Past JEE Main Entrance Papers Set-I
Overview
The three-dimensional rectangular coordinate system consists of three perpendicular axes: the \(x\)-axis, the \(y\)-axis, and the \(z\)-axis. In two-dimensional space, the coordinate plane is defined by a pair of perpendicular axes. These axes allow us to name any location within the plane. In three dimensions, we define coordinate planes by the coordinate axes, just as in two dimensions. There are three axes now, so there are three intersecting pairs of axes. Each pair of axes forms a coordinate plane: the \(x y\)-plane, the \(x z\)-plane, and the \(y z\)-plane (Figure below). We define the \(x y\)-plane formally as the following set: \(\{(x, y, 0): x, y \in R \}\). Similarly, the \(x z\)-plane and the \(y z\)-plane are defined as \(\{(x, 0, z): x, z \in R \}\) and \(\{(0, y, z): y, z \in R \}\), respectively.
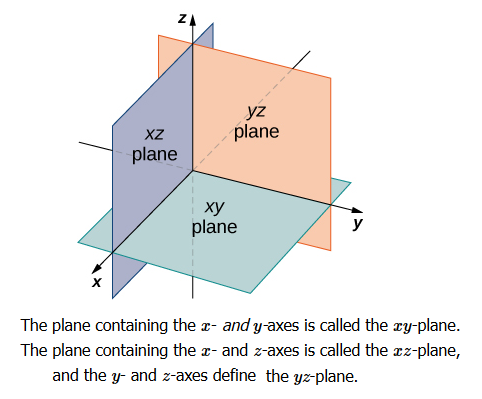
In two dimensions, the coordinate axes partition the plane into four quadrants. Similarly, the coordinate planes divide space between them into eight regions about the origin, called octants as shown in Figure below.
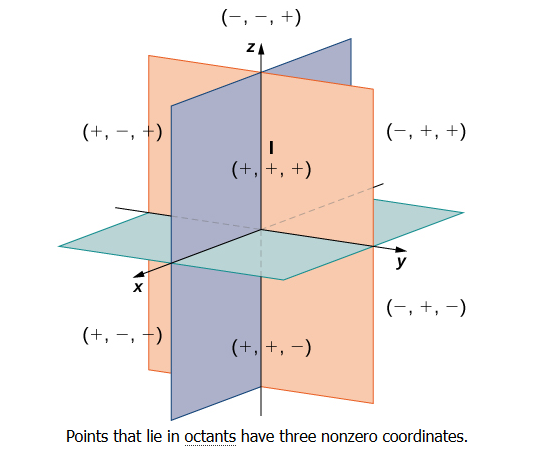
Coordinate of a point in space
An arbitrary point \(P\) in three-dimensional space is assigned coordinates \(\left(x_0, y_0, z_0\right)\) provided that
- The plane through \(P\) parallel to the \(y z\)-plane intersects the \(x\)-axis at \(\left(x_0, 0,0\right)\);
- The plane through \(P\) parallel to the \(x z\)-plane intersects the \(y\)-axis at \(\left(0, y_0, 0\right)\);
- The plane through \(P\) parallel to the \(x y\)-plane intersects the \(z\)-axis at \(\left(0,0, z_0\right)\).
- The space coordinates \(\left(x_0, y_0, z_0\right)\) are called the Cartesian coordinates of \(P\) or simply the rectangular coordinates of \(P\).
Let \(P\) be any point in the space, not in a coordinate plane, and through \(P\) pass planes parallel to the coordinate planes \(y z, z x\) and \(x y\) meeting the coordinate axes in the points \(A , B , C\) respectively. Three planes are
- ADPF || \(y z\)-plane
- BDPE || \(x z\)-plane
- CFPE || \(x y\)-plane
These planes determine a rectangular parallelopiped which has three pairs of rectangular faces (AD P F, O B E C),(B D P E, C F A O) and (A O B D, FPEC) (Shown in Figure below)
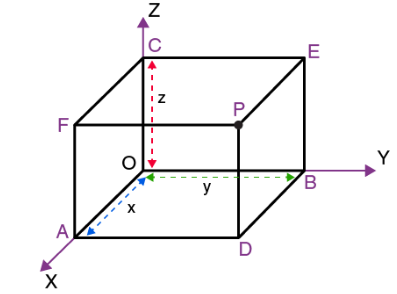
Hence the coordinates \(x, y z\) of a point \(P\) are the perpendicular distance of \(P\) from the three coordinate planes \(y z, z x\) and \(x y\), respectively.
Sign of coordinates of a point
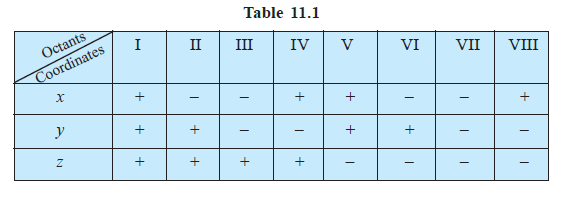
Distance formula
The distance between two points \(P \left(x_1, y_1, z_1\right)\) and \(Q \left(x_2, y_2\right.\), \(z_2\) ) is given by
\(
PQ =\sqrt{\left.x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}
\)
A paralleopiped is formed by planes drawn through the points \(\left(x_1, y_1, z_1\right)\) and \(\left(x_2, y_2, z_2\right)\) parallel to the coordinate planes. The length of edges are \(x_2-x_1, y_2-y_1, z_2-z_1\) and length of diagonal is \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}\).
Section formula
The coordinates of the point \(R\) which divides the line segment joining two points \(P \left(x_1, y_1, z_1\right)\) and \(Q \left(x_2, y_2, z_2\right)\) internally or externally in the ratio \(m: n\) are given by \(\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}, \frac{m z_2+n z_1}{m+n},\right),\left(\frac{m x_2-n x_1}{m-n}, \frac{m y_2-n y_1}{m-n}, \frac{m z_2-n z_1}{m-n}\right)\), respectively.
The coordinates of the mid-point of the line segment joining two points \(P \left(x_1, y_1, z_1\right)\) and \(Q \left(x_2, y_2, z_2\right)\) are \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2}\right)\).
The coordinates of the centroid of the triangle, whose vertices are \(\left(x_1, y_1, z_1\right),\left(x_2, y_2, z_2\right)\) and \(x_3, y_3, z_3\) are \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)\).
Quiz Summary
0 of 150 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 150 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 150
1. Question
If the shortest distance between the lines \(\frac{x-\lambda}{2}=\frac{y-4}{3}=\frac{z-3}{4}\) and \(\frac{x-2}{4}=\frac{y-4}{6}=\frac{z-7}{8}\) is \(\frac{13}{\sqrt{29}}\), then a value of \(\lambda\) is : [JEE Main 2024 (Online) 8th April Evening Shift]
CorrectIncorrectHint
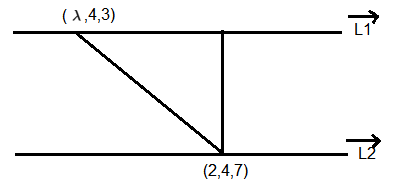
\(
\begin{aligned}
& \vec{l}_1=2 \hat{i}+3 \hat{j}+4 \hat{k} \\
& \vec{l}_2=4 \hat{i}+6 \hat{j}+8 \hat{k}
\end{aligned}
\)
\(
S . D .=\frac{|(2 \hat{i}+3 \hat{j}+4 \hat{k}) \times((2-\lambda) \hat{i}-4 \hat{k})|}{|2 \hat{i}+3 \hat{j}+4 \hat{k}|}
\)
\(
\begin{aligned}
& \frac{|(2 \hat{i}+3 \hat{j}+4 \hat{k}) \times((2-\lambda) \hat{i}+4 \hat{k})|}{\sqrt{29}}=\frac{13}{\sqrt{29}} \\
& |-8 \hat{j}-3(2-\lambda) \hat{k}+12 \hat{i}+4(2-\lambda) \hat{j}|=13 \\
& |12 \hat{i}-4 \lambda \hat{j}+(3 \lambda-6) \hat{k}|=13 \\
& 144+16 \lambda^2+(3 \lambda-6)^2=169 \\
& 16 \lambda^2+(3 \lambda-6)^2=25 \Rightarrow\lambda =1
\end{aligned}
\) -
Question 2 of 150
2. Question
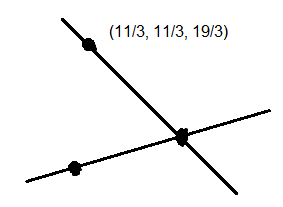
Consider the line \(L\) passing through the points \((1,2,3)\) and \((2,3,5)\). The distance of the point \(\left(\frac{11}{3}, \frac{11}{3}, \frac{19}{3}\right)\) from the line \(L\) along the line \(\frac{3 x-11}{2}=\frac{3 y-11}{1}=\frac{3 z-19}{2}\) is equal to [JEE Main 2024 (Online) 9th April Evening Shift]
CorrectIncorrectHint
\(
L: \frac{x-1}{1}=\frac{y-2}{1}=\frac{z-3}{2}=\mu
\)
Measured along \(L_2: \frac{x-\frac{11}{3}}{\frac{2}{3}}=\frac{y-\frac{11}{3}}{\frac{1}{3}}=\frac{z-\frac{19}{3}}{\frac{2}{3}}=\lambda\)
Any point on \(L_1:(\mu+1, \mu+2,2 \mu+3)\)
Any point on \(L_2\left(\frac{2}{3} \lambda+\frac{11}{3}, \frac{\lambda}{3}+\frac{11}{3}, \frac{2}{3} \lambda+\frac{19}{3}\right)\)
Now
\(
\begin{aligned}
& \mu+1=\frac{2}{3} \lambda+\frac{11}{3} \\
& \frac{\mu+2=\frac{\lambda}{3}+\frac{11}{3}}{\lambda=-3} \\
& \mu=\frac{2}{3}
\end{aligned}
\)
Point on \(L=\left(\frac{5}{3}, \frac{8}{3}, \frac{13}{3}\right)\)
\(
\begin{aligned}
& d=\sqrt{\left(\frac{11}{3}-\frac{5}{3}\right)^2+\left(\frac{8}{3}-\frac{11}{3}\right)^2+\left(\frac{19}{3}-\frac{13}{3}\right)^2} \\
& d=\sqrt{4+1+4} \\
& d=3
\end{aligned}
\) -
Question 3 of 150
3. Question
The shortest distance between the lines \(\frac{x-3}{4}=\frac{y+7}{-11}=\frac{z-1}{5}\) and \(\frac{x-5}{3}=\frac{y-9}{-6}=\frac{z+2}{1}\) is: [JEE Main 2024 (Online) 9th April Morning Shift]
CorrectIncorrectHint
Given lines are
\(
\begin{aligned}
& \frac{x-3}{4}=\frac{y-(-7)}{-11}=\frac{z-1}{5} \text { and } \\
& \frac{x-5}{3}=\frac{y-9}{-6}=\frac{z-(-2)}{1}
\end{aligned}
\)
Shortest distance between two lines,
\(
\begin{aligned}
& d=\frac{\left|\left(\vec{a}_2-\vec{a}_1\right) \cdot\left(\vec{b}_1 \times \vec{b}_2\right)\right|}{\left|\left(\vec{b}_1 \times \vec{b}_2\right)\right|} \\
& \vec{a}_2-\vec{a}_1=2 \hat{i}+16 \hat{j}-3 \hat{k} \text { and } \\
& \vec{b}_1 \times \vec{b}_2=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
4 & -11 & 5 \\
3 & -6 & 1
\end{array}\right|=19 \hat{i}+11 \hat{j}+9 \hat{k} \\
& \therefore \quad d=\frac{187}{\sqrt{563}}
\end{aligned}
\) -
Question 4 of 150
4. Question
Let the line \(L\) intersect the lines \(x-2=-y=z-1,2(x+1)=2(y-1)=z+1\) and be parallel to the line \(\frac{x-2}{3}=\frac{y-1}{1}=\frac{z-2}{2}\). Then which of the following points lies on \(L\) ? [JEE Main 2024 (Online) 9th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& L_1: \frac{x-2}{1}=\frac{y}{-1}=\frac{z-1}{1}=\lambda \\
& L_2: \frac{x+1}{(1 / 2)}=\frac{y-1}{(1 / 2)}=\frac{z+1}{1}=\mu
\end{aligned}
\)
Any point of \(L_1\) and \(L_2\) will be \((\lambda+2,-\lambda, \lambda+1)\) and \(\left(\frac{\mu}{2}-1, \frac{\mu}{2}+1, \mu-1\right)\)
Now DR of line \(<\lambda-\frac{\mu}{2}+3,-\lambda-\frac{\mu}{2}-1, \lambda-\mu+2>\)
Now \(\frac{\lambda-\frac{\mu}{3}+3}{3}=\frac{-\lambda-\frac{\mu}{2}-1}{1}=\frac{\lambda-\mu+2}{2}\)
\(
\left.\begin{array}{c}
\lambda-\frac{\mu}{3}+3=-3 \lambda-\frac{3 \mu}{2}-3 \ldots(1) \\
2\left(\lambda-\frac{\mu}{3}+3\right)=3(\lambda-\mu+2) \ldots(2)
\end{array}\right\} \lambda=\frac{-4}{3}, \mu=\frac{-2}{3}
\)
\(\therefore\) Points will be \(\left(\frac{2}{3}, \frac{4}{3}, \frac{-1}{3}\right)\) and \(\left(\frac{-4}{3}, \frac{2}{3}, \frac{-5}{3}\right)\)
\(\therefore \quad L\) will be \(\frac{x-\frac{2}{3}}{3}=\frac{y-\frac{4}{3}}{1}=\frac{z+\frac{1}{3}}{2}\)
\(\therefore \quad\left(\frac{-1}{3}, 1,-1\right)\) will satisfy \(L\) -
Question 5 of 150
5. Question
Let \(P(x, y, z)\) be a point in the first octant, whose projection in the \(x y\)-plane is the point \(Q\). Let \(O P=\gamma\), the angle between \(O Q\) and the positive \(x\)-axis be \(\theta\); and the angle between \(O P\) and the positive \(z\)-axis be \(\phi\), where \(O\) is the origin. Then the distance of \(P\) from the \(x\)-axis is [JEE Main 2024 (Online) 8th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \overrightarrow{O P}=x \hat{i}+y \hat{j}+z \hat{k} \\
& \overrightarrow{O Q}=x \hat{i}+y \hat{j} \\
& |O P|=\gamma=\sqrt{x^2+y^2+z^2} \\
& \cos \theta=\frac{x}{\sqrt{x^2+y^2}} \Rightarrow \cos ^2 \theta=\frac{x^2}{\gamma^2-z^2}=\frac{x^2}{\gamma^2-\gamma^2 \cos ^2 \phi} \\
& \cos \phi=\frac{z}{\sqrt{x^2+y^2+z^2}}=\frac{z}{\gamma}
\end{aligned}
\)
Distance of \(P\) from \(x\)-axis \(=\sqrt{y^2+z^2}\)
\(
\begin{aligned}
& d=\sqrt{\gamma^2-x^2} \\
& \Rightarrow x^2=\gamma^2 \sin ^2 \phi \cos ^2 \theta \\
& \Rightarrow d=\sqrt{\gamma^2-\gamma^2 \sin ^2 \phi \cos ^2 \theta} \\
& =\gamma \sqrt{1-\sin ^2 \phi \cos ^2 \theta}
\end{aligned}
\) -
Question 6 of 150
6. Question
If the shortest distance between the lines
\(
\begin{array}{ll}
L_1: \vec{r}=(2+\lambda) \hat{i}+(1-3 \lambda) \hat{j}+(3+4 \lambda) \hat{k}, & \lambda \in R \\
L_2: \vec{r}=2(1+\mu) \hat{i}+3(1+\mu) \hat{j}+(5+\mu) \hat{k}, & \mu \in R
\end{array}
\)
is \(\frac{m}{\sqrt{n}}\), where \(\operatorname{gcd}(m, n)=1\), then the value of \(m+n\) equals [JEE Main 2024 (Online) 8th April Morning Shift]CorrectIncorrectHint
\(
\begin{aligned}
& L_1: \vec{r}=(2+\lambda) \hat{i}+(1-3 \lambda) \hat{j}+(3+4 \lambda) \hat{k} \\
& L_1=2 \hat{i}+\hat{j}+3 \hat{k}+\lambda(\hat{i}-3 \hat{j}+4 \hat{k}) \\
& L_2: \vec{r}=2 \hat{i}+3 \hat{j}+5 \hat{k}+\mu(2 \hat{i}+3 \hat{j}+\hat{k}) \\
& \vec{a}_1=2 \hat{i}+\hat{j}+3 \hat{k} \\
& \vec{a}_2=2 \hat{i}+3 \hat{j}+5 \hat{k} \\
& \vec{a}_2-\vec{a}_1=2 \hat{j}+2 \hat{k} \\
& \vec{b}_1=\hat{i}-3 \hat{j}+4 \hat{k}, \vec{b}_2=2 \hat{i}+3 \hat{j}+\hat{k} \\
& \vec{b}_1 \times \vec{b}_2=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & -3 & 4 \\
2 & 3 & 1
\end{array}\right|
\end{aligned}
\)
\(
\begin{aligned}
& \hat{i}(-3-12)-\hat{j}(1-8)+\hat{k}(3+6) \\
& =-15 \hat{i}+7 \hat{j}+9 \hat{k} \\
& \left|\vec{b}_1 \times \vec{b}_2\right|=\sqrt{225+49+81} \\
& \left|\frac{\left(\vec{a}_2-\vec{a}_1\right) \cdot\left(\vec{b}_1 \times \vec{b}_2\right)}{\left|\vec{b}_1 \times \vec{b}_2\right|}\right|=\frac{14+18}{\sqrt{355}}=\frac{32}{\sqrt{355}} \\
& m+n=387
\end{aligned}
\) -
Question 7 of 150
7. Question
Let \(P (\alpha, \beta, \gamma)\) be the image of the point \(Q (3,-3,1)\) in the line \(\frac{x-0}{1}=\frac{y-3}{1}=\frac{z-1}{-1}\) and \(R\) be the point \((2,5,-1)\). If the area of the triangle \(P Q R\) is \(\lambda\) and \(\lambda^2=14 K\), then \(K\) is equal to : [JEE Main 2024 (Online) 6th April Evening Shift]
CorrectIncorrectHint
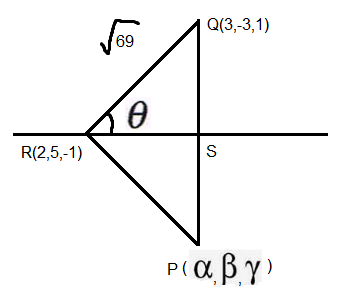
\(
\begin{aligned}
& RQ =\sqrt{1+64+4}=\sqrt{69} \\
& \overrightarrow{ RQ }=\hat{\ell}-8 \hat{ j }+2 \hat{ k } \\
& \overrightarrow{ RS }=\hat{\ell}+\hat{ j }-\hat{ k } \\
& \cos \theta=\frac{\overrightarrow{ RQ } \cdot \overrightarrow{ RS }}{|\overrightarrow{ RQ }||\overrightarrow{ RS }|}=\left|\frac{1-8-2}{\sqrt{69} \sqrt{3}}\right|=\frac{9}{3 \sqrt{23}} \\
& \cos \theta=\frac{3}{\sqrt{23}}=\frac{ RS }{ RQ }=\frac{ RS }{\sqrt{69}} \\
& RS =3 \sqrt{3} \\
& \sin \theta=\frac{\sqrt{14}}{\sqrt{23}}=\frac{ QS }{\sqrt{69}} \\
& QS =\sqrt{42} \\
& \operatorname{area}=\frac{1}{2} \cdot 2 QS \cdot RS =\sqrt{42} \cdot 3 \sqrt{3} \\
& \lambda=9 \sqrt{14} \\
& \lambda^2=81.14=14 k \\
& k =81
\end{aligned}
\) -
Question 8 of 150
8. Question
If \(A(3,1,-1), B\left(\frac{5}{3}, \frac{7}{3}, \frac{1}{3}\right), C(2,2,1)\) and \(D\left(\frac{10}{3}, \frac{2}{3}, \frac{-1}{3}\right)\) are the vertices of a quadrilateral \(A B C D\), then its area is [JEE Main 2024 (Online) 6th April Morning Shift]
CorrectIncorrectHint
\(A(3,1,-1), B\left(\frac{5}{3}, \frac{7}{3}, \frac{1}{3}\right), C(2,2,1), D\left(\frac{10}{3}, \frac{2}{3}, \frac{-1}{3}\right)\) are vertices of a quadrilateral.
\(
\begin{aligned}
& \overrightarrow{A C}=(2 \hat{i}+2 \hat{j}+\hat{k})-(3 \hat{i}+\hat{j}-\hat{k}) \\
& =-\hat{i}+\hat{j}+2 \hat{k} \\
& \overrightarrow{B D}=\left(\frac{10}{3} \hat{i}+\frac{2}{3} \hat{j}-\frac{1}{3} \hat{k}\right)-\left(\frac{5}{3} \hat{i}+\frac{7}{3} \hat{j}+\frac{1}{3} \hat{k}\right) \\
& \overrightarrow{B D}=\frac{5}{3} \hat{i}-\frac{5}{3} \hat{j}-\frac{2}{3} \hat{k} \\
& \text { Area }=\frac{1}{2}|\overrightarrow{A C} \times \overrightarrow{B D}| \\
& =\frac{1}{2}\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
-1 & 1 & 2 \\
\frac{5}{3} & \frac{-5}{3} & \frac{-2}{3}
\end{array}\right| \\
& =\frac{1}{2} \sqrt{\left(\frac{8}{3}\right)^2+\left(\frac{8}{3}\right)^2}\left[\because \overrightarrow{A C} \times \overrightarrow{B D}=\frac{8}{3} \hat{i}+\frac{8}{3} \hat{j}\right] \\
& =\frac{1}{2} \times \frac{8}{3} \times \sqrt{2}=\frac{4 \sqrt{2}}{3} \\
&
\end{aligned}
\) -
Question 9 of 150
9. Question
The shortest distance between the lines \(\frac{x-3}{2}=\frac{y+15}{-7}=\frac{z-9}{5}\) and \(\frac{x+1}{2}=\frac{y-1}{1}=\frac{z-9}{-3}\) is [JEE Main 2024 (Online) 6th April Morning Shift]
CorrectIncorrectHint
Given two lines are \(\frac{x-3}{2}=\frac{y-(-15)}{-7}=\frac{z-9}{5}\) and
\(
\frac{x-(-1)}{2}=\frac{y-1}{1}=\frac{z-9}{-3}
\)
Shortest distance between two lines are
\(
\begin{aligned}
& d=\frac{\left|\left(\vec{a}_2-\vec{a}_1\right) \cdot\left(\vec{b}_1 \times \vec{b}_2\right)\right|}{\left|\vec{b}_1 \times \vec{b}_2\right|} \\
& \therefore \quad \vec{a}_2-\vec{a}_1=-4 \hat{i}+16 \hat{j}+0 \hat{k} \\
& \vec{b}_1 \times \vec{b}_2=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
2 & -7 & 5 \\
2 & 1 & -3
\end{array}\right|=16 \hat{i}+16 \hat{j}+16 \hat{k} \\
& \therefore \quad d=\frac{|-64+16 \times 16|}{16 \sqrt{3}}=4 \sqrt{3}
\end{aligned}
\) -
Question 10 of 150
10. Question
Let \((\alpha, \beta, \gamma)\) be the image of the point \((8,5,7)\) in the line \(\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-2}{5}\). Then \(\alpha+\beta+\gamma\) is equal to : [JEE Main 2024 (Online) 5th April Evening Shift]
CorrectIncorrectHint
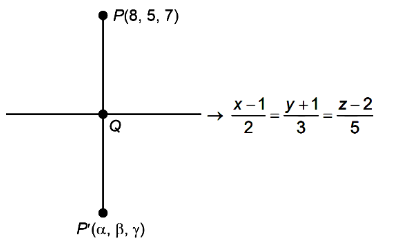
Let \(Q\) be general point.
\(
(x, y, z)=(2 \lambda+1,3 \lambda-1,5 \lambda+2)
\)
\(\therefore\) Now D.R. of P.Q
\(
\begin{aligned}
& P Q \Rightarrow(2 \lambda+1-8,3 \lambda-1-5,5 \lambda+2-7) \\
& =(2 \lambda-7,3 \lambda-6,5 \lambda-5)
\end{aligned}
\)
DR of line : \((2,3,5)\)
\(
\begin{array}{ll}
\therefore & 2(2 \lambda-7)+3(3 \lambda-6)+5(5 \lambda-5)=0 \\
\Rightarrow & \lambda=\frac{3}{2} \\
\therefore & Q\left(4, \frac{7}{2}, \frac{19}{2}\right) \\
\therefore & (\alpha, \beta, y) \equiv(0,2,12) \quad\left(Q \text { is mid point of } P \& P^{\prime}\right) \\
& \alpha+\beta+y \equiv 14
\end{array}
\) -
Question 11 of 150
11. Question
If the line \(\frac{2-x}{3}=\frac{3 y-2}{4 \lambda+1}=4-z\) makes a right angle with the line \(\frac{x+3}{3 \mu}=\frac{1-2 y}{6}=\frac{5-z}{7}\), then \(4 \lambda+9 \mu\) is equal to : [JEE Main 2024 (Online) 5th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& L_1: \frac{x-2}{(-3)}=\frac{y-\frac{2}{3}}{\left(\frac{4 \lambda+1}{3}\right)}={(4-z)} \\
& L_2: \frac{x+3}{3 \mu}=\frac{y-\frac{1}{2}}{-3}=\frac{z-5}{-7} \\
& \because L_1 \perp L_2 \\
& \Rightarrow(-3)(3 \mu)+\left(\frac{4 \lambda+1}{3}\right)(-3)+(-1)(-7)=0 \\
& -9 \mu-4 \lambda-1+7=0 \\
& \Rightarrow 4 \lambda+9 \mu=6
\end{aligned}
\) -
Question 12 of 150
12. Question
Let \(d\) be the distance of the point of intersection of the lines \(\frac{x+6}{3}=\frac{y}{2}=\frac{z+1}{1}\) and \(\frac{x-7}{4}=\frac{y-9}{3}=\frac{z-4}{2}\) from the point \((7,8,9)\). Then \(d ^2+6\) is equal to : [JEE Main 2024 (Online) 5th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& P_1:(3 k-6,2 k, k-1) \\
& P_2(4 \alpha+7,3 \alpha+9,2 \alpha+4) \\
& P_1 \equiv P_2 \\
& 3 k-6=4 \alpha+7 \Rightarrow 3 k-4 \alpha=13 \\
& 2 k=3 \alpha+9 \Rightarrow 2 k-3 \alpha=9 \\
& \therefore k=3, \alpha=-1 \\
& \therefore P_1:(3,6,2)
\end{aligned}
\)
Distance of \((3,6,2)\) and \((7,8,9)\)
\(
\begin{aligned}
& =\sqrt{16+4+49}=\sqrt{69}=d \\
& d^2+6=69+6=75
\end{aligned}
\) -
Question 13 of 150
13. Question
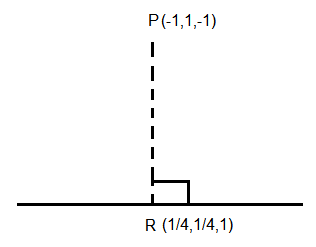
Let \(P\) be the point of intersection of the lines \(\frac{x-2}{1}=\frac{y-4}{5}=\frac{z-2}{1}\) and \(\frac{x-3}{2}=\frac{y-2}{3}=\frac{z-3}{2}\). Then, the shortest distance of \(P\) from the line \(4 x=2 y=z\) is [JEE Main 2024 (Online) 4th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& L_1: \frac{x-2}{1}=\frac{y-4}{5}=\frac{z-2}{1} \\
& L_2: \frac{x-3}{2}=\frac{y-2}{3}=\frac{z-3}{2}
\end{aligned}
\)
Point of intersection of \(L_1\) and \(L_2\) is \((-1,1,-1)\)
Distance of point \(P\) from \(L_3: 4 x=2 y=z\)
\(
L_3: \frac{x}{\frac{1}{4}}=\frac{y}{\frac{1}{2}}=\frac{z}{1}
\)
Any point on \(L_3\) be
\(
\begin{aligned}
& \left(\frac{\lambda}{4}, \frac{\lambda}{2}, \lambda\right) \\
& P R:\left\langle\frac{\lambda}{4}+1, \frac{\lambda}{2}-1, \lambda+1\right\rangle \\
& \because P R \perp\left\langle\frac{1}{4}, \frac{1}{2}, 1\right\rangle \\
& \Rightarrow\left(\frac{\lambda}{4}+1\right) \frac{1}{4}+\frac{1}{2}\left(\frac{\lambda}{2}-1\right)+\lambda+1=0 \\
& \frac{\lambda}{16}+\frac{1}{4}+\frac{\lambda}{4}-\frac{1}{2}+\lambda+1=0 \\
& \Rightarrow \quad \lambda=\frac{-4}{7}
\end{aligned}
\)
\(
\begin{aligned}
& \therefore R\left(\frac{-1}{7}, \frac{-2}{7}, \frac{-4}{7}\right) \\
& \text { Now } R P: \sqrt{\left(\frac{-1}{7}+1\right)^2+\left(\frac{-2}{7}-1\right)^2+\left(\frac{-4}{7}+1\right)^2} \\
& =\sqrt{\frac{36}{49}+\frac{81}{49}+\frac{9}{49}}=\frac{\sqrt{126}}{7}=\frac{3 \sqrt{14}}{7}
\end{aligned}
\) -
Question 14 of 150
14. Question
Let the point, on the line passing through the points \(P(1,-2,3)\) and \(Q(5,-4,7)\), farther from the origin and at a distance of 9 units from the point \(P\), be \((\alpha, \beta, \gamma)\). Then \(\alpha^2+\beta^2+\gamma^2\) is equal to : [JEE Main 2024 (Online) 4th April Morning Shift]
CorrectIncorrectHint
Line through \(P Q\)
\(
\frac{x-1}{4}=\frac{y+2}{-2}=\frac{z-3}{4}
\)
Any point on \(P Q\). be \(R(4 \lambda+1,-2 \lambda-2,4 \lambda+3)\)
\(
P R=9 \text { unit }
\)
\(
\begin{aligned}
& (P R)^2=81 \\
& (4 \lambda+1-1)^2+(-2 \lambda-2+2)^2+(4 \lambda+3-3)^2=81 \\
& 16 \lambda^2+4 \lambda^2+16 \lambda^2=81 \\
& 36 \lambda^2=81 \\
& \lambda= \pm \frac{9}{6}= \pm \frac{3}{2} \\
& \therefore R \text { can be }(7,-5,9) \text { or }(-5,1,-3)
\end{aligned}
\)
Distance from origin for both points be \(\sqrt{49+25+81}\) and \(\sqrt{25+1+9}=\sqrt{35}\)
\(\therefore\) Distance of \((7,-5,9)\) is farthest from origin
\(
\therefore(\alpha, \beta, \gamma)=(7,-5,9)
\)
Now \(7^2+(-5)^2+9^2=155\) -
Question 15 of 150
15. Question
Consider a \(\triangle A B C\) where \(A(1,3,2), B(-2,8,0)\) and \(C(3,6,7)\). If the angle bisector of \(\angle B A C\) meets the line \(B C\) at \(D\), then the length of the projection of the vector \(\overrightarrow{A D}\) on the vector \(\overrightarrow{A C}\) is : [JEE Main 2024 (Online) 1st February Evening Shift]
CorrectIncorrectHint
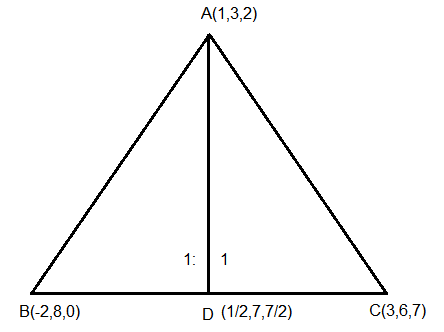
\(D\) divides \(B C\) in ratio \(1: 1\)
\(
\begin{aligned}
& D:\left(\frac{1}{2}, 7, \frac{7}{2}\right) \\
& \overrightarrow{A D}=\left(\frac{1}{2}-1\right) \hat{i}+(7-3) \hat{j}+\left(\frac{7}{2}-2\right) \hat{k} \\
& =-\frac{1}{2} \hat{i}+4 \hat{j}+\frac{3}{2} \hat{k} \\
& \overrightarrow{A C}=2 \hat{i}+3 \hat{j}+5 \hat{k}
\end{aligned}
\)
Projection of \(\overrightarrow{A D}\) on \(\overrightarrow{A C}\)
\(
=\frac{-1+12+\frac{15}{2}}{\sqrt{4+9+25}}=\frac{37}{2 \sqrt{38}}
\) -
Question 16 of 150
16. Question
Let \(P\) and \(Q\) be the points on the line \(\frac{x+3}{8}=\frac{y-4}{2}=\frac{z+1}{2}\) which are at a distance of 6 units from the point \(R (1,2,3)\). If the centroid of the triangle \(PQR\) is \((\alpha, \beta, \gamma)\), then \(\alpha^2+\beta^2+\gamma^2\) is : [JEE Main 2024 (Online) 1st February Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Any point on line } \frac{x+3}{8}=\frac{y-4}{2}=\frac{z+1}{2} \\
& \text { can be taken as }(8 \lambda-3,2 \lambda+4,2 \lambda-1) \\
& \text { If at a distance of } 6 \text { units from } R(1,2,3) \\
& \Rightarrow(8 \lambda-3-1)^2+(2 \lambda+4-2)^2+(2 \lambda-1-3)^2=36 \\
& \Rightarrow \lambda^2-\lambda=0 \text { \{on simplification \} } \\
& \Rightarrow \lambda=0, \lambda=1
\end{aligned}
\)
Here \(P \& Q\) are \((-3,4,-1)\) and \((5,6,1)\) Centroid of \(\triangle P Q R\)
\(
\begin{aligned}
& (\alpha, \beta, \gamma) \equiv\left(\frac{5-3+1}{3}, \frac{6+4+2}{3}, \frac{1-1+3}{3}\right) \\
& \Rightarrow \alpha=1, \beta=4, \gamma=1 \\
& \Rightarrow \alpha^2+\beta^2+\gamma^2=18
\end{aligned}
\) -
Question 17 of 150
17. Question
If the mirror image of the point \(P(3,4,9)\) in the line \(\frac{x-1}{3}=\frac{y+1}{2}=\frac{z-2}{1}\) is \((\alpha, \beta, \gamma)\), then \(14(\alpha+\beta+\gamma)\) is : [JEE Main 2024 (Online) 1st February Evening Shift]
CorrectIncorrectHint
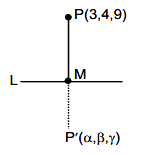
\(
L : \frac{x-1}{3}=\frac{y+1}{2}=\frac{z-2}{1}=\lambda, p (3,4,9)
\)
\(
\begin{aligned}
& M (3 \lambda+1,2 \lambda-1, \lambda+2) \\
& \overrightarrow{ PM }=(3 \lambda-2,2 \lambda-5, \lambda-7)
\end{aligned}
\)
DR’s of \(L :(3,2,1)\)
\(\overrightarrow{ PM } \perp\) line \(L\)
So, \(3(3 \lambda-2)+2(2 \lambda-5)+1(\lambda-7)=0\)
\(
\begin{aligned}
& 9 \lambda-6+4 \lambda-10+\lambda-7=0 \\
& 14 \lambda=23 \Rightarrow \lambda=\frac{23}{14} \\
& M \left(\frac{83}{14}, \frac{32}{14}, \frac{51}{14}\right)
\end{aligned}
\)
Now, As \(M\) is mid-point of \(pp ^{\prime}\)
\(\therefore\) co-ordinates of \(p ^{\prime}\) are
\(
\begin{gathered}
\frac{\alpha+3}{2}=\frac{83}{14} \Rightarrow \alpha=\frac{62}{7} \\
\frac{\beta+4}{2}=\frac{32}{14} \Rightarrow \beta=\frac{4}{7} \\
\frac{\gamma+9}{2}=\frac{51}{14} \Rightarrow \gamma=\frac{-12}{7}
\end{gathered}
\)
So, \(14(\alpha+\beta+\gamma)=14 \times \frac{54}{7} \Rightarrow 108\) -
Question 18 of 150
18. Question
If the shortest distance between the lines \(\frac{x-\lambda}{-2}=\frac{y-2}{1}=\frac{z-1}{1}\) and \(\frac{x-\sqrt{3}}{1}=\frac{y-1}{-2}=\frac{z-2}{1}\) is 1 , then the sum of all possible values of \(\lambda\) is : [JEE Main 2024 (Online) 1st February Morning Shift]
CorrectIncorrectHint
Given the two lines:
\(
\begin{aligned}
& L_1: \frac{x-\lambda}{-2}=\frac{y-2}{1}=\frac{z-1}{1} \\
& L_2: \frac{x-\sqrt{3}}{1}=\frac{y-1}{-2}=\frac{z-2}{1}
\end{aligned}
\)
We observe that these lines are not parallel as their directional vectors are not proportional. The directional vector for \(L_1\) is \((-2,1,1)\) and for \(L_2\) is \((1,-2,1)\). The shortest distance between two skew (non-intersecting and non-parallel) lines in the threedimensional space is along the line that is perpendicular to both lines. This implies we can find a vector that is perpendicular to both directional vectors by taking their cross product.
The directional vector for \(L_1\) is \(d_1=\langle-2,1,1\rangle\), and for \(L_2\) is \(d_2=\langle 1,-2,1\rangle\). The cross product of \(d_1\) and \(d_2\), which will be perpendicular to both lines, is given by:
\(
d=d_1 \times d_2=\left|\begin{array}{ccc}
i & j & k \\
-2 & 1 & 1 \\
1 & -2 & 1
\end{array}\right|
\)
Expanding the determinant gives:
\(
\begin{aligned}
& d= i ((1)(1)-(1)(-2))- j ((-2)(1)-(1)(1))+ k ((-2)(-2)-(1)(1)) \\
& d= i (1+2)- j (-2-1)+ k (4-1) \\
& d=3 i +3 j +3 k
\end{aligned}
\)
\(
d=\langle 3,3,3\rangle
\)
The shortest distance \(D\) between the two lines can then be given by the formula:
\(
D=\frac{\left|\left( a _2- a _1\right) \cdot d\right|}{\|d\|}
\)
Where \(a _1\) and \(a _{ 2 }\) are position vectors to any points on line \(L_1\) and line \(L_2\), respectively, and ‘.’ denotes the dot product.
From the lines’ equations, we can choose a point on each line (when the parameter is zero). Thus, for \(L_1\), let’s choose the point \(A(\lambda, 2,1)\), and for \(L_2\), let’s choose the point \(B(\sqrt{3}, 1,2)\). These points correspond to the vectors \(a _1=\langle\lambda, 2,1\rangle\) and \(a _2=\langle\sqrt{3}, 1,2\rangle\), respectively.
The vector \(a _2- a _1\) is:
\(
\begin{aligned}
& a _2- a _1=\langle\sqrt{3}, 1,2\rangle-\langle\lambda, 2,1\rangle \\
& a _2- a _1=\langle\sqrt{3}-\lambda, 1-2,2-1\rangle \\
& a _2- a _1=\langle\sqrt{3}-\lambda,-1,1\rangle
\end{aligned}
\)
We can now substitute this, along with \(d\), into the distance formula:
\(
\begin{aligned}
& D=\frac{|((\sqrt{3}-\lambda,-1,1\rangle) \cdot(3,3,3\rangle|}{\|(3,3,3)\|} \\
& D=\frac{|3(\sqrt{3}-\lambda)+3(-1)+3(1)|}{\sqrt{3^2+3^2+3^2}} \\
& D=\frac{|3 \sqrt{3}-3 \lambda-3+3|}{\sqrt{27}} \\
& D=\frac{|3 \sqrt{3}-3 \lambda|}{3 \sqrt{3}} \\
& D=\frac{|\sqrt{3}-\lambda|}{\sqrt{3}}
\end{aligned}
\)
Given that the shortest distance \(D\) between the lines is 1 , we can equate the above result to 1 , and solve for \(\lambda\) :
\(
\begin{aligned}
& \frac{|\sqrt{3}-\lambda|}{\sqrt{3}}=1 \\
& |\sqrt{3}-\lambda|=\sqrt{3}
\end{aligned}
\)
This absolute value equation gives us two possible cases:
Case 1: \(\sqrt{3}-\lambda=\sqrt{3}\), which gives \(\lambda=0\).
Case 2: \(\sqrt{3}-\lambda=-\sqrt{3}\), which gives \(\lambda=2 \sqrt{3}\).
Therefore, the sum of all possible values of \(\lambda\) is:
\(
\lambda_{\text {sum }}=\lambda_1+\lambda_2=0+2 \sqrt{3}=2 \sqrt{3}
\)
Hence, option \(B(2 \sqrt{3})\) is the correct answer. -
Question 19 of 150
19. Question
Let \((\alpha, \beta, \gamma)\) be the mirror image of the point \((2,3,5)\) in the line \(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\). Then, \(2 \alpha+3 \beta+4 \gamma\) is equal to [JEE Main 2024 (Online) 31st January Evening Shift]
CorrectIncorrectHint
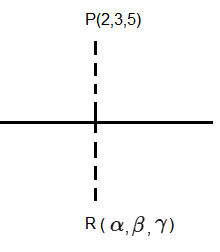
\(
\begin{aligned}
& \because \overrightarrow{ PR } \perp(2,3,4) \\
& \therefore \overrightarrow{ PR } \cdot(2,3,4)=0 \\
& (\alpha-2, \beta-3, \gamma-5) \cdot(2,3,4)=0 \\
& \Rightarrow 2 \alpha+3 \beta+4 \gamma=4+9+20=33
\end{aligned}
\) -
Question 20 of 150
20. Question
The shortest distance, between lines \(L_1\) and \(L_2\), where \(L_1: \frac{x-1}{2}=\frac{y+1}{-3}=\frac{z+4}{2}\) and \(L_2\) is the line, passing through the points \(A (-4,4,3), B (-1,6,3)\) and perpendicular to the line \(\frac{x-3}{-2}=\frac{y}{3}=\frac{z-1}{1}\), is [JEE Main 2024 (Online) 31st January Evening Shift]
CorrectIncorrectHint
\(
L _2=\frac{ x +4}{3}=\frac{ y -4}{2}=\frac{ z -3}{0}
\)
\(
\therefore S . D =\frac{\left|\begin{array}{ccc}
x _2- x _1 & y _2- y _1 & z _2- z _1 \\
2 & -3 & 2 \\
3 & 2 & 0
\end{array}\right|}{\left|\overrightarrow{ n _1} \times \overrightarrow{ n _2}\right|}
\)
\(
=\frac{\left|\begin{array}{ccc}
5 & -5 & -7 \\
2 & -3 & 2 \\
3 & 2 & 0
\end{array}\right|}{\left|\overrightarrow{ n _1} \times \overrightarrow{ n _2}\right|}
\)
\(
\begin{aligned}
& =\frac{141}{|-4 \hat{ i }+6 \hat{ j }+13 \hat{ k }|} \\
& =\frac{141}{\sqrt{16+36+169}} \\
& =\frac{141}{\sqrt{221}}
\end{aligned}
\) -
Question 21 of 150
21. Question
Let \(L_1: \vec{r}=(\hat{i}-\hat{j}+2 \hat{k})+\lambda(\hat{i}-\hat{j}+2 \hat{k}), \lambda \in R\) \(L_2: \vec{r}=(\hat{j}-\hat{k})+\mu(3 \hat{i}+\hat{j}+p \hat{k}), \mu \in R\), and \(L_3: \vec{r}=\delta(\ell \hat{i}+m \hat{j}+n \hat{k}), \delta \in R\) be three lines such that \(L_1\) is perpendicular to \(L_2\) and \(L_3\) is perpendicular to both \(L_1\) and \(L_2\). Then, the point which lies on \(L_3\) is [JEE Main 2024 (Online) 30th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& L _1 \perp L _2 \quad L _3 \perp L _1, L _2 \\
& 3-1+2 P =0 \\
& P =-1 \\
& \left|\begin{array}{ccc}
\hat{ i } & \hat{ j } & \hat{ k } \\
1 & -1 & 2 \\
3 & 1 & -1
\end{array}\right|=-\hat{ i }+7 \hat{ j }+4 \hat{ k } \\
& \therefore(-\delta, 7 \delta, 4 \delta) \text { will lie on } L _3 \\
& \text { For } \delta=1 \text { the point will be }(-1,7,4)
\end{aligned}
\) -
Question 22 of 150
22. Question
Let \((\alpha, \beta, \gamma)\) be the foot of perpendicular from the point \((1,2,3)\) on the line \(\frac{x+3}{5}=\frac{y-1}{2}=\frac{z+4}{3}\). Then \(19(\alpha+\beta+\gamma)\) is equal to : [JEE Main 2024 (Online) 30th January Morning Shift]
CorrectIncorrectHint
Let foot \(P (5 k -3,2 k +1,3 k -4)\)
DR’s \(\rightarrow A P: 5 k-4,2 k-1,3 k-7\)
DR’s \(\rightarrow\) Line \(: 5,2,3\)
Condition of perpendicular lines \((25 k-20)+(4 k-2)+(9 k-21)=0\)
Then \(k =\frac{43}{38}\)
Then \(19(\alpha+\beta+\gamma)=101\) -
Question 23 of 150
23. Question
Let \(A(2,3,5)\) and \(C(-3,4,-2)\) be opposite vertices of a parallelogram \(A B C D\). If the diagonal \(\overrightarrow{ BD }=\hat{i}+2 \hat{j}+3 \hat{k}\), then the area of the parallelogram is equal to : [JEE Main 2024 (Online) 30th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Area }=|\overrightarrow{ AC } \times \overrightarrow{ BD }| \\
& =\left|\begin{array}{ccc}
\hat{ i } & \hat{ j } & \hat{ k } \\
5 & -1 & 7 \\
1 & 2 & 3
\end{array}\right| \\
& =\frac{1}{2}|-17 \hat{ i }-8 \hat{ j }+11 \hat{ k }|=\frac{1}{2} \sqrt{474}
\end{aligned}
\) -
Question 24 of 150
24. Question
Let \(P (3,2,3), Q (4,6,2)\) and \(R (7,3,2)\) be the vertices of \(\triangle PQR\). Then, the angle \(\angle QPR\) is [JEE Main 2024 (Online) 29th January Evening Shift]
CorrectIncorrectHint
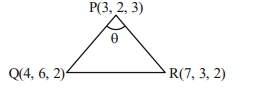
\(
\begin{aligned}
& \text { Direction ratio of } PR =(4,1,-1) \\
& \text { Direction ratio of } PQ =(1,4,-1) \\
& \text { Now, } \cos \theta=\left|\frac{4+4+1}{\sqrt{18} \cdot \sqrt{18}}\right| \\
& \theta=\frac{\pi}{3}
\end{aligned}
\) -
Question 25 of 150
25. Question
Let \(O\) be the origin and the position vectors of \(A\) and \(B\) be \(2 \hat{i}+2 \hat{j}+\hat{k}\) and \(2 \hat{i}+4 \hat{j}+4 \hat{k}\) respectively. If the internal bisector of \(\angle AOB\) meets the line \(AB\) at \(C\), then the length of \(O C\) is [JEE Main 2024 (Online) 29th January Morning Shift]
CorrectIncorrectHint
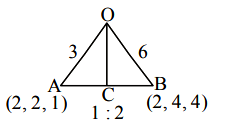
\(
\text { Length of } O C=\frac{\sqrt{136}}{3}=\frac{2 \sqrt{34}}{3}
\) -
Question 26 of 150
26. Question
Let \(P Q R\) be a triangle with \(R(-1,4,2)\). Suppose \(M(2,1,2)\) is the mid point of \(PQ\). The distance of the centroid of \(\triangle PQR\) from the point of intersection of the lines \(\frac{x-2}{0}=\frac{y}{2}=\frac{z+3}{-1}\) and \(\frac{x-1}{1}=\frac{y+3}{-3}=\frac{z+1}{1}\) is [JEE Main 2024 (Online) 29th January Morning Shift]
CorrectIncorrectHint
Centroid \(G\) divides MR in \(1: 2\)
\(
G (1,2,2)
\)
Point of intersection \(A\) of given lines is \((2,-6,0)\)
\(
AG =\sqrt{69}
\) -
Question 27 of 150
27. Question
Let the image of the point \((1,0,7)\) in the line \(\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}\) be the point \((\alpha, \beta, \gamma)\). Then which one of the following points lies on the line passing through \((\alpha, \beta, \gamma)\) and making angles \(\frac{2 \pi}{3}\) and \(\frac{3 \pi}{4}\) with \(y\)-axis and \(z\)-axis respectively and an acute angle with \(x\) axis? [JEE Main 2024 (Online) 27th January Evening Shift]
CorrectIncorrectHint
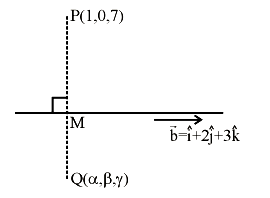
\(
L _1=\frac{ x }{1}=\frac{ y -1}{2}=\frac{ z -2}{3}=\lambda
\)
\(
\begin{aligned}
& M (\lambda, 1+2 \lambda, 2+3 \lambda) \\
& \overrightarrow{P M}=(\lambda-1) \hat{i}+(1+2 \lambda) \hat{j}+(3 \lambda-5) \hat{k}
\end{aligned}
\)
\(\overrightarrow{ PM }\) is perpendicular to line \(L _1\)
\(
\begin{aligned}
& \overrightarrow{ PM } \cdot \overrightarrow{ b }=0 \quad(\overrightarrow{ b }=\hat{ i }+2 \hat{ j }+3 \hat{ k }) \\
& \Rightarrow \lambda-1+4 \lambda+2+9 \lambda-15=0 \\
& 14 \lambda=14 \Rightarrow \lambda=1 \\
& \therefore M =(1,3,5) \\
& \overrightarrow{ Q }=2 \overrightarrow{ M }-\overrightarrow{ P } \quad[ M \text { is midpoint of } \overrightarrow{ P } \& \overrightarrow{ Q }] \\
& \overrightarrow{ Q }=2 \hat{ i }+6 \hat{ j }+10 \hat{ k }-\hat{ i }-7 \hat{ k } \\
& \overrightarrow{ Q }=\hat{ i }+6 \hat{ j }+3 \hat{ k } \\
& \therefore(\alpha, \beta, \gamma)=(1,6,3)
\end{aligned}
\)
Required line having direction cosine \((l, m, n)\)
\(
\begin{aligned}
& l^2+m^2+n^2=1 \\
& \Rightarrow l^2+\left(-\frac{1}{2}\right)^2+\left(-\frac{1}{\sqrt{2}}\right)^2=1 \\
& l^2=\frac{1}{4}
\end{aligned}
\)
\(\therefore l=\frac{1}{2}\) [Line make acute angle with \(x\)-axis]
Equation of line passing through \((1,6,3)\) will be
\(
\overrightarrow{ r }=(\hat{ i }+6 \hat{ j }+3 \hat{ k })+\mu\left(\frac{1}{2} \hat{ i }-\frac{1}{2} \hat{ j }-\frac{1}{\sqrt{2}} \hat{ k }\right)
\)
Option (3) satisfying for \(\mu=4\) -
Question 28 of 150
28. Question
The distance, of the point \((7,-2,11)\) from the line \(\frac{x-6}{1}=\frac{y-4}{0}=\frac{z-8}{3}\) along the line \(\frac{x-5}{2}=\frac{y-1}{-3}=\frac{z-5}{6}\), is : [JEE Main 2024 (Online) 27th January Morning Shift]
CorrectIncorrectHint
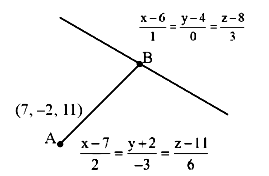
\(
B =(2 \lambda+7,-3 \lambda-2,6 \lambda+11)
\)
Point \(B\) lies on \(\frac{x-6}{1}=\frac{y-4}{0}=\frac{z-8}{3}\)
\(
\begin{aligned}
& \frac{2 \lambda+7-6}{1}=\frac{-3 \lambda-2-4}{0}=\frac{6 \lambda+11-8}{3} \\
& -3 \lambda-6=0 \\
& \lambda=-2 \\
& B \Rightarrow(3,4,-1) \\
& AB =\sqrt{(7-3)^2+(4+2)^2+(11+1)^2} \\
& =\sqrt{16+36+144} \\
& =\sqrt{196} \\
& =14
\end{aligned}
\) -
Question 29 of 150
29. Question
If the shortest distance between the lines \(\frac{x-4}{1}=\frac{y+1}{2}=\frac{z}{-3}\) and \(\frac{x-\lambda}{2}=\frac{y+1}{4}=\frac{z-2}{-5}\) is \(\frac{6}{\sqrt{5}}\), then the sum of all possible values of \(\lambda\) is : [JEE Main 2024 (Online) 27th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{x-4}{1}=\frac{y+1}{2}=\frac{z}{-3} \\
& \frac{x-\lambda}{2}=\frac{y+1}{4}=\frac{z-2}{-5}
\end{aligned}
\)
the shortest distance between the lines
\(
\begin{aligned}
& =\left|\frac{\overrightarrow{ a }-\overrightarrow{ b }) \cdot\left(\overrightarrow{ d _1} \times \overrightarrow{ d _2}\right)}{\left|\overrightarrow{ d _1} \times \overrightarrow{ d _2}\right|}\right| \\
& =\left|\frac{\left|\begin{array}{ccc}
\lambda-4 & 0 & 2 \\
1 & 2 & -3 \\
2 & 4 & -5
\end{array}\right|}{\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & 2 & -3 \\
2 & 4 & -5
\end{array}\right|}\right|
\end{aligned}
\)
\(
\begin{aligned}
& =\left|\frac{(\lambda-4)(-10+12)-0+2(4-4)}{|2 \hat{i}-1 \hat{j}+0 \hat{k}|}\right| \\
& \frac{6}{\sqrt{5}}=\left|\frac{2(\lambda-4)}{\sqrt{5}}\right| \\
& 3=|\lambda-4| \\
& \lambda-4= \pm 3 \\
& \lambda=7,1
\end{aligned}
\)
Sum of all possible values of \(\lambda\) is \(=8\) -
Question 30 of 150
30. Question
Let the foot of perpendicular of the point \(P(3,-2,-9)\) on the plane passing through the points \((-1,-2,-3),(9,3,4),(9,-2,1)\) be \(Q(\alpha, \beta, \gamma)\). Then the distance of \(Q\) from the origin is : [JEE Main 2023 (Online) 15th April Morning Shift]
CorrectIncorrectHint
The equation of the plane passing through points \(A(-1,-2,-3), B(9,3,4)\), and \(C(9,-2,1)\) can be written using the determinant :
\(
\left|\begin{array}{ccc}
x+1 & y+2 & z+3 \\
10 & 5 & 7 \\
10 & 0 & 4
\end{array}\right|=0
\)
Expanding the determinant, we get :
\(
2 x+3 y-5 z-7=0
\)
Next, we find the foot of the perpendicular from point \(P(3,-2,-9)\) to the plane. Using the coordinates of \(P\) and the equation of the plane, we can find the ratio of the perpendicular distance to the sum of the squares of the coefficients of \(x, y\), and \(z\) :
\(
\frac{2(3)+3(-2)-5(-9)-7}{2^2+3^2+(-5)^2}=\frac{-38}{38}
\)
We can now find the coordinates of the foot of the perpendicular, \(Q(\alpha, \beta, \gamma)\) :
\(
\frac{\alpha-3}{2}=\frac{\beta+2}{3}=\frac{\gamma+9}{-5}=-\frac{38}{38}
\)
Solving for \(\alpha, \beta\), and \(\gamma\) :
\(
\begin{aligned}
& \alpha=3-2\left(-\frac{38}{38}\right)=1 \\
& \beta=-2+3\left(-\frac{38}{38}\right)=-5 \\
& \gamma=-9-5\left(-\frac{38}{38}\right)=-4
\end{aligned}
\)
So, the coordinates of the foot of the perpendicular are \(Q(1,-5,-4)\). Now, we can find the distance of point \(Q\) from the origin :
\(
O Q=\sqrt{\alpha^2+\beta^2+\gamma^2}=\sqrt{1^2+(-5)^2+(-4)^2}=\sqrt{42}
\) -
Question 31 of 150
31. Question
Let the system of linear equations
\(
\begin{aligned}
& -x+2 y-9 z=7 \\
& -x+3 y+7 z=9 \\
& -2 x+y+5 z=8 \\
& -3 x+y+13 z=\lambda
\end{aligned}
\)
has a unique solution \(x=\alpha, y=\beta, z=\gamma\). Then the distance of the point \((\alpha, \beta, \gamma)\) from the plane \(2 x-2 y+z=\lambda\) is : [JEE Main 2023 (Online) 15th April Morning Shift]CorrectIncorrectHint
\(
\begin{aligned}
& -x+2 y-9 z=7-(1) \\
& -x+3 y-7 z=9-(2) \\
& -2 x+y+5 z=8-(3) \\
& (2)-(1) \\
& y+16 z=2 \dots(4)\\
& (3)-2 \times(1) \\
& -3 y+23 z=-6-(5) \\
& 3 \times(4)+(5) \\
& 71 z=0 \Rightarrow z=0 \\
& y=2 \\
& (-3,2,0) \rightarrow(\alpha, \beta, \gamma) \\
& \text { Put in }-3 x+y+13 z=\lambda \\
& \lambda=9+2=11
\end{aligned}
\)
The equation of the plane is:
\(
2 x-2 y+z=\lambda
\)
We already know that \(\lambda=11\). So the equation of the plane becomes:
\(
2 x-2 y+z=11
\)
Now, let’s find the distance \(d\) of the point \((\alpha, \beta, \gamma)=(-3,2,0)\) from the plane using the formula :
\(
d=\frac{|A x+B y+C z+D|}{\sqrt{A^2+B^2+C^2}}
\)
Plugging in the values for the point and the plane equation, we get:
\(
d=\frac{|2(-3)-2(2)+0-11|}{\sqrt{2^2+(-2)^2+1^2}}=\frac{|-6-4-11|}{\sqrt{4+4+1}}=\frac{21}{\sqrt{9}}=7
\)
So, the distance of the point \((-3,2,0)\) from the plane \(2 x-2 y+z=11\) is 7. -
Question 32 of 150
32. Question
Let \(S\) be the set of all values of \(\lambda\), for which the shortest distance between the lines \(\frac{x-\lambda}{0}=\frac{y-3}{4}=\frac{z+6}{1}\) and \(\frac{x+\lambda}{3}=\frac{y}{-4}=\frac{z-6}{0}\) is 13. Then \(8\left|\sum_{\lambda \in S} \lambda\right|\) is equal to [JEE Main 2023 (Online) 15th April Morning Shift]
CorrectIncorrectHint
Given the two lines :
\(
\frac{x-\lambda}{0}=\frac{y-3}{4}=\frac{z+6}{1} \frac{x+\lambda}{3}=\frac{y}{-4}=\frac{z-6}{0}
\)
Let’s find the direction vectors of these lines: \(\vec{d}_1=\langle 0,4,1\rangle\) and \(\vec{d}_2=\langle 3,-4,0\rangle\).
Now, let’s find the cross product of the direction vectors, which will give a vector that is perpendicular to both lines :
\(
\vec{n}=\vec{d}_1 \times \vec{d}_2=\langle 4,3,-12\rangle
\)
Let’s find the vector connecting a point on line 1 to a point on line 2 :
\(
\vec{c}=\langle 2 \lambda, 3,-12\rangle
\)
The shortest distance between the two lines is the projection of \(\vec{c}\) onto \(\vec{n}\) :
\(
d=\left|\frac{\vec{c} \cdot \vec{n}}{|\vec{n}|}\right|=\left|\frac{(2 \lambda)(4)+(3)(3)-(12)(-12)}{\sqrt{16+9+144}}\right|
\)
We are given that the shortest distance is 13 :
\(
\begin{aligned}
& 13=\left|\frac{8 \lambda+153}{13}\right| \\
& |8 \lambda+153|=169
\end{aligned}
\)
We have two cases:
Case-1: \(8 \lambda+153=169\)
\(
\lambda=\frac{16}{8}
\)
Case-2: \(8 \lambda+153=-169\)
\(
\lambda=\frac{-322}{8}
\)
Now, let’s calculate \(8\left|\sum_{\lambda \in S} \lambda\right|\) :
\(
8\left|\frac{16}{8}+\frac{-322}{8}\right|=8\left|\frac{-306}{8}\right|=306
\) -
Question 33 of 150
33. Question
The line, that is coplanar to the line \(\frac{x+3}{-3}=\frac{y-1}{1}=\frac{z-5}{5}\), is : [JEE Main 2023 (Online) 13th April Evening Shift]
CorrectIncorrectHint
Given two lines:
\(
\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}
\)
and \(\frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}\)
These lines are coplanar if the determinant of the matrix
\(
\left|\begin{array}{ccc}
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|=0
\)
Now let’s apply this condition to the given problem. The given line is :
\(
\frac{x+3}{-3}=\frac{y-1}{1}=\frac{z-5}{5}
\)
So, the coordinates of any point on this line are \((-3,1,5)\) and the direction ratios are \((-3,1,5)\).
Now, let’s calculate the determinants for each option and check which one equals zero.
For Option A :
\(
\frac{x+1}{-1}=\frac{y-2}{2}=\frac{z-5}{4}
\)
The coordinates of any point on this line are \((-1,2,5)\) and the direction ratios are \((-1,2,4)\).
The determinant is :
\(
\left|\begin{array}{ccc}
-1-(-3) & 2-1 & 5-5 \\
-3 & 1 & 5 \\
-1 & 2 & 4
\end{array}\right|=\left|\begin{array}{ccc}
2 & 1 & 0 \\
-3 & 1 & 5 \\
-1 & 2 & 4
\end{array}\right|
\)
Applying the formula :
\(
\begin{aligned}
& =2(1 \times 4-5 \times 2)-1((-3 \times 4)-(5 \times-1))+0((-3 \times 2)-(1 \times-1)) \\
& =2(4-10)-1(-12-(-5))+0(-6-(-1)) \\
& =2(-6)-1(-7)+0(-5) \\
& =-12+7+0 \\
& =-5
\end{aligned}
\)
The determinant for Option A is not equal to zero, so this line is not coplanar with the given line.
For Option B, we have :
\(
\frac{x+1}{-1}=\frac{y-2}{2}=\frac{z-5}{5}
\)
The coordinates of any point on this line are \((-1,2,5)\) and the direction ratios are \((-1,2,5)\).
\(
\left|\begin{array}{ccc}
-1-(-3) & 2-1 & 5-5 \\
-3 & 1 & 5 \\
-1 & 2 & 5
\end{array}\right|=\left|\begin{array}{ccc}
2 & 1 & 0 \\
-3 & 1 & 5 \\
-1 & 2 & 5
\end{array}\right|
\)
Applying the formula, we get:
\(
=2(5-10)-1(-15-(-5))+0(-6-(-1))=0
\)
So, the determinant for Option B equals zero, which confirms that the line in Option B is coplanar with the given line.
For Option C :
\(
\frac{x-1}{-1}=\frac{y-2}{2}=\frac{z-5}{5}
\)
The coordinates of any point on this line are \((1,2,5)\) and the direction ratios are \((-1,2,5)\).
The determinant is:
\(
\left|\begin{array}{ccc}
1-(-3) & 2-1 & 5-5 \\
-3 & 1 & 5 \\
-1 & 2 & 5
\end{array}\right|=\left|\begin{array}{ccc}
4 & 1 & 0 \\
-3 & 1 & 5 \\
-1 & 2 & 5
\end{array}\right|
\)
Applying the formula :
\(
=4(5-10)-1(-15-(-5))+0(-6-(-1))=-10
\)
For Option D:
\(
\frac{x+1}{1}=\frac{y-2}{2}=\frac{z-5}{5}
\)
The coordinates of any point on this line are \((-1,2,5)\) and the direction ratios are \((1,2,5)\).
The determinant is :
\(
\left|\begin{array}{ccc}
-1-(-3) & 2-1 & 5-5 \\
-3 & 1 & 5 \\
1 & 2 & 5
\end{array}\right|=\left|\begin{array}{ccc}
2 & 1 & 0 \\
-3 & 1 & 5 \\
1 & 2 & 5
\end{array}\right|
\)
Applying the formula :
\(
=2(5-10)-1(-15-5)+0(-6-1)=10
\)
So the determinant for Option \(D\) is not equal to zero, which means the line in Option D is not coplanar with the given line. -
Question 34 of 150
34. Question
The plane, passing through the points \((0,-1,2)\) and \((-1,2,1)\) and parallel to the line passing through \((5,1,-7)\) and \((1,-1,-1)\), also passes through the point : [JEE Main 2023 (Online) 13th April Evening Shift]
CorrectIncorrectHint
The first step is to find the normal vector to the desired plane. Since the plane is parallel to the line passing through the points \((5,1,-7)\) and \((1,-1,-1)\), the direction vector of that line is also parallel to the plane. The direction vector is the difference between the coordinates of the two points, which is \((5-1,1-(-1),-7-(-1))=(4,2,-6)\).
Next, let’s find another vector that is parallel to the plane. This vector can be obtained by taking the difference between the coordinates of the points \((0,-1,2)\) and \((-1,2,1)\), which the plane passes through. This gives us a vector of \((0-(-1),-1-2,2-1)=(1,-3,1)\).
The normal to the plane is perpendicular to both these vectors. It can be found by taking the cross product of the two vectors.
The cross product of vectors \((4,2,-6)\) and \((1,-3,1)\) is :
\(
\begin{aligned}
\vec{n} & =\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
4 & 2 & -6 \\
1 & -3 & 1
\end{array}\right|=\hat{i}(-16)-\hat{j}(+10)+\hat{k}(-14) \\
& =-16 \hat{i}-10 \hat{j}-14 \hat{k}
\end{aligned}
\)
The equation of the plane can now be written in the form :
\(
-16 x-10 y-14 z=d
\)
We can find the constant ‘d’ by substituting one of the points through which the plane passes, say \((0,-1,2)\) :
\(
d=-16 \cdot 0-10 .(-1)-14 \cdot 2=10-28=-18
\)
So, the equation of the plane is \(-16 x-10 y-14 z=-18\).
Now, we substitute the given options into the equation to check which one satisfies it :
Option A: \((-16.0-10.5-14 .(-2)=-18)=>-50+28=-22 \neq-18\), so A is not correct.
Option B: \((-16.2-10.0-14.1=-18)=>-32-14=-46 \neq-18\), so B is not correct.
Option C: \((-16.1-10 .(-2)-14.1=-18)=>-16+20-14=-10 \neq-18\), so \(C\) is not correct.
Option D: \((-16 .(-2)-10.5-14.0=-18)=>32-50=-18\), so \(D\) is correct.
So, the plane also passes through the point given in Option D, which is \((-2,5,0)\). -
Question 35 of 150
35. Question
Let \(N\) be the foot of perpendicular from the point \(P (1,-2,3)\) on the line passing through the points \((4,5,8)\) and \((1,-7,5)\). Then the distance of \(N\) from the plane \(2 x-2 y+z+5=0\) is : [JEE Main 2023 (Online) 13th April Evening Shift]
CorrectIncorrectHint
Equation of line \(\frac{x-4}{4-1}=\frac{y-5}{5-(-7)}=\frac{z-8}{8-5}\)
\(
\frac{x-4}{3}=\frac{y-5}{12}=\frac{z-8}{3}
\)
Let point \(N (3 \lambda+4,12 \lambda+5,3 \lambda+8)\)
\(
\begin{aligned}
& \overrightarrow{ PN }=(3 \lambda+4-1) \hat{i}+(12 \lambda+5-(-2)) \hat{j}+(3 \lambda+8-3) \hat{ k } \\
& \overrightarrow{ PN }=(3 \lambda+3) \hat{i}+(12 \lambda+7) \hat{ j }+(3 \lambda+5) \hat{ k }
\end{aligned}
\)
And parallel vector to line (say \(\vec{a}=3 \hat{i}+12 \hat{j}+3 \hat{k}\) )
Now, \(\overrightarrow{ PN } \cdot \overrightarrow{ a }=0\)
\(
\begin{aligned}
& (3 \lambda+3) 3+(12 \lambda+7) 12+(3 \lambda+5) 3=0 \\
& 162 \lambda+108=0 \Rightarrow \lambda=\frac{-108}{162}=\frac{-2}{3}
\end{aligned}
\)
So point \(N\) is \((2,-3,6)\)
Now distance of \(N (2,-3,6)\) from \(2 x-2 y+z+5=0\) is
\(
=\left|\frac{2(2)-2(-3)+6+5}{\sqrt{4+4+1}}\right|=7
\) -
Question 36 of 150
36. Question
Let the equation of plane passing through the line of intersection of the planes \(x+2 y+a z=2\) and \(x-y+z=3\) be \(5 x-11 y+b z=6 a-1\). For \(c \in Z\), if the distance of this plane from the point \((a,-c, c)\) is \(\frac{2}{\sqrt{a}}\), then \(\frac{a+b}{c}\) is equal to : [JEE Main 2023 (Online) 13th April Morning Shift]
CorrectIncorrectHint
Given the equation of the plane passing through the intersection of the two given planes:
\(
\begin{aligned}
& P:(x+2 y+a z-2)+\lambda(x-y+z-3)=0 \\
& \Rightarrow x(\lambda+1)+y(2-\lambda)+z(a+\lambda)-2-3 \lambda=0
\end{aligned}
\)
This is the same as the given equation \(5 x-11 y+b z=6 a-1\).
Now, comparing the coefficients of the corresponding variables in both equations:
\(
\frac{\lambda+1}{5}=\frac{2-\lambda}{-11}=\frac{a+\lambda}{b}=\frac{2+3 \lambda}{6 a-1}
\)
Solving for \(\lambda\) :
\(
\begin{aligned}
& -11 \lambda-11=10-5 \lambda \\
& 6 \lambda=-21 \Rightarrow \lambda=-\frac{7}{2}
\end{aligned}
\)
Now, substituting the value of \(\lambda\) back into the equations:
\(
\frac{2-\lambda}{-11}=\frac{2+3 \lambda}{6 a-1} \Rightarrow \frac{2+\frac{7}{2}}{-11}=\frac{2-\frac{21}{2}}{6 a-1}
\)
From this equation, we find the value of a :
\(
6 a-1=17 \Rightarrow a=3
\)
Now, substituting the value of \(a\) and \(\lambda\) into the equation:
\(
\begin{aligned}
& \frac{2-\lambda}{-11}=\frac{a+\lambda}{b} \Rightarrow-\frac{1}{2}=\frac{3-\frac{7}{2}}{b} \\
& \Rightarrow-\frac{b}{2}=-\frac{1}{2} \Rightarrow b=1
\end{aligned}
\)
Therefore, the point \((a,-c, c) \equiv(3,-c, c)\).
The given distance is \(\frac{2}{\sqrt{a}}=\frac{2}{\sqrt{3}}\).
The plane is: \(5 x-11 y+z=17\).
Now, let’s find the distance:
\(
\begin{aligned}
& \left|\frac{15+11 c+c-17}{\sqrt{147}}\right|=\frac{2}{\sqrt{3}} \\
& \Rightarrow c=-1, \frac{4}{3}
\end{aligned}
\)
Since \(c \in Z\), we have \(c=-1\).
Therefore, \(\frac{a+b}{c}=\frac{3+1}{-1}=-4\). -
Question 37 of 150
37. Question
The distance of the point \((-1,2,3)\) from the plane \(\vec{r} \cdot(\hat{i}-2 \hat{j}+3 \hat{k})=10\) parallel to the line of the shortest distance between the lines \(\vec{r}=(\hat{i}-\hat{j})+\lambda(2 \hat{i}+\hat{k})\) and \(\vec{r}=(2 \hat{i}-\hat{j})+\mu(\hat{i}-\hat{j}+\hat{k})\) is : [JEE Main 2023 (Online) 13th April Morning Shift]
CorrectIncorrectHint
Step 1: Determine the line of shortest distance between the given two lines:
Direction vector of line \(1: \vec{d}_1=2 \hat{i}+\hat{k}\)
Direction vector of line 2 : \(\overrightarrow{d_2}=\hat{i}-\hat{j}+\hat{k}\)
Now, let’s find the cross product \(\vec{N}=\vec{d}_1 \times \vec{d}_2\)
\(
\vec{N}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
2 & 0 & 1 \\
1 & -1 & 1
\end{array}\right|=(\hat{i}(0+1)-\hat{j}(2-1)+\hat{k}(-2-0))=\hat{i}-\hat{j}-2 \hat{k}
\)
So, the direction vector of the line of shortest distance is \(\vec{N}=\hat{i}-\hat{j}-2 \hat{k}\).Step 2: Find the equation of a line passing through point \(A(-1,2,3)\) and having the direction vector \(\vec{N}\) :
\(
\frac{x+1}{1}=\frac{y-2}{-1}=\frac{z-3}{-2}=\lambda
\)Step 3: Find the point \(P\) where the line intersects the given plane:
Let the coordinates of point \(P\) be in terms of \(\lambda\) :
\(
P(\lambda-1,-\lambda+2,-2 \lambda+3)
\)
Since \(P\) lies on the plane \(x-2 y+3 z=10\), we can substitute the coordinates of \(P\) in terms of \(\lambda\) into the equation of the plane:
\(
\begin{aligned}
& (\lambda-1)-2(-\lambda+2)+3(-2 \lambda+3)=10 \\
& \lambda=-2 \\
& P(-3,4,7)
\end{aligned}
\)
Step 4: Calculate the distance between points \(A\) and \(P\) :
\(
A P=\sqrt{(-3-(-1))^2+(4-2)^2+(7-3)^2}=2 \sqrt{6}
\) -
Question 38 of 150
38. Question
Let the lines \(l_1: \frac{x+5}{3}=\frac{y+4}{1}=\frac{z-\alpha}{-2}\) and \(l_2: 3 x+2 y+z-2=0=x-3 y+2 z-13\) be coplanar. If the point \(P (a, b, c)\) on \(l_1\) is nearest to the point \(Q (-4,-3,2)\), then \(|a|+|b|+|c|\) is equal to [JEE Main 2023 (Online) 12th April Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& (3 x +2 y + z -2)+\mu( x -3 y +2 z -13)=0 \\
& 3(3+\mu)+1 \cdot(2-3 \mu)-2(1+2 \mu)=0 \\
& 9-4 \mu=0 \\
& \mu=\frac{9}{4} \\
& 4(-15-8+\alpha-2)+9(-5+12+2 \alpha-13)=0 \\
& -100+4 \alpha-54+18 \alpha=0 \\
& \Rightarrow \alpha=7 \\
& \text { Let } P \equiv(3 \lambda-5, \lambda-4,-2 \lambda+7) \\
& \text { Direction ratio of } PQ (3 \lambda-1, \lambda-1,-2 \lambda+5) \\
& \text { But PQ } \perp \ell_1 \\
& \Rightarrow 3(3 \lambda-1)+1 \cdot(\lambda-1)-2(-2 \lambda+5)=0 \\
& \Rightarrow \lambda=1 \\
& P (-2,-3,5) \Rightarrow| a |+| b |+| c |=10
\end{aligned}
\) -
Question 39 of 150
39. Question
Let the plane \(P : 4 x-y+z=10\) be rotated by an angle \(\frac{\pi}{2}\) about its line of intersection with the plane \(x+y-z=4\). If \(\alpha\) is the distance of the point \((2,3,-4)\) from the new position of the plane \(P\), then \(35 \alpha\) is equal to : [JEE Main 2023 (Online) 12th April Morning Shift]
CorrectIncorrectHint
Equation of plane after rotation :
\(
\begin{aligned}
& (4 x-y+z-10)+\lambda(x+y-z-y)=0 \\
\Rightarrow & (4+\lambda) x+y(\lambda-1)+z(1-\lambda)-4 \lambda-10=0 \\
& \overrightarrow{n_1} \cdot \overrightarrow{n_2}=0 \\
\Rightarrow & (4+\lambda) 4+(\lambda-1)(-1)+(1-\lambda) 1=0 \\
\Rightarrow & 16+4 \lambda-\lambda+1+1-\lambda=0 \\
\Rightarrow & 2 \lambda=-18 \\
\Rightarrow & \lambda=-9
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \text { equation of plane : }-5 x-10 y+10 z+26=0 \\
& \text { Distance of plane from }(2,3,-4) \\
& \qquad=\left|\frac{-10-30-40+26}{\sqrt{100+100+26}}\right|=\frac{54}{15}=\alpha \\
& \therefore 35 \alpha=35 \cdot \frac{54}{15}=7 \times \frac{54}{3}=7 \times 18=126
\end{aligned}
\) -
Question 40 of 150
40. Question
Let the line passing through the points \(P (2,-1,2)\) and \(Q (5,3,4)\) meet the plane \(x-y+z=4\) at the point \(R\). Then the distance of the point \(R\) from the plane \(x+2 y+3 z+2=0\) measured parallel to the line \(\frac{x-7}{2}=\frac{y+3}{2}=\frac{z-2}{1}\) is equal to : [JEE Main 2023 (Online) 11th April Evening Shift]
CorrectIncorrectHint
Equation of line \(P Q\) :
\(
\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-2}{2}=\lambda
\)
Let \(R\) be \((3 \lambda+2,4 \lambda-1,2 \lambda+2)\)
\(R\) lies on plane \(x-y+z=4\)
\(
\begin{aligned}
& \therefore \quad 3 \lambda+2-4 \lambda+1+2 \lambda+2=4 \\
& \Rightarrow \quad \lambda=-1 \\
& \therefore \quad R(-1,-5,0)
\end{aligned}
\)
Let \(S R\) be \(: \frac{x+1}{2}=\frac{y+5}{2}=\frac{z-0}{1}=k\)
\(
\begin{aligned}
& \text { Point } S:(2 k-1,2 k-5, k) \\
& S \text { lies on plane: } x+2 y+3 z+2=0 \\
& \Rightarrow(2 k-1)+(4 k-10)+3 k+2=0 \\
& \Rightarrow 9 k-9=0 \Rightarrow k=1 \\
& \therefore S=(1,-3,1) \\
& \therefore S R=\sqrt{4+4+1}=3
\end{aligned}
\) -
Question 41 of 150
41. Question
Let \(P\) be the plane passing through the points \((5,3,0),(13,3,-2)\) and \((1,6,2)\). For \(\alpha \in N\), if the distances of the points \(A (3,4, \alpha)\) and \(B (2, \alpha, a)\) from the plane \(P\) are 2 and 3 respectively, then the positive value of a is : [JEE Main 2023 (Online) 11th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \overrightarrow{A B}=8 \hat{i}-2 \hat{k} \\
& \overrightarrow{A C}=-4 \hat{i}+3 \hat{j}+2 \hat{k} \\
& \overrightarrow{A B} \times \overrightarrow{A C}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
8 & 0 & -2 \\
-4 & 3 & 2
\end{array}\right| \\
& =6 \hat{i}-8 \hat{j}+24 \hat{k}
\end{aligned}
\)
Equation of plane : \(6 x-8 y+24 z=d\) passes through \((5,3,0)\)
\(
\begin{aligned}
& 6 \times 5-8 \times 3+24 \times 0=d \\
& \Rightarrow d=6
\end{aligned}
\)
\(
\begin{aligned}
& 6 x-8 y+24 z=6 \\
& \Rightarrow 3 x-4 y+12 z=3
\end{aligned}
\)
Distance of point \((3,4, \alpha)\)
\(
\frac{9-16+12 \alpha-3}{\sqrt{9+16+144}}=2 \Rightarrow \alpha=3
\)
Distance of point \((2, \alpha, a)\)
\(
\begin{aligned}
& \frac{3 \times 2-4 \times 3+12 \times a-3}{13}=3 \\
& \Rightarrow 12 a-9=39 \\
& \Rightarrow 12 a=48 \\
& \Rightarrow a=4
\end{aligned}
\) -
Question 42 of 150
42. Question
Let \((\alpha, \beta, \gamma)\) be the image of the point \(P (2,3,5)\) in the plane \(2 x+y-3 z=6\). Then \(\alpha+\beta+\gamma\) is equal to : [JEE Main 2023 (Online) 11th April Morning Shift]
CorrectIncorrectHint
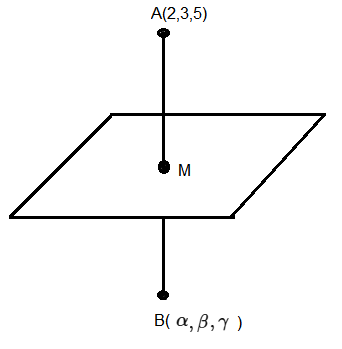
Co-ordinate of image of point \(P(2,3,5)\) in the plane \(2 x+y-3 z=6\) is
\(
\begin{aligned}
\frac{\alpha-2}{2} & =\frac{\beta-3}{1}=\frac{\gamma-5}{-3}=\frac{-2(2 \times 2+3-3 \times 5-6)}{2^2+1^2+(-3)^2} \\
\frac{\alpha-2}{2} & =\frac{\beta-3}{1}=\frac{\gamma-5}{-3}=2 \\
\frac{\alpha-2}{2} & =2, \frac{\beta-3}{1}=2, \frac{\gamma-5}{-3}=2 \\
\alpha & =6, \beta=5, \gamma=-1
\end{aligned}
\)
Hence, \(\alpha+\beta+\gamma=6+5-1=10\) -
Question 43 of 150
43. Question
If equation of the plane that contains the point \((-2,3,5)\) and is perpendicular to each of the planes \(2 x+4 y+5 z=8\) and \(3 x-2 y+3 z=5\) is \(\alpha x+\beta y+\gamma z+97=0\) then \(\alpha+\beta+\gamma=\) [JEE Main 2023 (Online) 11th April Morning Shift]
CorrectIncorrectHint
The equation of plane that passes through the point \((-2,3,5)\) is
\(
a(x+2)+b(y-3)+c(z-5)=0 \dots(i)
\)
The plane is perpendicular to
\(
\begin{aligned}
& 2 x+4 y+5 z=8 \text { and } 3 x-2 y+3 z=5 \\
& \therefore 2 a+4 b+5 c=0 \ldots \ldots \ldots(i i)
\end{aligned}
\)
and \(3 a-2 b+3 c=0\). (iii)
\(
\begin{aligned}
& \therefore \frac{ a }{\left|\begin{array}{cr}
4 & 5 \\
-2 & 3
\end{array}\right|}=\frac{- b }{\left|\begin{array}{ll}
2 & 5 \\
3 & 3
\end{array}\right|}=\frac{ c }{\left|\begin{array}{cc}
2 & 4 \\
3 & -2
\end{array}\right|} \\
& \Rightarrow \frac{ a }{22}=\frac{ b }{9}=\frac{ c }{-16}
\end{aligned}
\)
\(\therefore\) From Equation (i) equation of plane
\(
\begin{aligned}
& 22(x+2)+9(y-3)-16(z-5)=0 \\
& \Rightarrow 22 x+9 y-16 z+97=0
\end{aligned}
\)
Here, \(\alpha=22, \beta=9, \gamma=-16\)
\(
\therefore \alpha+\beta+\gamma=22+9-16=15
\) -
Question 44 of 150
44. Question
Let the image of the point \(P (1,2,6)\) in the plane passing through the points \(A (1,2,0), B (1,4,1)\) and \(C (0,5,1)\) be \(Q (\alpha, \beta, \gamma)\). Then \(\left(\alpha^2+\beta^2+\gamma^2\right)\) is equal to [JEE Main 2023 (Online) 10th April Evening Shift]
CorrectIncorrectHint
Equation of plane passing through the points \(A(1,2,0), B(1,4,1)\) and \(C(0,5,1)\) is
\(
\begin{aligned}
& \left|\begin{array}{ccc}
x-1 & y-2 & z-0 \\
0 & 2 & 1 \\
-1 & 3 & 1
\end{array}\right|=0 \\
& \Rightarrow x+y-2 z=3
\end{aligned}
\)
Now \(Q(\alpha, \beta, \gamma)\) is the image of the point \(P(1,2,6)\) in the plane \(x+y-2 z-3=0\)
\(
\begin{aligned}
& \therefore \frac{\alpha-1}{1}=\frac{\beta-2}{1}=\frac{\gamma-6}{-2}=\frac{-2[1+2-2(6)-3]}{1^2+1^2+(-2)^2} \\
& \Rightarrow \frac{\alpha-1}{1}=\frac{\beta-2}{1}=\frac{\gamma-6}{-2}=4 \\
& \Rightarrow \alpha=5, \beta=6, \gamma=-2
\end{aligned}
\)
Hence, \(\alpha^2+\beta^2+\gamma^2=5^2+6^2+(-2)^2=65\) -
Question 45 of 150
45. Question
Let the line \(\frac{x}{1}=\frac{6-y}{2}=\frac{z+8}{5}\) intersect the lines \(\frac{x-5}{4}=\frac{y-7}{3}=\frac{z+2}{1}\) and \(\frac{x+3}{6}=\frac{3-y}{3}=\frac{z-6}{1}\) at the points \(A\) and \(B\) respectively. Then the distance of the mid-point of the line segment \(AB\) from the plane \(2 x-2 y+z=14\) is : [JEE Main 2023 (Online) 10th April Evening Shift]
CorrectIncorrectHint
We have, \(\frac{x}{1}=\frac{6-y}{2}=\frac{z+8}{5}\) intersect the line \(\frac{x-5}{4}=\frac{y-7}{3}=\frac{z+2}{1}\) and \(\frac{x+3}{6}=\frac{3-y}{3}=\frac{z-6}{1}\)
Now, \(\frac{x}{1}=\frac{6-y}{2}=\frac{z+8}{5}=\lambda \dots(i)\).
\(
\Rightarrow x=\lambda, y=6-2 \lambda, z=5 \lambda-8
\)
Also, \(\frac{x-5}{4}=\frac{y-7}{3}=\frac{z+2}{1}=k \dots(ii)\).
\(\Rightarrow x=4 k+5, y=3 k+7, z=k-2\)
\(\frac{x+3}{6}=\frac{3-y}{3}=\frac{z-6}{1}=\mu \ldots \ldots \ldots \ldots(i i i)\)
\(
\Rightarrow x=6 \mu-3, y=3-3 \mu, z=\mu+6
\)
On solving Eqs. (i) and (ii), we get \(\lambda=1, k=-1\)
\(\therefore\) Co-ordinate of \(A\) is \((1,4,-3)\)
On solving Eqs. (i) and (iii), we get \(\lambda=3, \mu=1\)
\(\therefore\) Co-ordinate of \(\beta\) is \((3,0,7)\)
Co-ordinate of mid-point of \(A B\) is \(\left(\frac{1+3}{2}, \frac{4+0}{2}, \frac{-3+7}{2}\right)\) or \((2,2,2)\)
Perpendicular distance of mid-point of \(A B\) from the plane \(2 x-2 y+z=14\) is
\(
\frac{|2(2)-2(2)+2-14|}{\sqrt{2^2+(-2)^2+1^2}}=4
\) -
Question 46 of 150
46. Question
The shortest distance between the lines \(\frac{x+2}{1}=\frac{y}{-2}=\frac{z-5}{2}\) and \(\frac{x-4}{1}=\frac{y-1}{2}=\frac{z+3}{0}\) is : [JEE Main 2023 (Online) 10th April Morning Shift]
CorrectIncorrectHint
Given, the lines are
\(
\frac{x+2}{1}=\frac{y}{-2}=\frac{z-5}{2} \dots(i)
\)
and \(\frac{x-4}{1}=\frac{y-1}{2}=\frac{z+3}{0} \dots(ii)\)
Formula for shortest distance between two skew-lines,
\(
\begin{aligned}
& S D=\left|\frac{\left|\begin{array}{ccc}
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|}{\left|\begin{array}{ccc}
\hat{ i } & \hat{ j } & \hat{ k } \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|}\right|=\left|\frac{\left|\begin{array}{ccc}
6 & 1 & -8 \\
1 & -2 & 2 \\
1 & 2 & 0
\end{array}\right|}{\left|\begin{array}{ccc}
\hat{ i } & \hat{ j } & \hat{ k } \\
1 & -2 & 2 \\
1 & 2 & 0
\end{array}\right|}\right| \\
& =\left|\frac{6(-4)-1(-2)-8(4)}{|-4 \hat{ i }+2 \hat{ j }+4 \hat{ k }|}\right| \\
& =\left|\frac{-24+2-32}{\sqrt{36}}\right| \\
& =\left|\frac{-54}{6}\right|=|-9|=9 \\
&
\end{aligned}
\) -
Question 47 of 150
47. Question
Let two vertices of a triangle \(ABC\) be \((2,4,6)\) and \((0,-2,-5)\), and its centroid be \((2,1,-1)\). If the image of the third vertex in the plane \(x+2 y+4 z=11\) is \((\alpha, \beta, \gamma)\), then \(\alpha \beta+\beta \gamma+\gamma \alpha\) is equal to : [JEE Main 2023 (Online) 10th April Morning Shift]
CorrectIncorrectHint
Given that two vertex of a \(\triangle A B C\) be \(A(2,4,6)\) and \(B(0,-2,-5)\) and \(G=\) centroid \(=(2,1,-1)\) [Given]
Let, the other vertex is \(C(x, y, z)\)
According to the question,
\(
\begin{aligned}
& \frac{2+0+x}{3}=2 \\
& \Rightarrow x=4 \\
& \frac{4-2+y}{3}=1 \\
& \Rightarrow y=1 \\
& \frac{6-5+z}{3}=-1 \\
& \Rightarrow z=1
\end{aligned}
\)
Hence, third vertex is \(C(4,1,-4)\)
Now, if image of \(C(4,1,-4)\) in the plane \(x+2 y+4 z=11\) is \(D(\alpha, \beta, \gamma)\).
So, \(\frac{\alpha-4}{1}=\frac{\beta-1}{2}=\frac{\gamma+4}{4}=k\) (say)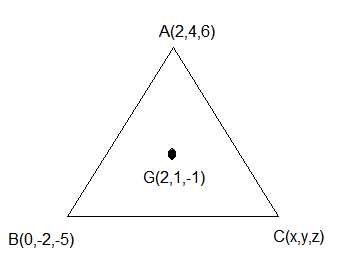
\(
\Rightarrow \alpha=k+4, \beta=2 k+1, \gamma=4 k-4
\)
Then, co-ordinates of \(D\) is \((k+4,2 k+1,4 k-4)\)
Let, \(E\) be the mid-point of \(C D\), which lies on the plane \(x+2 y+4 z=11\).
Then, co-ordinates of \(E\) is
\(
\left(\frac{k+8}{2}, \frac{2 k+2}{2}, \frac{4 k-8}{2}\right)=\left(\frac{k+8}{2}, k+1,2 k-4\right)
\)
Since, \(E\) lies on the plane, \(x+2 y+4 z-11=0\)
\(
\begin{aligned}
& \text { So, } \frac{k+8}{2}+2 k+2+8 k-16-11=0 \\
& \Rightarrow \frac{k+8+4 k+4+16 k-54}{2}=0 \\
& \Rightarrow 21 k=42 \\
& \Rightarrow k=2
\end{aligned}
\)
Hence, \(D \equiv(6,5,4) \equiv(\alpha, \beta, \gamma)\)
So, \(\alpha=6, \beta=5, \gamma=4\)
Now, \(\alpha \beta+\beta \gamma+\gamma \alpha=6 \times 5+5 \times 4+4 \times 6\)
\(
=30+20+24=74
\) -
Question 48 of 150
48. Question
Let \(P\) be the point of intersection of the line \(\frac{x+3}{3}=\frac{y+2}{1}=\frac{1-z}{2}\) and the plane \(x+y+z=2\). If the distance of the point \(P\) from the plane \(3 x-4 y+12 z=32\) is \(q\), then \(q\) and \(2 q\) are the roots of the equation: [JEE Main 2023 (Online) 10th April Morning Shift]
CorrectIncorrectHint
Given, equation of line is
\(
\begin{aligned}
& \frac{x+3}{3}=\frac{y+2}{1}=\frac{1-z}{2}=k \\
& \therefore x=3 k-3, y=k-2, z=1-2 k
\end{aligned}
\)
Since, given that \(P \equiv(3 k-3, k-2,1-2 k)\) be the point of intersection of the given line and the plane \(x+y+z=2\)
So, \((3 k-3)+(k-2)+(1-2 k)=2\)
\(
\Rightarrow 2 k-4=2 \Rightarrow k=3
\)
Thus, \(P=(6,1,-5)\)
Now, distance of point \(P\) from the plane \(3 x-4 y+12 z=32\) is
\(
\begin{aligned}
& q=\left|\frac{18-4-60-32}{\sqrt{9+16+144}}\right|=\left|\frac{-78}{\sqrt{169}}\right| \\
& \Rightarrow q=\left|\frac{-78}{13}\right|=\frac{78}{13}=6 \\
& \therefore q=6 \Rightarrow 2 q=12
\end{aligned}
\)
Thus, \(q\) and \(2 q\) are roots of the equation \(x^2-18 x+72=0\) -
Question 49 of 150
49. Question
For \(a , b \in Z\) and \(| a – b | \leq 10\), let the angle between the plane \(P : ax +y- z = b\) and the line \(l: x-1= a -y=z+1\) be \(\cos ^{-1}\left(\frac{1}{3}\right)\). If the distance of the point \((6,-6,4)\) from the plane \(P\) is \(3 \sqrt{6}\), then \(a^4+b^2\) is equal to : [JEE Main 2023 (Online) 8th April Evening Shift]
CorrectIncorrectHint
We have, \(\theta=\cos ^{-1} \frac{1}{3}\)
\(
\begin{aligned}
& \Rightarrow \cos \theta=\frac{1}{3} \\
& \therefore \sin \theta=\sqrt{1-\left(\frac{1}{3}\right)^2}=\sqrt{\frac{8}{9}}=\frac{2 \sqrt{2}}{3}
\end{aligned}
\)
The given plane and line are
\(
\begin{aligned}
& a x+y-z=b \\
& x-1=a-y=z+1 \\
& \therefore \sin \theta=\frac{a \cdot 1+(1)(-1)+(-1)(1)}{\sqrt{a^2+1^2+1^2} \sqrt{1^2+1^2+1^2}} \\
& \Rightarrow \frac{a-1-1}{\sqrt{a^2+2} \sqrt{3}}=\frac{2 \sqrt{2}}{3} \\
& \Rightarrow 3(a-2)=2 \sqrt{6} \sqrt{a^2+2} \\
& \Rightarrow 9\left(a^2+4-4 a\right)=24\left(a^2+2\right) \\
& \Rightarrow 9 a^2+36-36 a=24 a^2+48 \\
& \Rightarrow 15 a^2+36 a+12=0
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow 5 a^2+12 a+4=0 \\
& \Rightarrow 5 a^2+10 a+2 a+4=0 \\
& \Rightarrow 5 a(a+2)+2(a+2)=0 \\
& \Rightarrow a=\frac{-2}{5},-2
\end{aligned}
\)
So, \(a=-2[\because a \in Z]\)
Hence, the eqn. of plane is \(-2 x+y-z-b=0\)
\(
\begin{aligned}
& \text { Now, } d=\left|\frac{-12-6-4-b}{\sqrt{4+1+1}}\right|=3 \sqrt{6} \\
& \Rightarrow|-(b+22)|=18 \\
& \Rightarrow b=18-22=-4 \\
& \therefore a^4+b^2=(-2)^4+(-4)^2 \\
& =16+16=32
\end{aligned}
\) -
Question 50 of 150
50. Question
Let \(P\) be the plane passing through the line \(\frac{x-1}{1}=\frac{y-2}{-3}=\frac{z+5}{7}\) and the point \((2,4,-3)\). If the image of the point \((-1,3,4)\) in the plane \(P\) is \((\alpha, \beta, \gamma)\) then \(\alpha+\beta+\gamma\) is equal to : [JEE Main 2023 (Online) 8th April Evening Shift]
CorrectIncorrectHint
Equation of line : \(\frac{x-1}{1}=\frac{y-2}{-3}=\frac{z+5}{7}\)
Let \(B \equiv(2,4,-3)\)
\(
\begin{aligned}
& \text { So, } \overrightarrow{ AB }=(2-1) \hat{i}+(4-2) \hat{j}+(-3+5) \hat{k} \\
& =\hat{i}+2 \hat{j}+2 \hat{k} \\
& \vec{n}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & -3 & 7 \\
1 & 2 & 2
\end{array}\right|=(-6-14) \hat{i}-(2-7) \hat{j}+(2+3) \hat{k} \\
& =-20 \hat{i}+5 \hat{j}+5 \hat{k} \\
& =-5(4 \hat{i}-\hat{j}-\hat{k})
\end{aligned}
\)
\(\therefore\) Equation of plane is :
\(
\begin{aligned}
& 4(x-1)+(-1)(y-2)-1(z+5)=0 \\
& \Rightarrow 4 x-4-y+2-z-5=0 \\
& \Rightarrow 4 x-y-z-7=0
\end{aligned}
\)
\(\because\) Image of point \((-1,3,4)\) is \((\alpha, \beta, \gamma)\)
So, \(\frac{\alpha+1}{4}=\frac{\beta-3}{-1}=\frac{\gamma-4}{-1}=\frac{-2(-4-3-4-7)}{16+1+1}=2\)
\(
\Rightarrow \alpha=7, \beta=1, \gamma=2
\)
So, \(\alpha+\beta+\gamma=10\) -
Question 51 of 150
51. Question
The shortest distance between the lines \(\frac{x-4}{4}=\frac{y+2}{5}=\frac{z+3}{3}\) and \(\frac{x-1}{3}=\frac{y-3}{4}=\frac{z-4}{2}\) is : [JEE Main 2023 (Online) 8th April Morning Shift]
CorrectIncorrectHint
The given lines are
\(\frac{x-4}{4}=\frac{y+2}{5}=\frac{z+3}{3}\) and \(\frac{x-1}{3}=\frac{y-3}{4}=\frac{z-4}{2}\)
So, \(\vec{b}_1=4 \hat{i}+5 \hat{j}+3 \hat{k}\)
\(\vec{b}_2=3 \hat{i}+4 \hat{j}+2 \hat{k}\)
\(\vec{a}_1=4 \hat{i}-2 \hat{j}-3 \hat{k}\)
\(\vec{a}_2=\hat{i}+3 \hat{j}+4 \hat{k}\)
\(\therefore \vec{b}_1 \times \vec{b}_2=\left|\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k} \\ 4 & 5 & 3 \\ 3 & 4 & 2\end{array}\right|\)
\(=(10-12) \hat{i}-(8-9) \hat{j}+(16-15) \hat{k}\)
\(=-2 \hat{i}+\hat{j}+\hat{k}\)
\(
\begin{aligned}
& \text { Shortest distance, } d=\left|\frac{\left(\vec{a}_2-\vec{a}_1\right) \cdot\left(\vec{b}_1 \times \vec{b}_2\right)}{\left|\vec{b}_1 \times \vec{b}_2\right|}\right| \\
& =\left|\frac{(3 \hat{i}-5 \hat{j}-7 \hat{k}) \cdot(-2 \hat{i}+\hat{j}+\hat{k})}{\sqrt{4+1+1}}\right| \\
& =\left|\frac{-6-5-7}{\sqrt{6}}\right|=\frac{18}{\sqrt{6}}=3 \sqrt{6} \text { units }
\end{aligned}
\) -
Question 52 of 150
52. Question
If the equation of the plane containing the line \(x+2 y+3 z-4=0=2 x+y-z+5\) and perpendicular to the plane \(\vec{r}=(\hat{i}-\hat{j})+\lambda(\hat{i}+\hat{j}+\hat{k})+\mu(\hat{i}-2 \hat{j}+3 \hat{k})\) is \(a x+b y+c z=4\), then \((a-b+c)\) is equal to : [JEE Main 2023 (Online) 8th April Morning Shift]
CorrectIncorrectHint
Equation of plane \(P\) containing the given lines is
\(
\begin{aligned}
& (x+2 y+3 z-4)+\lambda(2 x+y-z+5)=0 \\
& \Rightarrow(1+2 \lambda) x+(2+\lambda) y+(3-\lambda) z+(-4+5 \lambda)=0
\end{aligned}
\)
Now, plane \(P\) is perpendicular to plane \(P ^{\prime}\)
\(
\vec{r}=(\hat{i}-\hat{j})+\lambda(\hat{i}+\hat{j}+\hat{k})+\mu(\hat{i}-2 \hat{j}+3 \hat{k})
\)
So, normal to plane \(P ^{\prime}\) is
\(
\begin{aligned}
& \vec{n}=(\hat{i}+\hat{j}+\hat{k}) \times(\hat{i}-2 \hat{j}+3 \hat{k}) \\
& \Rightarrow \vec{n}=5 \hat{i}-2 \hat{j}-3 \hat{k}
\end{aligned}
\)
\(\therefore P\) and \(P ^{\prime}\) are perpendicular
\(
\begin{aligned}
& \therefore 5(1+2 \lambda)-2(2+\lambda)-3(3-\lambda)=0 \\
& \Rightarrow 5+10 \lambda-4-2 \lambda-9+3 \lambda=0 \\
& \Rightarrow 11 \lambda=8 \Rightarrow \lambda=\frac{8}{11}
\end{aligned}
\)
\(
\therefore P:\left(1+\frac{16}{11}\right) x+\left(2+\frac{8}{11}\right) y+\left(3-\frac{8}{11}\right) z+\left(5 \times \frac{8}{11}-4\right)=0
\)
i.e., \(27 x+30 y+25 z=4\)
which is same as \(a x+b y+c z=4\)
\(\therefore a=27, b=30\) and \(c=25\)
\(
\Rightarrow a-b+c=27-30+25=22
\) -
Question 53 of 150
53. Question
A plane \(P\) contains the line of intersection of the plane \(\vec{r} \cdot(\hat{i}+\hat{j}+\hat{k})=6\) and \(\vec{r} \cdot(2 \hat{i}+3 \hat{j}+4 \hat{k})=-5\). If \(P\) passes through the point \((0,2,-2)\), then the square of distance of the point \((12,12,18)\) from the plane \(P\) is : [JEE Main 2023 (Online) 6th April Evening Shift]
CorrectIncorrectHint
Given plane \(\vec{r} \cdot(\hat{i}+\hat{j}+\hat{k})=6\) and
\(
\vec{r} \cdot(2 \hat{i}+3 \hat{j}+4 \hat{k})=-5
\)
Equation of plane passing through both plane
\(
\begin{aligned}
& P _1 \rightarrow(x \hat{i}+y \hat{j}+2 \hat{k})(\hat{i}+\hat{j}+\hat{k})=6 \\
& P _1=x+y+z=6 \\
& P _2 \rightarrow(x \hat{i}+y \hat{j}+z \hat{k}) \cdot(2 \hat{i}+3 \hat{j}+4 \hat{k})=-5 \\
& P _2 \rightarrow=2 x+3 y+4 z=-5 \\
& P _1+\lambda P _2=0 \\
& \Rightarrow(x+y+z-6)+\lambda(2 x+3 y+4 z+5)=0
\end{aligned}
\)
passes through \((0,2,-2)\)
\(
\begin{aligned}
& \Rightarrow(0+2-2-6)+\lambda(2 \times 0+3 \times 2+4 \times(-2)+5)=0 \\
& \Rightarrow \lambda=2
\end{aligned}
\)
Equation of plane
\(
5 x+7 y+9 z+4=0
\)
\(\therefore\) Distance of the point \((12,12,18)\) from the plane
\(
\begin{aligned}
d & =\frac{5 \times 12+7 \times 12+9 \times 18+4}{\sqrt{5^2+7^2+9^2}} \\
& =\frac{60+84+162+4}{\sqrt{155}}=\frac{310}{\sqrt{155}} \\
\therefore d^2 & =\frac{310 \times 310}{155}=620
\end{aligned}
\) -
Question 54 of 150
54. Question
Let the line \(L\) pass through the point \((0,1,2)\), intersect the line \(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\) and be parallel to the plane \(2 x+y-3 z=4\). Then the distance of the point \(P (1,-9,2)\) from the line \(L\) is : [JEE Main 2023 (Online) 6th April Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \Rightarrow[(1+2 \lambda) \hat{ i }+(1+3 \lambda) \hat{ j }+(1+4 \lambda) \hat{ k }] \\
& \quad(2 \hat{ i }+\hat{ j }-3 \hat{ k }) \\
& 2+4 \lambda+1+3 \lambda-3-12 \lambda=0 \\
& 5 \lambda=0 \Rightarrow \lambda=0
\end{aligned}
\)
Line \(\overrightarrow{ AB }, \overrightarrow{ r }=\hat{ j }+2 \hat{ k }+\mu(\hat{ i }+\hat{ j }+\hat{ k })\)
General form: \(Q (\mu, 1+\mu, 2+\mu)\)
\(
\begin{aligned}
& \therefore \overrightarrow{ PQ } \cdot \overrightarrow{ AB }=0 \\
& (\mu-1)+(10+\mu)+\mu=0 \\
& 3 \mu=-9 \Rightarrow \mu=-3
\end{aligned}
\)
\(
\therefore \text { distance }=\sqrt{16+49+9}=\sqrt{74}
\) -
Question 55 of 150
55. Question
If the equation of the plane passing through the line of intersection of the planes \(2 x-y+z=3,4 x-3 y+5 z+9=0\) and parallel to the line \(\frac{x+1}{-2}=\frac{y+3}{4}=\frac{z-2}{5}\) is \(a x+b y+c z+6=0\), then \(a+b+c\) is equal to : [JEE Main 2023 (Online) 6th April Morning Shift]
CorrectIncorrectHint
Equation of plane intersection of two plane
\(
\begin{aligned}
& P _1+\lambda P _2=0 \\
& P _1: 2 x-y+z=3 \text {, and } P _2: 4 x-3 y+5 z+9=0
\end{aligned}
\)
Equation of any plane passing through the intersection of given planes is
\(
\begin{aligned}
& (2 x-y+z-3)+\lambda(4 x-3 y+5 z+9)=0 \\
& \Rightarrow(2+4 \lambda) x+(-1-3 \lambda) y+(1+5 \lambda) z+(-3+9 \lambda)=0 \dots(i)
\end{aligned}
\)
Plane (i) is parallel to given line
\(
\begin{aligned}
& \therefore(-2)(2+4 \lambda)+4(-1-3 \lambda)+5(1+5 \lambda)=0 \\
& \Rightarrow-4-8 \lambda-4-12 \lambda+5+25 \lambda=0 \\
& \Rightarrow 5 \lambda-3=0 \\
& \Rightarrow \lambda=\frac{3}{5}
\end{aligned}
\)
Putting the value of \(\lambda\) in Eq. (i), we get
\(
\begin{aligned}
& (2 x-y+z-3)+\frac{3}{5}(4 x-3 y+5 z+9)=0 \\
& \Rightarrow 11 x-7 y+10 z+6=0 \\
& \therefore a=11, b=-7, c=10 \text { and } d=6 \\
& \therefore a+b+c=11-7+10=14
\end{aligned}
\) -
Question 56 of 150
56. Question
One vertex of a rectangular parallelopiped is at the origin \(O\) and the lengths of its edges along \(x, y\) and \(z\) axes are 3,4 and 5 units respectively. Let \(P\) be the vertex \((3,4,5)\). Then the shortest distance between the diagonal OP and an edge parallel to \(z\) axis, not passing through \(O\) or \(P\) is : [JEE Main 2023 (Online) 6th April Morning Shift]
CorrectIncorrectHint
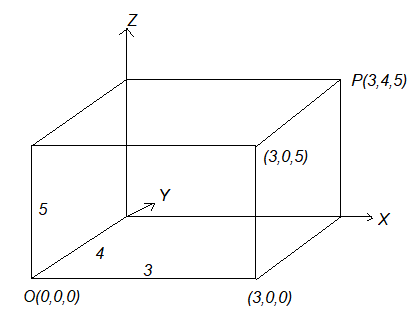
Equation of \(O P\) is
\(
\begin{aligned}
& \frac{x-0}{3-0}=\frac{y-0}{4-0}=\frac{z-0}{5-0} \\
& \Rightarrow \frac{x}{3}=\frac{y}{4}=\frac{z}{5}
\end{aligned}
\)
Equation of edge parallel to \(Z\)-axis is
\(
\frac{x-3}{0}=\frac{y-0}{0}=\frac{z-5}{1}
\)
\(\therefore\) Shortest distance
\(
=\frac{\left|\begin{array}{ccc}
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|}{\sqrt{\left(a_1 b_2-a_2 b_1\right)^2+\left(b_1 c_2-b_2 c_1\right)^2+\left(c_1 a_2-c_2 a_1\right)^2}}
\)
Here,
\(
\begin{aligned}
& x_1=0, y_1=0, z_1=0 \\
& x_2=3, y_2=0, z_2=5 \\
& a_1=3, b_1=4, c_1=5 \\
& a_2=0, b_2=0, c_2=1 \\
& \therefore\left|\begin{array}{ccc}
x_2-x_1 & y_2-y_1 & z_2-z_1 \\
a_1 & b_1 & c_1 \\
a_2 & b_2 & c_2
\end{array}\right|=\left|\begin{array}{ccc}
3 & 0 & 5 \\
3 & 4 & 5 \\
0 & 0 & 1
\end{array}\right|=4(3)=12 \\
& \text { and } \sqrt{\left(a_1 b_2-a_2 b_1\right)^2+\left(b_1 c_2-b_2 c_1\right)^2+\left(c_1 a_2-c_2 a_1\right)^2} \\
& =\sqrt{0+(4-0)^2+(0-3)^2} \\
& =\sqrt{16+9}=5 \\
& \therefore \text { Required shortest distance }=\frac{12}{5} \\
&
\end{aligned}
\) -
Question 57 of 150
57. Question
Let the plane \(P\) pass through the intersection of the planes \(2 x+3 y-z=2\) and \(x+2 y+3 z=6\), and be perpendicular to the plane \(2 x+y-z+1=0\). If \(d\) is the distance of \(P\) from the point \((-7,1,1)\), then \(d ^2\) is equal to : [JEE Main 2023 (Online) 1st February Evening Shift]
CorrectIncorrectHint
Plane \(P\), is passing through intersection of the two planes, so,
\(
\begin{aligned}
& 2 x+3 y-z-2+\lambda(x+2 y+3 z-6)=0 \\
& x(2+\lambda)+y(3+2 \lambda)+z(3 \lambda-1)-2-6 \lambda=0
\end{aligned}
\)
It is perpendicular with plane, \(2 x+y-2+1=0\)
So, \((2+\lambda) 2+(3+2 \lambda) 1+(3 \lambda-1)(-1)=0\)
\(
\lambda=-8
\)
So, plane \(p_1:-6 x-13 y-25 z+46=0\)
Distance of plane \(p\) from the point \((-7,1,1)\)
\(
\begin{aligned}
& d=\frac{|+42-13-25+46|}{\sqrt{36+169+625}}=\frac{50}{\sqrt{830}} \\
& d^2=\frac{2500}{830}=\frac{250}{83}
\end{aligned}
\) -
Question 58 of 150
58. Question
The shortest distance between the lines \(\frac{x-5}{1}=\frac{y-2}{2}=\frac{z-4}{-3}\) and \(\frac{x+3}{1}=\frac{y+5}{4}=\frac{z-1}{-5}\) is : [JEE Main 2023 (Online) 1st February Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& L _1: \frac{x-5}{1}=\frac{y-2}{2}=\frac{z-4}{-3} \\
& \overrightarrow{a_1}=5 \hat{i}+2 \hat{j}+4 \hat{k} \\
& \overrightarrow{r_1}=\hat{i}+2 \hat{j}-3 \hat{k} \\
& L _2: \frac{x+3}{1}=\frac{y+5}{4}=\frac{z-1}{-5} \\
& \overrightarrow{a_2}=-3 \hat{i}-5 \hat{j}+\hat{k} \\
& \overrightarrow{r_2}=\hat{i}+4 \hat{j}-5 \hat{k} \\
& \overrightarrow{r_1} \times \overrightarrow{r_2}=\left|\begin{array}{lll}
1 & \hat{i} & \hat{j} \\
1 & 2 & -3 \\
1 & 4 & -5
\end{array}\right| \\
& =2 \hat{i}+2 \hat{j}+2 \hat{k}
\end{aligned}
\)
\(
\begin{aligned}
& \text { Shortest distance (d) }=\left|\frac{\left(\overrightarrow{r_1} \times \overrightarrow{r_2}\right) \cdot\left(\overrightarrow{a_1}-\overrightarrow{a_2}\right)}{\left|\overrightarrow{r_1} \times \overrightarrow{r_2}\right|}\right| \\
& =\frac{36}{2 \sqrt{3}}=6 \sqrt{3}
\end{aligned}
\) -
Question 59 of 150
59. Question
Let the image of the point \(P(2,-1,3)\) in the plane \(x+2 y-z=0\) be \(Q\). Then the distance of the plane \(3 x+2 y+z+29=0\) from the point \(Q\) is : [JEE Main 2023 (Online) 1st February Morning Shift]
CorrectIncorrectHint
Equation of line PM \(\frac{x-2}{1}=\frac{y+1}{2}=\frac{z-3}{-1}=\lambda\)
Any point on line \(=(\lambda+2,2 \lambda-1,-\lambda+3)\)
For point ‘ \(m\) ‘ \((\lambda+2)+2(2 \lambda-1)-(3-\lambda)=0\)
\(
\begin{aligned}
& \Rightarrow \lambda=\frac{1}{2} \\
& \text { Point } m \left(\frac{1}{2}+2,2 \times \frac{1}{2}-1, \frac{-1}{2}+3\right) \\
& =\left(\frac{5}{2}, 0, \frac{5}{2}\right)
\end{aligned}
\)
For Image \(Q (\alpha, \beta, \gamma)\)
\(
\begin{aligned}
& \frac{\alpha+2}{2}=\frac{5}{2}, \frac{\beta-1}{2}=0 \\
& \frac{\gamma+3}{2}=\frac{5}{2} \\
& Q:(3,1,2) \\
& d=\left|\frac{3(3)+2(1)+2+29}{\sqrt{3^2+2^2+1^2}}\right| \\
& \Rightarrow d=\frac{42}{\sqrt{14}}=3 \sqrt{14}
\end{aligned}
\) -
Question 60 of 150
60. Question
Let the plane \(P : 8 x+\alpha_1 y+\alpha_2 z+12=0\) be parallel to the line \(L : \frac{x+2}{2}=\frac{y-3}{3}=\frac{z+4}{5}\). If the intercept of \(P\) on the \(y\)-axis is 1 , then the distance between \(P\) and \(L\) is : [JEE Main 2023 (Online) 31st January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& P : 8 x+\alpha_1 y +\alpha_2 z +12=0 \\
& L : \frac{ x +2}{2}=\frac{ y -3}{3}=\frac{ z +4}{5}
\end{aligned}
\)
\(\because P\) is parallel to \(L\)
\(
\begin{aligned}
& \Rightarrow 8(2)+\alpha_1(3)+5\left(\alpha_2\right)=0 \\
& \Rightarrow 3 \alpha_1+5\left(\alpha_2\right)=-16
\end{aligned}
\)
Also \(y\)-intercept of plane \(P\) is 1
\(
\Rightarrow \alpha_1=-12
\)
And \(\alpha_2=4\)
\(\Rightarrow\) Equation of plane \(P\) is \(2 x -3 y + z +3=0\)
\(\Rightarrow\) Distance of line \(L\) from Plane \(P\) is
\(
=\left|\frac{0-3(6)+1+3}{\sqrt{4+9+1}}\right|=\sqrt{14}
\) -
Question 61 of 150
61. Question
The foot of perpendicular from the origin \(O\) to a plane \(P\) which meets the coordinate axes at the points \(A , B , C\) is \((2, a , 4), a \in N\). If the volume of the tetrahedron \(OABC\) is 144 unit \(^3\), then which of the following points is NOT on \(P\) ? [JEE Main 2023 (Online) 31st January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& (2 \hat{i}+a \hat{j}+4 \hat{ k }) \cdot[( x -2) \hat{ i }+( y – a ) \hat{ j }+( z -4) \hat{ k }]=0 \\
& \Rightarrow 2 x + ay +4 z =20+ a ^2 \\
& \Rightarrow A \equiv\left(\frac{20+ a ^2}{2}, 0,0\right) \\
& B \equiv\left(0, \frac{20+ a ^2}{ a }, 0\right) \\
& C \equiv\left(0,0, \frac{20+ a ^2}{4}\right) \\
& \Rightarrow \text { Volume of tetrahedron } \\
& =\frac{1}{6}\left[\vec{a} \vec{b} \vec{c}\right]
\end{aligned}
\)
\(
\begin{aligned}
& \left.=\frac{1}{6} \overrightarrow{ a } \cdot \overrightarrow{( b } \times \overrightarrow{ c }\right) \\
& \Rightarrow \frac{1}{6}\left(\frac{20+ a ^2}{2}\right) \cdot\left(\frac{20+ a ^2}{ a }\right) \cdot\left(\frac{20+ a ^2}{4}\right)=144 \\
& \Rightarrow\left(20+ a ^2\right)^3=144 \times 48 \times a \\
& \Rightarrow a =2 \\
& \Rightarrow \text { Equation of plane is } 2 x +2 y +4 z =24 \\
& \text { Or } x + y +2 z =12 \\
& \Rightarrow(3,0,4) \quad \text { Not lies on the } \\
& x + y +2 z =12
\end{aligned}
\) -
Question 62 of 150
62. Question
Let \(P\) be the plane, passing through the point \((1,-1,-5)\) and perpendicular to the line joining the points \((4,1,-3)\) and \((2,4,3)\). Then the distance of \(P\) from the point \((3,-2,2)\) is : [JEE Main 2023 (Online) 31st January Evening Shift]
CorrectIncorrectHint
Equation of Plane :
\(
2(x-1)-3(y+1)-6(z+5)=0
\)
or \(2 x-3 y-6 z=35\)
\(
\Rightarrow \text { Required distance }=\frac{|2(3)-3(-2)-6(2)-35|}{\sqrt{4+9+36}}=5
\) -
Question 63 of 150
63. Question
If a point \(P (\alpha, \beta, \gamma)\) satisfying
\(
\left(\begin{array}{lll}
\alpha & \beta & \gamma
\end{array}\right)\left(\begin{array}{ccc}
2 & 10 & 8 \\
9 & 3 & 8 \\
8 & 4 & 8
\end{array}\right)=\left(\begin{array}{lll}
0 & 0 & 0
\end{array}\right)
\)
lies on the plane \(2 x+4 y+3 z=5\), then \(6 \alpha+9 \beta+7 \gamma\) is equal to : [JEE Main 2023 (Online) 31st January Evening Shift]CorrectIncorrectHint
Point \(P (\alpha, \beta, \gamma)\) lies on the plane \(2 x+4 y+3 z=5\),
\(
\therefore 2 \alpha+4 \beta+3 \gamma=5 \dots(1)
\)
Given, \(\left(\begin{array}{lll}\alpha & \beta & \gamma\end{array}\right)\left(\begin{array}{ccc}2 & 10 & 8 \\ 9 & 3 & 8 \\ 8 & 4 & 8\end{array}\right)=\left(\begin{array}{lll}0 & 0 & 0\end{array}\right)\)
\(
\therefore 2 \alpha+9 \beta+8 \gamma=0 \dots(2)
\)
and \(10 \alpha+3 \beta+4 \gamma=0 \dots(3)\)
and \(8 \alpha+8 \beta+8 \gamma=0 \dots(4)\)
Subtract (4) from (2)
\(
-6 \alpha+\beta=0 \Rightarrow \beta =6 \alpha
\)
From equation (4)
\(
\begin{aligned}
& 8 \alpha+48 \alpha+8 \gamma=0 \\
& \gamma=-7 \alpha
\end{aligned}
\)
From equation (1)
\(
\begin{aligned}
& 2 \alpha+24 \alpha-21 \alpha=5 \\
& 5 \alpha=5 \\
& \alpha=1 \\
& \beta=+6, \quad \gamma=-7 \\
& \therefore 6 \alpha+9 \beta+7 \gamma \\
& =6+54-49 \\
& =11
\end{aligned}
\) -
Question 64 of 150
64. Question
Let the shortest distance between the lines
\(L: \frac{x-5}{-2}=\frac{y-\lambda}{0}=\frac{z+\lambda}{1}, \lambda \geq 0\) and
\(L_1: x+1=y-1=4-z\) be \(2 \sqrt{6}\). If \((\alpha, \beta, \gamma)\) lies on \(L\),
then which of the following is NOT possible? [JEE Main 2023 (Online) 31st January Morning Shift]CorrectIncorrectHint
\(
\begin{aligned}
& \frac{x-5}{-2}=\frac{y-\lambda}{0}=\frac{z+\lambda}{1}, \lambda \geq 0 \\
& \frac{x+1}{1}=\frac{y-1}{1}=\frac{z-4}{-1} \\
& \vec{a}_1=5 \hat{i}+\lambda \hat{j}-\lambda \hat{k}, \vec{a}_2=-\hat{i}+\hat{j}+4 \hat{k} \\
& \vec{a}_1-\vec{a}_2=6 \hat{i}+(\lambda-1) \hat{j}-(\lambda+4) \hat{k} \\
& \vec{b}_1=-2 \hat{i}+\hat{k}, \vec{b}=\hat{i}+\hat{j}-\hat{k} \\
& \vec{b}_1 \times \vec{b}_2=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
-2 & 0 & 1 \\
1 & 1 & -1
\end{array}\right| \\
& =-\hat{i}-\hat{j}-2 \hat{k} \\
& \left(\vec{a}_1-\vec{a}_2\right) \cdot \vec{b}_1 \times \vec{b}_2=-6+1-\lambda+2 \lambda+8=\lambda+3 \\
& \text { and }\left|\vec{b}_1 \times \vec{b}_2\right|=\sqrt{6} \\
& \because \frac{|\lambda+3|}{\sqrt{6}}=2 \sqrt{6} \\
& \therefore \lambda=9, \because \lambda \geq 0 \\
& \therefore \quad L: \frac{x-5}{-2}=\frac{y-9}{0}=\frac{z+9}{1}=k \\
&
\end{aligned}
\)
\(
\therefore \quad \alpha=-2 k+5, \beta=9, \gamma=k-9
\)
Here \(k\) is real then
\(
\alpha+2 \gamma=-13 \neq 24 \text {. }
\)
But all other are in terms of \(k\) hence possible. -
Question 65 of 150
65. Question
A vector \(\vec{v}\) in the first octant is inclined to the \(x\)-axis at \(60^{\circ}\), to the \(y\)-axis at 45 and to the \(z\)-axis at an acute angle. If a plane passing through the points \((\sqrt{2},-1,1)\) and \((a, b, c)\), is normal to \(\vec{v}\), then : [JEE Main 2023 (Online) 30th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& l=\frac{1}{2}, m=\frac{1}{\sqrt{2}}, n=\cos \theta \\
& l^2+m^2+n^2=1 \\
& \Rightarrow \frac{1}{4}+\frac{1}{2}+n^2=1 \Rightarrow n^2=\frac{1}{4} \Rightarrow n=+\frac{1}{2}
\end{aligned}
\)
\(\theta\) is acute \(\therefore n=\frac{1}{2}\)
\(
\begin{aligned}
& \therefore \vec{v}=k\left(\frac{1}{2} \hat{i}+\frac{1}{\sqrt{2}} \hat{j}+\frac{1}{2} \widehat{k}\right), k \in R \\
& \vec{v}(\vec{a}-\vec{b})=0 \\
& (\sqrt{2}-a) \frac{1}{2}+(-1-b) \frac{1}{\sqrt{2}}+(1-c) \frac{1}{2}=0 \\
& \Rightarrow \frac{a}{2}+\frac{b}{\sqrt{2}}+\frac{c}{2}=\frac{1}{2} \\
& \Rightarrow a+\sqrt{2} b+c=1
\end{aligned}
\) -
Question 66 of 150
66. Question
If a plane passes through the points \((-1, k, 0),(2, k,-1),(1,1,2)\) and is parallel to the line \(\frac{x-1}{1}=\frac{2 y+1}{2}=\frac{z+1}{-1}\), then the value of \(\frac{k^2+1}{(k-1)(k-2)}\) is : [JEE Main 2023 (Online) 30th January Evening Shift]
CorrectIncorrectHint
Let \(P \equiv(-1, k, 0), Q \equiv(2, k,-1) \& R(1,1,2)\)
\(
\begin{aligned}
& \overrightarrow{P R}=2 \hat{i}+(1-k) \hat{j}+2 \widehat{k} \\
& \& \vec{Q} R=-\hat{i}+(1-k) \hat{j}+3 \widehat{k}
\end{aligned}
\)
\(\therefore\) Normal to plane will be
\(
\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \widehat{k} \\
2 & (1-k) & 2 \\
-1 & (1-k) & 3
\end{array}\right|=\hat{i}(1-k)-\hat{j}(8)+3 \widehat{k}(1-k)
\)
If line is parallel to this we have
\(
\begin{aligned}
& 1(1-k)+1(-8)+(-3)(1-k)=0 \\
& \Rightarrow 2(1-k)=-8 \\
& \Rightarrow 1-k=-4 \Rightarrow k=5 \\
& \therefore \frac{k^2+1}{(k-1)(k-2)}=\frac{26}{4.3}=\frac{13}{6}
\end{aligned}
\) -
Question 67 of 150
67. Question
The line \(l_1\) passes through the point \((2,6,2)\) and is perpendicular to the plane \(2 x+y-2 z=10\). Then the shortest distance between the line \(l_1\) and the line \(\frac{x+1}{2}=\frac{y+4}{-3}=\frac{z}{2}\) is : [JEE Main 2023 (Online) 30th January Morning Shift]
CorrectIncorrectHint
Equation of \(l_1=\frac{x-2}{2}=\frac{y-6}{1}=\frac{z-2}{-2}\)
Shortest distance with \(\frac{x+1}{2}=\frac{y+4}{-3}=\frac{z}{2}\) is
\(
\begin{aligned}
& =9 \text { units } \\
&
\end{aligned}
\) -
Question 68 of 150
68. Question
The plane \(2 x-y+z=4\) intersects the line segment joining the points \(A\) ( \(a,-2,4)\) and \(B (2, b,-3)\) at the point \(C\) in the ratio \(2: 1\) and the distance of the point \(C\) from the origin is \(\sqrt{5}\). If \(a b<0\) and \(P\) is the point \((a-b, b, 2 b-a)\) then \(C P^2\) is equal to : [JEE Main 2023 (Online) 29th January Evening Shift]
CorrectIncorrectHint
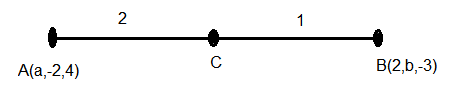
\(
\begin{aligned}
& C:\left(\frac{a+4}{3}, \frac{-2+2 b}{3}, \frac{4-6}{3}\right) \\
& =\left(\frac{a+4}{3}, \frac{-2+2 b}{3}, \frac{-2}{3}\right)
\end{aligned}
\)
\(
\begin{aligned}
& \text { C lies on plane } 2 x-y+z=4 \\
& 2\left(\frac{a+4}{3}\right)-\left(\frac{2 b-2}{3}\right)-\frac{2}{3}=4 \\
& \Rightarrow 2 a+8-2 b+2-2=12 \\
& \Rightarrow a-b=2 \ldots . \text { (i) }
\end{aligned}
\)
Now, \(O P=\sqrt{5}\)
\(
\begin{aligned}
& \left(\frac{a+4}{3}\right)^2+\left(\frac{2 b-2}{3}\right)^2+\frac{4}{9}=5 \text { and using (i) } \\
& a=\frac{11}{5}, 1 \\
& \Rightarrow b=\frac{1}{5},-1 \\
& \text { as also } \Rightarrow a=1, b=-1 \\
& P(2,-1,-3), c\left(\frac{5}{3}, \frac{-4}{3}, \frac{-2}{3}\right) \\
& C P^2=\frac{1}{9}+\frac{1}{9}+\frac{49}{9}=\frac{17}{3}
\end{aligned}
\) -
Question 69 of 150
69. Question
If the lines \(\frac{x-1}{1}=\frac{y-2}{2}=\frac{z+3}{1}\) and \(\frac{x-a}{2}=\frac{y+2}{3}=\frac{z-3}{1}\) intersect at the point \(P\), then the distance of the point \(P\) from the plane \(z=a\) is : [JEE Main 2023 (Online) 29th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{x-1}{1}=\frac{y-2}{2}=\frac{z+3}{1}=\lambda \text { (say) } \\
& \& \frac{x-a}{2}=\frac{y+2}{3}=\frac{z-3}{1}=\mu(\text { say) } \\
& \therefore \lambda+1=2 \mu+a \ldots \ldots . \text { (i) } \\
& 2 \lambda+2=3 \mu-2 \ldots . . \text { (ii) } \\
& \lambda-3=\mu+3 \ldots . \text { (iii) }
\end{aligned}
\)
By (i) & (ii)
\(
\begin{aligned}
& \Rightarrow 3 \mu-2=4 \mu+2 a+2 \\
& \mu=-2(1+a) \& \lambda=5-3 a
\end{aligned}
\)
Put \(\lambda \& \mu\) in (iii) we get
\(
\begin{aligned}
& a=-9 \\
& \mu=16 \\
& \lambda=22
\end{aligned}
\)
\(\therefore\) Point of intersection \(\equiv(23,46,19)\)
Distance from \(z=-9\) is 2 -
Question 70 of 150
70. Question
The shortest distance between the lines \(\frac{x-1}{2}=\frac{y+8}{-7}=\frac{z-4}{5}\) and \(\frac{x-1}{2}=\frac{y-2}{1}=\frac{z-6}{-3}\) is : [JEE Main 2023 (Online) 29th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \overrightarrow{r_1}=\hat{i}-8 \hat{j}+4 \widehat{k} \\
& \overrightarrow{r_2}=\hat{i}+2 \hat{j}+6 \widehat{k} \\
& \vec{a}=2 \hat{i}-7 \hat{j}+5 \widehat{k} \\
& \vec{b}=2 \hat{i}+\hat{j}-3 \widehat{k} \\
& \text { S.D. }=\frac{\left|\left[\overrightarrow{r_1}-\overrightarrow{r_2} \quad \vec{a} \quad \vec{b}\right]\right|}{|\vec{a} \times \vec{b}|}
\end{aligned}
\)
\(
\begin{aligned}
& {\left[\begin{array}{llll}
\overrightarrow{r_1}-\overrightarrow{r_2} & \vec{a} & \vec{b}
\end{array}\right]=\left|\begin{array}{ccc}
0 & -10 & -2 \\
2 & -7 & 5 \\
2 & 1 & -3
\end{array}\right|} \\
& \therefore 10(-16)-2(16)=-192 \\
& \left|\left[\begin{array}{llll}
\overrightarrow{r_1}-\overrightarrow{r_2} & \vec{a} & \vec{b}
\end{array}\right]\right|=192 \\
& \vec{a} \times \vec{b}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \widehat{k} \\
2 & -7 & 5 \\
2 & 1 & -3
\end{array}\right|=16 \hat{i}+16 \hat{j}+16 \widehat{k} \\
& \vec{a} \times \vec{b}=16 \sqrt{3} \\
& \text { S.D. }=\frac{192}{16 \sqrt{3}}=4 \sqrt{3} \\
&
\end{aligned}
\) -
Question 71 of 150
71. Question
The foot of perpendicular of the point \((2,0,5)\) on the line \(\frac{x+1}{2}=\frac{y-1}{5}=\frac{z+1}{-1}\) is \((\alpha, \beta, \gamma)\). Then, which of the following is NOT correct? [JEE Main 2023 (Online) 25th January Evening Shift]
CorrectIncorrectHint
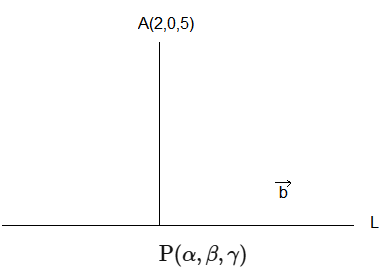
\(
L : \frac{ x +1}{2}=\frac{y-1}{5}=\frac{z+1}{-1}=\lambda \text { (let) }
\)
Let foot of perpendicular is
\(
\begin{aligned}
& P (2 \lambda-1,5 \lambda+1,-\lambda-1) \\
& \overrightarrow{ PA }=(3-2 \lambda) \hat{ i }-(5 \lambda+1) \hat{ j }+(6+\lambda) \hat{ k } \\
& \text { Direction ratio of line } \Rightarrow \overrightarrow{ b }=2 \hat{ i }+5 \hat{ j }-\hat{ k }
\end{aligned}
\)
Now, \(\Rightarrow \overrightarrow{ PA } \cdot \overrightarrow{ b }=0\)
\(
\begin{aligned}
& \Rightarrow 2(3-2 \lambda)-5(5 \lambda+1)-(6+\lambda)=0 \\
& \Rightarrow \lambda=\frac{-1}{6} \\
& P (2 \lambda-1,5 \lambda+1,-\lambda-1) \equiv P (\alpha, \beta, \gamma) \\
& \Rightarrow \alpha=2\left(-\frac{1}{6}\right)-1=-\frac{4}{3} \Rightarrow \alpha=-\frac{4}{3} \\
& \Rightarrow \beta=5\left(-\frac{1}{6}\right)+1=\frac{1}{6} \Rightarrow \beta=\frac{1}{6} \\
& \Rightarrow \gamma=-\lambda-1=\frac{1}{6}-1 \Rightarrow \gamma=-\frac{5}{6}
\end{aligned}
\) -
Question 72 of 150
72. Question
The shortest distance between the lines \(x+1=2 y=-12 z\) and \(x=y+2=6 z-6\) is : [JEE Main 2023 (Online) 25th January Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& L_1: \frac{x+1}{1}=\frac{y}{\frac{1}{2}}=\frac{z}{\frac{1}{12}} \\
& L_2: \frac{x}{1}=\frac{y+2}{1}=\frac{z-1}{\frac{1}{6}} \\
& \text { S.D }=\left|\frac{(-\hat{i}+2 \hat{j}-\hat{k}) \cdot(2 \hat{i}-3 \hat{j}+6 \hat{k})}{7}\right| \\
& =\left|\frac{-2-6-6}{7}\right|=2 \text { units }
\end{aligned}
\) -
Question 73 of 150
73. Question
The distance of the point \(P(4,6,-2)\) from the line passing through the point \((-3\), 2,3 ) and parallel to a line with direction ratios \(3,3,-1\) is equal to : [JEE Main 2023 (Online) 25th January Morning Shift]
CorrectIncorrectHint
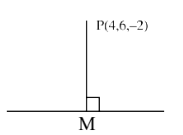
Equation of line is \(\frac{x+3}{3}\)
\(
\begin{aligned}
= & \frac{y-2}{3}=\frac{z-3}{-1}=\lambda \\
& (3 \lambda-3,3 \lambda+2,3-\lambda)
\end{aligned}
\)
D.R of \(PM (3 \lambda-7,3 \lambda-4,5-\lambda)\)
Since \(P M\) is perpendicular to line
\(
\begin{aligned}
& \Rightarrow 3(3 \lambda-7)+3(3 \lambda-4)-1(5-\lambda)=0 \\
& \Rightarrow \lambda=2 \\
& \Rightarrow M (3,8,1) \Rightarrow PM =\sqrt{14}
\end{aligned}
\) -
Question 74 of 150
74. Question
Consider the lines \(L_1\) and \(L_2\) given by
\(
\begin{aligned}
& L_1: \frac{x-1}{2}=\frac{y-3}{1}=\frac{z-2}{2} \\
& L_2: \frac{x-2}{1}=\frac{y-2}{2}=\frac{z-3}{3}
\end{aligned}
\)
A line \(L_3\) having direction ratios \(1,-1,-2\), intersects \(L_1\) and \(L_2\) at the points \(P\) and \(Q\) respectively. Then the length of line segment \(P Q\) is [JEE Main 2023 (Online) 25th January Morning Shift]CorrectIncorrectHint
\(
\begin{aligned}
& \text { Let, } \\
& P \equiv(2 \lambda+1, \lambda+3,2 \lambda+2) \text { and } Q(\mu+2,2 \mu+2,3 \mu+3) \\
& \text { d.r’s of } P Q \equiv<2 \lambda-\mu-1, \lambda-2 \mu+1,2 \lambda-3 \mu-1> \\
& \therefore \quad \frac{2 \lambda-\mu-1}{1}-\frac{\lambda-2 \mu-1}{-1}=\frac{2 \lambda-3 \mu-1}{-2} \\
& \therefore \quad-2 \lambda+\mu+1=\lambda-2 \mu+1 \text { and }-2 \lambda+4 \mu-2= \\
& -2 \lambda+3 \mu+1 \\
& \Rightarrow 3 \lambda-3 \mu=0 \text { and } \mu=3 \\
& \therefore \quad \lambda= \pm 3 \text { and } \mu=3 \\
& \therefore \quad P \equiv(7,6,8) \text { and } Q(5,8,12) \\
& \therefore|P O|=\sqrt{2^2+2^2+4^2}=\sqrt{24}=2 \sqrt{6}
\end{aligned}
\) -
Question 75 of 150
75. Question
If the foot of the perpendicular drawn from \((1,9,7)\) to the line passing through the point \((3,2,1)\) and parallel to the planes \(x+2 y+z=0\) and \(3 y-z=3\) is ( \(\alpha, \beta, \gamma)\), then \(\alpha+\beta+\gamma\) is equal to : [JEE Main 2023 (Online) 24th January Evening Shift]
CorrectIncorrectHint
Direction of line
\(
\begin{aligned}
\vec{b} & =\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & 2 & 1 \\
0 & 3 & -1
\end{array}\right| \\
& =\hat{i}(-5)-\hat{j}(-1)+\hat{k}(3) \\
& =-5 \hat{i}+\hat{j}+3 \hat{k}
\end{aligned}
\)
Equation of line
\(
\frac{x-3}{-5}=\frac{y-2}{1}=\frac{z-1}{3}
\)
Let foot of perpendicular be \(=(-5 k+3, k+2,3 k+1)\)
\(
\Rightarrow(-5 k+2)(-5)+(k-7)(1)+(3 k-6)(3)=0
\)
Or \(25 k-10+k-7+9 k-18=0\)
Or \(k=1\)
\(
\alpha+\beta+\gamma=-k+6=5
\) -
Question 76 of 150
76. Question
Let the plane containing the line of intersection of the planes
\(
\begin{aligned}
& P _1: x+(\lambda+4) y+z=1 \text { and } \\
& P _2: 2 x+y+z=2
\end{aligned}
\)
pass through the points \((0,1,0)\) and \((1,0,1)\). Then the distance of the point \((2 \lambda, \lambda,-\lambda)\) from the plane \(P_2\) is : [JEE Main 2023 (Online) 24th January Evening Shift]CorrectIncorrectHint
Equation of plane passing through point of intersection of \(P 1\) and \(P 2\)
\(
\begin{aligned}
& P _1+ kP _2=0 \\
& ( x +(\lambda+4) y + z -1)+ k (2 x + y + z -2)=0
\end{aligned}
\)
Passing through \((0,1,0)\) and \((1,0,1)\)
\(
\begin{aligned}
& (\lambda+4-1)+ k (1-2)=0 \\
& (\lambda+3)- k =0 \quad \ldots(1)
\end{aligned}
\)
Also passing \((1,0,1)\)
\(
\begin{aligned}
& (1+1-1)+ k (2+1-2)=0 \\
& 1+ k =0 \\
& k =-1
\end{aligned}
\)
put in (1)
\(
\begin{aligned}
& \lambda+3+1=0 \\
& \lambda=-4
\end{aligned}
\)
Then point \((2 \lambda, \lambda,-\lambda)\)
\(
\begin{aligned}
& (-8,-4,4) \\
& d=\left|\frac{-16-4+4-2}{\sqrt{6}}\right| \\
& d=\frac{18}{\sqrt{6}} \times \frac{\sqrt{6}}{\sqrt{6}}=3 \sqrt{6}
\end{aligned}
\) -
Question 77 of 150
77. Question
The distance of the point \((7,-3,-4)\) from the plane passing through the points \((2,-3,1),(-1,1,-2)\) and \((3,-4,2)\) is : [JEE Main 2023 (Online) 24th January Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& A(2,-3,1), B(-1,1,-2), C(3,-4,2) \\
& \overrightarrow{A B}=-3 \hat{i}+4 \hat{j}-3 \hat{k} \quad \overrightarrow{A C}=\hat{i}-\hat{j}+\hat{k} \\
& \vec{n}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
-3 & 4 & -3 \\
1 & -1 & 1
\end{array}\right|=\hat{i}-\hat{k}
\end{aligned}
\)
Let equation of plane is \(x-z+\lambda=0\) passes through point
\(
A(2,-3,1) \Rightarrow \lambda=-1
\)
Equation of plane is \(x-z-1=0\)
Distance of point \((7,-3,-4)\) from the plane \(x-z-1=0\) is \(5 \sqrt{2}\) -
Question 78 of 150
78. Question
The distance of the point \((-1,9,-16)\) from the plane \(2 x+3 y-z=5\) measured parallel to the line \(\frac{x+4}{3}=\frac{2-y}{4}=\frac{z-3}{12}\) is : [JEE Main 2023 (Online) 24th January Morning Shift]
CorrectIncorrectHint
Given, \(\frac{x+4}{3}=\frac{2-y}{4}=\frac{z-3}{12}\)
\(
\Rightarrow \frac{x+4}{3}=\frac{y-2}{-4}=\frac{z-3}{12}
\)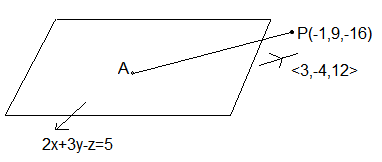
Equation of line passing through the point \(P (-1,9,-16)\) and parallel to line \(\frac{x+4}{3}=\frac{2-y}{4}=\frac{z-3}{12}\) is \(\frac{x+1}{3}=\frac{y-9}{-4}=\frac{z+16}{12}=\lambda\)
Any point on this line \(( A )=(3 \lambda-1,-4 \lambda+9,12 \lambda-16)\)
Point of intersection line and plane
\(
\begin{aligned}
& 2(3 \lambda-1)+3(-4 \lambda+9)-1(12 \lambda-16)=5 \\
\Rightarrow & 6 \lambda-2-12 \lambda+27-12 \lambda+16=5 \\
\Rightarrow & \lambda=2 \\
\therefore & \text { Point A }=(5,1,8) \\
\therefore & \text { Distance (AP) } \\
= & \sqrt{(5+1)^2+(9-1)^2+(-16-8)^2} \\
= & \sqrt{36+64+576} \\
= & 26 \text { units }
\end{aligned}
\) -
Question 79 of 150
79. Question
Let \(Q\) be the foot of perpendicular drawn from the point \(P(1,2,3)\) to the plane \(x+2 y+z=14\). If \(R\) is a point on the plane such that \(\angle P R Q=60^{\circ}\), then the area of \(\triangle P Q R\) is equal to : [JEE Main 2022 (Online) 29th July Evening Shift]
CorrectIncorrectHint
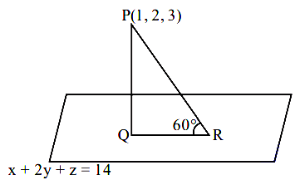
Length of perpendicular
\(
\begin{aligned}
& P Q=\left|\frac{1+4+3-14}{\sqrt{6}}\right|=\sqrt{6} \\
& Q R=(P Q) \cot 60^{\circ}=\sqrt{2}
\end{aligned}
\)
\(\therefore\) Area of \(\triangle PQR =\frac{1}{2}( PQ )( QR )=\sqrt{3}\) -
Question 80 of 150
80. Question
If \((2,3,9),(5,2,1),(1, \lambda, 8)\) and \((\lambda, 2,3)\) are coplanar, then the product of all possible values of \(\lambda\) is: [JEE Main 2022 (Online) 29th July Evening Shift]
CorrectIncorrectHint
\(\because A(2,3,9), B(5,2,1), C(1, \lambda, 8)\) and \(D (\lambda, 2,3)\) are coplanar.
\(
\therefore\left[\begin{array}{lll}
\overrightarrow{ AB } & \overrightarrow{ AC } & \overrightarrow{ AD }
\end{array}\right]=0
\)
\(
\begin{aligned}
& \left|\begin{array}{ccc}
3 & -1 & -8 \\
-1 & \lambda-3 & -1 \\
\lambda-2 & -1 & -6
\end{array}\right|=0 \\
& \Rightarrow[-6(\lambda-3)-1]-8(1-(\lambda-3)(\lambda-2))+(6+(\lambda-2)=0 \\
& \Rightarrow 3(-6 \lambda+17)-8\left(-\lambda^2+5 \lambda-5\right)+(\lambda+4)=8 \\
& \Rightarrow 8 \lambda^2-57 \lambda+95=0 \\
& \therefore \lambda_1 \lambda_2=\frac{95}{8}
\end{aligned}
\) -
Question 81 of 150
81. Question
If the foot of the perpendicular from the point \(A (-1,4,3)\) on the plane \(P : 2 x+ m y+ n z=4\), is \(\left(-2, \frac{7}{2}, \frac{3}{2}\right)\), then the distance of the point \(A\) from the plane \(P\), measured parallel to a line with direction ratios \(3,-1,-4\), is equal to : [JEE Main 2022 (Online) 29th July Morning Shift]
CorrectIncorrectHint
\(\left(-2, \frac{7}{2}, \frac{3}{2}\right)\) satisfies the plane \(P: 2 x+m y+n z=4\)
\(
-4+\frac{7 m}{2}+\frac{3 n}{2}=4 \Rightarrow 7 m+3 n=16 \dots(i)
\)
Line joining \(A(-1,4,3)\) and \(\left(-2, \frac{7}{2}, \frac{3}{2}\right)\) is perpendicular to
\(
\begin{aligned}
& P: 2 x+m y+n z=4 \\
& \frac{1}{2}=\frac{\frac{1}{2}}{m}=\frac{\frac{3}{2}}{n} \Rightarrow m=1 \& n=3
\end{aligned}
\)
Plane \(P: 2 x+y+3 z=4\)
Distance of \(P\) from \(A(-1,4,3)\) parallel to the line
\(
\frac{x+1}{3}=\frac{y-4}{-1}=\frac{z-3}{-4}: L
\)
for point of intersection of \(P \& L\)
\(
2(3 r-1)+(-r+4)+3(-4 r+3)=4 \Rightarrow r=1
\)
Point of intersection : \((2,3,-1)\)
Required distance \(=\sqrt{3^2+1^2+4^2}=\sqrt{26}\) -
Question 82 of 150
82. Question
Let the lines
\(\frac{x-1}{\lambda}=\frac{y-2}{1}=\frac{z-3}{2}\) and
\(\frac{x+26}{-2}=\frac{y+18}{3}=\frac{z+28}{\lambda}\) be coplanar
and \(P\) be the plane containing these two lines.
Then which of the following points does NOT lie on P? [JEE Main 2022 (Online) 28th July Evening Shift]CorrectIncorrectHint
\(
L_1: \frac{x-1}{\lambda}=\frac{y-2}{1}=\frac{z-3}{2}
\)
through a point \(\vec{a}_1 \equiv(1,2,3)\)
parallel to \(\overrightarrow{b_1} \equiv(\lambda, 1,2)\)
\(
L_2: \frac{x+26}{-2}=\frac{y+18}{3}=\frac{z+28}{\lambda}
\)
through a point \(\vec{a}_2=(-26,-18,-28)\)
parallel to \(\overrightarrow{b_2}=(-2,3,1)\)
If lines are coplanar then, \(\left(\overrightarrow{a_2}-\overrightarrow{a_1}\right) \cdot \overrightarrow{b_1} \times \overrightarrow{b_2}=0\)
\(
\Rightarrow\left|\begin{array}{ccc}
27 & 20 & 31 \\
\lambda & 1 & 2 \\
-2 & 3 & \lambda
\end{array}\right|=0 \Rightarrow \lambda=3
\)
Vector normal to the required plane \(\vec{n}=\overrightarrow{b_1} \times \overrightarrow{b_2}\)
\(
\Rightarrow \vec{n}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \widehat{k} \\
3 & 1 & 2 \\
-2 & 3 & 3
\end{array}\right|=-3 \hat{i}-13 \hat{j}+11 \widehat{k}
\)
Equation of plane
\(
\begin{aligned}
& \equiv((x-1),(y-2),(z-3)) \cdot(-3,-13,11)=0 \\
& \Rightarrow 3 x+13 y-11 z+4=0
\end{aligned}
\)
Checking the option gives \((0,4,5)\) does not lie on the plane. -
Question 83 of 150
83. Question
A plane \(P\) is parallel to two lines whose direction ratios are \(-2,1,-3\) and \(-1,2,-2\) and it contains the point \((2,2,-2)\). Let \(P\) intersect the co-ordinate axes at the points \(A , B , C\) making the intercepts \(\alpha, \beta, \gamma\). If \(V\) is the volume of the tetrahedron \(OABC\), where \(O\) is the origin, and \(p =\alpha+\beta+\gamma\), then the ordered pair \(( V , P )\) is equal to : [JEE Main 2022 (Online) 28th July Evening Shift]
CorrectIncorrectHint
Normal of plane P:
\(
\begin{aligned}
\vec{n} & =\left|\begin{array}{ccc}
i & j & k \\
-2 & 1 & -3 \\
-1 & 2 & -2
\end{array}\right| \\
& =4 i – j -3 k
\end{aligned}
\)
Equation of plane P which passes through (2,2,-2) is
\(
\begin{gathered}
4( x -2)-1( y -2)-3( z +2)=0 \\
4 x -8- y +2-3 z -6=0 \\
4 x – y -3 z =12 \\
\frac{ x }{3}+\frac{ y }{-12}+\frac{ z }{(-4)}=1 \\
\alpha=3, \beta=-12,\gamma=-4 \\
\alpha+\beta+\gamma=-13 \\
\text { Volume }=\frac{1}{6}[\alpha \times \beta] \times \gamma\\
=\frac{1}{6} \times 3 \times 12 \times-4 \\
=24
\end{gathered}
\) -
Question 84 of 150
84. Question
The foot of the perpendicular from a point on the circle \(x^2+y^2=1, z=0\) to the plane \(2 x+3 y+z=6\) lies on which one of the following curves? [JEE Main 2022 (Online) 28th July Morning Shift]
CorrectIncorrectHint
Any point on \(x^2+y^2=1, z=0\) is \(p(\cos \theta, \sin \theta, 0)\)
If foot of perpendicular of \(p\) on the plane \(2 x+3 y+z=6\) is \((h, k, l)\) then
\(
\begin{aligned}
& \frac{h-\cos \theta}{2}=\frac{k-\sin \theta}{3}=\frac{l-0}{1} \\
& =-\left(\frac{2 \cos \theta+3 \sin \theta+0-6}{2^2+3^2+1^2}\right)=r \text { (let) } \\
& h=2 r+\cos \theta, k=3 r+\sin \theta, l=r
\end{aligned}
\)
Hence, \(h-2 l=\cos \theta\) and \(k-3 l=\sin \theta\)
Hence, \((h-2 l)^2+(k-3 l)^2=1\)
When \(l=6-2 h-3 k\)
Hence required locus is
\(
\begin{aligned}
& (x-2(6-2 x-3 y))^2+(y-3(6-2 x-3 y))^2=1 \\
& \Rightarrow(5 x+6 y-12)^2+4(3 x+5 y-9)^2=1, z=6-2 x-3 y
\end{aligned}
\) -
Question 85 of 150
85. Question
If the length of the perpendicular drawn from the point \(P(a, 4,2), a >0\) on the line \(\frac{x+1}{2}=\frac{y-3}{3}=\frac{z-1}{-1}\) is \(2 \sqrt{6}\) units and \(Q\left(\alpha_1, \alpha_2, \alpha_3\right)\) is the image of the point \(P\) in this line, then \(a +\sum_{i=1}^3 \alpha_i\) is equal to : [JEE Main 2022 (Online) 27th July Evening Shift]
CorrectIncorrectHint
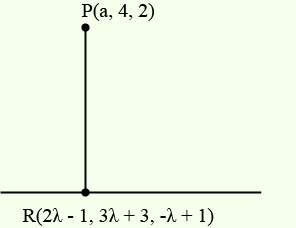
\(PR\) is perpendicular to given line, so
\(
\begin{aligned}
& 2(2 \lambda-1-a)+3(3 \lambda-1)-1(-\lambda-1)=0 \\
& \Rightarrow a=7 \lambda-2
\end{aligned}
\)
Now,
\(
\begin{aligned}
& \because P R=2 \sqrt{6} \\
& \Rightarrow(-5 \lambda+1)^2+(3 \lambda-1)^2+(\lambda+1)^2=24 \\
& \Rightarrow 5 \lambda^2-2 \lambda-3=0 \Rightarrow \lambda=1 \text { or }-\frac{3}{5} \\
& \because a>0 \text { so } \lambda=1 \text { and } a=5 \\
& \text { Now } \left.\sum_{i=1}^3 \alpha_i=2 \text { (Sum of co-ordinate of } R \right)-(\text { Sum of coordinates of } P ) \\
& =2(7)-11=3 \\
& a+\sum_{i=1}^3 \alpha_i=5+3=8
\end{aligned}
\) -
Question 86 of 150
86. Question
If the line of intersection of the planes \(a x+b y=3\) and \(a x+b y+c z=0, a >0\) makes an angle \(30^{\circ}\) with the plane \(y-z+2=0\), then the direction cosines of the line are : [JEE Main 2022 (Online) 27th July Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& P_1: a x+b y+0 z=3, \text { normal vector }: \vec{n}_1=(a, b, 0) \\
& P_2: a x+b y+c z=0, \text { normal vector }: \vec{n}_2=(a, b, c) \\
& \text { Vector parallel to the line of intersection }=\vec{n}_1 \times \vec{n}_2 \\
& \vec{n}_1 \times \vec{n}_2=(b c,-a c, 0)
\end{aligned}
\)
Vector normal to \(0 . x+y-z+2=0\) is \(\vec{n}_3=(0,1,-1)\)
Angle between line and plane is \(30^{\circ}\)
\(
\begin{aligned}
& \Rightarrow\left|\frac{0-a c+0}{\sqrt{b^2 c^2+c^2 a^2} \sqrt{2}}\right|=\frac{1}{2} \\
& \Rightarrow a^2=b^2
\end{aligned}
\)
Hence, \(\vec{n}_1 \times \vec{n}_2=(a c,-a c, 0)\)
Direction ratios \(=\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}, 0\right)\) -
Question 87 of 150
87. Question
If the plane \(P\) passes through the intersection of two mutually perpendicular planes \(2 x+k y-5 z=1\) and \(3 k x-k y+z=5, k<3\) and intercepts a unit length on positive \(x\)-axis, then the intercept made by the plane \(P\) on the \(y\)-axis is : [JEE Main 2022 (Online) 27th July Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& P_1: 2 x+k y-5 z=1 \\
& P_2: 3 k x-k y+z=5 \\
& \because P_1 \perp P_2 \Rightarrow 6 k-k^2+5=0 \\
& \Rightarrow k=1,5 \\
& \because k<3 \\
& \therefore k=1 \\
& P_1: 2 x+y-5 z=1 \\
& P_2: 3 x-y+z=5 \\
& P:(2 x+y-5 z-1)+\lambda(3 x-y+z-5)=0 \\
& \text { Positive x-axis intercept }=1 \\
& \Rightarrow \frac{1+5 \lambda}{2+3 \lambda}=1 \\
& \Rightarrow \lambda=\frac{1}{2} \\
& \therefore P: 7 x+y-4 z=7 \\
& \text { y intercept }=7 .
\end{aligned}
\) -
Question 88 of 150
88. Question
A vector \(\vec{a}\) is parallel to the line of intersection of the plane determined by the vectors \(\hat{i}, \hat{i}+\hat{j}\) and the plane determined by the vectors \(\hat{i}-\hat{j}, \hat{i}+\hat{k}\). The obtuse angle between \(\vec{a}\) and the vector \(\vec{b}=\hat{i}-2 \hat{j}+2 \hat{k}\) is : [JEE Main 2022 (Online) 26th July Evening Shift]
CorrectIncorrectHint
If \(\vec{n}_1\) is a vector normal to the plane determined by \(\hat{i}\) and \(\hat{i}+\hat{j}\) then
\(
\vec{n}_1=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \widehat{k} \\
1 & 0 & 0 \\
1 & 1 & 0
\end{array}\right|=\widehat{k}
\)
If \(\overrightarrow{n_2}\) is a vector normal to the plane determined by \(\hat{i}-\hat{j}\) and \(\hat{i}+\hat{k}\) then
\(
\bar{n}_2=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \widehat{k} \\
1 & -1 & 0 \\
1 & 0 & 1
\end{array}\right|=-\hat{i}-\hat{j}+\widehat{k}
\)
Vector \(\vec{a}\) is parallel to \(\vec{n}_1 \times \vec{n}_2\)
i.e. \(\vec{a}\) is parallel to \(\left|\begin{array}{ccc}\hat{i} & \hat{j} & \widehat{k} \\ 0 & 0 & 1 \\ -1 & -1 & 1\end{array}\right|=\hat{i}-\hat{j}\)
Given \(\vec{b}=\hat{i}-2 \hat{j}+2 \widehat{k}\)
Cosine of acute angle between
\(
\vec{a} \text { and } \vec{b}=\left|\frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot|\vec{b}|}\right|=\frac{1}{\sqrt{2}}
\)
Obtuse angle between \(\vec{a}\) and \(\vec{b}=\frac{3 \pi}{4}\) -
Question 89 of 150
89. Question
The length of the perpendicular from the point \((1,-2,5)\) on the line passing through \((1,2,4)\) and parallel to the line \(x+y-z=0=x-2 y+3 z-5\) is : [JEE Main 2022 (Online) 26th July Morning Shift]
CorrectIncorrectHint
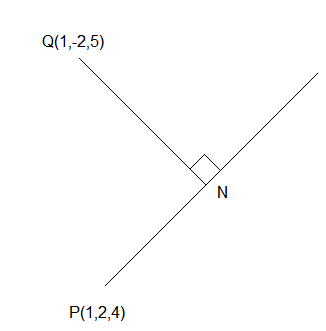
The line \(x+y-z=0=x-2 y+3 z-5\) is parallel to the vector
\(
\vec{b}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \widehat{k} \\
1 & 1 & -1 \\
1 & -2 & 3
\end{array}\right|=(1,4,-3)
\)
Equation of the line through \(P(1,2,4)\) and parallel to \(\vec{b}\)
\(
\frac{x-1}{1}=\frac{y-2}{-4}=\frac{z-4}{-3}
\)
Let \(N \equiv(\lambda+1,-4 \lambda+2,-3 \lambda+4)\)
\(
\overrightarrow{Q N}=(\lambda,-4 \lambda+4,-3 \lambda-1)
\)
\(\overrightarrow{Q N}\) is perpendicular to \(\vec{b}\)
\(
\begin{aligned}
& \Rightarrow(\lambda,-4 \lambda+4,-3 \lambda-1) \cdot(1,4,-3)=0 \\
& \Rightarrow \lambda=\frac{1}{2}
\end{aligned}
\)
Hence \(\overrightarrow{Q N}=\left(\frac{1}{2}, 2, \frac{-5}{2}\right)\) and \(|\overrightarrow{Q N}|=\sqrt{\frac{21}{2}}\) -
Question 90 of 150
90. Question
A plane \(E\) is perpendicular to the two planes \(2 x-2 y+z=0\) and \(x-y+2 z=4\), and passes through the point \(P(1,-1,1)\). If the distance of the plane \(E\) from the point \(Q(a, a, 2)\) is \(3 \sqrt{2}\), then \((P Q)^2\) is equal to : [JEE Main 2022 (Online) 25th July Evening Shift]
CorrectIncorrectHint
Let equation of plane be \(a(x-1)+b(y+1)+c(z-1)=0\)…..(1)
It is perpendicular to the given two planes
\(
\begin{aligned}
& 2 a-2 b+c=0 \\
& a-b+2 c=0 \\
& \Rightarrow \frac{a}{3}=\frac{b}{3}=\frac{c}{0}
\end{aligned}
\)
Equation of plane be \(x+y=0\)
Now \(\frac{|a+a|}{\sqrt{2}}=3 \sqrt{2} \Rightarrow|2 a|=6 \Rightarrow a= \pm 3\)
\(
\begin{aligned}
& P(3,3,2) \text { or } P(-3,-3,2), Q(1,-1,1) \\
& P Q^2=(3-1)^2+(3+1)^2+(2-1)^2=21
\end{aligned}
\) -
Question 91 of 150
91. Question
The shortest distance between the lines \(\frac{x+7}{-6}=\frac{y-6}{7}=z\) and \(\frac{7-x}{2}=y-2=z-6\) is : [JEE Main 2022 (Online) 25th July Evening Shift]
CorrectIncorrectHint
\(
L_1: \frac{x+7}{6}=\frac{y-6}{7}=\frac{z-0}{1}
\)
Any point on it \(\vec{a}_1(-7,6,0)\) and \(L _1\) is parallel to \(\vec{b}_1(-6,7,1)\) \(L_2: \frac{x-7}{-2}=\frac{y-2}{1}=\frac{z-6}{1}\)
Any point on it \(\vec{a}_2(7,2,6)\) and \(L _2\) is parallel to \(\vec{b}_2(-2,1,1)\)
Shortest distance between \(L _1\) and \(L _2\)
\(
=\left|\frac{\left.\left.\overrightarrow{\left(a_2\right.}-\overrightarrow{a_1}\right) \cdot \overrightarrow{\left(b_1\right.} \times \overrightarrow{b_2}\right)}{\left|\overrightarrow{b_1} \times \overrightarrow{b_2}\right|}\right|
\)
\(
=\left|\frac{(-14,4,-6) \cdot(3,2,4)}{\sqrt{9+4+16}}\right|
\)
\(
=2 \sqrt{29} .
\) -
Question 92 of 150
92. Question
Let \(P\) be the plane containing the straight line \(\frac{x-3}{9}=\frac{y+4}{-1}=\frac{z-7}{-5}\) and perpendicular to the plane containing the straight lines \(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}\) and \(\frac{x}{3}=\frac{y}{7}=\frac{z}{8}\). If \(d\) is the distance of \(P\) from the point \((2,-5,11)\), then \(d ^2\) is equal to : [JEE Main 2022 (Online) 25th July Morning Shift]
CorrectIncorrectHint
Let \(\langle a, b, c\rangle\) be direction ratios of plane containing lines \(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}\) and \(\frac{x}{3}=\frac{y}{7}=\frac{z}{8}\).
\(
\therefore \quad 2 a+3 b+5 c=0 \quad \ldots \text { (i) }
\)
and \(3 a+7 b+8 c=0 \quad \ldots(ii)\)
from eq. (i) and (ii) : \(\frac{a}{24-35}=\frac{b}{15-16}=\frac{c}{14-9}\)
\(\therefore\) D. R’s. of plane are \(<11,1,-5>\)
Let \(D\). R’s of plane \(P\) be \(<a_1, b_1, c_1>\) then.
\(
11 a_1+b_1-5 c_1=0 \dots(iii)
\)
and \(9 a_1-b_1-5 c_1=0 \dots(iv)\)
From eq. (iii) and (iv) :
\(
\frac{a_1}{-5-5}=\frac{b_1}{-45+55}=\frac{c_1}{-11-9}
\)
\(\therefore\) D.R’s of plane \(P\) are \(\langle 1,-1,2\rangle\)
Equation plane \(P\) is : \(1(x-3)-1(y+4)+2(z-7)=0\)
\(
\Rightarrow x-y+2 z-21=0
\)
Distance from point \((2,-5,11)\) is \(d=\frac{|2+5+22-2|}{\sqrt{6}}\)
\(
\therefore d^2=\frac{32}{3}
\) -
Question 93 of 150
93. Question
The distance of the point \((3,2,-1)\) from the plane \(3 x-y+4 z+1=0\) along the line \(\frac{2-x}{2}=\frac{y-3}{2}=\frac{z+1}{1}\) is equal to : [JEE Main 2022 (Online) 30th June Morning Shift]
CorrectIncorrectHint
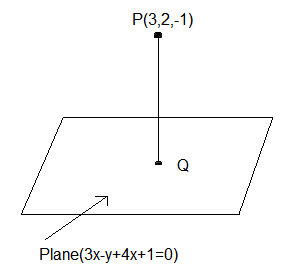
Line \(PQ\) is parallel to line \(\frac{2-x}{2}=\frac{y-3}{2}=\frac{z+1}{1}\)
\(\therefore D R\) of \(P Q=D R\) of line \(=<-2,2,1>\)
\(\therefore\) Equation of line \(P Q\) passing through \(P(3,2,-1)\) and \(D R=<-2,2,1\rangle\) is \(\frac{x-3}{-2}=\frac{y-2}{2}=\frac{z+1}{1}\)
Any General point on line \(P Q=\left(x_1, y_1, z_1\right)\)
\(
\begin{aligned}
& \therefore \frac{x_1-3}{-2}=\frac{y_1-2}{2}=\frac{z_1+1}{1}=\lambda \\
& \Rightarrow x_1=-2 \lambda+3 \\
& y_1=2 \lambda+2 \\
& z_1=\lambda-1
\end{aligned}
\)
\(
\therefore \text { Point } Q =(-2 \lambda+3,2 \lambda+2, \lambda-1)
\)
Point \(Q\) lies on the plane \(3 x-y+4 z+1=0\). So point \(Q\) satisfy the equation.
\(
\begin{aligned}
& 3(-2 \lambda+3)-(2 \lambda+2)+4(\lambda-1)+1=0 \\
& \Rightarrow-6 \lambda+9-2 \lambda-2+4 \lambda-4+1=0 \\
& \Rightarrow-4 \lambda+4=0 \\
& \Rightarrow \lambda=1 \\
& \therefore \text { Point } Q(-2 \times 1+3,2 \times 1+2,1-1) \\
& =(1,4,0)
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \text { Distance of the point } P (3,2,-1) \text { from the plane }=\text { Length of } PQ \\
& =\sqrt{(3-1)^2+(2-4)^2+(-1-0)^2} \\
& =\sqrt{2^2+(-2)^2+(-1)^2} \\
& =\sqrt{4+4+1} \\
& =\sqrt{9} \\
& =3
\end{aligned}
\) -
Question 94 of 150
94. Question
Let \(\frac{x-2}{3}=\frac{y+1}{-2}=\frac{z+3}{-1}\) lie on the plane \(p x-q y+z=5\), for some \(p , q \in R\). The shortest distance of the plane from the origin is : [JEE Main 2022 (Online) 29th June Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{x-2}{3}=\frac{y+1}{-2}=\frac{z+3}{-1}=\lambda \\
& (3 \lambda+2,-2 \lambda-1,-\lambda-3) \text { lies on plane } p x-q y+z=5 \\
& p(3 \lambda+2)-q(-2 \lambda-1)+(-\lambda-3)=5 \\
& \lambda(3 p+2 q-1)+(2 p+q-8)=0 \\
& 3 p+2 q-1=0\} p=15 \\
& 2 p+q-8=0\} q=-22
\end{aligned}
\)
Equation of plane \(15 x+22 y+z-5=0\)
Shortest distance from origin \(=\frac{|0+0+0-5|}{\sqrt{15^2+22^2+1}}\)
\(
\begin{aligned}
& =\frac{5}{\sqrt{710}} \\
& =\sqrt{\frac{5}{142}}
\end{aligned}
\) -
Question 95 of 150
95. Question
Let \(Q\) be the mirror image of the point \(P(1,2,1)\) with respect to the plane \(x+2 y+2 z=\) 16. Let \(T\) be a plane passing through the point \(Q\) and contains the line \(\vec{r}=-\widehat{k}+\lambda(\hat{i}+\hat{j}+2 \widehat{k}), \lambda \in R\). Then, which of the following points lies on \(T\) ? [JEE Main 2022 (Online) 29th June Evening Shift]
CorrectIncorrectHint
Given: Plane: \(x+2 y+2 z-16=0\)
And line: \(\vec{r}=-\widehat{k}+\lambda(\hat{i}+\hat{j}+2 \widehat{k})\)
So, equation of line in symmetric form is \(\frac{x-0}{1}=\frac{y-0}{1}=\frac{z+1}{2}\)
Now, mirror image of \(p(1,2,1)\) in plane \(x+2 y+2 z-16=0\) is
\(
\begin{aligned}
& \Rightarrow \frac{x-1}{1}=\frac{y-2}{2}=\frac{z-1}{2}=-2\left(\frac{1+2(2)+2(1)-16}{1^2+2^2+2^2}\right) \\
& \Rightarrow \frac{x-1}{1}=\frac{y-2}{2}=\frac{z-1}{2}=2 \\
& \Rightarrow x =3, y =6, z =5
\end{aligned}
\)
\(\therefore\) Coordinates of point \(Q\) are \((3,6,5)\)
Now, equation of plane \(T\) is \(\left|\begin{array}{ccc}x & y & z+1 \\ 1 & 1 & 2 \\ 3 & 6 & 6\end{array}\right|=0\)
\(
\begin{aligned}
& \Rightarrow x(6-12)-y(6-6)+(z+1)(6-3)=0 \\
& \Rightarrow-6 x+3 z+3=0 \\
& \Rightarrow 2 x-z-1=0
\end{aligned}
\)
So, \((1,2,1)\) lies on plane \(T\). -
Question 96 of 150
96. Question
If the mirror image of the point \((2,4,7)\) in the plane \(3 x-y+4 z=2\) is \((a, b, c)\), then \(2 a+\) \(b+2 c\) is equal to : [JEE Main 2022 (Online) 29th June Morning Shift]
CorrectIncorrectHint
We know mirror image of point \(\left(x_1, y_1, z_1\right)\) in the plane \(a x+b y+c z=d\)
\(
\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}=\frac{-2\left(a x_1+b y_1+c z_1-d\right)}{a^2+b^2+c^2}
\)
Here given point \((2,4,7)\) and plane \(3 x-y+4 z=2\) then mirror image is
\(
\begin{aligned}
& \frac{x-2}{3}=\frac{y-4}{-1}=\frac{z-7}{4}=\frac{-2(6-4+28-2)}{9+1+16} \\
& \Rightarrow \frac{x-2}{3}=\frac{y-4}{-1}=\frac{z-7}{4}=-\frac{28}{13} \\
& \therefore x=-\frac{58}{13}=a \\
& y=\frac{80}{13}=b \\
& z=-\frac{21}{13}=c \\
& \therefore 2 a+b+2 c \\
& =2\left(-\frac{58}{13}\right)+\frac{80}{13}+2\left(-\frac{21}{13}\right) \\
& =\frac{-116+80-42}{13}=\frac{-78}{13}=-6
\end{aligned}
\) -
Question 97 of 150
97. Question
Let the plane \(a x+b y+c z=d\) pass through \((2,3,-5)\) and is perpendicular to the planes \(2 x+y-5 z=10\) and \(3 x+5 y-7 z=12\). If \(a, b, c, d\) are integers \(d>0\) and gcd ( \(|a|,|b|,|c|\), d) \(=1\), then the value of \(a+7 b+c+20 d\) is equal to : [JEE Main 2022 (Online) 28th June Evening Shift]
CorrectIncorrectHint
Equation of pane through point \((2,3,-5)\) and perpendicular to planes \(2 x+y-5 z=10\) and \(3 x+5 y-7 z=12\) is
\(
\left|\begin{array}{ccc}
x-2 & y-3 & z+5 \\
2 & 1 & -5 \\
3 & 5 & -7
\end{array}\right|=0
\)
\(\therefore\) Equation of plane is \((x-2)(-7+25)-(y-3)\)
\(
\begin{aligned}
& (-14+15)+(z+5) \cdot 7=0 \\
& \therefore 18 x-y+7 z+2=0 \\
& \Rightarrow 18 x-y+7 z=-2 \\
& \therefore-18 x+y-7 z=2
\end{aligned}
\)
On comparing with \(a x+b y+c z=d\) where \(d >0\) is \(a =-18, b =1, c =-7, d =2\)
\(
\therefore a+7 b+c+20 d=22
\) -
Question 98 of 150
98. Question
If two distinct point \(Q , R\) lie on the line of intersection of the planes \(-x+2 y-z=0\) and \(3 x-5 y+2 z=0\) and \(P Q=P R=\sqrt{18}\) where the point \(P\) is \((1,-2,3)\), then the area of the triangle \(P Q R\) is equal to : [JEE Main 2022 (Online) 28th June Morning Shift]
CorrectIncorrectHint
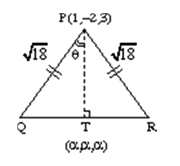
\(
\begin{aligned}
& -x+2 y-z=0 \\
& 3 x-5 y+2 z=0 \\
& \vec{n}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
-1 & 2 & -1 \\
3 & -5 & 2
\end{array}\right| \\
& =\hat{i}(-1)-\hat{j}(1)+\hat{k}(-1) \\
& \vec{n}=-\hat{i}-\hat{j}-\hat{k}
\end{aligned}
\)
Equation of LOI is \(\frac{x}{1}=\frac{y}{1}=\frac{z}{1}\)
DR: of \(PT \rightarrow \alpha-1, \alpha+2, \alpha-3\)
\(DR\) : of \(QR \rightarrow \quad 1, \quad 1,1\)
\(
\begin{aligned}
& \Rightarrow(\alpha-1) \times 1+(\alpha+2) \times 1+(\alpha-3) \times 1=0 \\
& 3 \alpha=2 \\
& \alpha=\frac{2}{3}
\end{aligned}
\)
\(
\begin{aligned}
& PT ^2=\frac{1}{9}+\frac{64}{9}+\frac{49}{9} \\
& PT ^2=\frac{114}{9} \\
& PT =\frac{\sqrt{114}}{3}
\end{aligned}
\)
\(
\cos \theta=\frac{\sqrt{114}}{3} \times \frac{1}{3 \sqrt{2}}=\frac{\sqrt{57}}{9}=\frac{\sqrt{19 \times 3}}{3 \times 3}=\frac{\sqrt{19}}{3 \sqrt{3}}
\)
\(
\begin{aligned}
& \cos 2 \theta=\frac{2 \times 19}{27}-1=\frac{11}{27} \\
& \sin 2 \theta=\sqrt{1-\left(\frac{11}{27}\right)^2}=\frac{\sqrt{38} \sqrt{16}}{27}=\frac{4}{27} \sqrt{38}
\end{aligned}
\)
\(
\begin{aligned}
& \text { Area }=\frac{1}{2} \times \sqrt{18} \sqrt{18} \times \frac{4}{27} \sqrt{38} \\
& =\frac{18}{2} \times \frac{4}{27} \sqrt{38}=\frac{36}{27} \sqrt{38}=\frac{4}{3} \sqrt{38}
\end{aligned}
\) -
Question 99 of 150
99. Question
The acute angle between the planes \(P_1\) and \(P_2\), when \(P_1\) and \(P_2\) are the planes passing through the intersection of the planes \(5 x+8 y+13 z-29=0\) and \(8 x-7 y+z-20=0\) and the points \((2,1,3)\) and \((0,1,2)\), respectively, is : [JEE Main 2022 (Online) 28th June Morning Shift]
CorrectIncorrectHint
Family of Plane’s equation can be given by
\(
(5+8 \lambda) x+(8-7 \lambda) y+(13+\lambda) z-(29+20 \lambda)=0
\)
\(P_1\) passes through \((2,1,3)\)
\(
\begin{aligned}
& \Rightarrow(10+16 \lambda)+(8-7 \lambda)+(39+3 \lambda)-(29+20 \lambda)=0 \\
& \Rightarrow-8 \lambda+28=0 \Rightarrow \lambda=\frac{7}{2}
\end{aligned}
\)
d.r, s of normal to \(P _1\)
\(
\left\langle 33, \frac{-33}{2}, \frac{33}{2}\right\rangle \text { or }\left\langle 1,-\frac{1}{2}, \frac{1}{2}\right\rangle
\)
\(P_2\) passes through \((0,1,2)\)
\(
\begin{aligned}
& \Rightarrow 8-7 \lambda+26+2 \lambda-(29+20 \lambda)=0 \\
& \Rightarrow 5-25 \lambda=0 \\
& \Rightarrow \lambda=\frac{1}{5}
\end{aligned}
\)
d.r, \(s\) of normal to \(P_2\)
\(
\left\langle\frac{33}{5}, \frac{33}{5}, \frac{66}{5}\right\rangle \text { or }\langle 1,1,2\rangle
\)
Angle between normals
\(
\begin{aligned}
& =\frac{\left(\hat{i}-\frac{1}{2} \hat{j}+\frac{1}{2} \hat{k}\right) \cdot(\hat{i}+\hat{j}+2 \hat{k})}{\frac{\sqrt{3}}{2}} \\
& \cos \theta=\frac{1-\frac{1}{2}+1}{3}=\frac{1}{2} \\
& \theta=\frac{\pi}{3} \\
&
\end{aligned}
\) -
Question 100 of 150
100. Question
Let the plane \(P: \vec{r} \cdot \vec{a}=d\) contain the line of intersection of two planes \(\vec{r} \cdot(\hat{i}+3 \hat{j}-\widehat{k})=6\) and \(\vec{r} \cdot(-6 \hat{i}+5 \hat{j}-\widehat{k})=7\). If the plane \(P\) passes through the point \(\left(2,3, \frac{1}{2}\right)\), then the value of \(\frac{|13 \vec{a}|^2}{|d|^2}\) is equal to: [JEE Main 2022 (Online) 28th June Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& P_1: x+3 y-z=6 \\
& P_2:-6 x+5 y-z=7
\end{aligned}
\)
Family of planes passing through line of intersection of \(P_1\) and \(P_2\) is given by \(x(1-6 \lambda)+y(3+5 \lambda)+z(-1-\lambda)-(6+7 \lambda)=0\)
It passes through \(\left(2,3, \frac{1}{2}\right)\)
\(
\begin{aligned}
& \text { So, } 2(1-6 \lambda)+3(3+5 \lambda)+\frac{1}{2}(-1-\lambda)-(6+7 \lambda)=0 \\
& \Rightarrow 2-12 \lambda+9+15 \lambda-\frac{1}{2}-\frac{\lambda}{2}-6-7 \lambda=0 \\
& \Rightarrow \frac{9}{2}-\frac{9 \lambda}{2}=0 \Rightarrow \lambda=1
\end{aligned}
\)
Required plane is
\(
\begin{aligned}
& -5 x+8 y-2 z-13=0 \\
& \text { Or } \vec{r} \cdot(-5 \hat{i}+8 \hat{j}-2 \widehat{k})=13 \\
& \frac{|13 \vec{a}|^2}{|d|^2}=\frac{13^2}{(13)^2} \cdot|\vec{a}|^2=93
\end{aligned}
\) -
Question 101 of 150
101. Question
Let the foot of the perpendicular from the point \((1,2,4)\) on the line \(\frac{x+2}{4}=\frac{y-1}{2}=\frac{z+1}{3}\) be \(P\). Then the distance of \(P\) from the plane \(3 x+4 y+12 z+23=0\) is : [JEE Main 2022 (Online) 27th June Evening Shift]
CorrectIncorrectHint
\(
L: \frac{x+2}{4}=\frac{y-1}{2}=\frac{z+1}{3}=t
\)
Let \(P=(4 t-2,2 t+1,3 t-1)\)
\(\because P\) is the foot of perpendicular of \((1,2,4)\)
\(
\begin{aligned}
& \therefore 4(4 t-3)+2(2 t-1)+3(3 t-5)=0 \\
& \Rightarrow 29 t=29 \Rightarrow t=1 \\
& \therefore P =(2,3,2)
\end{aligned}
\)
Now, distance of \(P\) from the plane \(3 x+4 y+12 z+23=0\), is
\(
\left|\frac{6+12+24+23}{\sqrt{9+16+144}}\right|=\frac{65}{13}=5
\) -
Question 102 of 150
102. Question
The shortest distance between the lines \(\frac{x-3}{2}=\frac{y-2}{3}=\frac{z-1}{-1}\) and \(\frac{x+3}{2}=\frac{y-6}{1}=\frac{z-5}{3}\), is : [JEE Main 2022 (Online) 27th June Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& L_1: \frac{x-3}{2}=\frac{y-2}{3}=\frac{z-1}{-1} \\
& L_2: \frac{x+3}{2}=\frac{y-6}{1}=\frac{z-5}{3} \\
& \text { Now, } \vec{p} \times \vec{q}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
2 & 3 & -1 \\
2 & 1 & 3
\end{array}\right|=10 \hat{i}-8 \hat{j}-4 \widehat{k} \\
& \text { and } \overrightarrow{a_2}-\overrightarrow{a_1}=6 \hat{i}-4 \hat{j}-4 \widehat{k} \\
& \therefore S . D .=\left|\frac{60+32+16}{\sqrt{100+64+16}}\right|=\frac{108}{\sqrt{180}}=\frac{18}{\sqrt{5}}
\end{aligned}
\) -
Question 103 of 150
103. Question
If two straight lines whose direction cosines are given by the relations \(l+m-n=0,3 l^2+m^2+c n l=0\) are parallel, then the positive value of \(c\) is : [JEE Main 2022 (Online) 27th June Morning Shift]
CorrectIncorrectHint
Given that the direction cosines satisfy \(l+m-n=0\), we find that \(n=l+m\).
The other equation is \(3 l^2+m^2+c n l=0\), and substituting \(n=l+m\) gives \(3 l^2+m^2+c l(l+m)=0\).
This simplifies to \((3+c) l^2+c l m+m^2=0\).
As the lines are parallel, they share the same direction ratios, so we can express \(l\) in terms of \(m\), say \(l=k m\). Substituting this into our equation gives
\(
(3+c)(k m)^2+c k m^2+m^2=0 \text {. }
\)
This simplifies to \(m^2\left[k^2(3+c)+k c+1\right]=0\).
Since \(m \neq 0\), we must have \(k^2(3+c)+k c+1=0\). Here, we consider the ratio \(k=\frac{l}{m}\) to be constant, since the lines are parallel. The equation then becomes a quadratic equation in \(k\).
As the lines are parallel, the discriminant of the quadratic equation must be equal to zero for the equation to have equal roots. Hence, the discriminant
\(
D=\left(c^2-4(3+c)\right)=0 \text {. }
\)
Solving this quadratic equation gives \(c^2-4 c-12=0\).
Factoring this equation gives \((c-6)(c+2)=0\).
Solving for \(c\) gives \(c=6,-2\).
However, we are looking for the positive value of \(c\), so \(c=6\).
Therefore, the correct answer is 6. -
Question 104 of 150
104. Question
If the plane \(2 x+y-5 z=0\) is rotated about its line of intersection with the plane \(3 x-y+4 z-7=0\) by an angle of \(\frac{\pi}{2}\), then the plane after the rotation passes through the point : [JEE Main 2022 (Online) 26th June Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& P_1: 2 x+y-52=0, P_2: 3 x-y+4 z-7=0 \\
& \text { Family of planes } P _1 \text { and } P _2 \\
& P: P_1+\lambda P_2 \\
& \therefore P:(2+3 \lambda) x+(1-\lambda) y+(-5+4 \lambda) z-7 \lambda=0 \\
& \because P \perp P_1 \\
& \therefore 4+6 \lambda+1-\lambda+25-20 \lambda=0 \\
& \lambda=2 \\
& \therefore P: 8 x-y+32-14=0
\end{aligned}
\)
It passes through the point \((1,0,2)\) -
Question 105 of 150
105. Question
If the lines \(\vec{r}=(\hat{i}-\hat{j}+\widehat{k})+\lambda(3 \hat{j}-\widehat{k})\) and \(\vec{r}=(\alpha \hat{i}-\hat{j})+\mu(2 \hat{i}-3 \hat{k})\) are co-planar, then the distance of the plane containing these two lines from the point ( \(\alpha\), \(0,0)\) is : [JEE Main 2022 (Online) 26th June Evening Shift]
CorrectIncorrectHint
\(\because\) Both lines are coplanar, so
\(
\begin{aligned}
& \left|\begin{array}{ccc}
\alpha-1 & 0 & -1 \\
0 & 3 & -1 \\
2 & 0 & -3
\end{array}\right|=0 \\
& \Rightarrow \alpha=\frac{5}{3}
\end{aligned}
\)
Equation of plane containing both lines
\(
\begin{aligned}
& \left|\begin{array}{ccc}
x-1 & y+1 & z-1 \\
0 & 3 & -1 \\
2 & 0 & -3
\end{array}\right|=0 \\
& \Rightarrow 9 x+2 y+6 z=13
\end{aligned}
\)
So, distance of \(\left(\frac{5}{3}, 0,0\right)\) from this plane
\(
=\frac{2}{\sqrt{81+4+36}}=\frac{2}{11}
\) -
Question 106 of 150
106. Question
Let \(\vec{a}=\hat{i}+\hat{j}+2 \widehat{k}, \vec{b}=2 \hat{i}-3 \hat{j}+\widehat{k}\) and \(\vec{c}=\hat{i}-\hat{j}+\widehat{k}\) be three given vectors. Let \(\vec{v}\) be a vector in the plane of \(\vec{a}\) and \(\vec{b}\) whose projection on \(\vec{c}\) is \(\frac{2}{\sqrt{2}}\). If \(\vec{v}\). \(\hat{j}=7\), then \(\vec{v} \cdot(\hat{i}+\widehat{k}) \text { is equal to: }\) [JEE Main 2022 (Online) 26th June Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Let } \vec{v}=\lambda_1 \vec{a}+\lambda_2 \vec{b} \text {, where } \lambda_1, \lambda_2 \in R . \\
& =\left(\lambda_1+2 \lambda_2\right) \hat{i}+\left(\lambda_1-3 \lambda_2\right) \hat{j}+\left(2 \lambda_1+\lambda_2\right) \widehat{k} \\
& \because \text { Projection of } \vec{v} \text { on } \vec{c} \text { is } \frac{2}{\sqrt{3}} \\
& \therefore \frac{\lambda_1+2 \lambda_2-\lambda_1+3 \lambda_2+2 \lambda_1+\lambda_2}{\sqrt{3}}=\frac{2}{\sqrt{3}} \\
& \therefore \lambda_1+3 \lambda_2=1 \ldots . \text { (i) }
\end{aligned}
\)
\(
\text { and } \vec{v} . \hat{j}=7 \Rightarrow \lambda_1-3 \lambda_2=7 \text {.. } \dots(ii)
\)
from equation (i) and (ii)
\(
\begin{aligned}
& \lambda_1=4, \lambda_2=-1 \\
& \therefore \vec{v}=2 \hat{i}+7 \hat{j}+7 \widehat{k} \\
& \therefore \vec{v} \cdot(\hat{i}+\widehat{k})=2+7 \\
& =9
\end{aligned}
\) -
Question 107 of 150
107. Question
If the two lines \(l_1: \frac{x-2}{3}=\frac{y+1}{-2}, z=2\) and \(l_2: \frac{x-1}{1}=\frac{2 y+3}{\alpha}=\frac{z+5}{2}\) are perpendicular, then an angle between the lines \(l_2\) and \(l_3: \frac{1-x}{3}=\frac{2 y-1}{-4}=\frac{z}{4}\) is : [JEE Main 2022 (Online) 26th June Morning Shift]
CorrectIncorrectHint
\(\because L _1\) and \(L _2\) are perpendicular, so
\(
\begin{aligned}
& 3 \times 1+(-2)\left(\frac{\alpha}{2}\right)+0 \times 2=0 \\
& \Rightarrow \alpha=3
\end{aligned}
\)
Now angle between \(I_2\) and \(I_3\),
\(
\begin{aligned}
& \cos \theta=\frac{1(-3)+\frac{\alpha}{2}(-2)+2(4)}{\sqrt{1+\frac{\alpha^2}{4}+4 \sqrt{9+4+16}}} \\
& \Rightarrow \cos \theta=\frac{2}{\frac{29}{2}} \Rightarrow \theta=\cos ^{-1}\left(\frac{4}{29}\right)=\sec ^{-1}\left(\frac{29}{4}\right)
\end{aligned}
\) -
Question 108 of 150
108. Question
Let the plane \(2 x+3 y+z+20=0\) be rotated through a right angle about its line of intersection with the plane \(x-3 y+5 z=8\). If the mirror image of the point \(\left(2,-\frac{1}{2}, 2\right)\) in the rotated plane is \(B(a, b, c)\), then : [JEE Main 2022 (Online) 26th June Morning Shift]
CorrectIncorrectHint
Consider the equation of plane,
\(
\begin{aligned}
& P:(2 x+3 y+z+20)+\lambda(x-3 y+5 z-8)=0 \\
& P:(2+\lambda) x+3(3-3 \lambda) y+1(1+5 \lambda) z+(20-8 \lambda)=0
\end{aligned}
\)
\(\because\) Plane \(P\) is perpendicular to \(2 x+3 y+z+20=0\)
So, \(4+2 \lambda+9-9 \lambda+1+5 \lambda=0\)
\(
\begin{aligned}
& \Rightarrow \lambda=7 \\
& P: 9 x-18 y+36 z-36=0
\end{aligned}
\)
or \(P: x-2 y+4 z=4\)
If image of \(\left(2,-\frac{1}{2}, 2\right)\) in plane \(P\) is \(( a , b , c )\) then
\(
\frac{a-2}{1}=\frac{b+\frac{1}{2}}{-2}=\frac{c-2}{4}
\)
and \(\left(\frac{a+2}{2}\right)-2\left(\frac{b-\frac{1}{2}}{2}\right)+4\left(\frac{c+2}{2}\right)=4\)
Clearly \(a=\frac{4}{3}, b=\frac{5}{6}\) and \(c=-\frac{2}{3}\)
So, \(a: b: c=8: 5:-4\) -
Question 109 of 150
109. Question
Let \(p\) be the plane passing through the intersection of the planes \(\vec{r} \cdot(\hat{i}+3 \hat{j}-\widehat{k})=5\) and \(\vec{r} \cdot(2 \hat{i}-\hat{j}+\widehat{k})=3\), and the point \((2,1,-2)\). Let the position vectors of the points \(X\) and \(Y\) be \(\hat{i}-2 \hat{j}+4 \widehat{k}\) and \(5 \hat{i}-\hat{j}+2 \widehat{k}\) respectively. Then the points : [JEE Main 2022 (Online) 25th June Evening Shift]
CorrectIncorrectHint
Let the equation of required plane
\(
\begin{aligned}
& \pi:(x+3 y-z-5)+\lambda(2 x-y+z-3)=0 \\
& \because(2,1,-2) \text { lies on it so, } 2+\lambda(-2)=0 \\
& \Rightarrow \lambda=1
\end{aligned}
\)
Hence, \(\pi: 3 x+2 y-8=0\)
\(
\begin{aligned}
& \because \pi_x=-9, \pi_y=5, \pi_{x+y}=4 \\
& \pi_{x-y}=-22 \text { and } \pi_{y-x}=6
\end{aligned}
\)
Clearly \(X\) and \(Y\) are on opposite sides of plane \(\pi\) -
Question 110 of 150
110. Question
Let \(Q\) be the mirror image of the point \(P(1,0,1)\) with respect to the plane \(S: x+y+z\) \(=5\). If a line \(L\) passing through \((1,-1,-1)\), parallel to the line \(P Q\) meets the plane \(S\) at \(R\), then \(Q R^2\) is equal to : [JEE Main 2022 (Online) 25th June Morning Shift]
CorrectIncorrectHint
As \(L\) is parallel to \(P Q\) d.r.s of \(S\) is \(<1,1,1>\)
\(
\therefore L \equiv \frac{x-1}{1}=\frac{y+1}{1}=\frac{z+1}{1}
\)
Point of intersection of \(L\) and \(S\) be \(\lambda\)
\(
\begin{aligned}
& \Rightarrow(\lambda+1)+(\lambda-1)+(\lambda-1)=S \\
& \Rightarrow \lambda=2 \\
& \therefore R \equiv(3,1,1) \\
& \text { Let } Q(\alpha, \beta, \gamma) \\
& \Rightarrow \frac{\alpha-1}{1}=\frac{\beta}{1}=\frac{\gamma-1}{1}=\frac{-2(-3)}{3} \\
& \Rightarrow \alpha=3, \beta=2, \gamma=3 \\
& \Rightarrow Q \equiv(3,2,3) \\
& (Q R)^2=0^2+(1)^2+(2)^2=5
\end{aligned}
\) -
Question 111 of 150
111. Question
If the shortest distance between the lines \(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{\lambda}\) and \(\frac{x-2}{1}=\frac{y-4}{4}=\frac{z-5}{5}\) is \(\frac{1}{\sqrt{3}}\), then the sum of all possible value of \(\lambda\) is : [JEE Main 2022 (Online) 24th June Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Let } \overrightarrow{a_1}=\hat{i}+2 \hat{j}+3 \widehat{k} \\
& \vec{a}_2=2 \hat{i}+4 \hat{j}+5 \widehat{k} \\
& \vec{p}=2 \hat{i}+3 \hat{j}+\lambda \widehat{k}, \vec{q}=\hat{i}+4 \hat{j}+5 \widehat{k} \\
& \therefore \vec{p} \times \vec{q}=(15-4 \lambda) \hat{i}-(10-\lambda) \hat{j}+5 \widehat{k} \\
& \vec{a}_2-\vec{a}_1=\hat{i}+2 \hat{j}+2 \widehat{k}
\end{aligned}
\)
\(\therefore\) Shortest distance
\(
\begin{aligned}
& =\left|\frac{(15-4 \lambda)-2(10-\lambda)+10}{\sqrt{(15-4 \lambda)^2+(10-\lambda)^2+25}}\right|=\frac{1}{\sqrt{3}} \\
& \Rightarrow 3(5-2 \lambda)^2=(15-4 \lambda)^2+(10-\lambda)^2+25 \\
& \Rightarrow 5 \lambda^2-80 \lambda+275=0
\end{aligned}
\)
\(\therefore\) Sum of values of \(\lambda=\frac{80}{5}=16\) -
Question 112 of 150
112. Question
Let the points on the plane \(P\) be equidistant from the points \((-4,2,1)\) and \((2,-2,3)\). Then the acute angle between the plane \(P\) and the plane \(2 x+y+3 z=1\) is : [JEE Main 2022 (Online) 24th June Evening Shift]
CorrectIncorrectHint
Let \(P(x, y, z)\) be any point on plane \(P_1\)
Then \((x+4)^2+(y-2)^2+(z-1)^2=(x-2)^2+(y+2)^2+(z-3)^2\)
\(
\begin{aligned}
& \Rightarrow 12 x-8 y+4 z+4=0 \\
& \Rightarrow 3 x-2 y+z+1=0
\end{aligned}
\)And \(P_2: 2 x+y+3 z=0\)
\(\therefore\) angle between \(P_1\) and \(P_2\)
\(
\cos \theta=\left|\frac{6-2+3}{14}\right| \Rightarrow \theta=\frac{\pi}{3}
\) -
Question 113 of 150
113. Question
Let the acute angle bisector of the two planes \(x-2 y-2 z+1=0\) and \(2 x-3 y-6 z\) \(+1=0\) be the plane \(P\). Then which of the following points lies on \(P\) ? [JEE Main 2021 (Online) 1st September Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& P_1: x-2 y-2 z+1=0 \\
& P_2: 2 x-3 y-6 z+1=0 \\
& \left|\frac{x-2 y-2 z+1}{\sqrt{1+4+4}}\right|=\left|\frac{2 x-3 y-6 z+1}{\sqrt{2^2+3^2+6^2}}\right| \\
& \frac{x-2 y-2 z+1}{3}= \pm \frac{2 x-3 y-6 z+1}{7}
\end{aligned}
\)Since \(a_1 a_2+b_1 b_2+c_1 c_2=20>0\)
\(\therefore\) Negative sign will give acute bisector
\(
\begin{aligned}
& 7 x-14 y-14 z+7=-[6 x-9 y-18 z+3] \\
& \Rightarrow 13 x-23 y-32 z+10=0 \\
& \left(-2,0,-\frac{1}{2}\right) \text { satisfy it. } \therefore \text { Ans. (b) }
\end{aligned}
\) -
Question 114 of 150
114. Question
The distance of line \(3 y-2 z-1=0=3 x-z+4\) from the point \((2,-1,6)\) is : [JEE Main 2021 (Online) 1st September Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& 3 y-2 z-1=0=3 x-z+4 \\
& 3 y-2 z-1=0 \\
& \text { D.R’s } \Rightarrow(0,3,-2) \\
& 3 x-z+4=0 \\
& \text { D.R’s } \Rightarrow(3,-1,0)
\end{aligned}
\)
Let DR’s of given line are a, b, c
Now, \(3 b-2 c=0 \& 3 a-c=0\)
\(
\begin{aligned}
& \therefore 6 a=3 b=2 c \\
& a: b: c=3: 6: 9
\end{aligned}
\)
Any point on line
\(
3 K-1,6 K+1,9 K+1
\)
Now, \(3(3 K-1)+6(6 K+1) 1+9(9 K+1)=0\)
\(
\Rightarrow K =\frac{1}{3}
\)
Point on line \(\Rightarrow(0,3,4)\)
Given point \((2,-1,6)\)
\(
\Rightarrow \text { Distance }=\sqrt{4+16+4}=2 \sqrt{6}
\) -
Question 115 of 150
115. Question
The distance of the point \((-1,2,-2)\) from the line of intersection of the planes \(2 x+\) \(3 y+2 z=0\) and \(x-2 y+z=0\) is : [JEE Main 2021 (Online) 31st August Evening Shift]
CorrectIncorrectHint
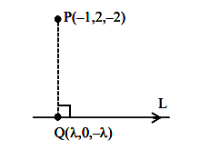
\(
\begin{aligned}
& P _1: 2 x +3 y +2 z =0 \\
& \Rightarrow \overrightarrow{n_1}=2 \hat{i}+3 \hat{j}+2 \widehat{k} \\
& P _2: x -2 y + z =0 \\
& \Rightarrow \overrightarrow{n_2}=\hat{i}-2 \hat{j}+\widehat{k}
\end{aligned}
\)
Direction vector of line \(L\) which is line of intersection of \(P_1 \& P_2\)
\(
\vec{r}=\vec{n}_1 \times \vec{n}_2=7 \hat{i}-7 \widehat{k}
\)
DR’s of \(L\) are \((1,0,-1)\)
\(\Rightarrow\) Equation of \(L : \frac{x}{1}=\frac{y}{0}=\frac{z}{-1}=\lambda\)
DR’s of \(\overrightarrow{P Q}=(\lambda+1,-2,2-\lambda)\)
\(
\begin{aligned}
& \because \overrightarrow{P Q} \perp \vec{r} \\
& \Rightarrow(\lambda+1)(1)+(-2)(0)+(2-\lambda)(-1)=0 \\
& \Rightarrow \lambda=\frac{1}{2} \Rightarrow Q\left(\frac{1}{2}, 0, \frac{-1}{2}\right) \\
& \Rightarrow P Q=\frac{\sqrt{34}}{2}
\end{aligned}
\) -
Question 116 of 150
116. Question
Let the equation of the plane, that passes through the point \((1,4,-3)\) and contains the line of intersection of the
planes \(3 x-2 y+4 z-7=0\)
and \(x+5 y-2 z+9=0\), be \(\alpha x +\beta y +\gamma z +3=0\), then \(\alpha+\beta+\gamma\) is equal to : [JEE Main 2021 (Online) 31st August Morning Shift]CorrectIncorrectHint
\(
\begin{aligned}
& 3 x-2 y+4 z-7+\lambda(x+5 y-2 z+9)=0 \\
& (3+\lambda) x+(5 \lambda-2) y+(4-2 \lambda) z+9 \lambda-7=0
\end{aligned}
\)
passing through \((1,4,-3)\)
\(
\begin{aligned}
& \Rightarrow 3+\lambda+20 \lambda-8-12+6 \lambda+9 \lambda-7=0 \\
& \Rightarrow \lambda=\frac{2}{3}
\end{aligned}
\)
\(\Rightarrow\) equation of plane is
\(
\begin{aligned}
& -11 x -4 y -8 z +3=0 \\
& \Rightarrow \alpha+\beta+\gamma=-23
\end{aligned}
\) -
Question 117 of 150
117. Question
The angle between the straight lines, whose direction cosines are given by the equations \(2 l+2 m-n=0\) and \(m n+n l+l m=0\), is : [JEE Main 2021 (Online) 27th August Evening Shift]
CorrectIncorrectHint
\(
\begin{aligned}
&\begin{aligned}
& n=2(\ell+m) \\
& \ell m+n(\ell+m)=0 \\
& \ell m+2(\ell+m)^2=0 \\
& 2 \ell^2+2 m^2+5 m \ell=0 \\
& 2\left(\frac{\ell}{m}\right)^2+2+5\left(\frac{\ell}{m}\right)=0 \\
& 2 t^2+5 t+2=0 \\
& (t+2)(2 t+1)=0 \\
& \Rightarrow t=-2 ;-\frac{1}{2}
\end{aligned}\\
&\begin{aligned}
& \text { (i) } \frac{\ell}{m}=-2 \\
& \frac{n}{m}=-2 \\
& (-2 m, m,-2 m) \\
& (-2,1,-2)
\end{aligned}\\
&\begin{aligned}
& \text { (ii) } \frac{\ell}{m}=-\frac{1}{2} \\
& n=-2 \ell \\
& (\ell,-2 \ell,-2 \ell) \\
& (1,-2,-2) \\
& \cos \theta=\frac{-2-2+4}{\sqrt{9} \sqrt{9}}=0 \\
& \Rightarrow \theta=\frac{\pi}{2}
\end{aligned}
\end{aligned}
\) -
Question 118 of 150
118. Question
The equation of the plane passing through the line of intersection of the planes \(\vec{r} \cdot(\hat{i}+\hat{j}+\widehat{k})=1\) and \(\vec{r} \cdot(2 \hat{i}+3 \hat{j}-\widehat{k})+4=0\) and parallel to the \(x\)-axis is : [JEE Main 2021 (Online) 27th August Evening Shift]
CorrectIncorrectHint
Equation of planes are
\(
\begin{aligned}
& \vec{r} .(\hat{i}+\hat{j}+\widehat{k})-1=0 \Rightarrow x+y+z-1=0 \\
& \text { and } \vec{r} .(2 \hat{i}+3 \hat{j}-\widehat{k})+4=0 \Rightarrow 2 x+3 y-z+4=0
\end{aligned}
\)
equation of planes through line of intersection of these planes is :-
\(
\begin{aligned}
& (x+y+z-1)+\lambda(2 x+3 y-z+4)=0 \\
& \Rightarrow(1+2 \lambda) x+(1+3 \lambda) y+(1-\lambda) z-1+4 \lambda=0
\end{aligned}
\)
But this plane is parallel to \(x\)-axis whose direction are \((1,0,0)\)
\(
\begin{aligned}
& \therefore(1+2 \lambda) 1+(1+3 \lambda) 0+(1-\lambda) 0=0 \\
& \lambda=-\frac{1}{2}
\end{aligned}
\)
\(\therefore\) Required plane is
\(
\begin{aligned}
& 0 x+\left(1-\frac{3}{2}\right) y+\left(1+\frac{1}{2}\right) z-1+4\left(\frac{-1}{2}\right)=0 \\
& \Rightarrow \frac{-y}{2}+\frac{3}{2} z-3=0 \\
& \Rightarrow y-3 z+6=0 \\
& \Rightarrow \vec{r} \cdot(\hat{j}-3 \widehat{k})+6=0
\end{aligned}
\) -
Question 119 of 150
119. Question
The distance of the point \((1,-2,3)\) from the plane \(x-y+z=5\) measured parallel to a line, whose direction ratios are \(2,3,-6\) is : [JEE Main 2021 (Online) 27th August Morning Shift]
CorrectIncorrectHint
The equation of the line through the point \((1,-2,3)\) and parallel to the given line is \(\frac{x-1}{2}=\frac{y+2}{3}=\)
\(
\frac{z-3}{-6}=\lambda
\)
The general point on this line \((2 \lambda+1,3 \lambda-2,-6 \lambda+3)\)
If this point lies in the given plane then
\(
\begin{aligned}
& (2 \lambda+1)-(3 \lambda-2)+(-6 \lambda+3)=5 \\
& \therefore \lambda=\frac{1}{7}
\end{aligned}
\)
Hence point of intersection is \(\left(\frac{9}{7}, \frac{-11}{7}, \frac{15}{7}\right)\)
The required distance \(=\) distance between the points \((1,-2,3)\) and \(\left(\frac{9}{7}, \frac{-11}{7}, \frac{15}{7}\right)\)
\(
=\sqrt{\left(1-\frac{9}{7}\right)^2+\left(-2+\frac{11}{7}\right)^2+\left(3-\frac{15}{7}\right)^2}=1 \text {. }
\) -
Question 120 of 150
120. Question
Equation of a plane at a distance \(\sqrt{\frac{2}{21}}\) from the origin, which contains the line of intersection of the planes \(x-y-z-1=0\) and \(2 x+y-3 z+4=0\), is : [JEE Main 2021 (Online) 27th August Morning Shift]
CorrectIncorrectHint
Required equation of plane
\(
\begin{aligned}
& P_1+\lambda P_2=0 \\
& (x-y-z-1)+\lambda(2 x+y-3 z+4)=0
\end{aligned}
\)Given that its dist. From origin is \(\frac{2}{\sqrt{21}}\)
\(
\begin{aligned}
& \text { Thus, } \frac{|4 \lambda-1|}{\sqrt{(2 \lambda+1)^2+(\lambda-1)^2+(-3 \lambda-1)^2}}=\frac{\sqrt{2}}{\sqrt{21}} \\
& \Rightarrow 21(4 \lambda-1)^2=2\left(14 \lambda^2+8 \lambda+3\right) \\
& \Rightarrow 336 \lambda^2-168 \lambda+21=28 \lambda^2+16 \lambda+6 \\
& \Rightarrow 308 \lambda^2-184 \lambda+15=0 \\
& \Rightarrow 308 \lambda^2-154 \lambda-30 \lambda+15=0 \\
& \Rightarrow(2 \lambda-1)(154 \lambda-15)=0 \\
& \Rightarrow \lambda=\frac{1}{2} \text { or } \frac{15}{154}
\end{aligned}
\)
for \(\lambda=\frac{1}{2}\) reqd. plane is \(4 x-y-5 z+2=0\) -
Question 121 of 150
121. Question
Let \(P\) be the plane passing through the point \((1,2,3)\) and the line of intersection of the planes \(\vec{r} \cdot(\hat{i}+\hat{j}+4 \widehat{k})=16\) and \(\vec{r} \cdot(-\hat{i}+\hat{j}+\widehat{k})=6\). Then which of the following points does NOT lie on P? [JEE Main 2021 (Online) 26th August Evening Shift]
CorrectIncorrectHint
\(
(x+y+4 z-16)+\lambda(-x+y+z-6)=0
\)Passes through \((1,2,3)\)
\(
\begin{aligned}
& -1+\lambda(-2) \Rightarrow \lambda=-\frac{1}{2} \\
& 2(x+y+4 z-16)-(-x+y+z-6)=0 \\
& 3 x+y+7 z-26=0
\end{aligned}
\) -
Question 122 of 150
122. Question
A plane \(P\) contains the line \(x+2 y+3 z+1=0=x-y-z-6\), and is perpendicular to the plane \(-2 x+y+z+8=0\). Then which of the following points lies on \(P\) ? [JEE Main 2021 (Online) 26th August Morning Shift]
CorrectIncorrectHint
Equation of plane \(P\) can be assumed as
\(
\begin{aligned}
& P: x+2 y+3 z+1+\lambda(x-y-z-6)=0 \\
& \Rightarrow P:(1+\lambda) x+(2-\lambda) y+(3-\lambda) z+1-6 \lambda=0 \\
& \Rightarrow \vec{n}_1=(1+\lambda) \hat{i}+(2-\lambda) \hat{j}+(3-\lambda) \widehat{k}
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \vec{n}_1 \cdot \vec{n}_2=0 \\
& \Rightarrow 2(1+\lambda)-(2-\lambda)-(3-\lambda)=0 \\
& \Rightarrow 2+2 \lambda-2+\lambda-3+\lambda=0 \Rightarrow \lambda=\frac{3}{4} \\
& \Rightarrow P: \frac{7 x}{4}+\frac{5}{4} y+\frac{9 z}{4}-\frac{14}{4}=0 \\
& \Rightarrow 7 x+5 y+9 z=14
\end{aligned}
\)
\((0,1,1)\) lies on \(P\). -
Question 123 of 150
123. Question
For real numbers \(\alpha\) and \(\beta \neq 0\), if the point of intersection of the straight lines \(\frac{x-\alpha}{1}=\frac{y-1}{2}=\frac{z-1}{3}\) and \(\frac{x-4}{\beta}=\frac{y-6}{3}=\frac{z-7}{3}\), lies on the plane \(x+2 y-z=8\), then \(\alpha-\beta\) is equal to : [JEE Main 2021 (Online) 27th July Evening Shift]
CorrectIncorrectHint
Let \(L_1: \frac{x-a}{1}=\frac{y-1}{2}=\frac{z-1}{3}=\lambda\) and \(L_2: \frac{x-4}{\beta}=\frac{y-6}{3}=\frac{z-7}{3}=\mu\)
Let point on line \(L_1\) be \((\lambda+a, 2 \lambda+1,3 \lambda+1)\) and a point on line \(L_2\) be \((\mu \beta+4,3 \mu+6,3 \mu+7)\)
For point of intersection
\(
\begin{aligned}
& \lambda+a=\mu \beta+4,2 \lambda+1=3 \mu+6 \& 3 \lambda+1=3 \mu+7 \\
& \lambda=1 \text { and } \mu=-1 \\
& \Rightarrow 1+a=-\beta+4 \Rightarrow a+\beta=3
\end{aligned}
\)
\(\therefore\) Point of intersection \((1+a, 3,4)\)
Above point lies on the plane \(x+2 y-z=8\),
\(
\begin{aligned}
& \Rightarrow 1+\alpha+6-4=8 \\
& \Rightarrow a=5, \beta=-2
\end{aligned}
\)
We get, \(\alpha-\beta=7\) -
Question 124 of 150
124. Question
Let the plane passing through the point \((-1,0,-2)\) and perpendicular to each of the planes \(2 x+y-z=2\) and \(x-y-z=3\) be \(a x+b y+c z+8=0\). Then the value of \(a+\) \(b+c\) is equal to : [JEE Main 2021 (Online) 27th July Morning Shift]
CorrectIncorrectHint
Given equation of plane is \(a x+b y+c z+8=0\)
Since it passes through the point \((-1,0,-2)\)
\(
\begin{aligned}
& \therefore-a-2 c+8=0 \\
& \Rightarrow a+2 c-8=0 \dots(1)
\end{aligned}
\)
and \(a x+b y+c z+8=0\) is perpendicular to \(2 x+y-z=2\) and \(x-y-z=3\)
\(
\begin{aligned}
& \therefore 2 a+b-c=0 \dots(2) \\
& a-b-c=0 \quad \cdots \dots(3)
\end{aligned}
\)
From (1), (2) and (3), we get
\(
\begin{aligned}
& a=2, b=-1 \text { and } c=3 \\
& \therefore a+b+c=4
\end{aligned}
\) -
Question 125 of 150
125. Question
Let the foot of perpendicular from a point \(P(1,2,-1)\) to the straight line \(L: \frac{x}{1}=\frac{y}{0}=\frac{z}{-1}\) be \(N\). Let a line be drawn from \(P\) parallel to the plane \(x + y +2 z =0\) which meets \(L\) at point \(Q\). If \(\alpha\) is the acute angle between the lines \(PN\) and \(PQ\), then \(\cos \alpha\) is equal to [JEE Main 2021 (Online) 25th July Morning Shift]
CorrectIncorrectHint
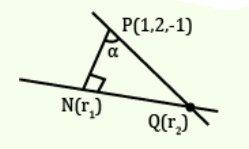
\(
\begin{aligned}
& L: \frac{x}{1}=\frac{y}{0}=\frac{z}{-1}=r \\
& N \equiv\left(r_1, 0,-r_1\right) \\
& P(1,2,-1)
\end{aligned}
\)
D.R’s of NP \(=\left(r_1-1,-2,-r_1+1\right) \perp\) with D.R’s \((1,0,-1)\)
\(
\begin{aligned}
& \Rightarrow r_1-1+0+r_1-1=0 \\
& \Rightarrow r_1=1 \\
& \Rightarrow N(1,0,-1) \\
& Q\left(r_2, 0,-r_2\right)
\end{aligned}
\)
D.R’s of normal of plane \(x+y+2 z=0\) are \((1,1,2)\)
D.R’s of \(P Q=\left(r_2-1,-2,-r_2+1\right)\) are perpendicular to \((1,1,2)\)
\(
\begin{aligned}
& \Rightarrow r_2-1-2-2 r_2+2=0 \\
& \Rightarrow r_2=-1 \\
& \Rightarrow Q(-1,0,1) \\
& N P=2, P Q=2 \sqrt{3} \\
& \cos a=\frac{N P}{P Q}=\frac{1}{\sqrt{3}}
\end{aligned}
\) -
Question 126 of 150
126. Question
Let \(L\) be the line of intersection of planes \(\vec{r} .(\hat{i}-\hat{j}+2 \widehat{k})=2\) and \(\vec{r}\). \((2 \hat{i}+\hat{j}-\widehat{k})=2\). If \(P(\alpha, \beta, \gamma)\) is the foot of perpendicular on \(L\) from the point \((1,2,0)\), then the value of \(35(\alpha+\beta+\gamma)\) is equal to : [JEE Main 2021 (Online) 22th July Evening Shift]
CorrectIncorrectHint
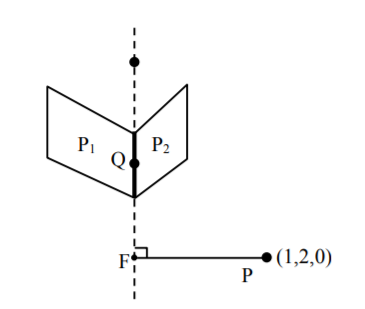
\(
\begin{gathered}
P_1: x-y+2 z=2 \\
P_2: 2 x+y-3=2
\end{gathered}
\)
Let line of Intersection of planes \(P _1\) and \(P _2\) cuts xy plane in point \(Q\).
\(\Rightarrow z\)-coordinate of point \(Q\) is zero
\(
\begin{aligned}
& \left.\Rightarrow \begin{array}{c}
x-y=2 \\
\text { and } 2 x+y=2
\end{array}\right\} \Rightarrow x=\frac{4}{3}, y=\frac{-2}{3} \\
& \Rightarrow Q\left(\frac{4}{3}, \frac{-2}{3}, 0\right)
\end{aligned}
\)
Vector parallel to the line of intersection
\(
\vec{a}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \widehat{k} \\
1 & -1 & 2 \\
2 & 1 & -1
\end{array}\right|=-\hat{i}+5 \hat{j}+3 \widehat{k}
\)
Equation of Line of intersection
\(
\frac{x-\frac{4}{3}}{-1}=\frac{y+\frac{2}{3}}{5}=\frac{z-0}{3}=\lambda \text { (say) }
\)
Let coordinates of foot of perpendicular be
\(
\begin{aligned}
& F\left(-\lambda+\frac{4}{3}, 5 \lambda-\frac{2}{3}, 3 \lambda\right) \\
& \overrightarrow{P F}=\left(-\lambda+\frac{1}{3}\right) \hat{i}+\left(5 \lambda-\frac{8}{3}\right) \hat{j}+(3 \lambda) \widehat{k} \\
& \overrightarrow{P F} \cdot \vec{a}=0 \\
& \Rightarrow \lambda-\frac{1}{3}+25 \lambda \frac{-40}{3}+9 \lambda=0 \\
& \Rightarrow 35 \lambda=\frac{41}{3} \Rightarrow \lambda=\frac{41}{105}
\end{aligned}
\)
Now, \(\alpha=-\lambda+\frac{4}{3}, \beta=5 \lambda-\frac{2}{3}, \gamma=3 \lambda\)
\(
\begin{aligned}
& \Rightarrow \alpha+\beta+\gamma=7 \lambda+\frac{2}{3} \\
& =7\left(\frac{41}{105}\right)+\frac{2}{3} \\
& =\frac{51}{15} \\
& \Rightarrow 35(\alpha+\beta+\gamma)=\frac{51}{15} \times 35=119
\end{aligned}
\) -
Question 127 of 150
127. Question
If the shortest distance between the straight lines \(3(x-1)=6(y-2)=2(z-1)\) and \(4(x-2)=2(y-\lambda)=(z-3), \lambda \in R\) is \(\frac{1}{\sqrt{38}}\), then the integral value of \(\lambda\) is equal to: [JEE Main 2021 (Online) 22th July Evening Shift]
CorrectIncorrectHint
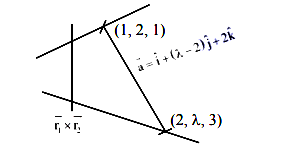
\(
\begin{aligned}
& L_1: \frac{(x-1)}{2}=\frac{(y-2)}{1}=\frac{(z-1)}{3} \overrightarrow{r_1}=2 \hat{i}+\hat{j}+3 \widehat{k} \\
& L_2: \frac{(x-2)}{1}=\frac{y-\lambda}{2}=\frac{z-3}{4} \overrightarrow{r_2}=\hat{i}+2 \hat{j}+4 \widehat{k}
\end{aligned}
\)
\(
\begin{aligned}
& \text { Shortest distance }=\text { Projection of } \vec{a} \text { on } \overrightarrow{r_1} \times \overrightarrow{r_2} \\
& =\frac{\left|\vec{a} \cdot\left(\overrightarrow{r_1} \times \overrightarrow{r_2}\right)\right|}{\left|\overrightarrow{r_1} \times \overrightarrow{r_2}\right|}
\end{aligned}
\)
\(
\begin{aligned}
& \left|\vec{a} .\left(\overrightarrow{r_1} \times \overrightarrow{r_2}\right)\right|=\left|\begin{array}{ccc}
1 & \lambda-2 & 2 \\
2 & 1 & 3 \\
1 & 2 & 4
\end{array}\right|=|14-5 \lambda| \\
& \left|\overrightarrow{r_1} \times \overrightarrow{r_2}\right|=\sqrt{38} \\
& \therefore \frac{1}{\sqrt{38}}=\frac{|14-5 \lambda|}{\sqrt{38}} \\
& \Rightarrow|14-5 \lambda|=1 \\
& \Rightarrow 14-5 \lambda=1 \text { or } 14-5 \lambda=-1 \\
& \Rightarrow \lambda=\frac{13}{5} \text { or } 3 \\
& \therefore \text { Integral value of } \lambda=3 .
\end{aligned}
\) -
Question 128 of 150
128. Question
The lines \(x=a y-1=z-2\) and \(x=3 y-2=b z-2,(a b \neq 0)\) are coplanar, if : [JEE Main 2021 (Online) 20th July Evening Shift]
CorrectIncorrectHint
Lines are \(x=a y-1=z-2\)
\(
\therefore \frac{x}{1}=\frac{y-\frac{1}{a}}{\frac{1}{a}}=\frac{z-2}{1} \ldots . \text { (i) }
\)
and \(x=3 y-2=b z-2\)
\(
\therefore \frac{x}{1}=\frac{y-\frac{2}{3}}{\frac{1}{3}}=\frac{z-\frac{2}{b}}{\frac{1}{6}} \ldots (ii)
\)
\(\therefore\) lines are co-planar
\(
\begin{aligned}
& \therefore\left|\begin{array}{ccc}
0 & -\frac{1}{a}+\frac{2}{3} & -2+\frac{2}{b} \\
1 & \frac{1}{a} & 1 \\
1 & \frac{1}{3} & \frac{1}{b}
\end{array}\right|=0 \\
& \therefore\left|\begin{array}{ccc}
0 & \frac{2}{3}-\frac{1}{a} & \frac{2}{b}-2 \\
0 & \frac{1}{a}-\frac{1}{3} & 1-\frac{1}{b} \\
1 & \frac{1}{3} & \frac{1}{b}
\end{array}\right|=0 \\
& \therefore \frac{1}{a}-\frac{1}{a b}=0 \\
& \Rightarrow b=1 \text { and } a \in R-\{0\}
\end{aligned}
\) -
Question 129 of 150
129. Question
Consider the line \(L\) given by the equation
\(
\frac{x-3}{2}=\frac{y-1}{1}=\frac{z-2}{1} .
\)
Let \(Q\) be the mirror image of the point \((2,3,-1)\) with respect to \(L\). Let a plane \(P\) be such that it passes through \(Q\), and the line \(L\) is perpendicular to \(P\). Then which of the following points is on the plane \(P\) ? [JEE Main 2021 (Online) 20th July Evening Shift]CorrectIncorrectHint
Plane \(p\) is \(\perp^r\) to line
\(
x-3 / 2=y-1 / 1=z-2 / 1
\)
& passes through pt. \((2,3)\) equation of plane \(p\)
\(
\begin{aligned}
& 2(x-2)+1(y-3)+1(z+1)=0 \\
& 2 x+y+z-6=0
\end{aligned}
\) -
Question 130 of 150
130. Question
If the equation of plane passing through the mirror image of a point \((2,3,1)\) with respect to line \(\frac{x+1}{2}=\frac{y-3}{1}=\frac{z+2}{-1}\) and containing the line \(\frac{x-2}{3}=\frac{1-y}{2}=\frac{z+1}{1}\) is \(\alpha x +\beta y +\gamma z =24\), then \(\alpha+\beta+\gamma\) is equal to : [JEE Main 2021 (Online) 17th March Evening Shift]
CorrectIncorrectHint
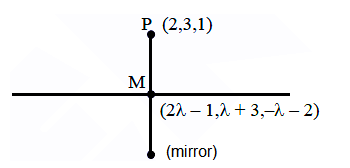
\(
\text { Line } \frac{x+1}{2}=\frac{y-3}{1}=\frac{z+2}{-1}
\)
\(
\begin{aligned}
& \overrightarrow{P M}=(2 \lambda-3, \lambda,-\lambda-3) \\
& \overrightarrow{P M} \perp(2 \hat{i}+\hat{j}-\hat{k}) \\
& 4 \lambda-6+\lambda+\lambda+3=0 \Rightarrow \lambda=\frac{1}{2} \\
& \therefore M \equiv\left(0, \frac{7}{2}, \frac{-5}{2}\right) \\
& \therefore \text { Reflection }(-2,4,-6)
\end{aligned}
\)
Plane \(:\left|\begin{array}{ccc}x-2 & y-1 & z+1 \\ 3 & -2 & 1 \\ 4 & -3 & 5\end{array}\right|=0\)
\(
\begin{aligned}
& \Rightarrow(x-2)(-10+3)-(y-1)(15-4)+(z+1)(-1)=0 \\
& \Rightarrow-7 x+14-11 y+11-z-1=0 \\
& \Rightarrow 7 x+11 y+z=24 \\
& \therefore \alpha=7, \beta=11, \gamma=1 \\
& \alpha+\beta+\gamma=19
\end{aligned}
\) -
Question 131 of 150
131. Question
The equation of the plane which contains the \(y\)-axis and passes through the point \((1,2,3)\) is : [JEE Main 2021 (Online) 17th March Morning Shift]
CorrectIncorrectHint
Let the equation of the plane is \(a(x-1)+b(y-2)+c(z-3)=0\)
Y-axis lies on it.
D.R.’s of \(y\)-axis are \(0,1,0\)
\(
\therefore 0 . a+1 . b+0 . c=0 \Rightarrow b=0
\)
\(\therefore\) Equation of plane is \(a(x-1)+c(z-3)=0\)
\(x=0, z=0\) also satisfy it \(-a-3 c=0 \Rightarrow a=-3 c\)
\(
\begin{aligned}
& -3 c(x-1)+c(z-3)=0 \\
& -3+3+z-3=0 \\
& 3 x-z=0
\end{aligned}
\) -
Question 132 of 150
132. Question
If the foot of the perpendicular from point \((4,3,8)\) on the line \(L_1: \frac{x-a}{l}=\frac{y-2}{3}=\frac{z-b}{4}, l \neq 0\) is \((3,5,7)\), then the shortest distance between the line \(L _1\) and line \(L_2: \frac{x-2}{3}=\frac{y-4}{4}=\frac{z-5}{5}\) is equal to : [JEE Main 2021 (Online) 16th March Evening Shift]
CorrectIncorrectHint
\((3,5,7)\) lie on given line \(L_1\)
\(
\begin{aligned}
& \frac{3-a}{l}=\frac{3}{3}=\frac{7-b}{4} \\
& \frac{7-b}{4}=1 \Rightarrow b=3 \\
& \frac{3-a}{l}=1 \Rightarrow 3-a=l \\
& M (4,3,8) \\
& N (3,5,7)
\end{aligned}
\)
DR’S of MN \(=(1,-2,1)\)
\(MN \perp\) line \(L _1\)
\(
\begin{aligned}
& (1)(l)+(-2)(3)+4(1)=0 \\
& \Rightarrow l=2 \\
& a=1
\end{aligned}
\)
\(
\begin{aligned}
& a =1, b =3, l =2 \\
& \frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4} \\
& \frac{x-2}{3}=\frac{y-4}{4}=\frac{z-5}{5} \\
& A=<1,2,3> \\
& B=<2,4,5> \\
& \overrightarrow{A B}=<1,2,2> \\
& \vec{p}=2 \hat{i}+3 \hat{j}+4 \widehat{k} \\
& \vec{q}=3 \hat{i}+4 \hat{j}+5 \widehat{k} \\
& \vec{p} \times \vec{q}=-\hat{i}+2 \hat{j}-\widehat{k}
\end{aligned}
\)
Shortest distance \(=\left|\frac{\overrightarrow{A B} \cdot(\vec{p} \times \vec{q})}{|\vec{p} \times \vec{q}|}\right|=\frac{1}{\sqrt{6}}\) -
Question 133 of 150
133. Question
If \((x, y, z)\) be an arbitrary point lying on a plane \(P\) which passes through the points \((42,0,0),(0,42,0)\) and \((0,0,42)\), then the value of the expression \(3+\frac{x-11}{(y-19)^2(z-12)^2}+\frac{y-19}{(x-11)^2(z-12)^2}+\frac{z-12}{(x-11)^2(y-19)^2}-\frac{x+y+z}{14(x-11)(y-19)(z-12)}\) is equal to : [JEE Main 2021 (Online) 16th March Evening Shift]
CorrectIncorrectHint
From intercept from, equation of plane is \(x+y+z=42\)
\(
\Rightarrow(x-11)+(y-19)+(z-12)=0
\)
let \(a=x-11, b=y-19, c=z-12\)
\(
a+b+c=0
\)
Now, given expression is
\(
\begin{aligned}
& 3+\frac{a}{b^2 c^2}+\frac{b}{a^2 c^2}+\frac{c}{a^2 b^2}-\frac{42}{14 a b c} \\
& 3+\frac{a^3+b^3+c^3-3 a b c}{a^2 b^2 c^2}
\end{aligned}
\)
If \(a+b+c=0\)
\(
\begin{aligned}
& \Rightarrow a ^3+ b ^3+ c ^3=3 abc \\
& \therefore 3+\frac{0}{a^2 b^2 c^2} \\
& =3
\end{aligned}
\) -
Question 134 of 150
134. Question
Let the position vectors of two points \(P\) and \(Q\) be \(3 \hat{i}-\hat{j}+2 \widehat{k}\) and \(\hat{i}+2 \hat{j}-4 \widehat{k}\), respectively. Let \(R\) and \(S\) be two points such that the direction ratios of lines \(P R\) and QS are \((4,-1,2)\) and \((-2,1,-2)\), respectively. Let lines PR and QS intersect at T. If the vector \(\overrightarrow{T A}\) is perpendicular to both \(\overrightarrow{P R}\) and \(\overrightarrow{Q S}\) and the length of vector \(\overrightarrow{T A}\) is \(\sqrt{5}\) units, then the modulus of a position vector of \(A\) is : [JEE Main 2021 (Online) 16th March Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& \vec{p}=3 \hat{i}-\hat{j}+2 \widehat{k} \& \vec{Q}=\hat{i}+2 \hat{j}-4 \widehat{k} \\
& \vec{v}_{P R}=(4,-1,2) \& \vec{v}_{Q S}=(-2,1,-2)
\end{aligned}
\)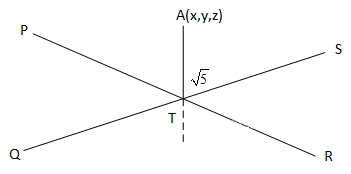
\(L_{P R}: \vec{r}=(3 \hat{i}-\hat{j}+2 \widehat{k})+\lambda(4,-1,2)\)
\(L_{Q S}: \vec{r}=(\hat{i}+2 \hat{j}-4 \widehat{k})+\mu(-2,1,-2)\)
Now \(T\) on \(PR =\langle 3+4 \lambda,-1-\lambda, 2+2 \lambda\rangle\)
Similarly T on QS \(=(1-2 \mu, 2+\mu,-4-2 \mu)\)
For \(\lambda \& \mu: 3+4 \lambda=1-2 \mu \Rightarrow \mu+2 \lambda=-1\} \lambda=2\) \(-1-\lambda=2+\mu \Rightarrow \mu+\lambda=-3 \quad\} \mu=-5\)
\(
\begin{aligned}
& \Rightarrow T :(11,-3,6) \\
& \text { D.R. of TA }=\vec{v}_{Q S} \times \vec{v}_{P R} \\
& =\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \widehat{k} \\
-2 & 1 & -2 \\
4 & -1 & 2
\end{array}\right|=0 \hat{i}-4 \hat{j}-2 \widehat{k} \\
& L_{T A}: \vec{r}=(11 \hat{i}-3 \hat{j}+6 \widehat{k})+\lambda(-4 \hat{j}-2 \widehat{k})
\end{aligned}
\)
Now \(A=(11,-3-4 \lambda, 6-2 \lambda)\)
Given, \(TA =\sqrt{5}\)
\(
\begin{aligned}
& (-3+4 \lambda+3)^2+(6+2 \lambda-6)^2=5 \\
& 16 \lambda^2+4 \lambda^2=5 \\
& 20 \lambda^2=5
\end{aligned}
\)
\(
\begin{array}{lll}
\lambda= \pm \frac{1}{2} & & \\
A:(11,-3-2,6-1) & ; & A:(11,-3+2,6+1) \\
|A|=\sqrt{121+25+25} & ; & |A|=\sqrt{121+1+49} \\
=\sqrt{171} & ; & \sqrt{171}
\end{array}
\) -
Question 135 of 150
135. Question
Let \(P\) be a plane \(l x+m y+n z=0\) containing the line, \(\frac{1-x}{1}=\frac{y+4}{2}=\frac{z+2}{3}\). If plane \(P\) divides the line segment \(AB\) joining points \(A(-3,-6,1)\) and \(B(2,4,-3)\) in ratio \(k\) : 1 then the value of \(k\) is equal to : [JEE Main 2021 (Online) 16th March Morning Shift]
CorrectIncorrectHint
Equation of the plane is given as \(l x+m y+n z=0\), means it is passing through the origin Equation of the plane passing through the origin and containing the line \(\frac{1-x}{1}=\frac{y+4}{2}=\frac{z+2}{3}\) is
\(
\left|\begin{array}{ccc}
x-1 & y+4 & z+2 \\
-1 & 2 & 3 \\
-1 & 4 & 2
\end{array}\right|=0 \Rightarrow-8 x-y-2 z=0 \Rightarrow 8 x+y+2 z=0
\)
Coordiantes of a point which divides the line segment joining the points \(A (-3,-6,1)\) and \(B (2,4,-3)\) in the ratio \(k : 1\) is \(\left(\frac{2 k+3}{k+1}, \frac{4 k-6}{k+1}, \frac{-3 k+1}{k+1}\right)\)
This point lies on the plane \(8 x+y+2 z=0\)
\(
8(2 k-3)+(4 k-6)+2(-3 k+1)=0 \Rightarrow 14 k=28 \Rightarrow k=2
\) -
Question 136 of 150
136. Question
If for \(a>0\), the feet of perpendiculars from the points \(A(a,-2 a, 3)\) and \(B(0,4,5)\) on the plane \(l x+m y+n z=0\) are points \(C(0,-a,-1)\) and \(D\) respectively, then the length of line segment \(C D\) is equal to : [JEE Main 2021 (Online) 16th March Morning Shift]
CorrectIncorrectHint
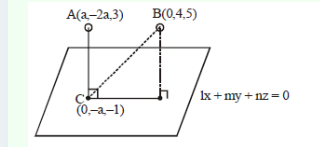
Direction cosines of plane \(=\lambda\) (direction cosines of line \(A C\) )
Direction cosines of plane \(=\lambda a,-\lambda a, 4 \lambda\)
Hence equation plane is: \(a x-a y+4 z=0\)
The point \(C\) lies on the plane
\(
a(0)-a(-a)+4(-1)=0 \Rightarrow a=2(\because a>0)
\)So plane is \(2 x-2 y+4 z=0, C=(0,-2,-1)\)
So for coordinates of D,
\(
\begin{aligned}
& {[x-0] / 2=[y-4] /-2=[z-5] / 4=-\left\{[2(0)-2(4)+4(5)] /\left[2^2+2^2+4^2\right]\right\}} \\
& D=(-1,5,3) \\
& C D=\sqrt{ } 66 \text { units }
\end{aligned}
\) -
Question 137 of 150
137. Question
If the mirror image of the point \((1,3,5)\) with respect to the plane \(4 x -5 y +2 z =8\) is \((\alpha, \beta, \gamma)\), then \(5(\alpha+\beta+\gamma)\) equals : [JEE Main 2021 (Online) 26th February Evening Shift]
CorrectIncorrectHint
Image of \((1,3,5)\) in the plane \(4 x-5 y+2 z=8\) is \((\alpha, \beta, \gamma)\)
\(
\begin{aligned}
& \Rightarrow \frac{\alpha-1}{4}=\frac{\beta-3}{-5}=\frac{\gamma-5}{2}=-\frac{(4(1)-5(3)+2(5)-8)}{4^2+5^2+2^2}=\frac{2}{5} \\
& \therefore \alpha=1+4\left(\frac{2}{5}\right)=\frac{13}{5} \\
& \beta=3-5\left(\frac{2}{5}\right)=1=\frac{5}{5} \\
& \gamma=5+2\left(\frac{2}{5}\right)=\frac{29}{5}
\end{aligned}
\)
Thus, \(5(\alpha+\beta+\gamma)=5\left(\frac{13}{5}+\frac{5}{5}+\frac{29}{5}\right)=47\) -
Question 138 of 150
138. Question
Let \(L\) be a line obtained from the intersection of two planes \(x+2 y+z=6\) and \(y+\) \(2 z =4\). If point \(P (\alpha, \beta, \gamma)\) is the foot of perpendicular from \((3,2,1)\) on \(L\), then the value of \(21(\alpha+\beta+\gamma)\) equals : [JEE Main 2021 (Online) 26th February Evening Shift]
CorrectIncorrectHint
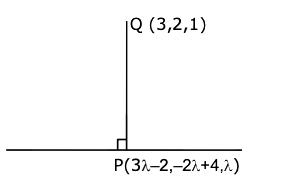
Finding the value of \(21(a+\beta+\gamma)\) :
Given equation of the line is \(x+2 y+z-6=0=y+2 z-4\)
\(
\frac{[x+2]}{3}=\frac{[y-4]}{-2}=\frac{z}{1}=\lambda
\)
Directional ration of \(P Q: 3 \lambda-5,-2 \lambda-2, \lambda-1\)
Directional ratio of \(y\) line are \((3,-2,1)\)
\(
\begin{aligned}
& x+2 y+z=6 \\
& (y+2 z=4) \times 2 \\
& x-3 z=-2 \\
& \quad \Rightarrow x=3 z-2 \\
& \quad \Rightarrow y=4-2 z \\
& 3 x+2=z-2 y-4=z
\end{aligned}
\)
Line of intersection of two planes is
\(
\begin{aligned}
& 3 x+2=-2 y-4=z=\lambda[\text { Let }] \\
& \because A P \perp \text { line } \\
& \therefore A P \cdot(3 i-2 \hat{j}+\hat{k})=0 \\
& (3 \lambda-5) \times 3+(-2 \lambda+2)(-2)+(\lambda-1) \times 1=0 \\
& 9 \lambda-15+4 \lambda-4+\lambda-1=0 \\
& 14 \lambda=20 \\
& \lambda=\frac{10}{7} \\
& \Rightarrow P\left(\frac{16}{7}, \frac{8}{7}, \frac{10}{7}\right) \\
& \Rightarrow \alpha+\beta+\gamma=\frac{16+8+10}{7}=\frac{34}{7} \\
& 21(\alpha+\beta+\gamma)=102
\end{aligned}
\) -
Question 139 of 150
139. Question
Consider the three planes
\(
P_1: 3 x+15 y+21 z=9,
\)
\(P_2: x-3 y-z=5\), and
\(
P_3: 2 x+10 y+14 z=5
\)
Then, which one of the following is true? [JEE Main 2021 (Online) 26th February Morning Shift]CorrectIncorrectHint
\(
\begin{aligned}
& P_1: 3 x+15 y+21 z=9 \\
& P_2: x-3 y-z=5 \\
& P_3: x+5 y+7 z=5 / 2
\end{aligned}
\)
\(\therefore P_1\) and \(P_3\) are parallel. -
Question 140 of 150
140. Question
If \((1,5,35),(7,5,5),(1, \lambda, 7)\) and \((2 \lambda, 1,2)\) are coplanar, then the sum of all possible values of \(\lambda\) is : [JEE Main 2021 (Online) 26th February Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& A (1,5,35), B (7,5,5), C (1, \lambda, 7), D (2 \lambda, 1,2) \\
& \overrightarrow{A B}=6 \hat{i}-30 \widehat{k} \\
& \overrightarrow{B C}=-6 \hat{i}(\lambda-5) \hat{j}+2 \widehat{k} \\
& \overrightarrow{C D}=(2 \lambda-1) \hat{i}+(1-\lambda) \hat{j}-5 \widehat{k}
\end{aligned}
\)
Points are coplanar
\(
\begin{aligned}
& \Rightarrow 0=\left|\begin{array}{ccc}
6 & 0 & -30 \\
-6 & \lambda-5 & 2 \\
2 \lambda-1 & 1-\lambda & -5
\end{array}\right| \\
& =6(-5 \lambda+25-2+2 \lambda)-30\left(-6+6 \lambda-\left(2 \lambda^2-\lambda-10 \lambda+5\right)\right) \\
& =6(-3 \lambda+23)-30\left(-2 \lambda^2+11 \lambda-5-6+6 \lambda\right) \\
& =6(-3 \lambda+23)-30\left(-2 \lambda^2+17 \lambda-11\right) \\
& =6\left(-3 \lambda+23+10 \lambda^2-85 \lambda+55\right) \\
& =6\left(10 \lambda^2-88 \lambda+78\right)=12\left(5 \lambda^2-44 \lambda+39\right) \\
& \Rightarrow 0=12\left(5 \lambda^2-44 \lambda+39\right) \\
& \Rightarrow 5 \lambda^2-44 \lambda+39=0
\end{aligned}
\)
this quadratic equation has two values \(\lambda_1\) and \(\lambda_2\)
\(
\therefore \lambda_1+\lambda_2=\frac{44}{5}
\) -
Question 141 of 150
141. Question
A plane passes through the points \(A(1,2,3), B(2,3,1)\) and \(C(2,4,2)\). If \(O\) is the origin and \(P\) is \((2,-1,1)\), then the projection of \(\overrightarrow{O P}\) on this plane is of length: [JEE Main 2021 (Online) 25th February Evening Shift]
CorrectIncorrectHint
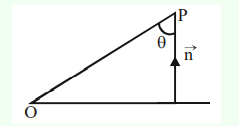
Normal to plane
\(
\begin{aligned}
& \vec{n}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & 1 & -2 \\
0 & 1 & 1
\end{array}\right| \\
& =3 \hat{i}-\hat{j}+\hat{k} \\
& \overrightarrow{O P}=2 \hat{i}-\hat{j}+\hat{k} \\
& \cos \theta=\frac{6+1+1}{\sqrt{6} \sqrt{11}}=\frac{8}{\sqrt{66}} \\
& \Rightarrow \sin \theta=\sqrt{\frac{2}{66}} \\
& \therefore \text { Projection of } \overrightarrow{O P} \text { on plane }=|\overrightarrow{O P}| \sin \theta \\
& =\sqrt{\frac{2}{11}}
\end{aligned}
\) -
Question 142 of 150
142. Question
The equation of the line through the point \((0,1,2)\) and perpendicular to the line \(\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-1}{-2}\) is : [JEE Main 2021 (Online) 25th February Morning Shift]
CorrectIncorrectHint
Given: \(\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-1}{-2}\)
Let \(\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-1}{-2}=\lambda\)
Any point on the line \((2 \lambda+1,3 \lambda-1,-2 \lambda+1)\)
Direction ratio of given line \(\overrightarrow{d_1}=(2,3,-2)\)
Direction ratio of the line to be found
\(
\overrightarrow{d_2}=(2 \lambda+1-0,3 \lambda-1-1,-2 \lambda+1-2)=(2 \lambda+1,3 \lambda-2,-2 \lambda-1)
\)
Since, \(\overrightarrow{d_1} . \overrightarrow{d_2}=0\)
\(
\begin{aligned}
& \Rightarrow 4 \lambda+2+9 \lambda-6+4 \lambda+2=0 \\
& \Rightarrow 17 \lambda-2=0 \\
& \Rightarrow \lambda=\frac{2}{17}
\end{aligned}
\)
Therefore,
\(
\begin{aligned}
& \overrightarrow{d_2}=\left(2\left(\frac{2}{17}\right)+1,3\left(\frac{2}{17}\right)-2,-2\left(\frac{2}{17}\right)-1\right) \\
& \rightarrow \\
& \Rightarrow d_2=\left(\frac{21}{17}, \frac{-28}{17}, \frac{-21}{17}\right) \\
& \rightarrow \\
& \Rightarrow d_2=(-3,4,3) \\
&
\end{aligned}
\)
Therefore the equation of the line is \(\frac{x}{-3}=\frac{y-1}{4}=\frac{z-2}{3}\). -
Question 143 of 150
143. Question
Let \(\alpha\) be the angle between the lines whose direction cosines satisfy the equations \(l+m-n=0\) and \(l^2+m^2-n^2=0\). Then the value of \(\sin ^4 \alpha+\cos ^4 \alpha\) is : [JEE Main 2021 (Online) 25th February Morning Shift]
CorrectIncorrectHint
\(
\begin{aligned}
& l^2+m^2+n^2=1 \\
& \therefore 2 n^2=1\left(\because l^2+ m ^2- n ^2=0\right) \\
& \Rightarrow n= \pm \frac{1}{\sqrt{2}} \\
& \therefore l^2+m^2=\frac{1}{2} \& l+m=\frac{1}{\sqrt{2}} \\
& \Rightarrow \frac{1}{2}-2 l m=\frac{1}{2} \\
& \Rightarrow l m=0 \text { or } m=0 \\
& \therefore l=0, m=\frac{1}{\sqrt{2}} \text { or } l=\frac{1}{\sqrt{2}} \\
& <0, \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}>\text { or }<\frac{1}{\sqrt{2}}, 0, \frac{1}{\sqrt{2}}> \\
& \therefore \cos \alpha=0+0+\frac{1}{2}=\frac{1}{2} \\
& \therefore \sin ^4 \alpha+\cos ^4 \alpha=1-\frac{1}{2} \sin ^2(2 \alpha)=1-\frac{1}{2} \cdot \frac{3}{4}=\frac{5}{8}
\end{aligned}
\) -
Question 144 of 150
144. Question
Let \(a, b \in R\). If the mirror image of the point \(P(a, 6,9)\) with respect to the line \(\frac{x-3}{7}=\frac{y-2}{5}=\frac{z-1}{-9}\) is \((20, b ,- a -9)\), then \(| a + b |\), is equal to : [JEE Main 2021 (Online) 24th February Evening Shift]
CorrectIncorrectHint
Given, \(P ( a , 6,9)\)
Equation of line \(\frac{x-3}{7}=\frac{y-2}{5}=\frac{z-1}{-9}\)
Image of point \(P\) with respect to line is point \(Q(20, b,-a-9)\)
Mid-point of \(P\) and \(Q =\left(\frac{a+20}{2}, \frac{6+b}{2}, \frac{-a}{2}\right)\)
This point lies on line
\(
\begin{aligned}
& \therefore \frac{\frac{a+20}{2}-3}{7}=\frac{\frac{6+b}{2}-2}{5}=\frac{\frac{-a}{2}-1}{-9} \\
& \Rightarrow \frac{a+14}{14}=\frac{b+2}{10}=\frac{a+2}{18} \\
& \Rightarrow \frac{a+14}{14}=\frac{a+2}{18} \text { and } \frac{b+2}{10}=\frac{a+2}{18}
\end{aligned}
\)
Solving, we get \(a=-56, b=-32\)
\(
\therefore|a+b|=|-56-32|=88
\) -
Question 145 of 150
145. Question
The vector equation of the plane passing through the intersection of the planes \(\vec{r} .(\hat{i}+\hat{j}+\widehat{k})=1\) and \(\vec{r} .(\hat{i}-2 \hat{j})=-2\), and the point \((1,0,2)\) is: [JEE Main 2021 (Online) 24th February Evening Shift]
CorrectIncorrectHint
Given, point \((1,0,2)\)
Equation of plane \(=\)
\(
\vec{r} \cdot(\hat{i}+\hat{j}+\widehat{k})=1 \text { and } \vec{r} \cdot(\hat{i}-2 \hat{j})=-2
\)
Equation of plane passing through the intersection of given planes is
\(
\begin{aligned}
& \vec{r} \cdot(\hat{i}+\hat{j}+\widehat{k})-1]+\lambda[\vec{r} \cdot(\hat{i}-2 \hat{j})+2]=0 \\
& \because \text { This plane passes through point }(1,0,2) \text { i.e., } \\
& \text { vector }(\hat{i}+2 \widehat{k}) \\
& \therefore[(\hat{i}+2 \widehat{k}) \cdot(\hat{i}+\hat{j}+\widehat{k})-1]+\lambda[(\hat{i}+2 \widehat{k}) \cdot(\hat{i}-2 \hat{j})+2]=0 \\
& \Rightarrow(3-1)+\lambda(1+2)=0 \\
& \Rightarrow 2+\lambda \times 3=0 \\
& \Rightarrow \lambda=-2 / 3
\end{aligned}
\)
Hence, equation of required plane is
\(
\begin{aligned}
& \left.\vec{r} \cdot(\hat{i}+\hat{j}+\widehat{k})-1]+\left(\frac{-2}{3}\right) \vec{r} \cdot(\hat{i}-2 \hat{j})+2\right]=0 \\
& \Rightarrow 3[\vec{r} \cdot(\hat{i}+\hat{j}+\widehat{k})-1]-2[\vec{r} \cdot(\hat{i}-2 \hat{j})+2]=0 \\
& \Rightarrow \vec{r} \cdot(\hat{i}+7 \hat{j}+3 \widehat{k})=7
\end{aligned}
\) -
Question 146 of 150
146. Question
The equation of the plane passing through the point \((1,2,-3)\) and perpendicular to the planes \(3 x+y-2 z=5\) and \(2 x-5 y-z=7\), is : [JEE Main 2021 (Online) 24th February Morning Shift]
CorrectIncorrectHint
Given, equation of planes are
\(
\begin{aligned}
& 3 x+y-2 z=5 \\
& 2 x-5 y-z=7
\end{aligned}
\)
and point \((1,2,3)\).
Normal vector of required plane \(= n =\left|\begin{array}{ccc}\hat{i} & \hat{j} & \widehat{k} \\ 3 & 1 & -2 \\ 2 & -5 & -1\end{array}\right|\)
\(
\begin{aligned}
& =\hat{i}(-1-10)-\hat{j}(-3+4)+\widehat{k}(-15-2) \\
& =-11 \hat{i}-\hat{j}-17 \widehat{k}
\end{aligned}
\)
Now, the equation of plane passing through \((1,2,-3)\) having normal vector \(-11 \hat{i}-\hat{j}\) \(-17 \widehat{k}\) is
\(
\begin{aligned}
& -[11(x-1)+(y-2)+17(z+3)]=0 \\
& \Rightarrow 11 x+y+17 z+38=0
\end{aligned}
\) -
Question 147 of 150
147. Question
The distance of the point \((1,1,9)\) from the point of intersection of the line \(\frac{x-3}{1}=\frac{y-4}{2}=\frac{z-5}{2}\) and the plane \(x+y+z=17\) is : [JEE Main 2021 (Online) 24th February Morning Shift]
CorrectIncorrectHint
Given, \(P(1,1,9)\).
Equation of plane \(x+y+z=17\)
Equation of line \(\Rightarrow \frac{x-3}{1}=\frac{y-4}{2}=\frac{z-5}{2}\)
\(
\begin{aligned}
& \Rightarrow \frac{x-3}{1}=\frac{y-4}{2}=\frac{z-5}{2}=\lambda \text { (let) } \\
& \Rightarrow x =\lambda+3 ; y =2 \lambda+4 ; z =2 \lambda+5
\end{aligned}
\)
\(\therefore\) The point we have is \((\lambda+3,2 \lambda+4,2 \lambda+5)\).
\(\because\) This point lies on the plane \(x+y+z=17\).
\(
\begin{aligned}
& \therefore \lambda+3+2 \lambda+4+2 \lambda+5=17 \\
& \Rightarrow \lambda=1
\end{aligned}
\)
\(\therefore\) The coordinate of point is \((4,6,7)\)
\(\therefore\) Required distance between \((1,1,9)\) and \((4,6,7)\) is
\(
\begin{aligned}
& =\sqrt{(4-1)^2+(6-1)^2+(7-9)^2} \\
& =\sqrt{9+25+4}=\sqrt{38}
\end{aligned}
\) -
Question 148 of 150
148. Question
A plane \(P\) meets the coordinate axes at \(A , B\) and \(C\) respectively. The centroid of \(\Delta\) \(A B C\) is given to be \((1,1,2)\). Then the equation of the line through this centroid and perpendicular to the plane \(P\) is : [JEE Main 2020 (Online) 6th September Evening Slot]
CorrectIncorrectHint
Let, Equation of plane is
\(
\begin{aligned}
& \frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1 \\
& A =(a, 0,0) B =(0, b , 0), C =(0,0, c ) \\
& \therefore \text { Centroid }=\left(\frac{a}{3}, \frac{b}{3}, \frac{c}{3}\right)=(1,1,2) \\
& \Rightarrow a=3, b =3, c =6 \\
& \therefore \text { Plane }: \frac{x}{3}+\frac{y}{3}+\frac{z}{6}=1 \\
& \Rightarrow 2 x +2 y + z =6
\end{aligned}
\)
The equation of the line through this centroid \((1,1,2)\) and perpendicular to the plane \(2 x+2 y+z=6\) is :
\(
\frac{x-1}{2}=\frac{y-1}{2}=\frac{z-2}{1}
\) -
Question 149 of 150
149. Question
The shortest distance between the lines
\(
\frac{x-1}{0}=\frac{y+1}{-1}=\frac{z}{1}
\)
and \(x+y+z+1=0,2 x-y+z+3=0\) is : [JEE Main 2020 (Online) 6th September Morning Slot]CorrectIncorrectHint
Plane through line of intersection is
\(
x+y+z+1+\lambda(2 x-y+z+3)=0
\)
It should be parallel to given line \(\frac{x-1}{0}=\frac{y+1}{-1}=\frac{z}{1}\)
\(
\therefore 0(1+2 \lambda)-1(1-\lambda)+1(1+\lambda)=0 \Rightarrow \lambda=0
\)
\(\therefore\) Required Plane : \(x+y+z+1=0\)
Shortest distance of \((1,-1,0)\) from this plane
\(
=\frac{|1-1+0+1|}{\sqrt{1^2+1^2+1^2}}=\frac{1}{\sqrt{3}}
\) -
Question 150 of 150
150. Question
If for some \(\alpha \in R\), the lines
\(L _1: \frac{x+1}{2}=\frac{y-2}{-1}=\frac{z-1}{1}\) and
\(L _2: \frac{x+2}{\alpha}=\frac{y+1}{5-\alpha}=\frac{z+1}{1}\) are coplanar,
then the line \(L_2\) passes through the point : [JEE Main 2020 (Online) 5th September Evening Slot]CorrectIncorrectHint
\(L _1: \frac{x+1}{2}=\frac{y-2}{-1}=\frac{z-1}{1}\) and
\(L _2: \frac{x+2}{\alpha}=\frac{y+1}{5-\alpha}=\frac{z+1}{1}\) are coplanar.
\(
\begin{aligned}
& \therefore\left|\begin{array}{ccc}
1 & 3 & 2 \\
2 & -1 & 1 \\
\alpha & 5-\alpha & 1
\end{array}\right|=0 \\
& \Rightarrow-1(-1+\alpha-5)+3(2-\alpha)-2(10-2 \alpha+\alpha)=0 \\
& \Rightarrow 6-\alpha+6-3 \alpha+2 \alpha-20=0 \\
& \Rightarrow-8-2 \alpha=0 \\
& \Rightarrow \alpha=-4
\end{aligned}
\)
\(\therefore\) Equation of \(L _2: \frac{x+2}{-4}=\frac{y+1}{9}=\frac{z+1}{1}\)
Check options \((2,-10,-2)\) lies on \(L_2\).