Past JEE Main Entrance Paper
Overview
Set and their representations
A set is a well-defined collection of objects. There are two methods of representing a set
- Roaster or tabular form
- Set builder form
The empty set
A set which does not contain any element is called the empty set or the void set or null set and is denoted by \(\{\} \text { or } \phi \text {. }\)
Finite and infinite sets
A set which consists of a finite number of elements is called a finite set otherwise, the set is called an infinite set.
Subsets
A set A is said to be a subset of set B if every element of \(A\) is also an element of \(B\). In symbols we write \(A \subset B\) if \(a \in A \Rightarrow a \in B\).
We denote
\(
\begin{aligned}
& \text { set of real numbers by } R \\
& \text { set of natural numbers by } N \\
& \text { set of integers by } Z \\
& \text { set of rational numbers by } Q \\
& \text { set of irrational numbers by } T
\end{aligned}
\)
We observe that
\(
\begin{aligned}
& N \subset Z \subset Q \subset R , \\
& T \subset R , Q \not \subset T , N \not \subset T
\end{aligned}
\)
Equal sets
Given two sets \(A\) and \(B\), if every elements of \(A\) is also an element of \(B\) and if every element of \(B\) is also an element of \(A\), then the sets \(A\) and \(B\) are said to be equal. The two equal sets will have exactly the same elements.
Intervals as subsets of \(R\)
Let \(a, b \in R\) and \(a<b\). Then
- An open interval denoted by \((a, b)\) is the set of real numbers \(\{x: a<x<b\}\)
- A closed interval denoted by \([a, b]\) is the set of real numbers \(\{x: a \leq x \leq b)\)
- Intervals closed at one end and open at the other are given by
\(
\begin{aligned}
& {[a, b)=\{x: a \leq x<b\}} \\
& (a, b]=\{x: a<x \leq b\}
\end{aligned}
\)
Power set
The collection of all subsets of a set A is called the power set of A. It is denoted by \(P ( A )\). If the number of elements in \(A =n\), i.e., \(n( A )=n\), then the number of elements in \(P ( A )=2^n\).
Universal set
This is a basic set; in a particular context whose elements and subsets are relevant to that particular context. For example, for the set of vowels in English alphabet, the universal set can be the set of all alphabets in English. Universal set is denoted by \(U\).
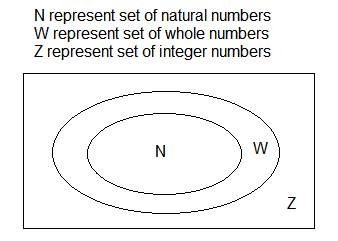
Venn diagrams
Venn Diagrams are the diagrams which represent the relationship between sets. For example, the set of natural numbers is a subset of set of whole numbers which is a subset of integers. We can represent this relationship through Venn diagram in the following way.
Operations on sets
Union of Sets : The union of any two given sets \(A\) and \(B\) is the set \(C\) which consists of all those elements which are either in \(A\) or in \(B\). In symbols, we write
\(
C = A \cup B =\{x \mid x \in A \text { or } x \in B \}
\)
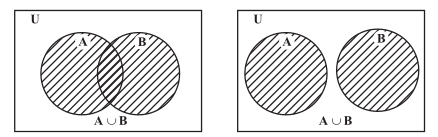
Some properties of the operation of union.
- \(A \cup B = B \cup A\)
- \(( A \cup B ) \cup C = A \cup( B \cup C )\)
- \(A \cup \phi= A\)
- \(A \cup A = A\)
- \(U \cup A = U\)
Intersection of sets: The intersection of two sets \(A\) and \(B\) is the set which consists of all those elements which belong to both A and B. Symbolically, we write \(A \cap B =\{x: x \in A\) and \(x \in B \}\).
When \(A \cap B =\phi\), then \(A\) and \(B\) are called disjoint sets.
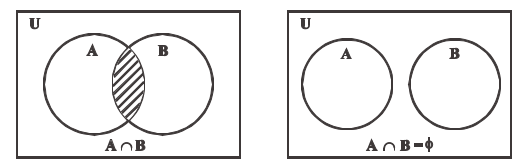
Some properties of the operation of intersection
- \(A \cap B = B \cap A\)
- \(( A \cap B ) \cap C = A \cap( B \cap C )\)
- \(\phi \cap A =\phi ; U \cap A = A\)
- \(A \cap A = A\)
- \(A \cap( B \cup C )=( A \cap B ) \cup( A \cap C )\)
- \(A \cup( B \cap C )=( A \cup B ) \cap( A \cup C )\)
Difference of sets: The difference of two sets \(A\) and \(B\), denoted by \(A – B\) is defined as set of elements which belong to \(A\) but not to \(B\). We write
also,
\(
\begin{aligned}
& A – B =\{x: x \in A \text { and } x \notin B \} \\
& B – A =\{x: x \in B \text { and } x \notin A \}
\end{aligned}
\)
Complement of a set: Let \(U\) be the universal set and \(A\) a subset of \(U\). Then the complement of \(A\) is the set of all elements of \(U\) which are not the elements of \(A\). Symbolically, we write
\(
A ^{\prime}=\{x: x \in U \text { and } x \notin A \} \text {. Also } A ^{\prime}= U – A
\)
Some properties of complement of sets
- Law of complements:
(a) \(A \cup A ^{\prime}= U\)
(b) \(A \cap A ^{\prime}=\phi\) - (ii) De Morgan’s law
(a) \((A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}\)
(b) \(( A \cap B )^{\prime}= A ^{\prime} \cup B ^{\prime}\) - \(\left( A ^{\prime}\right)^{\prime}= A\)
- \(U ^{\prime}=\phi\) and \(\phi^{\prime}= U\)
Formulae to solve practical problems on union and intersection of two sets
Let \(A , B\) and \(C\) be any finite sets. Then
- \(n( A \cup B )=n( A )+n( B )-n( A \cap B )\)
- If \(( A \cap B )=\phi\), then \(n( A \cup B )=n( A )+n\) (B)
- \(n( A \cup B \cup C )= n( A )+n( B )+n( C )-n( A \cap B )-n( A \cap C )-n( B \cap C ) +n( A \cap B \cap C )\)
Quiz Summary
0 of 45 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 45 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 45
1. Question
Let \(\mathrm{S}=\{1,2,3, \ldots, 100\}\). The number of non-empty subsets A of \(\mathrm{S}\) such that the product of elements in \(\mathrm{A}\) is even is: [Main Jan. 12, 2019(I)]
CorrectIncorrectHint
(b) Product of two even numbers is always even andthe product of two odd numbers is always odd.
\(\therefore\) Number of required subsets
\(=\) Total number of subsets – Total number of subsets having only odd numbers
\(
=2^{100}-2^{50}=2^{50}\left(2^{50}-1\right)
\)Explanation:
You are solving for the number of non-empty subsets of \(S=\{1,2,3, \ldots, 100\}\) where the product of elements in each subset is even.
What’s given in the problem
The set is \(S=\{1,2,3, \ldots, 100\}\).
We need to find the number of non-empty subsets.
The product of elements in the subset must be even.
A product of integers is even if and only if at least one of the integers is even.
A product of integers is odd if and only if all of the integers are odd.
How to solve?
Calculate the total number of non-empty subsets and subtract the number of non-empty subsets containing only odd numbers.Find the total number of non-empty subsets of \(S\):
The total number of elements in \(S\) is \(n=100\).
The total number of subsets is \(2^n=2^{100}\).
The total number of non-empty subsets is \(2^{100}-1\).Find the number of non-empty subsets containing only odd numbers:
The number of odd elements in \(S\) is 50 (i.e., \(\{1,3, \ldots, 99\}\) ).
The number of subsets formed only by odd numbers is \(2^{50}\).
The number of non-empty subsets formed only by odd numbers is \(2^{50}-1\).Calculate the number of non-empty subsets with an even product:
Subtract the number of non-empty subsets with an odd product from the total number of non-empty subsets.
Number of subsets with even product \(=\left(2^{100}-1\right)-\left(2^{50}-1\right)\).
Number of subsets with even product \(=2^{100}-2^{50}\).
This can be factored as \(2^{50}\left(2^{50}-1\right)\). -
Question 2 of 45
2. Question
Let \(\mathrm{S}=\{\mathrm{x} \in \mathrm{R}: \mathrm{x} \geq 0\) and \(2|\sqrt{\mathrm{x}}-3|+\sqrt{\mathrm{x}}(\sqrt{\mathrm{x}}-6)+6=0\). Then \(\mathrm{S}\): [Main 2018]
CorrectIncorrectHint
(b) You are solving for the set S containing non-negative real numbers x that satisfy the given equation.
What’s given in the problem
The set \(S\) is defined as \(S=\{x \in R: x \geq 0\) and \(2|\sqrt{x}-3|+\sqrt{x}(\sqrt{x}-6)+6=0\}\).
How to solve?
Solve the equation by substituting \(y=\sqrt{x}\) and considering two cases based on the absolute value.Step 1: Substitute \(\mathrm{y}=\sqrt{\mathrm{x}}\)
Let \(\mathrm{y}=\sqrt{\mathrm{x}}\).
The equation becomes \(2|y-3|+y(y-6)+6=0\).
Expand the term: \(2|y-3|+y^2-6 y+6=0\).Step 2: Consider Case 1: \(y \geq 3\)
If \(y \geq 3\), then \(|y-3|=y-3\).
Substitute into the equation: \(2(y-3)+y^2-6 y+6=0\).
Simplify: \(2 y-6+y^2-6 y+6=0\).
Combine terms: \(y^2-4 y=0\).
Factor: \(\mathrm{y}(\mathrm{y}-4)=0\).
Solutions for y are \(\mathrm{y}=0\) or \(\mathrm{y}=4\).
Since \(\mathrm{y} \geq 3\), we accept \(\mathrm{y}=4\).
Step 3: Consider Case 2: \(y<3\)
If \(y<3\), then \(|y-3|=-(y-3)=3-y\).
Substitute into the equation: \(2(3-y)+y^2-6 y+6=0\).
Simplify: \(6-2 y+y^2-6 y+6=0\).
Combine terms: \(y^2-8 y+12=0\).
Factor: \((y-2)(y-6)=0\).
Solutions for \(y\) are \(y=2\) or \(y=6\).
Since \(\mathrm{y}<3\), we accept \(\mathrm{y}=2\).Step 4: Convert back to x
For \(y=4: \sqrt{x}=4 \Longrightarrow x=4^2=16\).
For \(y=2: \sqrt{x}=2 \Longrightarrow x=2^2=4\).
Both \(x=16\) and \(x=4\) satisfy \(x \geq 0\).
The set \(S\) contains exactly two elements, \(S=\{4,16\}\). -
Question 3 of 45
3. Question
If \(f(x)+2 f\left(\frac{1}{x}\right)=3 x, x \neq 0\) and \(\mathrm{S}=\{\mathrm{x} \in \mathrm{R}: \mathrm{f}(\mathrm{x})=\mathrm{f}(-\mathrm{x})\}\); then \(\mathrm{S}\): [Main 2016]
CorrectIncorrectHint
(a) \(f(x)+2 f\left(\frac{1}{x}\right)=3 x \text { ..(i) }\)
\(f\left(\frac{1}{x}\right)+2 f(x)=\frac{3}{x} \text { ..(ii) }\)
Adding (i) and (ii)
\(
\Rightarrow f(x)+f\left(\frac{1}{x}\right)=x+\frac{1}{x} \text { ..(iii) }
\)
Substracting (i) from (ii)
\(
\Rightarrow f(x)-f\left(\frac{1}{x}\right)=\frac{3}{x}-3 x \text { ..(iv) }
\)
On adding (iii) and (iv)
\(
\begin{aligned}
&\Rightarrow f(x)=\frac{2}{x}-x \\
&f(x)=f(-x) \Rightarrow \frac{2}{x}-x=\frac{-2}{x}+x \Rightarrow x=\frac{2}{x} \\
&x^{2}=2 \quad \text { or } x=\sqrt{2},-\sqrt{2}
\end{aligned}
\) -
Question 4 of 45
4. Question
Let \(\mathrm{P}=\{\theta: \sin \theta-\cos \theta=\sqrt{2} \cos \theta\}\) and \(\mathrm{Q}=\{\theta: \sin \theta+\cos \theta=\sqrt{2} \sin \theta\}\) be two sets. Then [ JEE Main 2016 10th April]
CorrectIncorrectHint
(d) \(\mathrm{P}=\{\theta: \sin \theta-\cos \theta=\sqrt{2} \cos \theta\}\)
\(
\Rightarrow \sin \theta=(\sqrt{2}+1) \cos \theta \Rightarrow \tan \theta=\sqrt{2}+1
\)
Now, \(Q=\{\theta: \sin \theta+\cos \theta=\sqrt{2} \sin \theta\}\)
\(
\begin{aligned}
\Rightarrow \cos \theta=(\sqrt{2}-1) \sin \theta \Rightarrow \tan \theta=\frac{1}{\sqrt{2}-1} \times \frac{\sqrt{2}+1}{\sqrt{2}+1} \\
\Rightarrow \tan \theta=\sqrt{2}+1 \\
\therefore \quad \mathrm{P}=\mathrm{Q}
\end{aligned}
\) -
Question 5 of 45
5. Question
Let \(S=\{1,2,3,4\}\). The total number of unordered pairs of disjoint subsets of \(\mathrm{S}\) is equal to [2010]
CorrectIncorrectHint
(d) \(\mathrm{S}=\{1,2,3,4\}\)
Let \(\mathrm{A}\) and \(\mathrm{B}\) be disjoint subsets of \(\mathrm{S}\)
Now for any element \(a \in S\), has got three possibilities either, it is in A or B
or none
\(\Rightarrow\) For every element out of 4 elements there are three choices
\(\therefore\) Total options \(=3^{4}=81\)
Here \(\mathrm{A} \neq \mathrm{B}\) except when \(\mathrm{A}=\mathrm{B}=\phi\)
\(\therefore 81-1=80\) ordered pairs \((\mathrm{A}, \mathrm{B})\) are there for which \(\mathrm{A} \neq \mathrm{B}\)
Hence total number of unordered pairs of disjoint subsets \(=\frac{80}{2}+1=41\) -
Question 6 of 45
6. Question
Set A has \(m\) elements and set B has \(n\) elements. If the total number of subsets of A is 112 more than the total number of subsets of B, then the value of \(m \cdot n\) is _____ [Main Sep. 06, 2020]
CorrectIncorrectHint
(b) \(2^{m}=112+2^{n} \Rightarrow 2^{m}-2^{n}=112\)
\(
\Rightarrow 2^{n}\left(2^{m-n}-1\right)=2^{4}\left(2^{3}-1\right)
\)
\(
\therefore m=7, n=4 \Rightarrow m n=28
\) -
Question 7 of 45
7. Question
Let \(S=\{1,2,3, \ldots, 9\}\). For \(\mathrm{k}=1,2, \ldots, 5\), let \(\mathrm{N}_{\mathrm{k}}\) be the number of subsets of \(\mathrm{S}\), each containing five elements out of which exactly \(\mathrm{k}\) are odd. Then \(\mathrm{N}_{1}+\mathrm{N}_{2}+\mathrm{N}_{3}+\mathrm{N}_{4}+\mathrm{N}_{5}=\) [JEE 2017]
CorrectIncorrectHint
(d) Here set S contains 5 odd and 4 even numbers. Since each of \(\mathrm{N}_{\mathrm{K}}\) containing five elements out of which exactly are odd.
\(\begin{aligned}
&\therefore \mathrm{N}_{1}={ }^{5} \mathrm{C}_{1} \times{ }^{4} \mathrm{C}_{4}=5 \\
&\mathrm{~N}_{2}={ }^{5} \mathrm{C}_{2} \times{ }^{4} \mathrm{C}_{3}=40 \\
&\mathrm{~N}_{3}={ }^{5} \mathrm{C}_{3} \times{ }^{4} \mathrm{C}_{2}=60 \\
&\mathrm{~N}_{4}={ }^{5} \mathrm{C}_{4} \times{ }^{4} \mathrm{C}_{1}=20 \\
&\mathrm{~N}_{5}={ }^{5} \mathrm{C}_{5}=1 \\
&\therefore \mathrm{N}_{1}+\mathrm{N}_{2}+\mathrm{N}_{3}+\mathrm{N}_{4}+\mathrm{N}_{5}=126
\end{aligned}\) -
Question 8 of 45
8. Question
A survey shows that \(73 \%\) of the persons working in an office like coffee, whereas \(65 \%\) like tea. If \(x\) denotes the percentage of them, who like both coffee and tea, then \(x\) cannot be: [Main Sep. 05, 2020(I)]
CorrectIncorrectHint
(b) \(C \rightarrow\) person like coffee
\(T \rightarrow\) person like Tea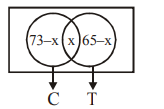
\(
\begin{aligned}
& n(C)=73 \\
& n(T)=65 \\
& n(C \cup T) \leq 100 \\
& n(C)+n(T)-n(C \cap T) \leq 100 \\
& 73+65-x \leq 100 \\
& x \geq 38 \\
& 73-x \geq 0 \Rightarrow x \leq 73 \\
& 65-x \geq 0 \Rightarrow x \leq 65 \\
& 38 \leq x \leq 65
\end{aligned}
\)\(
\Rightarrow x \neq 36 .
\) -
Question 9 of 45
9. Question
A survey shows that \(63 \%\) of the people in a city read newspaper \(A\) whereas \(76 \%\) read newspaper \(B\). If \(x \%\) of the people read both the newspapers, then a possible value of \(x\) can be: [Main Sep. 04,2020(I)]
CorrectIncorrectHint
(d) Let \(n(U)=100\), then \(n(A)=63, n(B)=76\)
\(
n(A \cap B)=x
\)
Now,
\(
\begin{aligned}
&n(A \cup B)=n(A)+n(B)-n(A \cap B) \leq 100 \\
&=63+76-x \leq 100 \\
&\Rightarrow x \geq 139-100 \Rightarrow x \geq 39 \\
&\because n(A \cap B) \leq n(A) \Rightarrow x \leq 63 \\
&\therefore 39 \leq x \leq 63
\end{aligned}
\)\(
\text { From options possible value of } x=55 \text {. }
\) -
Question 10 of 45
10. Question
\(\text { Let } \bigcup_{i=1}^{50} X_i=\bigcup_{i=1}^n Y_i=T \text {, }\) where each \(X_i\) contains 10 elements and each \(Y_i\) contains 5 elements. If each element of the set \(T\) is an element of exactly 20 of sets \(X_i^{\prime}\) ‘s and exactly 6 of sets \(Y_i^{\prime}\) ‘s, then \(n\) is equal to [JEE Main 2020 4th Sept Shift 2]
CorrectIncorrectHint
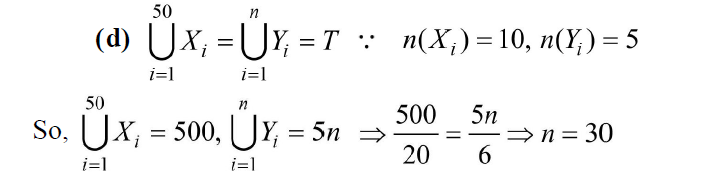
Explanation: \(\cup_{i=1}^{50} X_i=\mathrm{X}_1, \mathrm{X}_2, \ldots . ., \mathrm{X}_{50}=50\) sets. Given each sets having 10 elements.
So total elements \(=50 \times 10\)
\(\cup_{i=1}^n Y_i=\mathrm{Y}_1, \mathrm{Y}_2, \ldots . ., \mathrm{Y}_{\mathrm{n}}=\mathrm{n}\) sets. Given each sets having 5 elements.
So total elements \(=5 \times n\)
Now each element of set T contains exactly 20 of sets \(\mathrm{X}_{\mathrm{i}}\).
So number of effective elements in set \(T=\frac{50 \times 10}{20}\)
Also each element of set T contains exactly 6 of sets \(\mathrm{Y}_{\mathrm{i}}\).
So number of effective elements in set \(T=\frac{50 \times n}{6}\)
\(
\begin{aligned}
& \therefore \frac{50 \times 10}{20}=\frac{5 \times n}{6} \\
& \Rightarrow \mathrm{n}=30
\end{aligned}
\) -
Question 11 of 45
11. Question
Let \(Z\) be the set of integers. If \(A=\left\{x \in Z: 2^{(x+2)\left(x^{2}-5 x+6\right)}=1\right\}\) and \(B\{x \in Z:-3<2 x-1<9\}\), then the number of subsets of the set \(A \times B\), is: [Main Jan. 12, 2019 (II)]
CorrectIncorrectHint
\(
\begin{aligned}
A=\{x \in Z, \quad& 2^{(x+2)\left(x^{2}-5 x+6\right)}=2^{0} \\
&(x+2)\left(x^{2}-5 x+6\right)=0 \\
& x=-2,2,3
\end{aligned}
\)\(
\begin{aligned}
B=\{x \in Z, \quad&-3<2 x-1<9 \\
\Rightarrow &-2<2 x<10 \\
\Rightarrow &-1<x<5
\end{aligned}
\)\(
\begin{aligned}
&x=0,1,2,3,4 \\
&A \times B=\{(-2,0),(-2,1)(-2,2)(-2,3)(-2,4),(2,0),(2,1)(2,2),(2,3),(2,4)(3,0),(3,1) \\
&(3,2)(3,3),(3,4)] \\
&A \times B \text { elements }=15 \\
&\text { total subsets }=2^{15}
\end{aligned}
\) -
Question 12 of 45
12. Question
In a class of 140 students numbered 1 to 140, all even numbered students opted Mathematics course, those whose number is divisible by 3 opted Physics course and those whose number is divisible by 5 opted Chemistry course. Then the number of students who did not opt for any of the three courses is: [Main Jan. 10, 2019(II)]
CorrectIncorrectHint
(d) Let \(\mathrm{n}(\mathrm{A})=\) number of students opted Mathematics \(=70\),
\(\mathrm{n}(\mathrm{B})=\) number of students opted Physics \(=46\),
\(\mathrm{n}(\mathrm{C})=\) number of students opted Chemistry \(=28\),
\(\mathrm{n}(\mathrm{A} \cap \mathrm{B})=23\)
\(\mathrm{n}(\mathrm{B} \cap \mathrm{C})=9\)
\(\mathrm{n}(\mathrm{A} \cap \mathrm{C})=14\),
\(\mathrm{n}(\mathrm{A} \cap \mathrm{B} \cap \mathrm{C})=4\)
Nown( \(\mathrm{A} \cup \mathrm{B} \cup \mathrm{C})\)
\(=\mathrm{n}(\mathrm{A})+\mathrm{n}(\mathrm{B})+\mathrm{n}(\mathrm{C})-\mathrm{n}(\mathrm{A} \cap \mathrm{B})-\mathrm{n}(\mathrm{B} \cap \mathrm{C})-\mathrm{n}(\mathrm{A} \cap \mathrm{C})+\mathrm{n}(\mathrm{A} \cap \mathrm{B} \cap \mathrm{C})\) \(=70+46+28-23-9-14+4=102\)So number of students not opted for any course \(=\) Total \(-\mathrm{n}(\mathrm{A} \cup \mathrm{B} \cup \mathrm{C})\) \(=140-102=38\).
-
Question 13 of 45
13. Question
Let \(\mathrm{A}, \mathrm{B}\) and \(\mathrm{C}\) be sets such that \(\phi \neq A \cap B \subseteq C\). Then which of the following statements is not true? [Main April 12, 2019 (II)]
CorrectIncorrectHint
(d) Let \(A=\{1,2,3,4\}\)
\(B=\{3,4,5,6\}\)
\(C=\{1,2,3,4,7,8\}\)
Here \(A \cap B=\{3,4\} \subseteq C\)
\(A-C=\phi \subseteq B\)
but \(\mathrm{A} \nsubseteq \mathrm{B}\)
So not true (wrong) statement is d, If \(A-C \subseteq B\) then \(A \subseteq B\) -
Question 14 of 45
14. Question
In a certain town, \(25 \%\) of the families own a phone and \(15 \%\) own a car; \(65\%\) families own neither a phone nor a car and 2,000 families own both a car and a phone. Consider the following three statements: [Main Online April 10, 2015]
(A) \(5 \%\) families own both a car and a phone
(B) \(35 \%\) families own either a car or a phone
(C) 40,000 families live in the town
Then,CorrectIncorrectHint
(c) Step 1: Define the Variables
Let \(x\) be the total number of families in the town.Step 2: Identify the Percentages
– Families owning a phone: \(25 \%\) of \(x\)
– Families owning a car: \(15 \%\) of \(x\)
– Families owning neither a phone nor a car: \(65 \%\) of \(x\)
– Families owning both a car and a phone: 2000 familiesStep 3: Calculate Families Owning Either a Phone or a Car
Since \(65 \%\) of families own neither a phone nor a car, the percentage of families that own either a phone or a car is:
\(
100 \%-65 \%=35 \%
\)
Thus, the number of families owning either a phone or a car is:
\(
0.35 x
\)
Step 4: Use the Principle of Inclusion-Exclusion
According to the principle of inclusion-exclusion for two sets:
\(
n(P \cup C)=n(P)+n(C)-n(P \cap C)
\)
Where:
\(-n(P)=0.25 x\) (families with a phone)
\(-n(C)=0.15 x\) (families with a car)
\(-n(P \cap C)=2000\) (families with both)
Substituting the values we have:
\(
0.35 x=0.25 x+0.15 x-2000
\)
Step 5: Simplify the Equation
Combine like terms:
\(
0.35 x=0.40 x-2000
\)
Rearranging gives:
\(
\begin{aligned}
& 0.35 x-0.40 x=-2000 \\
& -0.05 x=-2000
\end{aligned}
\)
Step 6: Solve for \(x\)
Dividing both sides by -0.05 :
\(
x=\frac{2000}{0.05}=40000
\)
Step 7: Verify Each Statement
1. Statement A: \(5 \%\) of families own both a car and a phone.
– Calculation:
\(
\frac{2000}{40000} \times 100=5 \%
\)
– True.
2. Statement B: \(35 \%\) of families own either a car or a phone.
– Calculation:
\(0.35 \times 40000=14000\) families
– True.
3. Statement C: 40,000 families live in the town.
– True.Conclusion
All three statements (A, B, and C) are correct. -
Question 15 of 45
15. Question
If \(X\) and \(Y\) are two sets, then \(X \cap(X \cup Y)^{\prime}\) equals. [1979]
CorrectIncorrectHint
(c) We have \(\mathrm{X} \cap(\mathrm{Y} \cup \mathrm{X})^{\prime}=\mathrm{X} \cap\left(\mathrm{Y}^{\prime} \cap \mathrm{X}^{\prime}\right)\)
\(
\begin{aligned}
&=\mathrm{X} \cap \mathrm{Y}^{\prime} \cap \mathrm{X}^{\prime}=\mathrm{X} \cap \mathrm{X}^{\prime} \cap \mathrm{Y}^{\prime} \\
&=\phi \cap \mathrm{Y}^{\prime}=\phi
\end{aligned}
\) -
Question 16 of 45
16. Question
Let \(X=\{n \in N: 1 \leq n \leq 50\}\). If \(A=\{x \in X: n\) is a multiple of 2\(\} ; B=\{n \in X: n\) is a multiple of 7\(\}\), then the number of elements in the smallest subset of \(X\) containing both \(A\) and \(B\) is [Main Jan. 7, 2020(II)]
CorrectIncorrectHint
(c) From the given conditions,
\(
\begin{aligned}
&n(A)=25, n(B)=7 \text { and } n(A \cap B)=3 \\
&n(A \cup B)=n(A)+n(B)-n(A \cap B)=25+7-3=29
\end{aligned}
\) -
Question 17 of 45
17. Question
In a college of 300 students every student reads 5 newspapers and every newspaper is read by 60 students. The number of newpapers is [1998 – 2 Marks]
CorrectIncorrectHint
(c) Let the number of newspapers which are read be \(\mathrm{n}\). Then \(60 n=\) \((300)(5) \Rightarrow n=25\)
-
Question 18 of 45
18. Question
Suppose \(A_{1}, A_{2}, \ldots \ldots A_{30}\) are thirty sets each with five elements and \(B_{1}, B_{2}, \ldots \ldots B_{\mathrm{n}}\) are \(n\) sets each with three elements. Let \(\bigcup_{i=1}^{30} A_{i}=\bigcup_{j=1}^{n} B_{j}=S\). Assume that each element of \(\mathrm{S}\) belongs to exactly ten of the Ai’s and to exactly nine of the Bj’s. Find \(n\). [1981 – 2 Marks]
CorrectIncorrectHint
(b) Given that \(\bigcup_{i=1}^{30} A_{i}=\cup_{j=1}^{n} B_{j}=S \text { …(i) }\)
and each \(A_{i}^{\text {s }}\) contain 5 elements
So, total number of elements in \(A_{i}=5 \times 30=150\).
Since each element of \(S\) belongs to exactly ten of the \(A_{i}\) ‘s.
\(
\therefore n(S)=n\left[\bigcup_{i=1}^{30} A_{i}\right]=\frac{150}{10}=15 \text { …(ii) }
\)
Now, each \(\mathrm{B}_{\mathrm{j}}^{\text {s }}\) contain 3 elements
So, total number of elements in \(B_{j}=3 \times n=3 n\).
Since each element of \(\mathrm{S}\) belongs to exactly nine of the \(\mathrm{B}_{\mathrm{j}}{ }^{\prime {\text {s }}}\).
\(
\therefore n(S)=n\left[\bigcup_{j=1}^{n} B_{j}\right]=\frac{3 n}{9} \text { …(iii) }
\)
from (ii) and (iii)
\(
\frac{3 n}{9}=15 \Rightarrow n=45 \text {. }
\) -
Question 19 of 45
19. Question
Set \(A\) has 3 elements, and set \(B\) has 6 elements. What can be the minimum number of elements in the set \(A \cup B\)? [1980]
CorrectIncorrectHint
Concept:
If \(A\) and \(B\) are two sets then, \(n(A \cup B)=n(A)+n(B)-n(A \cap B)\)
Calculation:
Given: \(n(A)=3\) and \(n(B)=6\).
As we know that, if \(A\) and \(B\) are two sets then, \(n(A \cup B)=n(A)+n(B)-n(A \cap B)\)
\(
\Rightarrow n(A \cup B)=3+6-n(A \cap B)
\)
In order to minimize \(n(A \cup B)\) we have to maximize \(n(A \cap B)\).
If \(A\) is a subset of \(B\), then \(A \cap B=A \Rightarrow n(A \cap B)=n(A)=3\)
\(
\Rightarrow n(A \cup B)=3+6-3=6 \text {. }
\)
Hence, the minimum number of elements that \((A \cup B)\) can have is 6 . -
Question 20 of 45
20. Question
An investigator interviewed 100 students to determine their preferences for the three drinks : milk \((M)\), coffee \((C)\) and tea \((T)\). He reported the following : 10 students had all the three drinks \(M, C\) and \(T ; 20\) had \(M\) and \(C ; 30\) had \(C\) and \(T ; 25\) had \(M\) and \(T ; 12\) had \(M\) only; 5 had \(C\) only; and 8 had \(T\) only. Using a Venn diagram find how many did not take any of the three drinks. [1978]
CorrectIncorrectHint
(d) We have
\(
\begin{aligned}
&n(U)=100, \text { where } U \text { stands for universal set } \\
&n(M \cap C \cap T)=d=10 ; n(M \cap C)=b+d=20 ; \\
&n(C \cap \mathrm{T})=d+f=30 ; n(M \cap T)=d+e=25 \\
&\quad \Rightarrow b=10, f=20 \text { and } e=15 \\
&\quad n(\text { only } M)=a=12 ; n(\text { only } C)=c=5 ; n(\text { only } T)=\mathrm{g}=8
\end{aligned}
\)
Filling all the entries we obtain the Venn diagram as shown: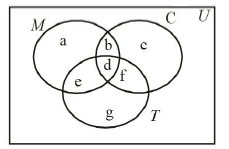
\(\begin{gathered}
\quad \therefore \quad n(M \cap C \cup T)=\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}+\mathrm{e}+\mathrm{f}+\mathrm{g} \\
=12+10+5+15+10+20+8=80 \\
\therefore \quad n(M \cup C \cup T)^{\prime}=100-80=20
\end{gathered}\) -
Question 21 of 45
21. Question
A relation on the set \(A=\{x:|x|<3, x \in Z\}\), where \(Z\) is the set of integers is defined by \(R=\{(x, y): y=|x|, x \neq-1\}\). Then the number of elements in the power set of \(R\) is: [Online April 12, 2014]
CorrectIncorrectHint
\(
\text { (b) } A =\{x:|x|<3, x \in Z\}
\)
\(
\begin{aligned}
& A =\{-2,-1,0,1,2\} \\
& R =\{(x, y): y=|x|, x \neq-1\} \\
& R =\{(-2,2),(0,0),(1,1),(2,2)\}
\end{aligned}
\)
\(R\) has four elements
Number of elements in the power set of \(R\)
\(
=2^4=16
\) -
Question 22 of 45
22. Question
Let \(X=\{1,2,3,4,5\}\). The number of different ordered pairs \((Y, Z)\) that can formed such that \(Y \subseteq X, Z \subseteq X\) and \(Y \cap Z\) is empty is : [JEE 2012]
CorrectIncorrectHint
(b) Let \(X=\{1,2,3,4,5\}\)
Total no. of elements \(=5\)
Each element has 3 options. Either set \(Y\) or set \(Z\) or none. \((\because Y \cap Z=\phi)\)
So, number of ordered pairs \(=3^5\)Explanation: The set \(X=\{1,2,3,4,5\}\).
\(Y \subseteq X\).
\(Z \subseteq X\).
\(Y \cap Z=\phi\).
How to solve?
Analyze the possible placements for each element of \(X\) to satisfy the given conditions.
For each element \(x \in X\), there are three possibilities:
\(x \in Y\) and \(x \notin Z\).
\(\quad x \notin Y\) and \(x \in Z\).
\(x \notin Y\) and \(x \notin Z\).
An element cannot be in both \(Y\) and \(Z\) because \(Y \cap Z=\phi\).
Since there are 5 elements in \(X\), and each element has 3 independent choices:
The total number of ordered pairs ( \(Y, Z\) ) is \(3^5\).
\(
3^5=243
\) -
Question 23 of 45
23. Question
If \(A, B\) and \(C\) are three sets such that \(A \cap B=A \cap C\) and \(A \cup B=A \cup C\), then [JEE 2009]
CorrectIncorrectHint
(b) Let \(x \in A\) and \(x \in B \Leftrightarrow x \in A \cup B\)
\(
\begin{aligned}
& \Leftrightarrow x \in A \cup C \quad(\because A \cup B=A \cup C) \\
& \Leftrightarrow x \in C
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \quad B=C . \\
& \text { Let } x \in A \text { and } x \in B \Leftrightarrow x \in A \cap B \\
& \Leftrightarrow x \in A \cap C \quad(\because A \cap B=A \cap C) \\
& \Leftrightarrow x \in C \\
& \therefore B=C
\end{aligned}
\) -
Question 24 of 45
24. Question
Let \(S=\{1,2,3,4\}\). The total number of unordered pair of disjoint subsets of \(S\) is equal to [IIT-JEE 2010, 5M]
CorrectIncorrectHint
For disoint sets, \(A \cap B=\phi\)
Each element in either \(A\) or \(B\) or neither.
\(\therefore\) Total ways \(=3^4=81 ; A=B\) iff \(A=B=\phi\)
Otherwise, \(A\) and \(B\) are interchangable
\(\therefore\) Number of unordered pair for disoint subsets of
\(
S=\frac{3^4+1}{2}=41
\) -
Question 25 of 45
25. Question
Let \(A\) and \(B\) be two sets containing 2 elements and 4 elements, respectively. The number of subsets of \(A \times B\) having 3 or more elements, is [JEE Main 2013, 4M]
CorrectIncorrectHint
\(\because A \times B\) has 8 elements.
\(\therefore\) Number of subsets \(=2^8=256\)
Number of subsets with zero element \(={ }^8 C_0=1\)
Number of subsets with one element \(={ }^8 C_1=8\)
Number of subsets with one elements \(={ }^8 C_2=28\)
Hence, Number of subsets of \(A \times B\) having 3 or more elements
\(
=256-(1+8+28)=256-37=219
\) -
Question 26 of 45
26. Question
If \(X=\left\{4^n-3 n-1: n \in N\right\}\) and \(Y=\{9(n-1): n=N\}\), where \(N\) is the set of natural numbers, then \(X \cup Y\) is equal to [JEE Main 2014, 4M]
CorrectIncorrectHint
Since, \(4^n-3 n-1=(1+3)^n-3 n-1\)
\(
\begin{aligned}
& =\left(1+{ }^n C_1 \cdot 3+{ }^n C_2 \cdot 3^2+{ }^n C_3 \cdot 3^3+\ldots+{ }^n C_n \cdot 3^n\right)-3 n-1 \\
& =3^2\left({ }^n C_2+{ }^n C_3 \cdot 3+\ldots+{ }^n C_n \cdot 3^{n-2}\right)
\end{aligned}
\)
\(\Rightarrow 4^n-3 n-1\) is a multiple of 9 for \(n \geq 2\)
For \(n=1,4^n-3 n-1=4-3-1=0\)
For \(n=2,4^n-3 n-1=16-6-1=9\)
\(\therefore 4^n-3 n-1\) is multiple of 9 for all \(n \in N\).
It is clear that \(X\) contains elements, which are multiples of 9 and \(Y\) contains all multiples of 9 .
\(
\therefore X \subseteq Y \text { i.e., } X \cup Y=Y
\) -
Question 27 of 45
27. Question
Let \(A\) and \(B\) be two sets containing four and two elements, respectively. Then, the number of subsets of the set \(A \times B\), each having atleast three elements is [JEE Main 2015, 4M]
CorrectIncorrectHint
\(
n(A)=4, n(B)=2 \Rightarrow n(A \times B)=8
\)
The number of subsets of \(A \times B\) having at least three elements
\(
\begin{aligned}
& ={ }^8 C_3+{ }^8 C_4+{ }^8 C_5+\ldots+{ }^8 C_8 \\
& =2^8-\left({ }^8 C_0+{ }^8 C_1+{ }^8 C_2\right) \\
& =256-(1+8+28)=219
\end{aligned}
\)Explanation: Cardinality of \(A \times B\) : Since set \(A\) has 4 elements and set \(B\) has 2 elements, their Cartesian product \(A \times B\) has \(4 \times 2=8\) elements.
Total number of subsets: A set with 8 elements has \(2^8=256\) subsets.
Subsets with fewer than 3 elements: We need to subtract the number of subsets with 0,1 , or 2 elements.
Subsets with 0 elements: 1 (the empty set)
Subsets with 1 element: \(\binom{8}{1}=8\)
Subsets with 2 elements: \(\binom{8}{2}=\frac{8 \times 7}{2 \times 1}=28\)
Subsets with 3 or more elements: Subtract the unwanted subsets from the total: \(256-1-8-28=219\).Note:
\(
\begin{aligned}
&\text { Combination Formula }\\
&{ }^n C_r=\frac{n!}{(n-r)!r!}
\end{aligned}
\) -
Question 28 of 45
28. Question
The number of elements in the set \(S=\{(x, y, z): x, y, z \in Z , x+2 y+3 z=42, x, y, z\) \(\geq 0\}\) equals {JEE Main 2024 1st Feb Shift 1]
CorrectIncorrectHint
\(
\begin{array}{ll}
x+2 y+3 z=42, & x, y, z \geq 0 \\
z=0 & x+2 y=42 \Rightarrow 22 \\
z=1 & x+2 y=39 \Rightarrow 20 \\
z=2 & x+2 y=36 \Rightarrow 19 \\
z=3 & x+2 y=33 \Rightarrow 17 \\
z=4 & x+2 y=30 \Rightarrow 16 \\
z=5 & x+2 y=27 \Rightarrow 14 \\
z=6 & x+2 y=24 \Rightarrow 13 \\
z=7 & x+2 y=21 \Rightarrow 11 \\
z=8 & x+2 y=18 \Rightarrow 10 \\
z=9 & x+2 y=15 \Rightarrow 8
\end{array}
\)
\(
\begin{array}{ll}
z=10 & x+2 y=12 \Rightarrow 7 \\
z=11 & x+2 y=9 \Rightarrow 5 \\
z=12 & x+2 y=6 \Rightarrow 4 \\
z=13 & x+2 y=3 \Rightarrow 2 \\
z=14 & x+2 y=0 \Rightarrow 1
\end{array}
\)
Total : 169 -
Question 29 of 45
29. Question
Let \(A=\{n \in N:\) H.C.F. \((n, 45)=1\}\) and
Let \(B=\{2 k: k \in\{1,2, \ldots, 100\}\}\). Then the sum of all the elements of \(A \cap B\) is [JEE Main 2022]CorrectIncorrectHint
Sum of elements in \(A \cap B\)
\(
\begin{aligned}
= & \underbrace{(2+4+6+\ldots+200)}_{\text {Multiple of } 2}-\underbrace{(6+12+\ldots+198)}_{\text {Multiple of } 2 \text { & } 3 \text { i.e. } 6} \\
& -\underbrace{(10+20+\ldots+200)}_{\text {Multiple of } 5 \text { & } 2 \text { i.e. } 10}+\underbrace{(30+60+\ldots+180)}_{\text {Multiple of } 2,5 \text { & 3 i.e. } 30} \\
= & 5264
\end{aligned}
\) -
Question 30 of 45
30. Question
\(
\text { Let } A =\{2,3,4,5, \ldots, 30\} \text { and } \simeq \text { be an equivalence relation on } A \times A \text {, defined by }( a , b ) \simeq( c , d ) \text {, if and }
\)
only if \(ad = bc\). Then the number of ordered pairs which satisfy this equivalence relation with ordered pair \((4,3)\) is equal to : [JEE Main 2021]CorrectIncorrectHint
\(
\begin{aligned}
& A =\{2,3,4,5, \ldots,, 30\} \\
& ( a , b ) \simeq( c , d ) \quad \Rightarrow ad = bc \\
& (4,3) \simeq(c, d) \quad \Rightarrow \quad 4 d=3 c \\
& \Rightarrow \frac{4}{3}=\frac{c}{d} \\
& \frac{c}{d}=\frac{4}{3} \quad \& c, d \in\{2,3, \ldots \ldots, 30\} \\
& ( c , d )=\{(4,3),(8,6),(12,9),(16,12),(20, \\
& 15),(24,18),(28,21)\}
\end{aligned}
\)
No. of ordered pair \(=7\) -
Question 31 of 45
31. Question
In a school, there are three types of games to be played. Some of the students play two types of games, but none play all the three games. Which Venn diagrams can justify the above statement? [JEE Main 2021]
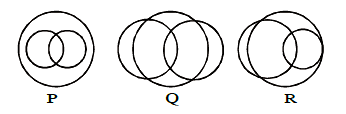 CorrectIncorrect
CorrectIncorrectHint
Let the types of games be denoted as \(A, B, C\).
In all the given Venn diagrams we can observe that there is at least one region where all \(A, B, C\) intersect i.e. \(A \cap B \cap C\)
Thus none of the given Venn diagrams represents the condition ‘Some of the students play two types of games, but none play all three games’ -
Question 32 of 45
32. Question
For any three sets \(A_1, A_2, A_3\), let \(B_1=A_1, B_2=A_2-A_1\) and \(B_3=A_3-\left(A_1 \cup A_2\right)\), then which one of the following statement is always true. [JEE (Orissa) 2002]
CorrectIncorrectHint
(a)
\(
\begin{aligned}
&\text { We have, } B_1=A_1 \Rightarrow B_1 \subset A_1\\
&\begin{aligned}
& B_2=A_2-A_1 \Rightarrow B_2 \subset A_2 \\
& B_3=A_3-\left(A_1 \cup A_2\right) \Rightarrow B_3 \subset A_3 \\
& B_1 \cup B_2 \cup B_3 \subset A_1 \cup A_2 \cup A_3 \\
& \because \quad A_1 \cup A_2 \cup A_3 \supset B_1 \cup B_2 \cup B_3
\end{aligned}
\end{aligned}
\) -
Question 33 of 45
33. Question
If \(A=\{1,2,3,4,5\}, B=\{2,4,6\}\) and \(C=\{3,4,6\}\), then \((A \cup B) \cap C\) is [JEE (Orissa) 2003]
CorrectIncorrectHint
(a)
\(
\begin{aligned}
& A \cup B=\{1,2,3,4,5\} \cup\{2,4,6\} \\
& A \cup B=\{1,2,3,4,5,6\}
\end{aligned}
\)
\(
\begin{aligned}
&\text { The intersection }(A \cup B) \cap C \text { contains elements common to both }(A \cup B) \text { and } C \text {. }\\
&\begin{aligned}
& (A \cup B) \cap C=\{1,2,3,4,5,6\} \cap\{3,4,6\} \\
& (A \cup B) \cap C=\{3,4,6\}
\end{aligned}
\end{aligned}
\) -
Question 34 of 45
34. Question
Let \(A\) be a set represented by the squares of natural numbers and \(x, y\) are any two elements of \(A\). Then, [JEE (Odisha 2007]
CorrectIncorrectHint
(b) The statement \(x y \in A\) is true. If \(x\) and \(y\) are elements of \(A\), which is the set of squares of natural numbers, then \(x=m^2\) and \(y=n^2\) for some natural numbers \(m\) and \(n\). Therefore, \(x y=m^2 n^2=(m n)^2\), and since \(m\) and \(n\) are natural numbers, \(m n\) is also a natural number, meaning \(x y\) is the square of a natural number and thus an element of \(A\).
The other options are not necessarily true. For example, \(5^2-3^2=25-9=16\), which is in \(A\), but \(3^2-5^2=9-25=-16\), which is not in \(A\). Similarly, \(x+y\) and \(\frac{x}{y}\) are not always in \(A\). For example, \(1^2+2^2=1+4=5\), which is not a perfect square. And \(\frac{4^2}{2^2}=\frac{16}{4}=4\), which is in \(A\), but \(\frac{2^2}{4^2}=\frac{4}{16}=\frac{1}{4}\), which is not a natural number. -
Question 35 of 45
35. Question
Let \(\mathbf{A}=\{(\alpha, \beta) \in \mathbb{R} \times \mathbb{R}:|\alpha-1| \leq 4\) and \(|\beta-5| \leq 6\}\) and \(\mathbf{B}=\left\{(\alpha, \beta) \in \mathbb{R} \times \mathbb{R}: 16(\alpha-2)^2+9(\beta-6)^2 \leq 144\right\}\). Then [JEE Main 2025]
CorrectIncorrectHint
(b)
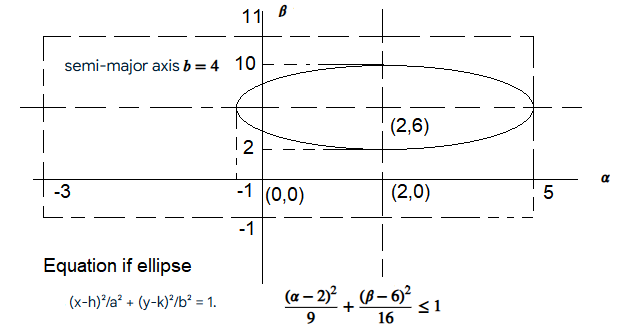
Given the sets \(A=\{(\alpha, \beta) \in \mathbb{R} \times \mathbb{R}:|\alpha-1| \leq 4\) and \(|\beta-5| \leq 6\}\) and \(B=\left\{(\alpha, \beta) \in \mathbb{R} \times \mathbb{R}: 16(\alpha-2)^2+9(\beta-6)^2 \leq 144\right\}\).
Let’s analyze set A first:
The condition \(|\alpha-1| \leq 4\) implies \(-4 \leq \alpha-1 \leq 4\), which means \(-3 \leq \alpha \leq 5\).
The condition \(|\beta-5| \leq 6\) implies \(-6 \leq \beta-5 \leq 6\), which means \(-1 \leq \beta \leq 11\).
So, set A is a rectangle defined by the inequalities \(-3 \leq \alpha \leq 5\) and \(-1 \leq \beta \leq 11\)
Now let’s analyze set \(B\) :
The inequality \(16(\alpha-2)^2+9(\beta-6)^2 \leq 144\) can be rewritten by dividing by 144:
\(
\begin{aligned}
& \frac{16(\alpha-2)^2}{144}+\frac{9(\beta-6)^2}{144} \leq 1 \\
& \frac{(\alpha-2)^2}{9}+\frac{(\beta-6)^2}{16} \leq 1
\end{aligned}
\)
This is the equation of an ellipse centered at \((2,6)\) with semi-major axis \(\boldsymbol{b}=\mathbf{4}\) (along the \(\boldsymbol{\beta}\)-axis, since \(\mathbf{1 6 > 9}\) ) and semi-minor axis \(\boldsymbol{a}=\mathbf{3}\) (along the \(\boldsymbol{\alpha}\) axis).
To determine the relationship between \(A\) and \(B\), it is necessary to check if one set is a subset of the other. Consider the boundary points of ellipse \(B\) and check if they fall within the bounds of rectangle \(A\).
The center of the ellipse is \((\mathbf{2 , 6})\).
The \(\alpha\)-values for the ellipse range from \(2-3=-1\) to \(2+3=5\). The \(\beta\)-values for the ellipse range from \(6-4=2\) to \(6+4=10\).
Comparing these ranges with the dimensions of rectangle A:
For \(\boldsymbol{\alpha}\) : The rectangle spans from -3 to 5. The ellipse spans from -1 to 5. The ellipse’s \(\boldsymbol{\alpha}\)-range is completely contained within the rectangle’s \(\boldsymbol{\alpha}\)-range.
For \(\boldsymbol{\beta}\) : The rectangle spans from -1 to 11. The ellipse spans from 2 to 10. The ellipse’s \(\boldsymbol{\beta}\)-range is completely contained within the rectangle’s \(\boldsymbol{\beta}\)-range.
Since both the \(\boldsymbol{\alpha}\) and \(\boldsymbol{\beta}\) ranges of the ellipse (set B) are contained within the corresponding ranges of the rectangle (set A), all points belonging to the ellipse are also contained within the rectangle.
Therefore, \(\boldsymbol{B} \subset \boldsymbol{A}\). -
Question 36 of 45
36. Question
Let \(\mathrm{A}=\left\{x \in(0, \pi)-\left\{\frac{\pi}{2}\right\}: \log _{(2 / \pi)}|\sin x|+\log _{(2 / \pi)}|\cos x|=2\right\}\) and \(\mathrm{B}=\{x \geqslant 0: \sqrt{x}(\sqrt{x}-4)-3|\sqrt{x}-2|+6=0\}\). Then \(\mathrm{n}(\mathrm{A} \cup \mathrm{B})\) is equal to : [JEE Main 2025]
CorrectIncorrectHint
(b) Set A is defined as \(\left\{x \in(0, \pi)-\left\{\frac{\pi}{2}\right\}: \log _{(2 / \pi)}|\sin x|+\log _{(2 / \pi)}|\cos x|=2\right\}\).
Set B is defined as \(\{x \geqslant 0: \sqrt{x}(\sqrt{x}-4)-3|\sqrt{x}-2|+6=0\}\).
The logarithm property \(\log _b M+\log _b N=\log _b(M N)\).
The definition of absolute value: \(|y|=y\) if \(y \geq 0\) and \(|y|=-y\) if \(y<0\).
How to solve?
Solve for the elements in set A and set B separately, then find the number of elements in their union.
Use the logarithm property: \(\log _{(2 / \pi)}(|\sin x||\cos x|)=2\).
Convert to exponential form: \(|\sin x \cos x|=\left(\frac{2}{\pi}\right)^2=\frac{4}{\pi^2}\). Use the identity \(\sin (2 x)=2 \sin x \cos x:\left|\frac{\sin (2 x)}{2}\right|=\frac{4}{\pi^2}\). This simplifies to \(|\sin (2 x)|=\frac{8}{\pi^2}\).
\(
\text { Since } \pi \approx 3.14, \pi^2 \approx 9.86 \text {, so } \frac{8}{\pi^2} \approx \frac{8}{9.86}<1 \text {. }
\)
In the domain \((0, \pi)-\left\{\frac{\pi}{2}\right\}, 2 x \in(0,2 \pi)-\{\pi\}\).
For \(|\sin (2 x)|=\frac{8}{\pi^2}\), there are four solutions for \(2 x\) in ( \(0,2 \pi\) ).
These solutions for \(2 x\) are \(\alpha, \pi-\alpha, \pi+\alpha, 2 \pi-\alpha\) where \(\sin (\alpha)=\frac{8}{\pi^2}\).
Thus, \(x=\frac{\alpha}{2}, \frac{\pi-\alpha}{2}, \frac{\pi+\alpha}{2}, \frac{2 \pi-\alpha}{2}\).
All these values are distinct and within \((0, \pi)-\left\{\frac{\pi}{2}\right\}\).
So, \(n(A)=4\).
Let \(y=\sqrt{x}\). The equation becomes \(y(y-4)-3|y-2|+6=0\).
This simplifies to \(y^2-4 y-3|y-2|+6=0\).
Case 1: \(y-2 \geq 0 \Longrightarrow y \geq 2\).
\(y^2-4 y-3(y-2)+6=0 \Longrightarrow y^2-7 y+12=0\).
\((y-3)(y-4)=0 \Longrightarrow y=3\) or \(y=4\).
Both \(y=3\) and \(y=4[latex] satisfy [latex]y \geq 2\).
So \(\sqrt{x}=3 \Longrightarrow x=9\) and \(\sqrt{x}=4 \Longrightarrow x=16\).Case 2: \(y-2<0 \Longrightarrow 0 \leq y<2\).
\(y^2-4 y-3(-(y-2))+6=0 \Longrightarrow y^2-4 y+3 y-6+6=0\).
\(y^2-y=0 \Longrightarrow y(y-1)=0\).
\(y=0\) or \(y=1\).
Both \(y=0\) and \(y=1\) satisfy \(0 \leq y<2\).
So \(\sqrt{x}=0 \Longrightarrow x=0\) and \(\sqrt{x}=1 \Longrightarrow x=1\).Thus, \(B=\{0,1,9,16\}\), so \(n(B)=4\).
The elements of A are of the form \(\frac{k \pi \pm \alpha}{2}\), which are irrational multiples of \(\pi\) or sums/differences involving \(\pi\).
The elements of \(B\) are integers \(\{0,1,9,16\}\).
Therefore, \(\mathrm{A} \cap \mathrm{B}=\phi\).
\(
n(A \cup B)=n(A)+n(B)-n(A \cap B)=4+4-0=8
\) -
Question 37 of 45
37. Question
Let \(A=\{1,2,3, \ldots, 10\}\) and \(B=\left\{\frac{m}{n}: m, n \in A, m<n\right.\) and \(\left.\operatorname{gcd}(m, n)=1\right\}\). Then \(n(B)\) is equal to : [JEE Main 2025]
CorrectIncorrectHint
(b) Set \(A=\{1,2,3, \ldots, 10\}\).
Set \(B=\left\{\frac{m}{n}: m, n \in A, m<n\right.\) and \(\left.\operatorname{gcd}(m, n)=1\right\}\).
How to solve?
To solve this, list all possible pairs \((m, n)\) from set \(A\) such that \(m<n\) and \(\operatorname{gcd}(m, n)=1\), then count the number of such pairs.
List all possible values for \(n\) from set \(A\).
\(
n \in\{2,3,4,5,6,7,8,9,10\} \text { since } m<n \text { and } m \geq 1 \text {. }
\)
For each value of \(n\), list all possible values for \(m\) such that \(m \in A, m<n\), and \(\operatorname{gcd}(m, n)=1\).
For \(n=2: m=1 . \operatorname{gcd}(1,2)=1\).
For \(n=3: m=1,2 . \operatorname{gcd}(1,3)=1, \operatorname{gcd}(2,3)=1\).
For \(n=4: m=1,3 . \operatorname{gcd}(1,4)=1, \operatorname{gcd}(3,4)=1\).
For \(n=5: m=1,2,3,4 . \operatorname{gcd}(1,5)=1, \operatorname{gcd}(2,5)=1, \operatorname{gcd}(3,5)=1, \operatorname{gcd}(4,5)=1\).
For \(n=6: m=1,5 . \operatorname{gcd}(1,6)=1, \operatorname{gcd}(5,6)=1\).
For \(n=7: m=1,2,3,4,5,6 . \operatorname{gcd}(m, 7)=1\) for all \(m<7\).
For \(n=8: m=1,3,5,7 . \operatorname{gcd}(1,8)=1, \operatorname{gcd}(3,8)=1, \operatorname{gcd}(5,8)=1, \operatorname{gcd}(7,8)=1\).
For \(n=9: m=1,2,4,5,7,8 . \operatorname{gcd}(1,9)=1, \operatorname{gcd}(2,9)=1, \operatorname{gcd}(4,9)=1, \operatorname{gcd}(5,9)=1\), \(\operatorname{gcd}(7,9)=1, \operatorname{gcd}(8,9)=1\).
For \(n=10: m=1,3,7,9 . \operatorname{gcd}(1,10)=1, \operatorname{gcd}(3,10)=1, \operatorname{gcd}(7,10)=1, \operatorname{gcd}(9,10)=1\).
Count the total number of valid pairs \((m, n)\).
\(
\text { Total count }=1+2+2+4+2+6+4+6+4=31 .
\)
The number of elements in set \(\boldsymbol{B}\) is 31.Alternate explanation:
To find the number of elements in set \(B\), we consider pairs \(\left(\frac{m}{n}\right)\) where \(m, n \in A\) with \(m<n\) and \(\operatorname{gcd}(m, n)=1\).
Here’s the breakdown for each possible \(m\) :
For \(m=1\) :
Possible values for \(n\) are \(2,3,4,5,6,7,8,9,10\).
Total pairs: 9.
For \(m=2\) :
Possible values for \(n\) are \(3,5,7,9\) (since these have \(\operatorname{gcd}(2, n)=1\) ).
Total pairs: 4.
For \(m=3\) :
Possible values for \(n\) are \(4,5,7,8,10\).
Total pairs: 5.
For \(m=4\) :
Possible values for \(n\) are \(5,7,9\).
Total pairs: 3.
For \(m=5\) :
Possible values for \(n\) are \(6,7,8,9\).
Total pairs: 4.
For \(m=6\) :
Possible value for \(n\) is 7.Total pairs: 1.
For \(m=7\) :Possible values for \(n\) are \(8,9,10\).
Total pairs: 3.
For \(m=8\) :
Possible value for \(\boldsymbol{n}\) is \(\mathbf{9}\).Total pairs: 1.
For \(m=9\) :
Possible value for \(n\) is 10.Total pairs: 1.
Adding all these up, the total number of elements in set \(B\) is:
\(
9+4+5+3+4+1+3+1+1=31
\) -
Question 38 of 45
38. Question
Let \(A=\{n \in[100,700] \cap \mathrm{N}: n\) is neither a multiple of 3 nor a multiple of 4\(\}\). Then the number of elements in \(A\) is [JEE Main 2024]
CorrectIncorrectHint
(a) You are finding the number of integers in the range \([100,700]\) that are neither multiples of 3 nor multiples of 4.
What’s given in the problem
The set \(A\) contains integers \(n\) such that \(100 \leq n \leq 700\).
\(n\) is not a multiple of 3.
\(n\) is not a multiple of 4.
The number of integers in a range \([a, b]\) is \(b-a+1\).
The Principle of Inclusion-Exclusion states \(|X \cup Y|=|X|+|Y|-|X \cap Y|\).
Calculate the total numbers, then subtract those divisible by 3 or 4 using the Inclusion-Exclusion Principle.
Calculate the total number of integers in the range:\(\text { Total numbers }=700-100+1=601\)
Find the count of numbers divisible by 3:
Smallest multiple of \(3 \geq 100\) is 102.
Largest multiple of \(3 \leq 700\) is 699.
Count of multiples of \(3=\frac{699-102}{3}+1=\frac{597}{3}+1=199+1=200\).
Find the count of numbers divisible by 4:
Smallest multiple of \(4 \geq 100\) is 100.
Largest multiple of \(4 \leq 700\) is 700.
Count of multiples of \(4=\frac{700-100}{4}+1=\frac{600}{4}+1=150+1=151\).
Find the count of numbers divisible by both 3 and 4 (i.e., by 12).
Smallest multiple of \(12 \geq 100\) is 108.
Largest multiple of \(12 \leq 700\) is 696.
Count of multiples of \(12=\frac{696-108}{12}+1=\frac{588}{12}+1=49+1=50\).
Apply the Inclusion-Exclusion Principle:
Numbers divisible by 3 or \(4=(\) Count of multiples of 3\()+(\) Count of multiples of 4\()-(\) Count of multiples of 12\()\). Numbers divisible by 3 or \(4=200+151-50=301\).
Number of elements in \(A=\) (Total numbers) – (Numbers divisible by 3 or 4 ).
Number of elements in \(A=601-301=300\). -
Question 39 of 45
39. Question
An organization awarded 48 medals in event ‘ \(A\) ‘, 25 in event ‘ \(B\) ‘ and 18 in event ‘ \(C\) ‘. If these medals went to total 60 men and only five men got medals in all the three events, then, how many received medals in exactly two of three events? [JEE Main 2023]
CorrectIncorrectHint
(c) This is a problem involving sets and the Principle of Inclusion-Exclusion.
Here’s how to solve this problem:
Define the sets and given information:
Let \(\boldsymbol{A}\) represent the set of men who received medals in event \(\boldsymbol{A}\).
Let \(\boldsymbol{B}\) represent the set of men who received medals in event \(\boldsymbol{B}\).
Let \(\boldsymbol{C}\) represent the set of men who received medals in event \(\boldsymbol{C}\).
Given information:
\(|A|=48\)
\(|B|=25\)
\(|C|=18\)
\(|A \cup B \cup C|=60\) (total men)
\(|\boldsymbol{A} \cap \boldsymbol{B} \cap \boldsymbol{C}|=5\) (men who received medals in all three events)
Apply the Principle of Inclusion-Exclusion:
The formula for the union of three sets is:
\(
|A \cup B \cup C|=|A|+|B|+|C|-(|A \cap B|+|A \cap C|+|B \cap C|)+|A \cap B \cap C|
\)
Substitute the given values into the formula:
\(
60=48+25+18-(|A \cap B|+|A \cap C|+|B \cap C|)+5
\)
Solve for the sum of the pairwise intersections:
\(
\begin{aligned}
& 60=91-(|A \cap B|+|A \cap C|+|B \cap C|)+5 \\
& 60=96-(|A \cap B|+|A \cap C|+|B \cap C|) \\
& |A \cap B|+|A \cap C|+|B \cap C|=96-60 \\
& |A \cap B|+|A \cap C|+|B \cap C|=36
\end{aligned}
\)
Calculate the number of men who received medals in exactly two events:
The sum of the pairwise intersections (36) includes the men who received medals in all three events multiple times. Each man who received medals in all three events is counted three times in this sum (once for each pair). Therefore, to find the number of men who received medals in exactly two events, subtract three times the number of men who received medals in all three events:
Exactly two events \(=(|\boldsymbol{A} \cap \boldsymbol{B}|+|\boldsymbol{A} \cap \boldsymbol{C}|+|\boldsymbol{B} \cap \boldsymbol{C}|)-3 \times|\boldsymbol{A} \cap \boldsymbol{B} \cap \boldsymbol{C}|\)
Exactly two events \(=36-3 \times 5\)
Exactly two events \(=\mathbf{3 6 – 1 5}\)
Exactly two events \(=21\)
Therefore, 21 men received medals in exactly two of the three events.Alternative,ly usinga Venn diagram:
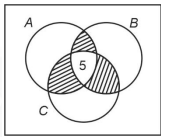
\(
\begin{aligned}
& n(A)=48, n(B)=25, n(C)=18 \\
& \text { Total men }=60=n(A \cup B \cup C) \\
& n(A \cap B \cap C)=5
\end{aligned}
\)
\(
n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A \cap B)-n(A \cap C)-n(B \cap C)+n(A \cap B \cap C)
\)
\(
60=48+25+18-[n(A \cap B)+n(B \cap C)+n(A \cap C)]+5 \Rightarrow n(A \cap B)+n(A \cap C)+n(B \cap C)=36
\)
\(
\begin{aligned}
&\text { Exactly two medals received in } 3 \text { events }\\
&=n(A \cap B)+n(B \cap C)+n(A \cap C)-3 n(A \cap B \cap C)=36-3(5)=21
\end{aligned}
\) -
Question 40 of 45
40. Question
Out of all the patients in a hospital 89% are found to be suffering from heart ailment and 98% are suffering from lungs infection. If K% of them are suffering from both ailments, then K can not belong to the set: [JEE Main 2021]
CorrectIncorrectHint
(c) Let H and L be the set of people suffering from heart ailment and lungs infections respectively.
\(
\begin{aligned}
& n (H)=89 \%, n (L)=98 \% \\
& n (H \cup L) \leq 100 \Rightarrow n (H)+n (L)-n (H \cap L) \leq 100
\end{aligned}
\)
Now \(100 \geq 89+98-n (H \cap L) \Rightarrow 87 \leq n(H \cap L)\)
Now \(n (H \cap L)=\min (n (H), n (L)) \leq 89\)
\(
\Rightarrow 87 \leq n (H \cap L) \leq 89
\)
\(\therefore n (H \cap L) \notin 79,81,83,85\) -
Question 41 of 45
41. Question
The number of elements in the set \(\{x \in R:(|x|-3)|x+4|=6\}\) is equal to : [JEE Main 2021]
CorrectIncorrectHint
(b) You are finding the number of real solutions for the given equation \((|x|-3)|x+4|=6\).
What’s given in the problem
The equation is \((|x|-3)|x+4|=6\).
We are looking for real solutions, \(x \in \mathbb{R}\).
How to solve?
Solve the equation by considering different cases based on the absolute value definitions.
Consider the case \(x \leq-4\).
In this case, \(|x|=-x\) and \(|x+4|=-(x+4)\).
The equation becomes \((-x-3)(-(x+4))=6\).
This simplifies to \((x+3)(x+4)=6\).
Expanding gives \(x^2+7 x+12=6\).
So, \(x^2+7 x+6=0\).
Factoring yields \((x+1)(x+6)=0\).
Solutions are \(x=-1\) or \(x=-6\).
Since we assumed \(x \leq-4\), only \(x=-6\) is a valid solution.
Consider the case \(-4<x<0\).
In this case, \(|x|=-x\) and \(|x+4|=x+4\).
The equation becomes \((-x-3)(x+4)=6\).
Expanding gives \(-x^2-7 x-12=6\).
So, \(x^2+7 x+18=0\).
Calculate the discriminant \(D=b^2-4 a c=7^2-4(1)(18)=49-72=-23\).
Since \(D<0\), there are no real solutions in this case.
Consider the case \(x \geq 0\).
In this case, \(|x|=x\) and \(|x+4|=x+4\).
The equation becomes \((x-3)(x+4)=6\).
Expanding gives \(x^2+x-12=6\).
So, \(x^2+x-18=0\).
Use the quadratic formula \(x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\).
\(
\begin{aligned}
& x=\frac{-1 \pm \sqrt{1^2-4(1)(-18)}}{2(1)} \\
& x=\frac{-1 \pm \sqrt{1+72}}{2} \\
& x=\frac{-1 \pm \sqrt{73}}{2}
\end{aligned}
\)
Since we assumed \(x \geq 0\), only \(x=\frac{-1+\sqrt{73}}{2}\) is a valid solution. Note that \(\sqrt{73} \approx 8.5\), so \(\frac{-1+8.5}{2}>0\).
The number of elements in the set is 2. -
Question 42 of 45
42. Question
Consider the two sets : \(A=\{m \in R\) : both the roots of \(x^2-(m+1) x+m+4=0\) are real} and \(B=[-3,5)\).
Which of the following is not true? [JEE Main 2020]CorrectIncorrectHint
(d) As roots are real so, \(D \geq 0\)
\(
\begin{aligned}
& (m+1)^2-4(m+4) \geq 0 \\
& \Rightarrow m^2-2 m-15 \geq 0 \\
& \Rightarrow(m-5)(m+3) \geq 0
\end{aligned}
\)
\(
m \in (-\infty,-3] \cup[5, \infty)
\)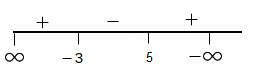
\(
\mathrm{A}=\{(-\infty,-3] \cup[5, \infty)\}
\)
\(
\text { Given } B=[-3,5)
\)
\(
A-B=(-\infty,-3) \cup[5, \infty)
\) -
Question 43 of 45
43. Question
If \(A=\{x \in R:|x|<2\}\) and \(B=\{x \in R:|x-2| \geq 3\}\); then : [JEE Main 2020]
CorrectIncorrectHint
(d) Set \(A=\{x \in R:|x|<2\}\).
Set \(B=\{x \in R:|x-2| \geq 3\}\).
How to solve
First, express sets \(A\) and \(B\) as intervals, then perform the set operations and compare with the given options.
Express set \(A\) as an interval.
The inequality \(|x|<2\) means that \(x\) is between -2 and 2 . \(A=(-2,2)\).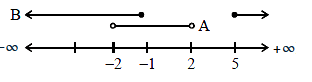
\(
\begin{aligned}
&\text { The inequality }|x-2| \geq 3 \text { means } x-2 \leq-3 \text { or } x-2 \geq 3 \text {. }\\
&\begin{aligned}
& x-2 \leq-3 \Longrightarrow x \leq-1 \\
& x-2 \geq 3 \Longrightarrow x \geq 5 \\
& B=(-\infty,-1] \cup[5, \infty)
\end{aligned}
\end{aligned}
\)\(
\begin{aligned}
&\begin{aligned}
& B-A=B \cap A^c . \\
& A^c=(-\infty,-2] \cup[2, \infty) . \\
& B-A=((-\infty,-1] \cup[5, \infty)) \cap((-\infty,-2] \cup[2, \infty)) . \\
& B-A=(-\infty,-2] \cup[5, \infty) . \\
& R-(-2,5)=(-\infty,-2] \cup[5, \infty) .
\end{aligned}\\
&\text { Option (d) states } B-A=R-(-2,5) \text {, which is correct. }
\end{aligned}
\) -
Question 44 of 45
44. Question
Two newspapers \(A\) and \(B\) are published in a city. It is known that \(25 \%\) of the city populations reads \(A\) and \(20 \%\) reads \(B\) while \(8 \%\) reads both \(A\) and \(B\). Further, \(30 \%\) of those who read \(A\) but not \(B\) look into advertisements and \(40 \%\) of those who read \(B\) but not \(A\) also look into advertisements, while \(50 \%\) of those who read both \(A\) and \(B\) look into advertisements. Then the percentage of the population who look into advertisement is : [JEE Main 2019]
CorrectIncorrectHint
(d) Let the population of the city be 100.
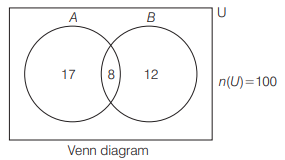
Then, \(n(A)=25, n(B)=20\) and \(n(A \cap B)=8\)
So, \(n(A \cap \bar{B})=17\) and \(n(\bar{A} \cap B)=12\)
According to the question, Percentage of the population who look into advertisement is
\(
\begin{aligned}
& =\left[\frac{30}{100} \times n(A \cap \bar{B})\right]+\left[\frac{40}{100} \times n(\bar{A} \cap B)\right]+\left[\frac{50}{100} \times n(A \cap B)\right] \\
& =\left(\frac{30}{100} \times 17\right)+\left(\frac{40}{100} \times 12\right)+\left(\frac{50}{100} \times 8\right) \\
& =5.1+4.8+4=13.9
\end{aligned}
\) -
Question 45 of 45
45. Question
Two sets \(A\) and \(B\) are as under :
\(\mathrm{A}=\{(\mathrm{a}, \mathrm{b}) \in \mathrm{R} \times \mathrm{R}:|\boldsymbol{a}-5|<1\) and \(|\mathrm{b}-5|<1\} ;\)
\(B=\left\{(a, b) \in R \times R: 4(a-6)^2+9(b-5)^2 \leq 36\right\} ;\)
Then [JEE Main 2018]CorrectIncorrectHint
(c) Set \(A\) is defined by the inequalities: \(|a-5|<1\) and \(|b-5|<1\).
Set \(B\) is defined by the inequality: \(4(a-6)^2+9(b-5)^2 \leq 36\).
The inequality \(|x-c|<r\) describes an open interval \((c-r, c+r)\).
The inequality \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2} \leq 1\) describes an ellipse centered at \((h, k)\) with semi-axes \(a\) and \(b\).
How to solve?
Analyze the geometric shapes represented by sets \(A\) and \(B\) and compare their regions.Analyze set \(A\):
The inequality \(|a-5|<1\) means \(-1<a-5<1\), which simplifies to \(4<a<6\).
The inequality \(|b-5|<1\) means \(-1<b-5<1\), which simplifies to \(4<b<6\).
Set \(A\) represents an open square region with vertices at \((4,4),(6,4),(6,6)\), and \((4,6)\).Analyze set \(B\):
Divide the inequality \(4(a-6)^2+9(b-5)^2 \leq 36\) by 36.
This gives \(\frac{4(a-6)^2}{36}+\frac{9(b-5)^2}{36} \leq \frac{36}{36}\).
Simplify to \(\frac{(a-6)^2}{9}+\frac{(b-5)^2}{4} \leq 1\).
Set \(B\) represents an ellipse centered at \((6,5)\) with a horizontal semi-axis of \(\sqrt{9}=3\) and a vertical semi-axis of \(\sqrt{4}=2\).Compare the regions:
The square \(A\) has \(a\) values from 4 to 6 and \(b\) values from 4 to 6.
The ellipse \(B\) has \(a\) values from \(6-3=3\) to \(6+3=9\) and \(b\) values from \(5-2=3\) to \(5+2=7\)
Hence, we can say entire set \(A\) is inside of the set \(B\).
\(
\text { Set } A \text { is a subset of set } B \text {. }
\)