NCERT Exemplar MCQs

Hint

\(
\text { Mean }=\bar{x}=\frac{f_i x_i}{f_i}=\frac{3+9+20+98+63+44+39+60}{42}=\frac{336}{42}=8
\)
\(
\text { M.D. }(\bar{x})=\frac{f_i\left|x_i-\bar{x}\right|}{f_i}=\frac{3(7)+3(5)+4(3)+14(1)+7(1)+4(3)+3(5)+4(7)}{42}
\)
\(
=\frac{21+15+12+14+7+12+15+28}{42}=\frac{62}{21}=2.95
\)

Hint

\(
\text { Mean }(\bar{x})=\frac{57+64+43+67+49+59+61+59+44+47}{10}=\frac{550}{10}=55
\)
\(
\begin{aligned}
& \text { Variance }\left(\sigma^2\right)=\frac{\left(x_i-\bar{x}\right)^2}{n} \\
& =\frac{2^2+9^2+12^2+12^2+6^2+4^2+6^2+4^2+11^2+8^2}{10} \\
& = \\
& \text { Standard deviation }(\sigma)=\sqrt{\sigma^2}=\sqrt{66.2}=8.13
\end{aligned}
\)

Hint

\(
\text { We have } \quad\left(x_i-\bar{x}\right)^2=\left(x_i^2-2 \bar{x} x_i+\bar{x}^2\right)
\)
\(
\begin{aligned}
& =\quad x_i^2+-2 \bar{x} x_i+\bar{x}^2 \\
& =\quad x_i^2-2 \bar{x} \quad x_i+(\bar{x})^2 \quad 1
\end{aligned}
\)
\(
\begin{aligned}
& =\quad x_i^2-2 \bar{x}(n \bar{x})+n \bar{x}^2 \\
& =\quad x_i^2-n \bar{x}^2
\end{aligned}
\)
Dividing both sides by \(n\) and taking their square root, we get \(\sigma=\sigma^{\prime}\).

Hint

\(
\text { Mean }(\bar{x})=\frac{f_i x_i}{f_i}=\frac{3 \times 6+6 \times 10+4 \times 14+7 \times 18}{20}=13
\)
\(
\text { Variance } \begin{aligned}
\left(\sigma^2\right) & =\frac{f_i\left(x_i-\bar{x}\right)^2}{f_i}=\frac{3(-7)^2+6(-3)^2+4(1)^2+7(5)^2}{20} \\
& =\frac{147+54+4+175}{20}=19
\end{aligned}
\)

Hint

\(
x^{\prime}=\frac{f_i y_i}{f_i}=\frac{-28}{70}=-0.4
\)
\(
\text { Mean }=\bar{x}=25.5+(-10)(0.4)=21.5
\)
Variance
\(
\left(\sigma^2\right)=\frac{h}{ N } \sqrt{ N f_i y_i^2-\left(f_i y_i\right)^2}
\)
\(
\begin{aligned}
& =\frac{10 \times 10}{70 \times 70}\left[70(124)-(-28)^2\right] \\
& =\frac{70(124)}{7 \times 7}-\frac{28 \times 28}{7 \times 7}=\frac{1240}{7}-16=161
\end{aligned}
\)
S.D. \((\sigma)=\sqrt{161}=12.7\)

Hint

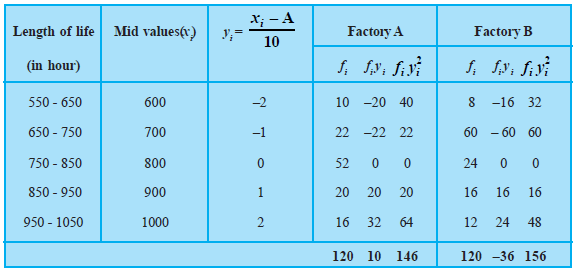
Here \(h=100\), let A (assumed mean \()=800\).

For Factory A:
Mean \((\bar{x})=800+\frac{10}{120} \times 100=816.67\) hours
\(
\text { S.D. }=\frac{100}{120} \sqrt{120(146)-100}=109.98
\)
Therefore, Coefficient of variation (C. V.) \(=\frac{\text { S.D. }}{\bar{x}} \times 100=\frac{109.98}{816.67} \times 100=13.47\)

For Factory A:
\(
\begin{aligned}
\text { Mean } & =800+\frac{-36}{120} \quad 100=770 \\
\text { S.D. } & =\frac{100}{120} \sqrt{120(156)-(-36)^2}=110
\end{aligned}
\)
Therefore, Coefficient of variation \(=\frac{\text { S.D. }}{\text { Mean }} \times 100=\frac{110}{770} \times 100=14.29\)
Since C.V. of factory B \(>\) C.V. of factory \(A \Rightarrow\) Factory \(B\) has more variability which means bulbs of factory \(A\) are more consistent.

Hint

(b) is the correct answer
M.D. \((\bar{x})=\frac{\left|x_i-\bar{x}\right|}{n}=\frac{4+3+3+3+0+3+2}{7}=2.57\)

Hint

(c) is the correct answer. When each observation is multiplied by 2 , then variance is also multiplied by 2 .

Hint

(a) is correct answer. If each observation is increased by a constant \(k\), then standard deviation is unchanged.

Hint

\(
\begin{array}{|c|c|c|c|c|}
\hline \text { Size }\left(x_i\right) & \text { Frequency }\left(f_i\right) & f_i x_i & d_i=\left|x_i-\bar{x}\right| & f_i d_i \\
\hline 20 & 6 & 120 & 1.65 & 9.90 \\
\hline 21 & 4 & 84 & 0.65 & 2.60 \\
\hline 22 & 5 & 110 & 0.35 & 1.75 \\
\hline 23 & 1 & 23 & 1.35 & 1.35 \\
\hline 24 & 4 & 96 & 2.35 & 9.40 \\
\hline \text { Total } & 20 & 433 & 6.35 & 25.00 \\
\hline
\end{array}
\)
Mean \(\bar{x}=\frac{\sum f_i x_i}{\sum f_i}=\frac{433}{20}=21.65\)
Mean deviation MD \(=\frac{\sum f_i d_i}{\sum f_i}=\frac{25}{20}=1.25\)
Here, the required \(MD =1.25\)

Hint

\(
\begin{array}{|c|c|c|c|c|}
\hline \begin{array}{c}
\text { Marks } \\
\text { obtained }
\end{array} & f_i & \text { c.f. } & d_i=\mid x_i-\text { Med } \mid & f_i d_i \\
\hline 10 & 2 & 2 & 2 & 4 \\
\hline 11 & 3 & 5 & 1 & 3 \\
\hline 12 & 8 & 13 & 0 & 0 \\
\hline 14 & 3 & 16 & 2 & 6 \\
\hline 15 & 4 & 20 & 3 & 12 \\
\hline \text { Total } & 20 & & & 25 \\
\hline
\end{array}
\)
\(
\text { Here } \sum f_i= N =20 \text { and } \sum f_i d_i=25
\)
\(
\text { Median }=\frac{1}{2}\left[\left(\frac{ N }{2}\right) \text { th observation }+\left(\frac{ N }{2}+1\right) \text { th observation }\right]
\)
\(
\begin{aligned}
& =\frac{1}{2}\left[\left(\frac{20}{2}\right) \text { th observation }+\left(\frac{20}{2}+1\right) \text { th observation }\right] \\
& =\frac{1}{2}[10 \text { th observation }+11 \text { th observation }]=\frac{1}{2}[12+12]
\end{aligned}
\)
\(
\begin{aligned}
\therefore & \text { Median } & =12 \\
\therefore & \text { M.D. } & =\frac{\sum f_i d_i}{\sum f_i}=\frac{25}{20}=1.25
\end{aligned}
\)
Hence, the required \(MD =1.25\)

Hint

First \(n\) natural numbers are \(1,2,3, \ldots, n\). Here, \(n\) is odd.
\(
\therefore \text { Mean } \bar{x}=\frac{1+2+3+\cdots+n}{n}=\frac{\frac{n(n+1)}{2}}{n}=\frac{n+1}{2}
\)
The deviations of numbers from mean \(\left(\frac{n+1}{2}\right)\) are
\(
\begin{aligned}
& 1-\frac{n+1}{2}, 2-\frac{n+1}{2}, 3-\frac{n+1}{2}, \ldots, n-\frac{n+1}{2} \\
& \text { i.e., }-\frac{n-1}{2},-\frac{n-3}{2}, \ldots,-2,-1,0,1,2, \ldots, \frac{n-1}{2} .
\end{aligned}
\)
The absolute values of deviation from the mean i.e. \(\left|x_i-\bar{x}\right|\) are
\(
\frac{n-1}{2}, \frac{n-3}{2}, \ldots, 2,1,0,1,2, \ldots, \frac{n-1}{2}
\)
The sum of absolute values of deviations from the mean i.e.
\(
\begin{aligned}
& \left|x_i-\bar{x}\right| \\
& =2\left(1+2+3+\ldots \text { to } \frac{n-1}{2} \text { terms }\right) \\
& =2 \cdot \frac{\frac{n-1}{2}\left(\frac{n-1}{2}+1\right)}{2}=\frac{n-1}{2} \cdot \frac{n+1}{2}=\frac{n^2-1}{4} .
\end{aligned}
\)
\(\therefore\) Mean deviation about the mean
\(
=\frac{\sum\left|x_i-\bar{x}\right|}{n}=\frac{\frac{n^2-1}{4}}{n}=\frac{n^2-1}{4 n} .
\)

Hint

First \(n\) natural numbers are \(1,2,3,4,5,6, \ldots, n\) (even)
\(\therefore \quad\) Mean \(\bar{x}=\frac{1+2+3+4+\cdots+n}{n}=\frac{n(n+1)}{2 n}=\frac{n+1}{2}\)
\(
\begin{aligned}
\therefore MD = & \frac{1}{n}\left[\left|1-\frac{n+1}{2}\right|+\left|2-\frac{n+1}{2}\right|+\left|3-\frac{n+1}{2}\right|+\ldots+\left|\frac{n-2}{2}-\frac{n+1}{2}\right|\right. \\
& \left.+\left|\frac{n}{2}-\frac{n+1}{2}\right|+\left|\frac{n+2}{2}-\frac{n+1}{2}\right| \ldots+\left|n-\frac{n+1}{2}\right|\right] \\
= & \frac{1}{n}\left[\left|\frac{1-n}{2}\right|+\left|\frac{3-n}{2}\right|+\left|\frac{5-n}{2}\right|+\ldots+\left|\frac{-3}{2}\right|+\left|-\frac{1}{2}\right|\right. \\
& \left.+\left|\frac{1}{2}\right|+\ldots+\left|\frac{n-1}{2}\right|\right] \\
= & \frac{1}{n}\left[\frac{1}{2}+\frac{3}{2}+\cdots+\frac{n-1}{2}\right]\left(\frac{n}{2}\right) \text { terms } \\
= & \frac{1}{n}\left(\frac{n}{2}\right)^2=\frac{1}{n} \cdot \frac{n^2}{4}=\frac{n}{4}
\end{aligned}
\)
\(\left[\because\right.\) Sum of first odd \(n\) natural numbers \(\left.=n^2\right]\) Hence, the required \(MD =\frac{n}{4}\).

Hint

\(
\begin{array}{|c|c|c|c|c|c|c|c|c|}
\hline x_i & 1 & 2 & 3 & 4 & 5 & – & – & n \\
\hline x_i^2 & 1 & 4 & 9 & 16 & 25 & – & – & n^2 \\
\hline
\end{array}
\)
\(
\begin{aligned}
\sum x_i & =1+2+3+4+5+\cdots+n=\frac{n(n+1)}{2} \\
\sum x_i^2 & =1^2+2^2+3^2+\ldots+n^2=\frac{n(n+1)(2 n+1)}{6} \\
\therefore \text { S.D. }(\sigma) & =\sqrt{\frac{\sum x_i^2}{n}-\left(\frac{\sum x_i}{n}\right)^2}
\end{aligned}
\)
\(
\begin{aligned}
& =\sqrt{\frac{n(n+1)(2 n+1)}{6 n}-\frac{n^2(n+1)^2}{4 n^2}} \\
& =\sqrt{\frac{(n+1)(2 n+1)}{6}-\frac{(n+1)^2}{4}} \\
& =\sqrt{\frac{2 n^2+3 n+1}{6}-\frac{n^2+2 n+1}{4}} \\
& =\sqrt{\frac{4 n^2+6 n+2-3 n^2-6 n-3}{12}}=\sqrt{\frac{n^2-1}{12}}
\end{aligned}
\)
\(
\text { Hence, the required } SD =\sqrt{\frac{n^2-1}{12}}
\)

Hint

Given that \(n_1=25, \bar{x}_1=18.2\) and \(\sigma_1=3.25\)
and \(\quad n_2=15, \sum_{i=1}^{15} x_i=279\) and \(\sum_{i=1}^{15} x_i^2=5524\)
For the first set, we have
\(
\begin{aligned}
\sum x_1 & =25 \times 18.2=455 \\
\therefore \quad \sigma_1^2 & =\frac{\sum x_i^2}{25}-(18.2)^2 \\
\Rightarrow \quad(3.25)^2 & =\frac{\sum x_i^2}{25}-331.24 \\
\Rightarrow 10.5625+331.24 & =\frac{\sum x_i^2}{25} \Rightarrow \quad \sum x_i^2=25 \times(10.5625+331.24) \\
& =25 \times 341.8025=8545.06
\end{aligned}
\)
For the combined standard deviation of the 40 observation, \(n=40\)
and \(\quad \sum x_i^2=5524+8545.06=14069.06\)
\(
\begin{aligned}
\Rightarrow \quad \sum x_i & =455+279=734 \\
\therefore \quad S D & =\sqrt{\frac{14069.06}{40}-\left(\frac{734}{40}\right)^2}=\sqrt{351.7265-(18.35)^2} \\
& =\sqrt{351.7265-336.7225}=\sqrt{15.004}=3.87
\end{aligned}
\)
Hence, the required \(SD =3.87\)

Hint

\(
\begin{aligned}
& \text { Let } \quad x_i, i=1,2,3,4, \ldots, n_1 \\
& \text { and } y_j, j=1,2,3,4, \ldots, n_2 \\
& \therefore \quad \bar{x}_1=\frac{1}{n_1} \sum_{i=1}^n x_i \quad \text { and } \quad \bar{x}_2=\frac{1}{n_2} \sum_{j=1}^n y_j \\
& \Rightarrow \quad \sigma_1^2=\frac{1}{n_1} \sum_{i=1}^{n_1}\left(x_i-\bar{x}_1\right)^2 \quad \text { and } \quad \sigma_2^2=\frac{1}{n_2} \sum_{j=1}^{n_2}\left(y_i-\bar{x}_2\right)^2 \\
&
\end{aligned}
\)
Now mean of the combined series is given by
\(
\bar{x}=\frac{1}{n_1+n_2}\left[\sum_{i=1}^{n_1} x_i+\sum_{j=1}^{n_2} y_j\right]=\frac{n_1 \bar{x}_1+n_2 \bar{x}_2}{n_1+n_2}
\)
Therefore, \(\sigma^2\) of the combined series is
\(
\sigma^2=\frac{1}{n_1+n_2}\left[\sum_{i=1}^{n_1}\left(x_i-\bar{x}\right)^2+\sum_{j=1}^{n_2}\left(y_j-\bar{x}\right)^2\right]
\)
Now,
\(
\begin{aligned}
\sum_{i=1}^{n_1}\left(x_i-\bar{x}\right)^2= & \sum_{i=1}^{n_1}\left(x_i-\bar{x}_j+\bar{x}_j-\bar{x}\right)^2 \\
= & \sum_{i=1}^{n_1}\left(x_i-x_j\right)^2+n_1\left(\bar{x}_j-\bar{x}\right)^2 \\
& +2\left(\bar{x}_j-\bar{x}\right) \sum_{i=1}^{n_1}\left(x_i-\bar{x}_j\right)^2
\end{aligned}
\)
But \(\sum_{i=1}^n\left(x_i-\bar{x}_i\right)=0\)
\([\because\) The algebraic sum of the deviation of values of first series from their mean is zero]
Also \(\begin{aligned} \sum_{i=1}^{n_1}\left(x_i-\bar{x}\right)^2 & =n_1 s_1^2+n_1\left(\bar{x}_1-\bar{x}\right)^2 \\ & =n_1 s_1^2+n_1 d_1^2\end{aligned}\)
where \(d_1=\left(\bar{x}_1-\bar{x}\right)\)
Similarly, we have
\(
\sum_{j=1}^{n_2}\left(y_j-\bar{x}\right)^2=\sum_{j=1}^{n_2}\left(y_j-\bar{x}_i+\bar{x}_i-\bar{x}\right)^2=n_2 s_2^2+n_2 d_2^2
\)
where \(d_2=\left(\bar{x}_2-\bar{x}\right)\)
Now combined Standard Deviation (SD)
\(\begin{aligned} \sigma & =\sqrt{\frac{n_1\left(s_1^2+d_1^2\right)+n_2\left(s_2^2+d_2^2\right)}{n_1+n_2}} \\ \text { where } d_1 & =\bar{x}_1-\bar{x}=\bar{x}_1-\left(\frac{n_1 \bar{x}_1+n_2 \bar{x}_2}{n_1+n_2}\right)=\frac{n_2\left(\bar{x}_1-\bar{x}_2\right)}{n_1+n_2}\end{aligned}\)
and \(d_2=\bar{x}_2-\bar{x}=\bar{x}_2-\left(\frac{n_1 \bar{x}_1+n_2 \bar{x}_2}{n_1+n_2}\right)=\frac{n_1\left(\bar{x}_2-\bar{x}_1\right)}{n_1+n_2}\)
\(
\therefore \sigma^2=\frac{1}{n_1+n_2}\left[n_1 s_1^2+n_2 s_2^2+\frac{n_1 n_2^2\left(\bar{x}_1-\bar{x}_2\right)^2}{\left(n_1+n_2\right)^2}+\frac{n_2 n_1^2\left(\bar{x}_2-\bar{x}_1\right)^2}{\left(n_1+n_2\right)^2}\right]
\)
so, \(\sigma=\sqrt{\frac{n_1 s_1^2+n_2 s_2^2}{n_1+n_2}+\frac{n_1 n_2\left(\bar{x}_1-\bar{x}_2\right)^2}{\left(n_1+n_2\right)^2}}\).

Hint

Given that
\(
\begin{array}{ll}
\text { Given that } & n_1=20, \sigma_1=5, \bar{x}_1=17 \\
\text { and } & n_2=20, \sigma_2=5, \bar{x}_2=22
\end{array}
\)
Now we know for combined two series that
\(
\begin{aligned}
\sigma & =\sqrt{\frac{n_1 s_1^2+n_2 s_2^2}{n_1+n_2}+\frac{n_1 n_2\left(\bar{x}_1-\bar{x}_2\right)^2}{\left(n_1+n_2\right)^2}} \\
& =\sqrt{\frac{20 \times(5)^2+20 \times(5)^2}{20+20}+\frac{20 \times 20(17-22)^2}{(20+20)^2}} \\
& =\sqrt{\frac{1000}{40}+\frac{400 \times 25}{1600}}=\sqrt{25+\frac{25}{4}}=\sqrt{\frac{125}{4}} \\
& =\sqrt{31.25}=5.59
\end{aligned}
\)
Hence, the required \(SD =5.59\)

Hint

\(
\begin{array}{|c|c|c|c|}
\hline x & f_i & f_i x_i & f_i x_i^2 \\
\hline A & 2 & 2 A & 2 A ^2 \\
\hline 2 A & 1 & 2 A & 4 A ^2 \\
\hline 3 A & 1 & 3 A & 9 A ^2 \\
\hline 4 A & 1 & 4 A & 16 A ^2 \\
\hline 5 A & 1 & 5 A & 25 A ^2 \\
\hline 6 A & 1 & 6 A & 36 A ^2 \\
\hline & n=7 & \sum f_i x_i=22 A & \sum f_i x_i^2=92 A ^2 \\
\hline
\end{array}
\)
\(
\begin{array}{ll}
\therefore & \text { Variance } \sigma^2=\frac{\sum f_i x_i^2}{n}-\left(\frac{\sum f_i x_i}{n}\right)^2 \\
\Rightarrow & 160=\frac{92 A ^2}{7}-\left(\frac{22 A }{7}\right)^2 \Rightarrow 160=\frac{92 A ^2}{7}-\frac{484 A ^2}{49} \\
\Rightarrow & 160=\frac{644 A ^2-484 A ^2}{49} \Rightarrow 160=\frac{160 A ^2}{49} \\
\Rightarrow & A ^2=49 \Rightarrow A =7
\end{array}
\)
Hence, the value of \(A\) is 7.

Hint

\(
\begin{array}{|c|c|c|c|}
\hline x_i & f_i & f_i x_i & f_i x_i^2 \\
\hline 2 & 4 & 8 & 16 \\
\hline 3 & 9 & 27 & 81 \\
\hline 4 & 16 & 64 & 256 \\
\hline 5 & 14 & 70 & 350 \\
\hline 6 & 11 & 66 & 396 \\
\hline 7 & 6 & 42 & 294 \\
\hline & N =60 & \sum f_i x_i=277 & \sum f_i x_i^2=1393 \\
\hline
\end{array}
\)
\(
\begin{aligned}
\therefore \quad SD (\sigma) & =\sqrt{\frac{\sum f_i x_i^2}{ N }-\left(\frac{\sum f_i x_i}{ N }\right)^2}=\sqrt{\frac{1393}{60}-\left(\frac{277}{60}\right)^2} \\
& =\sqrt{23.23-(4.62)^2}=\sqrt{23.21-21.34} \\
& =\sqrt{1.87}=1.37
\end{aligned}
\)
Hence, the required \(S D=1.37\)

Hint

Given that \(\sum f_i=60\)
\(
\therefore \quad x-2+x+x^2+(x+1)^2+2 x+(x+1)=60
\)
\(
\begin{aligned}
4 x-2+x^2+x^2+2 x+1+x+1 & =60 \\
2 x^2+7 x-60 & =0 \\
2 x^2+15 x-8 x-60 & =0 \\
x(2 x+15)-4(2 x+15) & =0 \\
(2 x+15)(x-4) & =0 \\
2 x+15 & =0
\end{aligned}
\)
\(
\begin{array}{ll}
\therefore & x=-\frac{15}{2} \text { Rejected } \\
\therefore & x=4 \quad\left[\because \quad x \in I ^{+}\right]
\end{array}
\)
Now put \(x=4\) in the frequency distribution table
\(
\begin{array}{|c|c|c|c|c|}
\hline x_i & f_i & d_i=x_i-3 & f_i d_i & f_i d_i^2 \\
\hline 0 & 2 & -3 & -6 & 18 \\
\hline 1 & 4 & -2 & -8 & 16 \\
\hline 2 & 16 & -1 & -16 & 16 \\
\hline 3 & 25 & 0 & 0 & 0 \\
\hline 4 & 8 & 1 & 8 & 8 \\
\hline 5 & 5 & 2 & 10 & 20 \\
\hline & N =60 & & \sum f_i x_i=-12 & \sum f_i x_i^2=78 \\
\hline
\end{array}
\)
Let assumed mean \(A =3\)
\(
\text { Mean }= A +\frac{\sum f_i d_i}{ N }=3+\left(\frac{-12}{60}\right)=3-\frac{1}{5}=\frac{14}{5}=2.8
\)
and
\(
\begin{aligned}
SD (\sigma) & =\sqrt{\frac{\sum f_i d_i^2}{ N }-\left(\frac{\sum f_i d_i}{ N }\right)^2}=\sqrt{\frac{78}{60}-\left(\frac{-12}{60}\right)^2} \\
& =\sqrt{1.3-0.04}=\sqrt{1.26}=1.12
\end{aligned}
\)
Hence, the required mean \(=2.8\) and \(SD =1.12\)

Hint

Given that \(n_1=60, \bar{x}_1=650, s_1=8\)
and \(\quad n_2=80, \bar{x}_2=660, s_2=7\)
we know that for a combined series.
\(
\begin{aligned}
\sigma & =\sqrt{\frac{n_1 s_1^2+n_2 s_2^2}{n_1+n_2}+\frac{n_1 n_2\left(\bar{x}_1-\bar{x}_2\right)^2}{\left(n_1+n_2\right)^2}} \\
& =\sqrt{\frac{60 \times(8)^2+80 \times(7)^2}{60+80}+\frac{60 \times 80(650-660)^2}{(60+80)^2}} \\
& =\sqrt{\frac{6 \times 64+8 \times 49}{14}+\frac{60 \times 80 \times 100}{140 \times 140}} \\
& =\sqrt{\frac{192+196}{7}+\frac{1200}{49}}=\sqrt{\frac{388}{7}+\frac{1200}{49}} \\
& =\sqrt{\frac{3916}{49}}=\frac{62.58}{7}=8.9
\end{aligned}
\)
Hence, the required \(SD =8.9\)

Hint

Given that
\(
\begin{aligned}
& \bar{x}=50, n=100 \text { and } \operatorname{SD}(\sigma)=4 \\
& \bar{x}=\frac{\sum x_i}{ N } \Rightarrow 50=\frac{\sum x_i}{100} \Rightarrow \sum x_i=5000
\end{aligned}
\)
and variance \(\sigma^2=\frac{\sum f_i x_i^2}{ N }-\left(\frac{\sum f_i x_i}{ N }\right)^2\) \((4)^2=\frac{\sum f_i x_i^2}{100}-(50)^2 \Rightarrow 16=\frac{\sum f_i x_i^2}{100}-2500\)
\(
\begin{array}{ll}
\therefore & \sum f_i x_i^2=(2500+16) \times 100 \\
\Rightarrow & \sum f_i x_i^2=2516 \times 100=251600
\end{array}
\)
Hence, the required sum are 5000 and 251600 .

Hint

Given that \(n=18, \sum(x-5)=3, \sum(x-5)^2=43\)
\(
\therefore \quad \text { Mean }=A+\frac{\sum(x-5)}{n}=5+\frac{3}{18}=\frac{93}{18}=5.166=5.17
\)
\(
\begin{aligned}
\text { and } SD & =\sqrt{\frac{\sum(x-5)^2}{ N }-\left[\frac{\sum(x-5)}{ N }\right]^2}=\sqrt{\frac{43}{18}-\left(\frac{3}{18}\right)^2} \\
& =\sqrt{2.39-(0.166)^2}=\sqrt{2.39-0.027}=1.54
\end{aligned}
\)

Hint

\(
\begin{array}{|c|c|c|c|c|}
\hline x & f_i & x_i & f_i x_i & f_i x_i^2 \\
\hline 1-3 & 6 & 2 & 12 & 24 \\
\hline 3-5 & 4 & 4 & 16 & 64 \\
\hline 5-7 & 5 & 6 & 30 & 180 \\
\hline 7-10 & 1 & 8.5 & 8.5 & 72.25 \\
\hline & N =16 & & \sum f_i x_i=66.5 & \sum f_i x_i^2=340.25 \\
\hline
\end{array}
\)
\(
\begin{aligned}
\text { Mean } & =\frac{\sum f_i x_i}{ N }=\frac{66.5}{16}=4.15 \\
\text { Variance }\left(\sigma^2\right) & =\frac{\sum f_i x_i^2}{ N }-\left(\frac{\sum f x}{ N }\right)^2 \\
& =\frac{340.25}{16}-(4.15)^2=21.26-17.22=4.04
\end{aligned}
\)
Hence, the required mean \(=4.15\) and variance \(=4.04\)

Hint

\(
\begin{array}{|c|c|c|c|c|c|}
\hline \begin{array}{c}
\text { Class- } \\
\text { interval }
\end{array} & f_i & x_i & f_i x_i & d_i=\left|x_i-\bar{x}\right| & f_i d_i \\
\hline 0-4 & 4 & 2 & 8 & 7.2 & 28.8 \\
\hline 4-8 & 6 & 6 & 36 & 3.2 & 19.2 \\
\hline 8-12 & 8 & 10 & 80 & 0.8 & 6.4 \\
\hline 12-16 & 5 & 14 & 70 & 4.8 & 24.0 \\
\hline 16-20 & 2 & 18 & 36 & 8.8 & 17.6 \\
\hline & N =25 & & \sum f_i x_i=230 & & \sum f_i d_i=96.0 \\
\hline
\end{array}
\)
\(
\text { Mean }=\frac{\sum f_i x_i}{ N }=\frac{230}{25}=9.2
\)
and Mean deviation \(=\frac{\sum f_i d_i}{ N }=\frac{96}{25}=3.84\)
Hence, the required \(MD =3.84\)

Hint

\(
\begin{array}{|c|c|c|c|c|c|}
\hline \begin{array}{c}
\text { Class- } \\
\text { interval }
\end{array} & f_i & x_i & c . f . & d_i=\mid x_i-\text { Med } \mid & f_i d_i \\
\hline 0-6 & 4 & 3 & 4 & 11 & 44 \\
\hline 6-12 & 5 & 9 & 9 & 5 & 25 \\
\hline 12-18 & 3 & 15 & 12 & 1 & 3 \\
\hline 18-24 & 6 & 21 & 18 & 7 & 42 \\
\hline 24-30 & 2 & 27 & 20 & 13 & 26 \\
\hline & N =20 & & & & \sum f_i d_i=140 \\
\hline
\end{array}
\)
Median class \(=\left(\frac{ N }{2}\right)\) th term \(=\frac{20}{2}\) th term \(=10\) th term i.e. \(12-18\)
\(
\begin{aligned}
\therefore \quad \text { Median } & =l+\frac{N / 2-c f}{f} \times h \\
& =12+\frac{10-9}{3} \times 6=12+\frac{1}{3} \times 6=12+2=14 \\
\text { and } \quad \text { MD } & =\frac{\sum f_i d_i}{ N }=\frac{140}{20}=7
\end{aligned}
\)
Hence, the required \(MD =7\)

Hint

\(
\begin{array}{|r|c|c|c|c|c|}
\hline x & f_i & f_i x_i & d_i=x_i-\bar{x} & f_i d_i & f_i d_i^2 \\
\hline 2 & 1 & 2 & -4 & -4 & 16 \\
\hline 3 & 6 & 18 & -3 & -18 & 54 \\
\hline 4 & 6 & 24 & -2 & -12 & 24 \\
\hline 5 & 8 & 40 & -1 & -8 & 8 \\
\hline 6 & 8 & 48 & 0 & 0 & 0 \\
\hline 7 & 2 & 14 & 1 & 2 & 2 \\
\hline 8 & 2 & 16 & 2 & 4 & 8 \\
\hline 9 & 3 & 27 & 3 & 9 & 27 \\
\hline 10 & 0 & 0 & 4 & 0 & 0 \\
\hline 11 & 2 & 22 & 5 & 10 & 50 \\
\hline 12 & 1 & 12 & 6 & 6 & 36 \\
\hline 13 & 0 & 0 & 7 & 0 & 0 \\
\hline 14 & 0 & 0 & 8 & 0 & 0 \\
\hline 15 & 0 & 0 & 9 & 0 & 0 \\
\hline 16 & 1 & 16 & 10 & 10 & 100 \\
\hline & N =40 & \sum f_i x_i=239 & & \sum f_i d_i=-1 & \sum f_i d_i^2=325 \\
\hline
\end{array}
\)
\(
\begin{aligned}
\text { Mean } \bar{x} & =\frac{\sum f_i x_i}{ N }=\frac{239}{40}=5.9=6 \\
\therefore \quad SD =\sigma & =\sqrt{\frac{\sum f_i d_i^2}{ N }-\left(\frac{\sum f_i d_i}{ N }\right)^2}=\sqrt{\frac{325}{40}-\left(\frac{-1}{40}\right)^2} \\
& =\sqrt{8.125-0.000625} \\
& =\sqrt{8.124375}=2.85
\end{aligned}
\)
Here, the required mean \(=6\) and \(MD =2.85\)

Hint

\(
\begin{array}{|c|c|c|c|c|c|}
\hline \begin{array}{c}
\text { Class- } \\
\text { interval }
\end{array} & f_i & x_i & d_i=x_i- A & f_i d_i & f_i d_i^2 \\
\hline 200-201 & 13 & 200.5 & -2 & -26 & 52 \\
\hline 201-202 & 27 & 201.5 & -1 & -27 & 27 \\
\hline 202-203 & 18 & 202.5(A) & 0 & 0 & 0 \\
\hline 203-204 & 10 & 203.5 & 1 & 10 & 10 \\
\hline 204-205 & 1 & 204.5 & 2 & 2 & 4 \\
\hline 205-206 & 1 & 205.5 & 3 & 3 & 9 \\
\hline & N =70 & & & \sum f_i d_i=-38 & \sum f_i d_i^2=102 \\
\hline
\end{array}
\)
\(
\therefore \quad \text { Variance }=\sigma^2=\frac{\sum f_i d_i^2}{N}-\left(\frac{\sum f_i d_i}{N}\right)^2
\)
\(
=\frac{102}{70}-\left(\frac{-38}{70}\right)^2=1.457-0.292=1.165
\)
\(
\therefore \quad S D=\sigma=\sqrt{1.165}=1.08 g .
\)
Hence, the required variance \(=1.165\) and \(S D=1.08 g\)

Hint

\(
\begin{array}{|c|c|c|}
\hline x_i & x_i-a & \left(x_i-a\right)^2 \\
\hline a & 0 & 0 \\
\hline a+d & d & d^2 \\
\hline a+2 d & 2 d & 4 d^2 \\
\hline- & – & – \\
\hline- & – & – \\
\hline- & – & – \\
\hline a+(n-1) d & (n-1) d & (n-1)^2 d^2 \\
\hline
\end{array}
\)
We know that \(\sum x_i=\frac{n}{2}[2 a+(n-1) d]\)
\(
\begin{aligned}
& \therefore \quad \text { Mean }=\frac{\sum x_i}{n}=\frac{1}{n}\left[\frac{n}{2}\{2 a+(n-1) d\}\right]=\frac{1}{2}[2 a+(n-1) d] \\
& =a+\frac{n-1}{2} d \\
& \therefore \quad \sum\left(x_i-a\right)=d[1+2+3+\cdots+(n-1)]=\frac{d(n-1) n}{2} \\
& \text { and } \quad \sum\left(x_i-a\right)^2=d^2\left[1^2+2^2+3^2+\cdots+(n-1)^2\right] \\
&
\end{aligned}
\)
\(
\begin{aligned}
& =d^2 \cdot \frac{n(n-1)(2 n-1)}{6} \\
\sigma & =\sqrt{\frac{\sum\left(x_i-a\right)^2}{n}-\left(\frac{\sum\left(x_i-a\right)}{n}\right)^2}
\end{aligned}
\)
\(
\begin{aligned}
& =\sqrt{\frac{d^2 n(n-1)(2 n-1)}{6 n}-\left(\frac{d n(n-1)}{2 n}\right)^2} \\
& =\sqrt{\frac{d^2(n-1)(2 n-1)}{6}-\frac{d^2(n-1)^2}{4}} \\
& =d \sqrt{\frac{n-1}{2}\left(\frac{2 n-1}{3}-\frac{n-1}{2}\right)} \\
& =d \sqrt{\frac{n-1}{2}\left[\frac{4 n-2-3 n+3}{6}\right]} \\
& =d \sqrt{\left(\frac{n-1}{2}\right)\left(\frac{n+1}{6}\right)}=d \sqrt{\frac{n^2-1}{12}}
\end{aligned}
\)
\(
\text { Hence, the required } SD =d \sqrt{\frac{n^2-1}{12}}
\)

Hint

Case I: Ravi
\(
\begin{array}{|l|c|c|}
\hline x_i & d_i=x_i-45 & d_i^2 \\
\hline 25 & -20 & 400 \\
\hline 50 & 5 & 25 \\
\hline 45= A & 0 & 0 \\
\hline 30 & -15 & 225 \\
\hline 70 & 25 & 625 \\
\hline 42 & -3 & 9 \\
\hline 36 & -9 & 81 \\
\hline 48 & 3 & 9 \\
\hline 35 & -10 & 100 \\
\hline 60 & 15 & 225 \\
\hline \text { Total } & \sum d_i=-9 & \sum d_i^2=1699 \\
\hline
\end{array}
\)
\(
\begin{aligned}
& \therefore \quad \sigma=\sqrt{\frac{\sum d_i^2}{N}-\left(\frac{\sum d i}{N}\right)^2} \\
& =\sqrt{\frac{1699}{10}-\left(\frac{-9}{10}\right)^2}=\sqrt{169.09}=13.003 \\
& \bar{x}= A +\frac{\sum d i}{N}=45-\frac{9}{10}=44.1 \\
&
\end{aligned}
\)
Now for Hashina
\(
\begin{array}{|c|c|c|}
\hline x_i & d_i=x_i-55 & d_i^2 \\
\hline 10 & -45 & 2025 \\
\hline 70 & 15 & 625 \\
\hline 50 & -5 & 25 \\
\hline 20 & -35 & 1225 \\
\hline 95 & 40 & 1600 \\
\hline 55= A & 0 & 0 \\
\hline 42 & -13 & 169 \\
\hline 60 & 5 & 25 \\
\hline 48 & -7 & 49 \\
\hline 80 & 25 & 625 \\
\hline \text { Total } & \sum d_i=-20 & \sum d_i^2=6368 \\
\hline
\end{array}
\)
Assumed mean \(A =55\)
\(
\begin{aligned}
& \therefore \quad \sigma=\sqrt{\frac{\sum d_i^2}{N}}=\sqrt{\frac{6368}{10}}=25.2 \\
& \text { and } \bar{x}= A +\frac{\sum d_i}{N}=55-\frac{20}{10}=53
\end{aligned}
\)
and \(\bar{x}= A +\frac{\sum d_i}{N}=55-\frac{20}{10}=53\)
For Ravi CV \(=\frac{\sigma}{\bar{x}} \times 100=\frac{13.003}{44.1} \times 100=29.48\)
For Hashina CV \(=\frac{\sigma}{\bar{x}} \times 100=\frac{25.2}{53} \times 100=47.55\)
Hence, Hashina is more consistent and intelligent.

Hint

Given that \(n=100, \bar{x}=40, \sigma=10\)
\(\therefore \quad \bar{x}=\frac{\sum x_i}{N} \Rightarrow 40=\frac{\sum x_i}{100} \Rightarrow \sum x_i=4000\)
Corrected \(\sum x_i=4000-30-70+3+27=3930\)
and Corrected mean \(=\frac{3930}{100}=39.3\)
Now \(\quad \sigma^2=\frac{\sum x_i^2}{n}-(40)^2 \Rightarrow 100=\frac{\sum x_i^2}{100}-1600\)
\(
\begin{aligned}
& \Rightarrow \quad \sum x_i^2=1700 \times 100 \Rightarrow \quad \sum x_i^2=170000 \\
& \therefore \text { Corrected } \sum x_i^2=170000-(30)^2-(70)^2+(3)^2+(27)^2 \\
& =170000-900-4900+9+729=164938 \\
& \therefore \quad \text { Correct SD }=\sqrt{\frac{164938}{100}-(39.3)^2} \\
& =\sqrt{1649.38-1544.49} \\
& =\sqrt{104.89}=10.24 \\
&
\end{aligned}
\)
Hence, the required \(SD =10.24\).

Hint

Given that \(n=10, \bar{x}=45\) and \(\sigma^2=16\)
\(
\begin{aligned}
\therefore \quad \bar{x} & =\frac{\sum x_i}{n} \Rightarrow 45=\frac{\sum x_i}{10} \Rightarrow \sum x_i=450 \\
\text { Corrected } \sum x_i & =450-52+25 \\
& =423
\end{aligned}
\)
Corrected \(\sum x_i=450-52+25\)
\(\therefore\) Correct Mean \(\bar{x}=\frac{423}{10}=42.3\)
\(
\begin{aligned}
& \Rightarrow \quad 16=\frac{\sum x_i^2}{10}-2025 \Rightarrow \frac{\sum x_i^2}{10}=2041 \\
& \therefore \quad \sum x_i^2=20410 \\
& \therefore \text { Correct } \sum x_i^2=20410-(52)^2+(25)^2 \\
& =20410-2704+625 \\
& =18331 \\
&
\end{aligned}
\)
and corrected variance
\(
\begin{aligned}
\sigma^2 & =\frac{18331}{10}-(42.3)^2 \\
& =1833.1-1789.3=43.8
\end{aligned}
\)
Hence the required mean \(=42.3\) and variance \(=43.8\)

Hint

Observations are given by \(3,10,10,4,7,10\) and 5
\(
\therefore \quad \bar{x}=\frac{3+10+10+4+7+10+5}{7}=\frac{49}{7}=7
\)
\(
\begin{array}{|c|c|}
\hline x_i & d_i=\left|x_i-\bar{x}\right| \\
\hline 3 & 4 \\
\hline 10 & 3 \\
\hline 10 & 3 \\
\hline 4 & 3 \\
\hline 7 & 0 \\
\hline 10 & 3 \\
\hline 5 & 2 \\
\hline \text { Total } & \sum d_i=18 \\
\hline
\end{array}
\)
\(
MD =\frac{\sum d_i}{n}=\frac{18}{7}=2.57
\)

Hint

\(
MD =\frac{1}{n} \sum_{i=1}^n\left|x_i-\bar{x}\right|
\)
Hence, the correct option is \((b)\).

Hint

The lines of 5 bulbs are given by \(1357,1090,1666,1494,1623\)
\(
\begin{array}{rlrl}
\therefore & \text { Mean } & =\frac{1357+1090+1666+1494+1623}{23} \\
\Rightarrow & & \bar{x} & =\frac{7230}{5}=1446
\end{array}
\)
\(
\begin{array}{|c|c|}
\hline x_i & d_i=\left|x_i-\bar{x}\right| \\
\hline 1357 & 89 \\
\hline 1090 & 356 \\
\hline 1666 & 220 \\
\hline 1494 & 48 \\
\hline 1623 & 177 \\
\hline \text { Total } & \sum d_i=890 \\
\hline
\end{array}
\)
\(
\therefore \quad MD =\frac{\sum d_i}{n}=\frac{890}{5}=178
\)
Hence, the correct option is \((a)\).

Hint

Marks obtained are \(50,69,20,33,53,39,40,65\) and 59
Let us write in ascending order
\(
20,33,39,40,50,53,59,65,69 \text {. }
\)
Here \(n=9\)
\(
\therefore \quad \text { Median }=\frac{9+1}{2} \text { th term }=5 \text { th term i.e. } 50
\)
\(\therefore \quad\) Median \(=50\)
Now
\(
\begin{array}{|c|c|}
\hline x_i & d_i=\mid x_i-\text { Med } \\
\hline 20 & 30 \\
\hline 33 & 17 \\
\hline 39 & 11 \\
\hline 40 & 10 \\
\hline 50 & 0 \\
\hline 53 & 3 \\
\hline 59 & 9 \\
\hline 65 & 15 \\
\hline 69 & 19 \\
\hline \text { Total } & \sum d_i=114 \\
\hline
\end{array}
\)
\(
\begin{aligned}
& n=9 \text { and } \sum d_i=114 \\
& \therefore MD =\frac{\sum d_i}{n}=\frac{114}{9}=12.67
\end{aligned}
\)
Hence, the correct option is (c).

Hint

Given data are \(6,5,9,13,12,8\) and 10 \(\therefore \quad n=7\)
\(
\begin{array}{|c|c|}
\hline x_i & x_i^2 \\
\hline 6 & 36 \\
\hline 5 & 25 \\
\hline 9 & 81 \\
\hline 13 & 169 \\
\hline 12 & 144 \\
\hline 8 & 64 \\
\hline 10 & 100 \\
\hline \sum x_i=63 & \sum x_i^2=619 \\
\hline
\end{array}
\)
\(
\begin{aligned}
\therefore SD & =\sqrt{\frac{\sum x_i^2}{n}-\left(\frac{\sum x_i}{n}\right)^2} \\
& =\sqrt{\frac{619}{7}-\left(\frac{63}{7}\right)^2} \\
& =\sqrt{\frac{619}{7}-(9)^2} \\
& =\sqrt{\frac{619}{7}-81}
\end{aligned}
\)
\(
=\sqrt{\frac{619-567}{7}}=\sqrt{\frac{52}{7}}
\)
Hence, the correct option is \((a)\).

Hint

The formula for S.D \(=\sigma=\sqrt{\frac{\sum\left(x_i-\bar{x}\right)^2}{n}}\) Hence, the correct option is \((c)\).

Hint

\(
\begin{aligned}
& \text { Here } \quad \bar{x}=\frac{\sum x_i}{n} \\
& 50=\frac{\sum x_i}{100} \Rightarrow \sum x_i=5000 \\
& \therefore \quad SD =\sqrt{\frac{\sum x_i^2}{n}-\left(\frac{\sum x_i}{n}\right)^2} \\
& 5=\sqrt{\frac{\sum x_i^2}{100}-\left(\frac{5000}{100}\right)^2} \Rightarrow 25=\frac{\sum x_i^2}{100}-2500 \\
& \Rightarrow \quad \frac{\sum x_i^2}{100}=2500+25 \Rightarrow \frac{\sum x_i^2}{100}=2525 \\
&
\end{aligned}
\)
\(
\therefore \quad \sum x_i^2=2525 \times 100=252500
\)
Hence, the correct option is \((c)\)

Hint

Given observation are \(a, b, c, d\) and \(e\)
\(
\begin{array}{rlrl}
\therefore & & \text { Mean } & =m=\frac{a+b+c+d+e}{5} \\
\therefore & & \sum x_i=5 m
\end{array}
\)
Now mean of \(a+ K , b+ K , c+ K , d+ K\) and \(e+ K\) is
\(
\begin{aligned}
& =\frac{a+ K +b+ K +c+ K +d+ K +e+ K }{5} \\
& =\frac{(a+b+c+d+e)+5 K}{5}=\frac{5 m+5 K}{5}=m+ K
\end{aligned}
\)
\(
\begin{aligned}
\therefore \quad SD & =\sqrt{\frac{\sum\left(x_i+ K \right)^2}{N}-\left[\frac{\sum x_i+ K }{ N }\right]^2} \\
& =\sqrt{\frac{\sum\left(x_i^2+ K ^2+2 x_i K\right)}{ N }-(m+ K )^2} \\
& =\sqrt{\frac{\sum x_i^2}{N}+\frac{\sum K ^2}{N}+\frac{2 K \sum x_i}{N}-m^2- K ^2-2 m K} \\
& =\sqrt{\frac{\sum x_i^2}{N}+ K ^2+2 K m-m^2- K ^2-2 m K} \\
& =\sqrt{\frac{\sum x_i^2}{N}-m^2} \quad\left[\because \frac{\sum x_i}{N}=m\right] \\
& = S
\end{aligned}
\)

Hint

Here
\(
m=\frac{\sum x_i}{N}, \quad S=\sqrt{\frac{\sum x_i^2}{5}-\left(\frac{\sum x_i}{5}\right)^2}
\)
\(
\begin{aligned}
\therefore \quad SD & =\sqrt{\frac{ K ^2 \sum x_i^2}{5}-\left(\frac{ K \sum x_i}{5}\right)^2} \\
& =\sqrt{\frac{ K ^2 \sum x_i^2}{5}- K ^2\left(\frac{\sum x_i}{5}\right)^2} \\
& = K \sqrt{\frac{\sum x_i^2}{5}-\left(\frac{\sum x_i}{5}\right)^2} \\
& = K \cdot S
\end{aligned}
\)

Hint

Given that
\(
\begin{aligned}
& w_i=x_i+k, \bar{x}_i=48, \operatorname{SD}\left(x_i\right)=12, \\
& w_i=55 \text { and } \operatorname{SD}\left(w_i\right)=15 \\
& \bar{w}_i=\bar{x}_i+k
\end{aligned}
\)
then
( \(\bar{w}_i=\) mean of \(w_i\) ‘s and \(\bar{x}_i\) is the mean of \(x_i^{\prime} s\) )
\(
\begin{aligned}
55 & =48+k \dots(i) \\
SD \text { of } w_i & = SD \text { of } x_i \\
15 & =l \times 12 \\
l & =\frac{15}{12}=1.25 \dots(ii)
\end{aligned}
\)
from eq. (i) and (ii) we have
\(
k=\bar{w}_i-\bar{x}_i=55-1.25 \times 48=55-60=-5
\)
Here, the correct option is (a).

Hint

We know that SD of first \(n\) natural numbers \(\sqrt{\frac{n^2-1}{12}}\)
Here \(n=10\)
\(
\therefore \quad S D=\sqrt{\frac{(10)^2-1}{12}}=\sqrt{\frac{99}{12}}=\sqrt{8.25}=2.87
\)
Hence, the correct option is (d)

Hint

Given numbers are \(1,2,3,4,5,6,7,8,9,10\)
Numbers obtained when 1 is added to the above numbers is \(2,3,4,5,6,7,8,9,10\) and 11 .
\(
\begin{aligned}
\therefore \quad \sum x_i & =2+3+4+5+6+7+8+9+10+11 \\
& =\frac{10}{2}[2 \times 2+(10-1) \cdot 1] \\
& =5[4+9]=5 \times 13=65
\end{aligned}
\)
Now
\(
\begin{aligned}
\sum x_i^2 & =2^2+3^2+4^2+\ldots+11^2 \\
& =\left(1^2+2^2+3^2+4^2+\cdots+11^2\right)-(1)^2 \\
& =\frac{n(n+1)(2 n+1)}{6}-1=\frac{11 \times 12 \times 23}{6}-1 \\
& =22 \times 23-1=506-1=505
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \quad \text { Variance }\left(\sigma^2\right)=\frac{\sum x_i^2}{N}-\left(\frac{\sum x_i}{N}\right)^2=\frac{505}{10}-\left(\frac{65}{10}\right)^2 \\
& =\frac{505}{10}-\left(\frac{65}{10}\right)^2=50.5-(6.5)^2 \\
& =50.5-42.25=8.25 \\
&
\end{aligned}
\)

Hint

First 10 positive integers are \(1,2,3,4,5,6,7,8,9,10\) on multiplying each number by -1 , we get
\(
-1,-2,-3,-4,-5,-6,-7,-8,-9,-10
\)
on adding 1 to each of the number, we get
\(
0,-1,-2,-3,-4,-5,-6,-7,-8,-9
\)
\(
\therefore \quad \sum x_i=0-1-2-3-4-5-6-7-8-9=-45
\)
\(
\text { and } \sum x_i^2=0^2+(-1)^2+(-2)^2+(-3)^2+(-4)^2+\cdots+(-9)^2
\)
\(
\begin{aligned}
& =\frac{9 \times 10 \times 19}{6}=285\left[\because \sum n^2=\frac{n(n+1)(2 n+1)}{6}\right] \\
\therefore \quad SD & =\sqrt{\frac{\sum x_i^2}{N}-\left(\frac{\sum x_i}{N}\right)^2}=\sqrt{\frac{285}{10}-\left(\frac{-45}{10}\right)^2}
\end{aligned}
\)
\(
\begin{aligned}
& =\sqrt{\frac{285}{10}-\frac{2025}{100}}-\sqrt{\frac{2850-2025}{100}}=\sqrt{8.25} \\
\therefore \text { Variance } & =( SD )^2=(\sqrt{8.25})^2=8.25
\end{aligned}
\)

Hint

We know that variance \(\left(\sigma^2\right)=\frac{\sum x_i^2}{N}-\left(\frac{\sum x_i}{N}\right)^2\)
\(
=\frac{18000}{60}-\left(\frac{960}{60}\right)^2=300-256=44
\)

Hint

Here, we have
\(
\begin{aligned}
CV _1 & =50, CV _2=60 \\
\bar{x}_1 & =30 \text { and } \bar{x}_2=25
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \quad CV _1=\frac{\sigma_1}{\bar{x}_1} \times 100 \Rightarrow 50=\frac{\sigma_1}{30} \times 100 \Rightarrow \sigma_1=\frac{50 \times 30}{100}=15 \\
& \text { and } C V_2=\frac{\sigma_2}{\bar{x}_2} \times 100 \Rightarrow 60=\frac{\sigma_2}{25} \times 100 \Rightarrow \sigma_2=\frac{60 \times 25}{100}=15
\end{aligned}
\)
\(
\therefore \text { Difference } \sigma_1-\sigma_2=15-15=0
\)

Hint

Given that \(\sigma_{ C }=5\)
We know that \(C=\frac{5}{9}(F-32) \Rightarrow F=\frac{9 C}{5}+32\)
\(
\begin{array}{ll}
\therefore & \sigma_{ F }=\frac{9}{5} \sigma_{ C }=\frac{9}{5} \times 5=9 \\
\therefore & \sigma_{ F }^2=(9)^2=81
\end{array}
\)

Hint

\(
C V=\frac{S D}{\text { Mean }} \times 100
\)
Hence, the value of the filler is SD.

Hint

If \(\bar{x}\) is the mean of \(n\) observations of \(x\), then \(\sum_{i=1}^n\left(x_i-\bar{x}\right)=0\) and if ‘ \(a\) ‘ has the value other than \(\bar{x}\), then \(\sum_{i=1}^n\left(x_i-\bar{x}\right)^2\) is less than \(\sum\left(x_i-a\right)^2\).
Hence, the value of the fillers are 0 and less.

Hint

We know that \(S D=\sqrt{\text { variance }}=\sqrt{121}=11\) Hence, the value of the filler is 11 .

Hint

Since the standard deviation of any data is independent of any change in origin but is dependent of any change of scale. Hence, the value of the fillers are independent and dependent.

Hint

The sum of the squares of the deviations of the value of variable is minimum when taken about their arithmetic mean. Hence, the value of the filler is minimum.

Hint

The mean deviation of the data is least when measured from the median.
Hence, the value of the filler is least.

Hint

The standard deviations is greater than or equal to the mean deviation taken from the arithmetic mean. Hence, the value of the filler is .