CLASS-XI MATHEMATICS + IIT JEE MAIN

In three dimensions, the coordinate axes of a rectangular Cartesian coordinate system are three mutually perpendicular lines. The axes are called the \(x, y\) and \(z\)-axes.
The three planes determined by the pair of axes are the coordinate planes, called XY, YZ and ZX-planes.
The three coordinate planes divide the space into eight parts known as octants.
The coordinates of a point \(P\) in three dimensional geometry is always written in the form of triplet like \((x, y, z)\). Here \(x, y\) and \(z\) are the distances from the YZ, ZX and XY-planes.
(i) Any point on \(x\)-axis is of the form \((x, 0,0)\)
(ii) Any point on \(y\)-axis is of the form \((0, y, 0)\)
(iii) Any point on \(z\)-axis is of the form \((0,0, z)\).
Distance between two points \(P \left(x_1, y_1, z_1\right)\) and \(Q \left(x_2, y_2, z_2\right)\) is given by
\(
PQ =\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}
\)
The coordinates of the point \(R\) which divides the line segment joining two points \(P \left(x_1 y_1 z_1\right)\) and \(Q \left(x_2, y_2, z_2\right)\) internally and externally in the ratio \(m: n\) are given by
\(
\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}, \frac{m z_2+n z_1}{m+n}\right) \text { and }\left(\frac{m x_2-n x_1}{m-n}, \frac{m y_2-n y_1}{m-n}, \frac{m z_2-n z_1}{m-n}\right) \text {, }
\)
respectively.
The coordinates of the mid-point of the line segment joining two points \(P \left(x_1, y_1, z_1\right)\) and \(Q \left(x_2, y_2, z_2\right)\) are \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2}\right)\).
The coordinates of the centroid of the triangle, whose vertices are \(\left(x_1, y_1, z_1\right)\) \(\left(x_2, y_2, z_2\right)\) and \(\left(x_3, y_3, z_3\right)\), are \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+x_3}{3}\right)\).

Time limit: 0

Quiz Summary

0 of 81 Questions completed

Questions:

Information

You have already completed the quiz before. Hence you can not start it again.

Quiz is loading…

You must sign in or sign up to start the quiz.

You must first complete the following:

Results

Quiz complete. Results are being recorded.

Results

0 of 81 Questions answered correctly

Your time:

Time has elapsed

You have reached 0 of 0 point(s), (0)

Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)

Categories

Not categorized 0%

Current
Review
Answered
Correct
Incorrect

Question 1 of 81

1. Question
Which Octant the following points located:
(i) \((1,-1,3)\)
(ii) \((-1,2,4)\)
(iii) \((-2,-4,-7)\)
(iv) \((-4,2,-5)\)
- (i) IV octant, (ii) II octant, (iii) VII octant (iv) VI octant
- (i) I octant, (ii) II octant, (iii) VII octant (iv) VI octant
- (i) IV octant, (ii) II octant, (iii) VIII octant (iv) VI octant
- (i) IV octant, (ii) II octant, (iii) VII octant (iv) VII octant
Correct

Incorrect

Hint

(i) Location of \(P (1,-1,3)=(x,-y, z)=\) IV octant
(ii) Location of \(Q (-1,2,4)=(-x, y, z)=\) II octant
(iii) Location of \(R (-2,-4,-7)=(-x,-y,-z)=\) VII octant
(iv) Location of \(S(-4,2,-5)=(-x, y,-z)= VI\) octant
Question 2 of 81

2. Question
Name the octant in which each of the following points lie.
(i) \((1,2,3)\)
(ii) \((4,-2,3)\)
(iii) \((4,-2,-5)\)
(iv) \((4,2,-5)\)
(v) \((-4,2,5)\)
(vi) \((-3,-1,6)\)
(vii) \((2,-4,-7) \quad\)
(viii) \((-4,2,-5)\)
- (i) I octant, (ii) IV octant. (iii) VIII octant (iv) V octant (v) II octant (vi) III octant (vii) VIII octant (viii) VII octant
- (i) I octant, (ii) IV octant. (iii) VIII octant (iv) V octant (v) II octant (vi) III octant (vii) VIII octant (viii) VI octant
- (i) II octant, (ii) IV octant. (iii) VIII octant (iv) V octant (v) I octant (vi) III octant (vii) VIII octant (viii) VI octant
- (i) I octant, (ii) II octant. (iii) VIII octant (iv) V octant (v) II octant (vi) III octant (vii) VIII octant (viii) VI octant
Correct

Incorrect

Hint

(i) Point \((1,2,3)\) lies in I octant
(ii) Point \((4,-2,3)\) lies in IV octant
(iii) Point \((4,-2,-5)\) lies in VIII octant
(iv) Point \((4,2,-5)\) lies in \(V\) octant
(v) Point \((-4,2,5)\) lies in II octant
(vi) Point \((-3,-1,6)\) lies in III octant
(vii) Point \((2,-4,-7)\) lies in VIII octant
(viii) Point \((-4,2,-5)\) lies in VI octant
Question 3 of 81

3. Question
Let A, B, C be the feet of perpendiculars from a point \(P\) on \(x, y\), \(z\)-axis respectively. Find the coordinates of \(A, B\) and \(C\) in each of the following where the \(P\) is
(i) \((3,4,2)\)
(ii) \((-5,3,7)\)
(iii) \((4,-3,-5)\)
- \(
  \begin{aligned}
  & \text { (i) }(3,4,0),(0,4,5),(3,0,5) \text { (ii) }(-5,3,0),(0,3,7),(-5,0,7) \text { (iii) }(4,-3,0) \text {, } \\
  & (0,-3,-5),(4,0,-5)
  \end{aligned}
  \)
- \( \begin{aligned} & \text { (i) }(3,4,0),(0,4,5),(3,0,5) \text { (ii) }(-5,3,0),(0,3,7),(-5,0,7) \text { (iii) }(4,-3,0) \text {, } \\ & (0,-3,-5),(4,1,-5) \end{aligned} \)
- \( \begin{aligned} & \text { (i) }(3,4,0),(0,4,5),(3,2,5) \text { (ii) }(-5,3,0),(0,3,7),(-5,0,7) \text { (iii) }(4,-3,0) \text {, } \\ & (0,-3,-5),(4,0,-5) \end{aligned} \)
- \( \begin{aligned} & \text { (i) }(3,4,0),(0,4,5),(3,0,5) \text { (ii) }(-5,3,0),(0,3,7),(-5,0,7) \text { (iii) }(2,-3,0) \text {, } \\ & (0,-3,-5),(4,0,-5) \end{aligned} \)
Correct

Incorrect

Hint

The coordinates of \(A , B\) and \(C\) are
(i) \(A (3,0,0), B (0,4,0)\) and \(C (0,0,2)\)
(ii) \(A (-5,0,0), B (0,3,0)\) and \(C (0,0,7)\)
(iii) \(A (4,0,0), B (0,-3,0)\) and \(C (0,0,-5)\)
Question 4 of 81

4. Question
Let A, B, C be the feet of perpendiculars from a point \(P\) on the \(x y, y z\) and \(z x\) planes respectively. Find the coordinates of A, B, C in each of the following where the point \(P\) is
(i) \((3,4,5)\)
(ii) \((-5,3,7)\)
(iii) \((4,-3,-5)\).
- \(
  \begin{aligned}
  & \text { (i) }(3,2,0),(0,4,5),(3,0,5) \text { (ii) }(-5,3,0),(0,3,7),(-5,0,7) \text { (iii) }(4,-3,0) \text {, } \\
  & (0,-3,-5),(4,0,-5)
  \end{aligned}
  \)
- \( \begin{aligned} & \text { (i) }(3,4,0),(0,4,5),(3,0,5) \text { (ii) }(-5,3,0),(0,3,7),(-5,0,7) \text { (iii) }(4,-3,0) \text {, } \\ & (0,-31-5),(4,0,-5) \end{aligned} \)
- \( \begin{aligned} & \text { (i) }(3,4,0),(0,4,5),(3,0,5) \text { (ii) }(-5,3,0),(0,3,7),(-5,0,7) \text { (iii) }(4,-3,0) \text {, } \\ & (0,-3,-5),(4,0,-5) \end{aligned} \)
- \( \begin{aligned} & \text { (i) }(3,4,0),(0,4,3),(3,0,5) \text { (ii) }(-5,3,0),(0,3,7),(-5,0,7) \text { (iii) }(4,-3,0) \text {, } \\ & (0,-3,-5),(4,0,-5) \end{aligned} \)
Correct

Incorrect

Hint

The coordinates of \(A , B\) and \(C\) are
(i) \(A (3,4,0), B (0,4,5)\) and \(C (3,0,5)\)
(ii) \(A (-5,3,0), B (0,3,7)\) and \(C (-5,0,7)\)
(iii) \(A (4,-3,0), B (0,-3,-5)\) and \(C (4,0,-5)\)
Question 5 of 81

5. Question
How far apart are the points \((2,0,0)[latex] and [latex](-3,0,0)\) ?
- 2
- 5
- 7
- 10
Correct

Incorrect

Hint

Given points are \((2,0,0)\) and \((-3,0,0)\)
\(\therefore\) Distance between the given points
\(
=\sqrt{(2+3)^2+(0-0)^2+(0-0)^2}=\sqrt{25}=5
\)
Hence, the required distance \(=5\).
Question 6 of 81

6. Question
Find the distance from the origin to \((6,6,7)\).
- 5 units
- 10 units
- 20 units
- 11 units
Correct

Incorrect

Hint

Coordinates of the origin are \((0,0,0)\)
\(\therefore\) Distance from \((0,0,0)\) to \((6,6,7)\)
\(
\begin{aligned}
& =\sqrt{(6-0)^2+(6-0)^2+(7-0)^2} \\
& =\sqrt{36+36+49}=\sqrt{121} \\
& =11 \text { units. }
\end{aligned}
\)
Hence, the required distance \(=11\) units.
Question 7 of 81

7. Question
If \(x^2+y^2=1\), then the point \(\left(x, y, \sqrt{1-x^2-y^2}\right)\) is at a distance ____ unit from the origin.
- 3
- 4
- 5
- 1
Correct

Incorrect

Hint

Given point is \(\left(x, y, \sqrt{1-x^2-y^2}\right)\)
\(\therefore\) Distance between the origin and the point is
\(
\begin{aligned}
& =\sqrt{(x-0)^2+(y-0)^2+\left(\sqrt{1-x^2-y^2}-0\right)^2} \\
& =\sqrt{1}=1 .
\end{aligned}
\)
Question 8 of 81

8. Question
Are the point \(A (1,-1,3), B (2,-4,5)\) and \((5,-13,11)\) are collinear?
- yes
- no
- can't be determined
- none of these
Correct

Incorrect

Hint

Given points are \(A (1,-1,3), B (2,-4,5)\) and \(C (5,-13,11)\)
\(
\begin{aligned}
AB & =\sqrt{(2-1)^2+(-4+1)^2+(5-3)^2} \\
& =\sqrt{1+9+4}=\sqrt{14} \\
BC & =\sqrt{(5-2)^2+(-13+4)^2+(11-5)^2} \\
& =\sqrt{9+81+36}=\sqrt{126}=3 \sqrt{14} \\
AC & =\sqrt{(5-1)^2+(-13+1)^2+(11-3)^2} \\
& =\sqrt{16+144+64}=\sqrt{224}=4 \sqrt{14}
\end{aligned}
\)
Here we observe that \(\sqrt{14}+3 \sqrt{14}=4 \sqrt{14}\)
So \(AB + BC = AC\).
Hence, the given points are collinear.
Question 9 of 81

9. Question
Three consecutive vertices of a parallelogram \(ABCD\) are \(A (6,-2,4), B (2,4,-8)\), \(C(-2,2,4)\). Find the coordinates of the fourth vertex.
[Hint: Diagonals of a parallelogram have the same mid-point.]
- \((2,-6,16)\)
- \( (2,-4,12) \)
- \( (2,-4,16) \)
- \( (1,-4,16) \)
Correct

Incorrect

Hint

Let the coordinates of the fourth vertex \(D\) be \((x, y, z)\)
Mid-point of diagonal \(A C\) is \(P\left(\frac{6-2}{2}, \frac{-2+2}{2}, \frac{4+4}{2}\right) \equiv P(2,0,4)\)
Also, mid-point of \(B D\) is \(P\left(\frac{x+2}{2}, \frac{y+4}{2}, \frac{z-8}{2}\right)\).
Now, \(P\left(\frac{x+2}{2}, \frac{y+4}{2}, \frac{z-8}{2}\right) \equiv P(2,0,4)\)
One equating coordinates, we get
\(
\begin{aligned}
& \frac{x+2}{2}=2 \Rightarrow x=2 ; \\
& \frac{y+4}{2}=0 \Rightarrow y=-4 ; \\
& \frac{z-8}{2}=4 \Rightarrow z=16
\end{aligned}
\)
So, the coordinate of fourth vertex \(D\) are given as \((2,-4,16)\).
Question 10 of 81

10. Question
The triangle \(ABC\) with vertices \(A (0,4,1), B (2,3,-1)\) and \(C (4,5,0)\) is ____ angled.
- right
- not right
- none of the above
Correct

Incorrect

Hint

Given vertices are \(A(0,4,1), B(2,3,-1)\) and \(C(4,5,0)\)
\(
\begin{aligned}
AB & =\sqrt{(2-0)^2+(3-4)^2+(-1-1)^2} \\
& =\sqrt{4+1+4}=\sqrt{9}=3 \\
BC & =\sqrt{(4-2)^2+(5-3)^2+(0+1)^2} \\
& =\sqrt{4+4+1}=\sqrt{9}=3 \\
AC & =\sqrt{(4-0)^2+(5-4)^2+(0-1)^2} \\
& =\sqrt{16+1+1}=\sqrt{18}
\end{aligned}
\)
\(
\because \quad(3)^2+(3)^2=(\sqrt{18})^2 \text {. }
\)
So \(AB ^2+ BC ^2= AC ^2\)
Hence, \(\triangle ABC\) is a right angled triangle.
Question 11 of 81

11. Question
Find the third vertex of triangle whose centroid is origin and two vertices are \((2,4,6)\) and \((0,-2,-5)\)
- \((-2,-1,-1)\)
- \( (-2,-2,-1) \)
- \( (-1,-2,-1) \)
- \( (0,-2,-1) \)
Correct

Incorrect

Hint

Using formula for co-ordinates of centroid of a triangle, the coordinates of the centroid of the triangle, whose vertices are \(\left(x_1, y_1, z_1\right),\left(x_2, y_2, z_2\right)\) and \(\left(x_3, y_3, z_3\right)\) are
\(
\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)
\)
Given two vertices are \(A(2,4,6)\) and \(B(0,-2,-5)\)
Let the third vertex \(C(x, y, z)\)
\(\therefore\) Centroid of \(\triangle ABC\),
\(
\begin{aligned}
& G=\left(\frac{x+2+0}{3}, \frac{y+4-2}{3}, \frac{z+6-5}{3}\right) \\
& \Rightarrow G=\left(\frac{x+2}{3}, \frac{y+2}{3}, \frac{z+1}{3}\right)
\end{aligned}
\)
Simplifying using given coordinates of centroid
Given centroid is at origin
\(
\therefore G\left(\frac{x+2}{3}, \frac{y+2}{3}, \frac{z+1}{3}\right)=G(0,0,0)
\)
Comparing coordinates, we get
\(
\frac{x+2}{3}=0 \Rightarrow x=-2
\)
\(
\begin{aligned}
& \frac{y+2}{3}=0 \Rightarrow y=-2 \\
& \frac{z+1}{3}=0 \Rightarrow z=-1
\end{aligned}
\)
Therefore, third vertex of the triangle is \((-2,-2,-1)\)
Question 12 of 81

12. Question
Find the centroid of a triangle, the mid-point of whose sides are \(D (1,2,-3)\), \(E(3,0,1)\) and \(F(-1,1,-4)\).
- \((2,1,-2)\)
- \( (1,2,-2) \)
- \( (1,1,-2) \)
- \( (2,2,-2) \)
Correct

Incorrect

Hint

Let the coordinates of the vertices of \(\triangle A B C\) be \(A \left(x_1, y_1, z_1\right), B \left(x_2, y_2, z_2\right)\) and \(C \left(x_3, y_3, z_3\right)\).
\(
\begin{aligned}
& \text { Mid-point of } BC =(1,2,-3) \\
\therefore \quad & 1=\frac{x_2+x_3}{2} \Rightarrow x_2+x_3=2 \dots(i)
\end{aligned}
\)
\(
\begin{aligned}
2 & =\frac{y_2+y_3}{2} \Rightarrow y_2+y_3=4 \dots(ii) \\
-3 & =\frac{z_2+z_3}{2} \Rightarrow z_2+z_3=-6 \dots(iii)
\end{aligned}
\)
Mid-point of \(AB =(3,0,1)\)
\(
\therefore \quad 3=\frac{x_1+x_2}{2} \Rightarrow x_1+x_2=6 \dots(iv)
\)
\(
\begin{aligned}
& 0=\frac{y_1+y_2}{2} \Rightarrow y_1+y_2=0 \dots(v) \\
& 1=\frac{z_1+z_2}{2} \Rightarrow z_1+z_2=2 \dots(vi)
\end{aligned}
\)
Similarly, mid-point of \(AC =(-1,1,-4)\)
\(
\begin{aligned}
\therefore \quad-1 & =\frac{x_1+x_3}{2} \Rightarrow x_1+x_3=-2 \dots(vii)\\
1 & =\frac{y_1+y_3}{2} \Rightarrow y_1+y_3=2 \dots(viii)\\
-4 & =\frac{z_1+z_3}{2} \Rightarrow z_1+z_3=-8 \dots(ix)
\end{aligned}
\)
Adding eq. (i), (iv) and (vii) we get,
\(
\begin{aligned}
& 2 x_1+2 x_2+2 x_3=2+6-2=6 \\
& \Rightarrow \quad x_1+x_2+x_3=3 \\
& \Rightarrow \quad 6+x_3=3 \Rightarrow x_3=-3 \quad \text { [from eq. (iv)] } \\
& \Rightarrow \quad x_1+2=3 \Rightarrow x_1=1 \quad \text { [from eq. (i)] } \\
& \Rightarrow \quad x_2-2=3 \Rightarrow x_2=5 \quad \text { [from eq. (vii)] } \\
&
\end{aligned}
\)
\(
\text { So, } x_1=1, x_2=5 \text { and } x_3=-3 \text {. }
\)
Similarly, Adding (ii), (v) and (viii) we get
\(
\begin{aligned}
& 2\left(y_1+y_2+y_3\right)=4+0+2=6 \\
& \therefore \quad y_1+y_2+y_3=3 \\
& y_1+4=3 \Rightarrow y_1=-1 \\
& 0+y_3=3 \Rightarrow y_3=3 \\
& y_2+2=3 \Rightarrow y_2=1 \\
&
\end{aligned}
\)
So, \(y_1=-1, y_2=1, y_3=3\)
Adding (iii), (vi) and (ix) we have
\(
2\left(z_1+z_2+z_3\right)=-6+2-8=-12
\)
\(
\begin{aligned}
& \therefore \quad z_1+z_2+z_3=-6 \\
& z_1-6=-6 \quad \Rightarrow \quad z_1=0 \quad \text { [from eq. (iii)] } \\
& 2+z_3=-6 \Rightarrow z_3=-8 \quad \text { [from eq. (vi)] } \\
& \text { and } z_2-8=-6 \quad \Rightarrow \quad z_2=2 \\
&
\end{aligned}
\)
\(
\therefore z_1=1, z_2=1, z_3=-8
\)
So, the points are \(A (1,-1,0), B (5,1,2)\) and \(C (-3,3,-8)\).
\(\therefore\) Centroid of the triangle
\(
G=\left(\frac{1+5-3}{3}, \frac{-1+1+3}{3}, \frac{0+2-8}{3}\right)=(1,1,-2)
\)
Hence, the required coordinates \(=(1,1,-2)\).
Question 13 of 81

13. Question
The mid-points of the sides of a triangle are \((5,7,11),(0,8,5)\) and \((2,3,-1)\). Find its vertices.
- \((-3,4,-7),(7,2,5) \text { and }(-3,12,7)\)
- \( (-3,4,-7),(2,2,5) \text { and }(-3,12,17) \)
- \( (-1,4,-7),(7,2,5) \text { and }(-3,12,17) \)
- \( (-3,4,-7),(7,2,5) \text { and }(-3,12,17) \)
Correct

Incorrect

Hint

Given that The mid-points of the sides of a triangle \(A B C\) are \(D(5,7,11), E(0,8,5)\) and \(F(2,3,-1)\)
Let the vertices of triangle be \(A\left(x_1, y_1, z_1\right)\), \(B\left(x_2, y_2, z_2\right)\) and \(C\left(x_3, y_3, z_3\right)\).
Mid-point of \(A C\) is \(E\).
\(
\therefore \quad\left(\frac{x_1+x_3}{2}, \frac{y_1+y_3}{2}, \frac{z_1+z_3}{2}\right) \equiv(0,8,5)
\)
So, \(C\left(x_3, y_3, z_3\right) \equiv C\left(-x_1, 16-y_1, 10-z_1\right)\) (i)
Mid-point of \(A B[latex] is [latex]F\).
\(
\therefore \quad\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2}\right) \equiv(2,3,-1)
\)
\(
\text { So, } B\left(x_2, y_2, z_2\right) \equiv B\left(4-x_1, 6-y_1,-2-z_1\right) \dots(ii)
\)
Mid-point of \(B C\) is \(D\)
\(
\begin{aligned}
\therefore \quad \frac{-x_1+4-x_1}{2} & =5, \frac{16-y_1+6-y_1}{2}=7, \\
\frac{10-z_1-2-z_1}{2} & =11
\end{aligned}
\)
\(
\begin{array}{llr}
\Rightarrow & x_1=-3, y_1=4 \text { and } z_1=-7 \\
\therefore & A \equiv(-3,4,-7) \\
\text { So, } & B \equiv(7,2,5) & \text { [Using (ii)] } \\
\text { and } & C \equiv(3,12,17) \quad \text { [Using (i)] }
\end{array}
\)
Question 14 of 81

14. Question
Three vertices of a Parallelogram \(ABCD\) are \(A (1,2,3), B (-1,-2,-1)\) and \(C (2,3,2)\). Find the fourth vertex \(D\).
- \((4,7,6)\)
- \( (3,7,6) \)
- \( (4,7,3) \)
- \( (2,7,6) \)
Correct

Incorrect

Hint

\(
\text { Let the coordinates of } D \text { be }(a, b, c) \text {. }
\)
We know that the diagonals of a parallelogram bisect each other.
\(\therefore\) Mid-point of \(AC\) i.e. \(O =\left(\frac{1+2}{2}, \frac{2+3}{2}, \frac{3+2}{2}\right)\)
\(
=\left(\frac{3}{2}, \frac{5}{2}, \frac{5}{2}\right)
\)
\(
\text { Mid-point of } BD \text { i.e. } O =\left(\frac{a-1}{2}, \frac{b-2}{2}, \frac{c-1}{2}\right)
\)
Equating the corresponding coordinate, we have
\(
\begin{aligned}
& \frac{a-1}{2}=\frac{3}{2} \quad \Rightarrow \quad a=4 \\
& \frac{b-2}{2}=\frac{5}{2} \quad \Rightarrow \quad b=7
\end{aligned}
\)
and \(\frac{c-1}{2}=\frac{5}{2} \Rightarrow c=6\)
Hence, the coordinates of \(D=(4,7,6)\).
Question 15 of 81

15. Question
Find the coordinate of the points which trisect the line segment joining the points \(A (2,1,-3)\) and \(B (5,-8,3)\).
- \((4,-5,1),(1,-2,-1)\)
- \( (2,-5,1),(3,-2,-1) \)
- \( (4,-5,1),(3,-2,-1) \)
- \( (4,-5,1),(3,-2,-4) \)
Correct

Incorrect

Hint

Let \(C\) and \(D\) be the points which divide the given line \(AB\) into three equal parts.
Here \(AC : CB =1: 2\)
Let \(\left(x_1, y_1, z_1\right)\) be the coordinates of \(C\)
\(
\begin{aligned}
\therefore \quad x_1 & =\frac{1 \times 5+2 \times 2}{1+2}=3 \\
y_1 & =\frac{1 \times-8+2 \times 1}{1+2}=-2
\end{aligned}
\)
\(
z_1=\frac{1 \times 3+2 \times-3}{1+2}=-1
\)
So \(C=(3,-2,-1)\).
Now \(D[latex] is the mid-point [latex]=C B\)
Let the coordinates of \(D\) be \(\left(x_2, y_2, z_2\right)\)
\(
\begin{aligned}
& x_2=\frac{3+5}{2}=4 \\
& y_2=\frac{-8-2}{2}=-5 \\
& z_2=\frac{3-1}{2}=1
\end{aligned}
\)
So, \(D=(4,-5,1)\).
Hence, the required coordinates are \(C(3,-2,-1)\) and \(D(4,-5,1)\).
Question 16 of 81

16. Question
If the origin is the centriod of a triangle \(ABC\) having vertices \(A (a, 1,3)\), \(B (-2, b,-5)\) and \(C (4,7, c)\), find the values of \(a, b, c\).
- \(a=-2, b=-8, c=1\)
- \( a=-1, b=-8, c=2 \)
- \( a=-2, b=-8, c=2 \)
- \( a=-2, b=-4, c=2 \)
Correct

Incorrect

Hint

Coordinates of the centroid \(G =(0,0,0)\)
\(
\begin{aligned}
\therefore & 0 & =\frac{x_1+x_2+x_3}{3} \Rightarrow 0=\frac{a-2+4}{3} \Rightarrow a=-2 \\
& 0 & =\frac{y_1+y_2+y_3}{3} \Rightarrow 0=\frac{1+b+7}{3} \Rightarrow b=-8 \\
\text { and } & 0 & =\frac{z_1+z_2+z_3}{3} \Rightarrow 0=\frac{3-5+c}{3} \Rightarrow c=2
\end{aligned}
\)
Hence, the required values are \(a=-2, b=-8\) and \(c=2\).
Question 17 of 81

17. Question
Let \(A (2,2,-3), B (5,6,9)\) and \(C (2,7,9)\) be the vertices of a triangle. The internal bisector of the angle \(A\) meets \(BC\) at the point \(D\). Find the coordinates of \(D\).
- \(\left(\frac{3}{2}, \frac{13}{2}, 9\right)\)
- \( \left(\frac{7}{2}, \frac{13}{2}, 9\right) \)
- \( \left(\frac{7}{2}, \frac{23}{2}, 9\right) \)
- \( \left(\frac{-7}{2}, \frac{13}{2}, 9\right) \)
Correct

Incorrect

Hint

Given that \(AD\) is the internal bisector of \(\angle A\)
\(
\begin{aligned}
\therefore \quad \frac{ AB }{ AC } & =\frac{ BD }{ DC } \\
AB & =\sqrt{(5-2)^2+(6-2)^2+(9+3)^2} \\
& =\sqrt{9+16+144}=\sqrt{169}=13 \\
\therefore \quad AC & =\sqrt{(2-2)^2+(7-2)^2+(9+3)^2} \\
& =\sqrt{0+25+144}=13 \\
\therefore \quad \frac{ AB }{ AC } & =\frac{ BD }{ DC }=\frac{13}{13} \Rightarrow BD = DC
\end{aligned}
\)
\(\Rightarrow D\) is the mid-point of \(B C\)
\(
\begin{aligned}
\therefore \quad \text { Coordinates of } D & =\left(\frac{5+2}{2}, \frac{6+7}{2}, \frac{9+9}{2}\right) \\
& =\left(\frac{7}{2}, \frac{13}{2}, 9\right)
\end{aligned}
\)
Hence, the required coordinates are \(\left(\frac{7}{2}, \frac{13}{2}, 9\right)\).
Question 18 of 81

18. Question
Given that the three points \(A (2,3,4), B (-1,2,-3)\) and \(C (-4,1,-10)\) are collinear and find the ratio in which \(C\) divides \(AB\).
- \(\text { 4:1 externally }\)
- \( \text { 6:1 externally } \)
- \( \text { 3:1 externally } \)
- \( \text { 2:1 externally } \)
Correct

Incorrect

Hint

Given points are \(A (2,3,4), B (-1,2,-3)\) and \(C (-4,1,-10)\)
\(
\begin{aligned}
AB & =\sqrt{(2+1)^2+(3-2)^2+(4+3)^2} \\
& =\sqrt{9+1+49}=\sqrt{59} \\
BC & =\sqrt{(-1+4)^2+(2-1)^2+(-3+10)^2} \\
& =\sqrt{9+1+49}=\sqrt{59} \\
AC & =\sqrt{(2+4)^2+(3-1)^2+(4+10)^2} \\
& =\sqrt{36+4+196}=\sqrt{236}=2 \sqrt{59} \\
\therefore \quad AB + BC & = AC \\
\sqrt{59}+\sqrt{59} & =2 \sqrt{59}
\end{aligned}
\)
Hence, \(A , B\) and \(C\) are collinear and \(AC : BC =2 \sqrt{59}: \sqrt{59}=2: 1\) Hence, \(C\) divides \(AB\) is \(2: 1\) externally.
Question 19 of 81

19. Question
The mid-point of the sides of a triangle are \((1,5,-1),(0,4,-2)\) and \((2,3,4)\). Find its vertices. Also find the centriod of the triangle.
- \(\text { vertices are }(3,4,5),(-1,6,-7),(1,2,3) \text { and centroid is }\left(1,4, \frac{1}{3}\right)\)
- \( \text { vertices are }(3,2,5),(-1,6,-7),(1,2,3) \text { and centroid is }\left(1,4, \frac{1}{3}\right) \)
- \( \text { vertices are }(3,4,5),(-1,4,-7),(1,2,3) \text { and centroid is }\left(1,4, \frac{1}{3}\right) \)
- \( \text { vertices are }(3,4,5),(-1,6,-7),(1,2,6) \text { and centroid is }\left(1,4, \frac{1}{3}\right) \)
Correct

Incorrect

Hint

Let the vertices of the given triangle be \(A \left(x_1, y_1, z_1\right), B \left(x_2, y_2, z_2\right)\) and \(C \left(x_3, y_3, z_3\right)\).
\(D\) is the mid-point of \(B C\)
\(
\begin{aligned}
& \therefore \quad 1=\frac{x_2+x_3}{2} \Rightarrow x_2+x_3=2 \dots(i)\\
& 5=\frac{y_2+y_3}{2} \Rightarrow y_2+y_3=10 \dots(ii)\\
& -1=\frac{z_2+z_3}{2} \Rightarrow z_2+z_3=-2 \dots(iii)\\
&
\end{aligned}
\)
\(E\) is the mid-point of \(A B\)
\(
\begin{aligned}
\therefore \quad 0 & =\frac{x_1+x_2}{2} \quad \Rightarrow x_1+x_2=0 \dots(iv) \\
4 & =\frac{y_1+y_2}{2} \Rightarrow y_1+y_2=8 \dots(v) \\
-2 & =\frac{z_1+z_2}{2} \Rightarrow z_1+z_2=-4 \dots(vi)
\end{aligned}
\)
\(F\) is the mid-point of \(AC\)
\(
\begin{aligned}
\therefore \quad 2 & =\frac{x_1+x_3}{2} \Rightarrow x_1+x_3=4 \dots(vii)\\
3 & =\frac{y_1+y_3}{2} \Rightarrow y_1+y_3=6 \dots(viii)\\
4 & =\frac{z_1+z_3}{2} \Rightarrow z_1+z_3=8 \dots(ix)
\end{aligned}
\)
Adding eq. (i), (iv) and (vii) we get
\(
\begin{aligned}
2\left(x_1+x_2+x_3\right) & =2+0+4 \\
\therefore \quad x_1+x_2+x_3 & =3 \dots(x)
\end{aligned}
\)
Adding (ii), (v) and (viii) we get
\(
\Rightarrow \quad \begin{aligned}
2\left(y_1+y_2+y_3\right) & =10+8+6\\
y_1+y_2+y_3 & =12 \dots(xi)
\end{aligned}
\)
Adding (iii), (vi) and (ix) we get
\(
\begin{aligned}
2\left(z_1+z_2+z_3\right) & =-2-4+8 \\
z_1+z_2+z_3 & =1 \dots(xii)
\end{aligned}
\)
Solving teh above equations
Here, the coordinates of \(B (-1,6,-7)\) Hence, the required coordinates are
\(
\begin{aligned}
& A (1,2,3), B (-1,6,-7) \text { and } C (3,4,5) \\
& \text { and Centroid } G=\left(\frac{1-1+3}{3}, \frac{2+6+4}{3}, \frac{3-7+5}{3}\right) \\
& =\left(1,4, \frac{1}{3}\right) \text {. } \\
&
\end{aligned}
\)
Question 20 of 81

20. Question
The points \((0,-1,-7),(2,1,-9)\) and \((6,5,-13)\) are collinear. Find the ratio in which the first point divides the join of the other two.
- \(1: 2 \text { externally }\)
- \( 1: 3 \text { externally } \)
- \( 2: 3 \text { externally } \)
- \( 1: 4 \text { externally } \)
Correct

Incorrect

Hint

Let the given points are \(A (0,-1,-7), B (2,1,-9)\) and \(C (6,5,-13)\)
\(
\begin{aligned}
AB & =\sqrt{(2-0)^2+(1+1)^2+(-9+7)^2} \\
& =\sqrt{4+4+4}=\sqrt{12}=2 \sqrt{3} \\
BC & =\sqrt{(6-2)^2+(5-1)^2+(-13+9)^2} \\
& =\sqrt{16+16+16}=\sqrt{48}=4 \sqrt{3}
\end{aligned}
\)
\(
\begin{aligned}
AC & =\sqrt{(6-0)^2+(5+1)^2+(-13+7)^2} \\
& =\sqrt{36+36+36}=\sqrt{108}=6 \sqrt{3} \\
2 \sqrt{3}+4 \sqrt{3} & =6 \sqrt{3}
\end{aligned}
\)
\(
\begin{array}{ll}
\text { i.e. } & A B+B C=A C \\
\therefore & A B: A C=2 \sqrt{3}: 6 \sqrt{3}=1: 3
\end{array}
\)
\(
\text { Hence, point } A \text { divides } B \text { and } C \text { in } 1: 3 \text { externally. }
\)
Question 21 of 81

21. Question
What are the coordinates of the vertices of a cube whose edge is 2 units, one of whose vertices coincides with the origin and the three edges passing through the origin, coincides with the positive direction of the axes through the origin?
- \((2,0,0),(2,2,0),(0,2,0),(0,2,2)(0,0,2)(2,0,2),(0,0,0),(1,2,2)\)
- \( (2,0,0),(2,2,0),(0,2,0),(0,2,2)(0,0,2)(2,0,2),(0,0,0),(2,2,2) \)
- \( (2,0,0),(2,2,0),(2,2,0),(0,2,2)(0,0,2)(2,0,2),(0,0,0),(2,2,2) \)
- \( (2,0,0),(2,2,0),(0,2,0),(0,2,2)(0,0,2)(2,0,2),(1,0,0),(2,2,2) \)
Correct

Incorrect

Hint

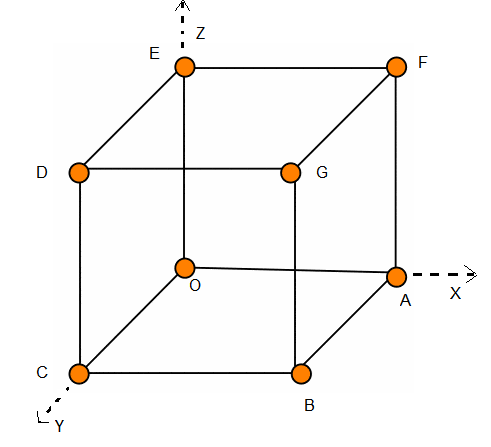
Given that each edge of the cuboid is 2 units.
\(\therefore\) Coordinates of the vertices are
\(
\begin{aligned}
& A (2,0,0), B (2,2,0), C (0,2,0) \\
& D (0,2,2), E (0,0,2), F (2,0,2), \\
& G (2,2,2) \text { and } O (0,0,0) \text {. }
\end{aligned}
\)
Question 22 of 81

22. Question
The distance of point \(P (3,4,5)\) from the \(y z\)-plane is
- 3 units
- 4 units
- 5 units
- 550
Correct

Incorrect

Hint

Given point is \(P (3,4,5)\)
\(\therefore\) Distance of \(P\) from \(y z\)-plane
\(
\begin{aligned}
& =\sqrt{(0-3)^2+(4-4)^2+(5-5)^2} \\
& =\sqrt{9}=3 \text { units }
\end{aligned}
\)
Question 23 of 81

23. Question
What is the length of foot of perpendicular drawn from the point \(P (3,4,5)\) on \(y\)-axis
- \(\sqrt{41}\)
- \(\sqrt{34}\)
- 5
- none of these
Correct

Incorrect

Hint

On \(y\)-axis, \(x=0\) and \(z=0\) and given point \(P (3,4,5)\)
\(\therefore\) The point \(A\) is \((0,4,0)\)
\(
\begin{aligned}
\therefore \quad PA & =\sqrt{(0-3)^2+(4-4)^2+(0-5)^2} \\
& =\sqrt{9+0+25}=\sqrt{34}
\end{aligned}
\)
Question 24 of 81

24. Question
Distance of the point \((3,4,5)\) from the origin \((0,0,0)\) is
- \(\sqrt{50}\)
- 3
- 4
- 5
Correct

Incorrect

Hint

Given points \(A (3,4,5)\) and the given \(O (0,0,0)\)
\(
\begin{aligned}
\therefore \quad OA & =\sqrt{(3-0)^2+(4-0)^2+(5-0)^2} \\
& =\sqrt{9+16+25}=\sqrt{50}
\end{aligned}
\)
Question 25 of 81

25. Question
If the distance between the points \((a, 0,1)\) and \((0,1,2)\) is \(\sqrt{27}\), then the value of \(a\) is
- 5
- \(\pm 5\)
- -5
- none of these
Correct

Incorrect

Hint

Let the given points be \(A (a, 0,1)\) and \(B (0,1,2)\)
\(
\begin{aligned}
\therefore \quad AB & =\sqrt{(a-0)^2+(0-1)^2+(1-2)^2} \\
\sqrt{27} & =\sqrt{a^2+1+1}
\end{aligned}
\)
Squaring both sides, we get
\(
27=a^2+2 \quad \Rightarrow \quad a^2=25 \quad \therefore a= \pm 5
\)
Question 26 of 81

26. Question
\(x\)-axis is the intersection of two planes
- \(x y\) and \(x z\)
- \(y z\) and \(z x\)
- \(x y\) and \(y z\)
- none of these
Correct

Incorrect

Hint

We know that on the \(x y\) and \(x z\)-planes, the line of intersection is \(x\)-axis.
Question 27 of 81

27. Question
Equation of \(y\)-axis is considered as
- \(x=0, y=0\)
- \(y=0, z=0\)
- \(z=0, x=0\)
- none of these
Correct

Incorrect

Hint

\(
\text { On } y \text {-axis, } x=0 \text { and } z=0
\)
Question 28 of 81

28. Question
The point \((-2,-3,-4)\) lies in the
- First octant
- Seventh octant
- Second octant
- Eighth octant
Correct

Incorrect

Hint

\(
\text { The point }(-2,-3,-4) \text { lies in seventh octant. }
\)
Question 29 of 81

29. Question
A plane is parallel to \(y z\)-plane so it is perpendicular to :
- \(x\)-axis
- \(y\)-axis
- z-axis
- none of these
Correct

Incorrect

Hint

\(
\text { Any plane parallel to } y z \text {-plane is perpendicular to } x \text {-axis. }
\)
Question 30 of 81

30. Question
The locus of a point for which \(y=0, z=0\) is
- equation of \(x\)-axis
- equation of \(y\)-axis
- equation at \(z\)-axis
- none of these
Correct

Incorrect

Hint

We know that one equation of \(x\)-axis, \(y=0, z=0\) Hence, the locus of the point is equation of \(x\)-axis.
Question 31 of 81

31. Question
The locus of a point for which \(x=0\) is
- \(x y\)-plane
- \(y z\)-plane
- \(z x\)-plane
- none of these
Correct

Incorrect

Hint

On the \(y z\)-plane, \(x=0\)
Hence, the locus of the point is \(y z\)-plane.
Question 32 of 81

32. Question
If a parallelopiped is formed by planes drawn through the points \((5,8,10)\) and \((3,6,8)\) parallel to the coordinate planes, then the length of diagonal of the parallelopiped is
- \(2 \sqrt{3}\)
- \(3 \sqrt{2}\)
- \(\sqrt{2}\)
- \(\sqrt{3}\)
Correct

Incorrect

Hint

Given points are \(A(5,8,10)\) and \(B(3,6,8)\)
\(
\begin{aligned}
\therefore \quad AB & =\sqrt{(5-3)^2+(8-6)^2+(10-8)^2} \\
& =\sqrt{4+4+4}=\sqrt{12}=2 \sqrt{3}
\end{aligned}
\)
Question 33 of 81

33. Question
\(L\) is the foot of the perpendicular drawn from a point \(P (3,4,5)\) on the \(x y\)-plane. The coordinates of point \(L\) are
- \((3,0,0)\)
- \((0,4,5)\)
- \((3,0,5)\)
- none of these
Correct

Incorrect

Hint

We know that on \(x y\)-plane, \(z=0\).
So, the coordinate of the point \(L\) are \((3,4,0)\).
Question 34 of 81

34. Question
\(L\) is the foot of the perpendicular drawn from a point \((3,4,5)\) on \(x\)-axis. The coordinates of \(L\) are
- \((3,0,0)\)
- \((0,4,0)\)
- \((0,0,5)\)
- none of these
Correct

Incorrect

Hint

We know that \(x\)-axis, \(y=0\) and \(z=0\).
So, the required coordinates are \((3,0,0)\).
Question 35 of 81

35. Question
The three axes OX, OY, OZ determine ____.
- Three cordinates planes
- represents origin
- represents 4 planes
- none of these
Correct

Incorrect

Hint

The three axes OX, OY and OZ determine three coordinate planes.
Hence, the filler value is three coordinate planes.
Question 36 of 81

36. Question
The three planes determine a rectangular parallelopiped which has _____ of rectangular faces.
- 2 pairs
- 3 pairs
- 1 pair
- 4 pairs
Correct

Incorrect

Hint

Three pairs. Hence, the value of the filler is three pairs.
Question 37 of 81

37. Question
The coordinates of a point are the perpendicular distance from the _____ on respective axes.
- given points
- origin
- plane
- none of these
Correct

Incorrect

Hint

Given points.
Hence, the value of the filler is given points.
Question 38 of 81

38. Question
The three coordinates planes divide the space into _____ parts.
- 4
- 6
- 8
- none of these
Correct

Incorrect

Hint

Eight. Hence, the values of the filler is eight.
Question 39 of 81

39. Question
If a point \(P\) lies in \(y z\)-plane, then the coordinates of a point on \(y z\)-plane is of the form _____.
- \((0, 0, z)\)
- \( (0, y, z) \)
- \( (0, y, x) \)
- \( (x, y, 0) \)
Correct

Incorrect

Hint

We know that on \(y z\)-plane, \(x=0\)
So, the coordinates of the required point is \((0, y, z)\). Hence, the value of the filler is \((0, y, z)\).
Question 40 of 81

40. Question
The equation of \(y z\)-plane is _____.
- \(z=0\).
- \(y=0\).
- \(z+x=0\).
- \(x=0\).
Correct

Incorrect

Hint

The equation of \(y z\)-plane is \(x=0\).
Hence, the value of the filler is \(x=0\).
Question 41 of 81

41. Question
If the point \(P\) lies on \(z\)-axis, then coordinates of \(P\) are of the form _____.
- \((0,0, y)\)
- \( (0,0, x) \)
- \( (0,0, z) \)
- \( (0,0, 0) \)
Correct

Incorrect

Hint

On the \(z\)-axis, \(x=0\) and \(y=0\).
\(\therefore\) The required coordinate is in the form of \((0,0, z)\).
Hence, the value of the filler is \((0,0, z)\).
Question 42 of 81

42. Question
The equation of \(z\)-axis are _____.
- \(x=0, y=0\)
- \( z=0, y=0 \)
- \( x=0, z=0 \)
- none of these
Correct

Incorrect

Hint

The equation of \(z\)-axis are, \(x=0\) and \(y=0\).
Hence, the value of the filler is \(x=0\) and \(y=0\).
Question 43 of 81

43. Question
A line is parallel to \(x y\)-plane if all the points on the line have equal _____.
- \(x \text { – cordinates }\)
- \( y \text { – cordinates } \)
- \( z \text { – cordinates } \)
- none of these
Correct

Incorrect

Hint

\(z\)-coordinates
Hence, the value of the filler is \(z\)-coordinates.
Question 44 of 81

44. Question
A line is parallel to \(x\)-axis if all the points on the line have equal ________.
- \(y\) and \(z\) coordinates.
- \(x\) and \(z\) coordinates.
- \(y\) and \(x\) coordinates.
- none of these
Correct

Incorrect

Hint

Hence, the value of the filler is \(y\) and \(z\) coordinates.
Question 45 of 81

45. Question
\(x=a\) represents a plane parallel to ____.
- \(x z\)-plane.
- \(y x\)-plane.
- \(y z\)-plane.
- none of these
Correct

Incorrect

Hint

\(x=a\) represents a plane parallel to \(y z\)-plane.
Question 46 of 81

46. Question
The plane parallel to \(y z\)-plane is perpendicular to _____.
- \(y \text {-axis }\)
- \( x \text {-axis } \)
- \( z \text {-axis } \)
- none of these
Correct

Incorrect

Hint

The plane parallel to \(y z\)-plane is perpendicular to \(x\)-axis. Hence, the value of the filler is \(x\)-axis.
Question 47 of 81

47. Question
The length of the longest piece of a string that can be stretched straight in a rectangular room whose dimensions are 10,13 and 8 units are _____.
- \(\sqrt{222}\)
- \( \sqrt{333} \)
- \( \sqrt{323} \)
- \( \sqrt{433} \)
Correct

Incorrect

Hint

The given dimensions are 10,13 and 8
Let \(a=10, b=13\) and \(c=8\)
\(
\begin{aligned}
\therefore \quad \text { Required length } & =\sqrt{a^2+b^2+c^2} \\
& =\sqrt{(10)^2+(13)^2+(8)^2} \\
& =\sqrt{100+169+64}=\sqrt{333}
\end{aligned}
\)
Hence, the value of the filler is \(\sqrt{333}\).
Question 48 of 81

48. Question
If the distance between the points \((a, 2,1)\) and \((1,-1,1)\) is 5 , then \(a\) ____.
- \(a=-3 \text { or } 4\)
- \( a=-3 \text { or } -5 \)
- \( a=-1 \text { or } 5 \)
- \( a=-3 \text { or } 5 \)
Correct

Incorrect

Hint

Given points are \((a, 2,1)\) and \((1,-1,1)\)
\(
\begin{aligned}
\therefore \quad \text { Distance } & =\sqrt{(a-1)^2+(2+1)^2+(1-1)^2} \\
5 & =\sqrt{a^2+1-2 a+9}
\end{aligned}
\)
Squaring both sides, we have
\(
\begin{aligned}
& 25=a^2-2 a+10 \\
& \Rightarrow \quad a^2-2 a-15=0 \\
& \Rightarrow \quad a^2-5 a+3 a-15=0 \\
& \Rightarrow \quad a(a-5)+3(a-5)=0 \\
& \Rightarrow \quad(a+3)(a-5)=0 \\
& \therefore \quad a=-3 \text { or } 5 \\
&
\end{aligned}
\)
Hence, the value of the filler is 5 or -3 .
Question 49 of 81

49. Question
If the mid-points of the sides of a triangle \(AB ; BC\); \(CA\) are \(D (1,2,-3), E (3,0,1)\) and \(F(-1,1,-4)\), then the centriod of the triangle \(A B C\) is _____.
- \((1,1,-2)\)
- \( (1,2,-2) \)
- \( (2,1,-2) \)
- \( (1,0,-2) \)
Correct

Incorrect

Hint

Given that mid-point of a triangle are \(D(1,2,-3), E(3,0,1)\) and \(F(-1,1,-4)\).
From Geometry of centroid, centroid of triangle is same as the centroid of the triangle formed by mid-points of the sides.
The coordinates of the centroid of the triangle, whose vertices are \(\left(x_1, y_1, z_1\right),\left(x_2, y_2, z_2\right)\) and \(\left(x_3, y_3, z_3\right)\) are \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)\)
\(\therefore\) Centroid of triangle
\(
\begin{aligned}
& =G\left(\frac{1+3-1}{3}, \frac{2+0+1}{3}, \frac{-3+1-4}{3}\right) \\
& =G(1,1,-2)
\end{aligned}
\)
Hence, \((1,1,-2)\) are the coordinates of the centroid.
Question 50 of 81

50. Question
Match each item under the Column I to its correct answer given under Column II.
\(
\begin{array}{|l|l|r|l|}
\hline & \text { Column I } & & \text { Column II } \\
\hline \text { (a) } & \text { In } x y \text {-plane } & \text { (i) } & \text { Ist octant } \\
\hline \text { (b) } & \text { Point }(2,3,4) \text { lies in the } & \text { (ii) } & y z \text {-plane } \\
\hline \text { (c) } & \begin{array}{l}
\text { Locus of the points } \\
\text { having } x \text {-coordinate } 0 \text { is }
\end{array} & \text { (iii) } & z \text {-coordinate is zero } \\
\hline \text { (d) } & \begin{array}{l}
\text { A line is parallel to } \\
x \text {-axis if and only }
\end{array} & \text { (iv) } & z \text {-axis } \\
\hline \text { (e) } & \begin{array}{l}
\text { If } x=0, y=0 \text { taken } \\
\text { together will represent } \\
\text { the }
\end{array} & \text { (v) } & \text { Parallel to } x y \text {-plane } \\
\hline \text { (f) } & \begin{array}{l}
z=c \text { represent the plane. }
\end{array} & \text { (vi) } & \begin{array}{l}
\text { If all the points on the } \\
\text { line have equal } y \text { and } \\
z \text {-coordinates }
\end{array} \\
\hline \text { (g) } & \begin{array}{l}
\text { Planes } x=a, y=b \\
\text { represent the line }
\end{array} & \text { (vii) } & \begin{array}{l}
\text { From the point on the } \\
\text { respective axes }
\end{array} \\
\hline \text { (h) } & \begin{array}{l}
\text { Coordinates of a point } \\
\text { are the distances from } \\
\text { the origin to the feet of } \\
\text { perpendiculars }
\end{array} & \text { (viii) } & \text { Parallel to } z \text {-axis } \\
\hline \text { (i) } & \begin{array}{l}
\text { A ball is a solid region } \\
\text { in the space enclosed } \\
\text { by a }
\end{array} & (i x) & \text { disc } \\
\hline \text { (j) } & \begin{array}{l}
\text { Region in the plane } \\
\text { enclosed by a circle is } \\
\text { known as a }
\end{array} & (x) & \text { sphere } \\
\hline
\end{array}
\)
- \(\text { (a) ↔ (iii) (b) ↔ (i) (c) ↔ (ii) (d) ↔ (vi) (e) } \leftrightarrow \text { (iv) (f) } \leftrightarrow \text { (v) (g) ↔ (viii) }\text { (h) } \leftrightarrow(\text { vii) (i) } \leftrightarrow( x )( j ) \leftrightarrow \text { (ix) }\)
- \(\text { (a) ↔ (iii) (b) ↔ (ii) (c) ↔ (i) (d) ↔ (vi) (e) } \leftrightarrow \text { (iv) (f) } \leftrightarrow \text { (v) (g) ↔ (viii) }\text { (h) } \leftrightarrow(\text { vii) (i) } \leftrightarrow( x )( j ) \leftrightarrow \text { (ix) }\)
- \(\text { (a) ↔ (iii) (b) ↔ (i) (c) ↔ (ii) (d) ↔ (vii) (e) } \leftrightarrow \text { (iv) (f) } \leftrightarrow \text { (v) (g) ↔ (viii) }\text { (h) } \leftrightarrow(\text { vi) (i) } \leftrightarrow( x )( j ) \leftrightarrow \text { (ix) }\)
- \(\text { (a) ↔ (iii) (b) ↔ (i) (c) ↔ (ii) (d) ↔ (vi) (e) } \leftrightarrow \text { (iv) (f) } \leftrightarrow \text { (v) (g) ↔ (viii) }\text { (h) } \leftrightarrow(\text { vii) (i) } \leftrightarrow( ix )( j ) \leftrightarrow \text { (x) }\)
Correct

Incorrect

Hint

(a) In \(x y\)-plane, \(z\)-coordinate is zero.
Hence, \((a) \leftrightarrow(i i i)\).
(b) The point \((2,3,4)\) lies in first octant.
Hence, \((b) \leftrightarrow(i)\).
(c) Locus of the points with \(x\)-coordinate is zero is \(y z\)-plane. Hence, \((c) \leftrightarrow(i i)\).
(d) A line is parallel to \(x\)-axis if and only if all the points on the line have equal \(y\) and \(z\)-coordinates.
Hence, \((d) \leftrightarrow(v i)\).
(e) \(x=0, y=0\) represent \(z\)-axis.
Hence, \((e) \leftrightarrow(i v)\).
(f) \(z=c\) represent a plane parallel to \(x y\)-plane.
Hence, \((f) \leftrightarrow(v)\).
(g) The planes \(x=a, y=b\) represent the line parallel to \(z\)-axis. Hence, \((g) \leftrightarrow\) (viii).
(h) Coordinates of a point are the distances from the origin to the feet of perpendicular from the point on the respective axes.
Hence, \((h) \leftrightarrow\) (vii).
(i) A ball is solid region in the space enclosed by a sphere. Hence, \((i) \leftrightarrow(x)\).
(j) The region in the plane enclosed by a circle is known as a disc. Hence, \((j) \leftrightarrow(i x)\).
Question 51 of 81

51. Question
The length of the foot of perpendicular drawn from the point \(P (3,4,5)\) on \(y\)-axis is
- 10
- \(\sqrt{34}\)
- \(\sqrt{113}\)
- \(5 \sqrt{2}\)
Correct

Incorrect

Hint

Let \(l\) be the foot of perpendicular from point \(P\) on the \(y\)-axis. Therefore, its \(x\) and \(z\)-coordinates are zero, i.e., \((0,4,0)\). Therefore, distance between the points ( 0 , \(4,0)\) and \((3,4,5)\) is \(\sqrt{9+25}\) i.e., \(\sqrt{34}\).
Question 52 of 81

52. Question
What is the perpendicular distance of the point \(P (6,7,8)\) from \(x y\)-plane?
- 8
- 7
- 6
- none of these
Correct

Incorrect

Hint

Let \(L\) be the foot of perpendicular drawn from the point \(P (6,7,8)\) to the \(x y\) plane and the distance of this foot \(L\) from \(P\) is \(z\)-coordinate of \(P\), i.e., 8 units.
Question 53 of 81

53. Question
\(20 L\) is the foot of the perpendicular drawn from a point \(P (6,7,8)\) on the \(x y\) plane. What are the coordinates of point \(L\) ?
- \((6,0,0)\)
- \((6,7,0)\)
- \((6,0,8)\)
- none of these
Correct

Incorrect

Hint

Since \(L\) is the foot of perpendicular from \(P\) on the \(x y\)-plane, \(z\)-coordinate is zero in the \(x y\)-plane. Hence, coordinates of \(L\) are \((6,7,0)\).
Question 54 of 81

54. Question
\(21 L\) is the foot of the perpendicular drawn from a point \((6,7,8)\) on \(x\)-axis. The coordinates of \(L\) are
- \((6,0,0)\)
- \((0,7,0)\)
- \((0,0,8)\)
- none of these
Correct

Incorrect

Hint

Since \(L\) is the foot of perpendicular from \(P\) on the \(x\)-axis, \(y\) and \(z\)-coordinates are zero. Hence, the coordinates of \(L\) are \((6,0,0)\).
Question 55 of 81

55. Question
What is the locus of a point for which \(y=0, z=0\) ?
- equation of \(x\)-axis
- equation of \(y\)-axis
- equation of \(z\)-axis
- none of these
Correct

Incorrect

Hint

Locus of the point \(y=0, z=0\) is \(x\)-axis, since on \(x\)-axis both \(y=0\) and \(z=0\).
Question 56 of 81

56. Question
\(23 L\), is the foot of the perpendicular drawn from a point \(P(3,4,5)\) on the \(x z\) plane. What are the coordinates of point \(L\) ?
- \((3,0,0)\)
- \((0,4,5)\)
- \((3,0,5)\)
- \((3,4,0)\)
Correct

Incorrect

Hint

Since \(L\) is the foot of perpendicular segment drawn from the point \(P(3,4,5)\) on the \(x z\)-plane. Since the \(y\)-coordinates of all points in the \(x z\)-plane are zero, coordinate of the foot of perpendicular are \((3,0,5)\).
Question 57 of 81

57. Question
A line is parallel to \(x y\)-plane if all the points on the line have equal _____.
- \(\)z[ latex]-coordinates
- \(\)x[ latex]-coordinates
- \(\)y[ latex]-coordinates
- none of these
Correct

Incorrect

Hint

A line parallel to xy-plane if all the points on the line have equal \(z\)-coordinates.
Question 58 of 81

58. Question
The equation \(x=b\) represents a plane parallel to ____ plane.
- \(x z\)
- \(x y\)
- \(y z\)
- none of these
Correct

Incorrect

Hint

Since \(x=0\) represent \(y z\)-plane, therefore \(x=b\) represent a plane parallel to \(y z\)-plane at a unit distance \(b\) from the origin.
Question 59 of 81

59. Question
Perpendicular distance of the point \(P (3,5,6)\) from \(y\)-axis is ____.
- \(\sqrt{25}\)
- \( \sqrt{15} \)
- \( \sqrt{35} \)
- \( \sqrt{45} \)
Correct

Incorrect

Hint

Since \(M\) is the foot of perpendicular from \(P\) on the \(y\)-axis, therefore, its \(x\) and \(z\)-coordinates are zero. The coordinates of \(M\) is \((0,5,0)\). Therefore, the perpendicular distance of the point \(P\) from \(y\)-axis \(\sqrt{3^2+6^2}=\sqrt{45}\).
Question 60 of 81

60. Question
\(L\) is the foot of perpendicular drawn from the point \(P (3,4,5)\) on \(z x\) planes. The coordinates of \(L\) are ____.
- \((3,1,5)\)
- \((0,0,5)\)
- \((3,0,5)\)
- \(\)(3,0,0)\(\)
Correct

Incorrect

Hint

Since \(L\) is the foot of perpendicular from \(P\) on the \(z x\)-plane, \(y\)-coordinate of every point is zero in the \(z x\)-plane. Hence, coordinate of \(L\) are \((3,0,5)\).
Question 61 of 81

61. Question
The length of the foot of perpendicular drawn from the point \(P (a, b, c)\) on \(z\)-axis is _____.
- \(\sqrt{a^2+b^2}\)
- \(\sqrt{a^2-b^2}\)
- \(\sqrt{-a^2+b^2}\)
- none of the above
Correct

Incorrect

Hint

The coordinates of the foot of perpendicular from the point \(P (a, b, c)\) on \(z\) axis is \((0,0, c )\). The distance between the point \(P (a, b, c)\) and \((0,0, c)\) is \(\sqrt{a^2+b^2}\).
Question 62 of 81

62. Question
The \(y\)-axis and \(z\)-axis, together determine a plane known as \(y z\)-plane.
- true
- false
Correct

Incorrect

Hint

True
Question 63 of 81

63. Question
The point \((4,5,-6)\) lies in the \(VI ^{\text th }}\) octant.
- true
- false
Correct

Incorrect

Hint

False, the point \((4,5,-6)\) lies in the \(V ^{ \text {th} }\) octant.
Question 64 of 81

64. Question
The \(x\)-axis is the intersection of two planes \(x y\)-plane and \(x z\) plane.
- true
- false
Correct

Incorrect

Hint

true
Question 65 of 81

65. Question
Three mutually perpendicular planes divide the space into 8 octants.
- true
- false
Correct

Incorrect

Hint

Three mutually perpendicular planes divide the space into 8 octants. True
Question 66 of 81

66. Question
The equation of the plane \(z=6\) represent a plane parallel to the \(x y\)-plane, having a \(z\)-intercept of 6 units.
- true
- false
Correct

Incorrect

Hint

True
Question 67 of 81

67. Question
The equation of the plane \(x=0\) represent the \(y z\)-plane.
- true
- false
Correct

Incorrect

Hint

true
Question 68 of 81

68. Question
The point on the \(x\)-axis with \(x\)-coordinate equal to \(x_0\) is written as \(\left(x_0, 0,0\right)\).
- true
- false
Correct

Incorrect

Hint

true
Question 69 of 81

69. Question
\(x=x_0\) represent a plane parallel to the \(y z\)-plane.
- true
- false
Correct

Incorrect

Hint

true
Question 70 of 81

70. Question
Match each item under the Column I to its correct answer given under Column II.
\(
\begin{array}{|l|l|r|l|}
\hline & \text { Column I } & & \text { Column II } \\
\hline \text { (a) } & \begin{array}{l}
\text { If the centriod of the triangle is } \\
\text { origin and two of its vertices } \\
\text { are (3, – 5, 7) and (–1, 7, – 6) } \\
\text { then the third vertex is }
\end{array} & \text { (i) } & \text { Parallelogram } \\
\hline \text { (b) } & \begin{array}{l}
\text { If the mid-points of the sides of } \\
\text { triangle are (1, 2, – 3), (3, 0, 1) } \\
\text { and (–1, 1, – 4) then the centriod is }
\end{array} & \text { (ii) } & \text { (–2, –2, –1) } \\
\hline \text { (c) } & \begin{array}{l}
\text { The points (3, – 1, – 1), (5, – 4, 0), } \\
\text { (2, 3, – 2) and (0, 6, – 3) are the } \\
\text { vertices of a }
\end{array} & \text { (iii) } & \text { as Isosceles right-angled triangle } \\
\hline \text { (d) } & \begin{array}{l}
\text { Point A(1, –1, 3), B (2, – 4, 5) and } \\
\text { C (5, – 13, 11) are }
\end{array} & \text { (iv) } & \text { (1, 1, – 2) } \\
\hline \text { (e) } & \begin{array}{l}
\text { Point A(2, 4, 3), B (4, 1, 9) and } \\
\text { C (10, – 1, 6) are the vertices of }
\end{array} & \text { (v) } & \text { Collinear } \\
\hline
\end{array}
\)
- \(\text { (a) } \leftrightarrow \text { (ii) }\), \(\text { (b) } \leftrightarrow \text { (iv) }\), \(\text { (c) } \leftrightarrow \text { (i) }\), \(\text { (d) } \leftrightarrow \text { (v) }\), \(\text { (e) } \leftrightarrow \text { (iii) }\)
- \(\text { (a) } \leftrightarrow \text { (ii) }\), \(\text { (b) } \leftrightarrow \text { (v) }\), \(\text { (c) } \leftrightarrow \text { (i) }\), \(\text { (d) } \leftrightarrow \text { (iv) }\), \(\text { (e) } \leftrightarrow \text { (iii) }\)
- \(\text { (a) } \leftrightarrow \text { (i) }\), \(\text { (b) } \leftrightarrow \text { (iv) }\), \(\text { (c) } \leftrightarrow \text { (ii) }\), \(\text { (d) } \leftrightarrow \text { (v) }\), \(\text { (e) } \leftrightarrow \text { (iii) }\)
- none of these
Correct

Incorrect

Hint

(a) Let \(A (3,-5,7), B (-1,7,-6), C (x, y, z)\) be the vertices of a \(\Delta ABC\) with centriod \((0\), 0,0 )
Therefore, \((0,0,0)=\left(\frac{3-1+x}{3}, \frac{-5+7+y}{3}, \frac{7-6+z}{3}\right)\). This implies \(\frac{x+2}{3}=0, \frac{y+2}{3}=0\), \(\frac{z+1}{3}=0\)
Hence \(x=-2, y=-2\), and \(z=-1\). Therefore (a) \(\leftrightarrow\) (ii)
(b) Let \(ABC\) be the given \(\triangle\) and \(DEF\) be the mid-points of the sides \(BC , CA , AB\), respectively. We know that the centriod of the \(\triangle ABC =\) centriod of \(\triangle DEF\).
Therefore, centriod of \(\triangle DEF\) is \(\left(\frac{1+3-1}{3}, \frac{2+0+1}{3}, \frac{-3+1-4}{3}\right)=(1,1,-2)\)
Hence (b) \(\leftrightarrow\) (iv)
(c) Mid-point of diagonal AC is \(\left(\frac{3+2}{2}, \frac{-1+3}{2}, \frac{-1-2}{2}\right)=\left(\frac{5}{2}, 1, \frac{-3}{2}\right)\)
Mid-point of diagonal BD is \(\left(\frac{5+0}{2}, \frac{-4+6}{2}, \frac{0-3}{2}\right)=\left(\frac{5}{2}, 1, \frac{-3}{2}\right)\)
Diagonals of parallelogram bisect each other. Therefore (c) \(\leftrightarrow\) (i)
(d)
\(
\begin{aligned}
& |A B|=\sqrt{(2-1)^2+(-4+1)^2+(5-3)^2}=\sqrt{14} \\
& |B C|=\sqrt{(5-2)^2+(-13+4)^2+(11-5)^2}=3 \sqrt{14} \\
& |A C|=\sqrt{(5-1)^2+(-13+1)^2+(11-3)^2}=4 \sqrt{14}
\end{aligned}
\)
Now \(|A B|+|B C|=|A C|\). Hence Points A, B, C are collinear. Hence (d) \(\leftrightarrow\) (v)
(e) \(AB =\sqrt{4+9+36}=7\)
\(
\begin{aligned}
& BC =\sqrt{36+4+9}=7 \\
& CA =\sqrt{64+25+9}=7 \sqrt{2}
\end{aligned}
\)
Now \(AB ^2+ BC ^2= AC ^2\). Hence \(ABC\) is an isosceles right angled triangle and hence (e) \(\leftrightarrow\) (iii)
Question 71 of 81

71. Question
The points \(P(2,4,6), Q(-2,-2,-2)\) and \(R (6,10,14)\) are collinear. Is this true?
- yes
- no
Correct

Incorrect

Hint

Three points are collinear if the sum of any two distances is equal to the third distance.
\(
\begin{aligned}
& P Q=\sqrt{(-2-2)^2+(-2-4)^2+(-2-6)^2}=\sqrt{16+36+64}=\sqrt{116}=2 \sqrt{29} \\
& QR =\sqrt{(6+2)^2+(10+2)^2+(14+2)^2}=\sqrt{64+144+256}=\sqrt{464}=4 \sqrt{29} \\
& PR =\sqrt{(6-2)^2+(10-4)^2+(14-6)^2}=\sqrt{16+36+64}=\sqrt{116}=2 \sqrt{29}
\end{aligned}
\)
Since \(QR = PQ + PR\). Therefore, the given points are collinear.
Question 72 of 81

72. Question
Find the coordinates of a point equidistant from the four points \(O (0,0,0)\), \(A (l, 0,0), B (0, m, 0)\) and \(C (0,0, n)\).
- \(\left(\frac{l}{2}, \frac{-m}{2}, \frac{n}{2}\right)\)
- \( \left(\frac{l}{2}, \frac{m}{2}, \frac{n}{2}\right) \)
- \( \left(\frac{-l}{2}, \frac{m}{2}, \frac{n}{2}\right) \)
- \( \left(\frac{l}{2}, \frac{m}{2}, \frac{-n}{2}\right) \)
Correct

Incorrect

Hint

Let \(P (x, y, z)\) be the required point. Then \(OP = PA = PB = PC\).
Now \(OP = PA \Rightarrow OP ^2= PA ^2 \Rightarrow x^2+y^2+z^2=(x-l)^2+(y-0)^2+(z-0)^2 \Rightarrow x=\frac{l}{2}\)
Similarly, \(OP = PB \Rightarrow y=\frac{m}{2}\) and \(OP = PC \Rightarrow z=\frac{n}{2}\)
Hence, the coordinate of the required point are \(\left(\frac{l}{2}, \frac{m}{2}, \frac{n}{2}\right)\).
Question 73 of 81

73. Question
Find the point on \(x\)-axis which is equidistant from the point \(A (3,2,2)\) and B \((5,5,4)\).
- \(\left(\frac{49}{4}, 0,1\right)\)
- \( \left(\frac{49}{4}, 1,0\right) \)
- \( \left(\frac{49}{4}, 0,0\right) \)
- \( \left(\frac{49}{2}, 0,0\right) \)
Correct

Incorrect

Hint

The point on the \(x\)-axis is of form \(P (x, 0,0)\). Since the points \(A\) and \(B\) are equidistant from \(P\). Therefore \(PA ^2= PB ^2\), i.e.,
\(
\begin{aligned}
& (x-3)^2+(0-2)^2+(0-2)^2=(x-5)^2+(0-5)^2+(0-4)^2 \\
& \Rightarrow 4 x=25+25+16-17 \text { i.e., } x=\frac{49}{4} .
\end{aligned}
\)
Thus, the point \(P\) on the \(x\)-axis is \(\left(\frac{49}{4}, 0,0\right)\) which is equidistant from \(A\) and \(B\).
Question 74 of 81

74. Question
Find the point on \(y\)-axis which is at a distance \(\sqrt{10}\) from the point \((1,2,3)\)
- \((1,2,0)\)
- \((0,2,1)\)
- \((0,2,0)\)
- \((0,-2,0)\)
Correct

Incorrect

Hint

Let the point \(P\) be on \(y\)-axis. Therefore, it is of the form \(P (0, y, 0)\).
The point \((1,2,3)\) is at a distance \(\sqrt{10}\) from \((0, y, 0)\). Therefore
\(
\begin{aligned}
& \sqrt{(1-0)^2+(2-y)^2+(3-0)^2}=\sqrt{10} \\
& \Rightarrow y^2-4 y+4=0 \Rightarrow(y-2)^2=0 \Rightarrow y=2
\end{aligned}
\)
Hence, the required point is \((0,2,0)\).
Question 75 of 81

75. Question
If a parallelopiped is formed by planes drawn through the points \((2,3,5)\) and \((5,9,7)\) parallel to the coordinate planes, then find the length of edges of a parallelopiped and length of the diagonal.
- 5 units
- 3 units
- 9 units
- 7 units
Correct

Incorrect

Hint

Length of edges of the parallelopiped are \(5-2,9-3,7-5\) i.e., \(3,6,2\).
Length of diagonal is \(\sqrt{3^2+6^2+2^2}=7\) units.
Question 76 of 81

76. Question
The points \((0,7,10),(-1,6,6)\) and \((-4,9,6)\) form a right angled isosceles triangle. Is this true?
- no
- yes
Correct

Incorrect

Hint

Let \(P (0,7,10), Q (-1,6,6)\) and \(R (-4,9,6)\) be the given three points.
Here \(PQ =\sqrt{1+1+16}=3 \sqrt{2}\)
\(
\begin{aligned}
& QR =\sqrt{9+9+0}=3 \sqrt{2} \\
& PR =\sqrt{16+4+16}=6
\end{aligned}
\)
Now \(PQ ^2+ QR ^2=(3 \sqrt{2})^2+(3 \sqrt{2})^2=18+18=36=( PR )^2\)
Therefore, \(\triangle PQR\) is a right angled triangle at \(Q\). Also \(PQ = QR\). Hence \(\triangle PQR\) is an isosceles triangle.
Question 77 of 81

77. Question
The points \((5,-1,1),(7,-4,7),(1-6,10)\) and \((-1,-3,4)\) are the vertices of a rhombus. Is this true?
- yes
- no
Correct

Incorrect

Hint

Let \(A (5,-1,1), B (7,-4,7), C (1,-6,10)\) and \(D (-1,-3,4)\) be the four points of a quadrilateral. Here
\(
\begin{aligned}
& AB =\sqrt{4+9+36}=7, BC =\sqrt{36+4+9}=7, CD =\sqrt{4+9+36}=7, \\
& DA =\sqrt{23+4+9}=7
\end{aligned}
\)
Note that \(AB = BC = CD = DA\). Therefore, \(ABCD\) is a rhombus.
Question 78 of 81

78. Question
Find the ratio in which the line segment joining the points \((2,4,5)\) and \((3,5,-4)\) is divided by the \(x z\)-plane.
- \(4: 5\)
- \(-4: 5\)
- \(-2: 5\)
- \(-14: 5\)
Correct

Incorrect

Hint

Let the joint of \(P (2,4,5)\) and \(Q (3,5,-4)\) be divided by \(x z\)-plane in the ratio \(k: 1\) at the point \(R (x, y, z)\). Therefore
\(
x=\frac{3 k+2}{k+1}, y=\frac{5 k+4}{k+1}, z=\frac{-4 k+5}{k+1}
\)
Since the point \(R (x, y, z)\) lies on the \(x z\)-plane, the \(y\)-coordinate should be zero,i.e.,
\(
\frac{5 k+4}{k+1}=0 \Rightarrow k=-\frac{4}{5}
\)
Hence, the required ratio is \(-4: 5\), i.e.; externally in the ratio \(4: 5\).
Question 79 of 81

79. Question
Find the coordinate of the point \(P\) which is five – sixth of the way from \(A\) \((-2,0,6)\) to \(B (10,-6,-12)\).
- \(=(4,-5,-9)\)
- \( =(8,-5,-9) \)
- \( =(8,5,-9) \)
- \( =(8,-5,9) \)
Correct

Incorrect

Hint

Let \(P (x, y, z)\) be the required point, i.e., \(P\) divides \(AB\) in the ratio \(5: 1\). Then
\(
P(x, y, z)=\left(\frac{5 \times 10+1 \times-2}{5+1}, \frac{5 \times-6+1 \times 0}{5+1}, \frac{5 \times-12+1 \times 6}{5+1}\right)=(8,-5,-9)
\)
Question 80 of 81

80. Question
Let \(A (3,2,0), B (5,3,2), C (-9,6,-3)\) be three points forming a triangle. \(A D\), the bisector of \(\angle B A C\), meets \(B C\) in \(D\). Find the coordinates of the point \(D\).
- \(=\left(\frac{19}{8}, \frac{57}{16}, \frac{17}{6}\right)\)
- \( =\left(\frac{19}{8}, \frac{57}{6}, \frac{17}{16}\right) \)
- \( =\left(\frac{19}{18}, \frac{57}{16}, \frac{17}{16}\right) \)
- \( =\left(\frac{19}{8}, \frac{57}{16}, \frac{17}{16}\right) \)
Correct

Incorrect

Hint

Note that
\(
\begin{aligned}
& AB =\sqrt{(5-3)^2+(3-2)^2+(2-0)^2}=\sqrt{4+1+4}=3 \\
& AC =\sqrt{(-9-3)^2+(6-2)^2+(-3-0)^2}=\sqrt{144+16+9}=13
\end{aligned}
\)
Since \(AD\) is the bisector of \(\angle BAC\), We have \(\frac{ BD }{ DC }=\frac{ AB }{ AC }=\frac{3}{13}\)
i.e., \(D\) divides \(BC\) in the ratio \(3: 13\). Hence, the coordinates of \(D\) are
\(
\left(\frac{3(-9)+13(5)}{3+13}, \frac{3(6)+13(3)}{3+13}, \frac{3(-3)+13(2)}{3+13}\right)=\left(\frac{19}{8}, \frac{57}{16}, \frac{17}{16}\right)
\)
Question 81 of 81

81. Question
Determine the point in \(y z\)-plane which is equidistant from three points \(A\) \((2,03)\) B \((0,3,2)\) and \(C(0,0,1)\).
- \((2,1,3)\)
- \( (0,-1,3) \)
- \( (0,1,3) \)
- \( (0,1,-3) \)
Correct

Incorrect

Hint

Since \(x\)-coordinate of every point in \(y z\)-plane is zero. Let \(P (0, y, z)\) be a point on the \(y z\)-plane such that \(PA = PB = PC\). Now
\(
\begin{aligned}
& PA = PB \Rightarrow(0-2)^2+(y-0)^2+(z-3)^2=(0-0)^2+(y-3)^2+(z-2)^2, \text { i.e. } z-3 y=0 \\
& \text { and } PB = PC \\
& \Rightarrow y^2+9-6 y+z^2+4-4 z=y^2+z^2+1-2 z \text {, i.e. } 3 y+z=6
\end{aligned}
\)
Simplifying the two equating, we get \(y=1, z=3\)
Here, the coordinate of the point \(P\) are \((0,1,3)\).

CLASS-XI MATHEMATICS + IIT JEE MAIN

NCERT Exemplar MCQs

Quiz Summary

Information

Results

Results

Categories

1. Question

Hint

2. Question

Hint

3. Question

Hint

4. Question

Hint

5. Question

Hint

6. Question

Hint

7. Question

Hint

8. Question

Hint

9. Question

Hint

10. Question

Hint

11. Question

Hint

12. Question

Hint

13. Question

Hint

14. Question

Hint

15. Question

Hint

16. Question

Hint

17. Question

Hint

18. Question

Hint

19. Question

Hint

20. Question

Hint

21. Question

Hint

22. Question

Hint

23. Question

Hint

24. Question

Hint

25. Question

Hint

26. Question

Hint

27. Question

Hint

28. Question

Hint

29. Question

Hint

30. Question

Hint

31. Question

Hint

32. Question

Hint

33. Question

Hint

34. Question

Hint

35. Question

Hint

36. Question

Hint

37. Question