NCERT Exemplar MCQs

Hint

We write the given equation in the form \(\left(x^2-2 x\right)+\left(y^2+4 y\right)=8\) Now, completing the squares, we get
\(
\begin{aligned}
& \left(x^2-2 x+1\right)+\left(y^2+4 y+4\right)=8+1+4 \\
& (x-1)^2+(y+2)^2=13
\end{aligned}
\)
Comparing it with the standard form of the equation of the circle, we see that the centre of the circle is \((1,-2)\) and radius is \(\sqrt{13}\).

Hint

The given equation is of the form \(x^2=-4 a y\) where \(a\) is positive.
Therefore, the focus is on \(y\)-axis in the negative direction and parabola opens downwards.
Comparing the given equation with standard form, we get \(a=2\).
Therefore, the coordinates of the focus are \((0,-2)\) and the the equation of directrix is \(y=2\) and the length of the latus rectum is \(4 a\), i.e., 8.

Hint

We have \(a e=5, \frac{a}{e}=\frac{36}{5}\) which give \(a^2=36\) or \(a=6\). Therefore, \(e=\frac{5}{6}\).
Now \(b=a \sqrt{1-e^2}=6 \sqrt{1-\frac{25}{36}}=\sqrt{11}\). Thus, the equation of the ellipse is \(\frac{x^2}{36}+\frac{y^2}{11}=1\).

Hint

The equation of the hyperbola can be written as \(\frac{x^2}{16}-\frac{y^2}{9}=1\), so \(a=4, b=3\) and \(9=16\left(e^2-1\right)\), so that \(e^2=\frac{9}{16}+1=\frac{25}{16}\), which gives \(e=\frac{5}{4}\). Vertices are \(( \pm a, 0)=\) \(( \pm 4,0)\) and foci are \(( \pm a e, 0)=( \pm 5,0)\).

Hint

Since the vertices are on the \(y\)-axes (with origin at the mid-point), the equation is of the form \(\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\).
As vertices are \((0, \pm 6), a=6, b^2=a^2\left(e^2-1\right)=36\left(\frac{25}{9}-1\right)=64\), so the required equation of the hyperbola is \(\frac{y^2}{36}-\frac{x^2}{64}=1\) and the foci are \((0, \pm a e)=(0, \pm 10)\).

Hint

By substitution of coordinates in the general equation of the circle given by \(x^2+y^2+2 g x+2 f y+ c =0\), we have
\(
\begin{aligned}
40 g+6 f+ c & =-409 \\
38 g+16 f+ c & =-425 \\
4 g-18 f+ c & =-85
\end{aligned}
\)
From these three equations, we get
\(
g=-7, f=-3 \text { and } c=-111
\)
Hence, the equation of the circle is
\(
\begin{aligned}
x^2+y^2-14 x-6 y-111 & =0 \\
(x-7)^2+(y-3)^2 & =13^2
\end{aligned}
\)
Therefore, the centre of the circle is \((7,3)\) and radius is 13.

Hint

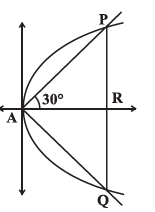
As shown in the figure APQ denotes the equilateral triangle with its equal sides of length \(l\) (say).
Here
\(
\begin{aligned}
AP & =l \operatorname{so~\mathrm {AR}}=l \cos 30^{\circ} \\
& =l \frac{\sqrt{3}}{2} \\
PR & =l \sin 30^{\circ}=\frac{l}{2} .
\end{aligned}
\)
Thus \(\left(\frac{l \sqrt{3}}{2}, \frac{l}{2}\right)\) are the coordinates of the point \(P\) lying on the parabola \(y^2=4 a x\).
Therefore, \(\quad \frac{l^2}{4}=4 a\left(\frac{l \sqrt{3}}{2}\right) \Rightarrow l=8 a \sqrt{3}\).
Thus, \(8 a \sqrt{3}\) is the required length of the side of the equilateral triangle inscribed in the parabola \(y^2=4 a x\).

Hint

Let \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) be the equation of the ellipse passing through the point \((-3,1)\).
Therefore, we have
\(
\begin{aligned}
& \frac{9}{a^2}+\frac{1}{b^2}=1 . \\
& 9 b^2+a^2=a^2 b^2
\end{aligned}
\)
or \(9 a^2\left(a^2-e^2\right)+a^2=a^2 a^2\left(1-e^2\right)\)
(Using \(b^2=a^2\left(1-e^2\right)\)
or \(a^2=\frac{32}{3}\)
\(
b^2=a^2\left(1-e^2\right)=\frac{32}{3}\left(1-\frac{2}{5}\right)=\frac{32}{5}
\)
Hence, the required equation of the ellipse is
\(
\begin{aligned}
& \frac{x^2}{\frac{32}{3}}+\frac{y^2}{\frac{32}{5}}=1 \\
& 3 x^2+5 y^2=32 .
\end{aligned}
\)

Hint

As the vertices are on the \(x\)-axis and their middle point is the origin, the equation is of the type \(\quad \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\).
Here \(b^2=a^2\left(e^2-1\right)\), vertices are \(( \pm a, 0)\) and directrices are given by \(x= \pm \frac{a}{e}\).
Thus \(a=6, \frac{a}{e}=4\) and so \(e=\frac{3}{2}\) which gives \(b^2=36\left(\frac{9}{4}-1\right)=45\)
Consequently, the required equation of the hyperbola is \(\frac{x^2}{36}-\frac{y^2}{45}=1\)

Hint

The correct choice is (a), since the equation can be written as \((x-1)^2+\) \((y-1)^2=1\) which represents a circle touching both the axes with its centre \((1,1)\) and radius one unit.

Hint

The correct option is (a). The point of intersection of \(3 x+y-14=0\) and \(2 x\) \(+5 y-18=0\) are \(x=4, y=2\), i.e., the point \((4,2)\)
Therefore, the radius is \(=\sqrt{9+16}=5\) and hence the equation of the circle is given by
\(
\begin{aligned}
(x-1)^2+(y+2)^2 & =25 \\
\text { or } \quad x^2+y^2-2 x+4 y-20 & =0 .
\end{aligned}
\)

Hint

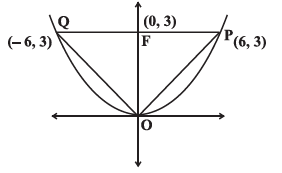
The correct option is (c). From the figure, \(O P Q\) represent the triangle whose area is to be determined. The area of the triangle
\(
=\quad \frac{1}{2} PQ \times OF =\frac{1}{2}(12 \times 3)=18
\)

Hint

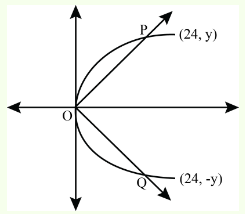
(b) is the correct choice. Let \(P\) and \(Q\) be points on the parabola \(y^2=6 x\) and \(OP , OQ\) be the lines joining the vertex \(O\) to the points \(P\) and \(Q\) whose abscissa are 24.
Thus
\(
\begin{aligned}
y^2 & =6 \times 24=144 \\
y & = \pm 12 .
\end{aligned}
\)
Therefore the coordinates of the points \(P\) and \(Q\) are \((24,12)\) and \((24,-12)\) respectively. Hence the lines are
\(
y= \pm \frac{12}{24} x \Rightarrow 2 y= \pm x .
\)

Hint

(b) is the correct choice. Let \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) be the equation of the ellipse. Then according to the given conditions, we have
\(
\begin{array}{lll}
\frac{9}{a^2}+\frac{1}{b^2}=1 & \text { and } & \frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{4} \\
\text { which gives } a^2=\frac{32}{3} & \text { and } & b^2=\frac{32}{5} .
\end{array}
\)
Hence, required equation of ellipse is \(3 x^2+5 y^2=32\)

Hint

(c) is the correct choice. Let \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) represent the hyperbola. Then according to the given condition, the length of transverse axis, i.e., \(2 a=7 \Rightarrow a=\frac{7}{2}\). Also, the point \((5,-2)\) lies on the hyperbola, so, we have
\(\frac{4}{49}(25)-\frac{4}{b^2}=1 \quad\) which gives
\(b^2=\frac{196}{51}\). Hence, the equation of the hyperbola is
\(
\frac{4}{49} x^2-\frac{51}{196} y^2=1
\)
State whether the statements in Examples 17 and 18 are correct or not. Justify.

Hint

True. From given conditions, we have
\(
\begin{aligned}
& x=2+4 \cos \theta \Rightarrow(x-2)=4 \cos \theta \\
\text { and } & y=-1+4 \sin \theta \Rightarrow y+1=4 \sin \theta .
\end{aligned}
\)
Squaring and adding, we get \((x-2)^2+(y+1)^2=16\).

Hint

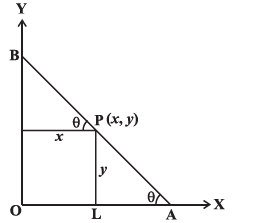
True. Let P \((x, y)\) be any point on the bar such that \(PA =a\) and \(PB =b\), clearly from the Fig. above.
\(
\begin{aligned}
& x= OL =b \cos \theta \text { and } \\
& y= PL =a \sin \theta
\end{aligned}
\)
These give \(\frac{x^2}{b^2}+\frac{y^2}{a^2}=1\), which is an ellipse.

Hint

As the circle is passing through the point \((4,5)\) and its centre is \((2,2)\) so its radius is \(\sqrt{(4-2)^2+(5-2)^2}=\sqrt{13}\). Therefore the required answer is \((x-2)^2+(y-2)^2=13\).

Hint

Let \((h, k)\) be the centre of the circle. Then \(k=h-1\). Therefore, the equation of the circle is given by \((x-h)^2+[y-(h-1)]^2=9\)
Given that the circle passes through the point \((7,3)\) and hence we get
\(
\begin{array}{r}
(7-h)^2+(3-(h-1))^2=9 \\
(7-h)^2+(4-h)^2=9
\end{array}
\)
\(
h^2-11 h+28=0
\)
which gives \((h-7)(h-4)=0 \quad \Rightarrow h=4\) or \(h=7\)
Therefore, the required equations of the circles are \(x^2+y^2-8 x-6 y+16=0\) or
\(
x^2+y^2-14 x-12 y+76=0
\)

Hint

Given that \(\frac{2 b^2}{a}=10\) and \(2 a e=2 b \Rightarrow b=a e\)
Again, we know that
\(
\begin{aligned}
b^2 & =a^2\left(1-e^2\right) \\
2 a^2 e^2 & =a^2 \Rightarrow e=\frac{1}{\sqrt{2}} \quad(\text { using } b=a e)
\end{aligned}
\)
Thus
\(
a=b \sqrt{2}
\)
\(
\begin{array}{rlrl}
& \text { Again } \frac{2 b^2}{a} =10 \\
\text { or } & b =5 \sqrt{2} . \quad \text { Thus we get } a=10
\end{array}
\)
Therefore, the required equation of the ellipse is
\(
\frac{x^2}{100}+\frac{y^2}{50}=1
\)

Hint

Using the definition of parabola, we have
\(
\sqrt{(x-2)^2+(y-3)^2}=\left|\frac{x-4 y+3}{\sqrt{17}}\right|
\)
Squaring, we get
\(
17\left(x^2+y^2-4 x-6 y+13\right)=x^2+16 y^2+9-8 x y-24 y+6 x
\)
or \(16 x^2+y^2+8 x y-74 x-78 y+212=0\)

Hint

Given that the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) is passing through the points \((3,0)\) and \((3 \sqrt{2}, 2)\), so we get \(a^2=9\) and \(b^2=4\).
Again, we know that \(b^2=a^2\left(e^2-1\right)\). This gives
\(
\begin{aligned}
4 & =9\left(e^2-1\right) \\
e^2 & =\frac{13}{9} \\
e & =\frac{\sqrt{13}}{3} .
\end{aligned}
\)

Hint

Given that the circle has a radius aand touches both axis. So the centre is \((a, a)\).
\((x-a)^2+(y-a)^2=a^2\)
\(
x^2+y^2-2 a x-2 a y+a^2=0
\)

Hint

We have variable point as \(x=\frac{2 a t}{1+t^2}\) and \(y=\frac{a\left(1-t^2\right)}{1+t^2}\)
\(
\begin{aligned}
& x^2+y^2=\frac{4 a^2 t^2}{\left(1+t^2\right)^2}+\frac{a^2\left(1+t^4-2 t^2\right)}{\left(1+t^2\right)^2} \\
& =\frac{a^2+a^2 t^4+2 a^2 t^2}{\left(1+t^2\right)^2} \\
& =\frac{a^2\left(1+t^2\right)^2}{\left(1+t^2\right)^2} \\
& =a^2
\end{aligned}
\)

Hint

As we know,
The equation of a circle with centre \((h, k)\) and radius as \(r\) units, is
\(
(x-h)^2+(y-k)^2=r^2
\)
Step 2. Put the values of given coordinates in general equation:
First, \((0,0)\)
\(
\begin{aligned}
& \Rightarrow(0-h)^2+(0-k)^2=r^2 \\
& \Rightarrow h^2+k^2=r^2
\end{aligned}
\)
Second, \((a, 0)\)
\(
\begin{aligned}
& \Rightarrow(a-h)^2+(0-k)^2=r^2 \\
& \Rightarrow a^2+h^2-2 a h+k^2=r^2 \dots(1)
\end{aligned}
\)
Third, \((0, b)\)
\(
\begin{aligned}
& \Rightarrow(0-h)^2+(b-k)^2=r^2 \\
& \Rightarrow h^2+b^2+k^2-2 b k=r^2 \dots(2)
\end{aligned}
\)
Step 3. By solving equation(1) and (2), respectively, we get
\(
\begin{aligned}
& a(a-2 h)=0 \\
& \Rightarrow a=0,2 h \\
& \Rightarrow h=\frac{a}{2} \\
& b(b-2 k)=0 \\
& \Rightarrow b=0,2 k \\
& \Rightarrow k=\frac{b}{2}
\end{aligned}
\)
\(\therefore\) The coordinates of centre are \(\left(\frac{a}{2}, \frac{b}{2}\right)\)

Hint

Given that, circle with centre \((1,2)\) touches \(x\)-axis.
Radius of the circle is, \(r=2\)
So, the equation of the required circle is:
\(
\begin{aligned}
& (x-1)^2+(y-2)^2=2^2 \\
& =>x^2-2 x+1+y^2-4 y+4=4 \\
& \Rightarrow x^2+y^2-2 x-4 y+1=0
\end{aligned}
\)

Hint

Given lines are \(3 x-4 y+4=0\) and \(6 x-8 y-7=0\).
These parallel lines are tangent to a circle.
\(\therefore \quad\) Diameter of the circle \(=\) Distance between the lines
\(
=\left|\frac{8-(-7)}{\sqrt{36+64}}\right|=\frac{15}{10}=\frac{3}{2}
\)
\(
\therefore \quad \text { Radius of the circle }=\frac{3}{4}
\)

Hint

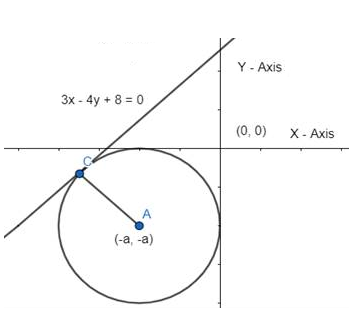
Perpendicular Distance (Between a point and line) \(=\frac{\left| ax _1+ by _1+ c \right|}{\sqrt{ a ^2+ b ^2}}\), whereas the point is \(\left(x_1, y_1\right)\) and the line is expressed as \(a x+b y+c=0\)
The line which touches the circle is \(3 x-4 y+8=0\), which is a tangent to the circle.
\(\therefore\) The perpendicular distance \(=\) a units (radius of the circle)
\(
\begin{aligned}
& a=\frac{\left|a x_1+b y_1+c\right|}{\sqrt{a^2+b^2}} \\
& a=\frac{|3(-a)-4(-a)+8|}{\sqrt{3^2+4^2}} \\
& a=\frac{|-3 a+4 a+8|}{\sqrt{9+16}} \\
& a=\frac{a+8}{5}  \\
& a=2
\end{aligned}
\)
Co-ordinates of the centre of the circle \(=(-2,-2)\)
SInce, the equation of a circle having centre \((h, k)\), having radlus as ” \(r\) ” unlts, Is
\(
\begin{aligned}
& (x-h)^2+(y-k)^2=r^2 \\
& (x-(-2))^2+(y-(-2))^2=2^2 \\
& x^2+y^2+4 x+4 y+4=0
\end{aligned}
\)

Hint

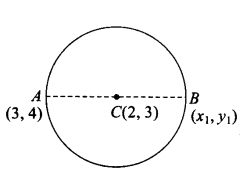
Given equation of the circle is:
\(
\begin{array}{ll}
& x^2+y^2-4 x-6 y+11=0 \\
\therefore \quad & 2 g=-4 \text { and } 2 f=-6
\end{array}
\)
So, the centre of the circle is \(C(-g,-f) \equiv C(2,3)\) \(A(3,4)\) is one end of the diameter.
Let the other end of the diameter be \(B\left(x_1, y_1\right)\)
Here, mid point of \(A B\) is \(C\).
\(
\begin{array}{ll}
\therefore & 2=\frac{3+x_1}{2} \text { and } 3=\frac{4+y_1}{2} \\
\Rightarrow & x_1=1 \text { and } y_1=2
\end{array}
\)
So, the coordinates of other end of the diameter are \((1,2)\)

Given equation of the circle is:
\(
\begin{array}{ll}
& x^2+y^2-4 x-6 y+11=0 \\
\therefore \quad & 2 g=-4 \text { and } 2 f=-6
\end{array}
\)
So, the centre of the circle is \(C(-g,-f) \equiv C(2,3)\) \(A(3,4)\) is one end of the diameter.
Let the other end of the diameter be \(B\left(x_1, y_1\right)\)
Here, mid point of \(A B\) is \(C\).
\(
\begin{array}{ll}
\therefore & 2=\frac{3+x_1}{2} \text { and } 3=\frac{4+y_1}{2} \\
\Rightarrow & x_1=1 \text { and } y_1=2
\end{array}
\)
So, the coordinates of other end of the diameter are \((1,2)\)

Hint

Given lines are \(3 x+y=14\) and \(2 x+5 y=18\).
Solving these equations we get point of intersection of the lines as \(A(4,2)/latex]
[latex]
\text { Radius }=\sqrt{(4-1)^2+\left(2-(-2)^2\right.}=\sqrt{9+16}=5
\)
So, equation of the required circle is:
\(
\begin{aligned}
& (x-1)^2+(y+2)^2=5^2 \\
& x^2+y^2-2 x+4 y-20=0
\end{aligned}
\)

Hint

Given line is \(y =\sqrt{3} x + k\) and the circle is \(x ^2+ y ^2=16\).
Centre of the circle is \((0,0)\) and radius is 4 .
Since the line \(y=\sqrt{3} x+k\) touches the circle, perpendicular distance from \((0,0)\) to line is equal to the radius of the circle.
\(
\therefore \quad\left|\frac{0-0+k}{\sqrt{3+1}}\right|=4 \Rightarrow \pm \frac{k}{2}=4 \Rightarrow k= \pm 8
\)

Hint

The given equation of circle is
\(
\begin{aligned}
& x^2+y^2-6 x+12 y+15=0 \dots(i) \\
& \therefore \text { centre }=(-g,-f)=(3,-6) \\
& \text { radius }=\sqrt{g^2+f^2-c}=\sqrt{9+36-15}=\sqrt{30}
\end{aligned}
\)
Now, the required equation of circle in concentric with (i) which means both have same centre (3. -6\()\)
Also,
Area of required circle \(=2 \times\) Area of \(\pi r^2=2 \times \pi(\sqrt{30})^2\)
\(
\begin{aligned}
& \Rightarrow R^2=60 \\
& \Rightarrow R=2 \sqrt{15}
\end{aligned}
\)
Thus,
the required circle is
\(
\begin{aligned}
& (x-3)^2+(y+6)^2=60 \\
& x^2+y^2-6 x+12 y-15=0
\end{aligned}
\)

Hint

Let the equation of an ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
Length of major axis \(=2 a\)
Length of minor axis \(=2 b\)

It is given that, length of latus rectum = half of minor axis
And the length of latus rectum \(=\frac{2 b^2}{a}\)
We have \(\frac{2 b^2}{a}=\frac{2 b}{2}\)
\(
\Rightarrow b =\frac{a}{2}
\)
Now \(b^2=a^2\left(1-e^2\right)\), where \(e\) is the eccentricity
\(
\begin{aligned}
& \Rightarrow b ^2=4 b ^2\left(1- e ^2\right) \\
& \Rightarrow 1=4\left(1- e ^2\right) \\
& \Rightarrow 1- e ^2=\frac{1}{4} \\
& \Rightarrow e ^2=1-\frac{1}{4} \\
& \Rightarrow e ^2=\frac{3}{4} \\
& \therefore e = \pm \frac{\sqrt{3}}{2}
\end{aligned}
\)
\(
\text { So, } e =\frac{\sqrt{3}}{2} \quad \ldots . .[\because \text { e is not }(-)]
\)

Hint

Given equation of ellipse, \(9 x^2+25 y^2=225\)
or \(\quad \frac{x^2}{25}+\frac{y^2}{9}=1\)
So, \(\quad a=5, b=3\)
Now, \(b^2=a^2\left(1-e^2\right)\)
\(\Rightarrow \quad 9=25\left(1-e^2\right) \Rightarrow \frac{9}{25}=1-e^2 \Rightarrow e^2=1-\frac{9}{25}=\frac{16}{25}\)
\(\therefore \quad e=\frac{4}{5}\)
Foci \(\equiv( \pm a e, 0) \equiv( \pm 5 \times(4 / 5), 0) \equiv( \pm 4,0)\)

Hint

Given: the distance between its foci be 10 and is denoted by \(2 c=10 \Rightarrow c=5\).
As we know that the eccentricity,\(e=\frac{c}{a}\)
\(
\begin{aligned}
& \Rightarrow \frac{5}{8}=\frac{5}{a} \\
& \therefore a=8
\end{aligned}
\)
Also \(c^2=a^2-b^2\)
\(
\begin{aligned}
& \Rightarrow b^2=a^2-c^2 \\
& =8^2-5^2 \\
& =64-25 \\
& \therefore b=39
\end{aligned}
\)
Thus, length of the latus rectum is \(=\frac{2 b^2}{a}\)
\(
\begin{aligned}
& =\frac{2(39)^2}{8} \\
& =\frac{39}{4}
\end{aligned}
\)

Hint

Let equation of the ellipse be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b)\) Given that, \(e=\frac{2}{3}\) and latus rectum \(=5\)
\(\therefore \quad \frac{2 b^2}{a}=5 \Rightarrow b^2=\frac{5 a}{2}\)
We know that, \(b^2=a^2\left(1-e^2\right)\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{5 a}{2}=a^2\left(1-\frac{4}{9}\right) \Rightarrow \frac{5}{2}=\frac{5 a}{9} \Rightarrow a=\frac{9}{2} \\
& \therefore \quad b^2=\frac{5 \times 9}{2 \times 2}=\frac{45}{4}
\end{aligned}
\)
So, the required equation of the ellipse is \(\frac{4 x^2}{81}+\frac{4 y^2}{45}=1\).

Hint

The equation of ellipse is \(\frac{x^2}{36}+\frac{y^2}{20}=1\).
\(
\therefore \quad a=6, b=2 \sqrt{5}
\)
We know that, \(b^2=a^2\left(1-e^2\right)\)
\(
\begin{array}{ll}
\Rightarrow & 20=36\left(1-e^2\right) \Rightarrow \frac{5}{9}=1-e^2 \Rightarrow e^2=\frac{4}{9} \\
& \therefore \quad e=\frac{2}{3}
\end{array}
\)
Now, directrices are: \(x= \pm \frac{a}{e}\)
\(\therefore\) Distance between direcrtrix \(=\frac{2 a}{e}=\frac{2 \times 6}{2 / 3}=18\)

Hint

Given parabola is \(y^2=8 x \dots(i)\)
Comparing with the equation of parabola \(y ^2=4 ax\)
\(
\begin{aligned}
& 4 a=8 \\
& \Rightarrow a=2
\end{aligned}
\)
Now focal distance \(=|x+a|\)
\(
\begin{aligned}
& \Rightarrow|x+a|=4 \\
& \Rightarrow(x+a)= \pm 4 \\
& \Rightarrow x+2= \pm 4 \\
& \Rightarrow x=4-2=2
\end{aligned}
\)
And \(x=-6\)
But \(x \neq-6\)
\(
\therefore x =2
\)
Put \(x=2\) in equation (i) we get
\(
\begin{aligned}
& y ^2=8 \times 2=16 \\
& \therefore y = \pm 4
\end{aligned}
\)
So, the coordinates of the point are \((2,4),(2,-4)\).

Hint

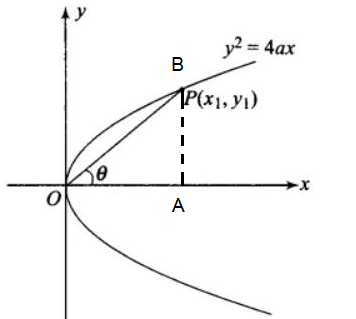
Let the coordinates of the point on the parabola be \(B \left(x_1, y_1\right)\).
Let \(B O\) be the line segment
In right triangle \(AOB\)
\(
\begin{aligned}
& \cos \theta=\frac{A O}{O B} \text { and } \sin \theta=\frac{A B}{O B} \\
& \Rightarrow \cos \theta=\frac{x_1}{O B} \text { and } \sin \theta=\frac{y_1}{O B}
\end{aligned}
\)
\(\therefore x_1= OB \cos \theta\) and \(y_1= OB \sin \theta\)
Now, the curve is passing through \(\left(x_1, y_1\right)\)
\(
\begin{aligned}
& \therefore\left(y_1\right)^2=4 a\left(x_1\right) \\
& \Rightarrow(O B \sin \theta)^2=4 a( OB \cos \theta) \\
& \Rightarrow O B^2 \sin ^2 \theta=4 a O B \cos \theta \\
& \Rightarrow O B=\frac{4 a \cos \theta}{\sin ^2 \theta}
\end{aligned}
\)

Hint

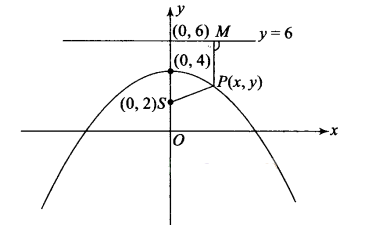
Given that the vertex of the parabola is \(A(0,4)\) and its focus is \(S(0,2)\). So, directrix of the parabola is \(y=6\).
Now by definition of the parabola for any point \(P(x, y)\) on the parabola, \(S P=P M\)
\(
\sqrt{(x-0)^2+(y-2)^2}=\left|\frac{0+y-6}{\sqrt{(0+1)}}\right|
\)
\(
\begin{aligned}
& x^2+y^2-4 y+4=y^2-12 y+36 \\
& x^2+8 y=32
\end{aligned}
\)

Hint

We have \(y^2=4 x\)
Substituting the value of \(y=m x+1\) in \(y^2=4 x\), we get
\(
\begin{aligned}
& (m x+1)^2=4 x \\
& \Rightarrow m^2 x^2+2 m x+1=4 x \\
& \Rightarrow m^2 x^2+(2 m-4) x+1=0 \dots(1)
\end{aligned}
\)
Since, a tangent touches the curve at a point, the roots of (1) must be equal.
\(
\begin{aligned}
& \therefore D=0 \\
& \Rightarrow(2 m-4)^2-4 m^2=0 \\
& \Rightarrow 4 m^2-16 m+16-4 m^2=0 \\
& \Rightarrow m=1
\end{aligned}
\)

Hint

Let the equation of the hyperbola be \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\).
Foci are \(( \pm a e, 0)\).
Distance between foci \(=2 a e=16\) (given)
Also, \(e=\sqrt{2}\) (Given)
\(\therefore \quad a=4 \sqrt{2}\)
We know that, \(b^2=a^2\left(e^2-1\right)\)
\(
\Rightarrow \quad b^2=(4 \sqrt{2})^2\left[(\sqrt{2})^2-1\right]=16 \times 2(2-1)=32
\)
So, the equation of hyperbola is: \(\frac{x^2}{32}-\frac{y^2}{32}=1\) or \(x^2-y^2=32\)

Hint

We have the hyperbola: \(9 y^2-4 x^2=36\)
\(
\frac{x^2}{9}-\frac{y^2}{4}=-1
\)
We know that \(a^2=b^2\left(e^2-1\right)\)
\(
\begin{array}{ll}
\therefore & 9=4\left(e^2-1\right) \\
\Rightarrow & e=\sqrt{1+\frac{9}{4}}=\frac{\sqrt{13}}{2}
\end{array}
\)

Hint

Let the equation of the hyperbola be \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\).
Given that eccentricity, \(e=\frac{3}{2}\) and foci \(( \pm a e, 0) \equiv( \pm 2,0)\)
\(
\begin{array}{ll}
\therefore & a e=2 \\
\Rightarrow & a \times \frac{3}{2}=2 \Rightarrow a=\frac{4}{3}
\end{array}
\)
We know that, \(b^2=a^2\left(e^2-1\right)\)
\(
\Rightarrow \quad b^2=\frac{16}{9}\left(\frac{9}{4}-1\right)=\frac{16}{9} \times \frac{5}{4}=\frac{20}{9}
\)
So, the equation of hyperbola is:
\(
\frac{x^2}{\frac{16}{9}}-\frac{y^2}{\frac{20}{9}}=1 \Rightarrow \frac{x^2}{16}-\frac{y^2}{20}=\frac{1}{9}
\)
\(
\frac{x^2}{4}-\frac{y^2}{5}=\frac{4}{9} \text {. }
\)

Hint

Given that lines \(2 x-3 y-5=0\) and \(3 x-4 y-1=0\) are diameters of the circle. Solving these lines we get point of intersection as \((1,-1)\), which is centre of the circle.
Also given that are of the circle is 154 sq. units.
Let the radius of the circle be \(r\).
Then, \(\quad \pi r^2=154\)
\(
\begin{array}{ll}
\Rightarrow & \frac{22}{7} \times r^2=154 \Rightarrow r^2=\frac{154 \times 7}{22}=49 \\
\therefore, r=7
\end{array}
\)
So, the equation of circle is:
\(
\begin{aligned}
& (x-1)^2+(y+1)^2=49 \\
& \Rightarrow \quad x^2-2 x+1+y^2+2 y+1=49 \quad \Rightarrow \quad x^2+y^2-2 x+2 y=47
\end{aligned}
\)

Hint

Centre lies on the line \(y-4 x+3=0\)
Let \(x = h\)
\(
\Rightarrow y =4 h -3
\)
So the center is of the form \((h, 4 h-3)\)
Distance of centre from \((2,3)\) and \((4,5)\) will be equal
\(
\begin{aligned}
& \Rightarrow(h-2)^2+(4 h-3-3)^2=(h-4)^2+(4 h-3-5)^2 \\
& \Rightarrow h =2
\end{aligned}
\)
So the centre is \((2,5)\)
\(
r =\sqrt{(2-2)^2+(5-3)^2}=2
\)
So the equation of the circle is
\(
\begin{aligned}
& (x-2)^2+(y-5)^2=2^2 \\
& x^2+y^2-4 x-10 y+25=0
\end{aligned}
\)

Hint

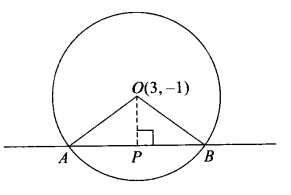
Given centre of the circle \(O(3,-1)\) Chord of the circle is \(A B\).
Given that equation of \(A B\) is \(2 x-5 y+18=0\).
Also, \(A B=6\)
Perpendicular distance from \(O\) to \(A B\) is:
\(
O P=\left|\frac{2(3)-5(-1)+18}{\sqrt{4+25}}\right|=\frac{29}{\sqrt{29}}=\sqrt{29}
\)
In \(\triangle O P B\), we have
\(
O B^2=O P^2+P B^2 \Rightarrow O B^2=29+9=38
\)
So, the radius of circle is \(\sqrt{38}\). Thus, equation of the circle is:
\(
(x-3)^2+(y+1)^2=38
\)

Hint

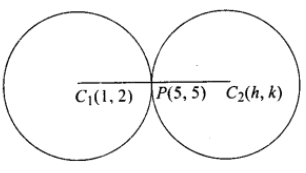
Given circle \(x^2+y^2-2 x-4 y-20=0\)
or \(\quad(x-1)^2+(y-2)^2=5^2\)
Centre of the this circle is \(C_1(1,2)\).
Now, the required circle of radius ‘ 5 ‘ touches the above circle at \(P(5,5)\).
Let the centre of the required circle be \(C_2(h, k)\).
Since the radius of the given circle and the required circle is same, point \(P\) is mid point of \(C_1\) and \(C_2\)
\(
\therefore \quad 5=\frac{1+h}{2} \Rightarrow h=9 \text { and } 5=\frac{2+k}{2} \Rightarrow k=8
\)
So, the equation of and required circle is:
\(
\begin{array}{ll}
& (x-9)^2+(y-8)^2=25 \\
\Rightarrow \quad & x^2-18 x+81+y^2-16 y+64=25 \\
\Rightarrow \quad & x^2+y^2-18 x-16 y+120=0
\end{array}
\)

Hint

Given that circle passes through the point \(A(7,3)\) and its radius is 3 .
Also, centre of the circle lies on the line \(y=x-1\).
Therefore, centre of the circle is \(C(h, h-1)\).
Now, radius of the circle is \(A C=3\) (given)
\(
\begin{array}{ll}
\therefore & (h-7)^2+(h-1-3)^2=9 \\
\Rightarrow & 2 h^2-22 h+56=0 \Rightarrow h^2-11 h+28=0 \\
\Rightarrow & (h-4)(h-7)=0 \\
\Rightarrow & h=4,7
\end{array}
\)
Thus, centre of the circle is \(C(4,3)\) or \(C(7,6)\).
Hence, equation of the circle can be:
\(
\begin{aligned}
& \quad(x-4)^2+(y-3)^2=9 \text { and }(x-7)^2+(y-6)^2=9 \\
& \Rightarrow \quad x^2+y^2-8 x-6 y+16=0 \text { and } x^2+y^2-14 x-12 y+76=0
\end{aligned}
\)

Hint

We know that the distance of any point on the parabola from its focus and its directrix is same.
(a) Given that, directrix, \(x=0\) and focus \(=(6,0)\)
So, for any point \(P ( x , y )\) on the parabola
Distance of \(P\) from directrix \(=\) Distance of \(P\) from focus \(=>x^2=(x-6)^2+y^2\)
\(\Rightarrow \quad y^2-12 x+36=0\)
(b) Given that, vertex \(=(0,4)\) and focus \(=(0,2)\)
Now distance between the vertex and directrix is same as the distance between the vertex and focus.
Directrix is \(y-6=0\)
For any point of \(P ( x , y )\) on the parabola
Distance of \(P\) from directrix \(=\) Distance of \(P\) from focus
\(
\begin{array}{ll}
\Rightarrow & |y-6|=\sqrt{(x-0)^2+(y-2)^2} \\
\Rightarrow & y^2-12 y+36=x^2+y^2-4 y+4 \\
\Rightarrow & x^2=32-8 y
\end{array}
\)
(c) Given that, focus at \((-1,-2)\) and directrix \(x-2 y+3=0\)
So, the equation of parabola is
\(
\begin{aligned}
& \sqrt{(x+1)^2+(y+2)^2}=\left|\frac{x-2 y+3}{\sqrt{1+4}}\right| \\
\Rightarrow \quad & x^2+2 x+1+y^2+4 y+4=\frac{1}{5}\left[x^2+4 y^2+9+6 x-4 x y-12 y\right] \\
\Rightarrow \quad & 4 x^2+4 x y+y^2+4 x+32 y+16=0
\end{aligned}
\)

Hint

Let \((x, y)\) be any point.
Given points are \((3,0)\) and \((9,0)\)
We have \(\sqrt{(x-3)^2+(y-0)^2}+\sqrt{(x-9)^2+(y-0)^2}=12\)
\(
\Rightarrow \sqrt{x^2+9-6 x+y^2}+\sqrt{x^2+81-18 x+y^2}=12
\)
Putting \(x^2+9-6 x+y^2=k\)
\(
\begin{aligned}
& \Rightarrow \sqrt{k}+\sqrt{72-12 x+k}=12 \\
& \Rightarrow \sqrt{72-12 x+k}=12-\sqrt{k}
\end{aligned}
\)
Squaring both sides, we have
\(
\begin{aligned}
& \Rightarrow 72-12 x + k =144+k-24 \sqrt{k} \\
& \Rightarrow 24 \sqrt{k}=144-72+12 x \\
& \Rightarrow 24 \sqrt{k}=72+12 x \\
& \Rightarrow 2 \sqrt{k}=6+ x
\end{aligned}
\)
Again squaring both sides, we get
\(
4 k=36+x^2+12 x
\)
Putting the value of \(k\), we have
\(
\begin{aligned}
& 4\left(x^2+9-6 x+y^2\right)=36+x^2+12 x \\
& \Rightarrow 4 x^2+36-24 x+4 y^2=36+x^2+12 x \\
& \Rightarrow 3 x^2+4 y^2-36 x=0
\end{aligned}
\)
Hence, the required equation is \(3 x^2+4 y^2-36 x=0\).

Hint

Let \(P(x, y)\) be a point.
We have \(\sqrt{(x-0)^2+(y-4)^2}=\frac{2}{3}\left|\frac{y-9}{1}\right|\)
Squaring both sides, we have
\(
\begin{aligned}
& x^2+(y-4)^2=\frac{4}{9}\left(y^2+81-18 y\right) \\
& \Rightarrow 9 x^2+9(y-4)^2=4 y^2+324-72 y \\
& \Rightarrow 9 x^2+9 y^2+144-72 y=4 y^2+324-72 y \\
& \Rightarrow 9 x^2+5 y^2+144-324=0 \\
& \Rightarrow 9 x^2+5 y^2-180=0
\end{aligned}
\)
Hence, the required equation is \(9 x^2+5 y^2-180=0\).

Hint

Let the points be \(P(x, y)\).
According to the question
Distance of \(P\) from \((4,0)\) – Distance of \(P\) from \((-4,0)=2\)
\(
\begin{array}{ll}
\Rightarrow & \sqrt{(x+4)^2+y^2}-\sqrt{(x-4)^2+y^2}=2 \\
\Rightarrow & \sqrt{(x+4)^2+y^2}=2+\sqrt{(x-4)^2+y^2}
\end{array}
\)
Squaring both sides, we get
\(
\begin{aligned}
& x^2+8 x+16+y^2=4+x^2-8 x+16+y^2+4 \sqrt{(x-4)^2+y^2} \\
\Rightarrow \quad & (4 x-1)=\sqrt{(x-4)^2+y^2}
\end{aligned}
\)
Again squaring both sides we get
\(
\begin{aligned}
& 16 x^2-8 x+1=x^2+16-8 x+y^2 \\
& \Rightarrow \quad 15 x^2-y^2=15 \text { which is a parabola. }
\end{aligned}
\)

Hint

(a) Given that, vertices \(=( \pm 5,0)\), foci \(=( \pm 7,0)\)
\(\therefore \quad a=5\) and \(a e=7\)
\(\Rightarrow e=\frac{7}{5}\)
Now \(b^2=a^2\left(e^2-1\right)=25\left(\frac{49}{25}-1\right)=49-25=24\)
So, the equation of hyperbola is
\(\frac{x^2}{25}-\frac{y^2}{24}=1\)
(b)
\(
\begin{aligned}
& \text { Vertices }=(0, \pm 7), e=\frac{4}{3} \\
& \therefore \quad b=7, e=\frac{4}{3}
\end{aligned}
\)
Now, \(a^2=b^2\left(e^2-1\right)=49\left(\frac{16}{9}-1\right)=\frac{343}{9}\)
So, the equation of hyperbola is:
\(
\begin{aligned}
& \frac{x^2}{a^2}-\frac{y^2}{b^2}=-1 \\
\Rightarrow & \frac{x^2}{343 / 9}-\frac{y^2}{49}=-1 \Rightarrow 9 x^2-7 y^2+343=0
\end{aligned}
\)
(c) Given that, foci \(=(0, \pm \sqrt{10})\)
\(\therefore \quad b e=\sqrt{10}\)
Also \(a^2=b^2\left(e^2-1\right)\)
\(
\Rightarrow a^2=b^2 e^2-b^2=10-b^2
\)
\(\therefore \quad\) Equation of the hyperbola is
\(
\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1 \text { or } \frac{x^2}{10-b^2}-\frac{y^2}{b^2}=-1
\)
Since, hyperbola passes through the point \((2,3)\).
\(
\begin{array}{ll}
\therefore & \frac{4}{10-b^2}-\frac{9}{b^2}=-1 \\
\Rightarrow & 4 b^2-9\left(10-b^2\right)=-b^2\left(10-b^2\right) \\
\Rightarrow & b^4-23 b^2+90=0 \Rightarrow\left(b^2-18\right)\left(b^2-5\right)=0 \\
\Rightarrow & b^2=5\left(b^2=18 \text { not possible as } a^2+b^2=10\right) \\
\therefore & a^2=10-5=5
\end{array}
\)
So, the equation of hyperbola is \(\frac{x^2}{5}-\frac{y^2}{5}=-1\) or \(y^2-x^2=5\)

Hint

Given equation of the circle is \(x^2+y^2+6 x+2 y=0\)
Centre is \((-3,-1)\)
If \(x+3 y=0\) is the equation of diameter
Then the centre \((-3,-1)\) will lie on \(x+3 y=0\)
\(
\begin{aligned}
& -3+3(-1)=0 \\
& \Rightarrow-6 \neq 0
\end{aligned}
\)
So, \(x+3 y=0\) is not the diameter of the circle.

Hint

Given circle is \(x^2+y^2-14 x-10 y-151=0\)
\(\therefore \quad\) Centre \(\equiv C(7,5)\)
And \(\quad\) Radius \(=\sqrt{49+25+151}=\sqrt{225}=15\)
Now distance between the point \(P(2,-7)\) and centre
\(
=\sqrt{(2-7)^2+(-7-5)^2}=\sqrt{25+144}=\sqrt{169}=13
\)
\(\therefore \quad\) Shortest distance of point \(P\) from the circle \(=|13-15|=2\)

Hint

True
Given circle is \(x^2+y^2=a^2\)
\(\therefore\) Radius \(=a\) and centre \(\equiv(0,0)\)
Now given that line \(l x+m y-1=0\) is tangent to the circle
\(\therefore\) Distance of \((0,0)\) from the line \(l x+m y-1=0\) is equal to radius ‘ \(a\) ‘.
\(
\Rightarrow \quad \frac{|0+0-1|}{\sqrt{l^2+m}}=a \Rightarrow l^2+m^2=\frac{1}{a^2}
\)
Thus, locus of \((l, m)\) is \(x^2+y^2=\frac{1}{a^2}\), which is circle.

Hint

Given circle is \(x^2+y^2-2 x+6 y+1=0\).
or \(\quad(x-1)^2+(y+3)^2=3^2\)
Centre is \(C(1,-3)\) and radius is 3 .
Distance of point \(P(1,2)\) from centre is 5 .
Thus, \(C P>\) radius
So, point \(P\) lies outside the circle.

Hint

True
Give line \(l x+m y+n=0\) and parabola \(y^2=4 a x\)
Solving line and parabola for their point of intersection, we get
\(
\frac{l}{4 a} y^2+m y+n=0
\)
Since line touches the parabola, above equation must have equal roots.
\(\therefore \quad\) Discriminant, \(D=0\)
\(\therefore \quad m^2-4\left(\frac{l}{4 a}\right) n=0 \Rightarrow a m^2=n l\)

Hint

False
We have equation of the ellipse is \(\frac{x}{16}+\frac{y^2}{25}=1\)
From the definition of the ellipse, we know that sum of the distances of any point \(P\) on the ellipse from the two foci is equal to the length of the major axis.
Here major axis \(=2 b=2 \times 5=10\)
\(S\) and \(S^{\prime}\) are foci, then \(S P+S^{\prime} P=10\)

Hint

True
Given line is \(2 x+3 y=12\) and the ellipse is \(4 x^2+9 y^2=72\).
Solving line and ellipse, we get
\(
\begin{array}{ll}
& (12-3 y)^2+9 y^2=72 \\
\Rightarrow & (4-y)^2+y^2=8 \Rightarrow 2 y^2-8 y+8=0 \Rightarrow y^2-4 y+4=0 \\
\Rightarrow \quad & (y-2)^2=0 \Rightarrow y=2 \\
\Rightarrow \quad & 2 x=12-3(2) \\
\Rightarrow \quad & x=3
\end{array} \quad \text { (from the equation of line) }
\)
So, point of contact is \((3,2)\).

Hint

True
Given equation of lines are:
\(
\begin{aligned}
& \sqrt{3} x-y-4 \sqrt{3} k=0 \\
& \text { and } \quad \sqrt{3} k x+k y-4 \sqrt{3}=0 \\
&
\end{aligned}
\)
From Eq. (i), \(k=\frac{\sqrt{3} x-y}{4 \sqrt{3}}\)
From Eq. (ii), \(k=\frac{4 \sqrt{3}}{\sqrt{3} x+y}\)
Equating the values of \(k\), we get
\(
\frac{\sqrt{3} x-y}{4 \sqrt{3}}=\frac{4 \sqrt{3}}{\sqrt{3} x+y}
\)
\(
\Rightarrow \quad 3 x^2-y^2=48
\)
\(\Rightarrow \quad \frac{x^2}{16}-\frac{y^2}{48}=1\), which is equation of hyperbola
\(\therefore \quad a^2=16\) and \(b^2=48\)
\(
\begin{array}{ll}
\Rightarrow & e^2=1+\frac{48}{16}=1+3=4 \\
\Rightarrow & e=2
\end{array}
\)

Hint

The perpendicular distance from centre \((3,-4)\) to the given line is, \(r=\frac{|5(3)+12(-4)-12|}{\sqrt{25+144}}=\frac{45}{13}\), which is radius of the circle So, the required equation of the circle is \((x-3)^2+(y+4)^2=\left(\frac{45}{13}\right)^2\).

Hint

Given equation of line are:
\(
\begin{aligned}
& y=x+2 \dots(i) \\
& 3 y=4 x \dots(ii) \\
& 2 y=3 x \dots(iii)
\end{aligned}
\)
Solving these lines, we get points of intersection \(A(6,8), B(4,6)\) and \(C(0,0)\).
Let the equation of circle circumscribing the given triangle be
\(
x^2+y^2+2 g x+2 f y+c=0
\)
Since the points \(A(6,9), B(4,6)\) and \(C(0,0)\) lie on this circle, we have
\(
36+64+12 g+16 f+c=0
\)
\(
\begin{aligned}
& \Rightarrow \quad 12 g+16 f+c=-100 \dots(iv) \\
& \text { Also, } 16+36+8 g+12 f+c=0 \\
& \Rightarrow \quad 8 g+12 f+c=–52 \dots(v)\\
& \text { And } \quad c=0 \dots(vi)
\end{aligned}
\)
Putting \(c=0\) in Eqs. (iv) and (v), we get
\(
\text { and } \quad \begin{aligned}
& 3 g+4 f=-25 \\
& 2 g+3 f=-13
\end{aligned}
\)
On solving these, we get \(g=-23\) and \(f=11\).
So, the equation of circle is:
\(
\Rightarrow \quad \begin{aligned}
& x^2+y^2-46 x+22 y+0=0 \\
& x^2+y^2-46 x+22 y=0
\end{aligned}
\)

Hint

Let equation of the ellipse be \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\).
According to the question, \(a=3\) and \(b=2\)
Now, \(b^2=a^2\left(1-e^2\right)\)
\(
\begin{array}{ll}
\therefore & e^2=1-\frac{b^2}{a^2}=1-\frac{4}{9}=\frac{5}{9} \\
\therefore & e=\frac{\sqrt{5}}{3}
\end{array}
\)
From the definition of the ellipse.for any point \(P\) on the ellipse, we have \(S P+S^{\prime} P=2 a, \quad\) where \(S\) and \(S^{\prime}\) are foci.
\(\therefore\) Length of the endless string \(=S P+S^{\prime} P+S S^{\prime}\)
\(
=2 a+2 a e=2(3)+2(3) \times \frac{\sqrt{5}}{3}=6+2 \sqrt{5}
\)

Hint

Given that, foci of the ellipse are \((0, \pm b e) \equiv(0, \pm 1)\)
\(
\therefore \quad b e=1
\)
Length of minor axis, \(2 a=1 \Rightarrow a=\frac{1}{2}\)
Now \(a^2=b^2\left(1-e^2\right)\)
\(
\Rightarrow \quad \frac{1}{4}=b^2-b^2 e^2=b^2-1 \Rightarrow b^2=\frac{5}{4}
\)
So, the equation of ellipse is \(\frac{x^2}{1 / 4}+\frac{y^2}{5 / 4}=1\) or \(4 x^2+\frac{4 y^2}{5}=1\)

Hint

Given that, focus at \(S(-1,-2)\) and directrix is \(x-2 y+3=0\)
Let any point on the parabola be \(P(x, y)\).
\(\therefore\) Length of perpendicular from \(S\) on the directrix \(=S P\)
\(
\begin{array}{ll}
\Rightarrow & \frac{(x-2 y+3)^2}{5}=(x+1)^2+(y+2)^2 \\
\Rightarrow & 5\left[x^2+2 x+1+y^2+4 y+4\right]=x^2+4 y^2+9-4 x y-12 y+6 x \\
\Rightarrow & 4 x^2+y^2+4 x+32 y+16=0
\end{array}
\)

Hint

Let the equation of parabola be \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1\)
\(
\begin{aligned}
& b=6 \\
& e=5 / 3 \\
& a^2=b^2\left(e^2-1\right) \\
& a^2=64 \\
& \frac{x^2}{64}-\frac{y^2}{36}=-1
\end{aligned}
\)
foci \(=(0, \pm b e) \equiv\left(0, \pm \frac{5}{3} \times 6\right)=(0, \pm 10)\)

Hint

Given that the centre of the circle is \((1,2)\)
\(
\begin{aligned}
& \text { Radius of the circle }=\sqrt{(4-1)^2+(6-2)^2} \\
& =\sqrt{9+16} \\
& =5
\end{aligned}
\)
So, the area of the circle \(=\pi r^2\)
\(
\begin{aligned}
& =\pi \times(5)^2 \\
& =25 \pi
\end{aligned}
\)

Hint

Since circle touches both axis
\(\Rightarrow\) equations of circle is of the form
\(
(x-a)^2+(y-a)^2=a^2
\)
i.e. \(x^2+a^2-2 a x+y^2-2 a y+a^2=a^2\)
i.e. \(x^2+y^2-2 a x-2 a y+a^2=0\)
Since circle passes through \((3,6)\)
\(
\Rightarrow(3)^2+(6)^2-2 a(3)-2 a(6)+a^2=0
\)
i.e. \(9+36-6 a-12 a+a^2=0\)
i.e. \(a^2-18 a+45=0\)
i.e. \(a^2-15 a-3 a+45=0\)
i.e. \(a (a-15)-3(a-15)=0\)
i.e. \(a=3\) or \(a=15\)
i.e. \((x-3)^2+(y-3)^2=9\)
i.e. \(x^2+y^2-2 \times 3 x-6 y+9=0\)
i.e. \(x^2+y^2-6 x-6 y+9=0\)

Hint

Circle with center as \(y\)-axis is of the form
\(
x^2+(y-b)^2=r^2
\)
also given, circle passes through origin
\(
\Rightarrow 0^2+\left(O-b^2\right)=r^2
\)
i.e \(r^2=b^2\)
i.e. equation of circle reduces to,
\(
x^2+(y-b)^2=b^2
\)
i.e. \(x^2+y^2-2 b y+b^2=b^2\)
i.e. \(x^2+y^2-2 b y=0\)
Given circle passes through \((2,3)\)
\(
\begin{aligned}
& \Rightarrow 4+9-2 b(3)=0 \\
& \text { i.e. } 6 b=13 \\
& \text { i.e. } b=13 / 6
\end{aligned}
\)
\(\therefore\) Equation of circle is \(x^2+y^2-2(13 / 6) y=0\)
i.e. \(3 x^2+3 y^2-13 y=0\)

Alternate: Centre of the circle lies on the \(y\)-axis.
So, let the centre be \(C(0, k)\).
Circle passes through \(O(0,0)\) and \(A(2,3)\).
\(
\begin{array}{ll}
\therefore & O C^2=A C^2 \\
\Rightarrow & k^2=(2-0)^2+(3-k)^2 \quad \Rightarrow k=13 / 6 \\
\therefore & \text { Centre } \equiv(0,13 / 6) \text { and radius }=13 / 6
\end{array}
\)
So, equation of the required circle is:
\(
\begin{aligned}
& (x-0)^2+(y-13 / 6)^2=(13 / 6)^2 \\
\Rightarrow \quad & 3 x^2+3 y^2-13 y=0 .
\end{aligned}
\)

Hint

Given, median of the equilateral triangle is 3a say LD
In \(\triangle\) LMD, we have
\(
\begin{aligned}
& ( LM )^2=( LD )^2+( MD )^2 \\
& \Rightarrow( LM )^2=9 a ^2+\left(\frac{ LM }{2}\right)^2 & \Rightarrow \frac{3}{4}( LM )^2=9 a ^2 & \Rightarrow( LM )^2=12 a ^2
\end{aligned}
\)
Again in triangle \(OMD\),
\(
\begin{aligned}
& (O M)^2=(O D)^2+(M D)^2 \\
& \Rightarrow R^2=(3 a-R)^2+\left(\frac{L M}{2}\right)^2 \\
& \Rightarrow R^2=9 a^2+R^2-6 a R+3 a^2 & \Rightarrow 6 a R=12 a^2 & \Rightarrow R=2 a
\end{aligned}
\)
So, equation of circle is
\(
\begin{aligned}
& (x-0)^2+(y-0)^2=(2 a)^2 & \Rightarrow x^2+y^2=4 a^2
\end{aligned}
\)

Alternate: \(\Rightarrow x^2+y^2=r^2\) is the required equation and since above circle passes through the vertices of equilateral triangle with medium \(3 a\). The centroid of an equilateral triangle is the center of its circumcircle and the radius of the circle is the distance of any vertex from centroid.
i. e. radius of circle=distance of centroid from any vertex
\(
\begin{aligned}
& =\frac{2}{3}(\text { median }) \\
& =\frac{2}{3}(3 a)(\text { given medium }=3 a)
\end{aligned}
\)
i.e. radius of circle \(=2 a\) \(\therefore\) equation of circle is \(x^2+y^2=(2 a)^2\)

Hint

Let \((h, k)\) be any point on the curve.
Distance of this point from the focus \(=\sqrt{( h -0)^2+( k -(-3))^2}\)
Distance of point \((h, k)\) from the directrix \(=\frac{k-3}{1}=k-3\)
Any point on the parabola is equidistant from its focus and dirextrix.
\(
\begin{aligned}
& \Rightarrow \sqrt{( h – o )^2+( k -(-3))^2}= k -3 \\
& \Rightarrow \sqrt{ h ^2+( k +3)^2}= k -3
\end{aligned}
\)
Squaring the above equation, we get
\(
\begin{aligned}
& \Rightarrow h^2+(k+3)^2=(k-3)^2 \\
& \Rightarrow h^2+k^2+6 k+9=k^2-6 k+9 \\
& \Rightarrow h^2=-12 k
\end{aligned}
\)
Subtitute \(k=y\) and \(h=x\), we get
\(
\Rightarrow x^2=-12 y
\)

Hint

Given that, parabola is \(y^2=4 a x\)
\(\therefore\) Length of latusrectum \(=4\) a
Since,the parabola passes through the point \((3,2)\)
Then, \(4=4 a(3)\)
\(
\begin{aligned}
& \Rightarrow a=\frac{1}{3} \\
& \Rightarrow 4 a=\frac{4}{3}
\end{aligned}
\)

Hint

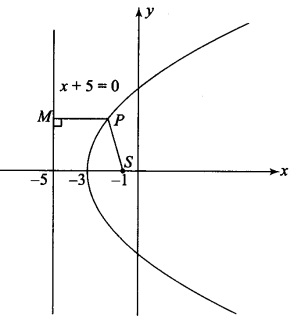
(a) Given that vertex \(\equiv(-3,0)\) and directrix, \(x+5=0\)
So, focus \(\equiv S(-1,0)\)
For any point of parabola \(P(x, y)\), we have
\(
\begin{array}{ll}
& S P=P M \\
\Rightarrow & \sqrt{(x+1)^2+y^2}=|x+5| \Rightarrow x^2+2 x+1+y^2=x^2+10 x+25 \\
\Rightarrow & y^2=8 x+24 \Rightarrow y^2=8(x+3)
\end{array}
\)

Hint

(a) Given that, focus of the ellipse is \(S(1,-1)\) and the equation of directrix is
\(
x-y-3=0
\)
Also, \(e=\frac{1}{2}\)
From definition of ellipse, for any point \(P(x, y)\) on the ellipse, we have \(S P=e P M\), where \(M\) is foot of the perpendicular from point \(P\) to the directrix.
\(
\begin{array}{ll}
\therefore & \sqrt{(x-1)^2+(y+1)^2}=\frac{1}{2} \frac{|x-y-3|}{\sqrt{2}} \\
\Rightarrow & 8 x^2-16 x+16+8 y^2+16 y=x^2+y^2+9-2 x y+6 y-6 x \\
\Rightarrow & 7 x^2+7 y^2+2 x y-10 x+10 y+7=0
\end{array}
\)

Hint

(d) Given ellipse is:
\(
\begin{array}{ll}
& 3 x^2+y^2=12 \\
\Rightarrow & \frac{x^2}{4}+\frac{y^2}{12}=1 \\
\therefore \quad & a^2=4 \Rightarrow a=2 \\
\text { and } \quad & b^2=12 \Rightarrow b=2 \sqrt{3}
\end{array}
\)
Since \(b>a\), length of latus rectum \(=\frac{2 a^2}{b}=\frac{2 \times 4}{2 \sqrt{3}}=\frac{4}{\sqrt{3}}\)

Hint

(b) Given that, \(\frac{x^2}{a^2}+\frac{\dot{y}^2}{b^2}=1, a<b\)
We know that, \(a^2=b^2\left(1-e^2\right)\)

Hint

(c) Let the equation of the hyperbola be \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\).
Length of latus rectum \(=8\)
\(
\therefore \quad \frac{2 b^2}{a}=8 \quad \Rightarrow \quad b^2=4 a \dots(i)
\)
Conjugate axis \(=\) half of the distance between the foci
\(
\therefore \quad 2 b=a e \dots(ii)
\)
Now, \(\quad b^2=a^2\left(e^2-1\right) \dots(iii)\)
From Eqs. (i) and (iii), we get
\(
\begin{aligned}
& \frac{a^2 e^2}{4}=a^2\left(e^2-1\right) \\
\Rightarrow \quad & e^2=4 e^2-4 \Rightarrow e^2=\frac{4}{3} \Rightarrow e=\frac{2}{\sqrt{3}}
\end{aligned}
\)

Hint

Let equation of hyperbola be \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \ldots(i)\)
According to the given condition, \(2 a e=16[latex] and [latex]e=\sqrt{2}\)
\(
\begin{aligned}
& \therefore 2 a(\sqrt{2})=16 \\
& \Rightarrow a=\frac{8}{\sqrt{2}} \\
& \Rightarrow a^2=32 \\
& \because b^2=a^2\left(e^2-1\right)=32(2-1)=32
\end{aligned}
\)
On putting the values of \(a^2\) and \(b^2\) in (i), we get
\(
\begin{aligned}
& \frac{x^2}{32}-\frac{y^2}{32}=1 \\
& \Rightarrow x^2-y^2=32
\end{aligned}
\)

Hint

Given that \(e =\frac{3}{2}\) and foci at \(( \pm 2,0)\)
We know that foci \(=( \pm ae , 0)\)
\(
\begin{aligned}
& \therefore ae =2 \\
& \Rightarrow a \times \frac{3}{2}=2 \\
& \Rightarrow a=\frac{4}{3} \\
& \Rightarrow a^2=\frac{16}{9}
\end{aligned}
\)
We know that \(b^2=a^2\left(e^2-1\right)\)
\(
\begin{aligned}
& \Rightarrow b^2=\frac{16}{9}\left(\frac{9}{4}-1\right) \\
& =\frac{16}{9} \times \frac{5}{4} \\
& =\frac{20}{9}
\end{aligned}
\)
So, the equation of the hyperbola is \(\frac{x^2}{\frac{16}{9}}-\frac{y^2}{\frac{20}{9}}=1\)
\(
\begin{aligned}
& \Rightarrow \frac{9 x^2}{16}-\frac{9 y^2}{20}=1 \\
& \Rightarrow \frac{x^2}{4}-\frac{y^2}{5}=\frac{4}{9}
\end{aligned}
\)
Hence, the required equation is \(\frac{x^2}{4}-\frac{y^2}{5}=\frac{4}{9}\).