Hint

Here the slope of the line is \(m=\tan \theta=\tan 30^{\circ}=\frac{1}{\sqrt{3}}\) and the given point is \((2,3)\).
Therefore, using point slope formula of the equation of a line, we have
\(
y-3=\frac{1}{\sqrt{3}}(x-2) \quad \text { or } x-\sqrt{3 y}+(3 \sqrt{3}-2)=0
\)

Hint

The normal form of the equation of the line is \(x \cos \omega+y \sin \omega=p\). Here \(p=4\) and \(\omega=30^{\circ}\). Therefore, the equation of the line is
\(
\begin{array}{l}
x \cos 30^{\circ}+y \sin 30^{\circ}=4 \\
x \frac{\sqrt{3}}{2}+y \frac{1}{2}=4 \quad \text { or } \quad \sqrt{3} x+y=8
\end{array}
\)

Hint

Let \(m\) be the slope of the line whose equation is to be found out which is perpendicular to the line \(x+y+7=0\). The slope of the given line \(y=(-1) x-7\) is -1 . Therefore, using the condition of perpendicularity of lines, we have \(m \times(-1)=-1\) or \(m=1\)
Hence, the required equation of the line is \(y-1=(1)(x-2)\) or \(y-1=x-2\) \(x-y-1=0\).

Hint

The equations of lines \(3 x+4 y=9\) and \(6 x+8 y=15\) may be rewritten as
\(
3 x+4 y-9=0 \text { and } 3 x+4 y-\frac{15}{2}=0
\)
Since, the slope of these lines are same and hence they are parallel to each other. Therefore, the distance between them is given by
\(
\left|\frac{9-\frac{15}{2}}{\sqrt{3^2+4^2}}\right|=\frac{3}{10}
\)

Hint

Changing the given equation of the line into intercept form, we have \(\frac{x}{\frac{p}{\cos \alpha}}+\frac{y}{\frac{p}{\sin \alpha}}=1\) which gives the coordinates \(\frac{p}{\cos \alpha}, 0\) and \(0, \frac{p}{\sin \alpha}\), where the line intersects \(x\)-axis and \(y\)-axis, respectively.
Let \((h, k)\) denote the mid-point of the line segment joining the points \(\frac{p}{\cos \alpha}, 0\) and \(0, \frac{p}{\sin \alpha}\),

Then \(h=\frac{p}{2 \cos \alpha}\) and \(k=\frac{p}{2 \sin \alpha} \quad\)
This gives \(\cos \alpha=\frac{p}{2 h}\) and \(\sin \alpha=\frac{p}{2 k}\)
Squaring and adding we get
\(
\frac{p^2}{4 h^2}+\frac{p^2}{4 k^2}=1 \quad \text { or } \quad \frac{1}{h^2}+\frac{1}{k^2}=\frac{4}{p^2} \text {. }
\)
Therefore, the required locus is \(\frac{1}{x^2}+\frac{1}{y^2}=\frac{4}{p^2}\).

Hint

The slope of the line \(\mathrm{AB}\) is \(\frac{1-0}{3-2}=1\) or \(\tan 45^{\circ}\) (see Fig.). After rotation of the line through \(15^{\circ}\), the slope of the line \(\mathrm{AC}\) in new position is \(\tan 60^{\circ}=\sqrt{3}\)

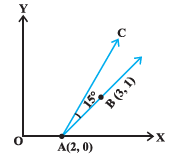
Therefore, the equation of the new line \(\mathrm{AC}\) is
\(
y-0=\sqrt{3}(x-2)
\)
or \(y-\sqrt{3} x+2 \sqrt{3}=0\)

Hint

Equation of the line passing through \((3,2)\) having slope \(\frac{3}{4}\) is given by
\(
\begin{aligned}
y-2 & =\frac{3}{4}(x-3) \\
4 y-3 x+1 & =0 \dots(1)
\end{aligned}
\)
Let \((h, k)\) be the points on the line such that
\(
(h-3)^2+(k-2)^2=25 \dots(2)
\)
Also, we have
\(
\begin{aligned}
4 k-3 h+1 & =0 \dots(3) \\
k & =\frac{3 h-1}{4} \dots(4)
\end{aligned}
\)
Putting the value of \(k\) in (2) and on simplifying, we get
\(
25 h^2-150 h-175=0
\)
\(
\begin{aligned}
h^2-6 h-7 & =0 \\
(h+1)(h-7) & =0 \Rightarrow h=-1, h=7
\end{aligned}
\)
Putting these values of \(k\) in (4), we get \(k=-1\) and \(k=5\). Therefore, the coordinates of the required points are either \((-1,-1)\) or \((7,5)\).

Hint

First we find the point of intersection of lines \(5 x-6 y-1=0\) and \(3 x+2 y+\) \(5=0\) which is \((-1,-1)\). Also the slope of the line \(3 x-5 y+11=0\) is \(\frac{3}{5}\). Therefore, the slope of the line perpendicular to this line is \(\frac{-5}{3}\). Hence, the equation of the required line is given by
\(
\begin{aligned}
y+1 & =\frac{-5}{3}(x+1) \\
5 x+3 y+8 & =0
\end{aligned}
\)

Alternatively: The equation of any line through the intersection of lines \(5 x-6 y-1=0\) and \(3 x+2 y+5=0\) is
\(
5 x-6 y-1+k(3 x+2 y+5)=0 \dots(1)
\)
Slope of this line is \(\frac{-(5+3 k)}{-6+2 k}\)
Also, slope of the line \(3 x-5 y+11=0\) is \(\frac{3}{5}\)
Now, both are perpendicular
\(
\text { so } \frac{-(5+3 k)}{-6+2 k} \times \frac{3}{5}=-1
\)
\(
k=45
\)
Therefore, equation of required line in given by
\(
\begin{array}{r}
5 x-6 y-1+45(3 x+2 y+5)=0 \\
5 x+3 y+8=0
\end{array}
\)

Hint

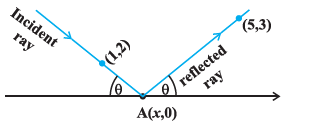
Let the incident ray strike \(x\)-axis at the point A whose coordinates be \((x, 0)\). From the figure, the slope of the reflected ray is given by
\(
\tan \theta=\frac{3}{5-x} \dots(1)
\)
Again, the slope of the incident ray is given by
\(
\begin{aligned}
\tan (\pi-\theta) & =\frac{-2}{x-1} \\
-\tan \theta & =\frac{-2}{x-1} \dots(2)
\end{aligned}
\)
Solving (1) and (2), we get
\(
\frac{3}{5-x}=\frac{2}{x-1} \quad \text { or } \quad x=\frac{13}{5}
\)
Therefore, the required coordinates of the point A are \(\frac{13}{5}, 0\)

Hint

Let \(A B C D\) be the given square and the coordinates of the vertex \(D\) be \((1,2)\). We are required to find the equations of its sides DC and AD.

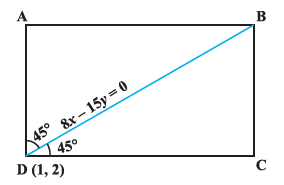
Given that BD is along the line \(8 x-15 y=0\), so its slope is \(\frac{8}{15}\). The angles made by BD with sides AD and DC is \(45^{\circ}\). Let the slope of DC be \(m\). Then
\(
\tan 45^{\circ}=\frac{m-\frac{8}{15}}{1+\frac{8 m}{15}}
\)
\(
15+8 m=15 m-8
\)
\(7 m=23\), which gives \(m=\frac{23}{7}\)
Therefore, the equation of the side \(\mathrm{DC}\) is given by
\(
y-2=\frac{23}{7}(x-1) \text { or } 23 x-7 y-9=0 .
\)
Similarly, the equation of another side \(\mathrm{AD}\) is given by
\(
y-2=\frac{-7}{23}(x-1) \text { or } 7 x+23 y-53=0 .
\)

Hint

(a) is the correct answer. The equation of the line \(x-y+3=0\) can be rewritten as \(y=x+3 \Rightarrow m=\tan \theta=1\) and hence \(\theta=45^{\circ}\).

Hint

(a) is correct answer. Slope of the line \(a x+b y=c\) is \(\frac{-a}{b}\), and the slope of the line \(a^{\prime} x+b^{\prime} y=c^{\prime}\) is \(\frac{-a^{\prime}}{b^{\prime}}\). The lines are perpendicular if
\(
\begin{aligned}
\tan \theta & =\frac{3}{5-x} \\
\frac{-a}{b} \quad \frac{-a^{\prime}}{b^{\prime}} & =-1 \text { or } a a^{\prime}+b b^{\prime}=0
\end{aligned}
\)

Hint

(b) is the correct answer. Let the slope of the line be \(m\). Then, its equation passing through \((1,2)\) is given by
\(
y-2=m(x-1) \dots(1)
\)
Again, this line is perpendicular to the given line \(x+y+7=0\) whose slope is -1
Therefore, we have
\(
\begin{aligned}
m(-1) & =-1 \\
m & =1
\end{aligned}
\)
Hence, the required equation of the line is obtained by putting the value of \(m\) in (1), i.e.,
\(
\begin{aligned}
y-2 & =x-1 \\
y-x-1 & =0
\end{aligned}
\)

Hint

(c) is the correct answer. The distance of the point \(\mathrm{P}(1,-3)\) from the line \(2 y-3 x-4=0\) is the length of perpendicular from the point to the line which is given by
\(
\left|\frac{2(-3)-3-4}{\sqrt{13}}\right|=\sqrt{13}
\)

Hint

(b) is the correct choice. Let \((h, k)\) be the coordinates of the foot of the perpendicular from the point \((2,3)\) on the line \(x+y-11=0\). Then, the slope of the perpendicular line is \(\frac{k-3}{h-2}\). Again the slope of the given line \(x+y-11=0\) is -1
Using the condition of perpendicularity of lines, we have
\(
\begin{aligned}
\frac{k-3}{h-2} \quad(-1) & =-1 \\
k-h & =1
\end{aligned}
\)
\(
k-h=1 \dots(1)
\)
Since \((h, k)\) lies on the given line, we have,
\(
h+k-11=0 \text { or } h+k=11 \dots(2)
\)
Solving (1) and (2), we get \(h=5\) and \(k=6\). Thus \((5,6)\) are the required coordinates of the foot of the perpendicular.

Hint

(a) is the correct choice. Let the line make intercept ‘ \(a\) ‘ on \(x\)-axis. Then, it makes intercept ‘ \(2 a\) ‘ on \(y\)-axis. Therefore, the equation of the line is given by
\(
\frac{x}{a}+\frac{y}{2 a}=1
\)
It passes through \((1,2)\), so, we have
\(
\frac{1}{a}+\frac{2}{2 a}=1 \text { or } a=2
\)
Therefore, the required equation of the line is given by
\(
\frac{x}{2}+\frac{y}{4}=1 \text { or } 2 x+y=4
\)

Hint

The correct choice is (d). We know that the equation of a line making intercepts \(a\) and \(b\) with \(x\)-axis and \(y\)-axis, respectively, is given by
\(
\frac{x}{a}+\frac{y}{b}=1 \text {. }
\)

Here we have
\(
1=\frac{a+0}{2} \text { and } 2=\frac{0+b}{2} \text {, }
\)
which give \(a=2\) and \(b=4\). Therefore, the required equation of the line is given by
\(
\frac{x}{2}+\frac{y}{4}=1 \text { or } 2 x+y-4=0
\)

Hint

The correct choice is (a). Let \((h, k)\) be the point of reflection of the given point \((4,-13)\) about the line \(5 x+y+6=0\). The mid-point of the line segment joining points \((h, k)\) and \((4,-13)\) is given by
\(
\frac{h+4}{2}, \frac{k-13}{2}
\)
This point lies on the given line, so we have
\(
5 \frac{h+4}{2}+\frac{k-13}{2}+6=0
\)
\(
5 h+k+19=0 \dots(1)
\)
Again the slope of the line joining points \((h, k)\) and \((4,-13)\) is given by \(\frac{k+13}{h-4}\). This line is perpendicular to the given line and hence \((-5) \frac{k+3}{h-4}=-1 \quad\)
This gives
\(
\begin{aligned}
5 k+65 & =h-4 \\
h-5 k-69 & =0 \dots(2)
\end{aligned}
\)
On solving (1) and (2), we get \(h=-1\) and \(k=-14\). Thus the point \((-1,-14)\) is the reflection of the given point.

Hint

The correct choice is (a). Let \((h, k)\) be the coordinates of the moving point. Then, we have
\(
\sqrt{(h-4)^2+k^2}=\frac{1}{2} \frac{h-16}{\sqrt{1^2+0}}
\)
\(
\begin{aligned}
(h-4)^2+k^2 & =\frac{1}{4}(h-16)^2 \\
4\left(h^2-8 h+16+k^2\right) & =h^2-32 h+256 \\
3 h^2+4 k^2 & =192
\end{aligned}
\)

Hence, the required locus is given by \(3 x^2+4 y^2=192\)

Hint

Equation of line in intercept form is: \(\frac{x}{a}+\frac{y}{b}=1\)
Here, we have \(a=b\).
So, equation of the line reduces to: \(\frac{x}{a}+\frac{y}{a}=1\) or \(x+y=a\)
Since the point \((1,-2)\) lies on the line, we get \(1-2=a\) or \(a=-1\).
Therefore, equation of the line is: \(x+y=-1\) or \(x+y+1=0\)

Hint

Slope of the line joining the points \((2,3)\) and \((3,-1)\) is
\(
\frac{-1-3}{3-2}=-4
\)
Slope of the required line which is perpendicular to it
\(
\begin{array}{l}
=\frac{-1}{-4} \\
=\frac{1}{4} \quad \ldots .\left[m_1 m_2=-1\right]
\end{array}
\)
Equation of the line passing through the point \((5,2)\) is
\(
\begin{array}{l}
y-2=\frac{1}{4}(x-5) \quad \ldots . .\left[y-y_1=m\left(x-x_1\right)\right] \\
\Rightarrow 4 y-8=x-5 \\
\Rightarrow x-4 y+3=0
\end{array}
\)
Hence, the required equation is \(x-4 y+3=0\).

Hint

\(
\text { Slope of the line }=(2-\sqrt{3})(x+5) \text { is: } m_{1}=(2-\sqrt{3})
\)
Slope of the line \(y=(2+\sqrt{3})(x-7)\) is: \(m_2=(2+\sqrt{3})\)
Let \(\theta\) be the angle between these lines. Then
\(
\tan \theta=\left|\frac{m_1-m_2}{1+m_1 m_2}\right|=\left|\frac{(2-\sqrt{3})-(2+\sqrt{3})}{1+(2-\sqrt{3})(2+\sqrt{3})}\right|=\left|\frac{-2 \sqrt{3}}{1+4-3}\right|=\sqrt{3}
\)
\(\therefore \quad \theta=\frac{\pi}{3}=60^{\circ}\), which is an acute angle
Thus, obtuse angle between the lines \(=180^{\circ}-60^{\circ}=120^{\circ}\)

Hint

Equation of line in intercept form is \(\frac{x}{a}+\frac{y}{b}=1\)
Given that, \(a+b=1 \dot{4} \Rightarrow b=14-a\)
So, equation of line is: \(\frac{x}{a}+\frac{y}{14-a}=1\)
Since it passes through the point \((3,4)\), we have
\(
\frac{3}{a}+\frac{4}{14-a}=1
\)
\(
\begin{array}{ll}
\Rightarrow & a^2-13 a+42=0 \Rightarrow \quad(a-7)(a-6)=0 \\
\therefore & a=7 \text { or } a=6
\end{array}
\)
When \(a=7\), then \(b=7\)
When \(a=6\), then \(b=8\)
Thus, equation of line is: \(\frac{x}{7}+\frac{y}{7}=1\), i.e., \(x+y=7\) or \(\frac{x}{6}+\frac{y}{8}=1\)

Hint

Let the required point be \((h, k)\) lies on the line \(x+y=4\)
i.e., \(h+k=4 \dots(i)\)

The distance of the point \((h, k)\) from the line \(4 x+3 y=10\) is:
\(
\begin{array}{l}
\left|\frac{4 h+3 k-10}{\sqrt{16+9}}\right|=1 \quad \text { (given) } \\
\Rightarrow \quad 4 h+3 k-10= \pm 5
\end{array}
\)

This gives two results:
\(
\begin{array}{l}
4 h+3 k=15 \dots(ii) \\
4 h+3 k=5 \dots(iii)
\end{array}
\)
Solving (i) and (ii), we get \((h, k) \equiv(3,1)\).
Solving (i) and (iii), we get \((h, k) \equiv(-7,11)\).

Hint

Slope of the line \(\frac{x}{a}+\frac{y}{b}=1\) is: \(m_1=-\frac{b}{a}\)
Slope of the line \(\frac{x}{a}-\frac{y}{b}=1\) is: \(m_2=\frac{b}{a}\)
Let \(\theta\) be angle between the given lines. Then
\(
\tan \theta=\left|\frac{m_1-m_2}{1+m_1 m_2}\right|=\left|\frac{-\frac{b}{a}-\frac{b}{a}}{1+\left(\frac{-b}{a}\right)\left(\frac{b}{a}\right)}\right|=\left|\frac{\frac{-2 b}{a}}{\frac{a^2-b^2}{a^2}}\right|
\)

Then, \(\tan \theta=\frac{2 a b}{a^2-b^2}\)

Hint

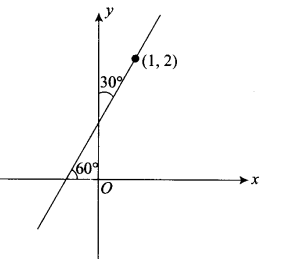
As shown in the figure line makes an angle \(30^{\circ}\) with \(y\)-axis, then it makes an angle \(60^{\circ}\) with \(x\)-axis.
\(\therefore\) Slope of the line \(=\tan 60^{\circ}=\sqrt{3}\)
So, the equation of line passing through \((1,2)\) and having slope \(\sqrt{3}\) is:
\(
\begin{aligned}
& y-2=\sqrt{3}(x-1) \\
\Rightarrow \quad & y-\sqrt{3} x-2+\sqrt{3}=0
\end{aligned}
\)

Hint

Given lines are:
\(
\begin{array}{l}
2 x+y=5 \dots(i)\\
x+3 y=-8 \dots(ii)
\end{array}
\)

Solving (i) and (ii), we get their point of intersection as \(\left(\frac{23}{5}, \frac{-21}{5}\right)\).
Slope of line \(3 x+4 y=7\) is \(\frac{-3}{4}\). So, the line parallel to this line has slope \(\frac{-3}{4}\).
Then the equation of the line passing through the point \(\left(\frac{23}{5}, \frac{-21}{5}\right)\) having slope \(\frac{-3}{4}\) is:
\(
\begin{aligned}
& y+\frac{21}{5}=\frac{-3}{4}\left(x-\frac{23}{5}\right) \\
\Rightarrow & 4 y+\frac{84}{5}=-3 x+\frac{69}{5} \Rightarrow 3 x+4 y=\frac{84-69}{5}=3 \\
\Rightarrow & 3 x+4 y+3=0
\end{aligned}
\)

Hint

Given line is:
\(
a x+b y+8=0 \Rightarrow \frac{x}{\frac{-8}{a}}+\frac{y}{\frac{-8}{b}}=1
\)

So, the intercepts are \(\frac{-8}{a}\) and \(\frac{-8}{b}\).
Another given line is:
\(
2 x-3 y+6=0 \Rightarrow \frac{x}{-3}+\frac{y}{2}=1
\)
So, the intercepts are -3 and 2 .
According to the question, we have
\(
\begin{aligned}
& \frac{-8}{a}=3 \text { and } \frac{-8}{b}=-2 \\
\therefore \quad & a=-\frac{8}{3}, b=4
\end{aligned}
\)

Hint

Let the line through the point \(P(-5,4)\) meets axis at \(A(h, 0)\) and \(B(0, k)\)
According to the question, we have \(A P: B P=1: 2\)
\(
\begin{array}{ll}
\therefore & (-5,4) \equiv\left(\frac{1 \times 0+2 \times h}{1+2}, \frac{1 \times k+2 \times 0}{1+2}\right) \\
\therefore & -5=\frac{2 h}{3} \text { and } 4=\frac{k}{3} \\
\Rightarrow & h=-15 / 2 \text { and } k=12
\end{array}
\)

Thus, equation of the line using intercept form is:
\(
\frac{x}{-15 / 2}+\frac{y}{12}=1 \Rightarrow 8 x-5 y+60=0
\)

Hint

Given that the line makes and angle \(120^{\circ}\) with positive direction of \(x\)-axis.
\(\therefore\) Slope of the line is \(\tan 120^{\circ}=-\sqrt{3}\)
So, equation of the required line is: \(y=-\sqrt{3} x+c \Rightarrow \sqrt{3} x+y-c=0\).
Now distance of this line from \((0,0)\) is 4 units.
\(
\begin{array}{ll}
\therefore & \frac{|\sqrt{3}(0)+0-c|}{\sqrt{3+1}}=4 \\
\Rightarrow & |c|=8 \Rightarrow c= \pm 8
\end{array}
\)

Thus, equation of the required lines is \(\sqrt{3} x+y \pm 8=0\).

Hint

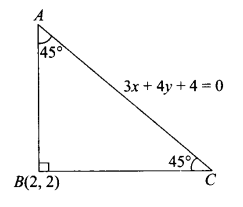
As shown in the figure, hypotenuse is along the line \(3 x+4 y+4=0\).
\(
\therefore \quad \text { Slope of } A C=\frac{-3}{4} \text {. }
\)
Since \(A B C\) is isosceles right angled triangle, \(\angle B A C=\angle A C B=45^{\circ}\).
Now, let the slope of the line making an angle \(45^{\circ}\) with \(A C\) be \(m\).
\(
\therefore \quad \tan 45^{\circ}=\left|\frac{m-\left(-\frac{3}{4}\right)}{1+m\left(-\frac{3}{4}\right)}\right| \Rightarrow \frac{4 m+3}{4-3 m}= \pm 1
\)
\(\Rightarrow \quad 4 m+3=4-3 m\) or \(4 m+3=3 m-4 \Rightarrow m=1 / 7\) or \(m=-7\)
So, if the slope of line \(B C\) is \(1 / 7\) then the slope of line \(A B\) is -7 .
So, equation of \(B C\) is: \(y-2=(1 / 7)(x-2) \Rightarrow x-7 y+12=0\).
Equation of \(A B\) is: \(y-2=-7(x-2) \Rightarrow 7 x+y-16=0\).

Hint

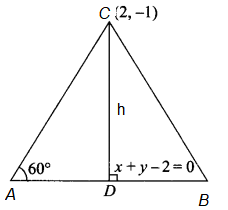
Considering \(C(2,-1)\) as vertex of the equilateral triangle.
The given equation of the base of the equilateral triangle is \(x+y=2\)
The perpendicular distance from the point \(\left(x_1, y_1\right)\) to a line \(a x+b y+c=0\) is given by
\(
d=\left|\frac{\left(a x_1+b y_1+c_1\right)}{\sqrt{\left(a^2+b^2\right)}}\right|
\)
Let’s consider the perpendicular distance to side \(A B\) be \(h\) Therefore, the perpendicular distance from \(C(2,-1)\) is given by
\(
h=\left|\frac{(2 \times 1-1 \times 1-2)}{\sqrt{\left(1^2+1^2\right)}}\right|
\)
\(
h=\frac{1}{\sqrt{2}} \cdots \ldots(i)
\)
We know that the height for an equilateral triangle is, \(h=\left(\frac{\sqrt{3}}{2}\right) a \ldots \ldots(i i)\), where \(a\) is the side and \(h\) is the altitude.
Step 2:Equating the equations \((i) \&(i i)\)
we get
\(
\begin{array}{l}
\Rightarrow \frac{1}{\sqrt{2}}=\frac{\sqrt{3} a}{2} \\
\Rightarrow \quad a=\sqrt{\frac{2}{3}}
\end{array}
\)

Hint

Let \(\left(x_1, y_1\right)\) be the coordinates of the given point \(P\) and \(m\) be the slope of the line.
\(\therefore\) Equation of the line is \(y-y_1=m\left(x-x_1\right) \dots(i)\)
Given points are \(A(2,0), B(0,2)\) and \(C(1,1)\).
Perpendicular distance from \(A(2,0)\) to the line (i) \(d_1\) (say)
\(
\mathrm{d}_1=\frac{0-y_1-m\left(2-x_1\right)}{\sqrt{1+m^2}}
\)
Perpendicular distance from \(B(0,2) d_2\) (say)
\(
\mathrm{d}_2=\frac{2-y_1-m\left(0-x_1\right)}{\sqrt{1+m^2}}
\)
Similarly, perpendicular distance from \(C(1,1) d_3\) (say)
\(
\mathrm{d}_3=\frac{1-y_1-m\left(1-x_1\right)}{\sqrt{1+m^2}}
\)
We have \(d_1+d_2+d_3=0\)
\(
\begin{array}{l}
\therefore \frac{0-y_1-m\left(2-x_1\right)}{\sqrt{1+m^2}}+\frac{2-y_1-m\left(0-x_1\right)}{\sqrt{1+m^2}}+\frac{1-y_1-m\left(1-x_1\right)}{\sqrt{1+m^2}}=0 \\
\Rightarrow-\mathrm{y}_1-2 \mathrm{~m}+\mathrm{mx}_1+2-\mathrm{y}_1+\mathrm{mx}_1+1-\mathrm{y}_1-\mathrm{m}+\mathrm{mx}_1=0 \\
\Rightarrow 3 \mathrm{mx}_1-3 \mathrm{y}_1-3 \mathrm{~m}+3=0
\end{array}
\)
\(
\Rightarrow \mathrm{mx}_1-\mathrm{y}_1-\mathrm{m}+1=0
\)
Since the point \((1,1)\) satisfies the above equation.

Hint

Let slope of the line be \(m\). Also, the line passes through the point \(A(1,2)\)
\(\therefore\) Equation of line is \(y-2=m(x-1)\) or \(m x-y+2-m=0 \dots(i)\)
Also the equation of the given line is \(x+y-4=0 \dots(ii)\) 
Let these lines meet at point \(B\).
Solving (i) and (ii), we get \(B \equiv\left(\frac{m+2}{m+1}, \frac{3 m+2}{m+1}\right)\)
Now, given that \(A B=\frac{\sqrt{6}}{3}\)
\(
\Rightarrow \quad A B^2=\frac{6}{9} \Rightarrow\left(\frac{m+2}{m+1}-1\right)^2+\left(\frac{3 m+2}{m+1}-2\right)^2=\frac{6}{9}
\)
\(
\begin{array}{ll}
\Rightarrow & \left(\frac{1}{m+1}\right)^2+\left(\frac{m}{m+1}\right)^2=\frac{2}{3} \Rightarrow \frac{1+m^2}{(1+m)^2}=\frac{2}{3} \\
\Rightarrow & 3+3 m^2=2+2 m^2+4 m \Rightarrow m^2-4 m+1=0 \\
\therefore & m=\frac{4 \pm \sqrt{16-4}}{2}=2 \pm \sqrt{3}=2+\sqrt{3} \text { or } 2-\sqrt{3} \\
\therefore & \tan \theta=2+\sqrt{3} \text { or } 2-\sqrt{3} \\
\therefore & \theta=75^{\circ} \text { or } \theta=15^{\circ}
\end{array}
\)

Hint

Equation of line in intercept form is \(\frac{x}{a}+\frac{y}{b}=1\).
Given that, \(\frac{1}{a}+\frac{1}{b}=\) constant \(=\frac{1}{k} \text { (say) }\)
\(\therefore \quad \frac{k}{a}+\frac{k}{b}=1\)
So, \((k, k)\) lies on \(\frac{x}{a}+\frac{k}{b}=1\)
Hence, the line passes through the fixed point \((k, k)\).

Hint

Let the line through the point \(P(-4, 3)\) meets axis at \(A(h, 0)\) and \(O(0, k)\)
Now according to the question \(A P: B P=5: 3\)
\(
\begin{array}{ll}
\therefore & (-4,3) \equiv\left(\frac{3 \times h+5 \times 0}{5+3}, \frac{3 \times 0+5 \times k}{5+3}\right) \equiv\left(\frac{3 h}{8}, \frac{5 k}{8}\right) \\
\Rightarrow & -4=\frac{3 h}{8} \text { and } 3=\frac{5 k}{8} \\
\Rightarrow & h=-\frac{32}{3} \text { and } k=\frac{24}{5}
\end{array}
\)

So, equation of the required line in intercept form is:
\(
\frac{x}{-32 / 3}+\frac{y}{24 / 5}=1 \Rightarrow 9 x-20 y+96=0
\)

Hint

The equations of the lines through the point of intersection of the lines \(x-y+1=0\) and \(2 x-3 y+5=0\) is given by
\(
\begin{array}{l}
x-y+1+a(2 x-3 y+5)=0 \\
\Rightarrow(1+2 a) x+y(-3 a-1)+5 a+1=0 \dots(1)
\end{array}
\)
The distance of the above line from the point is given by \(\frac{3(2 a+1)+2(-3 a-1)+5 a+1}{\sqrt{(2 a+1)^2+(-3 a-1)^2}}\)
\(
\begin{array}{l}
\therefore \frac{|3(2 a+1)+2(-3 a-1)+5 a+1|}{\sqrt{(2 a+1)^2+(-3 a-1)^2}}=\frac{7}{5} \\
\Rightarrow \frac{|5 a+2|}{\sqrt{13 a^2+10 a+2}}=\frac{7}{5} \\
\Rightarrow 25(5 a+2)^2=49\left(13 a^2+10 a+2\right) \\
\Rightarrow 6 a^2-5 a-1=0 \\
\Rightarrow a=1,-\frac{1}{6}
\end{array}
\)
Substituting the value of \(a\) in (1), we get \(3 x-4 y+6=0\) and \(4 x-3 y+1=0\)

Hint

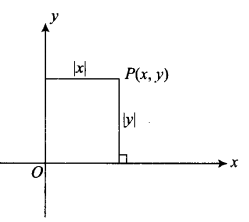
Let the coordinates of moving point \(P\) be \((x, y)\).
Given that, the sum of distances of this point in a plane from the axes is 1 .
\(
\begin{array}{ll}
\therefore & |x|+|v|=1 \\
\Rightarrow & \pm x \pm y=1 \\
\Rightarrow & x+y=1,-x-y=1 \\
& -x+y=1, x-y=1
\end{array}
\)
Hence, these equations gives us the locus of the point \(P\) which is a square.

Hint

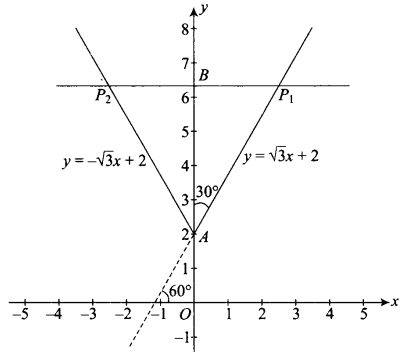
Given lines are: \(y-\sqrt{3} x=2\), for \(x \geq 0 \dots(i)\)
and \(\quad y+\sqrt{3} x=2\), for \(x \leq 0 \dots(ii)\)
Clearly, lines intersect at \(A(0,2)\).
Line (i) is inclined at an angle of \(60^{\circ}\) with +ve direction of \(x\)-axis.
Line (ii) is inclined at angle of \(120^{\circ}\) with \(+v e\) direction of \(x\)-axis.
\(P_1\) and \(P_2\) are points at distance 5 units from point \(A\) on the lines.
Clearly, angle bisector of lines is \(y\)-axis.
Foot of perpendicular from \(P_1\) and \(P_2\) on \(y\)-axis is \(B\).
Now, \(A P_1=5\)
\(
\therefore \quad \text { In } \triangle A B P_1, \frac{A B}{A P_1}=\cos 30^{\circ}
\)
\(
\begin{array}{ll}
\therefore & A B=\frac{5 \sqrt{3}}{2} \\
\therefore & O B=2+\frac{5 \sqrt{3}}{2}
\end{array}
\)
So, the coordinates of the foot of perpendicular are \(\left(0,2+\frac{5 \sqrt{3}}{2}\right)\).

Hint

Since \(p\) is the length of perpendicular from the origin on the line \(\frac{x}{a}+\frac{y}{b}=1\), we have
\(
p=\frac{|0+0-1|}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}}}=\frac{a b}{\sqrt{a^2+b^2}} \Rightarrow p^2=\frac{a^2 b^2}{a^2+b^2}
\)
Given that, \(a^2, p^2\) and \(b^2\) are in AP.
\(
\begin{array}{ll}
\therefore & 2 p^2=a^2+b^2 \\
\Rightarrow & \frac{2 a^2 b^2}{a^2+b^2}=a^2+b^2 \Rightarrow 2 a^2 b^2=\left(a^2+b^2\right)^2 \\
\Rightarrow & 2 a^2 b^2=a^4+b^4+2 a^2 b^2 \\
\Rightarrow & a^4+b^4=0
\end{array}
\)

Hint

(a) Let the equation of the line be \(y=m x+c\).
Given that, \(c=-3\) and \(m=\frac{3}{5}\).
So, equation of the line is: \(y=\frac{3}{5} x-3 \Rightarrow 5 y-3 x+15=0\)

Hint

(a) Equation of the according to the question is \(\frac{x}{a}+\frac{y}{a}\) \(\Rightarrow x+y=a\)
Required slope \(=-1\)

Hint

(b) Slope of the given line \(y=x\) is 1 .
Thus, slope of line perpendicular to \(y=x\) is -1 .
Line passes through the point \((3,2)\).
So, equation of the required line is: \(y-2=-1(x-3)=>x+y=5\)

Hint

(b) Slope of the given line \(+1=0\) is- 1 .
So, slope of line perpendicular to above line is 1 .
Line passes through the point \((1,2)\).
Therefore, equation of the required linens:
\(
y-2=1(x-1) \Rightarrow y-x-1=0
\)

Hint

(c) Intercepts of line are \(a\) and \(-b\); i.e., line passes through the points \((a, 0)\), \((0,-b)\).
\(\therefore \quad\) Slope of line, \(m_1=\frac{-b-0}{0-a}=\frac{b}{a}\)
Intercepts of line are \(b,-a\); i.e., line passes through the points \((b, 0),(0,-a)\).
\(\therefore \quad\) Slope of line, \(m_2=\frac{-a-0}{0-b}=\frac{a}{b}\)
If \(\theta\) is the angle between the lines, then
\(
\tan =\theta=\frac{\frac{b}{a}-\frac{a}{b}}{1+\frac{a}{b} \cdot \frac{b}{a}}=\frac{\frac{b^2-a^2}{a b}}{2}=\frac{b^2-a^2}{2 a b}
\)

Hint

Given points are \((2,-3)\) and \((4,-5)\)
Firstly the equation of line is found
We know that the equation of line when two points are given is \(\mathrm{y}-\mathrm{y}_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right)\)
Putting the values we get \(y-(-3)=\frac{-5-(-3)}{4-2}(x-2)\)
\(
\begin{array}{l}
y+3=\frac{-5+3}{2}(x-2) \\
y+3=-\frac{2}{2}(x-2) \\
y+3=-1(x-2) \\
y+3=-x+2 \\
x+y=2-3 \\
x+y=-1 \\
\frac{x}{-1}+\frac{y}{-1}=1 \text { in intercept form }
\end{array}
\)
Comparing the equation with intercept form of equation that is \(\frac{x}{a}+\frac{y}{b}=1\) the value of \(a=-1\) and \(b=-1\)
Hence, the correct option is (d)

Hint

(a) Given lines are:
\(2 x-3 y+5=0\) and \(3 x+4 y=0\)
Solving these lines, we get point of intersection as \(\left(\frac{-20}{17}, \frac{15}{17}\right)\) therefore Distance of this point from the line \(5 x-2 y=0\)
\(
=\frac{\left|5 \times\left(-\frac{20}{17}\right)-2\left(\frac{15}{17}\right)\right|}{\sqrt{25+4}}=\frac{\left|\frac{-100}{17}-\frac{30}{17}\right|}{\sqrt{29}}=\frac{130}{17 \sqrt{29}}
\)

Hint

(a) Slope of the given line \(\sqrt{3} x+y=1\) is, \(m_1=-\sqrt{3}\).

Let the slope of the required line which makes an angle of \(60^{\circ}\) with the above line is \(m\).
\(
\begin{array}{ll}
\therefore & \tan 60^{\circ}=\left|\frac{-\sqrt{3}-m}{1-\sqrt{3} m}\right| \Rightarrow\left|\frac{-\sqrt{3}-m}{1-\sqrt{3} m}\right|=\sqrt{3} \\
\Rightarrow & -\sqrt{3}-m=\sqrt{3}-3 m \text { or }-\sqrt{3}-m=-\sqrt{3}+3 m \\
\Rightarrow & m=\sqrt{3} \text { or } m=0
\end{array}
\)

Line is passing through the point \((3,-2)\).
Thus, the equation of the required line is: \(y+2=\sqrt{3}(x-3)\) or \(y+2=0\)
\(
\Rightarrow \quad \sqrt{3} x-y-2-3 \sqrt{3}=0 \text { and } y+2=0
\)

Hint

(a) Let the slope of the line be ‘ \(m\) ‘
Then equation of line passing through \((1,0)\) is:
\(
\begin{array}{ll}
& y-0=m(x-1) \\
\Rightarrow \quad & y-m x+m=0 \dots(i)
\end{array}
\)
It is given that the distance of the line from origin is \(\frac{\sqrt{3}}{2}\).
\(
\begin{array}{l}
\therefore \quad \frac{\sqrt{3}}{2}=\frac{|0-0+m|}{\sqrt{1+m^2}} \Rightarrow \frac{\sqrt{3}}{2}=\frac{|m|}{\sqrt{1+m^2}} \\
\Rightarrow \quad 3+3 m^2=4 \dot{m}^2 \Rightarrow m^2=3 \Rightarrow m= \pm \sqrt{3}
\end{array}
\)
So, equation of line is: \(\sqrt{3} x+y-\sqrt{3}=0\) or \(\sqrt{3} x-y-\sqrt{3}=0\).

Hint

(b) Let any point on the line \(y=m x+c_1\) be \(P\left(x_1, y_1\right)\).

The equation of the other line is: \(y=m x+c_2 \Rightarrow m x-y+c_2=0\)
Distance of point \(P\) from this line, \(d=\frac{\left|m x_1-y_1+c_2\right|}{\sqrt{m^2+1}}\)
Since \(P\) lies on the first line, we get
\(
\begin{aligned}
y_1 & =m x_1+c_1 \Rightarrow m x_1-y_1=-c_1 \\
\therefore \quad d & =\frac{\left|c_1-c_2\right|}{\sqrt{m^2+1}}
\end{aligned}
\)

Hint

Given equation is \(y=3 x+4 \dots(i)\)
\(
\Rightarrow 3 \mathrm{x}-\mathrm{y}+4=0
\)
Slope \(=3\)
Equation of any line passing through the point \((2,3)\) is
\(
y-3=m(x-2) \dots(ii)
\)
If equation (i) is perpendicular to eq. (ii)
Then \(\mathrm{m} \times 3=-1 \quad \ldots \ldots .\left[\because m_1 \times m_2=-1\right]\)
\(
\Rightarrow m=-\frac{1}{3}
\)
Putting the value of \(m\) in equation (ii) we get
\(
\begin{array}{l}
y-3=-\frac{1}{3}(x-2) \\
\Rightarrow 3 y-9=-x+2
\end{array}
\)
\(
\Rightarrow x+3 y=11 \dots(iii)
\)
Solving equation (i) and equation (iii) we get
\(
\begin{array}{l}
3 x-y=-4 \\
\Rightarrow y=3 x+4
\end{array}
\)
Putting the value of \(y\) in eq. (iii) we get
\(
\begin{array}{l}
x+3(3 x+4)=11 \\
\Rightarrow x+9 x+12=11 \\
\Rightarrow 10 x=-1 \\
\Rightarrow x=\frac{-1}{10}
\end{array}
\)
From equation (iv) we get
\(
\begin{array}{l}
y=3\left(\frac{-1}{10}\right)+4 \\
\Rightarrow y=\frac{-3}{10}+4 \\
\Rightarrow y=\frac{37}{10}
\end{array}
\)
So the required coordinates are \(\left(\frac{-1}{10}, \frac{37}{10}\right)\).

Hint

(a) Since, the middle point is \(P(3,2)\), then line meets axes at \(A(6,0)\) and \(B(0,4)\).
Answer:

Let the given line meets the axes at \(A(a, 0)\) and \(B(0, b)\)
Given that \((3,2)\) is the midpoint \(3=\frac{0+a}{2}\)
\(
\begin{array}{l}
\mathrm{a}=6 \text { and }2=\frac{0+b}{2} \\
\mathrm{~b}=4
\end{array}
\)
Intercept form of the line \(\mathrm{AB}\) is \(\frac{x}{a}+\frac{y}{b}=1\)
Putting the value of \(\mathrm{a}\) and \(\mathrm{b}\) in above equation, we get \(\frac{x}{6}+\frac{y}{4}=1\)
\(
\begin{array}{l}
\frac{2 x+3 y}{12}=1 \\
2 x+3 y=12
\end{array}
\)

Hint

(c) Line is parallel to the line \(y=3 x-1\).
So, slope of the line is’ 3 ‘.
Also, line passes through the point \((1,2)\).
So, equation of the line is: \(y-2=3(x-1)\)

Hint

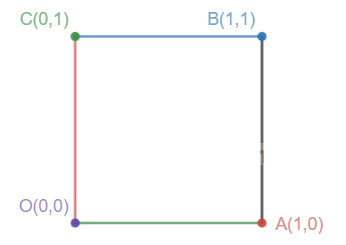
It is given that the lines \(x=0, y=0, x=1\) and \(y=1\) form a square of side 1 unit Let us form a square \(\mathrm{OABC}\) having corners \(\mathrm{O}(0,0)\) from the given lines with \(A(1,0), B(1,1)\) and \(C(0,1)\)
Now we have to find the equation of the diagonal \(A C\)
Equation of a line is found out by \(y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right)\)
\(
\begin{array}{l}
y-0=\frac{1-0}{0-1}(x-1) \\
y=-1(x-1) \\
y=-x+1
\end{array}
\)
\(
x+y=1
\)
Equation of diagonal OB is \(y-0=\frac{1-0}{1-0}(x-0)\) \(y=x\)

Hint

\(
a x+b y=1 \Rightarrow \text { Two parameters. }
\)

Hint

Let the reflection of \(A(4,1)\) in \(y=x\) be \(B(a, b)\) mid-point of \(A B\)
\(
\begin{array}{l}
=\left(\frac{4+a}{2}, \frac{1+b}{2}\right) \text { which lies on } \mathrm{y}=\mathrm{x} \\
\Rightarrow \frac{4+\mathrm{a}}{2}=\frac{1+b}{2}
\end{array}
\)
\(
\begin{array}{l}
\Rightarrow 4+a=1+b \\
\Rightarrow a-b=-3 \ldots (i)
\end{array}
\)
The slope of the line \(\mathrm{y}=\mathrm{x}\) is 1 and slope of \(\mathrm{AB}=\frac{b-1}{a-4}\)
\(
\begin{array}{l}
\therefore 1\left(\frac{b-1}{a-4}\right)=-1 \\
\Rightarrow b-1=-a+4 \\
\Rightarrow a+b=5 \quad . . . \text { (ii) }
\end{array}
\)

Solving equation (i) and equation (ii) we get
\(
\mathrm{a}=1 \text { and } \mathrm{b}=4
\)
\(\therefore\) The point after translation is \((1+2,4)\) or \((3,4)\)

Hint

Given equations are \(4 x+3 y+10=0\)…..(i)
\(
5 x-12 y+26=0 \dots(ii)
\)
And \(7 x+24 y-50=0 \dots(iii)\)
Let \(\left(x_1, y_1\right)\) be any point equidistant from equation (i), equation (ii) and equation (iii).
Distance of \(\left(x_1, y_1\right)\) from equation (i)
\(
\begin{array}{l}
=\left|\frac{4 x_1+3 y_1+10}{\sqrt{16+9}}\right| \\
=\left|\frac{4 x_1+3 y_1+10}{5}\right|
\end{array}
\)
Distance of \(\left(x_1, y_1\right)\) from equation (ii)
\(
\begin{array}{l}
=\left|\frac{5 x_1-12 y_1+26}{\sqrt{25+144}}\right| \\
=\left|\frac{5 x_1+12 y_1+26}{13}\right|
\end{array}
\)
Distance of \(\left(x_1, y_1\right)\) from equation (iii)
\(
\begin{array}{l}
=\left|\frac{7 x_1+24 y_1-50}{\sqrt{49+576}}\right| \\
=\left|\frac{7 x_1+24 y_1-50}{25}\right|
\end{array}
\)
If the point \(\left(x_1, y_1\right)\) is equidistant from the given lines, then
\(
\begin{array}{l}
\left|\frac{4 x_1+3 y_1+10}{5}\right|=\left|\frac{5 x_1-12 y_1+26}{13}\right| \\
=\left|\frac{7 x_1+2 y_1-50}{25}\right|
\end{array}
\)
We see that putting \(x_1=0\) and \(y_1=0\), the above relation is satisfied
i.e., \(\frac{10}{5}=\frac{26}{13}=\frac{50}{25}=2\)

Hint

(d) Slope of given line \(3 x+y=3\) is -3 .
\(\therefore \quad\) Slope of perpendicular line \(=\frac{1}{3}\) of the required line is: \(y-2=\frac{1}{3}(x-2) \Rightarrow x-3 y+4=0\)

Thus, equation of the requ For \(y\)-intercept, put \(x=0\).
\(0-3 y+4=0 \Rightarrow y=\frac{4}{3}\), which is \(y\)-intercept.

Hint

(b) Given lines are:
Given lines are \(3 x+4 y+5=0 \ldots . .\). (i)
\(
3 x+4 y-5=0 \dots(ii)
\)
and \(3 x+4 y+2=0 \dots(iii)\)
Since the coefficient of \(x\) and \(y\) are same equation \(i\), ii and iii are parallel to each other
We know that in case of \(\mathrm{i}\) and iii
\(d=\frac{\left|c_1-c_2\right|}{\sqrt{A^2+B^2}}=\frac{|5-2|}{\sqrt{3^2+(4)^2}}=\frac{|3|}{\sqrt{9+16}}=\left|\frac{3}{5}\right|\)
distance between two parallel lines is
Similarly in case of ii and iii distance between two parallel lines is
\(
d=\frac{\left|c_1-c_2\right|}{\sqrt{A^2+B^2}}=\frac{|-5-2|}{\sqrt{3^2+(4)^2}}=\frac{|-7|}{\sqrt{9+16}}=\left|-\frac{7}{5}\right|
\)
Ratio between the distance is \(\frac{3}{5}: \frac{7}{5}=3: 7\)

Hint

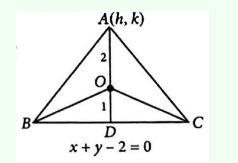
Let coordinates of the vertex \(A\) be \((h, k)\).
Now, \(A D\) is perpendicular to \(B C\)
\(
\begin{array}{l}
\therefore O A \perp B C \\
\Rightarrow \frac{k-0}{h-0} \times \frac{-1}{1}=-1 \\
\Rightarrow k=h \quad \ldots(i)
\end{array}
\)
Let coordinates of \(D\) be \((\alpha, \beta)\)
\(
\begin{array}{l}
\therefore \text { Coordinates of } O=\left(\frac{2 \alpha+h}{2+1}, \frac{2 \beta+k}{2+1}\right) \\
\Rightarrow \frac{2 \alpha+h}{3}=0, \\
\frac{2 \beta+k}{3}=0 \\
\Rightarrow \alpha=\frac{-h}{2}, \\
\beta=\frac{-k}{2}
\end{array}
\)
Now, \((\alpha, \beta)\) lies on \(x+y-2=0\)
\(
\begin{array}{l}
\therefore \alpha+\beta-2=0 \\
\Rightarrow \frac{-h}{2}+\frac{-k}{2}-2=0 \\
\Rightarrow h+k+4=0 \\
\Rightarrow 2 h+4=0 \\
\Rightarrow h=-2=k \text { (from }(i)) \\
\therefore \text { Vertex } A=(-2,-2)
\end{array}
\)

Hint

Given line is \(a x+b y+c=0 \dots(i)\)
Since, \(a, b\) and \(c\) are in A.P., we get
\(
b=\frac{a+c}{2} \text { or } a-2 b+c=0 \dots(ii)
\)
On comparing Eqs. (i) and (ii), we get
\(
x=1, y=-2
\)
So, \((1,-2)\) lies on the line.

Hint

Equation of straight line in intercept form \(=\frac{x}{a}+\frac{y}{b}=1\) where \(\mathrm{a}\) and \(\mathrm{b}\) are intercepts Given that \(\mathrm{a}=\mathrm{b}; \frac{x}{a}+\frac{y}{a}=1\)
\(
\begin{array}{l}
\frac{x+y}{a}=1 \\
{x}+{y}={a} \ldots . . \text { (i) }
\end{array}
\)
If equation ipasses through the point \((1,-2)\) we get \(1+(-2)=a\)
\(
\begin{array}{l}
1-2=a \\
a=-1
\end{array}
\)

Putting the value of \(a\) in equation \(i\) we get \(x+y=-1\)
\(
x+y+1=0
\)

Hint

Slope of the given line \(x-2 y=3\) is \(\frac{1}{2}\).
Let the slope of the required line be \(m\).
\(
\begin{array}{ll}
\therefore & \tan 45^{\circ}=\left|\frac{m-\frac{1}{2}}{1+\frac{1}{2} m}\right| \Rightarrow 1= \pm \frac{2 m-1}{2+m} \\
\Rightarrow & 2 m-1=2+m \text { or } 1-2 m=2+m \\
\Rightarrow & m=3 \text { or } m=-\frac{1}{3}
\end{array}
\)

Also, the required line passes through the point \((3,2)\).
So, equation of the line is: \(y-2=3(x-3)\) or \(y-2=-\frac{1}{3}(x-3)\)
\(
\therefore \quad 3 x-y-7=0 \text { or } x+3 y-9=0
\)

Hint

Given line is \(3 x-4 y-8=0\)
For point ( 3,4\(), 3(3)-4(4)-8=-15<0\)
For point \((2,-6), 3(2)-4(-6)-8=22>0\)
Hence, the points \((3,4)\) and \((2,-6)\) lies on opposite side of the line.

Hint

Let be the moving point & given point be \(A(3,-2)\)
\(
\begin{aligned}
A P & =\sqrt{(h-3)^2+(k+2)^2} \\
A P^2 & =(h-3)^2+(k+2)^2
\end{aligned}
\)
Distance from the point \(P(h, k)\) from the line \(5 x-12 y=13\) is
\(
\begin{array}{l}
\begin{aligned}
D & =\frac{\left|a x_1+b y_1+c\right|}{\sqrt{a^2+b^2}} \\
D & =\frac{|5 h-12 k-13|}{\sqrt{5^2+12^2}} \\
& =\frac{|5 h-12 k-13|}{13}
\end{aligned} \\
\text { Given, } A P^2=D
\end{array}
\)
\(
\begin{array}{c}
(h-3)^2+(k+2)^2=\frac{|5 h-12 k-13|}{13} \\
13\left(h^2-6 h+9+k^2+4 k+4\right)=(5 h-12 k-13)
\end{array}
\)
\(
0=13 h^2-78 h+117+13 k^2+52 k+52-5 h+12 k+13
\)
\(
\Rightarrow 13 h^2+13 k^2-83 h+64 k+182=0
\)
So the locus of the point is
\(
3 x^2+13 y^2-83 x+64 y+182=0
\)

Hint

Line \(x \sin \theta+y \cos \theta=p\) meets axes at \(A\left(\frac{p}{\sin \theta}, 0\right)\) and \(B\left(0, \frac{p}{\cos \theta}\right)\). Let \(P(h, k)\) be the mid-point of \(A B\).
Let \(P(h, k)\) be the mid-point of \(A B\).
\(\therefore \quad h=\frac{p}{2 \sin \theta}\) and \(k=\frac{p}{2 \cos \theta}\)
\(\therefore \quad \sin \theta=\frac{p}{2 h}\) and \(\cos \theta=\frac{p}{2 k}\)
Squaring and adding, we get
\(
\sin ^2 \theta+\cos ^2 \theta=\frac{p^2}{4 h^2}+\frac{p^2}{4 k^2} \quad \text { or } \mathrm{l}=\frac{p^2}{4 x^2}+\frac{p^2}{4 y^2}
\)
or \(\quad 4 x^2 y^2=p^2\left(x^2+y^2\right)\).

Hint

Let \(A\left(x_1, y_1\right) B\left(x_2, y_2\right)\) and \(C\left(x_3, y_3\right)\) be vertices of a triangle (ABC) with integer values.
area of \((\triangle \mathrm{ABC})=\frac{1}{2}\left\{x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right\}\)
Since \(x_i, y_i\); are integers
\(\Rightarrow\) area of \(\triangle(A B C) \dots(1)\) is rational
Let us suppose \(\Delta\) is an equilateral triangle
Then \(\Delta=\frac{\sqrt{3}}{4} a^2\)
where \(a=\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}\)
i. e. \(a^2=\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2\)
i. e. \(a^2\) is ration.
\(\therefore \Delta=\frac{\sqrt{3}}{4} a^2\) is irrational
Which contradicts eq(1)
Hence \(\Delta\) cannot be equilateral triangle.

Hint

Given points are \(A(-2,1), B(0,5)\) and \(C(-1,2)\) are collinear.
Slope of \(A B=\frac{5-1}{0+2}=2\)

Slope of \(B C=\frac{2-5}{-1-0}=3\)
Since the slopes are different, \(A, B\) and \(C\) are not collinear.

Hint

Equation of any line perpendicular to \(x \sec \theta+y \operatorname{cosec} \theta=a\) is
\(
x \operatorname{cosec} \theta-y \sec \theta=k \dots(i)
\)

If equation (i) passes through \(\left(a \cos ^3 \theta, a \sin ^3 \theta\right)\) then
\(
\begin{array}{l}
\mathrm{a} \cos ^3 \theta \cdot \operatorname{cosec} \theta-\mathrm{a} \sin ^3 \theta \cdot \sec \theta=\mathrm{k} \\
\Rightarrow \frac{a \cos ^3 \theta}{\sin \theta}-\frac{a \sin ^3 \theta}{\cos \theta}=\mathrm{k}
\end{array}
\)
\(\therefore\) Required equation is
\(
\begin{array}{l}
\mathrm{x} \cos \theta-\mathrm{y} \sin \theta=\frac{a \cos ^3 \theta}{\sin \theta}-\frac{a \sin ^3 \theta}{\cos \theta} \\
\Rightarrow \frac{x}{\sin \theta}-\frac{y}{\cos \theta}=a\left[\frac{\cos ^4 \theta-\sin ^4 \theta}{\sin \theta \cos \theta}\right] \\
\Rightarrow \frac{x \cos \theta-y \sin \theta}{\sin \theta \cos \theta}=a\left[\frac{\left(\cos ^2 \theta+\sin ^2 \theta\right)\left(\cos ^2 \theta-\sin ^2 \theta\right)}{\sin \theta \cos \theta}\right] \\
\Rightarrow \mathrm{x} \cos \theta-\mathrm{y} \sin \theta=\mathrm{a}\left(\cos ^2 \theta-\sin ^2 \theta\right) \\
\Rightarrow \mathrm{x} \cos \theta-\mathrm{y} \sin \theta=\mathrm{a} \cos 2 \theta
\end{array}
\)

Hint

Given equations are \(x+2 y-10=0 \dots(i)\)
And \(2 x+y+5=0 \dots(ii)\)
From equation (i) \(x=10-2 y \dots(iii)\)
Putting the value of \(x\) in equation (ii) we get
\(
\begin{array}{l}
2(10-2 y)+y+5=0 \\
\Rightarrow 20-4 y+y+5=0 \\
\Rightarrow-3 y+25=0 \\
\Rightarrow y=\frac{25}{3}
\end{array}
\)
Putting the value of \(y\) in equation (iii) we get
\(
\begin{array}{l}
x=10-2\left(\frac{25}{3}\right) \\
=\frac{30-50}{3} \\
=\frac{-20}{3} \\
\therefore \text { Point }=\left(\frac{-20}{3}, \frac{25}{3}\right)
\end{array}
\)
If the given line \(5 x+4 y=0\) passes through the point \(\left(\frac{-20}{3}, \frac{25}{3}\right)\)
\(
\begin{array}{l}
5\left(\frac{-20}{3}\right)+4\left(\frac{25}{3}\right)=0 \\
\Rightarrow \frac{-100}{3}+\frac{100}{3}=0 \\
\Rightarrow 0=0 \text { satisfied. }
\end{array}
\)
So, the given line passes through the point of intersection of the given lines.

Hint

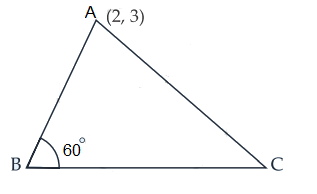
Let \(A B C\) be an equilateral triangle with vertex \((2,3)\) and the opposite side is \(x+y=2\) with slope -1 . Suppose slope of line \(A B\) is \(m\).
Since each angle of equilateral triangle is \(60^{\circ}\).
\(\therefore\) Angle between \(A B\) and \(B C\)
\(
\begin{array}{l}
\tan 60^{\circ}=\left|\frac{-1-m}{1+(-1) m}\right| \\
\Rightarrow \sqrt{3}=\left|\frac{1+m}{1-m}\right| \\
\Rightarrow \sqrt{3}= \pm\left(\frac{1+m}{1-m}\right)
\end{array}
\)
Taking (+) sign,
\(
\begin{array}{l}
\sqrt{3}=\frac{1+m}{1-m} \\
\Rightarrow \sqrt{3}-\sqrt{3} m=1+m \\
\Rightarrow \sqrt{3} m+m=\sqrt{3}-1 \\
\Rightarrow m(\sqrt{3}+1)=\sqrt{3}-1 \\
\Rightarrow{ }^` m=(\operatorname{sqrt}(3)-1) /(\operatorname{sqrt}(3)+1) \\
\Rightarrow m=\frac{\sqrt{3}-1}{\sqrt{3}+1} \times \frac{\sqrt{3}-1}{\sqrt{3}-1} \\
\Rightarrow m=\frac{3+1-2 \sqrt{3}}{3-1} \\
=2-\sqrt{3}
\end{array}
\)
Taking (-) sign,
\(
m=2+\sqrt{3}
\)
So, the equations of other two lines are \(y-3=(2 \pm \sqrt{3})(x-2)\)

Hint

Given equation of lines are \(4 x+y-1=0\) and \(7 x-3 y-35=0\).
Lines intersect at \((2,-7)\)
Now, the equation of a line passing through \((3,5)\) and \((2,-7)\) is:
\(
\begin{array}{l}
y-5=\frac{-7-5}{2-3}(x-3) \quad \Rightarrow \quad y-5=12(x-3) \\
\Rightarrow \quad 12 x-y-31=0 \dots(i)
\end{array}
\)
Distance from \((0,0)\) to the line (i), \(d_1=\frac{|-31|}{\sqrt{144+1}}=\frac{31}{\sqrt{145}}\)
\(\therefore\) Distance from \((8,34)\) to the line (i), \(d_2=\frac{|96-34-31|}{\sqrt{145}}=\frac{31}{\sqrt{145}}\)
So, \(d_1=d_2\)
Hence, the equation of line \(12 x-y-31=0\) is equidistant from \((0,0)\) and \((8,34)\) Hence, the given statement is True.

Hint

The given equation is \(\frac{x}{b}-\frac{y}{a}=0 \dots(i)\)
Equation of the line passing through \((0,0)\) and perpendicular to equation (i) is
\(\frac{x}{b}-\frac{y}{a}=0 \dots(ii)\)
Squaring and adding equation (i) and (ii) we get
\(
\begin{array}{l}
\left(\frac{x}{a}+\frac{y}{b}\right)^2+\left(\frac{x}{b}-\frac{y}{a}\right)^2=1+0 \\
\Rightarrow \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{2 x y}{a b}+\frac{x^2}{b^2}+\frac{y^2}{a^2}-\frac{2 x y}{a b}=1 \\
\Rightarrow x^2\left(\frac{1}{a^2}+\frac{1}{b^2}\right)+y^2\left(\frac{1}{b^2}+\frac{1}{a^2}\right)=1 \\
\Rightarrow\left(x^2+y^2\right)\left(\frac{1}{a^2}+\frac{1}{b^2}\right)=1 \\
\Rightarrow\left(x^2+y^2\right)\left(\frac{1}{c^2}\right)=1 \ldots\left[\because \frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{c^2}\right]
\end{array}
\)
\(
\Rightarrow x^2+y^2=c^2
\)

Hint

Given lines are
\(
\begin{array}{l}
a x+2 y+1=0 \dots(i) \\
b x+3 y+1=0 \dots(ii) \\
c x+4 y+1=0 \dots(iii)
\end{array}
\)
Solving (i) and (ii) by cross-multiplication method, we get
\(
\frac{x}{2-3}=\frac{-y}{a-b}=\frac{1}{3 a-2 b}
\)
So, the point of intersection is \(\left(\frac{1}{2 b-3 a}, \frac{a-b}{2 b-3 a}\right)\)
Since, this point lies on \(c x+4 y+1=0\), then
\(
\begin{aligned}
\quad \frac{c}{2 b-3 a}+\frac{4(a-b)}{2 b-3 a}+1 & =0 \\
\Rightarrow \quad c+4 a-4 b+2 b-3 a & =0 \quad \Rightarrow \quad 2 b=a+c
\end{aligned}
\)
Hence, \(a, b, c\) are in A.P.

Hint

The given points are \((3,-4)\) and \((-2,6),(-3,6)\) and \((9,-18)\).
Slope of the line joining the points \((3,-4)\) and \((-2,6)\)
\(
\begin{array}{l}
m_1=\frac{6+4}{-2-3} \\
=\frac{10}{-5} \\
=-2
\end{array}
\)

Slope of the line joining the points \((-3,6)\) and \((9,-18)\)
\(
\begin{array}{l}
m_2=\frac{-18-6}{9+3} \\
=\frac{-24}{12} \\
=-2
\end{array}
\)

Since \(m_1=m_2=-2\)
So, the lines are parallel and not perpendicular.

Hint

(a) Let \(P\left(x_1, y_1\right)\) be any point on the given line \(x+5 y=13\)
\(
\begin{aligned}
& x_1+5 y_1=13 \\
& 5 y_1=13-x_1 \ldots \text { (i) }
\end{aligned}
\)
Distance of the point \(P\left(x_1, y_1\right)\) from the equation \(12 x-5 y+26=0\)
\(
d=\frac{|A x+B y+C|}{\sqrt{A^2+B^2}}; 2= \pm\left(x_1+1\right)
\)
\(
\text { So } x_1=1 \ldots \text {…(ii) or } x_1=-3 \ldots \text {.. (iii) }
\)
Putting the value in equation (i) we get \(5 y_1=13-1=12\)
\(
y_1=\frac{12}{5}
\)
Putting the value of \(x_1=-3\) in the same equation we get \(5 y_1=13-(-3)=16\)
\(
y_1=\frac{16}{5}
\)
Hence, the required points on the given line are \(\left(1, \frac{12}{5}\right)\) and \(\left(-3, \frac{16}{5}\right)\) and \(-3,165\)
Hence, (a)-(iii)
(b) Let \(P x_1, y_1\) be any point lying in the equation \(x+y=4\)
\(
x_1+y_1=4 \ldots (i)
\)
Now, the distance of the point from the equation is \(d=\frac{|A x+B y+C|}{\sqrt{A^2+B^2}}\)
\(
4 x_1+3 y_1-10= \pm 5
\)
either \(4 x_1+3 y_1-10=5\) or \(4 x_1+3 y_1-10=-5\)
\(4 x_1+3 y_1=15 \dots(ii)\)
or \(4 x_1+3 y_1=5 \dots(iii)\)
From equation i we have \(y_1=4-x_1 \dots(iv)\)
Putting the value of \(y_1\) in equation ii we get \(4 x_1+34-x_1=15\)
\(4 x_1+12-3 x_1=15\); \(x_1=3\) Putting the value of \(x_1\) in equation (iv) we get \(y_1=4-3=1\)
Putting the value of \(y_1\) in equation iii we get \(4 x_1+34-x_1=5\)
\(
4 x_1+12-3 x_1=5, x_1=5-12=-7
\)
Putting the value of \(x_1\) in equation (iv), we get \(y_1=4-(-7)\)
\(y_1=4+7=11\)
Hence, the required points on the given line are \((3,1)\) and \((-7,11)\); Hence, b-i
(c) Given that \(A P=P Q=Q B\) and given points are \(A(-2,5)\) and \(B(3,1)\)
Firstly, we find the slope of the line joining the points \((-2,5)\) and \((3,1)\)
Slope of line joining two points \(=\frac{y_2-y_1}{x_2-x_1}\)
\(
m_{A B}=\frac{1-5}{3-(-2)}=-\frac{4}{3+2}=-\frac{4}{5}
\)
Now equation of line passing through the point \((-2,5) y-5=-4 / 5[x-(-2)]\)
\(5 y-25=-4(x+2)\)
\(4 x+5 y-17=0\) Let \(P\left(x_1, y_1\right)\) and \(Q\left(x_2 y_2\right)\) be any two points on the \(A B\)
\(P\left(x_1, y_1\right)\) divides the line \(A B\) in the ratio \(1: 2\)
\(
\begin{aligned}
& x_1=\frac{1 \times 3+2 \times (-2)}{1+2}=\frac{3-4}{3}=\frac{1}{3} \\
& y_1=\frac{1 \times 1+2 \times 5}{1+2}=\frac{1+10}{3}=\frac{11}{3}
\end{aligned}
\)
Now, \(Q \left( x _2, y _2\right)\) is the midpoint of PB \(x_2=\frac{3+\left(-\frac{1}{3}\right)}{2}=\frac{8}{6}=\frac{4}{3}\)
\(
y_2=\frac{1+113}{2}=\frac{3+11}{6}=\frac{14}{6}=\frac{7}{3}
\)
Hence, the coordinates of \(Q \left( x _2 y _2\right)\) is \((4 / 3,7 / 3)\); Hence, c-ii

Hint

a) Given equation is \((2 x+3 y+4)+\lambda(6 x-y+12)=0\)
\(
\begin{aligned}
& 2 x+3 y+4+6 \lambda x-\lambda y+12 \lambda=0 \\
& (2+6 \lambda) x+(3-\lambda) y+4+12 \lambda=0 \dots(i)
\end{aligned}
\)
If equation \(i\) is parallel to \(y\)-axis, then \(3-\lambda=0\)
\(
\lambda=3
\)
Hence, iv.
b) Given equation is \(2 x+3 y+4+\lambda 6 x-y+12=0\)
\(
\begin{aligned}
& 2 x+3 y+4+6 \lambda x-\lambda y+12 \lambda=0 \\
& (3-\lambda) y=-4-12 \lambda-(2+6 \lambda) x \\
& y=-\left(\frac{2+6 \lambda}{3-\lambda}\right) x+(-1)\left(\frac{4+12 \lambda}{3-\lambda}\right)
\end{aligned}
\)
Since, the above equation is in \(y=m x+b\) form
So the slope of equation (i) is \(m_1=-\left(\frac{2+6 \lambda}{3-\lambda}\right)\)
Now the second equation is \(7 x+y-4=0 \dots(ii)\)
\(
y=-7 x+4
\)
So, the slope of equation (ii) is \(m_2=-7\)
Now equation i is perpendicular to equation (ii)
\(
m_1 m_2=-1
\)
\(
\begin{aligned}
& -\left(\frac{2+6 \lambda}{3-\lambda}\right) *(-7)=-1 \\
& (2+6 \lambda) \star 7=-(3-\lambda)
\end{aligned}
\)
On solving we get \(\lambda=-17 / 41\)
Hence, (b)-(iii)
c) Given equation is \((2 x+3 y+4)+\lambda(6 x-y+12)=0\)
If the above equation passes through the point \((1,2)\) then \([2 \times 1+3 \times 2+4]+\lambda[6 \times 1-2+12]=0\)
\(
\begin{aligned}
& 2+6+4+\lambda(6+10)=0 \\
& 12+16 \lambda=0 \\
& 12=-16 \lambda \\
& \lambda=-12 / 16=-3 / 4
\end{aligned}
\)
Hence, (c)-(i)
d) Given equation is \((2 x+3 y+4)+\lambda(6 x-y+12)=0\)
\(
\begin{aligned}
& 2 x+3 y+4+6 \lambda x-\lambda y+12 \lambda=0 \\
& (2+6 \lambda) x+(3-\lambda) y+4+12 \lambda=0 .
\end{aligned}
\)
If equation (i) is parallel to \(x\) axis, then \(2+6 \lambda=0 \quad 6 \lambda=-2\)
\(
\lambda=-1 / 3
\)
(d)-(ii)

Hint

(a) Given equations are \(2 x-3 y=0 \dots(i)\)
And \(4 x-5 y=2 \dots(ii)\)
Equations of line passing through eq. (i) and (ii) we get
\(
(2 x-3 y)+k(4 x-5 y-2)=0 \dots(iii)
\)
If equation (iii) passes through \((2,1)\), we get
\(
(2 \times 2-3 \times 1)+k(4 \times 2-5 \times 1-2)=0
\)
\(
\Rightarrow k =-1
\)
So, the required equation is
\(
\Rightarrow x-y-1=0
\)
(b) Equation of any line passing through the point of intersection of the line \(2 x-3 y=0\) and \(4 x-5 y=2\) is
\(
\begin{aligned}
& (2 x -3 y )+ k (4 x -5 y -2)=0 \dots(i)\\
& \Rightarrow(2+4 k ) x +(-3-5 k ) y -2 k =0 \\
& \text { Slope }=\frac{-(2+4 k)}{-3-5 k}=\frac{2+4 k}{3+5 k}
\end{aligned}
\)
Slope of the given line \(x+2 y+1=0\) is \(-\frac{1}{2}\).
If they are perpendicular to each other then
\(
-\frac{1}{2}\left(\frac{2+4 k}{3+5 k}\right)=-1
\)
\(
\Rightarrow k =\frac{-2}{3}
\)
\(
\text { Putting the value of } k \text { is eq. (i) we get }
\)
\(
\Rightarrow 2 x-y=4
\)
(c) Given equations are
\(
\begin{aligned}
& 2 x-3 y=0 \dots(i) \\
& 4 x-5 y=2 \dots(ii)
\end{aligned}
\)
Equation of line passing through equation (i) and (ii) we get
\(
\begin{aligned}
& (2 x-3 y)+k(4 x-5 y-2)=0 \\
& \Rightarrow(2+4 k) x+(-3-5 k) y-2 k=0
\end{aligned}
\)
Slope \(=\frac{-(2+4 k)}{-3-5 k}=\frac{2+4 k}{3+5 k}\)
Slope of the given line \(3 x-4 y+5=0\) is \(\frac{3}{4}\).
If the two equations are parallel, then
\(
\begin{aligned}
& \frac{2+4 k}{3+5 k}=\frac{3}{4} \\
& \Rightarrow 8+16 k=9+15 k \\
& \Rightarrow 16 k-15 k=9-8 \\
& \Rightarrow k=1
\end{aligned}
\)
So, the equation of the required line is
\(
\Rightarrow 3 x-4 y-1=0
\)
(d) Given equations are
\(
\begin{aligned}
& 2 x-3 y=0 \\
& 4 x-5 y-2=0
\end{aligned}
\)
Equation of line passing through the intersection of equation (i) and (ii) we get
\(
\begin{aligned}
& (2 x-3 y)+k(4 x-5 y-2)=0 \\
& \Rightarrow(2+4 k) x+(-3-5 k) y-2 k=0
\end{aligned}
\)
Slope \(=\frac{2+4 k}{3+5 k}\)
Since the equation is equally inclined with axes
\(
\begin{aligned}
& \therefore \text { Slope }=\tan 135^{\circ}=\tan \left(180^{\circ}-45^{\circ}\right) \\
& =-\tan 45^{\circ}=-1
\end{aligned}
\)
So \(\frac{2+4 k}{3+5 k}=-1\)
\(
\Rightarrow 2+4 k =-3-5 k
\)
\(
\begin{aligned}
& \Rightarrow 4 k +5 k =-3-2 \\
& \Rightarrow 9 k =-5 \\
& \Rightarrow k =\frac{-5}{9}
\end{aligned}
\)
\(
\text { Required equation is }(2 x-3 y)-\frac{5}{0}(4 x-5 y-2)=0
\)
\(
\Rightarrow x+y-5=0
\)