NCERT Exemplar MCQs

Hint

Given that \(a_1=a\) and \(S _p=0\)
Sum of next \(q\) terms of the given A.P. \(= S _{p+q}- S _p\)
\(
\begin{aligned}
& \therefore \quad S _{p+q}=\frac{p+q}{2}[2 a+(p+q-1) d] \\
& \text { and } \quad S _p=\frac{p}{2}[2 a+(p-1) d]=0 \\
& \Rightarrow \quad 2 a+(p-1) d=0 \Rightarrow(p-1) d=-2 a \\
& \Rightarrow \quad d=\frac{-2 a}{p-1} \\
&
\end{aligned}
\)
Sum of next \(q\) terms \(= S _{p+q}- S _p\)
\(
\begin{aligned}
& =\frac{p+q}{2}[2 a+(p+q-1) d]-0 \\
& =\frac{p+q}{2}\left[2 a+(p+q-1)\left(\frac{-2 a}{p-1}\right)\right] \\
& =\frac{p+q}{2}\left[2 a+\frac{(p-1)(-2 a)}{p-1}-\frac{2 a q}{p-1}\right] \\
& =\frac{p+q}{2}\left[2 a-2 a-\frac{2 a q}{p-1}\right]=\frac{(p+q)}{2}\left(\frac{-2 a q}{p-1}\right) \\
& =\frac{-a(p+q) q}{p-1} \quad-a(p+q) q
\end{aligned}
\)
Hence, the required sum \(=\frac{-a(p+q) q}{p-1}\)

Hint

Let \(₹ x\) be saved in first year.
Annual increment \(=₹ 200\), which forms an A.P.
first term \(=a\) and common difference \(d=200\) \(n=20\) years
\(
\therefore \quad S _n=\frac{n}{2}[2 a+(n-1) d] \Rightarrow S _{20}=\frac{20}{2}[2 a+(20-1) 200]
\)
\(
\begin{aligned}
66000 & =10[2 a+3800] \Rightarrow 6600=2 a+3800 \\
2 a & =6600-3800 \Rightarrow 2 a=2800 \Rightarrow a=1400
\end{aligned}
\)

Hint

Given that fixed increment in the salary of a man
\(
=₹ 320 \text { each month }
\)
Initial salary \(=₹ 5200\) which makes an A.P.
whose first term \((a)=₹ 5200\) and common difference \((d)=₹ 320\)
(i) Salary for the tenth month
\(
\begin{aligned}
a_{10} & =a+(n-1) d \\
& =5200+(10-1) \times 320=5200+2880=₹ 8080
\end{aligned}
\)
(ii) Total earning during the first year ( 12 months)
\(
S_{12}=\frac{12}{2}[2 \times 5200+(12-1) \times 320] \left[\because \quad S _n=\frac{n}{2}[2 a+(n-1) d]\right]
\)
\(
=6[10400+3520]=6 \times 13920=₹ 83520
\)
Hence, the required amount is (i) ₹ 8080 (ii) ₹ 83520 .

Hint

Let the first term and common ratio of G.P. be \(a\) and \(r\), respectively.
Given that, \(p\) th term \(=q \quad \Rightarrow a r^{p-1}=q \dots(i)\)
\(
\text { and } \quad q \text { th term }=p \Rightarrow a r^{q-1}=p \dots(ii)
\)
On dividing Eq. (i) by Eq. (ii), we get
\(
\frac{a r^{p-1}}{a r^{q-1}}=\frac{q}{p} \Rightarrow r^{p-q}=\frac{q}{p} \Rightarrow r=\left(\frac{q}{p}\right)^{\frac{1}{p-q}}
\)
On substituting the value of \(r\) in Eq. (i), we get
\(
a\left(\frac{q}{p}\right)^{\frac{p-1}{p-q}}=q \Rightarrow a=q\left(\frac{p}{q}\right)^{\frac{p-1}{p-q}}
\)
\(
\begin{aligned}
(p+q) \text { th term, } T_{p+q} & = a \cdot p^{p+q-1} \\
& =q\left(\frac{p}{q}\right)^{\frac{p-1}{p-q}}\left(\frac{q}{p}\right)^{\frac{p+q-1}{p-q}}=q\left(\frac{p}{q}\right)^{\frac{p-1}{p-q}-\frac{p+q-1}{p-q}} \\
& =q\left(\frac{q}{p}\right)^{\frac{q}{p-q}}=\frac{q^{\frac{q}{p-q}+1}}{p^{\frac{q}{p-q}}}=\frac{q^{\frac{p}{p-q}}}{p^{\frac{q}{p-q}}}=\left(\frac{q^p}{p^q}\right)^{\frac{1}{p-q}}
\end{aligned}
\)

Hint

Here, \(a=5\) and \(d=2\)
Let the carpenter finish the job in \(n\) days. Then, \(S_n=192\)
\(
192=\frac{n}{2}[2 a+(n-1) d] \Rightarrow 192=\frac{n}{2}[2 \times 5+(n-1) 2]
\)
\(
\begin{aligned}
& 192=n[5+n-1] \Rightarrow n^2+4 n-192=0 \quad \Rightarrow \quad(n-12)(n+16)=0 \\
& n=12
\end{aligned}
\)

Hint

We know that, sum of interior angles of a polygon of side \(n\) is \((n-2) \times 180^{\circ}\).
Let \(t_n=(n-2) \times 180^{\circ}\)
Since \(t_n\) is linear in \(n\), it is \(n\)th term of some A.P.
\(
t_3=a=(3-2) \times 180^{\circ}=180^{\circ}
\)
Common difference, \(d=180^{\circ}\)
Sum of the interior angles for a 21 sided polygon is:
\(
t_{21}=(21-2) \times 180^{\circ}=3420^{\circ}
\)

Hint

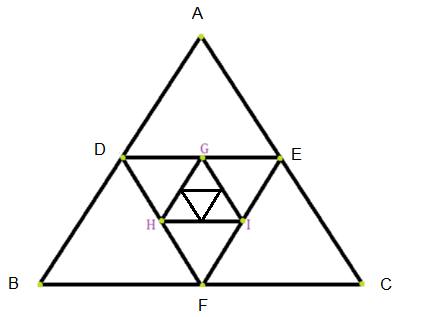
The side of the first equilateral \(\triangle ABC =20 cm\)
By joining the mid points of the sides of this triangle, we get the second equilateral triangle which each side \(=\frac{20}{2}=10 cm\)
\([\because \quad\) The line joining the mid-points of two sides of a triangle is \(1 / 2\) and parallel to third side of the triangle]
Similarly each side of the third equilateral triangle \(=\frac{10}{2}=5 cm\)
\(\therefore\) Perimeter of first triangle \(=20 \times 3=60 cm\)
Perimeter of the second triangle \(=10 \times 3=30 cm\)
and the perimeter of the third triangle \(=5 \times 3=15 cm\)
Therefore, the series will be \(60,30,15, \ldots\)
which is G.P. in which \(a=60\), and \(r=\frac{30}{60}=\frac{1}{2}\)
Now, we have to find the perimeter of the sixth inscribed equilateral triangle
\(
\begin{aligned}
\therefore \quad a_6 & =a r^{6-1} \\
& =60 \times\left(\frac{1}{2}\right)^5=60 \times \frac{1}{32}=\frac{15}{8} cm
\end{aligned}
\)
Hence, the required perimeter \(=\frac{15}{8} cm\)

Hint

We have,
the distance travelled to bring the first potato, \(a_1=2 \times 24=48 m\), the distance travelled to bring the second potato, \(a_2=2 \times(24+4)=56 m\), the distance travelled to bring the third potato, \(a_3=2 \times(24+4+4)=64 m\),
As, \(a_2-a_1=56-48=8\) and \(a_3-a_2=64-56=8\) i. e. \(a_2-a_1=a_3-a_2\)
So, \(a_1, a_2, a_3, \ldots\) are in A.P.
Also, \(a=48, d=8, n=20\)
Now,
\(
\begin{aligned}
& S_{20}=\frac{20}{2}[2 a+(20-1) d] \\
& =10[2 \times 48+19 \times 8] \\
& =10 \times(96+152) \\
& =10 \times 248 \\
& =2480
\end{aligned}
\)

Hint

Let the prize amount got by first place team be \(₹ a\)
Since, the prize money increases by the same amount for successive finishing places, therefore the series will be A.P.
\(
\therefore \quad \begin{aligned}
a_n & =275, n=16 \text { and } S _{16}=8000 \\
a_n & =a+(n-1) d \\
275 & =a+(16-1)(-d)
\end{aligned}
\)
\([\because\) Common difference \(d\) is \((-)\) as the series is decreasing \(]\)
\(
\Rightarrow \quad 275=a-15 d \dots(i)
\)
Now
\(
\begin{aligned}
S _n & =\frac{n}{2}[2 a+(n-1) d] \\
S _{16} & =\frac{16}{2}[2 a+15(-d)]
\end{aligned}
\)
\(
\Rightarrow \quad 8000=8[2 a-15 d] \Rightarrow 2 a-15 d=1000 \dots(ii)
\)
Solving eq. (i) and eq. (ii) we get
\(
a=725 \text { and } d=30
\)
Hence, the required award received by first place term \(=₹ 725\).

Hint

Given that \(a_1, a_2, a_3, a_4, \ldots, a_n\) are in A.P.
\(\therefore\) Common difference \(d=a_2-a_1=a_3-a_2=a_4-a_3=\ldots=a_n-a_{n-1}\)
\(
\begin{aligned}
& \text { If } a_2-a_1=d \text { then } \sqrt{a_2^2}-\sqrt{a_1^2}=d \\
& \Rightarrow \quad\left(\sqrt{a_2}-\sqrt{a_1}\right)\left(\sqrt{a_2}+\sqrt{a_1}\right)=d \quad\left[\because \quad a^2-b^2=(a+b)(a-b)\right]
\end{aligned}
\)
\(
\frac{1}{\sqrt{a_1}+\sqrt{a_2}}=\frac{\sqrt{a_2}-\sqrt{a_1}}{d}
\)
Similarly
\(
\frac{1}{\sqrt{a_2}+\sqrt{a_3}}=\frac{\sqrt{a_3}-\sqrt{a_2}}{d}
\)
\(
\begin{array}{cc}
\frac{1}{\sqrt{a_3}+\sqrt{a_4}}= & \frac{\sqrt{a_4}-\sqrt{a_3}}{d} \\
\cdots & \cdots \\
\frac{1}{\sqrt{a_{n-1}}+\sqrt{a_n}}= & \frac{\sqrt{a_n}-\sqrt{a_{n-1}}}{d}
\end{array}
\)
Adding the above terms, we get
\(
\frac{1}{\sqrt{a_1}+\sqrt{a_2}}+\frac{1}{\sqrt{a_2}+\sqrt{a_3}}+\frac{1}{\sqrt{a_3}+\sqrt{a_4}}+\cdots+\frac{1}{\sqrt{a_{n-1}}+\sqrt{a_n}}
\)
\(
\begin{gathered}
=\frac{1}{d}\left[\sqrt{a_2}-\sqrt{a_1}+\sqrt{a_3}-\sqrt{a_2}+\sqrt{a_4}-\sqrt{a_3}+\cdots \sqrt{a_n}-\sqrt{a_{n-1}}\right] \\
=\frac{1}{d}\left[\sqrt{a_n}-\sqrt{a_1}\right] \dots(i)
\end{gathered}
\)
\(
\begin{aligned}
& \text { Now } \quad a_n=a_1+(n-1) d \\
& \Rightarrow \quad a_n-a_1=(n-1) d \\
& \Rightarrow \quad \sqrt{a_n^2}-\sqrt{a_1^2}=(n-1) d \\
& \Rightarrow \quad\left(\sqrt{a_n}+\sqrt{a_1}\right)\left(\sqrt{a_n}-\sqrt{a_1}\right)=(n-1) d \\
& \Rightarrow \quad \sqrt{a_n}-\sqrt{a_1}=\frac{(n-1) d}{\sqrt{a_n}+\sqrt{a_1}} \\
& \Rightarrow \quad \frac{\sqrt{a_n}-\sqrt{a_1}}{d}=\frac{n-1}{\sqrt{a_n}+\sqrt{a_1}} \dots(ii)\\
&
\end{aligned}
\)
From Eq. (i) and eq. (ii) we get
\(
\begin{aligned}
& \frac{1}{\sqrt{a_1}+\sqrt{a_2}}+\frac{1}{\sqrt{a_2}+\sqrt{a_3}}+\frac{1}{\sqrt{a_3}+\sqrt{a_4}} \\
& +\cdots+\frac{1}{\sqrt{a_{n-1}}+\sqrt{a_n}}=\frac{n-1}{\sqrt{a_n}+\sqrt{a_1}}
\end{aligned}
\)

Hint

Given series
\(
\Rightarrow \quad\left(3^3-2^3\right)+\left(5^3-4^3\right)+\left(7^3-6^3\right)+\cdots
\)
\(
=\left(3^3+5^3+7^3+\cdots\right)-\left(2^3+4^3+6^3+\cdots\right)
\)
\(
\Rightarrow\left[3^3+5^3+7^3+\ldots(2 n+1)^3\right]-\left[2^3+4^3+6^3+\cdots(2 n)^3\right]
\)
\(
\begin{aligned}
& \therefore \quad T _n=(2 n+1)^3-(2 n)^3 \\
& =(2 n+1-2 n)\left[(2 n+1)^2+(2 n+1)(2 n)+(2 n)^2\right] \\
& {\left[\because a^3-b^3=(a-b)\left(a^2+a b+b^2\right)\right]} \\
& =1 \cdot\left[4 n^2+1+4 n+4 n^2+2 n+4 n^2\right] \\
& =12 n^2+6 n+1 \\
&
\end{aligned}
\)
(i)
\(
\begin{aligned}
S _n & =\sum T _n=12 \sum n^2+6 \sum n+n \\
& =12 \cdot \frac{n(n+1)(2 n+1)}{6}+\frac{6 n(n+1)}{2}+n \\
& =2 n(n+1)(2 n+1)+3 n(n+1)+n \\
& =n[2(n+1)(2 n+1)+3(n+1)+1] \\
& =n\left[2\left(2 n^2+3 n+1\right)+3 n+3+1\right] \\
& =n\left[4 n^2+6 n+2+3 n+4\right]=n\left[4 n^2+9 n+6\right] \\
& =4 n^3+9 n^2+6 n
\end{aligned}
\)
(ii)
\(
\begin{aligned}
S _{10} & =4(10)^3+9(10)^2+6(10)=4 \times 1000+900+60 \\
& =4000+960=4960
\end{aligned}
\)

Hint

\(
\text { [Hint: } a_n= S _n- S _{n-1} \text { ] }
\)
\(
\begin{array}{ll}
\text { Given that } & S _n=2 n+3 n^2 \\
\Rightarrow & S _1=2 \times 1+3(1)^2=5 \\
\Rightarrow & S _2=2 \times 2+3 \times 4=16 \\
\Rightarrow & S _3=2 \times 3+3 \times 9=33
\end{array}
\)
\(
\begin{aligned}
S_1 & =a_1=5 \\
S_2-S_1 & =a_2=16-5=11 \\
d & =a_2-a_1=11-5=6
\end{aligned}
\)
Now
\(
\begin{aligned}
T _r & =a_1+(r-1) d \\
& =5+(r-1) 6=5+6 r-6=6 r-1
\end{aligned}
\)
Hence, the required \(r\) th term is \(6 r-1\)

Hint

Let the numbers be \(a\) and \(b\).
Then, \(A=\frac{a+b}{2}\) or \(2 A=a+b \dots(i)\)
Also, \(G_1\) and \(G_2\) are geometric means between \(a\) and \(b\), then \(a, G_1, G_2, b\) are in G.P.
Let \(r\) be the common ratio.
Then, \(b=a r^{4-1}=a r^3 \Rightarrow \frac{b}{a}=r^3 \Rightarrow r=\left(\frac{b}{a}\right)^{1 / 3}\)
\(
\begin{array}{ll}
\therefore & G_1=a r=a\left(\frac{b}{a}\right)^{1 / 3}=a^{2 / 3} b^{1 / 3} \\
\text { and } & G_2=a r^2=a\left(\frac{b}{a}\right)^{2 / 3}=a^{1 / 3} b^{2 / 3} \\
\therefore & \frac{G_1^2}{G_2}+\frac{G_2^2}{G_1}=\frac{G_1^3+G_2^3}{G_1 G_2}=\frac{a^2 b+a b^2}{a b}=a+b=2 A
\end{array}
\)

Hint

Since \(\theta_1, \theta_2, \theta_3, \ldots, \theta_n\) are in A.P., we get
\(
\theta_2-\theta_1=\theta_3-\theta_2=\ldots=\theta_n-\theta_{n-1}=d \dots(i)
\)
Now,
\(
\begin{aligned}
\sec \theta_1 \sec \theta_2 & =\frac{1}{\sin d} \cdot \frac{\sin d}{\cos \theta_1 \cos \theta_2}=\frac{1}{\sin d} \cdot \frac{\sin \left(\theta_2-\theta_1\right)}{\cos \theta_1 \cos \theta_2} \\
& =\frac{1}{\sin d} \cdot \frac{\left(\sin \theta_2 \cos \theta_1-\cos \theta_2 \sin \theta_1\right)}{\cos \theta_1 \cos \theta_2}=\frac{\tan \theta_2-\tan \theta_1}{\sin d}
\end{aligned}
\)
Similarly, \(\sec \theta_2 \sec \theta_3=\frac{\tan \theta_3-\tan \theta_2}{\sin d} ; \sec \theta_3 \sec \theta_4=\frac{\tan \theta_4-\tan \theta_3}{\sin d}\); and so on.
\(
\therefore \quad \sec \theta_1 \sec \theta_2+\sec \theta_2 \sec \theta_3+\ldots+\sec \theta_{n-1} \sec \theta_n=\frac{\tan \theta_n-\tan \theta_1}{\sin d}
\)

Hint

Let first term and common difference of the A.P. be a and \(d\), respectively. Given, \(S_p=q\)
\(
\frac{p}{2}[2 a+(p-1) d]=q \quad \Rightarrow \quad 2 a+(p-1) d=\frac{2 q}{p} \dots(i)
\)
Also, \(S_q=p\)
\(
\Rightarrow \quad \frac{q}{2}[2 a+(q-1) d]=p \quad \Rightarrow \quad 2 a+(q-1) d=\frac{2 p}{q} \dots(ii)
\)
On subtracting Eq. (ii) from Eq. (i), we get
\(
(p-q) d=\frac{2 q}{p}-\frac{2 p}{q} \text { or }(p-q) d=\frac{2\left(q^2-p^2\right)}{p q}
\)
\(
\therefore \quad d=\frac{-2(p+q)}{p q} \dots(iii)
\)
On substituting the value of \(d[latex] into Eq. (i), we get
[latex]
\begin{array}{ll}
& 2 a+(p-1)\left(\frac{-2(p+q)}{p q}\right)=\frac{2 q}{p} \\
\Rightarrow & a=\frac{q}{p}+\frac{(p+q)(p-1)}{p q} \dots(iv)
\end{array}
\)
Now
\(
\begin{aligned}
S_{p+q} & =\frac{p+q}{2}[2 a+(p+q-1) d] \\
& =\frac{p+q}{2}\left[\frac{2 q}{p}+\frac{2(p+q)(p-1)}{p q}-\frac{2(p+q-1)(p+q)}{p q}\right] \\
& =(p+q)\left[\frac{q}{p}+\frac{(p+q)(p-1-p-q+1)}{p q}\right] \\
& =(p+q)\left[\frac{q}{p}+\frac{(p+q)(-q)}{p q}\right] \\
& =(p+q)\left[\frac{q}{p}-\frac{p+q}{p}\right]=-(p+q)
\end{aligned}
\)
Also,
\(
\begin{aligned}
S_{p-q} & =\frac{p-q}{2}[2 a+(p-q-1) d] \\
& =\frac{p-q}{2}\left[\frac{2 q}{p}+\frac{2(p+q)(p-1)}{p q}-\frac{(p-q-1) 2(p+q)}{p q}\right] \\
& =(p-q)\left[\frac{q}{p}+\frac{(p+q)(p-1-p+q+1)}{p q}\right] \\
& =(p-q)\left[\frac{q}{p}+\frac{(p+q) q}{p q}\right] \\
& =(p-q)\left[\frac{q}{p}+\frac{p+q}{p}\right]=(p-q) \frac{(p+2 q)}{p}
\end{aligned}
\)

Hint

Let \(A\) and \(d\) be the first term and common difference of \(A\).P., respectively. Also, let \(B\) and \(R\) be the first term and common ratio of G.P., respectively.
It is given that,
\(
\begin{aligned}
& A+(p-1) d=a \dots(i) \\
& A+(q-1) d=b \dots(ii) \\
& A+(r-1) d=c \dots(iii)
\end{aligned}
\)
Also,
\(
\begin{aligned}
& a=B R^{p-1} \dots(iv) \\
& b=B R^{q-1} \dots(v) \\
& c=B R^{r-1} \dots(vi)
\end{aligned}
\)
On subtracting Eq. (ii) from Eq. (i), we get
\(
a-b=d(p-q)
\)
On subtracting Eq. (iii) from Eq. (ii), we get
\(
b-c=d(q-r)
\)
On subtracting Eq. (i) from Eq. (iii), we get
\(
c-a=d(r-p)
\)
\(
\therefore \quad a^{b-c} \cdot b^{c-a} \cdot c^{a-b}
\)
\(
=\left(B R^{(p-1)}\right)^{d(q-r)}\left(B R^{(q-1)}\right)^{d(r-p)}\left(B R^{(r-1)}\right)^{d(p-q)}
\)
\(
=B^{d[(q-r)+(r-p)+(p-q)]} R^{d[(p-1)(q-r)+(q-1)(r-p)+(r-1)(p-q)]}
\)
\(
=B^0 R^0=1
\)

Hint

Given that
\(
\text { hat } \begin{aligned}
S _n & =3 n+2 n^2 \\
S _1 & =3(1)+2(1)^2=5 \\
S _2 & =3(2)+2(4)=14 \\
S _1 & =a_1=5 \\
S _2- S _1 & =a_2=14-5=9
\end{aligned}
\)
\(\therefore\) Common difference \(d=a_2-a_1=9-5=4\)

Hint

\(
\begin{aligned}
\text { Given that } & T _3 & =4 \\
\Rightarrow & a r^{3-1} & =4 \left[\because \quad T _n=a r^{n-1}\right] \\
\Rightarrow & a r^2 & =4
\end{aligned}
\)
Product of first 5 terms \(=a \cdot a r \cdot a r^2 \cdot a r^3 \cdot a r^4\)
\(
=a^5 r^{10}=\left(a r^2\right)^5=(4)^5
\)

Hint

Let the first term and common difference of given A.P. be a and d, respectively.
\(
\begin{aligned}
& & T _n & =a+(n-1) d \\
\therefore & & T _9 & =a+8 d \\
\text { and } & & T _{13} & =a+12 d
\end{aligned}
\)
As per the given condition
\(
\begin{aligned}
& & 9[a+8 d] & =13[a+12 d] \\
\Rightarrow & & 9 a+72 d & =13 a+156 d \Rightarrow-4 a=84 d \\
\Rightarrow & & a & =-21 d \dots(i)
\end{aligned}
\)
Now \(\quad T _{22}=a+21 d=-21 d+21 d=0 \quad\) [from eq. (i)]

Hint

Since \(x, 2 y, 3 z\) are in A.P.
\(
\begin{aligned}
\therefore & 2 y-x & =3 z-2 y \\
\Rightarrow & 4 y & =x+3 z \dots(i)
\end{aligned}
\)
Now \(x, y, z\) are in G.P.
\(\therefore \quad\) Common ratio \(r=\frac{y}{x}=\frac{z}{y} \dots(ii)\)
\(
\therefore \quad y^2=x z
\)
putting the value of \(x\) from eq. (i), we get
\(
\begin{aligned}
& y^2=(4 y-3 z) z \Rightarrow y^2=4 y z-3 z^2 \\
& \Rightarrow \quad 3 z^2-4 y z+y^2=0 \quad \Rightarrow \quad 3 z^2-3 y z-y z+y^2=0 \\
& \Rightarrow 3 z(z-y)-y(z-y)=0 \quad \Rightarrow \quad(3 z-y)(z-y)=0 \\
& \Rightarrow \quad 3 z-y=0 \text { and } z-y=0 \\
& \Rightarrow \quad 3 z=y \text { and } z \neq y [\because \quad z \text { and } y \text { are distinct numbers }] \\
&
\end{aligned}
\)
\(
\frac{z}{y}=\frac{1}{3} \Rightarrow r=\frac{1}{3} \quad \text { (from eq. (ii)) }
\)

Hint

The given series is A.P. whose first term is \(a\) and common difference is \(d\)
\(
\begin{array}{rlrl}
\therefore & & S _n & =\frac{n}{2}[2 a+(n-1) d]=q n^2 \\
\Rightarrow & & =2 a+(n-1) d=2 q n \dots(i) \\
& & S _m & =\frac{m}{2}[2 a+(m-1) d]=q m^2 \\
& & 2 a+(m-1) d & =2 q m \dots(ii)
\end{array}
\)
Solving eq. (i) and eq. (ii) we get
\(
\begin{array}{rlr}
2 a+(m-1) d & =\quad 2 q m \\
2 a+(n-1) d & =\quad 2 q n \\
\hline(-) \quad(-) \quad \quad & (-) \\
(m-n) d & =2 q m-2 q n \\
(m-n) d & =2 q(m-n) \\
\therefore \quad d & =2 q
\end{array}
\)
Putting the value of \(d\) in eq. (ii) we get
\(
2 a+(m-1) \cdot 2 q=2 q m \Rightarrow 2 a=2 q m-(m-1) 2 q
\)
\(
\begin{aligned}
2 a & =2 q(m-m+1) \Rightarrow 2 a=2 q \Rightarrow a=q \\
S _q & =\frac{q}{2}[2 a+(q-1) d]=\frac{q}{2}[2 q+(q-1) 2 q] \\
& =\frac{q}{2}\left[2 q+2 q^2-2 q\right]=\frac{q}{2} \times 2 q^2=q^3
\end{aligned}
\)

Hint

\(
\begin{aligned}
S _n & =\frac{n}{2}[2 a+(n-1) d] \\
\therefore \quad S _{2 n} & =\frac{2 n}{2}[2 a+(2 n-1) d] \\
S _{3 n} & =\frac{3 n}{2}[2 a+(3 n-1) d]
\end{aligned}
\)
As per the condition of the question, we have
\(
\begin{array}{rlrl}
& & S _{2 n}=3 \cdot S _n \\
\Rightarrow & & \frac{2 n}{2}[2 a+(2 n-1) d] & =3 \cdot \frac{n}{2}[2 a+(n-1) d] \\
\Rightarrow & & 2[2 a+(2 n-1) d] & =3[2 a+(n-1) d] \\
\Rightarrow & & 4 a+(4 n-2) d & =6 a+(3 n-3) d
\end{array}
\)
\(
\begin{aligned}
6 a+(3 n-3) d-4 a-(4 n-2) d & =0 \\
2 a+(3 n-3-4 n+2) d & =0 \quad \Rightarrow \quad 2 a+(-n-1) d=0
\end{aligned}
\)
\(
2 a-(n+1) d=0 \Rightarrow 2 a=(n+1) d \dots(i)
\)
\(
\begin{aligned}
\text { Now } S _{3 n}: S _n & =\frac{3 n}{2}[2 a+(3 n-1) d]: \frac{n}{2}[2 a+(n-1) d] \\
& =\frac{\frac{3 n}{2}[2 a+(3 n-1) d]}{\frac{n}{2}[2 a+(n-1) d]}=\frac{3[2 a+(3 n-1) d]}{2 a+(n-1) d} \\
& =\frac{3[(n+1) d+(3 n-1) d]}{(n+1) d+(n-1) d}
\end{aligned}
\)
\(
=\frac{3 d[n+1+3 n-1]}{d(n+1+n-1)}=\frac{3[4 n]}{2 n}=6
\)

Hint

We know that \(AM \geq GM\)
\(
\begin{array}{ll}
\therefore & \frac{4^x+4^{1-x}}{2} \geq \sqrt{4^x \cdot 4^{1-x}} \Rightarrow 4^x+4^{1-x} \geq 2 \sqrt{4^{x+1-x}} \\
\Rightarrow & 4^x+4^{1-x} \geq 2 \cdot 2 \Rightarrow 4^x+4^{1-x} \geq 4
\end{array}
\)

Hint

Given that \(\sum_{i=1}^n \frac{ S _r}{ s _r}=\frac{ S _1}{s_1}+\frac{ S _2}{s_2}+\frac{ S _3}{s_3}+\cdots+\frac{ S _n}{s_n}\)
Let \(T _n\) be the \(n\)th term of the above series
\(
\therefore \quad T _n=\frac{ S _n}{s_n}=\frac{\left[\frac{n(n+1)}{2}\right]^2}{\frac{n(n+1)}{2}}=\frac{n(n+1)}{2}=\frac{n^2+n}{2}
\)
Now sum of the given series
\(
\begin{aligned}
\sum T _n & =\frac{1}{2} \sum\left[n^2+n\right]=\frac{1}{2}\left[\sum n^2+\sum n\right] \\
& =\frac{1}{2}\left[\frac{n(n+1)(2 n+1)}{6}+\frac{n(n+1)}{2}\right] \\
& =\frac{1}{2} \cdot \frac{n(n+1)}{2}\left[\frac{2 n+1}{3}+1\right]=\frac{n(n+1)}{4}\left[\frac{2 n+1+3}{3}\right] \\
& =\frac{n(n+1)}{4} \cdot \frac{(2 n+4)}{3}=\frac{n(n+1)(n+2)}{6}
\end{aligned}
\)

Hint

Let \(S _n=2+3+6+11+18+\cdots+t_{50}\)
Using method of difference, we get
\(
\text { and } \quad \begin{aligned}
& S _n=2+3+6+11+18+\cdots+t_{50} \dots(i) \\
& S _n=0+2+3+6+11+\cdots+t_{49}+t_{50} \dots(ii)
\end{aligned}
\)
Subtracting eq. (ii) from eq. (i), we get
\(
\begin{aligned}
& 0=2+1+3+5+7+\cdots-t_{50} \text { terms } \\
& \Rightarrow \quad t_{50}=2+(1+3+5+7+\cdots \text { upto } 49 \text { terms }) \\
& \Rightarrow \quad t_{50}=2+\frac{49}{2}[2 \times 1+(49-1) 2]=2+\frac{49}{2}[2+96] \\
& =2+\frac{49}{2} \times 98=2+49 \times 49=49^2+2 \\
&
\end{aligned}
\)

Hint

Let the length, breadth and height of a rectangular block be \(\frac{a}{r}, a\) and \(a r\). [Since they are is G.P]
\(
\begin{aligned}
\text { Volume } & =l \times b \times h \\
216 & =\frac{a}{r} \times a \times a r \\
a^3 & =216 \Rightarrow a=6
\end{aligned}
\)
Now total surface area \(=2[l b+b h+l h]\)
\(
\begin{aligned}
& 252=2\left[\frac{a}{r} \cdot a+a \cdot a r+\frac{a}{r} \cdot a r\right] \Rightarrow 252=2\left[\frac{a^2}{r}+a^2 r+a^2\right] \\
& 252=2 a^2\left[\frac{1}{r}+r+1\right] \Rightarrow 252=2 \times(6)^2\left[\frac{1+r^2+r}{r}\right] \\
& 252=72\left[\frac{1+r^2+r}{r}\right] \Rightarrow \frac{252}{72}=\frac{1+r+r^2}{r}
\end{aligned}
\)
\(
\begin{aligned}
& \frac{7}{2}=\frac{1+r+r^2}{r} \Rightarrow 2+2 r+2 r^2=7 r \\
& 2 r^2-5 r+2=0 \Rightarrow 2 r^2-4 r-r+2=0 \\
& 2 r(r-2)-1(r-2)=0 \quad \Rightarrow \quad(r-2)(2 r-1)=0
\end{aligned}
\)
\(
\begin{array}{rlrl}
\Rightarrow & r-2 & =0 \text { and } & 2 r-1=0 \\
\therefore & r & =2, \frac{1}{2}
\end{array}
\)
Therefore, the three edge are:
If \(r=2\) then edges are \(3,6,12\)
If \(r=\frac{1}{2}\) then edges are \(12,6,3\)
So, the length of the longest edge \(=12\)

Hint

Since \(a, b\) and \(c\) are in G.P \(\therefore \quad \frac{b}{a}=\frac{c}{b}=r \quad\) (constant)
\(
\begin{array}{lrl}
\Rightarrow & b=a r \text { and } c=b r \Rightarrow c=a r \cdot r=a r^2 \\
\text { So } & \frac{a-b}{b-c}=\frac{a-a r}{a r-a r^2}=\frac{a(1-r)}{a r(1-r)}=\frac{1}{r}=\frac{a}{b}=\frac{b}{c}
\end{array}
\)
Hence, the correct value of the filler is \(\frac{a}{b}\) or \(\frac{b}{c}\)

Hint

Let A.P be \(a, a+d, a+2 d, a+3 d, \ldots, a+(n-1) d\)
Taking first and last term
\(
a_1+a_n=a+a+(n-1) d=2 a+(n-1) d
\)
Taking second and second last term
\(
a_2+a_{n-1}=(a+d)+[a+(n-2) d]=2 a+(n-1) d=a_1+a_n
\)
Taking third from the beginning and the third from the end
\(
a_3+a_{n-2}=(a+2 d)+[a+(n-3) d]=2 a+(n-1) d=a_1+a_n
\)
From the above pattern, we observe that the sum of terms equidistant from the beginning and the end in an A.P is equal to the [first term + last term]
Hence, the correct value of the filler is first term + last term.

Hint

\(
\begin{array}{lr}
\text { Given } & T _3=4 \\
\therefore & a r^2=4 \dots(i)
\end{array}
\)
Product of first five terms \(=a \cdot a r \cdot a r^2 \cdot a r^3 \cdot a r^4\)
\(=a^5 r^{10}=\left(a r^2\right)^5=(4)^5\) [from eq. (i)]
Hence, the correct value of the fillter is \((4)^5\).

Hint

Let us consider a G.P, \(a, a r\) and \(a r^2\)
If it is in A.P then \(a r-a \neq a r^2-a r\)
Hence, the given statement is True.

Hint

Let us consider a sequence of prime numbers \(2,3,5,7,11, \ldots\) It is clear that this progression is a sequence but sequence is not a progression because it does not follow a specific pattern. Here, the given statement is True.

Hint

Let us consider an A.P \(a, a+d, a+2 d, \ldots\)
\(
\begin{aligned}
& \therefore \quad a_2+a_4=a+d+a+3 d=2 a+4 d=2 a_3 \\
& \Rightarrow \quad a_3=\frac{a_2+a_4}{2} \\
& \frac{a_3+a_5}{2}=\frac{a+2 d+a+4 d}{2}=\frac{2 a+6 d}{2} \\
& \Rightarrow \quad=a+3 d=a_4 \\
&
\end{aligned}
\)
Hence, the given statement is True.

Hint

Let us consider two G.P.’s
\(
\begin{aligned}
& a_1, a_1 r_1, a_1 r_1^2, a_1 r_1^3 \cdots a_1 r_1^{n-1} \\
\text { and } & a_2, a_2 r_2, a_2 r_2^2, a_2 r_2^3, \cdots a_2 r_2^{n-1}
\end{aligned}
\)
Now Sum of two G.Ps
\(
\left(a_1+a_2\right)+\left(a_1 r_1+a_2 r_2\right)+\left(a_1 r_1^2+a_2 r_2^2\right) \cdots
\)
Now
\(
\frac{T_2}{T_1}=\frac{a_1 r_1+a_2 r_2}{a_1+a_2} \text { and } \frac{T_3}{T_2}=\frac{a_1 r_1^2+a_2 r_2^2}{a_1 r_1+a_2 r_2}
\)
But \(\frac{a_1 r_1+a_2 r_2}{a_1+a_2} \neq \frac{a_1 r_1^2+a_2 r_2^2}{a_1 r_1+a_2 r_2}\)
Now let us consider the difference G.P’s
\(
\begin{aligned}
& \left(a_1-a_2\right)+\left(a_1 r_1-a_2 r_2\right)+\left(a_1 r_1^2-a_2 r_2^2\right) \\
& \therefore \quad \frac{T_2}{T_1}=\frac{a_1 r_1-a_2 r_2}{a_1-a_2} \text { and } \frac{T_3}{T_2}=\frac{a_1 r_1^2-a_2 r_2^2}{a_1 r_1-a_2 r_2} \\
& \text { But } \quad \frac{T_2}{T_1} \neq \frac{T_3}{T_2}
\end{aligned}
\)
Hence, the given statement is False.

Hint

Let \(\quad S _n=a n^2+b n+c \quad\) (quadratic expression)
\(
S _1=a+b+c
\)
\(
\begin{aligned}
& a_1=a+b+c \\
& S _2=4 a+2 b+c \\
& a_2= S _2- S _1=(4 a+2 b+c)-(a+b+c)=3 a+b \\
& S _3=9 a+3 b+c \\
& a_3= S _3- S _2=(9 a+3 b+c)-(4 a+2 b+c)=5 a+b
\end{aligned}
\)
Common difference
\(
\begin{aligned}
d & =a_2-a_1=(3 a+b)-(a+b+c) \\
& =2 a-c \\
\text { and } d & =a_3-a_2=(5 a+b)-(3 a+b)=2 a
\end{aligned}
\)
Here, we observe that \(a_2-a_1 \neq a_3-a_2\)
So it does not represent an A.P
Hence, the given statement is False.

Hint

(a) \(4,1, \frac{1}{4}, \frac{1}{16}\)
Here, \(\frac{a_2}{a_1}=\frac{1}{4}, \frac{a_3}{a_2}=\frac{1 / 4}{1}=\frac{1}{4}\) and \(\frac{a_4}{a_3}=\frac{1 / 16}{1 / 4}=\frac{1}{4}\)
Hence it is G.P
\(\therefore \quad(a) \leftrightarrow(i i i)\)
(b) \(2,3,5,7\)
\(
\begin{aligned}
& \text { Here } \quad a_2-a_1=3-2=1 \\
& a_3-a_2=5-3=2 \\
& \therefore \quad a_2-a_1 \neq a_3-a_2 \\
&
\end{aligned}
\)
Hence it is not A.P
\(
\frac{a_2}{a_1}=\frac{3}{2}, \frac{a_3}{a_2}=\frac{5}{3}
\)
So, \(\quad \frac{3}{2} \neq \frac{5}{3}\)
So it is not G.P
Hence it is sequence
\(
\therefore \quad(b) \leftrightarrow(i i)
\)
(c) \(13,8,3,-2,-7\)
Here
\(
a_2-a_1=8-13=-5
\)
So, \(\quad \begin{aligned} & a_3-a_2=3-8=-5 \\ & a_2-a_1=a_3-a_2=-5\end{aligned}\)
So, it is an A.P
Hence \((c) \leftrightarrow(i)\)

Hint

(a) Let \(S _n=1^2+2^2+3^2+\cdots+n^2\)
\(K ^3-( K -1)^3=3 K ^2-3 K +1\)
For \(K=1\), \(1^3-0^3=3(1)^2-3(1)+1\)
For \(K=2\),
\(2^3-1^3=3(2)^2-3(2)+1\)
For \(K=3\),
\(
3^3-2^3=3(3)^2-3(3)+1
\)
For \(K =n, \quad n^3-(n-1)^3=3(n)^2-3(n)+1\)
Adding Column wise, we get
\(
\begin{aligned}
& n^3-0^3=3\left(1^2+2^2+3^2+\cdots+n^2\right) \\
& -3(1+2+3+\cdots+n)+n \\
& \Rightarrow \quad n^3=3 \cdot S _n-\frac{3 n(n+1)}{2}+n \\
& \Rightarrow \quad n^3+\frac{3 n(n+1)}{2}-n=3 \cdot S _n \\
& \Rightarrow \frac{2 n^3+3 n^2+3 n-2 n}{2}=3 \cdot S _n \\
& \Rightarrow \quad 6 \cdot S _n=2 n^3+3 n^2+n \\
& \Rightarrow \quad 6 \cdot S _n=n\left(2 n^2+3 n+1\right) \\
& \Rightarrow \quad 6 \cdot S _n=n\left[2 n^2+2 n+n+1\right] \\
& \Rightarrow \quad 6 \cdot S _n=n(n+1)(2 n+1) \\
& \Rightarrow \quad S _n=\frac{n(n+1)(2 n+1)}{6} \\
&
\end{aligned}
\)
Here \((a) \leftrightarrow\) (iii).
(b) Let \(S _n=1^3+2^3+3^3+\cdots+n^3\)
\(
K ^4-( K -1)^4=4 K ^3-6 K ^2+4 K -1
\)
For \(K =1 \quad 1^4-0^4=4(1)^3-6(1)^2+4(1)-1\)
For \(K=2 \quad 2^4-1^4=4(2)^3-6(2)^2+4(2)-1\)
For \(K=3 \quad 3^4-2^4=4(3)^3-6(3)^2+4(3)-1\)
For \(K =n \quad n^4-(n-1)^4=4(n)^3-6\left(n^2\right)+4(n)-1\)
Adding column wise, we get
\(
\begin{aligned}
\Rightarrow \quad n^4-0^4= & 4\left(1^3+2^3+3^3+\cdots n^3\right) \\
& -6\left(1^2+2^2+3^2+\cdots+n^2\right) \\
& +4(1+2+3+\ldots n)-n
\end{aligned}
\)
\(\Rightarrow \quad n^4=4 \cdot S _n-\frac{6 n(n+1)(2 n+1)}{6}+\frac{4 n(n+1)}{2}-n\)
\(
\begin{array}{cc}
\Rightarrow & n^4=4 \cdot S _n-n(n+1)(2 n+1)+2 n(n+1)-n \\
\Rightarrow & n^4+n(n+1)(2 n+1)-2 n(n+1)+n=4 \cdot S _n \\
\Rightarrow & n\left[n^3+(n+1)(2 n+1)-2 n-2+1\right]=4 \cdot S _n \\
\Rightarrow & n\left[n^3+2 n^2+3 n+1-2 n-1\right]=4 \cdot S _n \\
\Rightarrow & n\left[n^3+2 n^2+n\right]=4 \cdot S _n \\
\Rightarrow & \frac{n^2\left(n^2+2 n+1\right)}{4}= S _n \\
\Rightarrow & \frac{n^2(n+1)^2}{4}= S _n
\end{array}
\)
\(
S _n=\left[\frac{n(n+1)}{2}\right]^2
\)
Hence \((b) \leftrightarrow(i)\)
(c) Let
\(
\begin{aligned}
S _n & =2+4+6+\ldots .+2 n \\
& =2(1+2+3+\ldots .+n) \\
& =2 \frac{n(n+1)}{2} \\
& =n(n+1)
\end{aligned}
\)
Hence \((c) \leftrightarrow\) (ii)
(d) Let \(S _n=1+2+3+\cdots+n=\frac{n(n+1)}{2}\)
Hence \((d) \leftrightarrow(i v)\)

Hint

Let \(d\) be the common diffrence and \(n\) be the number of terms of the A.P.
Since the first term is \(a\) and the second term is \(b\)
Therefore,
\(
d=b-a
\)
Also, the last term is \(c\), so
\(
\begin{aligned}
& c=a+(n-1)(b- a )(\text { since } \quad d=b-a) \\
& \Rightarrow \\
& n-1=\frac{c-a}{b-a} \\
& n=1+\frac{c-a}{b-a}=\frac{b-a+c-a}{b-a}=\frac{b+c-2 a}{b-a} \\
& \text { Therefore, } \\
& S _n=\frac{n}{2}(a+l)=\frac{(b+c-2 a)}{2(b-a)}(a+c) \\
&
\end{aligned}
\)

Hint

Let \(A\) be the first term and \(D\) be the common difference of the A.P. It is given that
\(
\begin{gathered}
t_p=a \Rightarrow A +(p-1) D =a \dots(1) \\
t_q= b \Rightarrow A +(q-1) D =b \dots(2)
\end{gathered}
\)
Subtracting (2) from (1), we get
\(
\begin{aligned}
(p-1-q+1) D & =a-b \\
D & =\frac{a-b}{p-q} \dots(3)
\end{aligned}
\)
Adding (1) and (2), we get
\(
\begin{aligned}
& 2 A +(p+q-2) D =a+b \\
& \Rightarrow \quad 2 A +(p+q-1) D =a+b+ D \\
& \Rightarrow \quad 2 A +(p+q-1) D =a+b+\frac{a-b}{p-q} \dots(4) \\
& S _{p+q}=\frac{p+q}{2}[2 A +(p+q-1) D ] \\
& =\frac{p+q}{2}\left[a+b+\frac{a-b}{p-q}\right] \text { [(using … (3) and (4)] } \\
&
\end{aligned}
\)

Hint

Let \(a\) be the first term and \(d\) the common difference of the A.P. Also let \(S _1\) be the sum of odd terms of A.P. having \((2 n+1)\) terms. Then
\(
\begin{aligned}
& S _1=a_1+a_3+a_5+\ldots+a_{2 n+1} \\
& S _1=\frac{n+1}{2}\left(a_1+a_{2 n+1}\right) \\
& S _1=\frac{n+1}{2}[a+a+(2 n+1-1) d]
\end{aligned}
\)
\(
=(n+1)(a+n d)
\)
Similarly, if \(S _2\) denotes the sum of even terms, then
\(
\begin{aligned}
& S _2=\frac{n}{2}[2 a+2 n d]=n(a+n d) \\
& \frac{ S _1}{ S _2}=\frac{(n+1)(a+n d)}{n(a+n d)}=\frac{n+1}{n}
\end{aligned}
\)

Hint

After each year the value of the machine is \(80 \%\) of its value the previous year so at the end of 5 years the machine will depreciate as many times as 5 .
Hence, we have to find the \(6^{\text {th }}\) term of the GP. whose first term \(a_1\) is 1250 and common ratio \(r\) is . 8 .
Hence, value at the end 5 years \(=t_6=a_1 7^5=1250(.8)^5=409.6\)

Hint

We know that in an A.P., the sum of the terms equidistant from the beginning and end is always the same and is equal to the sum of first and last term.
Therefore
\(
d=b-a
\)
\(
\text { i.e., } \quad a_1+a_{24}=a_5+a_{20}=a_{10}+a_{15}
\)
\(
\begin{aligned}
& \text { It is given that }\left(a_1+a_{24}\right)+\left(a_5+a_{20}\right)+\left(a_{10}+a_{15}\right)=225 \\
& \Rightarrow\left(a_1+a_{24}\right)+\left(a_1+a_{24}\right)+\left(a_1+a_{24}\right)=225 \\
& \Rightarrow \quad 3\left(a_1+a_{24}\right)=225 \\
& \Rightarrow \quad a_1+a_{24}=75
\end{aligned}
\)
We know that \(S _n=\frac{n}{2}[a+l]\), where \(a\) is the first term and \(l\) is the last term of an A.P.
Thus, \(S _{24}=\frac{24}{2}\left[a_1+a_{24}\right]=12 \times 75=900\)

Hint

Let the three numbers in A.P. be \(a-d, a, a+d(d>0)[latex]
[latex]
\begin{array}{lr}
\text { Now } & (a- d ) a(a+ d )=224 \\
\Rightarrow & a\left(a^2-d^2\right)=224 \dots(1)
\end{array}
\)
Now, since the largest number is 7 times the smallest, i.e., \(a+d=7(a- d )\)
Therefore,
\(
d=\frac{3 a}{4}
\)
Substituting this value of \(d\) in (1), we get
\(
\begin{aligned}
a\left(a^2-\frac{9 a^2}{16}\right) & =224 \\
a & =8
\end{aligned}
\)
and \(d=\frac{3 a}{4}=\frac{3}{4} \times 8=6\)
Hence, the three numbers are \(2,8,14\).

Hint

The terms \(\left(x^2+x y+y^2\right),\left(z^2+x z+x^2\right)\) and \(\left(y^2+y z+z^2\right)\) will be in A.P. if
\(
\left(z^2+x z+x^2\right)-\left(x^2+x y+y^2\right)=\left(y^2+y z+z^2\right)-\left(z^2+x z+x^2\right)
\)
\(
\begin{aligned}
z^2+x z-x y-y^2 & =y^2+y z-x z-x^2 \\
x^2+z^2+2 x z-y^2 & =y^2+y z+x y
\end{aligned}
\)
\(
(x+z)^2-y^2=y(x+y+z)
\)
\(
\begin{aligned}
x+z-y & =y \\
x+z & =2 y
\end{aligned}
\)
which is true, since \(x, y, z\) are in A.P. Hence \(x^2+x y+y^2, z^2+x z+x^2, y^2+y z+z^2\) are in A.P.

Hint

Let \(r\) be the common ratio of the given GP. Then
\(
\begin{aligned}
\frac{b}{a}= & \frac{c}{b}=\frac{d}{c}=r \\
b & =a r, c=b r=a r^2, d=c r=a r^3 \\
a^2-b^2 & =a^2-a^2 r^2=a^2\left(1-r^2\right)
\end{aligned}
\)
\(
\begin{aligned}
& b^2-c^2=a^2 r^2-a^2 r^4=a^2 r^2\left(1-r^2\right) \\
& c^2-d^2=a^2 r^4-a^2 r^6=a^2 r^4\left(1-r^2\right)
\end{aligned}
\)
Therefore,
\(
\frac{b^2-c^2}{a^2-b^2}=\frac{c^2-d^2}{b^2-c^2}=r^2
\)
Hence, \(a^2-b^2, b^2-c^2, c^2-d^2\) are in G.P.

Hint

Let the A.P. be \(a, a+d, a+2 d, \ldots\). We are given
\(
a_1+a_2+\ldots+a_m=a_{m+1}+a_{m+2}+\ldots+a_{m+n} \dots(1)
\)
Adding \(a_1+a_2+\ldots+a_m\) on both sides of (1), we get
\(
\begin{aligned}
& 2\left[a_1+a_2+\ldots+a_m\right]=a_1+a_2+\ldots+a_m+a_{m+1}+\ldots+a_{m+n} \\
& 2 S _m= S _{m+n}
\end{aligned}
\)
Therefore, \(2 \frac{m}{2}\{2 a+(m-1) d\}=\frac{m+n}{2}\{2 a+(m+n-1) d\}\) Putting \(2 a+(m-1) d=x\) in the above equation, we get
\(
\begin{aligned}
m x & =\frac{m+n}{2}(x+n d) \\
\Rightarrow \quad(2 m-m-n) x & =(m+n) n d \\
(m-n) x & =(m+n) n d \dots(2)
\end{aligned}
\)
Similarly, if \(a_1+a_2+\ldots+a_m=a_{m+1}+a_{m+2}+\ldots+a_{m+p}\)
Adding \(a_1+a_2+\ldots+a_m\) on both sides
we get,
\(
2\left(a_1+a_2+\ldots+a_m\right)=a_1+a_2+\ldots+a_{m+1}+\ldots+a_{m+p}
\)
or, \(2 S _m= S _{m+p}\)
\(\Rightarrow \quad 2\left[\frac{m}{2}\{2 a+(m-1) d\}\right]=\frac{m+p}{2}\{2 a+(m+p-1) d\}\) which gives
i.e., \((m-p) x=(m+p) p d \dots(3)\)
Dividing (2) by (3), we get
\(
\begin{aligned}
\frac{(m-n) x}{(m-p) x} & =\frac{(m+n) n d}{(m+p) p d} \\
\Rightarrow \quad(m-n)(m+p) p & =(m-p)(m+n) n
\end{aligned}
\)
Dividing both sides by \(m n p\), we get
\(
\begin{aligned}
& (m+p)\left(\frac{1}{n}-\frac{1}{m}\right)=(m+n)\left(\frac{1}{p}-\frac{1}{m}\right) \\
= & (m+n)\left(\frac{1}{m}-\frac{1}{p}\right)=(m+p)\left(\frac{1}{m}-\frac{1}{n}\right)
\end{aligned}
\)

Hint

We have
\(
\begin{aligned}
& \sin d\left(\operatorname{cosec} a_1 \operatorname{cosec} a_2+\operatorname{cosec} a_2 \operatorname{cosec} a_3+\ldots+\operatorname{cosec} a_{n-1} \operatorname{cosec} a_n\right) \\
& =\sin d\left[\frac{1}{\sin a_1 \sin a_2}+\frac{1}{\sin a_2 \sin a_3}+\ldots+\frac{1}{\sin a_{n-1} \sin a_n}\right] \\
& =\frac{\sin \left(a_2-a_1\right)}{\sin a_1 \sin a_2}+\frac{\sin \left(a_3-a_2\right)}{\sin a_2 \sin a_3}+\ldots+\frac{\sin \left(a_n-a_{n-1}\right)}{\sin a_{n-1} \sin a_n} \\
& =\frac{\left.\sin a_2 \cos a_1-\cos a_2 \sin a_1\right)}{\sin a_1 \sin a_2}+\frac{\left.\sin a_3 \cos a_2-\cos a_3 \sin a_2\right)}{\sin a_2 \sin a_3}+\ldots+\frac{\left.\sin a_n \cos a_{n-1}-\cos a_n \sin a_{n-1}\right)}{\sin a_{n-1} \sin a_n} \\
& =\left(\cot a_1-\cot a_2\right)+\left(\cot a_2-\cot a_3\right)+\ldots+\left(\cot a_{n-1}-\cot a_n\right) \\
& =\cot a_1-\cot a_n
\end{aligned}
\)

Hint

\(
\text { Since } a, b, c, d \text { are in A.P., then A.M. > G.M., for the first three terms. }
\)
Therefore, \(b>\sqrt{a c}\) \(\left(\text { Here } \frac{a+c}{2}=b\right)\)
Squaring, we get
\(
b^2>a c \dots(1)
\)
Similarly, for the last three terms
\(
\begin{array}{ll}
AM > GM & \\
c>\sqrt{b d} & \left(\text { Here } \frac{b+d}{2}=c\right) \\
c^2>b d & \dots(2)
\end{array}
\)
Multiplying (1) and (2), we get
\(
\begin{aligned}
& b^2 c^2>(a c)(b d) \\
\Rightarrow & b c>a d
\end{aligned}
\)

Hint

Since \(a, b, c, d\) are in G.P.
again A.M. > G.M. for the first three terms
\(
\begin{array}{ll}
\frac{a+c}{2}>b & (\text { since } \sqrt{a c}=b)
\end{array}
\)
\(
\Rightarrow a+c>2 b \dots(1)
\)
Similarly, for the last three terms
\(
\begin{aligned}
& \frac{b+d}{2}>c & \text { (since } \sqrt{b d}=c \text { ) } \\
& \Rightarrow b+d>2 c \dots(2) \\
&
\end{aligned}
\)
Adding (1) and (2), we get
\(
\begin{aligned}
& (a+c)+(b+d)>2 b+2 c \\
& a+d>b+c
\end{aligned}
\)

Hint

We have \(a, b, c\) as three consecutive terms of A.P. Then
\(
b-a=c-b=d \text { (say) }
\)
\(
\begin{aligned}
& c-a=2 d \\
& a-b=-d
\end{aligned}
\)
Now \(x^{b-c} \cdot y^{c-a} \cdot z^{a-b}=x^{-d} \cdot y^{2 d} \cdot z^{-d}\)
\(
\left.=x^{-d}(\sqrt{x z})^{2 d} \cdot z^{-d} \quad \text { (since } y=(\sqrt{x z})\right) \text { as } x, y, z \text { are GP.) }
\)
\(
\begin{aligned}
& =x^{-d} \cdot x^d \cdot z^d \cdot z^{-d} \\
& =x^{-d+d} \cdot z^{d-d} \\
& =x^{\circ} z^{\circ}=1
\end{aligned}
\)

Hint

Given that \(f(x+y)=f(x) \cdot f(y) \text { and } f(1)=2\)
Therefore,
\(
\begin{aligned}
& f(2)=f(1+1)=f(1) \cdot f(1)=2^2 \\
& f(3)=f(1+2)=f(1) \cdot f(2)=2^3 \\
& f(4)=f(1+3)=f(1) \cdot f(3)=2^4
\end{aligned}
\)
and so on. Continuing the process, we obtain
\(
\begin{aligned}
f(k) & =2^k \text { and } f(a)=2^a \\
\sum_{k=1}^n f(a+k) & =\sum_{k=1}^n f(a) \cdot f(k) \\
& =f(a) \sum_{k=1}^n f(k) \\
& =2^a\left(2^1+2^2+2^3+\ldots+2^n\right) \\
& =2^a\left\{\frac{2 \cdot\left(2^n-1\right)}{2-1}\right\}=2^{a+1}\left(2^n-1\right)
\end{aligned} \dots(1)
\)
But, we are given
\(
\begin{aligned}
\sum_{k=1}^n f(a+k) & =16\left(2^n-1\right) \\
2^{a+1}\left(2^n-1\right) & =16\left(2^n-1\right) \\
2^{a+1} & =2^4 \Rightarrow a+1=4 \\
a & =3
\end{aligned}
\)

Hint

(C) is the correct answer. A sequence is a function \(f: N \rightarrow X\) having domain \(\subseteq N\)

Hint

since
A.M. \(>[latex] GM., [latex]\frac{x+y}{2}>\sqrt{x y}, \frac{y+z}{2}>\sqrt{y z}[latex] and [latex]\frac{z+x}{2}>\sqrt{z x}\)

Multiplying the three inequalities, we get
\(
\frac{x+y}{2} \cdot \frac{y+z}{2} \cdot \frac{y+z}{2}>\sqrt{(x y)(y z)(z x)}
\)
or, \(\quad(x+y)(y+z)(z+x)>8 x y z\)

Hint

\(
\begin{aligned}
& t_n=t_{n+1}+t_{n+2} \\
& \Rightarrow \quad a r^{n-1}=a r^n+a r^{n+1} \\
& \Rightarrow \quad 1=r+r^2 \\
& r=\frac{-1 \pm \sqrt{5}}{2} \text {, since } r>0 \\
& r=2 \frac{\sqrt{5}-1}{4}=2 \sin 18^{\circ} \\
&
\end{aligned}
\)

Hint

Let \(a, d\) be the first term and common difference respectively.
Therefore,
\(
\begin{aligned}
T _p & =a+(p-1) d=q \text { and } \dots(1)\\
T _{p+q} & =a+(p+q-1) d=0 \dots(2)
\end{aligned}
\)
Subtracting (1), from (2) we get \(q d=-q\)
Substituting in (1) we get \(a=q-(p-1)(-1)=q+p-1\)
Now
\(\)
\begin{aligned}
T _q & =a+(q-1) d=q+p-1+(q-1)(-1) \\
& =q+p-1-q+1=p
\end{aligned}

Hint

Let us take a G.P. with three terms \(\frac{a}{r}, a, a r\). Then
\(
\begin{aligned}
& S =\frac{a}{r}+a+a r=\frac{a\left(r^2+r+1\right)}{r} \\
& P =a^3, R =\frac{r}{a}+\frac{1}{a}+\frac{1}{a r}=\frac{1}{a}\left(\frac{r^2+r+1}{r}\right) \\
& \frac{ P ^2 R ^3}{ S ^3}=\frac{a^6 \cdot \frac{1}{a^3}\left(\frac{r^2+r+1}{r}\right)^3}{a^3\left(\frac{r^2+r+1}{r}\right)^3}=1
\end{aligned}
\)

Therefore, the ratio is \(1: 1\)

Hint

The first common term is 11 .
Now the next common term is obtained by adding L.C.M. of the common difference 4 and 5 , i.e., 20 .
Therefore, \(10^{\text {th }}\) common term \(= T _{10}\) of the AP whose \(a=11\) and \(d=20\)
\(
T _{10}=a+9 d=11+9(20)=191
\)

Hint

Let us consider a GP. \(a, a r, a r^2, \ldots\) with \(2 n\) terms. We have \(\frac{a\left(r^{2 n}-1\right)}{r-1}=\frac{5 a\left(\left(r^2\right)^n-1\right)}{r^2-1}\)
(Since common ratio of odd terms will be \(r^2\) and number of terms will be \(n\) )
\(
\begin{aligned}
& \Rightarrow \frac{a\left(r^{2 n}-1\right)}{r-1}=5 \frac{a\left(r^{2 n}-1\right)}{\left(r^2-1\right)} \\
& \Rightarrow a(r+1)=5 a, \text { i.e., } r=4
\end{aligned}
\)

Hint

We know A.M. \(\geq\) GM. for positive numbers.
Therefore, \(\frac{3^x+3^{1-x}}{2} \geq \sqrt{3^x \cdot 3^{1-x}}\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{3^x+3^{1-x}}{2} \geq \sqrt{3^x \cdot \frac{3}{3^x}} \\
& \Rightarrow \quad 3^x+3^{1-x} \geq 2 \sqrt{3}
\end{aligned}
\)