Motion in a Plane (Projectile Motion) Quiz-L1
Quiz Summary
0 of 118 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 118 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 118
1. Question
At the top of the trajectory of a projectile, the directions of its velocity and acceleration are
CorrectIncorrectHint
(d) Velocity is horizontal and acceleration is vertically downward. Therefore, at the top of the trajectory of a projectile, the direction of its velocity and acceleration are perpendicular to each other.
-
Question 2 of 118
2. Question
The value of acceleration at the top of the trajectory of a particle when thrown obliquely is
CorrectIncorrectHint
(d) Acceleration throughout the projectile motion remains constant and equal to \({g}\).
-
Question 3 of 118
3. Question
In the motion of a projectile falling freely under gravity, its (neglect air friction)
CorrectIncorrectHint
(a) An external force of gravity is present throughout the motion. So, momentum will not be conserved. Its total mechanical energy is conserved.
-
Question 4 of 118
4. Question
During the flight of a projectile thrown obliquely, which amongst the quantities remains constant?
CorrectIncorrectHint
\(
\text { (d) } a_x=0 \quad \therefore u_x=\text { constant }
\) -
Question 5 of 118
5. Question
A stone is projected with speed of \(50 \mathrm{~ms}^{-1}\) at an angle of \(60^{\circ}\) with the horizontal. The speed of the stone at highest point of trajectory is
CorrectIncorrectHint
(b) At highest point, vertical component of velocity is zero. Only horizontal component of velocity is present.
\(
v_x=u \cos \theta=50 \cos \left(60^{\circ}\right)=25 \mathrm{~ms}^{-1}
\) -
Question 6 of 118
6. Question
A football player throws a ball with a velocity of \(50 \mathrm{~ms}^{-1}\) at an angle \(30^{\circ}\) from the horizontal. The ball remains in the air for (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
\(
\text { (c) Time of flight, } T=\frac{2 u \sin \theta}{g}=\frac{2 \times 50 \times \sin 30^{\circ}}{10}=5 \mathrm{~s}
\) -
Question 7 of 118
7. Question
A particle is projected with a velocity of \(20 \mathrm{~ms}^{-1}\) at an angle of \(60^{\circ}\) to the horizontal. The particle hits the horizontal plane again during its journey. What will be the time of impact?
CorrectIncorrectHint
(a) The particle hits the horizontal plane again at time,
\(
T=\frac{2 u \sin \theta}{g}=\frac{40 \times \sin 60^{\circ}}{9.8}=3.53 \mathrm{~s}
\) -
Question 8 of 118
8. Question
If two balls are projected at angles \(45^{\circ}\) and \(60^{\circ}\) and the maximum heights reached are same, what is the ratio of their initial velocities?
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (b) } \frac{u_1^2 \sin ^2 45^{\circ}}{2 g}=\frac{u_2^2 \sin ^2 60^{\circ}}{2 g} \\
\therefore \quad \frac{u_1}{u_2}=\frac{\sin 60^{\circ}}{\sin 45^{\circ}}=\frac{\sqrt{3} / 2}{(1 \sqrt{2})}=\sqrt{3}: \sqrt{2} \\
\end{array}
\) -
Question 9 of 118
9. Question
If the initial velocity of a projection is doubled, keeping the angle of projection same, the maximum height reached by it will
CorrectIncorrectHint
(c) \(\quad H=\frac{u^2 \sin ^2 \theta}{2 g} \Rightarrow H \propto u^2\)
If initial velocity be doubled, then maximum height reached by the projectile will become four times. -
Question 10 of 118
10. Question
For a projectile, the ratio of maximum height reached to the square of flight time is (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(a) Maximum height, \(H=\frac{u^2 \sin ^2 \theta}{2 g}\) and time of flight, \(T=\frac{2 u \sin \theta}{g}\)
So,
\(
\frac{H}{T^2}=\frac{u^2 \sin ^2 \theta / 2 g}{4 u^2 \sin ^2 \theta / g^2}=\frac{g}{8}=\frac{5}{4}
\) -
Question 11 of 118
11. Question
A particle is projected from ground with speed \(u\) and at an angle \(\theta\) with horizontal. If at maximum height from ground, the speed of particle is \(1 / 2\) times of its initial velocity of projection, then find its maximum height attained.
CorrectIncorrectHint
(d) Given at maximum height,
\(
\begin{array}{l}
u \cos \theta=\frac{1}{2} u \Rightarrow \cos \theta=\frac{1}{2} \Rightarrow \theta=60^{\circ} \\
\therefore H=\frac{u^2 \sin ^2 \theta}{2 g}=\frac{u^2 \sin ^2 60^{\circ}}{2 g}=\frac{3 u^2}{8 g}
\end{array}
\) -
Question 12 of 118
12. Question
A projectile thrown with velocity \(v_0\) at an angle \(\alpha\) to the horizontal, has a range \(R\). It will strike a vertical wall at a distance \(R / 2\) from the point of projection with a speed of
CorrectIncorrectHint
(c) Projectile will strike at highest point of its path with velocity \(v_0 \cos \alpha\).
-
Question 13 of 118
13. Question
A particle is projected at an angle of \(45^{\circ}\) with a velocity of \(9.8 \mathrm{~ms}^{-1}\). The horizontal range will be (Take, \(g=9.8 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
\(
\text { (a) Horizontal range, } R=\frac{u^2 \sin 2 \theta}{g}=\frac{(9.8)^2 \sin 90^{\circ}}{9.8}=9.8 \mathrm{~m}
\) -
Question 14 of 118
14. Question
Two projectiles \(A\) and \(B\) are projected with same speed at angles \(30^{\circ}\) and \(60^{\circ}\) to the horizontal, then which one is wrong?
CorrectIncorrectHint
Given : Two projectiles A and B are projected with same speed at angles \(30^{\circ}\) and \(60^{\circ}\) to horizontal.
In projectile motion the time of flight, maximum height and range is given by \(\mathrm{T}=\frac{2 \mathrm{u} \sin \theta}{\mathrm{g}}, \mathrm{H}=\frac{\mathrm{u}^2 \sin ^2 \theta}{2 \mathrm{~g}}\) and \(\mathrm{R}=\frac{\mathrm{u}^2 \sin 2 \theta}{\mathrm{g}}\) for projectile A, \(\theta=30^{\circ}\) so \(\mathrm{T}_{\mathrm{a}}=\frac{2 \mathrm{u} \sin 30^{\circ}}{\mathrm{g}}=\frac{1}{2} \cdot \frac{2 \mathrm{u}}{\mathrm{g}}\)
\(\mathrm{H}_{\mathrm{a}}=\frac{\mathrm{u}^2 \sin ^2 30^{\circ}}{2 \mathrm{~g}}=\frac{1 \mathrm{u}^2}{42 \mathrm{~g}}\) and
\(
\mathrm{R}_{\mathrm{a}}=\frac{\mathrm{u}^2 \sin 60^{\circ}}{\mathrm{g}}=\frac{\sqrt{3} \mathrm{u}^2}{2 \mathrm{~g}}
\)
for projectile \(\mathrm{B}, \theta=60^{\circ}\) so \(\mathrm{T}_{\mathrm{b}}=\frac{2 \mathrm{u} \sin 60^{\circ}}{\mathrm{g}}=\frac{\sqrt{3}}{2} \cdot \frac{2 \mathrm{u}}{\mathrm{g}}\)
\(
\mathrm{H}_{\mathrm{b}}=\frac{\mathrm{u}^2 \sin ^2 60^{\circ}}{2 \mathrm{~g}}=\frac{3 \mathrm{u}^2}{42 \mathrm{~g}} \text { and }
\)
\(
\mathrm{R}_{\mathrm{b}}=\frac{\mathrm{u}^2 \sin 120^{\circ}}{\mathrm{g}}=\frac{\sqrt{3} \mathrm{u}^2}{2 \mathrm{~g}}
\)Hence, \(\mathrm{T}_{\mathrm{b}}=\sqrt{3} \cdot \mathrm{T}_{\mathrm{a}}\)
\(
\mathrm{H}_{\mathrm{b}}=3 \cdot \mathrm{H}_{\mathrm{a}}
\)
\(
\mathrm{R}_{\mathrm{b}}=\mathrm{R}_{\mathrm{a}}
\) -
Question 15 of 118
15. Question
A projectile fired with initial velocity \(u\) at some angle \(\theta\) has a range \(R\). If the initial velocity be doubled at the same angle of projection, then the range will be
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (d) } \quad R=\frac{u^2 \sin 2 \theta}{g} \\
\therefore \quad R \propto u^2 \\
\end{array}
\)If initial velocity be doubled at some angle of projection, then range will become four times.
-
Question 16 of 118
16. Question
An object is thrown along a direction inclined at an angle of \(45^{\circ}\) with the horizontal direction. The horizontal range of the particle is equal to
CorrectIncorrectHint
(d) \(\frac{R}{H}=\frac{\frac{u^2 \sin 2 \theta}{g}}{\frac{u^2 \sin ^2 \theta}{2 g}}=\frac{2 \sin \theta \cos \theta}{g} \times \frac{2 g}{\sin ^2 \theta}=4 \cot \theta\) \(\Rightarrow R=4 H \cot \theta\); If \(\theta=45^{\circ}\), then \(R=4 H \cot \left(45^{\circ}\right)=4 H\)
-
Question 17 of 118
17. Question
An object is projected at an angle of \(45^{\circ}\) with the horizontal. The horizontal range and the maximum height reached will be in the ratio
CorrectIncorrectHint
(d) \(R=4 H \cot \theta\)
If \(\theta=45^{\circ}\), then \(\frac{R}{H}=\frac{4}{1}\)
-
Question 18 of 118
18. Question
The horizontal range of a projectile is \(4 \sqrt{3}\) times of its maximum height. The angle of projection will be
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (c) Given, range, } R=4 \sqrt{3} H \\
\Rightarrow \frac{u^2 \sin \theta \cos \theta}{g}=4 \sqrt{3}\left(\frac{u^2 \sin ^2 \theta}{2 g}\right) \Rightarrow \tan \theta=\frac{1}{2 \sqrt{3}} \\
\therefore \quad \theta=16.1^{\circ}
\end{array}
\) -
Question 19 of 118
19. Question
A ball is projected with a velocity \(20 \sqrt{3} \mathrm{~ms}^{-1}\) at an angle \(60^{\circ}\) to the horizontal. The time interval after which the velocity vector will make an angle \(30^{\circ}\) to the horizontal is (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (b) } \tan 30^{\circ}=\frac{v_y}{v_x}=\frac{u_{y-} g t}{u_x}=\frac{\left(20 \sqrt{3} \sin 60^{\circ}\right)-10 t}{\left(20 \sqrt{3} \cos 60^{\circ}\right)} \\
\text { or } \quad 10=30-10 t \\
\therefore \quad t=2 \mathrm{~s} \\
\end{array}
\) -
Question 20 of 118
20. Question
A projectile is thrown with a velocity of \(10 \mathrm{~ms}^{-1}\) at an angle of \(60^{\circ}\) with horizontal. The interval between the moments when speed is \(\sqrt{5 g} \mathrm{~m} / \mathrm{s}\) is (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(a) \(\quad v^2=v_y^2+v_x^2\) or \(5 g=\left(u_y-g t\right)^2+u_x^2\)
Since, \(\quad v_y=u \sin 30^{\circ}=10 \sin 30^{\circ}=5 \sqrt{3} \mathrm{~ms}^{-1}\)
\(
v_x=u \cos 30^{\circ}=10 \cos 30^{\circ}=5 \mathrm{~ms}^{-1}
\)
or \(\quad 50=(5 \sqrt{3}-10 t)^2+(5)^2\)
\(
\therefore \quad(5 \sqrt{3}-10 t)= \pm 5
\)
\(
\begin{array}{l}
\Rightarrow \quad t_1=\frac{5 \sqrt{3}+5}{10} \text { and } t_2=\frac{5 \sqrt{3}-5}{10} \\
\therefore \quad t_1-t_2=1 \mathrm{~s} \\
\end{array}
\) -
Question 21 of 118
21. Question
A bomb is dropped from an aeroplane moving horizontally at constant speed. If air resistance is neglected, then the bomb
CorrectIncorrectHint
(a) Horizontal component of velocity of the bomb is same as velocity of the aeroplane. Therefore, the bomb falls exactly below the aeroplane.
-
Question 22 of 118
22. Question
A body is projected horizontally with a velocity of \(4 \mathrm{~ms}^{-1}\) from the top of a high tower. The velocity of the body after \(0.7 \mathrm{~s}\) is nearly (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (b) } v_y=g t=7 \mathrm{~ms}^{-1}, v_x=4 \mathrm{~ms}^{-1} \\
\therefore \quad v=\sqrt{v_x^2+v_y^2}=8 \mathrm{~ms}^{-1}
\end{array}
\) -
Question 23 of 118
23. Question
A particle is projected horizontally with speed \(20 \mathrm{~ms}^{-1}\) from the top of a tower. After what time, velocity of particle will be at \(45^{\circ}\) angle from initial direction of projection?
CorrectIncorrectHint
(b)
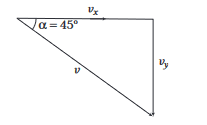
Let horizontal direction is \(x\) and \(y\) is downward direction.
After time \(t, v_x=u_x=20 \mathrm{~ms}^{-1}\)
Velocity in \(y\)-direction,
\(
\begin{array}{l}
v_y=u_y+a_y t=0+g t=g t \\
\tan \alpha=\frac{v_y}{v_x}=\frac{g t}{20} \\
\therefore 1=\frac{10 \times t}{20} \Rightarrow t=2 \mathrm{~s}
\end{array}
\) -
Question 24 of 118
24. Question
An aeroplane is travelling horizontally at a height of \(2000 \mathrm{~m}\) from the ground. The aeroplane when at a point \(P\), drops a bomb to hit a stationary target \(Q\) on the ground. In order that the bomb hits the target, what is the angle \(\theta\), the line \(P Q\) makes with the vertical?
(Take, \(g=10 \mathrm{~ms}^{-2}\) )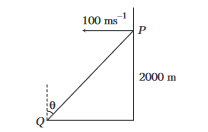
CorrectIncorrectHint
(a)
Let \(t\) be the time taken by bomb to hit the target.
\(
h=2000=\frac{1}{2} g t^2 \Rightarrow t=20 \mathrm{~s}
\)
\(
\begin{aligned}
R & =u t=(100)(20)=2000 \mathrm{~m} \\
\tan \theta & =\frac{R}{h}=\frac{2000}{2000}=1 \Rightarrow \theta=45^{\circ}
\end{aligned}
\) -
Question 25 of 118
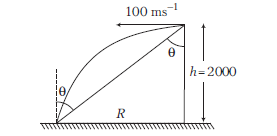
25. Question
An acroplane is flying at a constant height of \(1960 \mathrm{~m}\) with speed \(600 \mathrm{kmh}^{-1}\) above the ground towards point directly over a person struggling in flood water. At what angle of sight with the vertical should the pilot release a survival kit, if it is to reach the person in water? (Take, \(g=9.8 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(c) Plane is flying at a speed \(=600 \times \frac{5}{18}=\frac{500}{3} \mathrm{~ms}^{-1}\) horizontally (at a height \(1960 \mathrm{~m}\) )
Time taken by the kit to reach the ground,
\(
t=\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 1960}{9.8}}=20 \mathrm{~s}
\)
In this time, the kit will move horizontally by
\(
x=u t=\frac{500}{3} \times 20=\frac{10000}{3} \mathrm{~m}
\)
So, the angle of sight,
\(
\begin{aligned}
\tan \theta & =\frac{x}{h}=\frac{10000}{3 \times 1960}=\frac{10}{5.88} \\
& =1.7 \simeq \sqrt{3} \text { or } \theta=60^{\circ}
\end{aligned}
\) -
Question 26 of 118
26. Question
A ball is projected horizontally from the top of a tower with a velocity \(v_0\). It will be moving at an angle of \(60^{\circ}\) with the horizontal after time,
CorrectIncorrectHint
\(
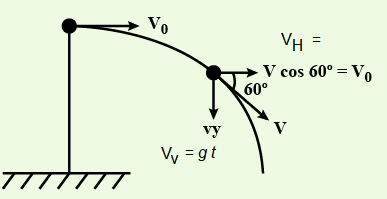
\begin{array}{ll}
\text { (b) } & \tan 60^{\circ}=\frac{v_V}{v_H}=\frac{g t}{v_0} \\
\therefore & t=\frac{\sqrt{3} v_0}{g}
\end{array}
\) -
Question 27 of 118
27. Question
A man standing on a hill top projects a stone horizontally with speed \(v_0\) as shown in figure. Taking the coordinate system as given in the figure. The coordinates of the point, where the stone will hit the hill surface are
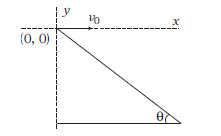CorrectIncorrectHint
\(
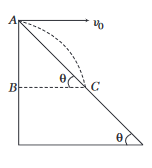
\begin{array}{l}
\text { (a) } \frac{A B}{B C}=\frac{\frac{1}{2} g t^2}{v_0 t}=\tan \theta \\
\therefore \quad t=\frac{2 v_0 \tan \theta}{g}
\end{array}
\)
Now, \(x\)-coordinate \(=v_0 t=\frac{2 v_0^2 \tan \theta}{g}\) and \(y\)-coordinate
\(
=-\frac{1}{2} g t^2=-\frac{2 v_0^2 \tan ^2 \theta}{g}
\) -
Question 28 of 118
28. Question
In a two dimensional motion, instantaneous speed \(v_0\) is a positive constant. Then which of the following are necessarily true?
CorrectIncorrectHint
(d) We know that,
Instantaneous speed, \(v=\frac{d s}{d t}\)
Since, \(v\) is a positive constant, hence in this situation, equal path lengths are traversed in equal intervals of time by the moving object. -
Question 29 of 118
29. Question
In a two dimensional motion, instantaneous speed \(v_0\) is a positive constant. Then, which of the following are necessarily true?
CorrectIncorrectHint
(c) As given motion is two dimensional motion and it is given that instantaneous speed \(v_0\) is positive constant. Acceleration is rate of change of velocity (instantaneous speed), hence it will also be in the plane of motion.
-
Question 30 of 118
30. Question
A particle velocity changes from \((2 \hat{\mathbf{i}}-3 \hat{\mathbf{j}}) \mathrm{ms}^{-1}\) to \((3 \hat{\mathbf{i}}-2 \hat{\mathbf{j}}) \mathrm{ms}^{-1}\) in \(2 \mathrm{~s}\). If its mass is \(1 \mathrm{~kg}\), the acceleration \(\left(\mathrm{ms}^{-2}\right)\) is
CorrectIncorrectHint
\(
\text { (b) } \mathbf{a}=\frac{\mathbf{v}_f-\mathbf{v}_i}{t}=\frac{(3 \hat{\mathbf{i}}-2 \hat{\mathbf{i}})-(2 \hat{\mathbf{j}}-3 \hat{\mathbf{j}})}{2}=\frac{\hat{\mathbf{i}}+\hat{\mathbf{j}}}{2}
\) -
Question 31 of 118
31. Question
A projectile is thrown at an angle \(\theta\) with the horizontal and its range is \(R_1\). It is then thrown at an angle \(\theta\) with vertical and the range is \(R_2\), then
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (c) We know that, } R_\theta=R_{90^{\circ}-\theta} \\
\therefore \quad R_1=R_2
\end{array}
\)Explanation:
Let the velocity of projection = \(u\)
when thrown at an angle \(\theta\) with horizontal range \(R_1=\frac{u^2 \sin 2 \theta}{g}\)
when thrown with an an \(\theta\) with vertical
\(
\begin{aligned}
R_2 & =\frac{u^2 \sin 2(90-\theta)}{g} \\
& =\frac{u^2 \sin (180-2 \theta)}{g}
\end{aligned}
\)
\(
\begin{array}{l}
R_2=\frac{u^2 \sin 2 \theta}{g} \\
\Rightarrow R_1=R_2
\end{array}
\) -
Question 32 of 118
32. Question
Figure shows four paths for a kicked football. Ignoring the effects of air on the flight, rank the paths according to initial horizontal velocity component highest first.
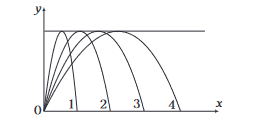CorrectIncorrectHint
(d) \(R=\frac{u^2 \sin 2 \theta}{g}=\frac{2 u_x u_y}{g}\)
\(\therefore\) Range \(\propto\) Horizontal initial velocity component \(\left(u_x\right)\)
In path 4 , range is maximum, so football has maximum horizontal velocity component in this path and in path 1 , range is minimum. So, horizontal velocity component is minimum. -
Question 33 of 118
33. Question
Which of the following is the graph between the height \((h)\) of a projectile and time \((t)\), when it is projected from the ground?
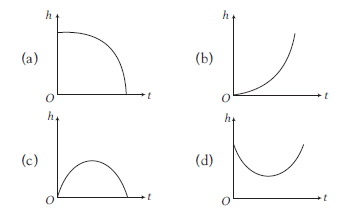CorrectIncorrectHint
(c) Projectile motion is a form of motion experienced by an object or particle (a projectile) that is projected in a gravitational field, such as from Earth ‘s surface, and moves along a curved path under the action of gravity only.
-
Question 34 of 118
34. Question
Which of the following is the altitude-time graph for a projectile thrown horizontally from the top of the tower?
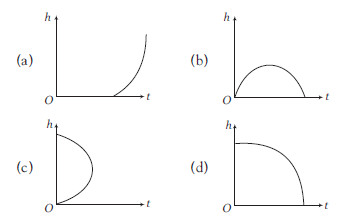CorrectIncorrectHint
A projectile thrown horizontally moves under the effect of gravity. Hence its vertical acceleration in the downward direction is +g, where g is the acceleration due to gravity.
-
Question 35 of 118
35. Question
The horizontal range of a projectile fired at an angle of \(15^{\circ}\) is \(50 \mathrm{~m}\). If it is fired with the same speed at an angle of \(45^{\circ}\), its range will be
CorrectIncorrectHint
(c) Given, \(\quad \theta=15^{\circ}\) and \(R=50 \mathrm{~m}\)
Range, \(R=\frac{u^2 \sin 2 \theta}{g}\)
Putting all the given values in the formula, we get
\(
\begin{array}{l}
R=50 \mathrm{~m}=\frac{u^2 \sin \left(2 \times 15^{\circ}\right)}{g} \\
\Rightarrow 50 \times g=u^2 \sin 30^{\circ}=u^2 \times \frac{1}{2} \Rightarrow 50 \times g \times 2=u^2 \\
\Rightarrow \quad u^2=50 \times 9.8 \times 2=980 \\
\Rightarrow \quad u=\sqrt{980} \\
=31.304 \mathrm{~ms}^{-1} \\
\text { For } \theta=45^{\circ}, R=\frac{u^2 \sin 2 \times 45^{\circ}}{g}=\frac{u^2}{g} \quad\left(\because \sin 90^{\circ}=1\right) \\
\Rightarrow \quad R=\frac{(14 \sqrt{5})^2}{g}=\frac{14 \times 14 \times 5}{9.8}=100 \mathrm{~m} \\
\end{array}
\) -
Question 36 of 118
36. Question
A body is thrown horizontally from the top of a tower of height \(5 \mathrm{~m}\). It touches the ground at a distance of \(10 \mathrm{~m}\) from the foot of the tower. The initial velocity of the body is (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (c) } s=u \times \sqrt{\frac{2 h}{g}} \Rightarrow 10=u \sqrt{2 \times \frac{5}{10}} \\
\Rightarrow \quad u=10 \mathrm{~ms}^{-1}
\end{array}
\) -
Question 37 of 118
37. Question
Velocity and acceleration of a particle at|some instant of time are \(v=(3 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}) \mathrm{ms}^{-1}\) and \(\mathbf{a}=-(6 \hat{\mathbf{i}}+8 \hat{\mathbf{j}}) \mathrm{ms}^{-2}\), respectively. At the same instant particle is at origin, maximum \(x\)-coordinate of particle will be
CorrectIncorrectHint
we know \(\overrightarrow{{v}}=\overrightarrow{{u}}+\overrightarrow{{at}}\)
\(
\begin{array}{l}
\Rightarrow \vec{v}=3 \hat{i}+4 \hat{j}-(6 \hat{i}+8 \hat{j}) t \\
\Rightarrow \vec{v}=(3-6 t) \hat{i}+(4-8 t) \hat{j} \\
\Rightarrow \vec{v}=v_x \hat{i}+v_y \hat{j}
\end{array}
\)Now \(\frac{\mathrm{dx}}{\mathrm{dt}}={v}_{\mathrm{x}}=3-6 \mathrm{t}\)
For \({x}\) maximum \({v}_{x}=0 \Rightarrow 3-6 \mathrm{t}=0 \Rightarrow \mathrm{t}=\frac{1}{2}\) second
\(
\begin{array}{l}
\frac{d x}{d t}=(3-6 t) \\
\Rightarrow \int_0^{x_{\max }} d x=\int_0^{\frac{1}{2}}(3-6 t) d t \\
\Rightarrow x_{\max }-0=\left[3 t-\frac{6 t^2}{2}\right]_0^{\frac{1}{2}} \\
\Rightarrow x_{\max }=\left[3 \times \frac{1}{2}-3\left(\frac{1}{2}\right)^2\right]-(0-0)=\frac{3}{2}-\frac{3}{4}=\frac{3}{4}=0.75 \mathrm{~m}
\end{array}
\)Alternate:Â
\(
\begin{aligned}
\text { (b) Given, } u_x & =3 \mathrm{~ms}^{-1}, a_x=-6 \mathrm{~ms}^{-1} \\
X_{\max } & =\frac{u_x^2}{2\left|a_x\right|}=\frac{9}{12}=0.75 \mathrm{~m}
\end{aligned}
\) -
Question 38 of 118
38. Question
Two paper screens \(A\) and \(B\) are separated by a distance of \(100 \mathrm{~m}\). A bullet pierces \(A\) and then \(B\). The hole in \(B\) is \(10 \mathrm{~cm}\) below the hole in \(A\). If the bullet is travelling horizontally at the time of hitting \(A\), then the velocity of the bullet at \(A\) is
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (d) } \quad h=\frac{1}{2} g t^2 \quad \text { (In vertical direction) } \\
\Rightarrow \quad t=\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 0.1}{10}}=0.141 \mathrm{~s} \\
\end{array}
\)Now, in horizontal direction, \(v_x=\frac{s_x}{t}=\frac{100}{0.141} \approx 700 \mathrm{~ms}^{-1}\)
-
Question 39 of 118
39. Question
Two stones having different masses \(m_1\) and \(m_2\) are projected at an angle \(\alpha\) and \(\left(90^{\circ}-\boldsymbol{\alpha}\right)\) with same speed from same point. The ratio of their maximum heights is
CorrectIncorrectHint
(d) Maximum height, \(H=\frac{u^2 \sin ^2 \alpha}{2 g} \Rightarrow H \propto \sin ^2 \alpha\)
\(
\therefore \quad \frac{H_1}{H_2}=\frac{\sin ^2 \alpha}{\sin ^2\left(90^{\circ}-\alpha\right)}=\tan ^2 \alpha
\) -
Question 40 of 118
40. Question
Two projectiles \(A\) and \(B\) are thrown from the same point with velocities \(v\) and \(v / 2\), respectively. If \(B\) is thrown at angle \(45^{\circ}\) with horizontal, what is the inclination of \(A\) when their ranges are the same?
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (d) Given, } R_A=R_B \\
\Rightarrow \quad \frac{v^2 \sin 2 \theta}{g}=\frac{(v / 2)^2 \sin 90^{\circ}}{g} \\
\Rightarrow \quad \sin 2 \theta=\frac{1}{4} \text { or } \theta=\frac{1}{2} \sin ^{-1}\left(\frac{1}{8}\right)
\end{array}
\) -
Question 41 of 118
41. Question
A particle moves in the \(X Y\)-plane according to the law \(x=k t, y=k t(1-\alpha t)\), where \(k\) and \(\alpha\) are positive constants and \(t\) is time. The trajectory of the particle is
CorrectIncorrectHint
(b) \(x=k t \Rightarrow t=\frac{x}{k}\)
Now, \(y=k\left(\frac{x}{k}\right)\left(1-\alpha \cdot \frac{x}{k}\right)\)
or \(y=x-\frac{\alpha x^2}{k}\) -
Question 42 of 118
42. Question
The maximum range of a gun on horizontal terrain is \(1 \mathrm{~km}\). If \(g=10 \mathrm{~ms}^{-2}\), what must be the muzzle velocity of the shell?
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (c) } R_{\max }=\frac{u^2}{g} \text { at } \theta=45^{\circ} \\
\therefore \quad u=\sqrt{g R_{\max }}=100 \mathrm{~ms}^{-1}
\end{array}
\) -
Question 43 of 118
43. Question
The equation of trajectory of a projectile is \(y=\sqrt{3} x-\frac{g}{2} x^2\), the angle of its projection is
CorrectIncorrectHint
(c) Compare the given equation with
\(
\begin{aligned}
y & =x \tan \theta-\frac{g x^2}{2 u^2 \cos ^2 \theta} \\
\Rightarrow \quad \tan \theta & =\sqrt{3} \Rightarrow \theta=60^{\circ}
\end{aligned}
\) -
Question 44 of 118
44. Question
A projectile is thrown upward with a velocity \(v_0\) at an angle \(\alpha\) to the horizontal. The change in velocity of the projectile when it strikes the same horizontal plane is
CorrectIncorrectHint
(b) \(\Delta v=a \Delta t\) (As, \(a=\) constant)
\(
=(-g \hat{\mathbf{j}})\left(\frac{2 v_0 \sin \alpha}{g}\right)=\left(-2 v_0 \sin \alpha\right) \hat{\mathbf{j}}
\)
i.e. Change in velocity is \(2 v_0 \sin \alpha\), vertically downwards. -
Question 45 of 118
45. Question
The maximum height attained by a projectile is increased by \(10 \%\) by increasing its speed of projection, without changing the angle of projection. The percentage increase in the horizontal range will be
CorrectIncorrectHint
(c) We know that, \(\mathrm{R}=\frac{\mathrm{u}^2 \sin 2 \theta}{\mathrm{g}}\)
When the speed of projection is increased by \(5 \%, u^{\prime}=1.05 \mathrm{u}\)
So, \(R^{\prime}=\frac{(1.05 u)^2 \sin 2 \theta}{g} =\frac{1.1025 u^2 \sin 2 \theta}{g}=1.1025 R\)
\(R^{\prime}\) is approximately \(1.1 \mathrm{R}\).
Now, percentage increase in range \(=\frac{1.1 R-R}{R} \times 100=10 \%\) -
Question 46 of 118
46. Question
A body is projected at an angle of \(30^{\circ}\) with the horizontal with momentum p. At its highest point, the magnitude of the momentum is
CorrectIncorrectHint
(a) At highest point, velocity will remain \(v \cos 30^{\circ}\) or \(\frac{\sqrt{3} v}{2}\). Therefore, momentum will also remain \(p \cos 30^{\circ}=\frac{\sqrt{3} p}{2}\)
-
Question 47 of 118
47. Question
A projectile is fired from ground level at an angle \(\theta\) above the horizontal. The elevation angle \(\phi\) of the highest point as seen from the launch point is related to \(\theta\) by the relation
CorrectIncorrectHint
\(
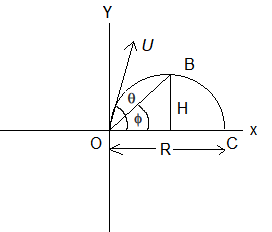
\begin{array}{ll}
\text { (c) } \tan \phi=\frac{H}{R / 2}=\frac{2 H}{R}=\frac{\left(u^2 \sin ^2 \theta / g\right)}{u^2 \sin 2 \theta / g} \\
\Rightarrow \quad \tan \phi=\frac{\sin ^2 \theta}{2 \sin \theta \cos \theta}=\frac{\tan \theta}{2}
\end{array}
\) -
Question 48 of 118
48. Question
A ball is thrown up with a certain velocity at an angle \(\theta\) to the horizontal. The kinetic energy \(\mathrm{KE}\) of the ball varies with horizontal displacement \(x\) as
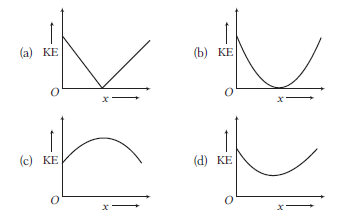CorrectIncorrectHint
(d) The kinetic energy of projectile first decreases from ground to highest point and after that increases upto ground. At highest point, kinetic energy will be minimum but not zero.
-
Question 49 of 118
49. Question
A body projected with velocity \(u\) at projection angle \(\theta\) has horizontal range \(R\). For the same velocity and projection angle, its range on the moon surface will be \(\left(g_{\text {moon }}=g_{\text {earth }} / 6\right)\)
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (d) } R \propto \frac{1}{g} \\
\therefore R_{\text {moon }}=6 R_{\text {earth }} \quad\left(\because g_{\text {moon }}=\frac{1}{6} g_{\text {carth }}\right)
\end{array}
\) -
Question 50 of 118
50. Question
Three balls of same masses are projected with equal speeds at angle \(15^{\circ}, 45^{\circ}, 75^{\circ}\), and their ranges are respectively \(R_1, R_2\) and \(R_3\), then
CorrectIncorrectHint
(d) At \(45^{\circ}\), range is maximum. At \(15^{\circ}\) and \(75^{\circ}\), ranges are equal.
\(
\begin{array}{l}
\text { As, } R_\theta=R_{90^{\circ}-\theta} \\
\because R_{15^{\circ}}=R_{75^{\circ}}<R_{45^{\circ}} \\
\Rightarrow \quad R_1=R_3<R_2
\end{array}
\) -
Question 51 of 118
51. Question
A projectile is thrown with an initial velocity of \((a \hat{\mathbf{i}}+b \hat{\mathbf{j}}) \mathrm{ms}^{-1}\). If the range of the projectile is twice the maximum height reached by it, then
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (c) } R=2 H \text { or } \frac{2 u_x u_y}{g}=\frac{2 u_y^2}{2 g} \\
\text { or } \quad 2 u_x=u_y \text { or } 2 a=b
\end{array}
\) -
Question 52 of 118
52. Question
The ratio of the speed of a projectile at the point of projection to the speed at the top of its trajectory is \(x\). The angle of projection with the horizontal is
CorrectIncorrectHint
(d) Speed of projectile at the point of projection \(=u\)
Speed of projectile at the top of its trajectory \(=u \cos \theta\)
\(
\frac{u}{u \cos \theta}=x \text { or } \cos \theta=\frac{1}{x} \Rightarrow \theta=\cos ^{-1}\left(\frac{1}{x}\right)
\) -
Question 53 of 118
53. Question
A man can throw a stone such that it acquires maximum horizontal range \(80 \mathrm{~m}\). The maximum height to which it will rise for the same projectile (in metre) is
CorrectIncorrectHint
(b) At \(\theta=45^{\circ}, R_{\max }=\frac{u^2}{g}=80\)
\(
\therefore \quad u^2=800 \mathrm{~ms}^{-2}
\)Now, \(\quad H=\frac{u^2 \sin ^2 45^{\circ}}{2 g}=\frac{(800)(1 / 2)}{20}=20 \mathrm{~m}\)
-
Question 54 of 118
54. Question
The velocity at the maximum height of a projectile is half of its initial velocity of projection \((u)\). Its range on horizontal plane is
CorrectIncorrectHint
(d) Given, \(u \cos \theta=\frac{u}{2} \Rightarrow \theta=60^{\circ}\)
Now, \(R=\frac{u^2 \sin 2 \theta}{g}=\frac{u^2 \sin 120^{\circ}}{g}=\frac{\sqrt{3} u^2}{2 g}\) -
Question 55 of 118
55. Question
A projectile is thrown from a point in a horizontal plane such that the horizontal and vertical velocities are \(9.8 \mathrm{~ms}^{-1}\) and \(19.6 \mathrm{~ms}^{-1}\). It will strike the plane after covering distance of
CorrectIncorrectHint
\(
\text { (a) } R=\frac{2 u_x u_y}{g}=\frac{2 \times 9.8 \times 19.6}{9.8}=39.2 \mathrm{~m}
\) -
Question 56 of 118
56. Question
The greatest height to which a man can throw a stone is \(h\). The greatest distance to which he can throw it will be
CorrectIncorrectHint
(c) Maximum height, \(H=\frac{u^2}{2 g}=h\) (Given)
Now, \(\quad R_{\max }=\frac{u^2 \sin 90^{\circ}}{g}=\frac{u^2}{g}=2 h\)
Alternate:
For greatest height \(\theta=90^{\circ}\)
\(
\begin{array}{l}
\mathrm{H}_{\max }=\frac{\mathrm{u}^2 \sin ^2\left(90^{\circ}\right)}{2 \mathrm{~g}}=\frac{\mathrm{u}^2}{2 \mathrm{~g}}=\mathrm{h} \text { (given) } \\
\mathrm{R}_{\max }=\frac{\mathrm{u}^2 \sin ^2 2\left(45^{\circ}\right)}{\mathrm{g}}=\frac{\mathrm{u}^2}{\mathrm{~g}}=2 \mathrm{~h}
\end{array}
\) -
Question 57 of 118
57. Question
Four bodies \(P, Q, R\) and \(S\) are projected with equal velocities having angles of projection \(15^{\circ}, 30^{\circ}, 45^{\circ}\) and \(60^{\circ}\) with the horizontal respectively. The body having shortest range is
CorrectIncorrectHint
(a) When the angle of projection is very far from \(45^{\circ}\), then range will be minimum. Therefore, the body \(P\) with angle of projection \(15^{\circ}\) will have a shortest range.
-
Question 58 of 118
58. Question
A stone is projected in air. Its time of flight is \(3 \mathrm{~s}\) and range is \(150 \mathrm{~m}\). Maximum height reached by the stone is (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(d) Time of flight, \(T=\frac{2 u_y}{g}=3\)
\(\therefore \quad u_y=15 \mathrm{~ms}^{-1}\)
Now, \(H=\frac{u_y^2}{2 g}=\frac{(15)^2}{20}=11.25 \mathrm{~m}\) -
Question 59 of 118
59. Question
A boy throws a ball with a velocity \(u\) at an angle \(\theta\) with the horizontal. At the same instant, he starts running with uniform velocity to catch the ball before it hits the ground. To achieve this, he should run with a velocity of
CorrectIncorrectHint
(a) Velocity of boy should be equal to the horizontal component of velocity of ball, i.e. \(u \cos \theta\).
-
Question 60 of 118
60. Question
Galileo writes that for angle of projection of a projectile at angle \(\left(45^{\circ}-\theta\right)\) and \(\left(45^{\circ}+\theta\right)\), the horizontal ranges described by the projectile are in the ratio of (if \(\theta \leq 45^{\circ}\) )
CorrectIncorrectHint
(c) For angle \(\left(45^{\circ}-\theta\right), R=\frac{u^2 \sin \left(90^{\circ}-2 \theta\right)}{g}=\frac{u^2 \cos 2 \theta}{g}\)
For angle \(\left(45^{\circ}+\theta\right), R=\frac{u^2 \sin \left(90^{\circ}+2 \theta\right)}{g}=\frac{u^2 \cos 2 \theta}{g}\)
Thus, ratio becomes 1: 1 . -
Question 61 of 118
61. Question
If time of flight of a projectile is \(10 \mathrm{~s}\). Range is \(500 \mathrm{~m}\). The maximum height attained by it will be
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (a) Time of flight, } T=\frac{2 u \sin \theta}{g}=10 \mathrm{~s} \\
\Rightarrow \quad u \sin \theta=50 \mathrm{~ms}^{-1} \\
\therefore \quad H=\frac{u^2 \sin ^2 \theta}{2 g}=\frac{(u \sin \theta)^2}{2 g}=\frac{50 \times 50}{2 \times 10}=125 \mathrm{~m}
\end{array}
\) -
Question 62 of 118
62. Question
A body of mass \(m\) is thrown upwards at an angle \(\theta\) with the horizontal with velocity \(v\). While rising up the velocity of the mass after \(t\) seconds will be
CorrectIncorrectHint
(c) Instantaneous velocity of rising mass after \(t\) second will be
\(
v_t=\sqrt{v_x^2+v_y^2}
\)
where, \(v_x=v \cos \theta=\) horizontal component of velocity
\(v_y=v \sin \theta-g t=\) vertical component of velocity.
\(
\begin{array}{ll}
\Rightarrow & v_t=\sqrt{(v \cos \theta)^2+(v \sin \theta-g t)^2} \\
\Rightarrow & v_t=\sqrt{v^2+g^2 t^2-(2 v \sin \theta) g t}
\end{array}
\) -
Question 63 of 118
63. Question
A stone is thrown at an angle \(\theta\) with the horizontal, reaches a maximum height \(H\). Then, the time of flight of stone will be
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (b) } H=\frac{u^2 \sin ^2 \theta}{2 g} \text { and } T=\frac{2 u \sin \theta}{g} \Rightarrow T^2=\frac{4 u^2 \sin ^2 \theta}{g^2} \\
\therefore \quad \frac{T^2}{H}=\frac{8}{g} \Rightarrow T=\sqrt{\frac{8 H}{g}}=2 \sqrt{\frac{2 H}{g}}
\end{array}
\) -
Question 64 of 118
64. Question
A ball is thrown up with a certain velocity at an angle \(\theta\) to the horizontal. The kinetic energy \(\mathrm{KE}\) of the ball varies with height \(h\) as
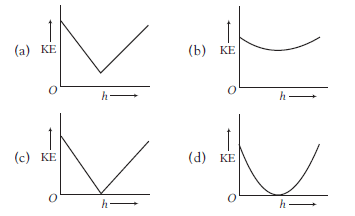CorrectIncorrectHint
(a) \(K=K_0-m g h\); Here \(K=\) kinetic energy at height \(h\), \(K_0=\) initial kinetic energy. Variation of \(K\) with \(h\) is linear. At highest point, kinetic energy is not zero.
-
Question 65 of 118
65. Question
For a given velocity, a projectile has the same range \(R\) for two angles of projection. If \(t_1\) and \(t_2\) are the time of flight in the two cases, then \(t_1 t_2\) is equal to
CorrectIncorrectHint
(a) \(R=\frac{u^2 \sin 2 \theta}{g}\) at angles \(\theta\) and \(90^{\circ}-\theta\)
Now, \(t_1=\frac{2 u \sin \theta}{g}\) and \(t_2=\frac{2 u \sin \left(90^{\circ}-\theta\right)}{g}=\frac{2 u \cos \theta}{g}\)
\(\therefore \quad t_1 t_2=\frac{2}{g}\left(\frac{u^2 \sin 2 \theta}{g}\right)=\frac{2 R}{g}\) -
Question 66 of 118
66. Question
A cricket ball is hit for a six by the bat at an angle of \(45^{\circ}\) to the horizontal with kinetic energy \(K\). At the highest point, the kinetic energy of the ball is
CorrectIncorrectHint
(c)
Kinetic Energy, \(\mathrm{K}=1 / 2 \mathrm{mv}^2\)
At the highest point, vertical component of velocity becomes zero and only the horizontal component is left that is given by
\(
\begin{array}{l}
u_x=u \cos \theta \\
\theta=45^{\circ}, \text { so } \cos \theta=1 / \sqrt{ } 2 \\
u_x=u / \sqrt{ } 2
\end{array}
\)Kinetic energy \(\mathrm{K}\) at the highest point \(=1 / 2 \mathrm{~m}(\mathrm{u} / \sqrt{ } 2)^2=\left(1 / 2 \times\left(\mathrm{mu}^2\right)\right) / 2\)
\(
=\mathrm{K} / 2
\)Â
-
Question 67 of 118
67. Question
The equation of motion of a projectile is
\(
y=12 x-\frac{3}{4} x^2
\)
What is the range of the projectile?CorrectIncorrectHint
\(
\text { (b) Substitute } y=0, \quad 0=12 x-\frac{3}{4} x^2 \Rightarrow x=16 \mathrm{~m}
\) -
Question 68 of 118
68. Question
A ball of mass \(m\) is projected from the ground with an initial velocity \(u\) making an angle of \(\theta\) with the vertical. What is the change in velocity between the point of projection and the highest point?
CorrectIncorrectHint
(a) \(\Delta v=a \Delta t=a \cdot\left(\frac{T}{2}\right)=(-g \hat{\mathbf{j}})\left(\frac{u \cos \theta}{g}\right)=(-u \cos \theta) \hat{\mathbf{j}}\)
Therefore, change in velocity is \(u \cos \theta\) in downward direction.
Explanation: As the projectile moves upwards vertical component of velocity changes only, there will be no effect on the horizontal component of velocity.
When velocity is broken in horizontal \((\mathrm{ucos} \theta\) ) and vertical \((\operatorname{usin} \theta)\) components then only vertical components decreases up to zero at peak point and then starts decreasing in Negative direction. -
Question 69 of 118
69. Question
The equation of projectile is \(Y=\sqrt{3} X-\frac{1}{2} g X^2\). The velocity of projection is
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (b) Comparing with } y=x \tan \theta-\frac{g x^2}{2 u^2 \cos ^2 \theta} \text {, we have } \\
\qquad \begin{aligned}
\tan \theta & =\sqrt{3} \text { or } \theta=60^{\circ} \text { and } u^2 \cos ^2 \theta=1 \\
\text { or } \quad u & =\sec \theta=\sec 60^{\circ}=2 \mathrm{~ms}^{-1}
\end{aligned}
\end{array}
\) -
Question 70 of 118
70. Question
The range of a projectile when launched at an angle \(\theta\) is same as when launched at angle \(2 \theta\). What is the value of \(\theta\) ?
CorrectIncorrectHint
(b) Range of projectile launched at an angle \(\theta\) is same as the range of projectile launched at angle \(2 \theta\).
\(
\begin{array}{l}
\Rightarrow \quad \frac{u^2 \sin 2(2 \theta)}{g}=\frac{u^2 \sin 2 \theta}{g} \\
\Rightarrow \quad \sin 2(2 \theta)=\sin 2 \theta \\
\Rightarrow \quad 2 \sin 2 \theta \cos 2 \theta=2 \sin \theta \cos \theta \\
4 \sin \theta \cos \theta \cos 2 \theta=2 \sin \theta \cos \theta \\
\Rightarrow \quad 4 \cos 2 \theta=2 \Rightarrow \cos 2 \theta=\frac{1}{2} \\
\Rightarrow \quad \cos 2 \theta=\cos 60^{\circ} \\
\Rightarrow \quad 2 \theta=60^{\circ} \\
\therefore \quad \theta=30^{\circ} \\
\end{array}
\) -
Question 71 of 118
71. Question
A particle is thrown with a speed \(u\) at an angle \(\theta\) with the horizontal. When the particle makes an angle \(\phi\) with the horizontal, its speed changes to \(v\), where
CorrectIncorrectHint
Initial horizontal speed = final horizontal speed
\(
\begin{aligned}
\Rightarrow u \cos \theta & =v \cos \phi \\
\Rightarrow v & =\frac{u \cos \theta}{\cos \phi}=u \cos \theta \sec \phi
\end{aligned}
\) -
Question 72 of 118
72. Question
An aeroplane moving horizontally with a speed of \(720 \mathrm{kmh}^{-1}\) drops a food pocket, while flying at a height of \(396.9 \mathrm{~m}\). The time taken by a food pocket to reach the ground and its horizontal range is (Take \(g=9.8 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(d) \(T=\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 3969}{9.8}}=9 \mathrm{~s}\)
and \(u=720 \mathrm{~km} / \mathrm{h}=200 \mathrm{~m} / \mathrm{s}\)
\(\)\therefore \quad R=u \times T=200 \times 9=1800 \mathrm{~m}[/latex -
Question 73 of 118
73. Question
A bullet is to be fired with a speed of \(2000 \mathrm{~ms}^{-1}\) to hit a target \(200 \mathrm{~m}\) away on a level ground. If \(g=10 \mathrm{~ms}^{-2}\), the gun should be aimed
CorrectIncorrectHint
(c) Let \(t\) be time taken by the bullet to hit the target.
\(
\begin{array}{ll}
\therefore & 200 \mathrm{~m}=2000 \mathrm{~ms}^{-1} t \\
\Rightarrow & t=\frac{200 \mathrm{~m}}{2000 \mathrm{~ms}^{-1}}=\frac{1}{10} \mathrm{~s}
\end{array}
\)
For vertical motion, here \(u=0\)
\(
\therefore \quad h=\frac{1}{2} g t^2
\)
\(
h=\frac{1}{2} \times 10 \times\left(\frac{1}{10}\right)^2=\frac{1}{20} \mathrm{~m}=5 \mathrm{~cm}
\)
\(\therefore\) Gun should be aimed \(5 \mathrm{~cm}\) above the target. -
Question 74 of 118
74. Question
A projectile has the maximum range \(500 \mathrm{~m}\). If the projectile is thrown up a smooth inclined plane of \(30^{\circ}\) with the same (magnitude) velocity, the distance covered by it along the inclined plane till it stops will be
CorrectIncorrectHint
(b) \(\quad R_{\max }=\frac{u^2}{g}=500\)
Now, \(s=\frac{u^2}{2 a}=\frac{u^2}{2 g \sin 30^{\circ}}=\frac{u^2}{g}=500 \mathrm{~m}\) -
Question 75 of 118
75. Question
A projectile \(A\) is thrown at an angle \(30^{\circ}\) to the horizontal from point \(P\). At the same time, another projectile \(B\) is thrown with velocity \(v_2\) upwards from the point \(Q\) vertically below the highest point \(A\) would reach. For \(B\) to collide with \(A\), the ratio \(\frac{v_2}{v_1}\) should be
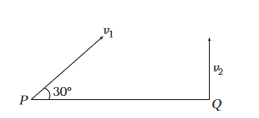CorrectIncorrectHint
(c) Vertical component of velocity of projectile \(A\) should be equal to vertical velocity of projectile \(B\).
or \(\quad v_1 \sin 30^{\circ}=v_2 \quad\) or \(\frac{v_1}{2}=v_2\)
\(\therefore \quad \frac{v_2}{v_1}=\frac{1}{2}\) -
Question 76 of 118
76. Question
A ball is thrown from a point \(O\) aiming a target at angle \(30^{\circ}\) with the horizontal, so that the ball hits the target at \(B\) but the ball hits at point \(A\), a vertical distance \(h\) below \(B\). If the initial velocity of the ball is \(20 \mathrm{~ms}^{-1}\) and the horizontal distance between \(O\) and \(C\) is \(10 \mathrm{~m}\). Find the value of \(h\).
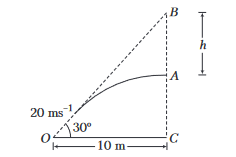CorrectIncorrectHint
(a) In moving horizontal distance \(10 \mathrm{~m}\), the ball will fall by distance \(\frac{1}{2} g t^2\).
\(
\begin{aligned}
\text { As, } \quad R & =u \cos \theta t \\
\Rightarrow \quad 10 & =20 \times \cos 30^{\circ} t=20 \times \frac{\sqrt{3}}{2} t \Rightarrow t=\frac{1}{\sqrt{3}} \mathrm{~s} \\
A B & =h=\frac{1}{2} g t^2=\frac{1}{2} \times g \times\left(\frac{1}{\sqrt{3}}\right)^2=\frac{g}{6} \mathrm{~m}
\end{aligned}
\) -
Question 77 of 118
77. Question
A ball is thrown from a point with a speed \(v_0\) at an angle of projection \(\theta\). From the same point and at the same instant, a person starts running with a constant speed \(v_0 / 2\) to catch the ball. Will the person be able to catch the ball? If yes, what should be the angle of projection?
CorrectIncorrectHint
(a) Person will catch the ball, if his velocity will be equal to horizontal component of velocity of the ball.
\(
\Rightarrow \frac{v_0}{2}=v_0 \cos \theta \Rightarrow \cos \theta=\frac{1}{2} \Rightarrow \theta=60^{\circ}
\) -
Question 78 of 118
78. Question
The initial velocity of a particle of mass \(2 \mathrm{~kg}\) is \((4 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}) \mathrm{ms}^{-1}\). A constant force of \(-20 \hat{\mathbf{j}} \mathrm{N}\) is applied on the particle. Initially, the particle was at \((0,0)\). Find the \(x\)-coordinate of the point, where its \(y\)-coordinate is again zero.
CorrectIncorrectHint
(a) We can see that it is like a projectile motion, with
\(
\begin{array}{l}
u_x=4 \mathrm{~ms}^{-1}, u_y=4 \mathrm{~ms}^{-1} \text { and } a_y=10 \mathrm{~ms}^{-2} . \\
x \text {-coordinate }=\text { Range }=\frac{2 u_x u_y}{g}=\frac{2 \times 4 \times 4}{10}=3.2 \mathrm{~m}
\end{array}
\) -
Question 79 of 118
79. Question
An object of mass \(m\) is projected with a momentum \(p\) at such an angle that its maximum height is \(1 / 4\) th of its horizontal range. Its minimum kinetic energy in its path will be
CorrectIncorrectHint
(b) It is given that, \(H=\frac{R}{4}\)
\(
\therefore \quad \frac{u^2 \sin ^2 \theta}{2 g}=\frac{2 u^2 \sin \theta \cos \theta}{4 g} \text { or } \tan \theta=1 \Rightarrow \theta=45^{\circ}
\)At highest point, momentum will remain \(\frac{p}{\sqrt{2}}\).
\(
\therefore \quad K=\frac{(p / \sqrt{2})^2}{2 m}=\frac{p^2}{4 m}
\) -
Question 80 of 118
80. Question
The equation of motion of a projectile are given by \(x=36 t \mathrm{~m}\) and \(2 y=96 t-9.8 t^2 \mathrm{~m}\). The angle of projection is
CorrectIncorrectHint
(a) It is given that, \(x=36 t\)
\(
\begin{array}{l}
\therefore \quad v_x=\frac{d x}{d t}=36 \mathrm{~ms}^{-1} \text { and } y=48 t-4.9 t^2 \\
\therefore \quad v_y=48-9.8 t \\
\text { At } \quad t=0 \quad v_x=36 \mathrm{~ms}^{-1} \text { and } v_y=48 \mathrm{~ms}^{-1} \\
\end{array}
\)So, angle of projection, \(\theta=\tan ^{-1}\left(\frac{v_y}{v_x}\right)\)
\(
\begin{aligned}
& =\tan ^{-1}\left(\frac{48}{36}\right)=\tan ^{-1}\left(\frac{4}{3}\right) \\
\theta & =\sin ^{-1}\left(\frac{4}{5}\right)
\end{aligned}
\) -
Question 81 of 118
81. Question
Two stones are projected so as to reach the same distance from the point of projection on a horizontal surface. The maximum height reached by one exceeds the other by an amount equal to half the sum of the height attained by them. Then, angle of projection of the stone which attains smaller height is
CorrectIncorrectHint
(c) It is given that, \(H_1-H_2=\frac{H_1+H_2}{2}\) or \(H_1=3 H_2\)
\(
\begin{array}{ll}
\therefore & \frac{u^2 \sin ^2 \theta}{2 g}=3\left(\frac{u^2 \sin ^2\left(90^{\circ}-\theta\right)}{2 g}\right) \\
\Rightarrow & \tan ^2 \theta=3 \\
\therefore & \tan \theta=\sqrt{3} \text { or } \theta=60^{\circ}
\end{array}
\)Therefore, the other angle is \(90^{\circ}-\theta\) or \(30^{\circ}\).
-
Question 82 of 118
82. Question
An arrow is shot into air. Its range is \(200 \mathrm{~m}\) and its time of flight is \(5 \mathrm{~s}\). If \(g=10 \mathrm{~ms}^{-2}\), then horizontal component of velocity and the maximum height will be respectively
CorrectIncorrectHint
(b) Time of flight, \(T=\frac{2 u_y}{g}\)
\(
\Rightarrow \quad u_y=\frac{g T}{2}=25 \mathrm{~ms}^{-1}
\)
Now, \(H=\frac{u_y^2}{2 g}=\frac{(25)^2}{20}=31.25 \mathrm{~m}\)
Further, \(\quad R=u_x T\)
\(
\Rightarrow \quad u_x=\frac{R}{T}=40 \mathrm{~ms}^{-1}
\) -
Question 83 of 118
83. Question
A body is projected from the ground with a velocity \(\mathbf{v}=(3 \hat{\mathbf{i}}+10 \hat{\mathbf{j}}) \mathrm{ms}^{-1}\). The maximum height attained and the range of the body respectively are (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(a) Given, \(\mathbf{v}=(3 \hat{\mathbf{i}}+10 \hat{\mathbf{j}}) \mathrm{ms}^{-1}, v_x=3 \mathrm{~ms}^{-1}, v_y=10 \mathrm{~ms}^{-1}\)
\(
\begin{array}{l}
H=\frac{v_y^2}{2 g}=\frac{100}{2 \times 10}=5 \mathrm{~m} \\
R=v_x \times T=v_x \times \frac{2 v_y}{g}=6 \mathrm{~m}
\end{array}
\) -
Question 84 of 118
84. Question
A cricket fielder can throw the cricket ball with a speed \(v_0\). If he throws the ball while running with speed \(u\) at an angle \(\theta\) to the horizontal, what is the effective angle to the horizontal at which the ball is projected in air as seen by a spectator?
CorrectIncorrectHint
(b) Consider the diagram below.
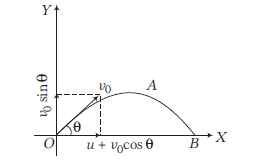
Initial velocity in \(x\)-direction, \(u_x=u+v_0 \cos \theta\) Initial velocity in \(y\)-direction, \(u_y=v_0 \sin \theta\) where, angle of projection is \(\theta\). Now, we can write
\(
\begin{aligned}
\tan \theta & =\frac{u_y}{u_x}=\frac{v_0 \sin \theta}{u+v_0 \cos \theta} \\
\Rightarrow \quad \theta & =\tan ^{-1}\left(\frac{v_0 \sin \theta}{u+v_0 \cos \theta}\right)
\end{aligned}
\) -
Question 85 of 118
85. Question
A particle is projected with a velocity of \(30 \mathrm{~ms}^{-1}\), at an angle of \(\theta_0=\tan ^{-1}\left(\frac{3}{4}\right)\). After \(1 \mathrm{~s}\), the particle is moving at an angle \(\theta\) to the horizontal, where \(\tan \theta\) will be equal to (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(d) \(u_x=u \cos \theta_0=30 \times \frac{4}{5}=24 \mathrm{~ms}^{-1}\)
and \(u_y=u \sin \theta_0=30 \times \frac{3}{5}=18 \mathrm{~ms}^{-1}\)
After \(1 \mathrm{~s}, u_x\) will remain same and \(u_y\) will decrease by \(10 \mathrm{~ms}^{-1}\) or it will become \(8 \mathrm{~ms}^{-1}\).
\(
\therefore \quad \tan \theta=\frac{v_y}{v_x}=\frac{8}{24}=\frac{1}{3}
\) -
Question 86 of 118
86. Question
A bomber plane moves horizontally with a speed of \(500 \mathrm{~ms}^{-1}\) and a bomb released from it, strikes the ground in \(10 \mathrm{~s}\). Angle at which it strikes the ground will be (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(a) Horizontal component of velocity, \(v_x=500 \mathrm{~ms}^{-1}\) and vertical component of velocity while striking the ground,
\(
v_y=0+10 \times 10=100 \mathrm{~ms}^{-1}
\)
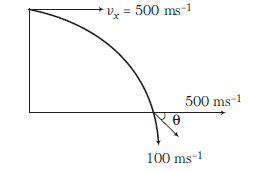
\(\therefore\) Angle with which it strikes the ground,
\(
\theta=\tan ^{-1}\left(\frac{v_y}{v_x}\right)=\tan ^{-1}\left(\frac{100}{500}\right)=\tan ^{-1}\left(\frac{1}{5}\right)
\) -
Question 87 of 118
87. Question
Two balls are thrown simultaneously from ground with same velocity of \(10 \mathrm{~ms}^{-1}\) but different angles of projection with horizontal. Both balls fall at same distance \(5 \sqrt{3} \mathrm{~m}\) from point of projection. What is the time interval between balls striking the ground?
CorrectIncorrectHint
(a) Given, \(5 \sqrt{3}=\frac{(10)^2 \sin 2 \theta}{g}\) or \(\sin 2 \theta=\frac{\sqrt{3}}{2}\)
\(
\therefore \quad 2 \theta=60^{\circ} \text { or } \theta=30^{\circ}
\)Two different angles of projection are therefore \(\theta\) and \(90^{\circ}-\theta\) or \(30^{\circ}\) and \(60^{\circ}\).
\(
\begin{array}{ll}
\therefore & T_1=\frac{2 u \sin 30^{\circ}}{g}=1 \mathrm{~s} \\
\therefore & T_2=\frac{2 u \sin 60^{\circ}}{g}=\sqrt{3} \mathrm{~s}
\end{array}
\)Hence, \(\Delta t=T_2-T_1=(\sqrt{3}-1) \mathrm{s}\)
-
Question 88 of 118
88. Question
A particle moves along a parabolic path \(y=-9 x^2\) in such a way that the \(x\)-component of velocity remains constant and has a value \(1 / 3 \mathrm{~ms}^{-1}\). The acceleration of the particle is
CorrectIncorrectHint
(d) Comparing with the trajectory of projectile in which particle is projected from certain height horizontally \(\left(\theta=0^{\circ}\right)\).
\(
y=x \tan \theta-\frac{g x^2}{2 u^2 \cos ^2 \theta}
\)Putting \(\theta=0^{\circ}\) and \(g=a=18 u^2=2 \mathrm{~ms}^{-2}\)
\(
\left(\because y=-9 x^2, u=\frac{1}{3} \mathrm{~ms}^{-1}\right)
\) -
Question 89 of 118
89. Question
A projectile can have same range from two angles of projection with same initial speed. If \(h_1\) and \(h_2\) be the maximum heights, then
CorrectIncorrectHint
\(
\text { (d) } R=\frac{u^2 \sin \theta}{g} \text { at angles } \theta \text { and } 90^{\circ}-\theta
\)
\(
h_1=\frac{u^2 \sin ^2 \theta}{2 g} \text { and } h_2=\frac{u^2 \sin ^2\left(90^{\circ}-\theta\right)}{2 g}=\frac{u^2 \cos ^2 \theta}{2 g}
\)
\(
\begin{aligned}
& h_1 h_2=\left(\frac{u^2 \sin 2 \theta}{g}\right)^2 \cdot \frac{1}{16}=\frac{R^2}{16} \\
\therefore \quad & R=4 \sqrt{h_1 h_2}
\end{aligned}
\) -
Question 90 of 118
90. Question
A ball is projected from ground with a speed of \(20 \mathrm{~ms}^{-1}\) at an angle of \(45^{\circ}\) with horizontal. There is a wall of \(25 \mathrm{~m}\) height at a distance of \(10 \mathrm{~m}\) from the projection point. The ball will hit the wall at a height of
CorrectIncorrectHint
(b) Since, \(u \sin \theta \times t=10 \mathrm{~m}\)
\(
\begin{aligned}
\Rightarrow & 20 \sin 45^{\circ} t & =10 \\
\Rightarrow & t & =\frac{10}{20 \sin 45^{\circ}}=\frac{1}{\sqrt{2}} \mathrm{~s}
\end{aligned}
\)
Now, \(y=\left(20 \sin 45^{\circ}\right) t-\frac{1}{2} g t^2\)
\(
=20 \times \frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}-\frac{1}{2} \times 10 \times \frac{1}{2}=7.5 \mathrm{~m}
\) -
Question 91 of 118
91. Question
A boy can throw a stone up to a maximum height of \(10 \mathrm{~m}\). The maximum horizontal distance that the boy can throw the same stone up to will be
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (d) } H_{\max }=\frac{u^2}{2 g}=10 \left(\because \theta=90^{\circ}\right) \\
\Rightarrow \quad u^2=200 \Rightarrow \quad R_{\max }=\frac{u^2}{g}=20 \mathrm{~m}
\end{array}
\) -
Question 92 of 118
92. Question
At the height \(80 \mathrm{~m}\), an aeroplane is moving with \(150 \mathrm{~ms}^{-1}\). A bomb is dropped from it so as to hit a target. At what distance from the target should the bomb be dropped? (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(a) The horizontal distance covered by bomb,
\(
B C=v_H \times \sqrt{\frac{2 h}{g}}=150 \sqrt{\frac{2 \times 80}{10}}=600 \mathrm{~m}
\)
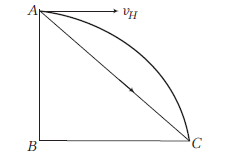
\(\therefore\) The distance of target from dropping point of bomb,
\(
A C=\sqrt{(A B)^2+(B C)^2}=\sqrt{(80)^2+(600)^2}=605.3 \mathrm{~m}
\) -
Question 93 of 118
93. Question
A ball is projected upwards from the top of a tower with velocity \(25 \mathrm{~ms}^{-1}\) making an angle of \(30^{\circ}\) with the horizontal. If the height of the tower is \(70 \mathrm{~m}\), after what time from the instant of throwing, will the ball reach the ground? (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
\(
\begin{array}{lr}
\text { (c) } s_y=u_y t+\frac{1}{2} a_y t^2 \text { or }-70=25 t-5 t^2 \\
\Rightarrow 5 t^2-25 t-70=0 \\
\Rightarrow t^2-5 t-14=0 \\
\Rightarrow t=7, t=-2 \\
\therefore t=7 \mathrm{~s}
\end{array}
\) -
Question 94 of 118
94. Question
From the top of a tower of height \(40 \mathrm{~m}\), a ball is projected upwards with a speed of \(20 \mathrm{~ms}^{-1}\) at an angle of elevation of \(30^{\circ}\). The ratio of the total time taken by the ball to hit the ground to its time of flight (time taken to come back to the same elevation) is (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(a) From \(s_y=u_y t+\frac{1}{2} a_y t^2\), we have
\(
-40=\left(20 \sin 30^{\circ}\right) t-5 t^2 \text { or } t^2-2 t-8=0
\)
Solving this, we get \(t=4 \mathrm{~s}\)
\(
\begin{aligned}
T & =\frac{2 \mu \sin \theta}{g}=\frac{2 \times 20 \times \sin 30^{\circ}}{10}=2 \mathrm{~s} \\
\Rightarrow \quad \frac{t}{T} & =2: 1
\end{aligned}
\) -
Question 95 of 118
95. Question
The coordinates of a moving particle at any time \(t\) are given by \(x=c t\) and \(y=b t^2\). The speed of the particle is given by
CorrectIncorrectHint
(b) Given, \(x=c t \quad \Rightarrow v_x=\frac{d x}{d t}=c\)
Also, \(y=b t^2 \Rightarrow v_y=\frac{d y}{d t}=2 b t\)
\(
\begin{aligned}
\therefore \text { Speed } & =|\mathbf{v}|=\sqrt{v_x^2+v_y^2}=\sqrt{(c)^2+(2 b t)^2} \\
& =\sqrt{c^2+4 b^2 t^2}
\end{aligned}
\) -
Question 96 of 118
96. Question
A ball rolls off the edge of a horizontal table top \(4 \mathrm{~m}\) high. If it strikes the floor at a point \(5 \mathrm{~m}\) horizontally away from the edge of the table, what was its speed at the instant it left the table?
CorrectIncorrectHint
\(
\text { (c) Using, } h=\frac{1}{2} g t^2 \text {, we get }
\)
\(
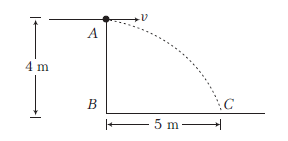
\begin{aligned}
h_{A B} & =\frac{1}{2} g t_{A C}^2 \\
\text { or } t_{A C} & =\sqrt{\frac{2 h_{A B}}{g}}=\sqrt{\frac{2 \times 4}{9.8}}=0.9 \mathrm{~s}
\end{aligned}
\)Further, \(\quad B C=v t_{A C}\) or
\(
v=\frac{B C}{t_{A C}}=\frac{5}{0.9}=5.55 \mathrm{~ms}^{-1}
\) -
Question 97 of 118
97. Question
A ball is thrown from the ground to a wall \(3 \mathrm{~m}\) high at a distance of \(6 \mathrm{~m}\) and falls \(18 \mathrm{~m}\) away from the wall, the angle of projection of ball is
CorrectIncorrectHint
\(
\text { (b) Here, } R=\frac{u^2 \sin 2 \theta}{g}=24 \dots(i)
\)
\(
\begin{array}{l}
y=x \tan \theta-\frac{g x^2}{2 u^2 \cos ^2 \theta} \\
3=6 \tan \theta-\frac{36 g}{2 u^2 \cos ^2 \theta} \dots(ii)
\end{array}
\)
From Eq. (i), we get
\(
\frac{g}{u^2}=\frac{\sin 2 \theta}{24}=\frac{\sin \theta \cos \theta}{12}
\)
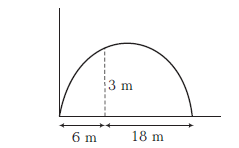
Substituting in Eq. (ii), we get
\(
3=6 \tan \theta-\frac{3}{2} \tan \theta=\frac{9}{2} \tan \theta \Rightarrow \theta=\tan ^{-1}\left(\frac{2}{3}\right)
\) -
Question 98 of 118
98. Question
The horizontal range and maximum height attained by a projectile are \(R\) and \(H\), respectively. If a constant horizontal acceleration \(a=g / 4\) is imparted to the projectile due to wind, then its horizontal range and maximum height will be
CorrectIncorrectHint
(d) \(H^{\prime}=H\) (as vertical component of acceleration has not changed)
\(
\begin{aligned}
R^{\prime} & =u_x T+\frac{1}{2} a_x T^2=R+\frac{1}{2} \times \frac{g}{4} \times \frac{4 u^2 \sin ^2 \theta}{g^2} \\
& =R+\frac{u^2 \sin ^2 \theta}{2 g}=(R+H)
\end{aligned}
\) -
Question 99 of 118
99. Question
An object is projected with a velocity of \(20 \mathrm{~ms}^{-1}\) making an angle of \(45^{\circ}\) with horizontal. The equation for trajectory is \(h=A x-B x^2\), where \(h\) is height, \(x\) is horizontal distance, \(A\) and \(B\) are constants. The ratio \(A: B\) is (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(d) Standard equation of projectile motion,
\(
y=x \tan \theta-\frac{g x^2}{2 u^2 \cos ^2 \theta}
\)Comparing with given equation,
\(
A=\tan \theta \text { and } B=\frac{g}{2 u^2 \cos ^2 \theta}
\)So,
\(
\frac{A}{B}=\frac{\tan \theta \times 2 u^2 \cos ^2 \theta}{g}=40: 1
\)
(As \(\theta=45^{\circ}, u=20 \mathrm{~ms}^{-1}, g=10 \mathrm{~ms}^{-2}\) ) -
Question 100 of 118
100. Question
If the instantaneous velocity of a particle projected as shown in figure is given by \(\mathbf{v}=a \hat{\mathbf{i}}+(b-c t) \hat{\mathbf{j}}\). where \(a, b\) and \(c\) are positive constants, the range on the horizontal plane will be
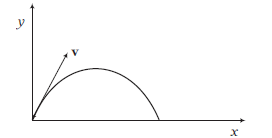CorrectIncorrectHint
(a) \(u_x=a, u_y=b, g=c\)
\(\therefore\) Horizontal range, \(R=\frac{2 u_x u_y}{g}=\frac{2 a b}{c}\) -
Question 101 of 118
101. Question
Two particles are simultaneously projected in opposite directions horizontally from a given point in space, where gravity \(g[latex] is uniform. If [latex]u_1\) and \(u_2\) be their initial speeds, then the time \(t\) after which their velocities are mutually perpendicular is given by
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (a) Given, } \mathbf{v}_1 \perp \mathbf{v}_2 \\
\therefore \quad \mathbf{v}_1 \cdot \mathbf{v}_2=0 \\
\text { or }\left(u_1 \hat{\mathbf{i}}-g t \hat{\mathbf{j}}\right) \cdot\left(-u_2 \hat{\mathbf{i}}-g t \hat{\mathbf{j}}\right)=0 \\
\therefore \quad g^2 t^2=u_1 u_2 \text { or } t=\frac{\sqrt{u_1 u_2}}{g}
\end{array}
\) -
Question 102 of 118
102. Question
A projectile is fired at an angle of \(30^{\circ}\) to the horizontal such that the vertical component of its initial velocity is \(80 \mathrm{~ms}^{-1}\). Its time of flight is \(T\). Its velocity at \(t=T / 4\) has a magnitude of nearly
CorrectIncorrectHint
\(
\begin{aligned}
\text { (d) } \tan 30^{\circ} & =\frac{u_y}{u_x} \\
\therefore \quad \frac{1}{\sqrt{3}} & =\frac{80}{u_x} \text { or } u_x=80 \sqrt{3} \mathrm{~ms}^{-1} \\
T & =\frac{2 u_y}{g}=\frac{2 \times 80}{10}=16 \mathrm{~s}
\end{aligned}
\)
\(
\text { At } t=\frac{T}{4}=4 \mathrm{~s} \Rightarrow v_x=u_x=80 \sqrt{3} \mathrm{~ms}^{-1} \text { and } v_y=u_y+a_y t
\)
\(
v_y=80+(-10)(4)=40 \mathrm{~ms}^{-1}
\)
\(
\therefore \text { Velocity }=\sqrt{\left(80 \sqrt{3)^2}+(40)^2\right.}=144.2 \mathrm{~ms}^{-1}
\) -
Question 103 of 118
103. Question
A projectile is thrown with some initial velocity at an angle \(\alpha\) to the horizontal. Its velocity when it is at the highest point is \((2 / 5)^{1 / 2}\) times the velocity when it is at height half of the maximum height. Find the angle of projection \(\alpha\) with the horizontal.
CorrectIncorrectHint
\(
\text { (c) }(u \cos \alpha)=\sqrt{\frac{2}{5}} \sqrt{(u \cos \alpha)^2+\left\{(u \sin \alpha)^2-2 g h\right\}} \dots(i)
\)
\(
\text { Here, } \quad h=\frac{H}{2}=\frac{u^2 \sin ^2 \alpha}{4 g} \dots(ii)
\)
Solving Eqs. (i) and (ii), we get
\(
\alpha=60^{\circ}
\) -
Question 104 of 118
104. Question
A very broad elevator is going up vertically with a constant acceleration of \(2 \mathrm{~ms}^{-2}\). At the instant when its velocity is \(4 \mathrm{~ms}^{-1}\), a ball is projected from the floor of the lift with a speed of \(4 \mathrm{~ms}^{-1}\) relative to the floor at an elevation of \(30^{\circ}\). The time taken by the ball to return the floor is (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(b) The motion relative to elevator,
\(
a_r=a_b-a_e=(-10)-(+2)=-12 \mathrm{~ms}^{-2}
\)Now, \(T=\frac{2 u_y}{\left|a_r\right|}=\frac{2 \times u \sin \theta}{\left|a_r\right|}=\frac{2 \times 4 \times \sin 30^{\circ}}{12}=\frac{1}{3} \mathrm{~s}\)
-
Question 105 of 118
105. Question
A grasshopper can jump a maximum distance of \(1.6 \mathrm{~m}\). How far can it go in \(10 \mathrm{~s}\) ?
CorrectIncorrectHint
(c) \(\quad R_{\max }=\frac{u^2}{g}=1.6 \mathrm{~m}\) (At \(\theta=45^{\circ}\) ) or \(u=\sqrt{16}=4 \mathrm{~ms}^{-1}\)
Now, \(\quad T=\frac{2 u_y}{g}=\frac{2(4 / \sqrt{2})}{10}=\frac{4}{5 \sqrt{2}} \mathrm{~s}\)
\(\therefore\) Total distance travelled in \(10 \mathrm{~s}=1.6 \times \frac{10}{4 / 5 \sqrt{2}}=20 \sqrt{2} \mathrm{~m}\) -
Question 106 of 118
106. Question
A body of mass \(1 \mathrm{~kg}\) is projected with velocity \(50 \mathrm{~ms}^{-1}\) at an angle of \(30^{\circ}\) with the horizontal. At the highest point of its path, a force \(10 \mathrm{~N}\) starts acting on body for \(5 \mathrm{~s}\) vertically upward besides gravitational force. What is the horizontal range of the body? (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(d) For \(5 \mathrm{~s}\), weight of the body is balanced by the given force. Hence, it will move in a straight line as shown in the figure.
\(
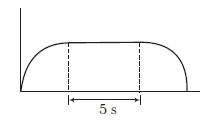
\begin{aligned}
R & =\frac{u^2 \sin 2 \theta}{g}+(u \cos \theta)(5) \\
& =\frac{(50)^2 \cdot \sin 60^{\circ}}{10}+\left(50 \times \cos 30^{\circ}\right)(5)=250 \sqrt{3} \mathrm{~m}
\end{aligned}
\) -
Question 107 of 118
107. Question
A projectile is thrown at an angle \(\theta\) such that it is just able to cross a vertical wall at its highest point as shown in the figure.
The angle \(\theta\) at which the projectile is thrown is given by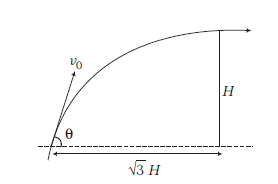
CorrectIncorrectHint
(c) From the given diagram, \(\frac{R / 2}{H}=\frac{\sqrt{3} H}{H}=\sqrt{3}\)
or \(\frac{\left(v_0^2 \sin \theta \cos \theta\right) / g}{\left(v_0^2 \sin ^2 \theta\right) / 2 g}=\sqrt{3} \Rightarrow 2 \cot \theta=\sqrt{3}\)\(
\tan \theta=\frac{2}{\sqrt{3}} \text { or } \theta=\tan ^{-1}\left(\frac{2}{\sqrt{3}}\right)
\) -
Question 108 of 118
108. Question
A jet aeroplane is flying at a constant height of \(2 \mathrm{~km}\) with a speed \(360 \mathrm{kmh}^{-1}\) above the ground towards a target and releases a bomb. After how much time, it will hit the target and what will be the horizontal distance of the aeroplane from the target, so that the bomb should hit the target? (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
\(
\text { (b) Given, } H=2000 \mathrm{~m}, u=360 \mathrm{kmh}^{-1}
\)
\(
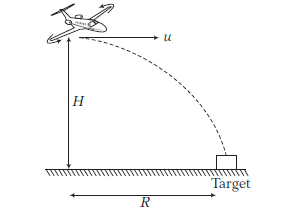
u=360 \times \frac{5}{18}=100 \mathrm{~ms}^{-1}
\)The time taken by the bomb to hit the target is
\(
T=\sqrt{\frac{2 H}{g}}=\sqrt{\frac{2 \times 2000}{10}}=20 \mathrm{~s}
\)The horizontal distance of the aeroplane from the target,
\(
R=u \sqrt{\frac{2 H}{g}}=100 \times 20=2000 \mathrm{~m}=2 \mathrm{~km}
\) -
Question 109 of 118
109. Question
Balls \(A\) and \(B\) are thrown from two points lying on the same horizontal plane separated by a distance \(120 \mathrm{~m}\). Which of the following is true?
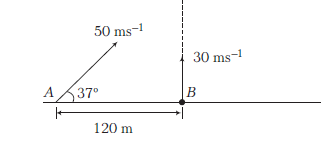CorrectIncorrectHint
(c) Two balls will meet, if \(\left(50 \cos 37^{\circ}\right) t_A=120[latex] or [latex]t_A=3 \mathrm{~s}\)
Vertical component of \(A\) is \(50 \sin 37^{\circ}\) or \(30 \mathrm{~ms}^{-1}\), so they will meet, if thrown simultaneously.
\(
h_A=h_B=30 \times 3-\frac{1}{2} \times 10 \times(3)^2=45 \mathrm{~m}
\) -
Question 110 of 118
110. Question
Two particles are projected from the same point with same speed \(u\) at angles of projection \(\alpha\) and \(\beta\) from horizontal. The maximum heights attained by them are \(h_1\) and \(h_2\) respectively, \(R\) is the range for both. If \(t_1\) and \(t_2\) are their times of flight respectively, then which amongst the option(s) is/are incorrect?
CorrectIncorrectHint
(d) (a) Range becomes equal at complimentary angle. Hence,
\(
\beta=90^{\circ}-\alpha \text { or } \alpha+\beta=90^{\circ}=\pi / 2
\)
\(
\begin{array}{l}
\text { (b) } \quad h_1=\frac{u^2 \sin ^2 \alpha}{2 g} \\
\Rightarrow \quad h_2=\frac{u^2 \cos ^2 \alpha}{2 g} \\
\text { (As, } \beta=90^{\circ}-\alpha \text { ) } \\
\therefore 4 \sqrt{h_1 h_2}=\frac{2 u^2 \sin \alpha \cos \alpha}{g}=\frac{u^2 \sin 2 \alpha}{g}=R \\
\end{array}
\)
(c) \(\quad \frac{t_1}{t_2}=\frac{(2 u \sin \alpha / g)}{(2 u \cos \alpha / g)}=\tan \alpha\)
(d) \(\sqrt{\frac{h_1}{h_2}}=\tan \alpha\) -
Question 111 of 118
111. Question
A particle is projected from the ground at an angle \(\theta\) with the horizontal with an initial speed \(u\). Time after which velocity vector of the projectile is perpendicular to the initial velocity.
CorrectIncorrectHint
(a) Since, \(\quad \mathbf{v} \perp \mathbf{u}\) or \(\mathbf{v} \cdot \mathbf{u}=0\)
\(
\begin{array}{r}
(\mathbf{u}+g t) \cdot \mathbf{u}=0 \\
\mathbf{u} \cdot \mathbf{u}+(g \cdot \mathbf{u}) t=0 \\
u^2+g u t \cos \left(90^{\circ}+\theta\right)=0
\end{array}
\)
(Angle between \(\mathbf{u}\) and \(g\) is \(90^{\circ}+\theta\) )
\(
\begin{aligned}
u-g t \sin \theta & =0 \\
t & =\frac{u}{g \sin \theta}
\end{aligned}
\) -
Question 112 of 118
112. Question
A particle is projected from horizontal making an angle of \(53^{\circ}\) with initial velocity of \(100 \mathrm{~ms}^{-1}\). The time taken by the particle to make angle \(45^{\circ}\) from horizontal is
CorrectIncorrectHint
(c) Component (100 \(\left.\cos 53^{\circ}\right) 60 \mathrm{~ms}^{-1}\) will remain unchanged. Velocity will make \(45^{\circ}\) with horizontal when vertical component also becomes \(\pm 60 \mathrm{~ms}^{-1}\).
\(
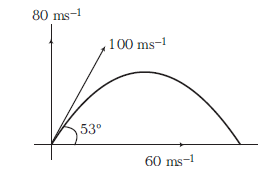
\begin{array}{l}
\text { Using } \quad v=u+a t \quad \text { (In vertical direction) } \\
+60=80+(-10) t_1 \\
\therefore \quad t_1=2 \mathrm{~s} \Rightarrow-60=80+(-10) t_2 \\
\therefore \quad t_2=14 \mathrm{~s} \\
\end{array}
\) -
Question 113 of 118
113. Question
A large number of bullets are fired in all directions with same speed \(v\). What is the maximum area on the ground on which these bullets will spread?
CorrectIncorrectHint
(b) Area in which bullet will spread \(=\pi r^2\)
For maximum area, \(r=R_{\max }=\frac{v^2}{g} \quad\left(\right.\) When \(\left.\theta=45^{\circ}\right)\)
Maximum area \(=\pi R_{\max }^2=\pi\left(\frac{v^2}{g}\right)^2=\frac{\pi v^4}{g^2}\) -
Question 114 of 118
114. Question
For a ground-to-ground projectile, an object is at point \(A\) at \(t=\frac{T}{3}\), at point \(B\) at \(t=\frac{5 T}{6}\) and reaches the ground at \(t=T\). The difference in heights between points \(A\) and \(B\) is
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (d) As, } T=\frac{2 u_y}{g} \Rightarrow u_y=\frac{g T}{2} \\
\Rightarrow \quad h_A=u_y t_A-\frac{1}{2} g t_A^2=u_y\left(\frac{2 u_y}{3 g}\right)-\frac{1}{2} g\left(\frac{2 u_y}{3 g}\right)^2 \\
=\frac{4}{9} \frac{u_y^2}{g}=\left(\frac{4}{9 g}\right)\left(\frac{g T}{2}\right)^2=\frac{g T^2}{9} \quad\left(\because u_y=\frac{g T}{2}\right) \\
\Rightarrow \quad h_B=u_y\left(\frac{5}{6} \times \frac{2 u_y}{g}\right)-\frac{1}{2} \times g \times\left(\frac{5}{6} \times \frac{2 u_y}{g}\right)^2 \\
=\frac{5}{18} \frac{u_y^2}{g}=\frac{5}{18 g}\left(\frac{g T}{2}\right)^2=\frac{5}{72} g T^2 \\
\therefore \quad h_A-h_B=\frac{g T^2}{24} \\
\end{array}
\) -
Question 115 of 118
115. Question
A cart is moving horizontally along a straight line with a constant speed of \(30 \mathrm{~ms}^{-1}\). A projectile is to be fired from the moving cart in such a way that it will return to the cart (at the same point on cart) after the cart has moved \(80 \mathrm{~m}\). At what velocity (relative to the cart) must projectile be fired? (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(c) The time taken by cart to cover \(80 \mathrm{~m}\),
\(
\frac{s}{v}=\frac{80}{30}=\frac{8}{3} \mathrm{~s}
\)The projectile must be fired (relative to cart) in vertically upward direction.
i.e. \(\quad a=-g=-10 \mathrm{~ms}^{-2}, v^{\prime}=0\) and \(t=\frac{8 / 3}{2}=\frac{4}{3} \mathrm{~s}\)
\(\therefore \quad v^{\prime}=u+a t\) or \(0=u-10 \times \frac{4}{3}\) or \(u=\frac{40}{3} \mathrm{~ms}^{-1}\) -
Question 116 of 118
116. Question
Two second after projection, a projectile is travelling in a direction inclined at \(30^{\circ}\) with the horizontal. After 1 more second, it is travelling horizontally. Then, (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (a) } T / 2=2+1=3 \mathrm{~s} \text { or } T=6 \mathrm{~s} \\
\Rightarrow \quad \frac{2 u_y}{g}=6 \\
\therefore \quad u_y=30 \mathrm{~ms}^{-1} \\
\text { Further, } \tan 30^{\circ}=\frac{v_y}{v_x}=\frac{u_y-g t}{u_x}=\frac{30-20}{u_x} \\
\text { or } \quad u_x=10 \sqrt{3} \mathrm{~ms}^{-1} \\
\text { or } u=\sqrt{u_x^2+u_y^2}=20 \sqrt{3} \mathrm{~ms}^{-1} \\
\qquad \tan \theta=\frac{u_y}{u_x}=\frac{30}{10 \sqrt{3}}=\sqrt{3} \text { or } \theta=60^{\circ}
\end{array}
\) -
Question 117 of 118
117. Question
A ball rolls off top of a stair way with a horizontal velocity \(u \mathrm{~ms}^{-1}\). If the steps are \(h\) metres high and \(b\) metres wide, the ball will just hit the edge of \(n\)th step, if \(n\) equals to
CorrectIncorrectHint
(c) If the ball hits the \(n\)th step, the horizontal and vertical distances traversed are \(n b\) and \(n h\), respectively. Let \(t\) be the time taken by the ball for these horizontal and vertical displacement. Then, velocity along horizontal direction remains constant \(=u\), initial vertical velocity is zero.
\(
\begin{aligned}
\therefore \quad n b & =u t \dots(i)\\
n h & =0+(1 / 2) g t^2 \dots(ii)
\end{aligned}
\)From Eqs. (i) and (ii), we get by eliminating \(t\),
\(
n h=(1 / 2) g(n b / u)^2 \Rightarrow n=\frac{2 h u^2}{g b^2}
\) -
Question 118 of 118
118. Question
A hill is \(500 \mathrm{~m}\) high. Supplies are to be sent across the hill using a canon that can hurl packets at a speed of \(125 \mathrm{~ms}^{-1}\) over the hill. The canon is located at a distance of \(800 \mathrm{~m}\) from the foot of hill and can be moved on the ground at a speed of \(2 \mathrm{~ms}^{-1}\), so that its distance from the hill can be adjusted. What is the shortest time in which a packet can reach on the ground across the hill? (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(d) Given, speed of packets \(=125 \mathrm{~ms}^{-1}\)
Height of the hill \(=500 \mathrm{~m}\).
To cross the hill, the vertical component of the velocity should be sufficient to cross such height.
\(
\begin{aligned}
u_y & \geq \sqrt{2 g h} \\
& \geq \sqrt{2 \times 10 \times 500} \geq 100 \mathrm{~ms}^{-1}
\end{aligned}
\)
But
\(
u^2=u_x^2+u_y^2
\)
\(\therefore\) Horizontal component of initial velocity,
\(
\begin{aligned}
u_x & =\sqrt{u^2-u_y^2} \\
& =\sqrt{(125)^2-(100)^2} \\
& =75 \mathrm{~ms}^{-1}
\end{aligned}
\)
Time taken to reach the top of the hill,
\(
t=\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 500}{10}}=10 \mathrm{~s}
\)
Time taken to reach the ground from the top of the hill,
\(
t^{\prime}=t=10 \mathrm{~s}
\)
Horizontal distance travelled in \(10 \mathrm{~s}\),
\(
\begin{aligned}
x & =u_x \times t=75 \times 10 \\
& =750 \mathrm{~m}
\end{aligned}
\)
\(\therefore\) Distance through which canon has to be moved
\(
=800-750=50 \mathrm{~m}
\)
Speed with which canon can move \(=2 \mathrm{~ms}^{-1}\)
\(\therefore\) Time taken by canon, \(t^{\prime}=\frac{50}{2}\)
\(
\Rightarrow \quad=25 \mathrm{~s}
\)
\(\therefore\) Total time taken by a packet to reach on the ground
\(
\begin{array}{l}
=t^{\prime \prime}+t+t^{\prime} \\
=25+10+10=45 \mathrm{~s}
\end{array}
\)