Motion in a Plane (Projectile Motion-Entrance Paper) Quiz-L2
Quiz Summary
0 of 60 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 60 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 60
1. Question
When an object is shot from the bottom of a long smooth inclined plane kept at an angle \(60^{\circ}\) with horizontal, it can travel a distance \(x_1\) along the plane. But when the inclination is decreased to \(30^{\circ}\) and the same object is shot with the same velocity, it can travel \(x_2\) distance. Then, \(x_1: x_2\) will be [NEET 2019]
CorrectIncorrectHint
(b) The motion of the object shot in two cases can be depicted as below
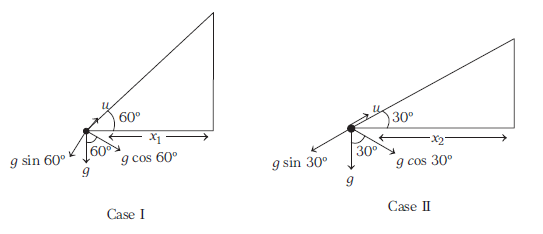
Using third equation of motion, \(v^2=u^2-2 g h\)
As the object stops finally, so \(v=0\)
For inclined motion, \(g=g \sin \theta\) and \(h=x\)
Substituting these values in Eq. (i), we get
\(
\begin{array}{ll}
\Rightarrow & u^2=2 g \sin \theta x \\
\Rightarrow & x=\frac{u^2}{2 g \sin \theta}
\end{array}
\)
\(
\text { For case I: } \quad x_1=\frac{u^2}{2 g \sin 60^{\circ}}
\)
\(
\text { For case II: } \quad \begin{aligned}
x_2 & =\frac{u^2}{2 g \sin 30^{\circ}} \\
\because \quad \frac{x_1}{x_2} & =\frac{u^2}{2 g \sin 60^{\circ}} \times \frac{2 g \sin 30^{\circ}}{u^2} \\
& =\frac{1}{2} \times \frac{2}{\sqrt{3}}=\frac{1}{\sqrt{3}} \text { or } 1: \sqrt{3}
\end{aligned}
\) -
Question 2 of 60
2. Question
Two bullets are fired horizontally and simultaneously towards each other from roof tops of two buildings \(100 \mathrm{~m}\) apart and of same height of \(200 \mathrm{~m}\) with the same velocity of \(25 \mathrm{~ms}^{-1}\). When and where will the two bullets collides?
(Take, \(g=10 \mathrm{~ms}^{-2}\) ) [NEET (Odisha) 2019]CorrectIncorrectHint
(a) Given, distance between the two buildings, \(d=100 \mathrm{~m}\)
Height of each tower, \(h=200 \mathrm{~m}\)
Speed of each bullet, \(v=25 \mathrm{~ms}^{-1}\)
The situation can be shown as below.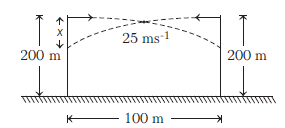
where, \(x\) be the vertical distance travelled from the top of the building and \(t\) be the time at which they collide.
As two bullets are fired toward each other, so their relative velocity will be
\(
v_{\text {rel }}=25-(-25)=50 \mathrm{~ms}^{-1}
\)
Then, time, \(\quad t=\frac{d}{v_{\text {rel }}}=\frac{100}{50}=2 \mathrm{~s}\)
The distance or height at which they collide is calculated from equation of motion,
\(
x=u t+\frac{1}{2} a t^2
\)
The bullet is initially at rest, i.e. \(u=0\) and as it is moving under the effect of gravity \(a=-g\), so
The bullet is initially at rest, i.e. \(u=0\) and as it is moving under the effect of gravity \(a=-g\), so
\(
\begin{array}{l}
x=-\frac{1}{2} g t^2 \\
x=-\frac{1}{2} \times 10(2)^2=-20 \mathrm{~m}
\end{array}
\)
The negative sign shows that the bullets will collide \(20 \mathrm{~m}\) below the top of tower, i.e. at a height of \((200-20)=180 \mathrm{~m}\) from the ground after \(2 \mathrm{~s}\). -
Question 3 of 60
3. Question
Assertion: The maximum height of projectile is always \(25 \%\) of the maximum range.
Reason: For maximum range, projectile should be projected at \(90^{\circ}\). [AIIMS 2018]CorrectIncorrectHint
(c) To obtain maximum range, angle of projection must be \(45^{\circ}\), i.e. \(\theta=45^{\circ}\).
\(
\begin{aligned}
& R_{\max }=\frac{u^2 \sin \left(2 \times 45^{\circ}\right)}{g}=\frac{u^2}{g} \\
\because & H_{\max }=\frac{u^2 \sin ^2 45^{\circ}}{2 g}=\frac{u^2}{4 g}=\frac{R_{\max }}{4}
\end{aligned}
\)
So, \(H_{\max }\) is \(25 \%\) of \(R_{\max }\) -
Question 4 of 60
4. Question
What is the range of a projectile thrown with velocity \(98 \mathrm{~ms}^{-1}\) with angle \(30^{\circ}\) from horizontal ? [JIPMER 2018]
CorrectIncorrectHint
(a) Given, \(u=98 \mathrm{~ms}^{-1}\) and \(\theta=30^{\circ}\)
\(\because\) Range of a projectile,
\(
\begin{array}{l}
R=\frac{u^2 \sin (2 \theta)}{g}=\frac{98 \times 98 \times \sin 60^{\circ}}{9.8} \\
R=490 \sqrt{3} \mathrm{~m}
\end{array}
\) -
Question 5 of 60
5. Question
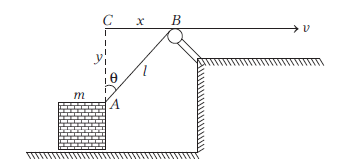
A block is dragged on a smooth plane with the help of a rope which moves with a velocity \(v\) as shown in the figure. The horizontal velocity of the block is [AIIMS 2017]
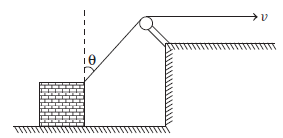 CorrectIncorrect
CorrectIncorrectHint
(a) Let at any instant of time, the length \(A B\) be \(l\), here angle \(\theta\) and length \(l\) vary with time, then using Pythagoras theorem in \(\triangle A B C\),
\(
x^2+y^2=l^2
\)On differentiating both sides w.r.t \(t\), we get or \(2 x \frac{d x}{d t}+2 y \frac{d y}{d t}=2 l \frac{d l}{d t}\)
As, there is no vertical motion of the block, so
\(
\frac{d y}{d t}=0, \frac{d x}{d t}=v_x \text { and } \frac{d l}{d t}=v
\)
\(
\begin{aligned}
2 x v_x & =2 l v \\
v_x & =\frac{l}{x} v \quad \text { or } \quad v_x=\frac{v}{\left(\frac{x}{l}\right)}=\frac{v}{\sin \theta}
\end{aligned}
\) -
Question 6 of 60
6. Question
Assertion: When \(\theta=45^{\circ}\) or \(135^{\circ}\), the value of \(R\) remains the same, only the sign changes.
Reason: \(R=\frac{u^2 \sin 2 \theta}{g}\) [AIIMS 2017]CorrectIncorrectHint
\(
\text { (a) Horizontal range, } R=\frac{u^2 \sin 2 \theta}{g}
\)When \(\theta=45^{\circ}\), maximum horizontal range,
\(
R_{\max }=\frac{u^2}{g} \sin 90^{\circ}=\frac{u^2}{g}
\)
When \(\theta=135^{\circ}\), maximum horizontal range,
\(
R=\frac{u^2}{g} \sin 270^{\circ}=\frac{-u^2}{g}
\)
Negative sign implies opposite direction. -
Question 7 of 60
7. Question
The \(x\) and \(y\)-coordinates of a particle moving in a plane are given by \(x(t)=a \cos (p t)\) and \(y(t)=b \sin (p t)\), where \(a, b(<a)\) and \(p\) are positive constants of appropriate dimensions and \(t\) is time. Then, which of the following is not true? [JIPMER 2017]
CorrectIncorrectHint
(d) Given, \(x=a \cos (p t), y=b \sin (p t)\) \(\therefore \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\), i.e. equation of ellipse
Now,
\(
\begin{array}{l}
\mathbf{r}=x \hat{\mathbf{i}}+y \hat{\mathbf{j}}=a \cos (p t) \hat{\mathbf{i}}+b \sin (p t) \hat{\mathbf{j}} \\
\mathbf{v}=\frac{d \mathbf{r}}{d t}=-p a \sin (p t) \hat{\mathbf{i}}+p b \cos (p t) \hat{\mathbf{j}} \\
\mathbf{a}=\frac{d \mathbf{v}}{d t}=-p^2 a \cos (p t) \hat{\mathbf{i}}-p^2 b \sin (p t) \hat{\mathbf{j}}
\end{array}
\)
\(
\text { At } \quad \begin{aligned}
t & =\frac{\pi}{2 p}, \\
\mathbf{v} & =-p a \hat{i} \text { and } \mathbf{a}=-p^2 \hat{\mathbf{j}}
\end{aligned}
\)
Thus, velocity is perpendicular to acceleration.
Also, \(a=-p^2 b\), i.e. directed towards a fixed point as \(p\) and \(b\) are positive constants.
\(
\begin{array}{ll}
\text { As, } & v=\frac{d r}{d t} \Rightarrow \Delta r=\int_0^{\frac{\pi}{2 p}} v d t \\
\Rightarrow & \Delta r=[a \cos (p t) \hat{\mathbf{i}}+b \sin (p t) \hat{\mathbf{j}}]_0^{\frac{\pi}{2 p}}=-a \hat{\mathbf{i}}+b \hat{\mathbf{j}} \\
\text { So, } & |\mathbf{r}|=\sqrt{a^2+b^2}
\end{array}
\) -
Question 8 of 60
8. Question
A particle moves, so that its position vector is given by \(\mathbf{r}=\cos \omega t \hat{\mathbf{x}}+\sin \omega t \hat{\mathbf{y}}\), where \(\omega\) is a constant. Which of the following is true? [NEET 2016]
CorrectIncorrectHint
(b) Position vector of the particle is given by
\(
\mathbf{r}=\cos \omega t \hat{\mathbf{x}}+\sin \omega t \hat{\mathbf{y}}
\)
where, \(\omega\) is a constant.
Velocity of the particle is
\(
\begin{aligned}
\mathbf{v} & =\frac{d \mathbf{r}}{d t}=\frac{d}{d t}(\cos \omega t \hat{\mathbf{x}}+\sin \omega t \hat{\mathbf{y}}) \\
& =(-\sin \omega t) \omega \hat{\mathbf{x}}+(\cos \omega t) \omega \hat{\mathbf{y}} \\
& =-\omega(\sin \omega t \hat{\mathbf{x}}-\cos \omega t \hat{\mathbf{y}})
\end{aligned}
\)
Acceleration of the particle,
\(
\begin{aligned}
\mathbf{a} & =\frac{d \mathbf{v}}{d t}=\frac{d}{d t}(-\omega \sin \omega t \hat{\mathbf{x}}+\omega \cos \omega t \hat{\mathbf{y}}) \\
& =-\omega^2 \cos \omega t \hat{\mathbf{x}}-\omega^2 \sin \omega t \hat{\mathbf{y}} \\
\Rightarrow \quad \mathbf{a} & =-\omega^2 \mathbf{r}=\omega^2(-\mathbf{r})
\end{aligned}
\)
Assuming the particle is at \(P\), then its position vector is directed as shown in the diagram.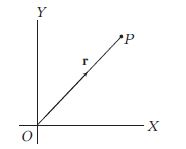
Therefore, acceleration is directed towards \(-\mathbf{r}\), i.e. towards \(O\) (origin).
\(
\begin{aligned}
\mathbf{v} \cdot \mathbf{r} & =-\omega(\sin \omega t \hat{\mathbf{x}}-\cos \omega t \hat{\mathbf{y}}) \cdot(\cos \omega t \hat{\mathbf{x}}+\sin \omega t \hat{\mathbf{y}}) \\
& =-\omega[\sin \omega t \cdot \cos \omega t+0+0-\sin \omega t \cdot \cos \omega t] \\
& =-\omega(0)=0 \\
\Rightarrow \mathbf{v} & \perp \mathbf{r}
\end{aligned}
\)
Thus, velocity is perpendicular to \(\mathbf{r}\) -
Question 9 of 60
9. Question
A particle is projected with an angle of projection \(\theta\) to the horizontal line passing through the points \((P, Q)\) and \((Q, P)\) referred to horizontal and vertical axes (can be treated as \(X\)-axis and \(\)Y\(\)-axis, respectively). The angle of projection can be given by [AIIMS 2015]
CorrectIncorrectHint
(a) The equation of trajectory,
\(
\begin{aligned}
y & =x \tan \alpha\left[1-\frac{x}{R}\right] \text { (Gives) } \\
Q & =P \tan \theta\left[1-\frac{P}{R}\right] \dots(i) \\
\text { and } \quad P & =Q \tan \theta\left[1-\frac{Q}{R}\right] \dots(ii)
\end{aligned}
\)On dividing Eq. (i) by Eq. (ii), we get
\(
\begin{aligned}
\frac{Q^2}{P^2} & =\frac{[1-P / R]}{[1-Q / R]} \\
\frac{1}{R}\left[P^3-Q^3\right] & =P^2-Q^2
\end{aligned}
\)
\(
R=\frac{P^3-Q^3}{P^2-Q^2}=\frac{P^2+P Q+Q^2}{P+Q}
\)
\(
\begin{aligned}
\frac{Q}{P} & =\tan \theta\left[1-\frac{P(P+Q)}{P^2+P Q+Q^2}\right] \\
& =\tan \theta\left[\frac{P^2+P Q+Q^2-P^2-P Q}{P^2+P Q+Q^2}\right] \\
\tan \theta & =\frac{P^2+Q^2+P Q}{P Q} \\
\theta & =\tan ^{-1}\left[\frac{P^2+P Q+Q^2}{P Q}\right]
\end{aligned}
\) -
Question 10 of 60
10. Question
An object is thrown towards the tower which is at a horizontal distance of \(50 \mathrm{~m}\) with an initial velocity of \(10 \mathrm{~ms}^{-1}\) and making an angle \(30^{\circ}\) with the horizontal. The object hits the tower at certain height. The height from the bottom of the tower, where the object hits the tower is (Take, \(g=10 \mathrm{~ms}^{-2}\) ) [EAMCET 2015]
CorrectIncorrectHint
(a) Consider the diagram below
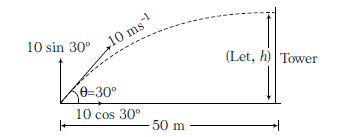
For horizontal motion, \(50=10 \cos 30^{\circ} \times t\)
\(
\Rightarrow \quad t=\frac{5}{\cos 30^{\circ}}=\frac{5}{\frac{\sqrt{3}}{2}}=\frac{10}{\sqrt{3}}
\)
For vertical motion,
\(
\begin{aligned}
h & =10 \sin 30^{\circ} \times \frac{10}{\sqrt{3}}-\frac{1}{2} \times 10 \times\left(\frac{10}{\sqrt{3}}\right)^2 \\
& =10 \times \frac{1}{2} \times \frac{10}{\sqrt{3}}-\frac{100}{\sqrt{3}} \times \frac{5}{\sqrt{3}}=\frac{100}{\sqrt{3}}\left(\frac{1}{2}-\frac{5}{\sqrt{3}}\right) \\
& =\frac{50}{\sqrt{3}}\left[1-\frac{10}{\sqrt{3}}\right] \mathrm{m}
\end{aligned}
\) -
Question 11 of 60
11. Question
The range of a projectile is \(R\) when the angle of projection is \(40^{\circ}\). For the same velocity of projection and range, the other possible angle of projection is [Kerala CEE 2015]
CorrectIncorrectHint
(b)
\(
\begin{array}{l}
\text { Range }=\frac{\mathrm{u}^2 \sin 2 \theta}{\mathrm{g}} \\
\text { Range }=\frac{\mathrm{u}^2(2 \sin \theta \cos \theta)}{\mathrm{g}}=\frac{\mathrm{u}^2\left(2 \sin \left(90^{\circ}-\theta\right) \cos \left(90^{\circ}-\theta\right)\right)}{\mathrm{g}}
\end{array}
\)Range of projectile is same for \(\theta\) and \(90^{\circ}-\theta\).
Given, \(\theta=40^{\circ}\)
Another angle \(=90^{\circ}-\theta=90^{\circ}-40^{\circ}=50^{\circ}\) -
Question 12 of 60
12. Question
A particle is projected with a velocity \(v\), so that its horizontal range twice the greatest height attained. The horizontal range is [KCET 2015]
CorrectIncorrectHint
(a)
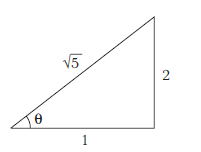
Given, a particle having horizontal range is twice the greatest height attained by it, i.e. \(\mathrm{R}=2 \mathrm{H}\)
\(
\begin{array}{ll}
& \frac{v^2 \sin 2 \theta}{g}=\frac{2 v^2 \sin ^2 \theta}{2 g} \\
\Rightarrow & 2 \sin \theta \cos \theta=\sin ^2 \theta \Rightarrow \tan \theta=2 \\
\Rightarrow & \sin \theta=\frac{2}{\sqrt{5}} \Rightarrow \cos \theta=\frac{1}{\sqrt{5}} \\
\therefore \quad & R=\frac{v^2 \sin 2 \theta}{g}=\frac{v^2 \times 2 \sin \theta \cos \theta}{g} \\
\Rightarrow \quad & R=v^2 \times \frac{2}{g} \times \frac{2}{\sqrt{5}} \times \frac{1}{\sqrt{5}} \\
\text { i.e. } & R=\frac{4 v^2}{5 g}
\end{array}
\) -
Question 13 of 60
13. Question
If the angle of projection of a projector with same initial velocity exceed or fall short of \(45^{\circ}\) by equal amount \(\alpha\), then the ratio of horizontal ranges is [Kerala CEE 2014]
CorrectIncorrectHint
(d) Given, \(\theta_1=\theta_2=45^{\circ}\)
\(
\begin{array}{l}
\theta_1+\theta_2=\left(45^{\circ}+\alpha\right)+\left(45^{\circ}-\alpha\right)=90^{\circ} \\
u_1=u_2=u \Rightarrow R_1=R_2=\text { ? } \\
R_1=\frac{u_1^2 \sin \left(\theta_1+\theta_2\right)}{g} \\
\Rightarrow \quad R_1=\frac{u^2 \sin 90^{\circ}}{g}=\frac{u^2}{g} \dots(i)\\
\Rightarrow \quad R_2=\frac{u^2 \sin 90^{\circ}}{g}=\frac{u^2}{g} \\
\end{array}
\)Similarly, \(R_2=\frac{u_2^2 \sin \left(\theta_1+\theta_2\right)}{g} \dots(ii)\)
\(
\Rightarrow \quad R_2=\frac{u^2 \sin 90^{\circ}}{g}=\frac{u^2}{g}
\)
The ratio of horizontal ranges
\(
\frac{R_1}{R_2}=\frac{u^2 / g}{u^2 / g}=1: 1 \Rightarrow \quad R_1: R_2=1: 1
\) -
Question 14 of 60
14. Question
A particle is moving such that its position coordinates \((x, y)\) are \((2 m, 3 m)\) at time \(t=0,(6 m, 7 m)\) at time \(t=2 \mathrm{~s}\) and \((13 \mathrm{~m}, 14 \mathrm{~m})\) at time \(t=5 \mathrm{~s}\). Average velocity vector \(\left(v_{\text {av }}\right)\) from \(t=0\) to \(5 \mathrm{~s}\) is [CBSE AIPMT 2014]
CorrectIncorrectHint
Average velocity,
\(
\begin{aligned}
\mathbf{v}_{\mathrm{av}} & =\frac{\text { Net displacement }}{\text { Time taken }} \\
& =\frac{(13-2) \hat{\mathbf{i}}+(14-3) \hat{\mathbf{j}}}{5} \\
& =\frac{11 \hat{\mathbf{i}}+11 \hat{\mathbf{j}}}{5}=\frac{11}{5}(\hat{\mathbf{i}}+\hat{\mathbf{j}})
\end{aligned}
\) -
Question 15 of 60
15. Question
A cricket ball thrown across a field is at heights \(h_1\) and \(h_2\) from the point of projection at times \(t_1\) and \(t_2\) respectively after the throw. The ball is caught by a fielder at the same height as that of projection. The time of flight of the ball in this journey is [WB JEE 2014]
CorrectIncorrectHint
\(
\text { (c) For vertical motion, } h_1=u \sin \theta t_1-\frac{1}{2} g t_1^2 \text { (For } h_1 \text { ) }
\)
\(
\begin{array}{c}
t_1=\frac{h_1+\frac{1}{2} g t_1^2}{u \sin \theta} \dots(i) \\
h_2=u \sin \theta t_2-\frac{1}{2} g t_2^2 \text { (For } h_2 \text { ) }
\end{array}
\)
\(
t_2=\frac{h_2+\frac{1}{2} g t_2^2}{u \sin \theta} \dots(ii)
\)
On dividing Eq. (i) by Eq. (ii), we get
\(
\frac{t_1}{t_2}=\frac{\left(h_1+\frac{1}{2} g t_1^2\right) / u \sin \theta}{\left(h_2+\frac{1}{2} g t_2^2\right) / u \sin \theta}
\)
\(
\Rightarrow \quad h_1 t_2-h_2 t_1=\frac{g}{2}\left(t t_2^2-t_1^2 t_2\right)
\)
The time of flight of the ball,
\(
\begin{aligned}
T & =\frac{2 u \sin \theta}{g}=\frac{2}{g}(u \sin \theta) \\
& =\frac{2}{g}\left(\frac{h_1+1 / 2 g t_1^2}{t_1}\right) \text { [From Eq. (i)] }
\end{aligned}
\)
\(
\begin{array}{l}
=\frac{2}{t_1}\left(\frac{h_1}{g}+\frac{t_1^2}{2}\right) \\
=\frac{h_1}{t_1} \times \frac{2}{g}+t_1=\frac{h_1}{t_1} \times\left(\frac{t_1 t_2^2-t_1^2 t_2}{h_{t_2}-h_2 t_1}\right)+t_1
\end{array}
\)
\(
=\frac{h_1 t_1 t_2^2-h_1 t_1^2 t_2+h_1 t_1^2 t_2-h_2 t_1^3}{t_1\left(h_1 t_2-h_2 t_1\right)}=\left(\frac{h_1 t_2^2-h_2 t_1^2}{h_1 t_2-h_2 t_1}\right)
\) -
Question 16 of 60
16. Question
For an object thrown at \(45^{\circ}\) to the horizontal, the maximum height \(H\) and horizontal range \(R\) are related as [PMT 2014]
CorrectIncorrectHint
(c) As we know that, maximum height of a projectile is given by
\(
H_{\max }=\frac{u^2 \sin ^2 \theta}{2 g}
\)
where, \(u=\) initial velocity of projectile
\(g=\) acceleration due to gravity
and \(\theta=\) angle of projection.
As per question,
\(
H_{\max }=\frac{v^2 \sin ^2 45^{\circ}}{2 g} \dots(i) \left(\text { As, } u=v, \theta=45^{\circ}\right)
\)
Now, range of a projectile is given by
\(
\begin{array}{l}
R=\frac{u^2 \sin 2 \theta}{g} \\
\Rightarrow \quad R=\frac{v^2 \sin \left(2 \times 45^{\circ}\right)}{g} \\
\Rightarrow \quad R=\frac{v^2 \sin 90^{\circ}}{g} \dots(ii) \\
\end{array}
\)
On dividing Eq. (i) by Eq. (ii), we get
\(
\begin{array}{l}
\frac{H_{\max }}{R}=\frac{v^2 \sin ^2 45^{\circ} \times g}{2 g \times v^2 \sin 90^{\circ}}=\frac{1}{4 \times 1} \\
\Rightarrow \quad R=4 H_{\max }=4 H \\
\end{array}
\) -
Question 17 of 60
17. Question
A body is projected horizontally from the top of a tower with a velocity of \(10 \mathrm{~ms}^{-1}\). If it hits the ground at an angle of \(45^{\circ}\), then the vertical component of velocity when it hits ground (in \(\mathrm{ms}^{-1}\) ) is [EAMCET 2014]
CorrectIncorrectHint
(d) The horizontal component of velocity,
\(
v_x=u=10 \mathrm{~ms}^{-1}
[latex]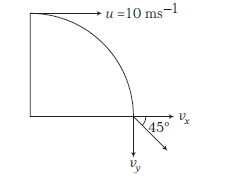
[latex]
\begin{array}{l}
\text { Now, } \tan \theta=\tan 45^{\circ}=\frac{v_y}{v_x}=\frac{v_y}{10} \\
\Rightarrow \quad v_y=10 \mathrm{~ms}^{-1}
\end{array}
\) -
Question 18 of 60
18. Question
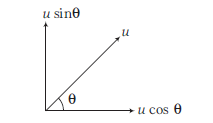
A body is projected with an angle \(\theta\). The maximum height reached is \(h\). If the time of flight is \(4 \mathrm{~s}\) and \(g=10 \mathrm{~ms}^{-2}\), then value of \(h\) is [EAMCET 2014]
CorrectIncorrectHint
\(
\text { (b) As, } \quad t=\frac{2 u \sin \theta}{g} \Rightarrow 4=\frac{2 u \sin \theta}{g} \dots(i)
\)
\(
\begin{array}{l}
\Rightarrow \quad u \sin \theta=2 g \\
\text { and } \quad h=\frac{u^2 \sin ^2 \theta}{2 g}=\frac{4 g^2}{2 g} \quad \text { [From Eq.(i)] } \\
\Rightarrow \quad h=20 \mathrm{~m} \\
\end{array}
\) -
Question 19 of 60
19. Question
The velocity of a projectile at the initial point \(A\) is \((2 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}) \mathrm{ms}^{-1}\). Its velocity (in \(\mathrm{ms}^{-1}\) ) at point \(B\) is [NEET 2013]
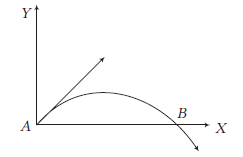 CorrectIncorrect
CorrectIncorrectHint
(c) From the question’s figure, the \(x\)-component remain unchanged, while the \(y\)-component is reverse. Then, the velocity at point \(B\) is \((2 \hat{\mathbf{i}}-3 \hat{\mathbf{j}}) \mathrm{ms}^{-1}\).
-
Question 20 of 60
20. Question
A projectile is thrown with initial velocity \(u_0\) and angle \(30^{\circ}\) with the horizontal. If it remains in the air for 1 s, what was its initial velocity? [J & K CET 2013]
CorrectIncorrectHint
(b) Time of flight, \(T=\frac{2 u \sin \theta}{g}\)
Given, \(u=u_0, T=1 \mathrm{~s}, \theta=30^{\circ}, g=9.8 \mathrm{~ms}^{-2}\)
\(
u_0=g=9.8 \mathrm{~ms}^{-1}
\) -
Question 21 of 60
21. Question
A projectile is projected at \(10 \mathrm{~ms}^{-1}\) by making at an angle \(60^{\circ}\) to the horizontal. After some time, its velocity makes an angle of \(30^{\circ}\) to the horizontal. Its speed at this instant is [KCET 2013]
CorrectIncorrectHint
(a) As the velocity makes an angle of \(30^{\circ}\) with horizontal, so the horizontal component of velocity at the instant will be \(v \cos 30^{\circ}\).
\(
\begin{array}{l}
\Rightarrow \quad v \cos 30^{\circ}=5 \\
\Rightarrow v=\frac{5}{\cos 30^{\circ}}=\frac{5}{\sqrt{3} / 2}=\frac{10}{\sqrt{3}} \mathrm{~ms}^{-1}
\end{array}
\) -
Question 22 of 60
22. Question
Two particles are projected upwards with the same initial velocity \(v_0\) in two different angles of projection such that their horizontal ranges are the same. The ratio of the heights of their highest point will be [UP CPMT 2013]
CorrectIncorrectHint
(a) As the horizontal ranges are the same.
\(
\begin{array}{l}
\therefore \quad \frac{v_0^2 \sin 2 \theta_1}{g}=\frac{v_0^2 \sin 2 \theta_2}{g} \\
\text { So, } \quad \sin 2 \theta_1=\sin 2 \theta_2 \\
\text { or } \quad 2 \theta_1=\pi-2 \theta_2 \\
\Rightarrow \quad \theta_1+\theta_2=\pi / 2 \\
\therefore \quad\left(h_1\right)_{\max }=\frac{v_0^2 \sin ^2 \theta_1}{2 g} \\
\end{array}
\)
\(
\begin{array}{l}
\text { and } \quad\left(h_2\right)_{\max }=\frac{v_0^2 \sin ^2 \theta_2}{2 g} \\
\therefore \quad \frac{\left(h_1\right)_{\max }}{\left(h_2\right)_{\max }}=\frac{\sin ^2 \theta_1}{\sin ^2 \theta_2}=\frac{\sin ^2 \theta_1}{\cos ^2 \theta_1}=\tan ^2 \theta_1 \\
{\left[\because \sin ^2 \theta_2=\sin ^2\left(\frac{\pi}{2}-\theta_2\right)=\cos ^2 \theta / 2\right]}
\end{array}
\) -
Question 23 of 60
23. Question
The velocity vector of the motion described by the position vector of a particle \(r=2 t \hat{\mathbf{i}}+t^2 \hat{\mathbf{j}}\) is given by
CorrectIncorrectHint
(a) Given, \(\mathbf{r}=2 t \hat{\mathbf{i}}+t^2 \hat{\mathbf{j}}\)
Velocity vector, \(\mathbf{v}=\frac{d \mathbf{r}}{d t}\) and using \(\frac{d}{d x} x^n=n x^{n-1}\)
We have, \(\frac{d \mathbf{r}}{d t}=2 \hat{\mathbf{i}}+2 t \hat{\mathbf{j}}\) -
Question 24 of 60
24. Question
The horizontal range and the maximum height of a projectile are equal. The angle of projection of the projectile is [CBSE AIPMT 2012]
CorrectIncorrectHint
(b) Given, \(R=H\)
\(
\text { Range, } R=\frac{u^2(2 \sin \theta \cos \theta)}{g}
\)
Height, \(H=\frac{u^2 \sin ^2 \theta}{2 g}\)
Hence, \(\frac{u^2(2 \sin \theta \cos \theta)}{g}=\frac{u^2 \sin ^2 \theta}{2 g}\)
\(
\begin{aligned}
2 \cos \theta & =\frac{\sin \theta}{2} \\
\Rightarrow \quad \tan \theta & =4 \Rightarrow \theta=\tan ^{-1}(4)
\end{aligned}
\) -
Question 25 of 60
25. Question
Trajectories of two projectiles are shown in figure, let \(T_1\) and \(T_2\) be the periods and \(u_1\) and \(u_2\) are their speeds of projections, then [UP CPMT 2012]
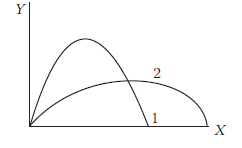 CorrectIncorrect
CorrectIncorrectHint
(d) Maximum height and time of flight depends upon the vertical component of initial velocity.
\(
\begin{array}{l}
H_1>H_2 \\
\Rightarrow \quad u_{y_1}>u_{y_2} \\
\text { Range } \quad R_2>R_1 \\
\text { So, } \quad u_2>u_1 \\
\end{array}
\) -
Question 26 of 60
26. Question
If for the same range, the two heights attained are \(20 \mathrm{~m}\) and \(80 \mathrm{~m}\), then the range will be [BHU 2012]
CorrectIncorrectHint
(d) According to given condition,
\(
\begin{aligned}
\frac{h_1}{h_2} & =\frac{\sin ^2 \theta}{\sin ^2\left(90^{\circ}-\theta\right)}=\frac{20}{80} \\
\Rightarrow \quad \tan ^2 \theta & =\frac{1}{4} \Rightarrow \tan \theta=\frac{1}{2} \\
\sin \theta & =\frac{1}{\sqrt{5}} \text { and } \cos \theta=\frac{2}{\sqrt{5}}
\end{aligned}
\)
So, \(\quad h=\frac{u^2 \sin ^2 \theta}{2 g}\)
\(\Rightarrow \quad 20=\frac{u^2}{10 g}\) or \(\frac{u^2}{g}=200\)
\(\therefore \quad\) The range, \(R=\frac{u^2 \times 2 \sin \theta \cos \theta}{g}=\frac{200 \times 2 \times 2}{\sqrt{5} \times \sqrt{5}}\)
\(
=\frac{200 \times 4}{5}=160 \mathrm{~m}
\) -
Question 27 of 60
27. Question
A ball thrown by one player reaches the other in \(2 \mathrm{~s}\). The maximum height attained by the ball above the point of projection will be (Take, \(g=10 \mathrm{~ms}^{-2}\) ) [BHU 2012]
CorrectIncorrectHint
(b) Since, the ball reaches from one player to another in \(2 \mathrm{~s}\), so the time period of the flight, \(T=2 \mathrm{~s}\)
\(
\Rightarrow \quad \frac{2 u \sin \theta}{g}=2 \mathrm{~s}
\)Here, \(u\) is the initial velocity and \(\theta\) is the angle of projection.
\(
\Rightarrow \quad u \sin \theta=g \dots(i)
\)Now, we know that the maximum height of the projection,
\(
H=\frac{u^2 \sin ^2 \theta}{2 g} \text { or } H=\frac{(u \sin \theta)^2}{2 g}
\)On putting the value of \(u \sin \theta\) from Eq. (i), we get
\(
H=\frac{g^2}{2 g}=\frac{g}{2} \text { or } H=\frac{g}{2}=\frac{10}{2} \mathrm{~m} \text { or } H=5 \mathrm{~m}
\) -
Question 28 of 60
28. Question
Assertion: In case of projectile motion, the magnitude of rate of change of velocity is variable.
Reason: In projectile motion, magnitude of velocity first. decreases and then increases during the motion.CorrectIncorrectHint
(d) \(\left|\frac{d v}{d t}\right|=|a|=9.8 \mathrm{~ms}^{-2}=\) constant and it is true that in case of projectile motion, the magnitude of velocity first decreases and then increases during the motion.
-
Question 29 of 60
29. Question
Assertion: At highest point of a projectile, dot product of velocity and acceleration is zero.
Reason: At highest point, velocity and acceleration are mutually perpendicular.CorrectIncorrectHint
(a) At highest point, velocity is horizontal and acceleration is vertical, i.e. both are perpendicular to each other and hence, their dot product is zero.
-
Question 30 of 60
30. Question
Assertion: If a particle is projected vertically upwards with velocity \(u\), the maximum height attained by the particle is \(h_1\). The same particle is projected at angle \(30^{\circ}\) from horizontal with the same speed \(u\). Now the maximum height is \(h_2\). Thus, \(h_1=4 h_2\).
Reason: In first case, \(v=0\) at highest point and in second case, \(v \neq 0\) at highest point.CorrectIncorrectHint
\(
\begin{array}{l}
\text { (b) } h_1=\frac{u^2}{2 g}, h_2=\frac{u^2 \sin ^2 30^{\circ}}{2 g}=\frac{u^2}{8 g} \\
\Rightarrow h_1=4 h_2
\end{array}
\)Also, at highest point, \(v=0\) in first case and \(v \neq 0\) in second case.
-
Question 31 of 60
31. Question
A particle \((A)\) is dropped from a height and another particle \((B)\) is thrown in horizontal direction with speed of \(5 \mathrm{~m} / \mathrm{s}\) from the same height. The correct statement is
CorrectIncorrectHint
(a) For both cases, \(t=\sqrt{\frac{2 h}{g}}=\) constant.
Because, initial vertical downward component of velocity will be zero for both the particles and both move under the effect of \(g\).
-
Question 32 of 60
32. Question
A ball is rolled off the edge of a horizontal table at a speed of \(4 \mathrm{~ms}^{-1}\). It hits the ground after \(0.4 \mathrm{~s}\).
Which statement given below is true?CorrectIncorrectHint
(a) Vertical component of velocity of ball at point \(P\).
\(
\begin{aligned}
u_V & =0+g t \\
& =10 \times 0.4=4 \mathrm{~ms}^{-1}
\end{aligned}
\)
Horizontal component of velocity \(=\) initial velocity
\(
\Rightarrow \quad v_H=4 \mathrm{~m} / \mathrm{s}
\)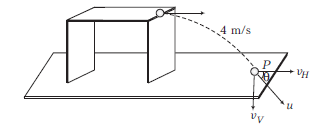
So, the speed with which it hits the ground, \(v=\sqrt{v_H^2+v_V^2}=4 \sqrt{2} \mathrm{~m} / \mathrm{s}\) and \(\tan \theta=\frac{v_V}{v_H}=\frac{4}{4}=1 \Rightarrow \theta=45^{\circ}\)
It means the ball hits the ground at an angle of \(45^{\circ}\) to the horizontal.
Height of the table \(h=\frac{1}{2} g t^2=\frac{1}{2} \times 10 \times(0.4)^2=0.8 \mathrm{~m}\)
Horizontal distance travelled by the ball from the edge of table \(h=u t=4 \times 0.4=1.6 \mathrm{~m}\) -
Question 33 of 60
33. Question
I. In projectile motion, the angle between instantaneous velocity vector and acceleration vector can be anything between 0 to \(\pi\) (excluding the limiting case.)
II. In projectile motion, acceleration vector is always pointing vertically downwards. (Neglect air friction).
Which of the following statement(s) is/are correct?CorrectIncorrectHint
(c) The angle between instantaneous velocity vector and acceleration vector before attaining the maximum height is acute \((0\) to \(\pi / 2)\) and after is obtuse ( \(\pi / 2\) to \(\pi\) ). At the highest point, it is perpendicular \((\pi / 2)\).
-
Question 34 of 60
34. Question
I. Particle-1 is dropped from a tower and particle-2 is projected horizontal from the same tower, then both the particles reach the ground simultaneously.
II. Both the particles strike the ground with different speeds.
Which of the following statement(s) is/are correct?CorrectIncorrectHint
(c)
\(
\begin{array}{l}
t_1=t_2=\sqrt{\frac{2 h}{g}} \quad \text { (where, } h=\text { height of tower) } \\
v_1=\sqrt{2 g h}
\end{array}
\)While \(v_2=\sqrt{v_1^2+v_0^2}\) (where, \(v_0=\) initial horizontal velocity)
Therefore, both statements are correct. -
Question 35 of 60
35. Question
A particle is projected from ground with velocity \(u\) at angle \(\theta\) from horizontal. Match the following two columns and mark the correct option from the codes given below.
\(
\begin{array}{|c|c|c|}
\hline & \text { Column I } & \text { Column II } \\
\hline \text { (A) } & \begin{array}{l}
\text { Average velocity between initial and } \\
\text { final points }
\end{array} & (p) u \sin \theta \\
\hline \text { (B) } & \begin{array}{l}
\text { Change in velocity between initial } \\
\text { and final points }
\end{array} & (q) u \cos \theta \\
\hline \text { (C) } & \begin{array}{l}
\text { Change in velocity between initial } \\
\text { and peak points }
\end{array} & (r) \text { zero } \\
\hline \text { (D) } & \begin{array}{l}
\text { Average velocity between initial and } \\
\text { highest points }
\end{array} & (s) \text { None } \\
\hline
\end{array}
\)CorrectIncorrectHint
(c)
A) average velocity between initial and final point is
\(
v_{\text {ave }}=\frac{R}{T}=\frac{u \cos \theta T}{T}=U \cos \theta
\)
B) change in velocity between initial and final point is
\(
g T=g \frac{2 u \sin \theta}{g}=2 u \sin \theta
\)
C) change in velocity between initial and peak point is
\(
g \frac{T}{2}=u \sin \theta
\)
D) average velocity between initial and peak point is
\(
\hat{i} u \cos \theta+\frac{\hat{j} u \sin \theta}{2}
\) -
Question 36 of 60
36. Question
A particle is projected horizontally from a tower with velocity \(10 \mathrm{~ms}^{-1}\). Taking, \(g=10 \mathrm{~ms}^{-2}\). Match the following two columns at time \(t=1 \mathrm{~s}\) and mark the correct option from the codes given below.
\(
\begin{array}{|c|c|c|}
\hline & \text { Column I } & \text { Column II } \\
\hline \text { (A) } & \begin{array}{l}
\text { Horizontal component of velocity } \\
\end{array} & (p) 5 \text { SI units } \\
\hline \text { (B) } & \begin{array}{l}
\text { Vertical component of velocity } \\
\end{array} & (q) 10 \mathrm{SI} \text { unit } \\
\hline \text { (C) } & \begin{array}{l}
\text { Horizontal displacement } \\
\end{array} & (r) 15 \text { SI unit } \\
\hline \text { (D) } & \begin{array}{l}
\text { Vertical displacement } \\
\end{array} & (s) 20 \text { SI unit } \\
\hline
\end{array}
\)CorrectIncorrectHint
(d) In horizontal projectile motion,
Horizontal component of velocity,
\(
u_x=u=10 \mathrm{~ms}^{-1}
\)
Vertical component of velocity,
\(
u_y=g t=10 \times 1=10 \mathrm{~ms}^{-1}
\)
Horizontal displacement
\(
=u \times t=10 \times(1)=10 \mathrm{~m}
\)Vertical displacement \(=\frac{1}{2} g t^2=\frac{1}{2} \times 10 \times(1)^2=5 \mathrm{~m}\)
-
Question 37 of 60
37. Question
The maximum range of a gun or horizontal range is \(16 \mathrm{~km}\). If \(\mathrm{g}=10 \mathrm{~ms}^{-2}\). The muzzle velocity of the shell must be :[AIPMT 1990, AIIMS 2002]
CorrectIncorrectHint
\(
R=\frac{u^2 \sin 2 \theta}{g}
\)For maximum range \(\theta=45^{\circ}, \sin 2 \theta=1\)
\(
\therefore R_{\max }=\frac{u^2}{g}
\)Given, \(R=16 \mathrm{~km}=16 \times 10^3 \mathrm{~m}\)
\(
\begin{array}{l}
g=10 \mathrm{~m} / \mathrm{s}^2 \\
\Rightarrow u^2=16 \times 10^3 \times 10 \\
\Rightarrow u=400 \mathrm{~m} / \mathrm{s}
\end{array}
\) -
Question 38 of 60
38. Question
A ball whose kinetic energy is \(\mathrm{E}\), is thrown at an angle of \(45^{\circ}\) with the horizontal, its kinetic energy at the highest point of its flight will be :[AIPMT 1997, 2000]
CorrectIncorrectHint
A ball is projected at an angle of \(45^{\circ}\) with the horizontal. This is a projectile motion.
Let the initial velocity of the ball is \(u\).
Now, the horizontal component of the velocity will be, \(u \cos 45^{\circ}=\frac{u}{\sqrt{2}}\)
Again, the vertical component of the velocity will be, \(u \sin 45^{\circ}=\frac{u}{\sqrt{2}}\)
In a projectile motion, at the highest point of its flight, the vertical component of the velocity becomes zero and the velocity of the object is given only by the horizontal component of the velocity.
So, at the height of point of flight of a projectile motion, the velocity of the object will be \(\frac{u}{\sqrt{2}}\).
Now, initially the kinetic energy of the ball is \(E\) when the object starts moving with velocity \(u\).
So, we can write that,
\(
E=\frac{1}{2} m u^2
\)
Where, \(m\) is the mass of the ball.
Now, at the highest point of flight, the ball is moving with velocity \(\frac{u}{\sqrt{2}}\). so, its kinetic energy will be,
\(
E_f=\frac{1}{2} m\left(\frac{u}{\sqrt{2}}\right)^2=\frac{1}{4} m u^2
\)
Now, dividing the second equation with the first equation we get that,
\(
\begin{array}{l}
\frac{E_f}{E}=\frac{\frac{1}{4} m u^2}{\frac{1}{2} m u^2} \\
E_f=\frac{E}{2}
\end{array}
\)So, the kinetic energy of the ball at its highest point of flight will be, \(\frac{E}{2}\).
-
Question 39 of 60
39. Question
A body is projected at such an angle that the horizontal range is three times the greatest height. The angle of projection is : [AIIMS 1998, DPMT 2000]
CorrectIncorrectHint
Let the body be projected at an angle \(\theta\) with initial speed \(u\).
The maximum height attained by the body is given by
\(
H=\frac{u^2 \sin ^2 \theta}{2 g}
\)
And the range of the projectile,
\(
R=\frac{u^2 \sin 2 \theta}{g}=\frac{2 u^2 \sin \theta \cos \theta}{g}
\)
Now given \(R=3 H\)
\(
\begin{array}{l}
\Rightarrow \quad \frac{2 u^2 \sin \theta \cos \theta}{g}=\frac{3 \times u^2 \sin ^2 \theta}{2 g} \\
\Rightarrow \quad \frac{\sin \theta}{\cos \theta}=\tan \theta=\frac{4}{3} \\
\Rightarrow \theta=\tan ^{-1}\left(\frac{4}{3}\right)=53^{\circ}
\end{array}
\) -
Question 40 of 60
40. Question
A projectile can have the same range \(R\) for two angles of projection. If \(t_1\) and \(t_2\) be the times of flight in the two cases : [AIPMT 1999, UP PMT 2001, KCET 2003, RPMT 2008]
CorrectIncorrectHint
Range is same for angles of projection \(\theta\) and \((90-\theta)\)
\(
\begin{array}{l}
t_1=2 u \sin \theta / g \\
t_2=[2 u \sin (90-\theta)] / g=2 u \cos \theta / g .
\end{array}
\)
Hence, \(t_1 t_2=4\left(u^2 \sin \theta \cos \theta / g^2\right)=2 / g\left[u^2 \sin \theta / g\right]\)
\(=(2 / g) R\)., Where \({R}\) is range.
Hence, \(t_1 t_2 \propto R\) because \(R\) is constant. -
Question 41 of 60
41. Question
Two projectiles of same mass and with same velocity are thrown at angle \(60^{\circ}\) and \(30^{\circ}\) with the horizontal, then which quantity will remain same : [AIPMT 2000, JIPMER 2002]
CorrectIncorrectHint
As \(\theta_2=\left(90-\theta_1\right)\),
So range of projectile,
\(
\begin{array}{l}
R_1=\frac{v_0^2 \sin 2 \theta}{g}=\frac{v_0^2 2 \sin \theta \cos \theta}{g} \\
R_2=\frac{v_0^2 2 \sin \left(90-\theta_1\right) \cos \left(90-\theta_1\right)}{g} \\
R_2=\frac{v_0^2 2 \cos \theta_1 \sin \theta_1}{g}=R_1
\end{array}
\) -
Question 42 of 60
42. Question
At the uppermost point of a projectile its velocity and acceleration are at angle of : [AIIMS 2002]
CorrectIncorrectHint
As per the problem we have to find the angle between the velocity and acceleration at the highest point. Now when a particle is projected an angle of \(\theta\), having some initial velocity u moving along a curved path under constant acceleration acting in downward direction can be represented as given,
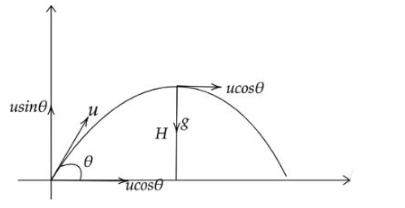
As per the diagram \(\mathrm{H}\) is the highest point of the projectile motion and at the highest point the velocity acting is \(u \cos \theta\) and the acceleration acting on the particle is the constant acceleration and it is acting in downward direction and it the acceleration due to gravity. Hence acceleration and velocity are perpendicular to each other. Now from the above figure and from the above discussion we can conclude that the angle between the velocity and acceleration at the highest point is \(90^{\circ}\).
-
Question 43 of 60
43. Question
A force \(\overrightarrow{\mathrm{F}}=6 \mathrm{t}^2 \hat{\mathrm{i}}+4 \mathrm{t} \hat{j}\) is acting on a particle of mass \(3 \mathrm{~kg}\) then what will be velocity of particle at \(t=3\) second and if at \(t=0\), particle is at rest :[AIPMT 2002]
CorrectIncorrectHint
\(
\begin{array}{l}
\mathrm{F}=m a \quad \therefore a=\frac{{\mathrm{F}}}{m}=\frac{1}{3}\left(6 t^2 \hat{i}+4 t \hat{j}\right)=2 t^2 \hat{i}+\frac{4}{3} t \hat{j} \\
a=\frac{d \mathrm{~V}}{d t} \quad \therefore v=\int_0^t a d t=\int_0^3 2 t^2 \hat{i} d t+\int_0^3 \frac{4}{3} t \hat{j} d t=18 \hat{i}+6 \hat{j}
\end{array}
\) -
Question 44 of 60
44. Question
For angles of projection of a projectile at angles \(\left(45^{\circ}-\theta\right)\) and \(\left(45^{\circ}+\theta\right)\), the horizontal ranges described by the projectile are in the ratio of : [AIPMT 2006]
CorrectIncorrectHint
Let \(u\) be the initial velocity of the projectile.
Range of a projectile is given by:
\(
\mathrm{R}=\frac{\mathrm{u}^2 \sin 2 \theta}{\mathrm{g}}
\)
Step 2: Ratio of \(R_1 \& R_2\)
At \(\theta_1=45^{\circ}-\theta, R=R_1\)
\(
\mathrm{R}_1=\frac{\mathrm{u}^2 \sin 2\left(45^{\circ}-\theta\right)}{\mathrm{g}}=\frac{\mathrm{u}^2 \sin \left(90^{\circ}-2 \theta\right)}{\mathrm{g}}
\)
At \(\theta_2=45^{\circ}+\theta, \mathrm{R}=\mathrm{R}_2\)
\(
R_2=\frac{u^2 \sin 2\left(45^{\circ}+\theta\right)}{g}=\frac{u^2 \sin \left(90^{\circ}+2 \theta\right)}{g}
\)
The ratio of \(R_1\) and \(R_2\) is given by
\(
\frac{R_1}{R_2}=\frac{\sin \left(90^{\circ}-2 \theta\right)}{\sin \left(90^{\circ}+2 \theta\right)}=\frac{\cos 2 \theta}{\cos 2 \theta}=1
\)
Hence the ratio of the range of the projectile is \(1: 1\). -
Question 45 of 60
45. Question
A particle starting from the origin \((0,0)\) moves in a straight line in the \((x, y)\) plane. Its coordinates at a later time are \((\sqrt{3}, 3)\). The path of the particle makes with the \({x}\) – axis an angle of :[AIPMT 2007]
CorrectIncorrectHint
Let, \(\theta\) be the angle which the particle makes with an \(\mathrm{x}\)-axis.
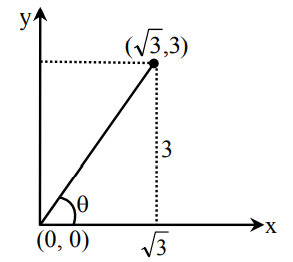
From the given figure:
\(
\tan \theta=\frac{y}{x}=\frac{3}{\sqrt{3}}=\sqrt{3} \Rightarrow \theta=\tan ^{-1} \sqrt{3}=60^{\circ} .
\) -
Question 46 of 60
46. Question
A particle of mass \(\mathrm{m}\) is projected with velocity \(\mathrm{v}\) making an angle of \(45^{\circ}\) with the horizontal. When the particle lands on the ground level, the magnitude of the change in its momentum will be : [AIPMT 2008]
CorrectIncorrectHint
The formula for momentum is given below:
\(
p=m v
\)
From the question, momentum change when the particle reaches ground level is asked.
Thus, the horizontal momentum remains unchanged.
\(
\begin{array}{l}
\Delta p=\Delta p_{\text {vertical }} \\
\Delta p_{\text {vertical }}=(\text { Final momentum })_{\text {vertical }}-(\text { Initial momentum })_{\text {vertical }} \\
\text { Initial momentum }=m v \sin 45 \\
\text { Final momentum }=-({mv} \sin 45) \\
\Delta p_{\text {vertical }}=-(m v \sin 45)-(m v \sin 45) \\
=-(2 m v \sin 45) \\
\Delta p_{\text {vertical }}=2 m v \times \frac{1}{\sqrt{2}} \\
\Delta p_{\text {vertical }}=\sqrt{2}(m v) .
\end{array}
\) -
Question 47 of 60
47. Question
Two projectiles are fired from the same point with the same speed at angles of projection \(60^{\circ}\) and \(30^{\circ}\) respectively. Which one of the following is true : [AIIMS 2009]
CorrectIncorrectHint
The horizontal range is the same when angle of projection is \(\theta\) or \(\left(90^{\circ}-\theta\right)\).
-
Question 48 of 60
48. Question
The speed of a projectile at its maximum height is half of its initial speed. The angle of projection is : [AIPMT (Mains) 2010]
CorrectIncorrectHint
Let \(\mathrm{v}\) be velocity of a projectile at maximum height \(\mathrm{H}\)
\(
\mathrm{v}=\mathrm{u} \cos \theta
\)According to given problem, \(\mathrm{v}=\frac{\mathrm{u}}{2}\)
\(
\begin{array}{l}
\therefore \frac{\mathrm{u}}{2}=\mathrm{u} \cos \theta \Rightarrow \cos \theta=\frac{1}{2} \\
\theta=60^{\circ}
\end{array}
\)
-
Question 49 of 60
49. Question
A particle has initial velocity \((3 \hat{\mathrm{i}}+4 \hat{\mathrm{j}})\) and has acceleration \((0.4 \hat{\mathrm{i}}+0.3 \hat{\mathrm{j}})\). Its speed after \(\)10 \mathrm{~s}\(\) is : [AIPMT (Pre) 2010]
CorrectIncorrectHint
Step 1: Given data
Initial velocity, \(u=3 \hat{i}+4 \hat{j}\)
Acceleration, \(a=0.4 \hat{i}+0.3 \hat{j}\)
Time, \(t=10 \mathrm{~s}\)
Step 2: Find Final velocity
Final velocity \((v)\) is given by using the first equation of motion,
\(
\begin{aligned}
v & =u+a t \\
v & =3 \hat{i}+4 \hat{j}+(0.4 \hat{i}+0.3 \hat{j}) 10 \\
v & =7 \hat{i}+7 \hat{j} \\
V & =\sqrt{7^2+7^2} \\
V & =7 \sqrt{ } 2 \text { units }
\end{aligned}
\) -
Question 50 of 60
50. Question
A missile is fired for maximum range with an initial velocity of \(20 \mathrm{~m} / \mathrm{s}\). If \(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2\), the range of the missile is : [AIPMT (Pre) 2011]
CorrectIncorrectHint
Given:
initial velocity \(\mathrm{u}=20 \mathrm{~m} / \mathrm{s}\)
\(
\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2
\)
We know that, for maximum range the angle of projection \(\theta=45^{\circ}\)
so,
\(
\mathrm{R}_{\max }=\frac{\mathrm{u}^2 \sin 2 \theta}{\mathrm{g}}=\frac{20^2 \sin 90^{\circ}}{10}=\frac{20 \times 20}{10}=40 \mathrm{~m} \text {. }
\) -
Question 51 of 60
51. Question
A projectile is fired at an angle of \(45^{\circ}\) with the horizontal. Elevation angle of the projectile at its highest point as seen from the point of projection, is : [AIPMT (Mains) 2011]
CorrectIncorrectHint
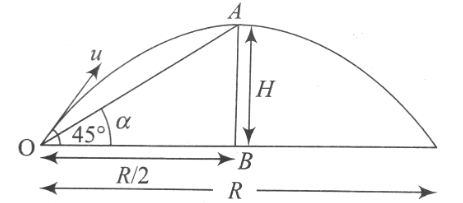
Height of projectile
\(
H=\frac{u^2 \sin ^2 \theta}{2 g}=\frac{u^2 \sin ^2 45^{\circ}}{2 g}
\)
\(
H=\frac{u^2}{4 g} \ldots \ldots(i)
\)
Range of projectile \(R=\frac{u^2 \sin 2 \theta}{g}=\frac{u^2 \sin 90^{\circ}}{g}\) \(\Rightarrow R=\frac{u^2}{g}\)
\(
\begin{array}{l}
\tan \alpha=\frac{H}{R / 2} \\
\operatorname{In} \triangle O A B=\frac{u^2 / 4 g}{u^2 / 2 g} \\
\tan \alpha=\frac{1}{2} \Rightarrow \alpha=\tan ^{-1}\left(\frac{1}{2}\right)
\end{array}
\) -
Question 52 of 60
52. Question
The speed of a swimmer in still water is \(20 \mathrm{~m} / \mathrm{s}\). The speed of river water is \(10 \mathrm{~m} / \mathrm{s}\) and is flowing due east. If he is standing on the south bank and wishes to cross the river along the shortest path the angle at which he should make his strokes w.r.t. north is given by : [NEET(UG)-2019]
CorrectIncorrectHint
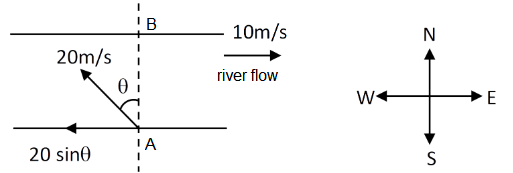
For shortest path(AB), velocity along river flow is zero. Horizontal compaonent should cancel out.
\(
\begin{array}{l}
20 \sin \theta=10 \Rightarrow \sin \theta=\frac{10}{20}=\frac{1}{2} \\
\theta=30^{\circ} \text { west }
\end{array}
\) -
Question 53 of 60
53. Question
A bullet is fired from a gun at the speed of \(280 \mathrm{~ms}^{-1}\) in the direction \(30^{\circ}\) above the horizontal. The maximum height attained by the bullet is \(\left(\mathrm{g}=9.8 \mathrm{~ms}^{-2}, \sin 30^{\circ}=0.5\right)\) : [NEET 2023]
CorrectIncorrectHint
\(
\begin{array}{l}
\mathrm{H}_{\max }=\frac{\mathrm{u}^2 \sin ^2 \theta}{2 \mathrm{~g}} \\
=\frac{(280)^2\left(\sin 30^{\circ}\right)^2}{2(9.8)} \\
=1000 \mathrm{~m}
\end{array}
\) -
Question 54 of 60
54. Question
A ball is projected from point A with velocity \(20 \mathrm{~m} \mathrm{~s}^{-1}\) at an angle \(60^{\circ}\) to the horizontal direction. At the highest point \(\mathrm{B}\) of the path (as shown in figure), the velocity \(v\mathrm{~ms}^{-1}\) of the ball will be: [NEET Manipur 2023]
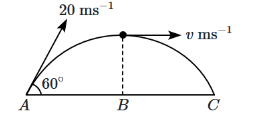 CorrectIncorrect
CorrectIncorrectHint
At the top most point of its trajectory particle will have only horizontal component of velocity
\(
\begin{array}{l}
\mathrm{V}=v \cos \theta \\
=20 \times \frac{1}{2} \\
=10 \mathrm{~m} / \mathrm{s}
\end{array}
\) -
Question 55 of 60
55. Question
A particle is executing uniform circular motion with velocity \(\vec{v}\) and acceleration \(\vec{a}\). Which of the following is true? [NEET Manipur 2023]
CorrectIncorrectHint
Direction of velocity and centripetal acceleration changes continuously so \(\vec{v}\) is not constant and \(\vec{a}\) is not a constant.
-
Question 56 of 60
56. Question
A cricket ball is thrown by a player at a speed of \(20 \mathrm{~m} / \mathrm{s}\) in a direction \(30^{\circ}\) above the horizontal. The maximum height attained by the ball during its motion is
\(
\left(g=10 \mathrm{~m} / \mathrm{s}^2\right)
\) [NEET 2022]CorrectIncorrectHint
Maximum height reached by the ball
\(
\begin{array}{l}
H=\frac{v^2 \sin ^2 \theta}{2 g} \\
=\frac{(20)^2 \sin ^2 30^{\circ}}{2 g} \\
H=5 m
\end{array}
\) -
Question 57 of 60
57. Question
A ball is projected with a velocity, \(10 \mathrm{~ms}^{-1}\), at an angle of \(60^{\circ}\) with the vertical direction. Its speed at the highest point of its trajectory will be [NEET 2022]
CorrectIncorrectHint
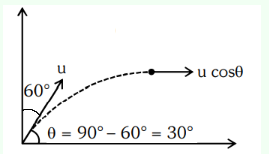
At highest point only horizontal component of velocity remains
\(
u_x=u \cos \theta=10 \cos 30^{\circ}=5 \sqrt{3} m s^{-1}
\) -
Question 58 of 60
58. Question
A particle moving in a circle of radius \(\mathrm{R}\) with a uniform speed takes a time \(\mathrm{T}\) to complete one revolution. If this particle were projected with the same speed at an angle ‘ \(\theta\) ‘ to the horizontal, the maximum height attained by it equals \(4 \mathrm{R}\). The angle of projection, \(\theta\), is then given by : [NEET 2021]
CorrectIncorrectHint
\(
\begin{array}{l}
T=\frac{2 \pi R}{V} \\
V=\frac{2 \pi R}{T} \\
H=\frac{u^2 \sin ^2 \theta}{2 g} \\
4 R=\frac{4 \pi^2 R^2 \sin ^2 \theta}{T^2 2 g} \\
\sin ^2 \theta=\frac{8 R T^2 g}{4 \pi^2 R^2} \\
\sin ^2 \theta=\sqrt{\frac{2 T^2 g}{\pi^2 R}} \\
\theta=\sin ^{-1}\left(\frac{2 T^2 g}{\pi^2 R}\right)^{1 / 2}
\end{array}
\) -
Question 59 of 60
59. Question
A car starts from rest and accelerates at \(5 \mathrm{~m} / \mathrm{s}^2\). At \(t=4 \mathrm{~s}\), a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at \(t=6 s\) ? (Take \(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2\) ) [NEET 2021]
CorrectIncorrectHint
velocity of car at \(t=4 \mathrm{sec}\) is
\(
\begin{array}{l}
v=u+a t \\
v=0+5(4) \\
=20 \mathrm{~m} / \mathrm{s}
\end{array}
\)
At \(t=6 \mathrm{sec}\)
acceleration is due to gravity
\(
\therefore a=g=10 \mathrm{~m} / \mathrm{s}
\)
\(v_x=20 \mathrm{~m} / \mathrm{s}\) (due to car)
\(
v_y=u+a t
\)
\(
\begin{array}{l}
=0+g(2) \text { (downward) } \\
=20 \mathrm{~m} / \mathrm{s} \text { (downward) } \\
\mathrm{v}=\sqrt{v_x^2+v_y^2} \\
=\sqrt{20^2+20^2} \\
=20 \sqrt{2} \mathrm{~m} / \mathrm{s} .
\end{array}
\) -
Question 60 of 60
60. Question
A stone tied to the end of a string of \(1 \mathrm{~m}\) long is whirled in a horizontal circle with a constant speed. If the stone makes 22 revoluations in 44 seconds, what is the magnitude and direction of acceleration of the stone? [AIPMT 2005]
CorrectIncorrectHint
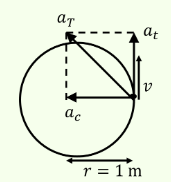
Radial acceleration or centripetal accceleration is given by:
\(
a_c=\frac{v^2}{r}=\omega^2 r
\)
Frequency of revolution is, \(f=\frac{n}{t}\) where \(n\) is the number of revolutions, and \(t\) is the time taken to make that revolution.
\(
\begin{array}{l}
f=\frac{22}{44}=\frac{1}{2} \mathrm{~s}^{-1} \\
\Rightarrow \omega=2 \pi f=\pi \mathrm{rad} / \mathrm{s} \\
\therefore a_c=\omega^2 r=\pi^2 \times 1=\pi^2 \mathrm{~m} / \mathrm{s}^2
\end{array}
\)
Tangential acceleration is the rate of change of speed w.r.t time:
\(
\Rightarrow a_t=\frac{d v}{d t}=0
\)
\(\because\) speed is constant
Hence net acceleration of stone \(\vec{a}\) given by:
\(
\begin{array}{l}
\vec{a}=\vec{a}_c+\vec{a}_t=\vec{a}_c=\pi^2 \mathrm{~m} / \mathrm{s}^2 \\
\therefore|\vec{a}|=\left|\vec{a}_c\right|=\pi^2 \mathrm{~m} / \mathrm{s}^2
\end{array}
\)
Direction is along the radius towards the centre i.e. radially inwards.