Laws of Motion Quiz-L1
Quiz Summary
0 of 55 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 55 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 55
1. Question
If an electron is subjected to a force of \(10^{-25} \mathrm{~N}\) in an \(X\)-ray machine, then find out the time taken by the electron to cover a distance of \(0.2 \mathrm{~m}\). (Take, mass of an electron \(=10^{-30} \mathrm{~kg}\) )
CorrectIncorrectHint
The acceleration of the electron, \(a=\frac{F}{m}=\frac{10^{-25}}{10^{-30}}=10^5 \mathrm{~ms}^{-2}\)
The time taken by the electron \((t)\) to cover the distance \((s)\) of \(0.2 \mathrm{~m}\) can be given by
\(
\begin{array}{rlrl}
s & =u t+\frac{1}{2} a t^2 \\
\Rightarrow 0.2 & =0+\frac{1}{2} \times 10^5 \times t^2 \\
\Rightarrow t^2 & =0.4 \times 10^{-5}=4 \times 10^{-6} \Rightarrow t=2 \times 10^{-3} \mathrm{~s}
\end{array}
\) -
Question 2 of 55
2. Question
A bullet of mass \(0.06 \mathrm{~kg}\) moving with a speed of \(90 \mathrm{~ms}^{-1}\) enters a heavy wooden block and is stopped after a distance of \(60 \mathrm{~cm}\). What is the average resistive force exerted by the block on the bullet?
CorrectIncorrectHint
The retardation \(a\) of the bullet is given by
\(
\begin{array}{r}
a=-\frac{u^2}{2 s}=\frac{-90 \times 90}{2 \times 0.6} \quad\left(\text { From, } v^2=u^2+2 a s, v=0\right) \\
\left(\because \text { Given, } s=60 \mathrm{~cm}=0.6 \mathrm{~m}, u=90 \mathrm{~ms}^{-1}\right)
\end{array}
\)
\(
\Rightarrow \quad a=-6750 \mathrm{~ms}^{-2}
\)From second law of motion,
Retarding force, \(F=m a=0.06 \times 6750\)
\(
\Rightarrow \quad F=405 \mathrm{~N}
\) -
Question 3 of 55
3. Question
A stone of mass \(1 \mathrm{~kg}\) is thrown with a velocity of \(20 \mathrm{~ms}^{-1}\) across the frozen surface of a lake and it comes to rest after travelling a distance of \(50 \mathrm{~m}\). What is the magnitude of the force opposing the motion of the stone?
CorrectIncorrectHint
Given, \(u=20 \mathrm{~ms}^{-1}, v=0, s=50 \mathrm{~m}\) and \(m=1 \mathrm{~kg}\)
To calculate force, we have the formula \(F=m a\), but we have to first calculate acceleration \(a\).
Using the third equation of motion, i.e.
\(
\begin{array}{rlrl}
v^2 & =u^2+2 a s \\
& & (0)^2 & =(20)^2+2 \times a \times 50 \\
\Rightarrow & 100 a & =-400 \\
\Rightarrow & & a & =-4 \mathrm{~ms}^{-2}
\end{array}
\)Acceleration \(a=-4 \mathrm{~ms}^{-2}\) (-ve sign shows that speed of the stone decreases, i.e. retardation)
Now,
\(
\begin{aligned}
F & =m a=(1 \mathrm{~kg}) \times\left(-4 \mathrm{~ms}^{-2}\right) \\
& =-4 \mathrm{~kg}-\mathrm{ms}^{-2}=-4 \mathrm{~N}
\end{aligned}
\)Thus, force of opposition between the stone and the ice is \(-4 \mathrm{~N}\). The negative value of force shows that the opposing force acts in a direction opposite to the direction of motion.
-
Question 4 of 55
4. Question
A block of \(6 \mathrm{~kg}\) is resting on a frictionless plane. It is struck by a jet releasing water at a rate of \(3 \mathrm{kgs}^{-1}\) at a speed of \(4 \mathrm{~ms}^{-1}\). Calculate the acceleration of the block.
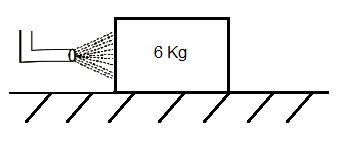 CorrectIncorrect
CorrectIncorrectHint
Force exerting on block, \(F=v \frac{d m}{d t}=4 \times 3=12 \mathrm{~N}\)
So, acceleration of the block, \(a=\frac{F}{m}=\frac{12}{6}=2.0 \mathrm{~ms}^{-2}\) -
Question 5 of 55
5. Question
A force of \(50 \mathrm{~N}\) acts in the direction as shown in figure. The block of mass \(5 \mathrm{~kg}\), resting on a smooth horizontal surface. Find out the acceleration of the block.
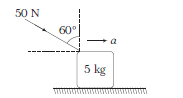 CorrectIncorrect
CorrectIncorrectHint
Free body diagram is shown below.
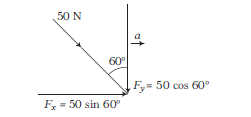
where, \(F_x=\) horizontal component of the force and \(\quad F_y=\) vertical component of the force.
Horizontal component of the force \(=50 \sin 60^{\circ}=\frac{50 \sqrt{3}}{2} \mathrm{~N}\) Acceleration of the block, \(a\)
\(
\begin{aligned}
& =\frac{\text { Component of force in the direction of acceleration }}{\text { Mass }} \\
& =\frac{50 \sqrt{3}}{2} \times \frac{1}{5}=5 \sqrt{3} \mathrm{~ms}^{-2}
\end{aligned}
\) -
Question 6 of 55
6. Question
A force \(\mathbf{F}=(6 \hat{\mathbf{i}}-8 \hat{\mathbf{j}}+10 \hat{\mathbf{k}}) N\) produces acceleration of \(\sqrt{2} \mathrm{~ms}^{-2}\) in a body. Calculate the mass of the body.
CorrectIncorrectHint
\(\because\) Acceleration, \(a=\frac{|\mathrm{F}|}{m}\)
\(
\Rightarrow \text { Mass, } m=\frac{|\mathbf{F}|}{a}=\frac{\sqrt{6^2+8^2+10^2}}{\sqrt{2}}=10 \mathrm{~kg}
\) -
Question 7 of 55
7. Question
A force \(\mathrm{F}=\left(2 t \hat{\mathbf{i}}+3 t^2 \hat{\mathbf{j}}\right) N\) acts on an object moving in XY-plane. Find magnitude of change in momentum of the object in time interval \(t=0\) to \(t=2 \mathrm{~s}\).
CorrectIncorrectHint
Given, \(\mathbf{F}=\left(2 t \hat{\mathbf{i}}+3 t^2 \hat{\mathbf{j}}\right) N \Rightarrow \frac{d \mathbf{p}}{d t}=2 t \hat{\mathbf{i}}+3 t^2 \hat{\mathbf{j}}\)
\(
\begin{array}{ll}
\Rightarrow & d \mathbf{p}=2 t d t \hat{\mathbf{i}}+3 t^2 d \hat{\mathbf{j}} \\
\Rightarrow & \int d \mathbf{p}=2 \int_0^2 t d t \hat{\mathbf{i}}+3 \int_0^2 t^2 d t \hat{\mathbf{j}} \\
\Rightarrow & \Delta \mathbf{p}=\left[t^2\right]_0^2 \hat{\mathbf{i}}+\left[t^3\right]_0^2 \hat{\mathbf{j}} \\
\Rightarrow & \Delta \mathbf{p}=4 \hat{\mathbf{i}}+8 \hat{\mathbf{j}} \\
\Rightarrow & |\Delta \mathbf{p}|=\sqrt{16+64}=\sqrt{80} \approx 9 \mathrm{~kg} \mathrm{~ms}^{-1}
\end{array}
\) -
Question 8 of 55
8. Question
Let us consider two forces \(F_1\) and \(F_2\) acting on a body of mass \(2 \mathrm{~kg}\) as shown in the figure. \(F_1=10 \mathrm{~N}\), \(F_2=2 N\), what will be the acceleration?
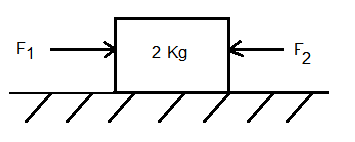 CorrectIncorrect
CorrectIncorrectHint
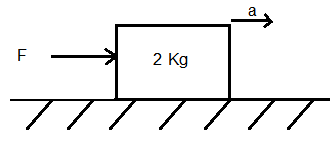
Unbalanced external force, \(F=F_1-F_2=10-2=8 \mathrm{~N}\)
So,\(F=m a\)
\(\Rightarrow\) Acceleration,
\(
a=\frac{F}{m}=\frac{8}{2}=4 \mathrm{~ms}^{-2}
\)The body moves in direction of \(F_1\)
-
Question 9 of 55
9. Question
A baseball player hits back the ball straight in the direction of the bowler without changing its initial speed of \(12 \mathrm{~ms}^{-1}\). If the mass of the ball is \(0.15 \mathrm{~kg}\), then find the impulse imparted to the ball. (Consider the ball in linear motion)
CorrectIncorrectHint
Given, \(m=0.15 \mathrm{~kg}, v=12 \mathrm{~ms}^{-1}\) and \(u=-12 \mathrm{~ms}^{-1}\) Change in momentum,
\(
\begin{gathered}
p_2-p_1=m(v-u)=0.15[12-(-12)]=0.15 \times 24 \\
p_2-p_1=3.60 \mathrm{~kg}-\mathrm{ms}^{-1} \\
\text { Impulse, } I=p_2-p_1 \Rightarrow I=3.6 \mathrm{~N}-\mathrm{s}
\end{gathered}
\) -
Question 10 of 55
10. Question
A hammer of mass \(1 \mathrm{~kg}\) moving with a speed of \(6 \mathrm{~ms}^{-1}\) strikes a wall and comes to rest in \(0.1 \mathrm{~s}\). Calculate
(i) impulse of the force,
(ii) average retarding force that stops the hammer
(iii) and average retardation of the hammer.CorrectIncorrectHint
(i) Impulse \(=F \times t=m(v-u)=1(0-6)=-6 \mathrm{~N}-\mathrm{s}\)
(ii) Average retarding force that stops the hammer,
\(
F=\frac{\text { Impulse }}{\text { Time }}=\frac{6}{0.1}=60 \mathrm{~N}
\)
(iii) Average retardation, \(a=\frac{F}{m}=\frac{60}{1}=60 \mathrm{~ms}^{-2}\) -
Question 11 of 55
11. Question
A cricket ball of mass \(150 \mathrm{~g}\) is moving with a velocity of \(12 \mathrm{~ms}^{-1}\) and is hit by a bat, so that the ball is turned back with a velocity of \(20 \mathrm{~ms}^{-1}\). If the duration of contact between the ball and bat is \(0.01 \mathrm{~s}\), find the impulse and the average force exerted on the ball by the bat.
CorrectIncorrectHint
According to given question, change in momentum of the ball,
\(
\Delta p=p_f-p_i=m(v-u)=150 \times 10^{-3}[20-(-12)]=4.8 \mathrm{~N}-\mathrm{s}
\)So, by impulse-momentum theorem, impulse, \(I=\Delta p=4.8 \mathrm{~N}-\mathrm{s}\) and by time averaged definition of force in case of impulse
\(
\Rightarrow \quad F_{\mathrm{av}}=\frac{I}{\Delta t}=\frac{\Delta p}{\Delta t}=\frac{4.80}{0.01}=480 \mathrm{~N}
\) -
Question 12 of 55
12. Question
Figure shows an estimated force-time graph for a baseball struck by a bat.
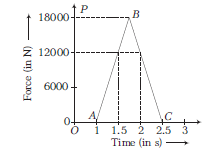
From this curve, determine
(i) impulse delivered to the ball
(ii) and average force exerted on the ball.CorrectIncorrectHint
(i) Impulse \(=\) Area under \(F\) – \(t\) curve
\(
\begin{aligned}
& =\text { Area of } \triangle A B C=\frac{1}{2} \times O P \times A C=\frac{1}{2} \times 18000 \times(2.5-1) \\
& =1.35 \times 10^4 \mathrm{~kg}-\mathrm{ms}^{-1} \text { or } \mathrm{N}-\mathrm{s}
\end{aligned}
\)
(ii) Average force \(=\frac{\text { Impulse }}{\text { Time }}=\frac{1.35 \times 10^4}{(2.5-1)}=9000 \mathrm{~N}\) -
Question 13 of 55
13. Question
A block of mass \(25 \mathrm{~kg}\) is raised by a \(50 \mathrm{~kg}\) man in two different ways as shown in figure. What is the action on the floor by the man in the two cases? If the floor yields to a normal force of \(700 \mathrm{~N}\), which mode should the man adopt to lift the block without the floor yielding? (Take, \(g=9.8 \mathrm{~ms}^{-2}\) )
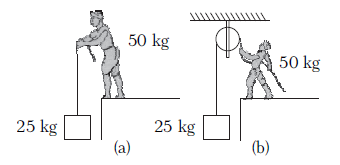 CorrectIncorrect
CorrectIncorrectHint
In mode (a), the man applies a force equal to \(25 \mathrm{~kg}\) weight in upward direction. According to Newton’s third law of motion, there will be a downward force of reaction on the floor.
\(\therefore\) Total action on the floor by the man
\(
\begin{aligned}
& =50 \mathrm{~kg}-\mathrm{wt}+25 \mathrm{~kg}-\mathrm{wt} \\
& =75 \mathrm{~kg}-\mathrm{wt} \\
& =75 \times 9.8 \mathrm{~N}=735 \mathrm{~N}
\end{aligned}
\)
In mode (b), the man applies a downward force on rope equal to \(25 \mathrm{~kg}\)-wt. According to Newton’s third law, the reaction will be in the upward direction by the rope on the man, so he becomes light by \(25 \mathrm{~kg}\)-wt.
\(\therefore\) Total action on the floor by the man
\(
\begin{aligned}
& =50 \mathrm{~kg} \text {-wt}-25 \mathrm{~kg} \text {-wt } \\
& =25 \mathrm{~kg} \text {-wt } \\
& =25 \times 9.8 \mathrm{~N}=245 \mathrm{~N}
\end{aligned}
\)As the floor yields to a downward force of \(700 \mathrm{~N}\), so the man should adopt mode (b).
-
Question 14 of 55
14. Question
A bullet of mass \(10 \mathrm{~g}\) is fired from a gun of mass \(1 \mathrm{~kg}\). If the recoil velocity is \(5 \mathrm{~ms}^{-1}\). Find the velocity of the muzzle.
CorrectIncorrectHint
From the law of conservation of momentum,
\(
m_G v_G=m_B v_B
\)
where, \(m_G, v_G=\) mass and velocity of gun
\(m_B, v_B=\) mass and velocity of bullet
\(
\Rightarrow \quad v_B=\frac{m_G v_G}{m_B}=\frac{1 \times 5}{10 \times 10^{-3}}=500 \mathrm{~ms}^{-1}
\) -
Question 15 of 55
15. Question
On a mine site a rock is exploded. On explosion, rock breaks into three parts. Two parts go off at right angles to each other. Of these two, \(1 \mathrm{~kg}\) first part is moving with a velocity of \(12 \mathrm{~ms}^{-1}\) and \(2 \mathrm{~kg}\) second part is moving with a velocity of \(8 \mathrm{~ms}^{-1}\). If the third part flies off with a velocity \(4 \mathrm{~ms}^{-1}\), what will be its mass?
CorrectIncorrectHint
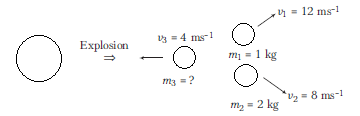
From the law of conservation of momentum,
\(
\begin{aligned}
p_3 & =\sqrt{p^2+p_2^2} \\
\Rightarrow \quad m_3 \times 4 & =\sqrt{(1 \times 12)^2+(2 \times 8)^2}=20 \\
\Rightarrow \quad m_3 & =5 \mathrm{~kg}
\end{aligned}
\) -
Question 16 of 55
16. Question
Two objects each of mass \(5 \mathrm{~kg}\) are moving in the same straight line but in the opposite directions towards each other with same speed of \(3 \mathrm{~m} / \mathrm{s}\). They stick to each other after collision. What will be the velocity of the combined object after collision?
CorrectIncorrectHint
Given,
\(
\begin{aligned}
m_1 & =m_2=5 \mathrm{~kg}, \\
u_1 & =3 \mathrm{~m} / \mathrm{s}, u_2=-3 \mathrm{~m} / \mathrm{s}
\end{aligned}
\)Before collision,
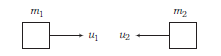
Let the velocity of the combined object be \(v\). Then, after collision,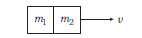
Total momentum of the system before collision is
\(
m_1 u_1+m_2 u_2=5 \times 3+5 \times(-3)=0
\)Total momentum of the system after collision is
\(
m_1 v+m_2 v=\left(m_1+m_2\right) v=(5+5) v=10 v
\)According to the law of conservation of momentum, Momentum before collision \(=\) Momentum after collision
\(
\therefore, 0=10 v \Rightarrow v=0
\)Hence, the velocity of the combined object after collision is zero.
-
Question 17 of 55
17. Question
A ball of mass \(m\) strikes a rigid wall with speed \(v\) and gets reflected without any loss of speed, as shown in the figure.
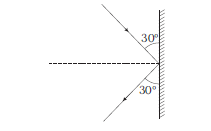
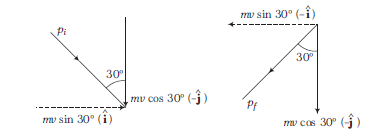
(i) What is the magnitude of the impulse imparted to the ball by the wall?
(ii) What is the direction of the force on the wall due to the ball?CorrectIncorrectHint
According to the question,
\(
\begin{aligned}
& \text { (i) } \mathbf{p}_i=m v \sin 30^{\circ} \hat{\mathbf{i}}-m v \cos 30^{\circ} \hat{\mathbf{j}}, \mathbf{p}_f=-m v \sin 30^{\circ} \hat{\mathbf{i}}-m v \cos 30^{\circ} \hat{\mathbf{j}} \\
& \therefore \text { Impulse }=\Delta \mathbf{p}=\mathbf{p}_f-\mathbf{p}_i=-2 m v \sin 30^{\circ} \hat{\mathbf{i}}=-m v \hat{\mathbf{i}} \\
& \text { Magnitude of impulse }=|\Delta \mathbf{p}|=m v
\end{aligned}
\)
(ii) Negative sign of the impulse shows that it is along negative \(x\)-direction. Since, impulse and force are in the same direction, the force on the ball is along the negative direction of \(X\)-axis. Hence, the force on the wall will be along positive \(X\)-axis.
-
Question 18 of 55
18. Question
Inertia of an object is directly dependent on
CorrectIncorrectHint
1. According to Newton’s first law of motion, “A body continues to be in its state of rest or uniform motion along a given direction, until and unless an external force is applied on it.” This is also known as the law of inertia.
2. Inertia is the property of a body by which it is unable to change its position of rest or uniform motion.
3. The mass of a body can be defined as the measure of inertia of a body.
4. Thus, inertia depends upon mass. The greater the mass of a body, the greater will be the inertia and the more difficult it will be to move the body. -
Question 19 of 55
19. Question
A body of mass \(6 \mathrm{~kg}\) is acted upon by a force, so that its velocity changes from \(3 \mathrm{~ms}^{-1}\) to \(5 \mathrm{~ms}^{-1}\), then change in momentum is
CorrectIncorrectHint
(d) Given, mass, \(m=6 \mathrm{~kg}\)
Velocity, \(\Delta v=v_2-v_1=5-3=2 \mathrm{~ms}^{-1}\)
\(\therefore\) Momentum, \(\Delta p=m \Delta v=6 \times 2=12 \mathrm{~N}-\mathrm{s}\) -
Question 20 of 55
20. Question
The momentum \(p\) (in \(\mathrm{kg}-\mathrm{ms}^{-1}\) ) of a particle is varying with time \(t\) (in second) as \(p=2+3 t^2\). The force acting on the particle at \(t=3 \mathrm{~s}\) will be
CorrectIncorrectHint
(a) Given, \(p=2+3 t^2\)
Differentiate w.r.t. \(t\), we get
\(
\frac{d p}{d t}=0+3 \times 2 t=6 t
\)If \(t=3 \mathrm{~s}\), then \(\frac{d p}{d t}=6 \times 3=18 \mathrm{~N}\)
\(\therefore\) Force acting on the particle \(=18 \mathrm{~N}\) -
Question 21 of 55
21. Question
A body is acted upon by balanced forces,
CorrectIncorrectHint
If a body is acted upon by balanced forces then the net force acting on the body is zero.
We know from Newton’s law of motion \(\mathrm{F}=\mathrm{ma}\)
If \(\mathrm{F}=0\) then \(\mathrm{a}=0\)
Thus, the body will not accelerate. It will either be at rest or move with a constant velocity. -
Question 22 of 55
22. Question
A force of 72 dyne is inclined to the horizontal at an angle of \(60^{\circ}\), find the acceleration of a mass of \(9 \mathrm{~g}\) which moves in the effect of this force in a horizontal direction.
CorrectIncorrectHint
(b) Given,
\(
\begin{aligned}
F & =72 \text { dyne } \Rightarrow F=72 \times 10^{-5} \mathrm{~N}, \\
\theta & =60^{\circ}, m=9 \mathrm{~g}=9 \times 10^{-3} \mathrm{~kg} \\
F^{\prime} & =m a
\end{aligned}
\)In this case, \(F^{\prime}=F \cos 60^{\circ}\)
\(
\begin{aligned}
\Rightarrow \quad a & =\frac{F^{\prime}}{m}=\frac{F \cos 60^{\circ}}{9 \times 10^{-3}} \\
& =\frac{72 \times 10^{-5} \times \cos 60^{\circ}}{9 \times 10^{-3}}=8 \times 10^{-2} \times \frac{1}{2} \\
& =4 \times 10^{-2} \mathrm{~ms}^{-1}=4 \mathrm{cms}^{-1}
\end{aligned}
\) -
Question 23 of 55
23. Question
A man of mass \(60 \mathrm{~kg}\) is standing on a horizontal conveyor belt. When the belt is given an acceleration of \(1 \mathrm{~ms}^{-2}\), the man remains stationary with respect to the moving belt. If \(g=10 \mathrm{~ms}^{-2}\), the net force acting on the man is
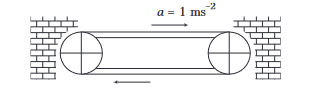 CorrectIncorrect
CorrectIncorrectHint
(d) Given, \(m=60 \mathrm{~kg}\) and \(a=1 \mathrm{~ms}^{-2}\)
\(\therefore\) Net force, \(F_{\text {net }}=\) Mass \(\times\) Acceleration \(=60 \times 1=60 \mathrm{~N}\) -
Question 24 of 55
24. Question
A constant force acting on a body of mass \(3 \mathrm{~kg}\) change its speed from \(2 \mathrm{~ms}^{-1}\) to \(3.5 \mathrm{~ms}^{-1}\) in \(25 \mathrm{~s}\), in the direction of the motion of the body. What is the magnitude and direction of the force?
CorrectIncorrectHint
(a) Given, \(m=3 \mathrm{~kg}, \Delta v=35-2=15 \mathrm{~ms}^{-1}\) and \(\Delta t=25 \mathrm{~s}\)
Force, \(F=m a=m \frac{\Delta v}{\Delta t}=3 \times \frac{1.5}{25}=0.18 \mathrm{~N}\), in the direction of motion
-
Question 25 of 55
25. Question
A body of mass \(5 \mathrm{~kg}\) is acted upon by two perpendicular force \(8 \mathrm{~N}\) and \(6 \mathrm{~N}\), find the magnitude and direction of the acceleration.
CorrectIncorrectHint
(b) Given, \(m=5 \mathrm{~kg}, F_1=8 \mathrm{~N}\) and \(F_2=6 \mathrm{~N}\)
Resultant force, \(F=\sqrt{8^2+6^2}=10 \mathrm{~N}\)
\(
\therefore a=\frac{F}{m}=\frac{10}{5}=2 \mathrm{~ms}^{-2}
\)
and \(\theta=\cos ^{-1}\left(\frac{6}{10}\right)=\cos ^{-1}(0.6)\), from \(6 \mathrm{~N}\) -
Question 26 of 55
26. Question
A ball of mass \(m\) is moving towards a player with velocity \(v\). If player stopped it, then impulse applied by the player is
CorrectIncorrectHint
Impulse = change in momentum
\(
=m { (v_f-v_i) }
\)
\(
\begin{aligned}
v_f & =0 \\
& =m(0-\vec{v}) \\
& =-m \vec{v}
\end{aligned}
\) -
Question 27 of 55
27. Question
A constant retarding force of \(50 \mathrm{~N}\) is applied to a body of mass \(20 \mathrm{~kg}\) moving initially with a speed of \(15 \mathrm{~ms}^{-1}\). How much time does the body take to stop?
CorrectIncorrectHint
(a) Given, \(F=50 \mathrm{~N}, m=20 \mathrm{~kg}\) and \(v=15 \mathrm{~ms}^{-1}\)
Impulse \(=F \Delta t=m v\)
\(\therefore\) Time, \(\Delta t=\frac{m v}{F}=\frac{20 \times 15}{50}=6 \mathrm{~s}\) -
Question 28 of 55
28. Question
A ball of mass \(1 \mathrm{~kg}\) is dropped from height \(9.8 \mathrm{~m}\), strikes with ground and rebounds at height of \(4.9 \mathrm{~m}\), if the time of contact between ball and ground is \(0.1 \mathrm{~s}\), then find impulse and average force acting on ball.
CorrectIncorrectHint
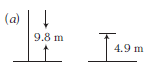
\(
\begin{aligned}
& v^2=u^2+2 g h \\
& v^2=0+2 \times 9.8 \times 9.8
\end{aligned}
\)
\(
\begin{aligned}
v^2 & =\sqrt{2 \times 9.8 \times 9.8} \\
\Rightarrow \quad v & =9.8 \sqrt{2} \mathrm{~m} / \mathrm{s} \\
\text { Again, } v^2 & =u^2-2 g h \\
0 & =u^2-2 \times 9.8 \times 4.9 \\
\Rightarrow \quad u^2 & =\sqrt{(9.8)^2} \Rightarrow u=9.8 \mathrm{~m} / \mathrm{s}
\end{aligned}
\)
\(
\begin{aligned}
\text { Impulse } & =m[v-(-u)] \\
& =1[9.8 \sqrt{2}+9.8]=9.8(\sqrt{2}+1) \\
& =9.8 \times 2.4=23.52 \mathrm{~N}\mathrm{-s}
\end{aligned}
\)
\(
\text { Average force }=\frac{\text { Impulse }}{\text { Time }}=\frac{23.52}{0.1}=235.2 \mathrm{~N}
\) -
Question 29 of 55
29. Question
A body of mass \(5 \mathrm{~kg}\) is moving with velocity of \(\mathbf{v}=(2 \hat{\mathbf{i}}+6 \hat{\mathbf{j}}) \mathrm{ms}^{-1}\) at \(t=0 \mathrm{~s}\). After time \(t=2 \mathrm{~s}\), velocity of body is \((10 \hat{\mathbf{i}}+6 \hat{\mathbf{j}})\), then change in momentum of body is
CorrectIncorrectHint
(a) Here, mass, \(m=5 \mathrm{~kg}\)
Change in velocity, \(\Delta \mathbf{v}=v_f-v_i=[(10-2) \hat{\mathbf{i}}+(6-6) \hat{\mathbf{j}}]=8 \hat{\mathbf{i}}\)
Change in momentum \(=m \Delta \mathbf{v}=5[8 \hat{\mathbf{i}}]=40 \hat{\mathbf{i}} \mathrm{kg}-\mathrm{ms}^{-1}\) -
Question 30 of 55
30. Question
If impulse \(I\) varies with time \(t\) as \(F\left(\mathrm{~kg}-\mathrm{ms}^{-1}\right)=20 t^2-40 t\). The change in momentum is minimum at
CorrectIncorrectHint
(b) Impulse is defined as rate of change of momentum. For change in momentum to be minimum,
\(
\begin{aligned}
\frac{d}{d t}\left(20 t^2-40 t\right) & =0 \\
40 t-40 & =0 \Rightarrow t=1 \mathrm{~s}
\end{aligned}
\) -
Question 31 of 55
31. Question
A ball of mass \(0.5 \mathrm{~kg}\) moving with a velocity of \(2 \mathrm{~ms}^{-1}\) strikes a wall normally and bounces back with the same velocity. If the time of contact between the ball and the wall is one millisecond, the average force exerted by the wall on the ball is
CorrectIncorrectHint
\(
\text { (a) } F_{\mathrm{av}}=m a_{\mathrm{av}}=m \frac{\Delta v}{\Delta t}=\frac{0.5[2-(-2)]}{10^{-3}}=2000 \mathrm{~N}
\) -
Question 32 of 55
32. Question
An initially stationary device lying on a frictionless floor explodes into two pieces and slides across the floor. One piece is moving in positive \(x\)-direction, then other piece is moving in
CorrectIncorrectHint
(c) From law of conservation of momentum, \(p_i=p_f\)
and initial momentum, \(p_i=m u=m(0)=0\)
\(\therefore p_f\) should also be zero.
Hence, other piece will move in negative \(x\)-direction. -
Question 33 of 55
33. Question
A bullet of mass \(0.1 \mathrm{~kg}\) is fired with a speed of \(100 \mathrm{~ms}^{-1}\). The mass of gun being \(50 \mathrm{~kg}\), then the velocity of recoil becomes
CorrectIncorrectHint
(d) From the law of conservation of momentum, total initial momentum \(=\) total final momentum
\(
\begin{aligned}
& \Rightarrow \quad m_1 \mu_1+m_2 u_2=m v_1+m v_2 \\
& \therefore \quad 0.1 \times 0+50 \times 0=0.1 \times 100+50\left(-v_2\right) \\
& \Rightarrow \quad 0=10-50 v_2 \\
& \therefore \quad v_2=\frac{10}{50}=0.2 \mathrm{~ms}^{-1} \\
&
\end{aligned}
\) -
Question 34 of 55
34. Question
A ball is moving with speed \(20 \mathrm{~ms}^{-1}\) collides with a smooth surface as shown in figure. The magnitude of change in velocity of the ball will be
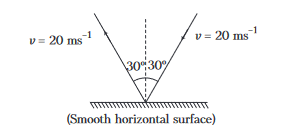 CorrectIncorrect
CorrectIncorrectHint
(b) From the given figure,
Initial velocity, \(\mathbf{v}_i=\left(-20 \sin 30^{\circ} \hat{\mathbf{i}}-20 \cos 30^{\circ} \hat{\mathbf{j}}\right) \mathrm{m} / \mathrm{s}\)
Final velocity, \(\mathbf{v}_f=\left(-20 \sin 30^{\circ} \hat{\mathbf{i}}+20 \cos 30^{\circ} \hat{\mathbf{j}}\right) \mathrm{m} / \mathrm{s}\)
Change in velocity, \(\Delta \mathbf{v}=\mathbf{v}_f-\mathbf{v}_i\)
[/latex]
\begin{aligned}
& \Delta \mathbf{v}=\left(-20 \sin 30^{\circ} \hat{\mathbf{i}}+20 \cos 30^{\circ} \hat{\mathbf{j}}\right) \\
& \Delta \mathbf{v}=2 \times 20 \cos 30^{\circ} \hat{\mathbf{j}} \quad-\left(-20 \sin 30^{\circ} \hat{\mathbf{i}}-20 \cos 30^{\circ} \hat{\mathbf{j}}\right) \\
& \Delta \mathbf{v}=2 \times 20 \times \frac{\sqrt{3}}{2} \hat{\mathbf{j}} \Rightarrow \Delta \mathbf{v}=20 \sqrt{3} \mathbf{j}
\end{aligned}
[/latex]Magnitude, \(|\Delta \mathbf{v}|=20 \sqrt{3} \mathrm{~m} / \mathrm{s}\)
-
Question 35 of 55
35. Question
Resolve horizontally and vertically a force \(F=8 \mathrm{~N}\) which makes an angle of \(45^{\circ}\) with the horizontal.
CorrectIncorrectHint
Horizontal component of \(\mathbf{F}\) is
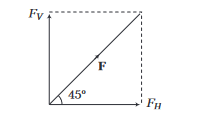
\(
\begin{aligned}
F_H & =F \cos 45^{\circ} \\
& =(8)\left(\frac{1}{\sqrt{2}}\right)=4 \sqrt{2} \mathrm{~N}
\end{aligned}
\)
and vertical component of \(\mathbf{F}\) is
\(
\begin{aligned}
F_V & =F \sin 45^{\circ} \\
& =(8)\left(\frac{1}{\sqrt{2}}\right)=4 \sqrt{2} \mathrm{~N}
\end{aligned}
\) -
Question 36 of 55
36. Question
Resolve a weight of \(10 \mathrm{~N}\) in two directions which are parallel and perpendicular to a slope inclined at \(30^{\circ}\) to the horizontal.
CorrectIncorrectHint
Component perpendicular to the plane,
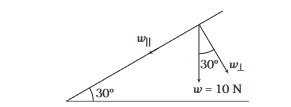
\(
w_{\perp}=w \cos 30^{\circ}=(10) \frac{\sqrt{3}}{2}=5 \sqrt{3} \mathrm{~N}
\)
and component parallel to the plane,
\(
w_{||}=w \sin 30^{\circ}=(10)\left(\frac{1}{2}\right)=5 \mathrm{~N}
\) -
Question 37 of 55
37. Question
An object is in equilibrium under four concurrent forces in the directions shown in figure. Find the magnitude of \(\mathrm{F}_1\) and \(\mathrm{F}_2\).
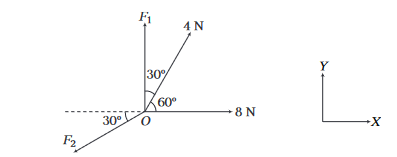 CorrectIncorrect
CorrectIncorrectHint
The object is in equilibrium.
\(
\begin{aligned}
& \Sigma F_x=0 \\
& \therefore 8+4 \cos 60^{\circ}-F_2 \cos 30^{\circ}=0 \\
& 8+2-F_2 \frac{\sqrt{3}}{2}=0 \\
& F_2=\frac{20}{\sqrt{3}} \mathrm{~N} \\
& \text { Similarly, } \quad \Sigma F_y=0 \\
& \therefore F_1+4 \sin 60^{\circ}-F_2 \sin 30^{\circ}=0 \\
& F_1+\frac{4 \sqrt{3}}{2}-\frac{F_2}{2}=0 \\
& F_1=\frac{F_2}{2}-2 \sqrt{3} \\
& =\frac{10}{\sqrt{3}}-2 \sqrt{3} \\
& F_1=\frac{4}{\sqrt{3}} \mathrm{~N} \\
&
\end{aligned}
\) -
Question 38 of 55
38. Question
Determine the tensions \(T_1\) and \(T_2\) in the strings as shown in figure.
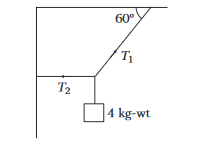 CorrectIncorrect
CorrectIncorrectHint
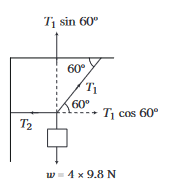
Resolving the tension \(T_1\) along horizontal and vertical directions. As the body is in equilibrium,
\(\mathrm{T}_1 \sin 60^{\circ}=4 \times 9.8 \mathrm{~N} \dots(i)\) and
\(T_1 \cos 60^{\circ}=T_2 \dots(ii)\)
From Eq. (i), we get
\(
T_1=\frac{4 \times 9.8}{\sin 60^{\circ}}=\frac{4 \times 9.8 \times 2}{\sqrt{3}}=45.26 \mathrm{~N}
\)
Putting this value in Eq. (ii), we get
\(
T_2=T_1 \cos 60^{\circ}=45.26 \times 0.5=22.63 \mathrm{~N}
\)Note Tension is a type of force produced in strings.
-
Question 39 of 55
39. Question
One end of a string \(0.5 \mathrm{~m}\) long is fixed to a point \(A\) and the other end is fastened to a small object of weight \(8 \mathrm{~N}\). The object is pulled aside by a horizontal force \(F\), until it is \(0.3 \mathrm{~m}\) from the vertical through \(A\). Find the magnitudes of the tension \(T\) in the string and the force \(F\).
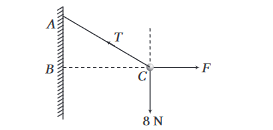 CorrectIncorrect
CorrectIncorrectHint
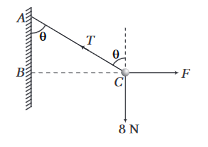
\(A C=0.5 \mathrm{~m}, B C=0.3 \mathrm{~m}\)
\(\therefore A B=0.4 \mathrm{~m}\)
and if \(\angle B A C=\theta\)
Then, \(\cos \theta=\frac{A B}{A C}=\frac{0.4}{0.5}=\frac{4}{5}\)
and \(\quad \sin \theta=\frac{B C}{A C}=\frac{0.3}{0.5}=\frac{3}{5}\)
Here, the object is in equilibrium under three concurrent forces. So, we can apply Lami’s theorem,
\(
\frac{F}{\sin \left(180^{\circ}-\theta\right)}=\frac{8}{\sin \left(90^{\circ}+\theta\right)}=\frac{T}{\sin 90^{\circ}}
\)\(
\begin{aligned}
\frac{F}{\sin \theta} & =\frac{8}{\cos \theta}=T \\
T & =\frac{8}{\cos \theta} \\
& =\frac{8}{4 / 5}=10 \mathrm{~N} \\
F & =\frac{8 \sin \theta}{\cos \theta} \\
& =\frac{(8)(3 / 5)}{(4 / 5)}=6 \mathrm{~N}
\end{aligned}
\) -
Question 40 of 55
40. Question
A block of mass \(m\) is at rest on a rough wedge as shown in figure. What is the force exerted by the wedge on the block?
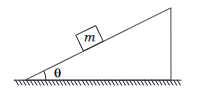 CorrectIncorrect
CorrectIncorrectHint
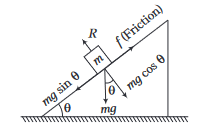
Since, the block is permanently at rest, it is in equilibrium. Net force on it should be zero. In this case, only two forces are acting on the block.
(i) Weight \(=m g\) (downwards)
(ii) Contact force (resultant of normal reaction and friction force) applied by the wedge on the block.For the block to be in equilibrium, these two forces should be equal and opposite. Therefore, force exerted by the wedge on the block is \(m g\) (upwards).
Explanation:
From Newton’s third law of motion, force exerted by the block on the wedge is also \(\mathrm{mg}\) but downwards. The result can also be obtained in a different manner. The normal force on the block is \(R\) or \(N=m g \cos \theta\) and the friction force on the block is \(f=m g \sin \theta(\operatorname{not} \mu m g \cos \theta)\) because it is not the case of limiting friction.
These two forces are mutually perpendicular.
\(\therefore\) Net contact force would be \(\sqrt{N^2+f^2}\) or \(\sqrt{(m g \cos \theta)^2+(m g \sin \theta)^2}\) which is equal to \(m g\). -
Question 41 of 55
41. Question
Four forces act on a point object. The object will be in equilibrium, if
CorrectIncorrectHint
The equilibrium condition is obtained when the net force acting on the body is zero. All of the above choice is true.
-
Question 42 of 55
42. Question
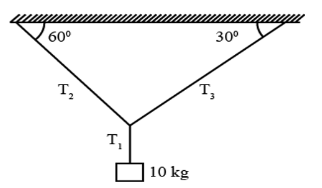
A block of mass \(10 \mathrm{~kg}\) is suspended by three strings as shown in the figure. The tension \(T_2\) is
 CorrectIncorrect
CorrectIncorrectHint
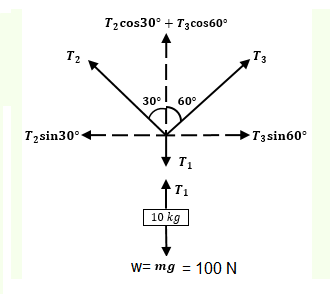
For horizontal equilibrium: \(T_3 \sin 60^{\circ}=T_2 \sin 30^{\circ} \therefore T_3=\frac{T_2}{\sqrt{3}}\)
Now, for vertical equilibrium:
\(
T_2 \cos 30^{\circ}+T_3 \cos 60^{\circ}=T_1 \dots(1)
\)
\(
\mathrm{T}_1=\mathrm{mg}=10 \times 10=100 \mathrm{~N}
\)
Substituting the value of \(T_1\) and \(T_3\) in equation (1), we get
\(
\begin{aligned}
\frac{\sqrt{3} T_2}{2}+\frac{T_2}{\sqrt{3}} \times \frac{1}{2} & =100 \\
\frac{8 T_2}{4 \sqrt{3}} & =100 \\
T_2 & =50 \sqrt{3} \mathrm{~N}
\end{aligned}
\) -
Question 43 of 55
43. Question
An object is resting at the bottom of two strings which are inclined at an angle of \(120^{\circ}\) with each other. Each string can withstand a tension of \(20 \mathrm{~N}\). The maximum weight of the object that can be sustained without breaking the strings is
CorrectIncorrectHint
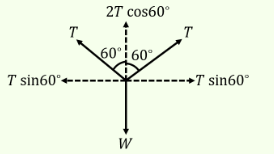
Considering the forces acting in the vertically upward direction, \(2 \mathrm{~T} \cos 60^{\circ}=\mathrm{W}\)
\(
\mathrm{W}_{\max }=\mathrm{T}_{\max }=20 \mathrm{~N}
\)
In the horizontal direction, the component of the forces cancel out. -
Question 44 of 55
44. Question
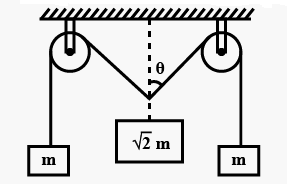
The pulleys and strings shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle \(\theta\) should be
 CorrectIncorrect
CorrectIncorrectHint
Since both blocks (left and right, \(m\)) are similar and tension in the strings are \(\mathrm{mg}\). It has zero acceleration, as the system is in equilibrium.
For the block on the left is \(T-m g=m a=m(0)\)
For the blockin the right is \(T-m g=m a=m(0)\)
Equilibrium of \(\sqrt{2} m: 2 T \cos \theta=\sqrt{2} m g\)
\(
\begin{aligned}
& \Rightarrow 2 m g \cos \theta=\sqrt{2} m g \\
& \Rightarrow \cos \theta=\frac{1}{\sqrt{2}} \\
& \Rightarrow \theta=45^{\circ}
\end{aligned}
\) -
Question 45 of 55
45. Question
A non-uniform \(\operatorname{rod} A B\) of weight \(w\) is supported horizontally in a vertical plane by two light strings \(P A\) and \(Q B\) as shown in the figure. \(G\) is the centre of gravity of the rod. If \(P A\) and \(Q B\) make angles \(30^{\circ}\) and \(60^{\circ}\) respectively with the vertical, the ratio \(\frac{A G}{B G}\) is
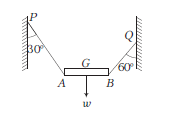 CorrectIncorrect
CorrectIncorrectHint

\(
\begin{aligned}
T_1 \cos 60^{\circ}= & T_2 \cos 30^{\circ} \\
\frac{T_1}{2} & =\frac{\sqrt{3} T_2}{2}
\end{aligned}
\)‘
\(
T_1=\sqrt{3} T_2 \dots(i)
\)
\(
\begin{aligned}
& \therefore \quad \frac{\sqrt{3} T_1}{2} \times A G=\frac{T_2}{2} \times B G \\
& \Rightarrow \quad \frac{A G}{B G}=\frac{T_2}{\sqrt{3} T_1} \\
& \text { But } \quad \frac{T_2}{T_1}=\frac{1}{\sqrt{3}} \quad \text { [from Eq. (i)] }\\
& \text { Hence, } \quad \frac{A G}{B G}=\frac{1}{3} \\
&
\end{aligned}
\) -
Question 46 of 55
46. Question
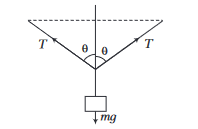
A weight \(w\) is suspended from the mid-point of a rope, whose ends are at the same level. In order to make the rope perfectly horizontal, the force applied to each of its ends must be
CorrectIncorrectHint
For equilibrium of body,
\(
m g=2 T \cos \theta
\)
\(
T=\frac{m g}{2 \cos \theta}
\)
For the string to be horizontal,
\(
\begin{aligned}
\theta & =90^{\circ} \\
T & =\frac{m g}{2 \cos 90^{\circ}} \\
\Rightarrow \quad T & =\infty
\end{aligned}
\) -
Question 47 of 55
47. Question
The below figure is the part of a horizontally stretched net. Section \(A B\) is stretched with a force of \(10 \mathrm{~N}\). The tensions in the sections \(B C\) and \(B F\) are
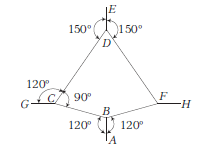 CorrectIncorrect
CorrectIncorrectHint
As shown the figure below
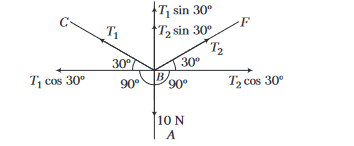
\(
\begin{aligned}
T_1 \cos 30^{\circ} & =T_2 \cos 30^{\circ} \\
\text { Let, }T_1 & =T_2=T
\end{aligned}
\)
Again, \(T_1 \sin 30^{\circ}+T_2 \sin 30^{\circ}=10 \Rightarrow 2 T \sin 30^{\circ}=10\)
\(\Rightarrow \quad 2 T \cdot \frac{1}{2}=10 \Rightarrow T=10 \mathrm{~N}\)
Thus, the tension in section \(B C\) and \(B F\) are \(10 \mathrm{~N}\) and \(10 \mathrm{~N}\), respectively. -
Question 48 of 55
48. Question
A body of mass \(60 \mathrm{~kg}\) suspended by means of three strings, \(P, Q\) and \(R\) as shown in the figure is in equilibrium. The tension in the string \(P\) is
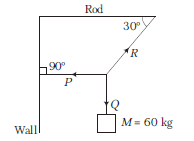 CorrectIncorrect
CorrectIncorrectHint
The given figure can be drawn as
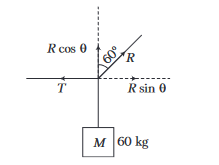
Taking component of forces,
\(
\begin{aligned}
R \cos \theta=M g \Rightarrow & R \cos 60^{\circ}=M g \dots(i) \\
\text { and } & R \sin 60^{\circ}=T \dots(ii)
\end{aligned}
\)
and
\(
R \sin 60^{\circ}=T
\)By Eqs. (i) and (ii), we get
\(
\begin{aligned}
\Rightarrow & & \tan 60^{\circ} & =\frac{T}{M g} \Rightarrow T=M g \tan 60^{\circ} \\
\text { or } & & T & =60 \times g \times \sqrt{3}=103.9 \mathrm{kgf}
\end{aligned}
\) -
Question 49 of 55
49. Question
A man of mass \(50 \mathrm{~g}\) stands on a frame of mass \(30 \mathrm{~g}\). He pulls on a light rope which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium, what force man must exert on the rope?
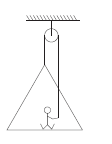 CorrectIncorrect
CorrectIncorrectHint
(a) The mass of the frame is \(m=30 \mathrm{~kg}\)
The mass of the man is \(M=50 \mathrm{~kg}\)
The man is standing on the frame. So, the total mass of the system is \(M+m=50 \mathrm{~kg}+30 \mathrm{~kg}=80 \mathrm{~kg}\)
Now the frame is on a pulley, the other end of the rope is on the hand of the man. The man is pulling the rope to make the system to be in equilibrium.
Let the man is pulling the rope with a force \(\mathrm{F}\) and the tension on the rope will be \(\mathrm{T}\). Again, the frame is also attached to one end of the rope. The weight of the frame is downward. So, we have another tension \(T\) on the rope which is also acting upward.
For the system to be in equilibrium, the downward force on the system should be equal to the upward force.
Total downward force \(m\) the system will be,
\(
\begin{array}{l}
(M+m) g = 80 g
\end{array}
\)
The total upward force will be,
\(
T+T=2 T
\)
Now, these two forces will be equal.
\(
\begin{array}{l}
2 T=80 g \\
T=\frac{80 g}{2} \\
T=40 g
\end{array}
\)
Since the force with which the man is pulling the rope is equal to the tension on the rope, we can say that the system will be in equilibrium when the man pulls the rope with a force \(40 g\). -
Question 50 of 55
50. Question
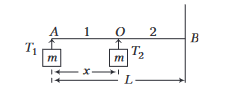
Two particles of equal mass are connected to a rope \(A B\) of negligible mass, such that one is at end \(A\) and the other dividing the length of the rope in the ratio \(1: 2\) from \(A\). The rope is rotated about end \(B\) in a horizontal plane. Ratio of the tensions in the smaller part to the other is (ignore effect of gravity)
CorrectIncorrectHint
(d) Let \(x\) be distance from \(A\) to \(O\) and \(L\) be the total length of string. Then, ratio of tensions is
\(
\frac{T_1}{T_2}=\frac{x}{L}=\frac{1}{3}
\)
-
Question 51 of 55
51. Question
A body is under the action of two mutually perpendicular forces of \(3 \mathrm{~N}\) and \(4 \mathrm{~N}\). The resultant force acting on the body is
CorrectIncorrectHint
The resultant force will be
\(
F_R=\left|\mathbf{F}_R\right|=\sqrt{3^2+4^2+2 \times 3 \times 4 \cos 90^{\circ}}=5 \mathrm{~N}
\) -
Question 52 of 55
52. Question
Two equals forces are acting at a point with an angle of \(60^{\circ}\) between them. If the resultant force is equal to \(40 \sqrt{3} \mathrm{~N}\), the magnitude of each force is
CorrectIncorrectHint
(a) Let equal forces \(F_1=F_2=F\) newton
Angle between the forces, \(\theta=60^{\circ}\)
Resultant force, \(R=40 \sqrt{3} \mathrm{~N}\)
Now,
\(
R=\sqrt{F_1^2+F_2^2+2 F_1 F_2 \cos \theta}
\)
\(
\begin{array}{l}
\therefore \quad 40 \sqrt{3}=\sqrt{F^2+F^2+2 F F \cos 60^{\circ}} \\
\Rightarrow \quad 40 \sqrt{3}=\sqrt{2 F^2+2 F^2 \times \frac{1}{2}} \\
\Rightarrow \quad F=40 \mathrm{~N} \\
\end{array}
\) -
Question 53 of 55
53. Question
When a force \(F\) acts on a body of mass \(m\), the acceleration produced in the body is \(a\). If three equal forces \(F_1=F_2=F_3=F\) act on the same body as shown in figure. The acceleration produced is
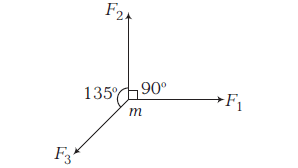 CorrectIncorrect
CorrectIncorrectHint
Let us find the net magnitude of forces \(F_1\) and \(F_2\) which are perpendicular to each other and this net force be written as \(F_{12}\) so,
\(
F_{12}=\sqrt{F^2+F^2}
\)
\(F_{12}=\sqrt{2} F\) Which will be in direction just opposite to that of \(F_3\).
Now, two forces acting on the body of mass \(m\) respectively \(F_{12}=\sqrt{2} F\) and \(F_3=F\).
Both forces are in opposite direction,
Hence net force act on the body of mass \(m\) is,
\(
\begin{array}{l}
F_{\text {net }}=\sqrt{2} F-F \\
\Rightarrow F_{\text {net }}=(\sqrt{2}-1) F
\end{array}
\)
Now, let us assume that net acceleration is denoted by \(a^{\prime}\) then by newton’ second law we have:
\(
(\sqrt{2}-1) F=m a^{\prime}
\)
We also know that, \(F=m a\) put this value in above equation, we get,
\(
(\sqrt{2}-1) a=a^{\prime}
\)
Net acceleration is \(a^{\prime}=(\sqrt{2}-1) a\) -
Question 54 of 55
54. Question
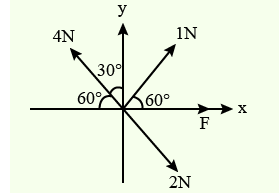
Three forces acting on a body are shown in the figure. To have the resultant force only along the \(y\)-direction, the magnitude of the minimum additional force needed is
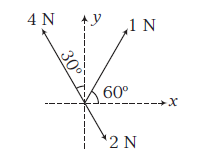 CorrectIncorrect
CorrectIncorrectHint
Let the additional force \(\mathrm{F}\) be directed along the positive \({x}\)-direction Taking \({x}\)-components, the total should be zero
\(
x+1 \cos 60^{\circ}+2 \cos 60^{\circ}-4 \sin 30^{\circ}=0
\)
\(
x=0.5 \mathrm{~N}
\) -
Question 55 of 55
55. Question
A ball of mass \(1 \mathrm{~kg}\) hangs in equilibrium from two strings \(O A\) and \(O B\) as shown in figure. What are the tensions in strings \(O A\) and \(O B\) ? (Take, \(g=10 \mathrm{~ms}^{-2}\) )
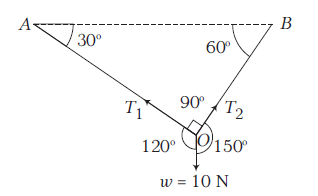 CorrectIncorrect
CorrectIncorrectHint
(c) Apply Lami’s theorem at \(O\),
\(
\begin{aligned}
\frac{T_1}{\sin 150^{\circ}} & =\frac{T_2}{\sin 120^{\circ}}=\frac{10}{\sin 90^{\circ}}=\frac{10}{1}=10 \\
\therefore \quad T_1 & =10 \sin 150^{\circ}=10 \times \frac{1}{2}=5 \mathrm{~N} \\
T_2 & =10 \sin 120^{\circ} \\
& =10 \times \frac{\sqrt{3}}{2}=5 \sqrt{3} \mathrm{~N}
\end{aligned}
\)