Kinematics (motion in one dimension) Quiz-L2
Quiz Summary
0 of 100 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 100 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 100
1. Question
The acceleration of a particle is increasing linearly with time \(t\) as \(b t\). The particle starts from the origin with an initial velocity \(v_0\). The distance travelled by the particle in time \(t\) will be
CorrectIncorrectHint
(a)
\(
\begin{array}{c}
a=b t \\
\therefore \quad \int_{v_0}^v d v=\int a d t=\int_0^t b t \cdot d t \Rightarrow v=v_0+\frac{b t^2}{2}
\end{array}
\)Further integrating the above equation w.r.t. time, we get
\(
s=v_0 t+\frac{b t^3}{6}
\) -
Question 2 of 100
2. Question
The acceleration \(a\) (in \(\mathrm{ms}^{-2}\) ), of a particle is given by \(a=3 t^2+2 t+2\) where \(t\) is the time. If the particle starts out with a velocity \(v=2 \mathrm{~ms}^{-1}\) at \(t=0\), then the velocity at the end of \(2 \mathrm{~s}\) is
CorrectIncorrectHint
(d)
\(
d v=a d t
\)
\(
\therefore \quad \int_2^v d v=\int_0^2\left(3 t^2+2 t+2\right) d t=\left[t^3+t^2+2 t\right]_0^2
\)
or \(\quad v=18 \mathrm{~ms}^{-1}\) -
Question 3 of 100
3. Question
A particle is moving such that \(s=t^3-6 t^2+18 t+9\), where \(s\) is in metre and \(t\) is in second. The minimum velocity attained by the particle is
CorrectIncorrectHint
(c) \(s=t^3-6 t^2+18 t+9 \Rightarrow v=\frac{d s}{d t}=3 t^2-12 t+18\)
\(v\) is minimum or maximum at time \(t\), which can be calculated as
\(
\begin{aligned}
a & =\frac{d v}{d t}=6 t-12=0 \\
\Rightarrow \quad t & =2 \mathrm{~s}
\end{aligned}
\)
At \(t=2 \mathrm{~s}\),
\(\frac{d^2 v}{d t^2}=6>0\), i.e. \(v\) is minimum at \(t=2 \mathrm{~s}\)
\(
v_{\min }=3(2)^2-12(2)+18=6 \mathrm{~m} / \mathrm{s}
\) -
Question 4 of 100
4. Question
Which of the following graph represents the uniform motion?
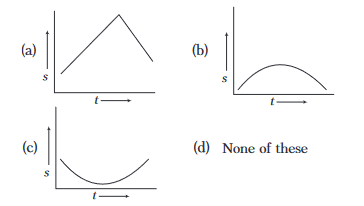 CorrectIncorrect
CorrectIncorrectHint
(d) Uniform motion means uniform velocity or constant slope of \(s-t\) graph.
-
Question 5 of 100
5. Question
A particle shows distance-time curve as given in this figure. The maximum instantaneous velocity of the particle is around the point
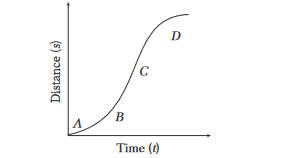 CorrectIncorrect
CorrectIncorrectHint
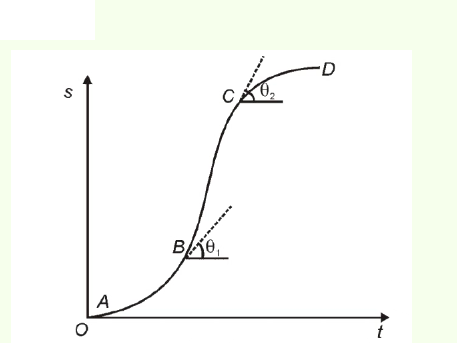
Slope of s-t graph gives instantaneous velocity
Slope \(=\tan \theta\)
Slope at \(A\) and \(D\) is very less
For \(B\) and \(C, \theta_2>\theta_1\)
\(\operatorname{tan} \theta_2>\tan \theta_1\)
Hence instantaneous velocity is maximum at \(C\). -
Question 6 of 100
6. Question
From the displacement-time graph, find out the velocity of a moving body.
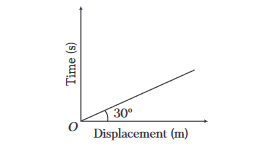 CorrectIncorrect
CorrectIncorrectHint
(c) Slope of the s-t graph is velocity, \(v=\tan \theta\)
But it is valid only when angle is measured with time axis.
So, for the given graph, angle from time axis
\(
=90^{\circ}-30^{\circ}=60^{\circ}
\)
Now,
\(
v=\tan 60^{\circ}=\sqrt{3} \mathrm{~ms}^{-1}
\) -
Question 7 of 100
7. Question
The distance-time graph of a particle at time \(t\) makes angle \(45^{\circ}\) with the time axis. After one second, it makes angle \(60^{\circ}\) with the time axis. What is the average acceleration of the particle?
CorrectIncorrectHint
(a) \(v_i=\) slope of \(s-t\) graph \(=\tan 45^{\circ}=1 \mathrm{~ms}^{-1}\)
\(v_f=\) slope of \(s-t\) graph \(=\tan 60^{\circ}=\sqrt{3} \mathrm{~ms}^{-1}\)Now, \(a_{\mathrm{av}}=\frac{v_f-v_i}{\Delta t}=\frac{\sqrt{3}-1}{1}=(\sqrt{3}-1)\) units
-
Question 8 of 100
8. Question
The \(v-t\) graph of a moving object is shown in the figure. The maximum acceleration is
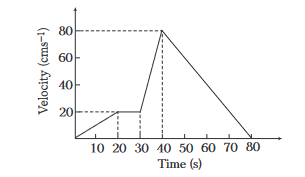 CorrectIncorrect
CorrectIncorrectHint
(d) Maximum acceleration means maximum change in velocity in minimum time interval.
In time interval, \(t=30 \mathrm{~s}\) to \(t=40 \mathrm{~s}\)
\(
\therefore \quad a=\frac{\Delta v}{\Delta t}=\frac{80-20}{40-30}=\frac{60}{10}=6 \mathrm{cms}^{-2}
\) -
Question 9 of 100
9. Question
The variation of velocity of a particle with time moving along a straight line is illustrated in the adjoining figure. The distance travelled by the particle in \(4 \mathrm{~s}\) is
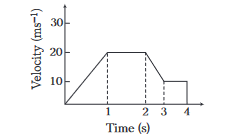 CorrectIncorrect
CorrectIncorrectHint
\(
\text { (b) Distance }=\text { Area under } v \text { – } t \text { graph }=A_1+A_2+A_3+A_4
\)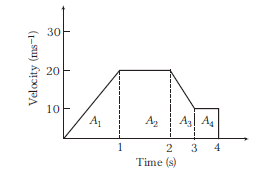
\(
\begin{array}{l}
=\frac{1}{2} \times 1 \times 20+(20 \times 1)+\frac{1}{2}(20+10) \times 1+(10 \times 1) \\
=10+20+15+10=55 \mathrm{~m}
\end{array}
\) -
Question 10 of 100
10. Question
A lift is going up. The variation in the speed of the lift is as given in the graph. What is the height to which the lift takes the passengers?
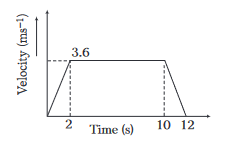 CorrectIncorrect
CorrectIncorrectHint
\(
\text { (c) } \text { Distance }=\text { Area of trapezium }=\frac{1}{2} \times 3.6 \times(12+8)=36 \mathrm{~m}
\) -
Question 11 of 100
11. Question
The velocity-time graph of a body moving in a straight line is shown in the figure. The displacement and distance travelled by the body in \(6 \mathrm{~s}\) are respectively
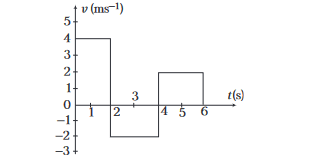 CorrectIncorrect
CorrectIncorrectHint
Displacement is equal to area under the velocity time graph with proper sign.
\(\therefore\) Displacement \(=4 \times 2-2 \times 2+2 \times 2=8 \mathrm{~m}\)
Distance is equal to total area under the speed time graph.
\(\therefore\) Distance \(=4 \times 2+2 \times 2+2 \times 2=16 \mathrm{~m}\). -
Question 12 of 100
12. Question
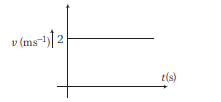
The \(x-t\) equation is given as \(x=2 t+1\). The corresponding \(v\) – \(t\) graph is
CorrectIncorrectHint
\(
\text { (b) } v=\frac{d x}{d t}=2 \mathrm{~ms}^{-1}=\text { constant }
\)
-
Question 13 of 100
13. Question
Which of the following graphs correctly represents velocity-time relationship for a particle released from rest to fall freely under gravity?
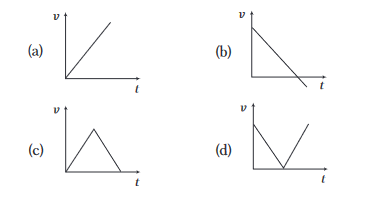 CorrectIncorrect
CorrectIncorrectHint
(a) Velocity will continuously increase (starting from rest).
-
Question 14 of 100
14. Question
A particle projected vertically upwards returns to the ground in time \(T\). Which graph represents the correct variation of velocity \((v)\) against time \((t)\) ?
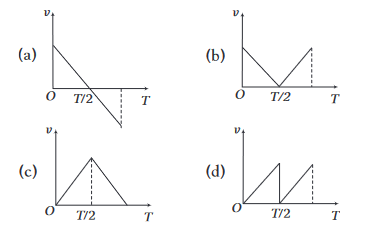 CorrectIncorrect
CorrectIncorrectHint
(a) Velocity first decreases in upwards direction, then increases in downward direction.
-
Question 15 of 100
15. Question
The velocity-time graph is shown in the figure, for a particle. The acceleration of particle is
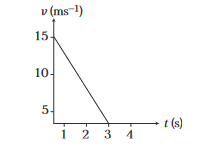 CorrectIncorrect
CorrectIncorrectHint
\(
\text { (c) } a=\text { Slope of } v t \text { graph }=-\frac{15}{3}=-5 \mathrm{~ms}^{-2}
\) -
Question 16 of 100
16. Question
The \(v-t\) plot of a moving object is shown in the figure. The average velocity of the object during the first \(10 \mathrm{~s}\) is
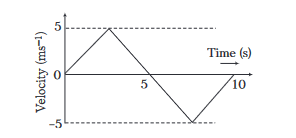 CorrectIncorrect
CorrectIncorrectHint
(a) Since, total displacement is zero, hence average velocity is also zero.
-
Question 17 of 100
17. Question
Which of the following graphs cannot possibly represent one dimensional motion of a particle?
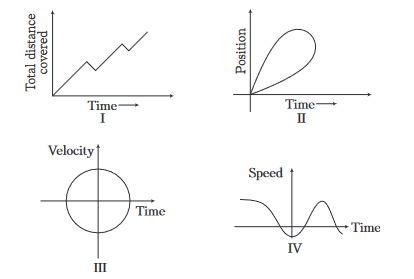 CorrectIncorrect
CorrectIncorrectHint
(d) I is not possible because total distance covered by a particle cannot decrease with time. II is not possible because at a particular time, position cannot have two values. III is not possible because at a particular time, velocity cannot have two values. IV is not possible because speed can never be negative.
-
Question 18 of 100
18. Question
If the velocity \(v\) of a particle moving along a straight line decreases linearly with its displacement \(s\) from \(20 \mathrm{~ms}^{-1}\) to a value approaching zero at \(s=30 \mathrm{~m}\), then acceleration of the particle at \(v=10 \mathrm{~ms}^{-1}\) is
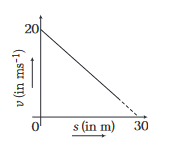 CorrectIncorrect
CorrectIncorrectHint
\(
\text { (d) } a=v\left(\frac{d v}{d s}\right)=(10)\left(-\frac{20}{30}\right)=-\frac{20}{3} \mathrm{~ms}^{-2}
\) -
Question 19 of 100
19. Question
\(v^2\) versus \(s\) graph of a particle moving in a straight line is shown in the figure below. From the graph some conclusions are drawn. State which amongst the following statement(s) is wrong?
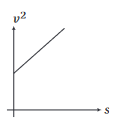 CorrectIncorrect
CorrectIncorrectHint
(b) For uniformly accelerated motion, \(v^2=u^2+2 a\) s, i.e.
\(v^2\) versus \(s\) graph is a straight line with intercept \(u^2\) and slope
\(2 a\). Since, intercept is non-zero, initial velocity is non-zero. -
Question 20 of 100
20. Question
A graph between the square of the velocity of a particle and the distance $s$ moved by the particle is shown in the figure below. The acceleration of the particle is
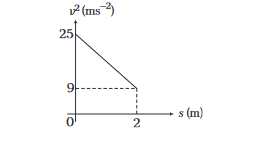 CorrectIncorrect
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (b) } v^2=u^2+2 a s, \text { slope }=2 a=-\frac{16}{2}=-8 \mathrm{~ms}^{-2} \\
\text { or } \quad a=-4 \mathrm{~ms}^{-2}
\end{array}
\) -
Question 21 of 100
21. Question
A particle starts from rest at \(t=0\) and undergoes an acceleration a in \(\mathrm{ms}^{-2}\) with time \(t\) in second which is as shown?
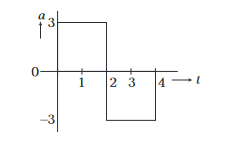
Which one of the following plot represents velocity \(v\) (in \(\mathrm{ms}^{-1}\) ) versus time \(t\) (in s)?
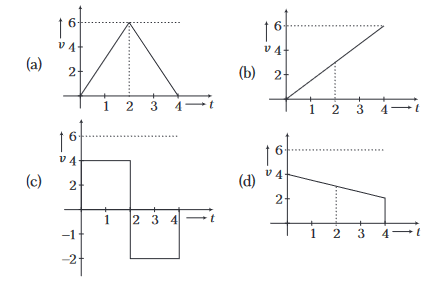 CorrectIncorrect
CorrectIncorrectHint
(a) Taking the motion from 0 to \(2 \mathrm{~s}\),
\(
\begin{array}{l}
u=0, a=3 \mathrm{~ms}^{-2}, t=2 \mathrm{~s}, v=? \\
v=u+a t=0+3 \times 2=6 \mathrm{~ms}^{-1}
\end{array}
\)Taking the motion from \(2 \mathrm{~s}\) to \(4 \mathrm{~s}\),
\(
v=6+(-3)(2)=0 \mathrm{~ms}^{-1}
\) -
Question 22 of 100
22. Question
A \(100 \mathrm{~m}\) long train crosses a man travelling at \(5 \mathrm{kmh}^{-1}\), in opposite direction in \(7.2 \mathrm{~s}\), then the velocity of train is
CorrectIncorrectHint
\(
\text { (d) } 7.2=\frac{100}{(v+5)(5 / 18)} \text { or } v=45 \mathrm{~ms}^{-1}
\) -
Question 23 of 100
23. Question
Two parallel rail tracks run north-south. Train \(A\) moves north with a speed of \(54 \mathrm{kmh}^{-1}\) and train \(B\) moves south with a speed of \(90 \mathrm{kmh}^{-1}\). Find the relative velocity of \(B\) w.r.t. \(A\).
CorrectIncorrectHint
(a) Let positive direction of motion be from south to north.
Given,
\(
\begin{array}{l}
\mathbf{v}_A=+54 \mathrm{kmh}^{-1}=15 \mathrm{~ms}^{-1}, \\
\mathbf{v}_B=-90 \mathrm{kmh}^{-1}=-25 \mathrm{~ms}^{-1}
\end{array}
\)
\(\therefore\) The relative velocity of \(B\) w.r.t. \(A\),
\(
\mathbf{v}_{B A}=\mathbf{v}_B-\mathbf{v}_A=-25-15=-40 \mathrm{~ms}^{-1}
\)
i.e. The train \(B\) appears to \(A\) to move with a speed of \(40 \mathrm{~ms}^{-1}\) from north to south. -
Question 24 of 100
24. Question
Two bodies are held separated by \(9.8 \mathrm{~m}\) vertically one above the other. They are released simultaneously to fall freely under gravity. After \(2 \mathrm{~s}\), the relative distance between them is
CorrectIncorrectHint
(c) Both the particles will fall same distance in same time interval.
So, the relative separation will remain unchanged. -
Question 25 of 100
25. Question
A particle \((A)\) moves due north at \(3 \mathrm{kmh}^{-1}\) and another particle \((B)\) moves due west at \(4 \mathrm{kmh}^{-1}\). The relative velocity of \(A\) with respect to \(B\) is (Take, \(\tan 37^{\circ}=3 / 4\) )
CorrectIncorrectHint
\(
\text { (b) } \mathbf{v}_{A B}=\mathbf{v}_A-\mathbf{v}_B
\)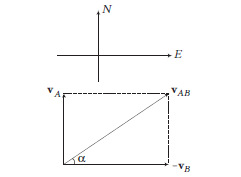
\(
\begin{aligned}
v_{A B} & =\sqrt{v_A^2+v_B^2}=5 \mathrm{kmh}^{-1} \\
\alpha & =\tan ^{-1}\left(\frac{v_A}{v_B}\right)=\tan ^{-1}\left(\frac{3}{4}\right) \\
& =37^{\circ} \text { east of north }
\end{aligned}
\) -
Question 26 of 100
26. Question
A man standing on a road has to hold his umbrella at \(30^{\circ}\) with the vertical to keep the rain away. He throws the umbrella and starts running at \(10 \mathrm{kmh}^{-1}\). He finds that raindrops are hitting his head vertically. What is the speed of rain with respect to ground?
CorrectIncorrectHint
(b) Velocity of rain is at \(30^{\circ}\) in vertical direction. So, its horizontal component is \(v_R \sin 30^{\circ}=\frac{v_R}{2}\). When man starts walking with \(10 \mathrm{kmh}^{-1}\) rain appears vertical. So, horizontal component \(\frac{v_R}{2}\) is balanced by his speed of \(10 \mathrm{kmh}^{-1}\). Thus, \(\frac{v_R}{2}=10\) or \(v_R=20 \mathrm{kmh}^{-1}\)
Alternate:
When the man is at rest with respect to the ground, the rain comes to him at an angle \(30^{\circ}\) with the vertical. This is the direction of the velocity of raindrops with respect to the ground. The situation when the man runs is shown in the figure
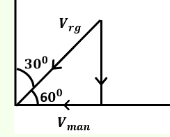
\(
\begin{array}{l}
\mathrm{V}_{\mathrm{rg}}=\text { velocity of rain drops with respect to ground. } \\
\mathrm{V}_{\text {man }}=\text { velocity of man }=10 \mathrm{~km} / \mathrm{h} \\
\text { Hence, } \cos \theta=\frac{10}{\mathrm{~V}_{\mathrm{rg}}} \\
\Rightarrow \cos 60^{\circ}=\frac{10}{\mathrm{~V}_{\mathrm{rg}}} \\
\Rightarrow \frac{1}{2}=\frac{10}{\mathrm{~V}_{\mathrm{rg}}} \\
\Rightarrow \mathrm{V}_{\mathrm{rg}}=20 \mathrm{~km} / \mathrm{h}
\end{array}
\)
Hence, velocity of rain drops with respect to the ground is \(20 \mathrm{~km} / \mathrm{h}\). -
Question 27 of 100
27. Question
A stationary man observes that the rain is falling vertically downward. When he starts running with a velocity of \(12 \mathrm{kmh}^{-1}\), he observes that the rain is falling at an angle \(60^{\circ}\) with the vertical. The actual velocity of rain is
CorrectIncorrectHint
\(
\begin{array}{ll}
\text { (c) } \tan 60^{\circ}=\frac{v_H}{v_V} \text { or } \sqrt{3}=\frac{12}{v_V} \\
\therefore & v_V=4 \sqrt{3} \mathrm{kmh}^{-1}
\end{array}
\)Alternate:
Let \(\vec{V}_m\) be the velocity of the running man.
Let the velocity of the rain be \(\vec{V}_r\)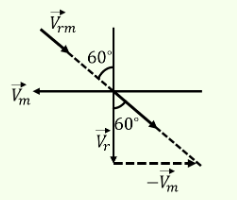
From the figure, we can say \(\tan 60^{\circ}=\frac{\left|\overrightarrow{\mathrm{V}_{\mathrm{m}}}\right|}{\left|\overrightarrow{\mathrm{V}_{\mathrm{r}}}\right|}\)
\(
\begin{array}{l}
\sqrt{3}=\frac{12}{\left|\vec{V}_r\right|} \\
\therefore\left|\vec{V}_r\right|=4 \sqrt{3} \mathrm{~km} / \mathrm{h}
\end{array}
\) -
Question 28 of 100
28. Question
A boy is running on the plane road with velocity \(v\) with a long hollow tube in his hand. The water is falling vertically downwards with velocity \(u\). At what angle to the vertical, he must inclined the tube, so that the water drops enter it without touching its sides?
CorrectIncorrectHint
(a) \(\tan \theta=\frac{v_H}{v_V}=\frac{v}{u}\)
or \(\quad \theta=\tan ^{-1}\left(\frac{v}{u}\right)\)
-
Question 29 of 100
29. Question
The speed of boat is \(5 \mathrm{kmh}^{-1}\) in still water. It crosses a river of width \(1 \mathrm{~km}\) along the shortest possible path in \(15 \mathrm{~min}\). Then, velocity of river will be
CorrectIncorrectHint
Shortest path that is, Width of river \(=1 \mathrm{Km}\)
Speed of boat in still water \(v_{br}=5 \mathrm{Kmhr}^{-1}\)
Time taken by boat to cross the river \(\mathrm{t}=15 \mathrm{~min}=\frac{1}{4} \mathrm{hr}\)
Let the speed of river \(=v_r\)
The vector diagram is shown below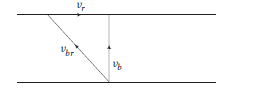
Calculating the velocity of river:
By observing the vector diagram we can calculate the velocity along the shortest path as below:
Speed in the direction of shortest path \(=\frac{\text { shortest path }}{\text { time }}\)
And also we know that
\(
\text { time }=\frac{\text { shortest path }}{\sqrt{{v_{br}}^2-\mathrm{v_r}^2}}
\)
\(
\Rightarrow \frac{1}{4}=\frac{1}{\sqrt{25-{v_r}^2}}
\)
\(
{v_r}=3 \mathrm{Kmh}^{-1}
\)Therefore the speed of river is equal to \(3 \mathrm{Kmh}^{-1}\).
-
Question 30 of 100
30. Question
\(A\) ship \(X\) moving due north with speed \(v\) observes that another ship \(Y\) is moving due west with same speed \(v\). The actual velocity of \(Y\) is
CorrectIncorrectHint
\(
\text { (b) } \mathbf{v}_x=-v \hat{\mathbf{j}}
\)
\(
\begin{array}{ll}
\therefore \quad \mathbf{v}_Y=\mathbf{v}_{Y X}+\mathbf{v}_X=-\hat{\mathbf{i}}+v \hat{\mathbf{j}} \\
\left|\mathbf{v}_Y\right|=\sqrt{2} v
\end{array}
\)
Direction of \(\mathbf{v}_Y\) is north-west. -
Question 31 of 100
31. Question
A river is flowing from west to east at a speed of \(8 \mathrm{~m}\) per \(\mathrm{min}\). A man on the south bank of the river, capable of swimming at \(20 \mathrm{~m} / \mathrm{min}\) in still water, wants to swim across the river in the shortest time. He should swim in a direction,
CorrectIncorrectHint
(a) To reach the opposite bank of the river in minimum time, the swimmer should swim at right angles to the direction of flow of river. He should swim in a direction due north
-
Question 32 of 100
32. Question
The rowing speed of a man relative to water is \(5 \mathrm{kmh}^{-1}\) and the speed of water flow is \(3 \mathrm{kmh}^{-1}\). At what angle to the river flow should he head, if he wants to reach a point on the other bank, directly opposite to starting point?
CorrectIncorrectHint
(a)
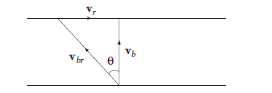
\(
\begin{array}{l}
\mathrm{v}_{\mathrm{{br}}}=5 \mathrm{~km} / \mathrm{h} \\
\mathrm{v}_{\mathrm{r}}=3 \mathrm{~km} / \mathrm{h}
\end{array}
\)
To reach the directly opposite point the man should move along the line joining the two points in other words due to the resultant velocity his body should flow perpendicular to river flow.
To do this we need to cancel out the speed of water to avoid the drifting. Suppose he moves at angle \(90+\theta\) from the direction of flow. Thus his speed component opposite to that of river is \(\mathrm{v}_{\mathrm{br}} \sin \theta\) that should cancel \(\mathrm{v}_{\mathrm{r}}\).
\(
\sin \theta=\frac{v_r}{v_{k \pi}}=\frac{3}{5}, \theta=37^{\circ}
\)
The required angle is therefore
\(
90^{\circ}+\theta=90^{\circ}+37^{\circ}=127^{\circ}
\) -
Question 33 of 100
33. Question
A man wants to reach point \(B\) on the opposite bank of a river flowing at a speed as shown in figure. With what minimum speed and in which direction should the man swim relative to water, so that he can reach point \(B\) ?
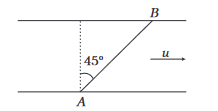 CorrectIncorrect
CorrectIncorrectHint
(c) Let \(v\) be the speed of boatman in still water. Resultant of \(v\) and \(u\) should be along \(A B\). Components of \(\mathbf{v}_b\) (absolute velocity of boatman) along \(x\) and \(y\)-directions are,
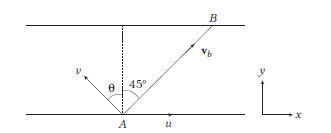
\(
v_x=u-v \sin \theta \text { and } v_y=v \cos \theta
\)
Further, \(\tan 45^{\circ}=\frac{v_y}{v_x}\) or \(1=\frac{v \cos \theta}{u-v \sin \theta}\)
\(
\therefore \quad v=\frac{u}{\sin \theta+\cos \theta}=\frac{u}{\sqrt{2} \sin \left(\theta+45^{\circ}\right)}
\)
\(v\) is minimum at,
\(
\theta+45^{\circ}=90^{\circ} \text { or } \theta=45^{\circ} \text { and } v_{\min }=\frac{u}{\sqrt{2}}
\) -
Question 34 of 100
34. Question
Two trains, each \(50 \mathrm{~m}\) long moving parallel towards each other at speeds \(10 \mathrm{~ms}^{-1}\) and \(15 \mathrm{~ms}^{-1}\) respectively, at what time will they pass each other?
CorrectIncorrectHint
(b) \(v_r=10+15=25 \mathrm{~ms}^{-1}\)
where, \(v_r\) is relative velocity.
\(
\therefore \quad t=\frac{50+50}{25}=4 \mathrm{~s}
\) -
Question 35 of 100
35. Question
A ball is dropped from the top of a building \(100 \mathrm{~m}\) high. At the same instant, another ball is thrown upwards with a velocity of \(40 \mathrm{~ms}^{-1}\) from the bottom of the building. The two balls will meet after
CorrectIncorrectHint
(b) Relative acceleration \(=0\) relative velocity is \(40 \mathrm{~ms}^{-1}\) and relative separation is \(100 \mathrm{~m}\).
\(
\therefore \quad t=\frac{100}{40}=25 \mathrm{~s}
\) -
Question 36 of 100
36. Question
A boy walks to his school at a distance of \(6 \mathrm{~km}\) with constant speed of \(2.5 \mathrm{kmh}^{-1}\) and walks back with a constant speed of \(4 \mathrm{kmh}^{-1}\). His average speed for round trip expressed (in \(\mathrm{kmh}^{-1}\) ), is
CorrectIncorrectHint
(b)
\(
\begin{aligned}
\text { Average speed of a boy } & =\frac{2 v_1 v_2}{v_1+v_2}=\frac{2 \times 2.5 \times 4}{2.5+4} \\
& =\frac{20}{6.5}=\frac{40}{13} \mathrm{~km} / \mathrm{h}
\end{aligned}
\) -
Question 37 of 100
37. Question
The distance travelled by a particle starting from rest and moving with an acceleration \(\frac{4}{3} \mathrm{~ms}^{-2}\), in the third second is
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (a) } s_n=u+\frac{a}{2}(2 n-1) \\
\Rightarrow \quad s_3=0+\frac{4 / 3}{2}(2 \times 3-1) \Rightarrow s_3=\frac{10}{3} \mathrm{~m}
\end{array}
\) -
Question 38 of 100
38. Question
A vehicle travels half the distance \(l\) with speed \(v_1\) and the other half with speed \(v_2\), then its average speed is
CorrectIncorrectHint
(c) Time taken to travel first half distance, \(t_1=\frac{l / 2}{v_1}=\frac{l}{2 v_1}\) Time taken to travel second half distance, \(t_2=\frac{l}{2 v_2}\)
\(
\text { Total time }=t_1+t_2=\frac{l}{2 v_1}+\frac{l}{2 v_2}=\frac{l}{2}\left(\frac{1}{v_1}+\frac{1}{v_2}\right)
\)
We know that, \(v_{\text {av }}=\) Average speed
\(
=\frac{\text { total distance }}{\text { total time }}=\frac{l}{\frac{l}{2}\left(\frac{1}{v_1}+\frac{1}{v_2}\right)}=\frac{2 v_1 v_2}{v_1+v_2}
\) -
Question 39 of 100
39. Question
Which of the following speed-time \((v-t)\) graphs is physically not possible?
 CorrectIncorrect
CorrectIncorrectHint
(d) In all the given graphs, we have more than one value of speed corresponding to a single time. However, the graph must have a unique value of speed corresponding to a single time. Thus, all the three graphs are not possible.
-
Question 40 of 100
40. Question
A particle moves in a straight line with a constant acceleration. It changes its velocity from \(10 \mathrm{~ms}^{-1}\) to \(20 \mathrm{~ms}^{-1}\) while passing through a distance \(135 \mathrm{~m}\) in \(t\) second. The value of \(t\) (in second) is
CorrectIncorrectHint
(b) From third equation of motion, \(v^2=u^2+2 a s\)
\(
\Rightarrow \quad a=\frac{v^2-u^2}{2 \mathrm{~s}}=\frac{(20)^2-(10)^2}{2 \times 135}=\frac{300}{270}=\frac{10}{9} \mathrm{~ms}^{-2}
\)
From first equation of motion,
\(
v=u+a t \Rightarrow t=\frac{v-u}{a}=\frac{20-10}{10 / 9}=\frac{10}{10 / 9}=9 \mathrm{~s}
\) -
Question 41 of 100
41. Question
A man walks on a straight road from his home to a market \(2.5 \mathrm{~km}\) away with a speed of \(5 \mathrm{kmh}^{-1}\). Finding the market closed, he instantly turns and walks back home with a speed of \(7.5 \mathrm{kmh}^{-1}\). The average speed of the man over the interval of time 0 to \(50 \mathrm{~min}\) is equal to
CorrectIncorrectHint
(c) Man walks from his home to market with a speed of \(5 \mathrm{~kmh}^{-1}\). Distance \(=2.5 \mathrm{~km}\) and time
\(
=\frac{d}{v}=\frac{2.5}{5}=\frac{1}{2}=30 \mathrm{~min}
\)
and he returns back with speed of \(7.5 \mathrm{~kmh}^{-1}\) in rest a time of \(20 \mathrm{~min}\).
Distance \(=7.5 \times \frac{20}{60}=2.5 \mathrm{~km}\)
So, average speed \(=\frac{\text { total distance }}{\text { total time }}=\frac{(2.5+2.5)}{(50 / 60) \mathrm{h}}=\frac{30}{5} \mathrm{~km} / \mathrm{h}\) -
Question 42 of 100
42. Question
A car moving with a velocity of \(10 \mathrm{~ms}^{-1}\) can be stopped by the application of a constant force \(F\) in a distance of \(20 \mathrm{~m}\). If the velocity of the car is \(30 \mathrm{~ms}^{-1}\), it can be stopped by this force in
CorrectIncorrectHint
(d) \(s \propto u^2\). If \(u\) becomes 3 times, then \(s\) will become 9 times, i.e. \(9 \times 20=180 \mathrm{~m}\)
-
Question 43 of 100
43. Question
A body \(A\) starts from rest with an acceleration \(a_1\). After 2 seconds, another body \(B\) starts from rest with an acceleration \(a_2\). If they travel equal distance in the 5th second, after the start of \(A\), then the ratio \(a_1: a_2\) is equal to
CorrectIncorrectHint
(a) Distance travelled by body \(A\) in 5 th second and distance travelled by body \(B\) in 3rd second of its motion are equal.
\(
\begin{aligned}
0+\frac{a_1}{2}(2 \times 5-1) & =0+\frac{a_2}{2}(2 \times 3-1) \\
9 a_1 & =5 a_2 \Rightarrow \frac{a_1}{a_2}=\frac{5}{9}
\end{aligned}
\) -
Question 44 of 100
44. Question
The displacement-time graph of a moving particle is shown below. The instantaneous velocity of the particle is negative at the point
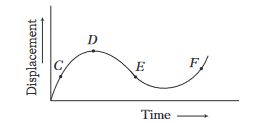 CorrectIncorrect
CorrectIncorrectHint
(a) \(\because\) Slope of displacement-time graph at the point \(E\) is negative. Thus, at the point \(E\), the instantaneous velocity of the particle is negative.
-
Question 45 of 100
45. Question
Figure given shows the distance-time graph of the motion of a car. It follows from the graph that the car is
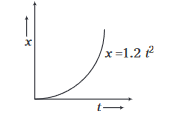 CorrectIncorrect
CorrectIncorrectHint
(d) Since \(x=1.2 t^2\), comparing it with equation of motion
\(
x=\frac{1}{2} a t^2 \text {. }
\)
Thus, the motion is uniformly accelerated.Note: Since, slope is increasing parabolically at a constant rate hence, motion of car is uniformly accelerated.
-
Question 46 of 100
46. Question
The velocity of a body depends on time according to the equation \(v=\frac{t^2}{10}+20\). The body is undergoing
CorrectIncorrectHint
(c) It is given that, \(v=\frac{t^2}{10}+20\)
Differentiating both sides w.r.t. time, we get
\(
\frac{d v}{d t}=\frac{2 t}{10}+0=\frac{t}{5}
\)
\(\therefore\) Acceleration, \(a=\frac{d v}{d t}=\frac{t}{5} \neq\) constant
Hence, it is a case of non-uniform acceleration. -
Question 47 of 100
47. Question
The velocity \(v\) of a particle as a function of its position \((x)\) is expressed as \(v=\sqrt{c_1-c_2 x}\), where \(c_1\) and \(c_2\) are positive constants. The acceleration of the particle is
CorrectIncorrectHint
(b) Given, \(v=\sqrt{c_1-c_2 x}\)
We know that, \(a=v \frac{d v}{d x}\)
\(
\begin{aligned}
\Rightarrow \quad a & =\sqrt{c_1-c_2 x} \cdot \frac{d}{d x} 9\left(\sqrt{c_1-c_2 x}\right) \\
& =\frac{1}{2}\left(-c_2\right)=-\frac{c_2}{2}
\end{aligned}
\) -
Question 48 of 100
48. Question
A person walks up a stalled escalator in \(90 \mathrm{~s}\). When he is just standing on the same moving escalator, then he is carried for \(60 \mathrm{~s}\). The time it would take him to walk up the moving escalator will be
CorrectIncorrectHint
(d) \(v_1=\frac{s}{90}, v_2=\frac{s}{60}\)
Now, \(t=\frac{s}{v_1+v_2}=\frac{s}{\frac{s}{90}+\frac{s}{60}}\)
\(
=\frac{90 \times 60}{90+60}=36 \mathrm{~s}
\) -
Question 49 of 100
49. Question
Particle \(A\) is moving along \(X\)-axis. At time \(t=0\), it has velocity of \(10 \mathrm{~ms}^{-1}\) and acceleration \(-4 \mathrm{~ms}^{-2}\). Particle \(B\) has velocity of \(20 \mathrm{~ms}^{-1}\) and acceleration \(-2 \mathrm{~ms}^{-2}\). Initially both the particles are at origin. At time \(t=2 \mathrm{~s}\), distance between the two particles is
CorrectIncorrectHint
(a) At \(t=2 \mathrm{~s} ; x_A=10 \times 2-\frac{1}{2} \times 4 \times(2)^2=12 \mathrm{~m}\) and \(x_B=20 \times 2-\frac{1}{2} \times 2 \times(2)^2=36 \mathrm{~m}\)
\(\therefore\) Distance between \(A\) and \(B\) at that instant is \(36-12=24 \mathrm{~m}\). -
Question 50 of 100
50. Question
The displacement of a body along \(X\)-axis depends on time as \(\sqrt{x}=t+1\). Then, the velocity of body
CorrectIncorrectHint
(a) Given, \(\sqrt{x}=t+1\)
Squaring both sides, we get
\(
x=(t+1)^2=t^2+2 t+1
\)
Differentiating it w.r.t. time \(t\), we get
\(
\frac{d x}{d t}=2 t+2
\)
Velocity, \(v=\frac{d x}{d t}=2 t+2\)This shows velocity increases with respect to time linearly.
-
Question 51 of 100
51. Question
A car starts moving along a line, first with acceleration \(a=5 \mathrm{~ms}^{-2}\) starting from rest, then uniformly and finally decelerating at the same rate \(a\) and comes to rest. The total time of motion is \(25 \mathrm{~s}\). The average speed during the time is \(20 \mathrm{~ms}^{-1}\). How long does particle move uniformly?
CorrectIncorrectHint
\(
\text { (d) Average velocity }=\frac{\text { Total displacement }}{\text { Total time }}
\)
or \(\quad 20=\frac{\frac{1}{2} \times a \times t^2+(a t)(25-2 t)+\frac{1}{2} \times a \times t^2}{25}\)
Solving this equation with \(a=5 \mathrm{~ms}^{-2}\), we get
\(
t=5 \mathrm{~s}
\)Thus, the particle moved uniformly for \((25-2 t)\) or \(15 \mathrm{~s}\).
-
Question 52 of 100
52. Question
A cyclist starts from the centre \(O\) of a circular park of radius one kilometre, reaches the edge \(P\) of the park, then cycles along the circumference and returns to the centre along \(Q O\) as shown in the figure. If the round trip takes ten minutes, the net displacement and average speed of the cyclist (in metre and kilometre per hour) is
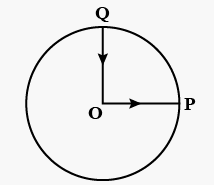 CorrectIncorrect
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (d) Net displacement }=0 \text { and total distance }=O P+P Q+Q O \\
\qquad=1+\frac{2 \pi \times 1}{4}+1=\frac{14.28}{4} \mathrm{~km} \\
\text { Average speed }=\frac{14.28}{4 \times 10 / 60}=\frac{6 \times 14.28}{4}=21.42 \mathrm{~km} / \mathrm{h}
\end{array}
\) -
Question 53 of 100
53. Question
A body starts from rest with uniform acceleration \(a\). The acceleration of the body as function of time \(t\) is given by the equation \(a=p t\), where \(p\) is a constant, then the displacement of the particle in the time interval \(t=0\) to \(t=t_1\) will be
CorrectIncorrectHint
(d) Integrate twice to convert \(a\) – \(t\) equation into \(s\) – \(t\) equation.
\(
\begin{array}{lc}
\because & a=\frac{v}{t} \Rightarrow v=a t \\
\Rightarrow & \int d v=\int a \cdot d t \Rightarrow v=\int p t \cdot d t=\frac{p t^2}{2} \\
\because & s=v \times t \Rightarrow d s=v d t \\
\Rightarrow & \int d s=\int_0^{t_1} v d t \Rightarrow s=\frac{1}{6} p t_1^3
\end{array}
\) -
Question 54 of 100
54. Question
A particle moves along a straight line \(O X\). At a time \(t\) (in seconds), the distance \(x=40+12 t-t^3\). How long would the particle travel before coming to rest?
CorrectIncorrectHint
(c) Distance travelled by the particle is \(x=40+12 t-t^3\)
We know that, speed is defined as the rate of change of distance, i.e. \(\quad v=\frac{d x}{d t}\)
\(
v=\frac{d}{d t}\left(40+12 t-t^3\right)=0+12-3 t^2
\)
But final velocity, \(v=0\)
\(
\begin{array}{l}
\therefore \quad 12-3 t^2=0 \Rightarrow t^2=\frac{12}{3}=4 \\
\Rightarrow \quad t=2 \mathrm{~s} \\
\end{array}
\)
Hence, distance travelled by the particle before coming to rest is given by
\(
x=40+12(2)-(2)^3=40+24-8=64-8=56 \mathrm{~m}
\) -
Question 55 of 100
55. Question
A bullet emerges from a barrel of length \(1.2 \mathrm{~m}\) with a speed of \(640 \mathrm{~ms}^{-1}\). Assuming constant acceleration, the approximate time that it spends in the barrel after the gun is fired, is
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (b) Given, } s=1.2 \mathrm{~m}, v=640 \mathrm{~ms}^{-1} \text {, } \\
a=\text { ?; } u=0 ; t=\text { ? } \\
2 a s=v^2-u^2 \\
\Rightarrow \quad 2 a \times 1.2=640 \times 640 \\
\Rightarrow \quad a=\frac{8 \times 64 \times 100}{3} \\
v=u+a t \\
\Rightarrow \quad t=\frac{v}{a}=\frac{640 \times 3}{8 \times 64 \times 100}=37.5 \times 10^{-3} \mathrm{~s} \approx 40 \mathrm{~ms} \\
\end{array}
\) -
Question 56 of 100
56. Question
The ratios of the distance traversed, in successive intervals of time by a body, falling from rest, are
CorrectIncorrectHint
(a) Here, \(u=0, a=g\)
Distance travelled in \(n\)th second is given by
\(
\begin{array}{ll}
& D_n=u+\frac{a}{2}(2 n-1) \\
\therefore \quad & D_n \propto(2 n-1) \\
\therefore \quad & D_1: D_2: D_3: D_4: D_5 \ldots=1: 3: 5: 7: 9: \ldots
\end{array}
\) -
Question 57 of 100
57. Question
A particle starts from rest. Its acceleration (a) versus time \((t)\) graph as shown in the figure. The maximum speed of the particle will be
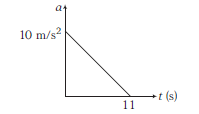 CorrectIncorrect
CorrectIncorrectHint
(b) The area under acceleration-time graph gives change in velocity.
As acceleration is zero at the end of \(11 \mathrm{~s}\), i.e. \(\quad v_{\max }=\) Area of \(\triangle O A B=\frac{1}{2} \times 11 \times 10=55 \mathrm{~ms}^{-1}\) -
Question 58 of 100
58. Question
A ball is dropped onto the floor from a height of \(10 \mathrm{~m}\). It rebounds to a height of \(5 \mathrm{~m}\). If the ball was in contact with the floor for \(0.01 \mathrm{~s}\), what was its average acceleration during contact? (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(a)
\(
\begin{aligned}
a_{\mathrm{av}} & =\frac{v_f-v_i}{\Delta t} \quad \text { (As they are in opposite direction) } \\
& =\frac{\sqrt{2 g h_f}+\sqrt{2 g h_i}}{\Delta t}=\frac{\sqrt{2 \times 10 \times 5}+\sqrt{2 \times 10 \times 10}}{0.01} \\
& =2414 \mathrm{~ms}^{-2}
\end{aligned}
\)Alternate:
When dropped from the height \(10 \mathrm{~m}\) from rest, the velocity with which the ball hits the ground is
\(\mathrm{v_i}=\sqrt{2 \mathrm{gh}}=\sqrt{2 \times 10 \times 10}=\sqrt{196}=14.14 \mathrm{~m} / \mathrm{s}\) in vertically downward direction.
After the ball rebounds, it reaches maximum height of \(2.5 \mathrm{~m}\)
so velocity just after the rebound is
\(\mathrm{v_f}=\sqrt{2 \times 10 \times 5}=\sqrt{49}=10 \mathrm{~m} / \mathrm{s}\) in vertically upward direction.
So average acceleration is \((10-(-14.14)) / 0.01=2414 \mathrm{~m} / \mathrm{s}^2\) in vertically upward direction. -
Question 59 of 100
59. Question
Two boys are standing at the ends \(A\) and \(B\) of a ground, where \(A B=a\). The boy at \(B\) starts running in a direction perpendicular to \(A B\) with velocity \(v_1\). The boy at \(A\) starts running simultaneously with velocity \(v\) and catches the other boy in a time \(t\), where \(t\) is
CorrectIncorrectHint
(b) Let two boys meet at point \(C\) after time ‘ \(t\) ‘ from the starting. Then, \(A C=v t, B C=v_1 t\) (see figure)
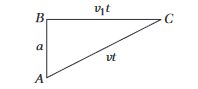
\(
(A C)^2=(A B)^2+(B C)^2 \Rightarrow v^2 t^2=a^2+v_1^2 t^2
\)
By solving, we get
\(
t=\sqrt{\frac{a^2}{v^2-v_1^2}}
\) -
Question 60 of 100
60. Question
A boggy of uniformly moving train is suddenly detached from train and stops after covering some distance. Then, which amongst the following option is correct about the relation between the distance covered by the boggy and distance covered by the train in the same time?
CorrectIncorrectHint
(b) Let \(a\) be the retardation of boggy, then distance covered by it be \(s_b\). If \(u\) is the initial velocity of boggy after detaching from train (i.e. uniform speed of train)
\(
v^2=u^2+2 a s \Rightarrow 0=u^2-2 a s
\)
\(
\Rightarrow \quad s_b=\frac{u^2}{2 a}
\)
Time taken by boggy to stop
\(
v=u+a t \Rightarrow 0=u-a t \Rightarrow t=\frac{u}{a}
\)
In this time \(t\), distance travelled by train, \(s_t=u t=\frac{u^2}{a}\) Hence, ratio \(\frac{s_b}{s_t}=\frac{1}{2}\). -
Question 61 of 100
61. Question
A body moves for a total of nine second starting from rest with uniform acceleration and then with uniform retardation, which is twice the value of acceleration and then stops. The duration of uniform acceleration is
CorrectIncorrectHint
(d)
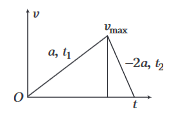
Let acceleration is \(a\) and retardation is \(-2 a\).
Then, for accelerated motion,
\(
t_1=\frac{v}{a} \dots(i)
\)
For retarding motion,
\(
t_2=\frac{v}{2 a} \dots(ii)
\)
Given, \(t_1+t_2=9 \Rightarrow \frac{v}{a}+\frac{v}{2 a}=9 \Rightarrow \frac{3 v}{2 a}=9 \Rightarrow \frac{v}{a}=6\)
Hence, duration of acceleration, \(t_1=\frac{v}{a}=6 \mathrm{~s}\). -
Question 62 of 100
62. Question
The displacement \(x\) of a particle varies with time \(t\) as \(x=a e^{-\alpha t}+b e^{\beta t}\), where \(a, b, \alpha\) and \(\beta\) are positive constants. The velocity of the particle will
CorrectIncorrectHint
(d) Given, \(x=a e^{-\alpha t}+b e^{\beta t}\)
So, velocity, \(v=\frac{d x}{d t}=-a \alpha e^{-\alpha t}+b \beta e^{\beta t}\) \(a=\frac{d v}{d t}=a \alpha^2 e^{-\alpha t}+b \beta^2 e^{\beta t}=+\) ve all time.
\(\therefore v\) will go on increasing. -
Question 63 of 100
63. Question
A stone is allowed to fall freely from rest. The ratio of the time taken to fall through the first metre and the second metre distance is
CorrectIncorrectHint
\(
\text { (b) } 1=\frac{1}{2} g t_1^2 \text { or } t_1=\sqrt{\frac{2}{g}}
\)
\(
2=\frac{1}{2} g t^2 \text { or } t=\sqrt{\frac{4}{g}}
\)
But
\(
t_2=t-t_1=\sqrt{\frac{4}{g}}-\sqrt{\frac{2}{g}}
\)
\(
\begin{aligned}
\therefore \quad \frac{t_1}{t_2} & =\frac{\sqrt{2 / g}}{\sqrt{4 / g}-\sqrt{2 / g}}=\frac{\sqrt{2}}{2-\sqrt{2}} \\
& =\frac{\sqrt{2}(2+\sqrt{2})}{2}=(\sqrt{2}+1)
\end{aligned}
\) -
Question 64 of 100
64. Question
Amongst the following equation of motion, which represents uniformly accelerated motion?
CorrectIncorrectHint
(c) \(t=\sqrt{\frac{x+a}{b}}\) or \((x+a)=b t^2\) or \(x=-a+b t^2\) Comparing this equation with general equation of uniformly accelerated motion, \(s=s_i+u t+\frac{1}{2} a t^2\) we see that \(s_i=-a, u=0\) and acceleration \(=2 b\).
-
Question 65 of 100
65. Question
A point initially at rest moves along \(X\)-axis. Its acceleration varies with time as \(a=(6 t+5) \mathrm{ms}^{-2}\). If it starts from origin, then the distance covered in \(2 \mathrm{~s}\) is
CorrectIncorrectHint
(b) Given, acceleration, \(a=6 t+5\)
\(
\therefore \quad a=\frac{d v}{d t}=6 t+5, d v=(6 t+5) d t
\)
Integrating it, we have
\(
\int_0^v d v=\int_0^t(6 t+5) d t
\)
\(v=3 t^2+5 t+C\), where \(C\) is a constant of integration.
When \(t=0, v=0\), so \(C=0\)
\(
\therefore \quad v=\frac{d s}{d t}=3 t^2+5 t \text { or } d s=\left(3 t^2+5\right) d t
\)
Integrating it within the conditions of motion, i.e. as \(t\) changes from 0 to \(2 \mathrm{~s}, s\) changes from 0 to \(s\), we have
\(
\begin{aligned}
& \int_0^s d s =\int_0^2\left(3 t^2+5 t\right) d t \\
\therefore & s =\left[t^3+\frac{5}{2} t^2\right]_0^2=8+10=18 \mathrm{~m}
\end{aligned}
\) -
Question 66 of 100
66. Question
A particle moves a distance \(x\) in time \(t\) according to equation \(x=(t+5)^{-1}\). The acceleration of particle is proportional to
CorrectIncorrectHint
(a) Given, \(x=\frac{1}{t+5}\)
Differentiating both sides w.r.t. \(t\), we get
\(
\frac{d x}{d t}=-\frac{1}{(t+5)^2} \times 1
\)
\(\therefore\) Velocity, \(v=\frac{d x}{d t}=-\frac{1}{(t+5)^2} \dots(i)\)
Again, differentiating both sides w.r.t. \(t\), we get
\(
\frac{d v}{d t}=\frac{1 \times 2}{(t+5)^3}(1)=\frac{2}{(t+5)^3} \dots(ii)
\)
Now, from Eqs. (i) and (ii), we get
\(
\frac{d v}{d t}=-2 v \times \frac{1}{(t+5)}=(-2 v)(\sqrt{v})=-2(v)^{3 / 2}
\)
\(\therefore\) Acceleration, \(a=\frac{d v}{d t}=-2 v^{3 / 2} \Rightarrow a \propto(\text { velocity })^{3 / 2}\) -
Question 67 of 100
67. Question
A particle moves along a straight line. Its position at any instant is given by \(x=32 t-\frac{8 t^3}{4}\), where \(x\) is in metre and \(t\) is in second. Find the acceleration of the particle at the instant when particle is at rest.
CorrectIncorrectHint
(b) \(v=\frac{d x}{d t}=32-6 t^2, v=0\) at \(t=2.30 \mathrm{~s}\)
\(
a=\frac{d v}{d t}=-12 t
\)At \(2.30 \mathrm{~s}\),
\(
a=-27.6 \mathrm{~ms}^{-2}
\) -
Question 68 of 100
68. Question
Two particles \(P\) and \(Q\) simultaneously start moving from point \(A\) with velocities \(15 \mathrm{~ms}^{-1}\) and \(20 \mathrm{~ms}^{-1}\) respectively. The two particles move with accelerations equal in magnitude but opposite in direction. When \(P\) overtakes \(Q\) at \(B\), then its velocity is \(30 \mathrm{~ms}^{-1}\). The velocity of \(Q\) at point \(B\) will be
CorrectIncorrectHint
(b) For \(P, 30=15+a t\) or at \(=15 \mathrm{~ms}^{-1}\)
For \(Q, v=20-a t\) or \(v=20-15=5 \mathrm{~ms}^{-1}\)
-
Question 69 of 100
69. Question
A man is \(45 \mathrm{~m}\) behind the bus when the bus start accelerating from rest with acceleration \(2.5 \mathrm{~ms}^{-2}\). With what minimum velocity should the man start running to catch the bus?
CorrectIncorrectHint
(c) Let the man will catch the bus after \(t\) second. So, he will cover distance \(u t\).
Similarly, distance travelled by the bus will be \(\frac{1}{2} a t^2\).
For the given condition,
\(
\begin{aligned}
& u t=45+\frac{1}{2} a t^2=45+1.25 t^2 \quad\left(\text { As, } a=2.5 \mathrm{~ms}^{-2}\right) \\
\Rightarrow \quad & u=\frac{45}{t}+1.25 t
\end{aligned}
\)
To find the minimum value of \(u\)
\(
\frac{d u}{d t}=0 \Rightarrow \frac{d u}{d t}=\frac{-45}{t^2}+1.25=0
\)So, we get \(t=6 \mathrm{~s}\), then \(u=\frac{45}{6}+(1.25 \times 6)=15 \mathrm{~ms}^{-1}\)
-
Question 70 of 100
70. Question
A point moves in a straight line, so that its displacement \(x\) at time \(t\) is given by \(x^2=t^2+1\). Its acceleration is
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (b) } x^2=t^2+1 \text { or } 2 x \cdot \frac{d x}{d t}=2 t \text { or } x \cdot \frac{d x}{d t}=t \\
\therefore \quad v=\frac{d x}{d t}=\frac{t}{x}=\frac{t}{\sqrt{t^2+1}} \\
\quad a=\frac{d v}{d t}=\frac{d^2 x}{d t^2}=\frac{\sqrt{t^2+1}-\frac{t^2}{\sqrt{t^2+1}}}{\left(t^2+1\right)}=\frac{1}{\left(t^2+1\right)^{3 / 2}}=\frac{1}{x^3}
\end{array}
\) -
Question 71 of 100
71. Question
A point moves with uniform acceleration and \(v_1, v_2\) and \(v_3\) denote the average velocities in the three successive intervals of time \(t_1, t_2\) and \(t_3\). Which of the following relations is correct?
CorrectIncorrectHint
(b) Average velocity in uniformly accelerated motion is given by
\(
v_{\mathrm{av}}=\frac{s}{t}=\frac{u t+\frac{1}{2} a t^2}{t}=u+\frac{1}{2} a t
\)
Now, \(v_1=u+\frac{1}{2} a t_1, v_2=\left(u+a t_1\right)+\frac{1}{2} a t_2\)
\(
\begin{array}{l}
\text { and } v_3=u+a\left(t_1+t_2\right)+\frac{1}{2} a t_3 \\
\therefore\left(v_1-v_2\right):\left(v_2-v_3\right)=\left(t_1+t_2\right):\left(t_2+t_3\right)
\end{array}
\) -
Question 72 of 100
72. Question
The velocity-time graph for a particle moving along \(X\)-axis is shown in the figure. The corresponding displacement-time graph is correctly shown by
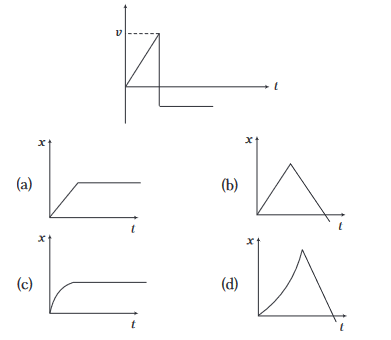 CorrectIncorrect
CorrectIncorrectHint
(d) Motion is first uniformly accelerated in positive direction, then it is uniform in negative direction.
-
Question 73 of 100
73. Question
The vertical height of point \(P\) above the ground is twice that of \(Q\). A particle is projected downward with a speed of \(5 \mathrm{~ms}^{-1}\) from \(P\) and at the same time, another particle is projected upward with the same speed from \(Q\). Both particles reach the ground simultaneously, then
CorrectIncorrectHint
\(
\text { (c) } h=-5 t+5 t^2 \text { and } 2 h=5 t+5 t^2
\)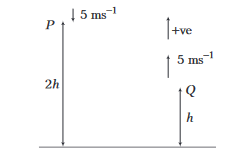
From these two equations, we get \(t=3 \mathrm{~s}\) and \(h=\) distance between \(P\) and \(Q=30 \mathrm{~m}\).
-
Question 74 of 100
74. Question
A body falling from a high Minaret travels \(40 \mathrm{~m}\) in the last 2 seconds of its fall to ground. Height of Minaret in metre is (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(b) Let height of Minaret be \(H\) and body take time \(T\) to fall from top to bottom.
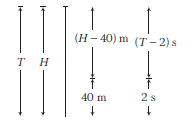
\(
H=\frac{1}{2} g T^2 \dots(i)
\)
In last \(2 \mathrm{~s}\), body travels distance of \(40 \mathrm{~m}\), so in \((T-2)\) second, distance travelled \(=(H-40) \mathrm{m}\)
\(
\Rightarrow \quad(H-40)=\frac{1}{2} g(T-2)^2 \dots(ii)
\)
By solving Eqs. (i) and (ii), we get
\(
T=3 \mathrm{~s} \text { and } H=45 \mathrm{~m}
\) -
Question 75 of 100
75. Question
The acceleration-time \((a-t)\) graph for a particle moving along a straight line starting from rest is shown in figure. Which of the following graph is the best representation of variation of its velocity \((v)\) with time \((t)\) ?
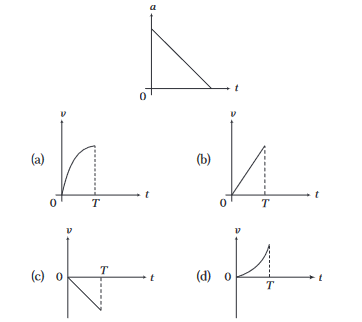 CorrectIncorrect
CorrectIncorrectHint
(a) Given acceleration-time graph is shown in figure.
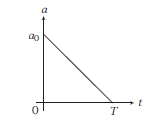
Let \(a(t=0)=a_0=\) constant
From the graph, we have
\(
\begin{aligned}
\frac{t}{T}+\frac{a}{a_0} & =1 \\
\Rightarrow \quad a_0 t+a T & =a_0 T \dots(i)
\end{aligned}
\)
Also, we know that,
\(
a=\frac{d v}{d t} \dots(ii)
\)
From Eqs. (i) and (ii), we get
\(
\frac{a_0 T-a_0 t}{T}=\frac{d v}{d t}
\)
Integrating both sides, we get
\(
\begin{aligned}
\quad \int_0^t\left(a_0 T-a_0 t\right) d t & =T \int_0^v d v \\
\Rightarrow \quad a_0 T t-\frac{a_0 t^2}{2} & =T v \Rightarrow v=a_0 t-\frac{a_0}{2 T} t^2
\end{aligned}
\)Therefore, \(v\)-t graph must be parabolic.
Now, at \(t=0, v=0\)
\(
t=T, v=\frac{a_0 T}{2}=\text { constant }
\)
These conditions are satisfied by graph (a). -
Question 76 of 100
76. Question
The given graph shows the variation of velocity with displacement. Which one of the graphs given below correctly represents the variation of acceleration with displacement?
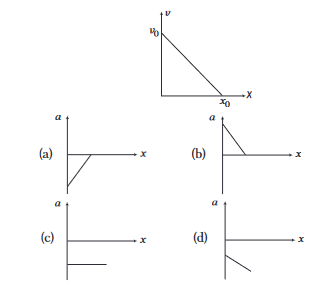 CorrectIncorrect
CorrectIncorrectHint
(a) Given line has positive intercept but negative slope. So, its equation can be written as
\(
v=-m x+v_0\left(\text { where, } m=\tan \theta=\frac{v_0}{x_0}\right) \dots(i)
\)
By differentiating with respect to time, we get
\(
\frac{d v}{d t}=-m \frac{d x}{d t}=-m v
\)
Now, substituting the value of \(v\) from Eq. (i), we get
\(
\begin{aligned}
\frac{d v}{d t} & =-m\left(-m x+v_0\right)=m^2 x-m v_0 \\
\therefore \quad a & =m^2 x-m v_0
\end{aligned}
\)
i.e. The graph between \(a\) and \(x\) should have positive slope but negative intercept on \(a\)-axis. So, graph (a) is correct. -
Question 77 of 100
77. Question
The displacement \(x\) of a particle in a straight line motion is given by \(x=1-t-t^2\). The correct representation of the motion is
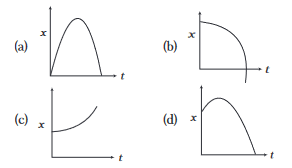 CorrectIncorrect
CorrectIncorrectHint
(b) \(\frac{d x}{d t}=v=-1-2 t\)
Comparing with \(v=u+a t\), we get
\(
u=-1 \mathrm{~ms}^{-1} \text { and } a=-2 \mathrm{~ms}^{-2} \text {. }
\)
At \(t=0, x=1 \mathrm{~m}\) Then, \(u\) and \(a\) both are negative. Hence, \(x\)-coordinate of particle will go on decreasing. -
Question 78 of 100
78. Question
Among the four graph shown in the figure, there is only one graph for which average velocity over the time interval \((0, T)\) can vanish for a suitably chosen \(T\). Which one is it?
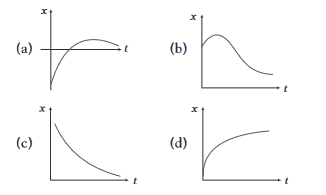 CorrectIncorrect
CorrectIncorrectHint
(b) In graph (b) for one value of displacement, there are two different points of time. Hence, for one time, the average velocity is positive and for other time is equivalent negative.
As there are opposite velocities in the interval 0 to \(T\), hence average velocity can vanish in (b). This can be seen in the figure alongside. Here, \(O A=B T\) (same displacement) for two different points of time.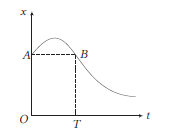
-
Question 79 of 100
79. Question
A lift is coming from 8th floor and is just about to reach 4th floor. Taking ground floor as origin and positive direction upwards for all quantities, which one of the following is correct?
CorrectIncorrectHint
(a) As the lift is coming in downward directions, displacement will be negative. We have to see whether the motion is accelerating or retarding.
We know that due to downward motion, displacement will be negative. When the lift reaches 4 th floor and is about to stop, hence motion is retarding in nature, hence \(x<0 ; a>0\). As displacement is in negative direction, velocity will also be negative, i.e. \(v<0\).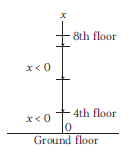
-
Question 80 of 100
80. Question
The displacement of a particle is given by \(x=(t-2)^2\), where \(x\) is in metre and \(t\) in second. The distance covered by the particle in first 4 seconds is
CorrectIncorrectHint
(b) Given, \(\quad x=(t-2)^2\)
Velocity, \(\quad v=\frac{d x}{d t}=\frac{d}{d t}(t-2)^2=2(t-2) \mathrm{ms}^{-1}\)
Acceleration, \(a=\frac{d v}{d t}=\frac{d}{d t}[2(t-2)]=2(1-0)=2 \mathrm{~ms}^{-2}\)
When \(t=0 ; v=-4 \mathrm{~ms}^{-1}, t=2 \mathrm{~s} ; v=0 \mathrm{~ms}^{-1}\)
\(
t=4 \mathrm{~s} ; v=4 \mathrm{~ms}^{-1}
\)
\(v\)-t graph is shown in figure below.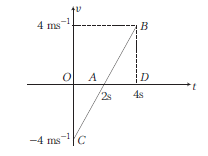
\(
\begin{aligned}
\text { Distance travelled } & =\text { Area under the } v \text { – } t \text { graph } \\
& =\mid \text { Area } O A C \mid+ \text { Area } A B D \\
& =\left|\frac{4 \times 2}{2}\right|+\frac{1}{2} \times 2 \times 4=8 \mathrm{~m}
\end{aligned}
\) -
Question 81 of 100
81. Question
A body falls freely from the top of a tower. It covers \(36 \%\) of the total height in the last second before striking the ground level. The height of the tower is
CorrectIncorrectHint
(d) Let height of tower is \(h\) and body takes \(t\) time to reach to ground when it fall freely.
\(
\therefore \quad h=\frac{1}{2} g t^2 \dots(i)
\)
In last second, i.e. t-th second body travels \(=0.36 \mathrm{~h}\)
It means in rest of the time, \(i . e\) in \((t-1)\) second, it travels
\(
=h-0.36 h=0.64 h
\)
Now, applying equation of motion for \((t-1)\) second
\(
0.64 h=\frac{1}{2} g(t-1)^2 \dots(ii)
\)From Eqs. (i) and (ii), we get
\(
t=5 \mathrm{~s} \text { and } h=125 \mathrm{~m}
\) -
Question 82 of 100
82. Question
A particle moving along \(X\)-axis has acceleration \(f\), at time \(t\), given \(f=f_0\left(1-\frac{t}{T}\right)\), where \(f_0\) and \(T\) are constants. The particle at \(t=0\) has zero velocity. When \(f=0\), the particle’s velocity \(\left(v_x\right)\) is
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (a) Acceleration, } f=f_0\left(1-\frac{t}{T}\right) \\
\frac{d v}{d t}=f_0 \cdot\left(1-\frac{t}{T}\right) \quad\left(\because f=\frac{d v}{d t}\right) \\
\end{array}
\)
\(
\begin{aligned}
d v & =f_0 \cdot\left(1-\frac{t}{T}\right) d t \Rightarrow \int d v=\int f_0\left(1-\frac{t}{T}\right) d t \\
v & =f_0 t-f_0 \frac{t^2}{2 T}+C \dots(i)
\end{aligned}
\)
where, \(C\) is constant.
When \(t=0, v=0\) thus from Eq. (i), \(C=0\)
\(
v=f_0 t-\frac{f_0}{T} \cdot \frac{t^2}{2} \dots(ii)
\)
As, \(\quad f=f_0\left(1-\frac{t}{T}\right)\)
When \(f=0\)
\(
\therefore \quad f_0\left(1-\frac{t}{T}\right)=0 ; f_0 \neq 0 \Rightarrow t=T
\)
Putting \(t=T\) in Eq. (ii), we get
\(
v=f_0 T-\frac{f_0}{T} \cdot \frac{T^2}{2}=\frac{f_0 T}{2}
\) -
Question 83 of 100
83. Question
An elevator car whose floor to ceiling distance is \(2.7 \mathrm{~m}\) starts ascending with a constant acceleration of \(1.2 \mathrm{~ms}^{-2} .2 \mathrm{~s}\) after the start, a bolt falls from the ceiling of the car. The free fall time of the bolt is (Take, \(g=9.8 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(d) Relative to lift,
\(
\begin{array}{l}
u_r=0, a_r=(9.8+1.2)=11 \mathrm{~ms}^{-2} \\
s_r=\frac{1}{2} a r^2 \Rightarrow 2.7=\frac{1}{2} \times 11 \times t^2 \Rightarrow t=\sqrt{\frac{5.4}{11}} \mathrm{~s}
\end{array}
\) -
Question 84 of 100
84. Question
A parachutist after bailing out falls \(50 \mathrm{~m}\) without friction when parachute opens, it decelerates at \(2 \mathrm{~ms}^{-2}\). He reaches the ground with speed of \(3 \mathrm{~m} / \mathrm{s}\). At what height did he bail out?
CorrectIncorrectHint
(a) After bailing out from point \(A\), parachutist falls freely under gravity. The velocity acquired by it will be \(v\).
From \(v^2=u^2+2 a s=0+2 \times 9.8 \times 50=980\)
\(
\text { (As, } \left.u=0, a=9.8 \mathrm{~ms}^{-2}, s=50 \mathrm{~m}\right)
\)
At point \(B\), parachute opens and it moves with retardation of \(2 \mathrm{~ms}^{-2}\) and reach at ground (point \(C\) with velocity of \(3 \mathrm{~ms}^{-1}\) ). For the part \(B C\) by applying the equation \(v^2=u^2+2 a s\)
\(
v=3 \mathrm{~ms}^{-1}, u=\sqrt{980} \mathrm{~ms}^{-1}, a=-2 \mathrm{~ms}^{-2}, s=h
\)
\(
\begin{aligned}
(3)^2 & =(\sqrt{980})^2+2 \times(-2) \times h \\
9 & =980-4 h \\
h & =\frac{980-9}{4}=\frac{971}{4}=242.7 \cong 243 \mathrm{~m}
\end{aligned}
\)
So, the total height by which parachutist bails out
\(
=50+243=293 \mathrm{~m}
\) -
Question 85 of 100
85. Question
Two cars \(A\) and \(B\) are travelling in the same direction with velocities \(v_1\) and \(v_2\left(v_1>v_2\right)\). When the car \(A\) is at a distance \(d\) ahead of the car \(B\), the driver of the car \(A\) applied the brake producing a uniform retardation \(a\). There will be no collision when
CorrectIncorrectHint
(c) Initial relative velocity \(=v_1-v_2\), final relative velocity \(=0\)
From
\(
\begin{array}{ll}
\text { From } & v^2=u^2-2 a s \Rightarrow 0=\left(v_1-v_2\right)^2-2 \times a \times s \\
\Rightarrow & s=\frac{\left(v_1-v_2\right)^2}{2 a}
\end{array}
\)
If the distance between two cars is \(s\), then collision will take place. To avoid collision \(d>s\)
\(
\therefore \quad d>\frac{\left(v_1-v_2\right)^2}{2 a}
\)
where, \(d=\) actual initial distance between two cars. -
Question 86 of 100
86. Question
Water drops fall at regular intervals from a tap which is \(5 \mathrm{~m}\) above the ground. The third drop is leaving the tap at the instant, the first drop touches the ground. How far above the ground is the second drop at that instant?
CorrectIncorrectHint
(b) Time taken by first drop to reach the ground, \(t=\sqrt{\frac{2 h}{g}}\) \(\Rightarrow \quad t=\sqrt{\frac{2 \times 5}{10}}=1 \mathrm{~s}\)
As the water drops fall at regular intervals from a tap, therefore time difference between any two drops \(=\frac{1}{2} \mathrm{~s}\).
In this given time, distance of second drop from the tap
\(
=\frac{1}{2} g\left(\frac{1}{2}\right)^2=\frac{10}{8}=1.25 \mathrm{~m}
\)Its distance from the ground \(=5-1.25=3.75 \mathrm{~m}\)
-
Question 87 of 100
87. Question
A body is thrown vertically up with a velocity \(u\). It passes three points \(A, B\) and \(C\) in its upward journey with velocities \(\frac{u}{2}, \frac{u}{3}\) and \(\frac{u}{4}\), respectively. The ratio of the separations between points \(A\) and \(B\) and between \(B\) and \(C\), i.e. \(\frac{A B}{B C}\) is
CorrectIncorrectHint
(d)
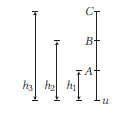
\(
\begin{aligned}
A & \Rightarrow \frac{u^2}{4}-u^2=-2 g h_1 \\
B & \Rightarrow \frac{u^2}{9}-u^2=-2 g h_2 \\
C & \Rightarrow \frac{u^2}{16}-u^2=-2 g h_3
\end{aligned}
\)
\(
\therefore \quad A B=\frac{u^2}{2 g}\left(\frac{8}{9}-\frac{3}{4}\right)=\frac{u^2}{2 g} \cdot \frac{5}{36}
\)
\(
B C=\frac{u^2}{2 g}\left(\frac{15}{16}-\frac{8}{9}\right)=\frac{u^2}{2 g} \cdot \frac{7}{144}
\)
\(
\frac{A B}{B C}=\frac{5}{36} \times \frac{144}{7}=\frac{20}{7}
\) -
Question 88 of 100
88. Question
A ball is dropped vertically from a height \(d\) above the ground. It hits the ground and bounces up vertically to a height \(d / 2\) Neglecting subsequent motion and air resistance, its velocity \(v\) varies with the height \(h\) above the ground can be plotted as
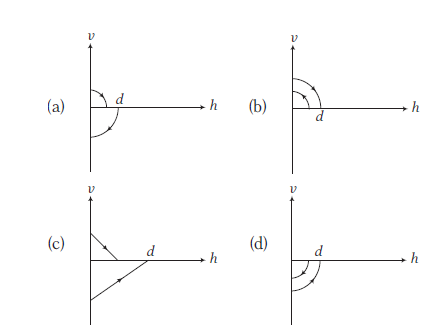 CorrectIncorrect
CorrectIncorrectHint
(a) For the given condition, initial height \(h=d\) and velocity of the ball is zero. When the ball moves downward, its velocity increases and it will be maximum, when the ball hits the ground and just after the collision, it becomes half and in opposite direction. As the ball moves upwards, its velocity again decreases and becomes zero at height \(d / 2\). This explanation match with graph (a).
-
Question 89 of 100
89. Question
The position \(x\) of a particle with respect to time \(t\) along \(X\)-axis is given by \(x=9 t^2-t^3\), where \(x\) is in metres and \(t\) in second. What will be the position of this particle when it achieves maximum speed along the positive \(x\)-direction?
CorrectIncorrectHint
(c) The position \(x\) of a particle w.r.t. time \(t\) along \(X\)-axis,
\(
x=9 t^2-t^3 \dots(i)
\)
Differentiating Eq. (i) w.r.t. time, we get speed, i.e.
\(
\begin{array}{l}
v=\frac{d x}{d t}=\frac{d}{d t}\left(9 t^2-t^3\right) \\
v=18 t-3 t^2 \dots(ii)
\end{array}
\)
Again, differentiating Eq. (ii) w.r.t. time, we get acceleration, i.e.
\(
\begin{aligned}
a & =\frac{d v}{d t}=\frac{d}{d t}\left(18 t-3 t^2\right) \\
\Rightarrow \quad a & =18-6 t \dots(iii)
\end{aligned}
\)
Now, when speed of particle is maximum, its acceleration is zero.
\(
\begin{array}{rlrl}
a =0 \\
\Rightarrow & 18-6 t & =0 \\
\Rightarrow & & t =3 \mathrm{~s}
\end{array}
\)
Putting in Eq. (i), we obtain position of particle at that time
\(
\begin{aligned}
x & =9(3)^2-(3)^3=9(9)-27 \\
& =81-27=54 \mathrm{~m}
\end{aligned}
\) -
Question 90 of 100
90. Question
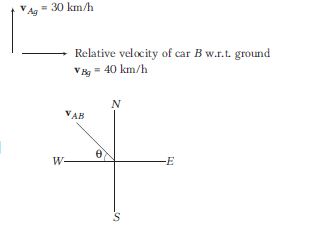
A car \(A\) moves along north with velocity \(30 \mathrm{~km} / \mathrm{h}\) and another car \(B\) moves along east with velocity \(40 \mathrm{~km} / \mathrm{h}\). The relative velocity of \(A\) with respect to \(B\) is
CorrectIncorrectHint
(c) Relative velocity of car \(A\) w.r.t. ground \(\mathbf{v}_{A g}=30 \mathrm{~km} / \mathrm{h}\)
Relative velocity of car \(B\) w.r.t. ground \(\mathbf{v}_{B g}=40 \mathrm{~km} / \mathrm{h}\)
\(\therefore\) Relative velocity of \(A\) w.r.t. \(B\),
\(
\begin{aligned}
& \mathbf{v}_{A B}=\mathbf{v}_{A g}-\mathbf{v}_{B g}=\mathbf{v}_{A g}+\left(-\mathbf{v}_{B g}\right) \\
& \left|\mathbf{v}_{A B}\right|=\sqrt{(30)^2+(40)^2}=50 \mathrm{~km} / \mathrm{h} \\
\therefore & \tan \theta=\frac{30}{40}=\frac{3}{4} \\
\Rightarrow & \quad \theta=\tan ^{-1}(3 / 4) \mathrm{N} \text { of west }
\end{aligned}
\)
-
Question 91 of 100
91. Question
Rain is falling vertically downward with velocity \(4 \mathrm{~m} / \mathrm{s}\). A man is moving horizontally with velocity \(3 \mathrm{~m} / \mathrm{s}\), the velocity of rain with respect to man is
CorrectIncorrectHint
(d)

Relative velocity of man w.r.t. ground \(\mathbf{v}_{m g}=3 \mathrm{~m} / \mathrm{s}\)
Relative velocity of rain w.r.t. ground, \(\mathbf{v}_{\mathrm{rg}}=4 \mathrm{~m} / \mathrm{s}\)
Relative velocity of rain w.r.t. \(\operatorname{man}, \mathbf{v}_{r m}=\) ?
\(
\mathbf{v}_{m m}=\mathbf{v}_{r g}-\mathbf{v}_{m g}=\mathbf{v}_{r g}+\left(-\mathbf{v}_{m g}\right)
\)
\(
\begin{aligned}
\mathbf{v}_{\mathrm{rm}} & =5 \mathrm{~m} / \mathrm{s} \\
\tan \alpha & =\frac{3}{4}, \quad \tan \beta=\frac{4}{3}
\end{aligned}
\)
\(\mathbf{v}_{m m}=5 \mathrm{~m} / \mathrm{s}\) at \(\tan ^{-1}\left(\frac{3}{4}\right)\) with vertical or at \(\tan ^{-1}\left(\frac{4}{3}\right)\) with horizontal. -
Question 92 of 100
92. Question
A ship is travelling due east at a speed of \(15 \mathrm{~km} / \mathrm{h}\). Find the speed of a boat heading \(30^{\circ}\) east of north, if it always appears due north from the ship.
CorrectIncorrectHint
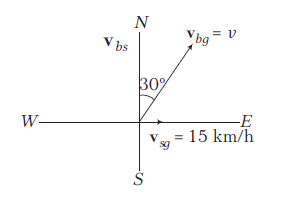
where, \(\mathbf{v}_{b g}\) is the velocity of boat w.r.t. ground and \(\mathbf{v}_{s g}\) is the velocity of ship w.r.t. ground.
Relative velocity of boat w.r.t. ship \(\mathbf{v}_{b s}\) is along north. \(\mathbf{v}_{b s}\) is resultant of \(\mathbf{v}_{b g}\) and \(\mathbf{v}_{s g}\) in opposite direction.
\(
\begin{aligned}
v \cos 30^{\circ} & =v_{b s} \\
v \sin 30^{\circ} & =15 \Rightarrow v=30 \mathrm{~km} / \mathrm{h}
\end{aligned}
\) -
Question 93 of 100
93. Question
A man takes \(3 \mathrm{~h}\) to cover a certain distance along the flow of river and takes \(6 \mathrm{~h}\) to cover the same distance opposite to the flow of river. In how much time, he will cross this distance in still water?
CorrectIncorrectHint
\(u: v_{r g}\) (velocity of river w.r.t. ground)
\(v: v_{m r}\) (velocity of man w.r.t. river)
Along the flow, \(v_{m g}=v+u, 3=\frac{d}{v+u} \dots(i)\)
where, \(v_{m g}\) is velocity of man w.r.t. ground.
Opposite to the flow,
\(
\begin{aligned}
v_{m g} & =v-u, 6=\frac{d}{v-u} \dots(ii) \\
\Rightarrow \quad t_0 & =\frac{d}{v}=4 \mathrm{~h}
\end{aligned}
\) -
Question 94 of 100
94. Question
A river \(500 \mathrm{~m}\) wide is flowing at a rate of \(4 \mathrm{~m} / \mathrm{s}\). A boat is sailing at a velocity of \(10 \mathrm{~m} / \mathrm{s}\) with respect to the water in a direction perpendicular to the river. The time taken by the boat to reach the opposite bank is
CorrectIncorrectHint
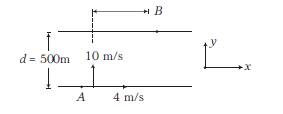
\(
\begin{array}{rlrl}
y & \text { displacement } & =\text { velocity } \times \text { time } \\
\Rightarrow \quad 500 & =10 t \\
\Rightarrow \quad & t =50 \mathrm{~s}
\end{array}
\) -
Question 95 of 100
95. Question
A ship is travelling due east at \(10 \mathrm{~km} / \mathrm{hr}\). Another ship heading \(30^{\circ}\) east of north is always due north from the first ship. The speed of the second ship in \(\mathrm{km} / \mathrm{hr}\) is
CorrectIncorrectHint
The condition of both the ships are shown in figure \((A)\) and figure \((B)\) shows the condition of ship 2 when it is always due north to the ship 1.
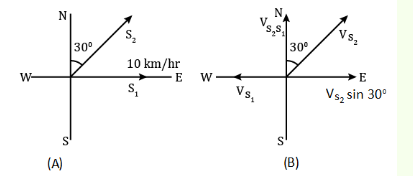
So, east component of both ships must be same.
\(
\begin{array}{l}
\therefore \mathrm{v}_{\mathrm{s} 2} \sin 30^{\circ}=\mathrm{v}_{\mathrm{s} 1} \\
\mathrm{v}_{\mathrm{s} 2}=\frac{10}{\frac{1}{2}}=20 \mathrm{~km} / \mathrm{hr}
\end{array}
\) -
Question 96 of 100
96. Question
A man weighing \(80 \mathrm{~kg}\) is standing in a trolley weighing \(320 \mathrm{~kg}\). The trolley is resting on frictionless horizontal rails. If the man starts walking on the trolley with a speed of \(1 \mathrm{~m} / \mathrm{s}\), then after \(4 \mathrm{sec}\) his displacement relative to the ground will be
CorrectIncorrectHint
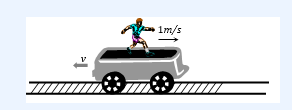
If the man starts walking on the trolley in the forward direction then whole system will move in backward direction with same momentum. Trolley will move back with a velocity \(v^{\prime}=\frac{m v}{M+m}\)
In 4 sec the net distance of the man moved \(=x=v t-v^{\prime} t=1 \times 4-\frac{320 \times 1}{320+80}=3.2 \mathrm{~m}\) -
Question 97 of 100
97. Question
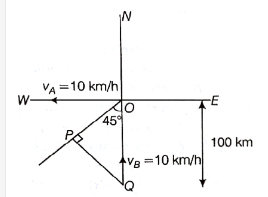
A ship A is moving westwards with a speed of \(10 \mathrm{~km} \mathrm{~h}^{-1}\) and a ship B, \(100 \mathrm{~km}\) south of A is moving northwards with a speed of \(10 \mathrm{~km} \mathrm{~h}^{-1}\). The time after which the distance between them becomes the shortest, is:
CorrectIncorrectHint
It is clear from the diagram that the shortest distance between the ship A and \(\mathrm{B}\) is \(\mathrm{PQ}\).
Here, \(\operatorname{Sin} 45^{\circ}=\frac{\mathrm{PQ}}{\mathrm{OQ}}\)
\(
\Longrightarrow \mathrm{PQ}=100 \times \frac{1}{\sqrt{2}}=50 \sqrt{2} \mathrm{~m}
\)
Also,
\(
\mathrm{V}_{\mathrm{AB}}=\sqrt{\mathrm{V}_{\mathrm{A}}^2+\mathrm{V}_{\mathrm{B}}^2}=\sqrt{10^2+10^2}=10 \sqrt{2} \mathrm{~km} / \mathrm{h}
\)
So, the time taken to reach shortest path is
\(
\mathrm{t}=\frac{\mathrm{PQ}}{\mathrm{V}_{\mathrm{AB}}}=\frac{50 \sqrt{2}}{10 \sqrt{2}}=5 \mathrm{~h}
\)
-
Question 98 of 100
98. Question
A river is flowing with a speed of \(1 \mathrm{~km} / \mathrm{hr}\). A swimmer wants to go to point ‘ \(\mathrm{C}\) ‘ starting from ‘A’. He swims with a speed of \(5 \mathrm{~km} / \mathrm{hr}\), at an angle \(\theta\) with respect to the river. If \(A B=B C=400 \mathrm{~m}\). Then
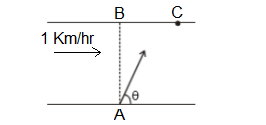 CorrectIncorrect
CorrectIncorrectHint
Time to cross river \((t)=\frac{A B}{V_{m r} \sin \theta}=\frac{0.4}{5 \sin \theta}\)
Drift:
\(
\begin{array}{l}
B C=\left(v_{m r} \cos \theta+v_r\right) t \\
\Rightarrow 0.4=(5 \cos \theta+1) \times \frac{0.4}{5 \sin \theta} \\
\Rightarrow 5 \sin \theta-5 \cos \theta=1 \\
\Rightarrow 25 \sin ^2 \theta+25 \cos ^2 \theta-50 \sin \theta \cos \theta=1 \\
\Rightarrow 25 \sin 2 \theta=24 \\
\Rightarrow \sin 2 \theta=\frac{24}{25} \\
\Rightarrow \theta=53^{\circ}
\end{array}
\) -
Question 99 of 100
99. Question
Two men P \& Q are standing at corners A \& B of square ABCD of side \(8 \mathrm{~m}\). They start moving along the track with constant speed \(2 \mathrm{~m} / \mathrm{s}\) and \(10 \mathrm{~m} / \mathrm{s}\) respectively. The time when they will meet for the first time, is equal to:
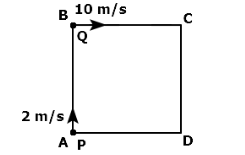 CorrectIncorrect
CorrectIncorrectHint
(b) Relative speed of \(Q\) with respect to \(P\) is given by \((10-2) \mathrm{m} / \mathrm{s}=8 \mathrm{~m} / \mathrm{s}\)
So, if we assume \(P\) is at rest, then we can say that \(Q\) is moving towards \(P\) with speed \(8 \mathrm{~m} / \mathrm{s}\)
To reach \(P, Q\) will have to cover distance of \(B C+C D+D A=3 \times 8=24 \mathrm{~m}\)
\(
\text { time }=\frac{24}{8}=3 \text { seconds }
\) -
Question 100 of 100
100. Question
A boat is sent across a river in perpendicular direction with a velocity of \(8 \mathrm{~km} / \mathrm{hr}\). If the resultant velocity of boat is \(10 \mathrm{~km} / \mathrm{hr}\) then velocity of the river is
CorrectIncorrectHint
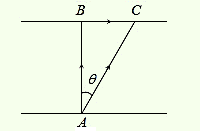
\(
\begin{array}{l}
\text { Given } \overrightarrow{A B}=\text { velocity of boat }=8 \mathrm{~km} / \mathrm{hr} \\
\mathrm{\vec{AC}}=\text { Resultant velocity of boat }=10 \mathrm{~km} / \mathrm{hr} \\
\overrightarrow{\mathrm{BC}}=\text { Velocity of river }=\sqrt{\mathrm{AC}^2-\mathrm{AB}^2} \\
=\sqrt{(10)^2-(8)^2}=6 \mathrm{~km} / \mathrm{hr} .
\end{array}
\)