Kinematics (motion in one dimension) Quiz-L1
Quiz Summary
0 of 63 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 63 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 63
1. Question
Which of the following is a one-dimensional motion?
CorrectIncorrectHint
(d) Motion of train on straight track is a one dimensional motion whereas everything else is a two dimensional or three dimensional activity.
-
Question 2 of 63
2. Question
A person moves towards east for \(3 \mathrm{~m}\), then towards north for \(4 \mathrm{~m}\) and then moves vertically up by \(5 \mathrm{~m}\). What is his distance now from the starting point?
CorrectIncorrectHint
Now, write the final position vector of the particle as follows.
\(
\vec{r}=3 \hat{i}+4 \hat{j}+5 \hat{k}
\)The distance of the person from the origin is calculated by finding the magnitude of the position vector as,
\(
\begin{array}{l}
|\vec{r}|=\sqrt{3^2+4^2+5^2} \\
\Rightarrow \sqrt{9+16+25} \\
\Rightarrow 5 \sqrt{2}
\end{array}
\) -
Question 3 of 63
3. Question
A particle moves in a circle of radius \(R\) from \(A\) to \(B\) as shown in figure. The distance covered by the object is
CorrectIncorrectHint
\(
\text { (a) Distance }=\text { Length } A B=2 \pi R \times \frac{60}{360}=\frac{\pi R}{3}
\) -
Question 4 of 63
4. Question
A wheel of radius \(1 \mathrm{~m}\) rolls forward half a revolution on a horizontal ground. The magnitude of displacement of the point of the wheel initially in contact with the ground is
CorrectIncorrectHint
(c) Horizontal distance covered by the wheel in half revolution \(=\pi R\)
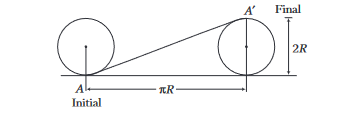
So, the displacement of the point which was initially in
\(
\begin{aligned}
\text { contact with ground } & =A A^{\prime}=\sqrt{(\pi R)^2+(2 R)^2} \\
& =R \sqrt{\pi^2+4}=\sqrt{\pi^2+4} \quad(\mathrm{As}, R=1 \mathrm{~m})
\end{aligned}
\) -
Question 5 of 63
5. Question
The three initial and final position of a man on the \(X\)-axis are given as
(i) \((-8 \mathrm{~m}, 7 \mathrm{~m})\)
(ii) \((7 \mathrm{~m},-3 \mathrm{~m})\)
(iii) \((-7 \mathrm{~m}, 3 \mathrm{~m})\)
Which pair gives the negative displacement?CorrectIncorrectHint
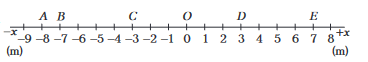
(i) The displacement of the man from \(A\) to \(E\) is \(\Delta x=x_2-x_1=7 \mathrm{~m}-(-8 \mathrm{~m})=+15 \mathrm{~m}\) directed in the positive \(x\)-direction.
(ii) The displacement of the man from \(E\) to \(C\) is \(\Delta x=-3 \mathrm{~m}-(7 \mathrm{~m})=-10 \mathrm{~m}\) directed in the negative \(x\)-direction.
(iii) The displacement of the man from \(B\) to \(D\) is \(\Delta x=3 \mathrm{~m}-(-7 \mathrm{~m})=+10 \mathrm{~m}\) directed in the positive \(x\)-direction. -
Question 6 of 63
6. Question
The numerical ratio of displacement to the distance covered is always
CorrectIncorrectHint
(c) Since, displacement is always less than or equal to distance but never greater than distance. Hence, numerical ratio of displacement to the distance covered is always equal to or less than one.
-
Question 7 of 63
7. Question
A particle moves along a circular path of radius \(R\). The distance and displacement of a particle after one complete revolution is
CorrectIncorrectHint
\(
\begin{aligned}
\text { circumference of circle } & =2 \pi R \\
\text { distance } & =2 \pi R
\end{aligned}
\)
\(\Delta x=x_f – x_i\)
\(
x_f=x_i
\)
displacement \(=\Delta x=0\) -
Question 8 of 63
8. Question
A particle starts from the origin, goes along \(X\)-axis to the point \((20 \mathrm{~m}, 0)\) and then returns along the same line to the point \((-20 \mathrm{~m}, 0)\). The distance and displacement of the particle during the trip are
CorrectIncorrectHint
The starting point for the particle is origin as shown in figure.
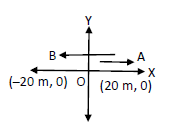
The Distance traveled by the particle is:
\(
\begin{array}{l}
\mathrm{D}=20+20+20 \\
=60 \mathrm{~m}
\end{array}
\)
The displacement is the distance between the initial and the final points. Displacement \(\Rightarrow \mathrm{OB}=20 \mathrm{~m}\) in the negative direction
The distance is \(60 \mathrm{~m}\) and displacement is \(20 \mathrm{~m}\) in negative direction. -
Question 9 of 63
9. Question
A car has to cover the distance \(60 \mathrm{~km}\). If half of the total time, it travels with speed \(80 \mathrm{kmh}^{-1}\) and in rest half time, its speed becomes \(40 \mathrm{kmh}^{-1}\), the average speed of car will be
CorrectIncorrectHint
\(
\text { (a) } v_{\mathrm{av}}=\frac{\text { Total distance }}{\text { Total time }}=\frac{80 t+40 t}{2 t}=60 \mathrm{kmh}^{-1}
\) -
Question 10 of 63
10. Question
During the first \(18 \mathrm{~min}\) of a \(60 \mathrm{~min}\) trip, a car has an average speed of \(11 \mathrm{~m} \mathrm{~min}^{-1}\). What should be the average speed for remaining \(42 \mathrm{~min}\), so that car is having an average speed of \(21 \mathrm{~m} \mathrm{~min}^{-1}\) for the entire trip?
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (a) } 21=\frac{11 \times 18+42 \times v}{60} \\
\therefore \quad v=25.3 \mathrm{~m} \mathrm{~min}^{-1} \\
\end{array}
\) -
Question 11 of 63
11. Question
A man walks on a straight road from his home to a market \(2.5 \mathrm{~km}\) away with a speed of \(5 \mathrm{kmh}^{-1}\). Finding the market closed, he instantly turns and walks back home with a speed of \(7.5 \mathrm{kmh}^{-1}\). The average speed of the man over the interval of time 0 to \(40 \mathrm{~min}\) is equal to
CorrectIncorrectHint
(d) Man walks from his home to market with a speed of \(5 \mathrm{kmh}^{-1}\). Distance \(=2.5 \mathrm{~km}\) and time \(=\frac{2.5}{5}=\frac{1}{2} \mathrm{~h}=30 \mathrm{~min}\) and he returns back with speed of \(7.5 \mathrm{~km} / \mathrm{h}\) in rest time, i.e. \(10 \mathrm{~min}\).
\(
\text { Distance }=7.5 \times \frac{10}{60}=1.25 \mathrm{~km}
\)
\(
\begin{aligned}
\text { So, average speed } & =\frac{\text { total distance }}{\text { total time }} \\
& =\frac{(2.5+1.25) \mathrm{km}}{(40 / 60) \mathrm{h}}=\frac{45}{8} \mathrm{kmh}^{-1}
\end{aligned}
\) -
Question 12 of 63
12. Question
A particle is constrained to move on a straight line path. It returns to the starting point after \(10 \mathrm{~s}\). The total distance covered by the particle during this time is \(30 \mathrm{~m}\). Which of the following statements about the motion of the particle is true?
CorrectIncorrectHint
(d) Displacement of the particle will be zero because it comes back to its starting point.
\(
\text { Average speed }=\frac{\text { Total distance }}{\text { Total time }}=\frac{30 \mathrm{~m}}{10 \mathrm{~s}}=3 \mathrm{~ms}^{-1}
\) -
Question 13 of 63
13. Question
A \(150 \mathrm{~m}\) long train is moving with a uniform velocity of \(45 \mathrm{kmh}^{-1}\). The time taken by the train to cross a bridge of length \(850 \mathrm{~m}\) is
CorrectIncorrectHint
\(
\text { (c) } t=\frac{d}{v}=\frac{150+850}{45 \times \frac{5}{18}}=80 \mathrm{~s}
\) -
Question 14 of 63
14. Question
An insect crawls a distance of \(4 \mathrm{~m}\) along north in \(10 \mathrm{~s}\) and then a distance of \(3 \mathrm{~m}\) along east in \(5 \mathrm{~s}\). The average velocity of the insect is
CorrectIncorrectHint
\(
\text { (c) } v_{\mathrm{av}}=\frac{\text { Total displacement }}{\text { Total time }}=\frac{\sqrt{(4)^2+(3)^2}}{10+5}=\frac{1}{3} \mathrm{~ms}^{-1}
\) -
Question 15 of 63
15. Question
A particle traversed (3/4) th of the circle of radius \(R\) in time \(t\). The magnitude of the average velocity of the particle in this time interval is
CorrectIncorrectHint
\(
\text { (c) } v_{\text {av }}=\frac{\text { Displacement }}{\text { Time }}=\frac{\sqrt{2} R}{t}
\) -
Question 16 of 63
16. Question
A boy is running over a circular track with uniform speed of \(10 \mathrm{~ms}^{-1}\). What is the average velocity for movement of boy along semicircle (in \(\mathrm{ms}^{-1}\) )?
CorrectIncorrectHint
\(
\text { (d) } v_{\mathrm{av}}=\frac{\text { Displacement }}{\text { Time }}=\frac{2 R}{(\pi R / v)}=\frac{2 v}{\pi}=\frac{20}{\pi} \mathrm{ms}^{-1}
\) -
Question 17 of 63
17. Question
Acceleration of a particle changes when
CorrectIncorrectHint
(c) Acceleration is a vector quantity. So, it changes when either magnitude or direction of velocity changes or both changes.
-
Question 18 of 63
18. Question
If a particle moves with an acceleration, then which of the following can remain constant?
CorrectIncorrectHint
(d) If the particle is accelerating then the velocity can not be constant. But the speed can be constant if the acceleration produced by the force is only change the direction of motion. For example in uniform circular motion, acceleration is non-zero, velocity is not constant but speed is constant.
-
Question 19 of 63
19. Question
The average velocity of a body moving with uniform acceleration travelling a distance of \(3.06 \mathrm{~m}\) is \(0.34 \mathrm{~ms}^{-1}\). If the change in velocity of the body is \(0.18 \mathrm{~ms}^{-1}\), then during this time, its uniform acceleration is
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (b) } \text { Time }=\frac{\text { Distance }}{\text { Average velocity }}=\frac{3.06}{0.34}=9 \mathrm{~s} \\
\text { Acceleration }=\frac{\text { Change in velocity }}{\text { Time }}=\frac{0.18}{9}=0.02 \mathrm{~m} / \mathrm{s}^2
\end{array}
\) -
Question 20 of 63
20. Question
A car travelling with a velocity of \(80 \mathrm{~km} / \mathrm{h}\) slowed down to \(44 \mathrm{~km} / \mathrm{h}\) in \(15 \mathrm{~s}\). The retardation is
CorrectIncorrectHint
(a)
\(
\begin{aligned}
a & =\frac{\text { Change in velocity }}{\text { Time taken }}=\frac{v_f-v_i}{t} \\
& =\frac{\left(44 \times \frac{5}{18}\right)-\left(80 \times \frac{5}{18}\right)}{15}=-0.67 \mathrm{~m} / \mathrm{s}^2
\end{aligned}
\)Negative sign represents the retardation.
-
Question 21 of 63
21. Question
An object is moving along the path \(O A B O\) with constant speed, then
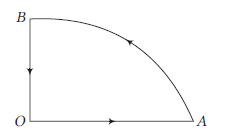CorrectIncorrectHint
(d) For path \(O A\) and \(B O\), the magnitude of velocity (speed) and direction is constant, hence acceleration is zero.
For path \(A B\), since this path is a curve, so the direction of the velocity changes every moment but the magnitude of velocity (speed) remains constant.
Since, the direction of velocity is changing, i.e. there must be some acceleration along the path \(A B\). -
Question 22 of 63
22. Question
Velocity of a body moving along a straight line with uniform acceleration \((a)\) reduces by \(\frac{3}{4}\) of its initial velocity in time \(t_0\). The total time of motion of the body till its velocity becomes zero is
CorrectIncorrectHint
(a)
\(
\begin{array}{l}
u-\frac{3 u}{4}=u-a t_0 \\
a=\frac{3 u}{4 t_0} \text { or } \frac{u}{a}=\frac{4}{3} t_0
\end{array}
\)Now, \(0=u-a t\) or \(t=\frac{u}{a}=\frac{4}{3} t_0\)
-
Question 23 of 63
23. Question
The displacement of a body in \(8 \mathrm{~s}\) starting from rest with an acceleration of \(20 \mathrm{~cms}^{-2}\) is
CorrectIncorrectHint
\(
\text { (c) } s=\frac{1}{2} a t^2=\frac{1}{2} \times(0.2)(64)=6.4 \mathrm{~m}=640 \mathrm{~cm}
\) -
Question 24 of 63
24. Question
The motion of a particle is described by the equation \(v=a t\). The distance travelled by the particle in the first \(4 \mathrm{~s}\) is
CorrectIncorrectHint
\(
\text { (d) } s=\frac{1}{2} a t^2 \Rightarrow s=\frac{1}{2} \times a \times(4)^2 \Rightarrow s=8 a
\) -
Question 25 of 63
25. Question
A particle starts with a velocity of \(2 \mathrm{~ms}^{-1}\) and moves in a straight line with a retardation of \(0.1 \mathrm{~ms}^{-2}\). The first time at which the particle is \(15 \mathrm{~m}\) from the starting point is
CorrectIncorrectHint
\(
\text { (a) } 15=2 t-\frac{1}{2} \times(0.1) t^2 \text { or } t=10 \mathrm{~s}
\) -
Question 26 of 63
26. Question
A particle starts from rest, accelerates at \(2 \mathrm{~ms}^{-2}\) for \(10 \mathrm{~s}\) and then moves with constant speed of \(20 \mathrm{~ms}^{-1}\) for \(30 \mathrm{~s}\) and then decelerates at \(4 \mathrm{~ms}^{-2}\) till it stops after next \(5 \mathrm{~s}\). What is the distance travelled by it?
CorrectIncorrectHint
(a)
\(
\begin{aligned}
s & =s_1+s_2+s_3 \\
& =\frac{1}{2} \times 2 \times(10)^2+(20)(30)+\frac{1}{2} \times 4 \times(5)^2 \\
& =100+600+50=750 \mathrm{~m}
\end{aligned}
\) -
Question 27 of 63
27. Question
A body is moving with uniform velocity of \(8 \mathrm{~ms}^{-1}\). When the body just crossed another body, the second one starts and moves with uniform acceleration of \(4 \mathrm{~ms}^{-2}\). The time after which two bodies meet, will be
CorrectIncorrectHint
(b) Displacements of both should be equal.
or \(\quad 8 t=\frac{1}{2} \times 4 \times t^2\) or \(t=4 \mathrm{~s}\) -
Question 28 of 63
28. Question
Two bodies \(A\) and \(B\) start from rest from the same point with a uniform acceleration of \(2 \mathrm{~ms}^{-2}\). If \(B\) starts one second later, then the two bodies are separated at the end of the next second, by
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (c) } \quad s_B=\frac{1}{2} \times 2 \times(1)^2=1 \mathrm{~m} \\
s_A=\frac{1}{2} \times 2 \times(2)^2=4 \mathrm{~m} \\
\therefore \quad s_A-s_B=3 \mathrm{~m}
\end{array}
\) -
Question 29 of 63
29. Question
A train accelerating uniformly from rest attains a maximum speed of \(40 \mathrm{~ms}^{-1}\) in \(20 \mathrm{~s}\). It travels at this speed for \(20 \mathrm{~s}\) and is brought to rest by uniform retardation in further \(40 \mathrm{~s}\). What is the average velocity during this period?
CorrectIncorrectHint
(c) \(\quad 40=(20) a_1 \Rightarrow a_1=2 \mathrm{~ms}^{-2}\)
Further \(40=(40) a_2\)
\(
\therefore \quad a_2=1 \mathrm{~ms}^{-2}
\)Therefore, acceleration is \(2 \mathrm{~ms}^{-2}\) and retardation is \(1 \mathrm{~ms}^{-2}\).
\(
\text { Now, } \begin{aligned}
s_1 & =\frac{1}{2} a_1 t_1^2=\frac{1}{2} \times 2 \times(20)^2=400 \mathrm{~m} \\
s_2 & =v_{\max } t_2=40 \times 20=800 \mathrm{~m} \\
s_3 & =\frac{v_{\max }^2}{2 a_2}=\frac{(40)^2}{2 \times 1}=800 \mathrm{~m}
\end{aligned}
\)
\(
\begin{array}{l}
\text { Now, average velocity }=\frac{\text { total displacement }}{\text { total time }} \\
\qquad=\frac{400+800+800}{20+20+40}=25 \mathrm{~ms}^{-1}
\end{array}
\) -
Question 30 of 63
30. Question
A particle starts from rest and traverses a distance \(l\) with uniform acceleration, then moves uniformly over a further distance \(2 l\) and finally comes to rest after moving a further distance \(3 l\) under uniform retardation. Assuming entire motion to be rectilinear motion, the ratio of average speed over the journey to the maximum speed on its ways is
CorrectIncorrectHint
(c) Let \(v_m\) be the maximum speed,
\(
\begin{array}{l}
v_m=a_1 t_1=\sqrt{2 a_1 l} (\because u=0) \\
t_2=\frac{2 l}{v_m} \text { and } v_m=a_2 t_3=\sqrt{2 a_2(3 l)}
\end{array}
\)
Now, average speed, \(v_{\mathrm{av}}=\frac{l+2 l+3 l}{t_1+t_2+t_3}\)
\(
\begin{aligned}
v_{\text {av }} & =\frac{6 l}{\left(v_m / a_1\right)+\left(2 l / v_m\right)+\left(v_m / a_2\right)} \\
& =\frac{6 l}{\left(\frac{v_m}{v_m^2 / 2 l}\right)+\left(\frac{2 l}{v_m}\right)+\left(\frac{v_m}{v_m^2 / 6 l}\right)}=\frac{6 l}{\left(10 l / v_m\right)}=\frac{3 v_m}{5} \\
\Rightarrow \quad \frac{v_{\text {av }}}{v_m} & =\frac{3}{5}
\end{aligned}
\) -
Question 31 of 63
31. Question
A body travelling with uniform acceleration crosses two points \(A\) and \(B\) with velocities \(20 \mathrm{~ms}^{-1}\) and \(30 \mathrm{~ms}^{-1}\), respectively. The speed of the body at mid-point of \(A\) and \(B\) is
CorrectIncorrectHint
(b) \((30)^2=(20)^2+2 a(2 s)\) or \(\quad 2 a s=250\)
Now, \(v^2=u^2+2 a s \Rightarrow v^2=(20)^2+250 \Rightarrow v^2=650\)
\(
\therefore \quad v=25.5 \mathrm{~ms}^{-1}
\) -
Question 32 of 63
32. Question
If a body starts from rest and travels \(120 \mathrm{~cm}\) in the 6th second, then what is the acceleration?
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (c) } s_n=u+\frac{a}{2}(2 n-1) \Rightarrow 1.2=0+\frac{a}{2}(2 \times 6-1) \\
\Rightarrow a=\frac{1.2 \times 2}{11}=0.218 \mathrm{~ms}^{-2}
\end{array}
\) -
Question 33 of 63
33. Question
If a stone is thrown up with a velocity of \(9.8 \mathrm{~ms}^{-1}\), then how much time will it take to come back?
CorrectIncorrectHint
\(
\text { (b) } t=\frac{2 u}{g} \Rightarrow t=\frac{2 \times 9.8}{10}=1.96 \approx 2 \mathrm{~s}
\) -
Question 34 of 63
34. Question
If a ball is thrown vertically upwards with speed \(u\), the distance covered during the last \(t\) second of its ascent is
CorrectIncorrectHint
(d) Let \(t\) second of upward journey \(=\) first \(t\) second of downward journey (with zero initial velocity).
\(
\therefore \text { Desired distance }=\frac{1}{2} g t^2
\) -
Question 35 of 63
35. Question
A person throws balls into air after every second. The next ball is thrown when the velocity of the first ball is zero. How high do the ball rise above his hand?
CorrectIncorrectHint
(b) Time taken to reach maximum height is \(1 \mathrm{~s}\).
Height \(=\) free fall distance in \(1 \mathrm{~s}=\frac{1}{2} g t^2=5 \mathrm{~m}\)
-
Question 36 of 63
36. Question
A particle is thrown vertically upwards. Its velocity at half of the height is \(10 \mathrm{~ms}^{-1}\). Then, the maximum height attained by it is (Take, \(g=10 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
\(
\text { (b) } h=\frac{(10)^2}{2 g}=5 \mathrm{~m}
\)\(
\therefore \text { Total height }=2 h=10 \mathrm{~m}
\) -
Question 37 of 63
37. Question
When a ball is thrown up vertically with velocity \(v_0\), it reaches a maximum height of \(h\). If one wishes to triple the maximum height, then the ball should be thrown with velocity,
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (a) } H_{\max } \propto v^2 \\
\Rightarrow \quad v \propto \sqrt{H_{\max }}
\end{array}
\)
i.e. To triple the maximum height, ball should be thrown with velocity \(\sqrt{3} v_0\). -
Question 38 of 63
38. Question
A stone thrown upward with a speed \(u\) from the top of the tower reaches the ground with a speed \(3 u\). The height of the tower is
CorrectIncorrectHint
\(
\begin{aligned}
\text { (b) } & v^2Â =u^2+2 g h \\
\Rightarrow & (3 u)^2Â =(-u)^2+2 g h \\
\Rightarrow & h =\frac{4 u^2}{g}
\end{aligned}
\) -
Question 39 of 63
39. Question
A body thrown vertically up from the ground passes the height of \(10.2 \mathrm{~m}\) twice in an interval of \(10 \mathrm{~s}\). What was its initial velocity?
CorrectIncorrectHint
\(
\text { (a) } t_{A B C}=10 \mathrm{~s} \Rightarrow t_{A B}=5 \mathrm{~s}
\)
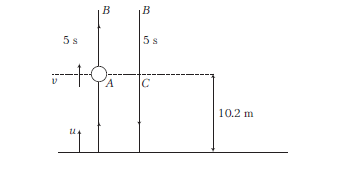
At \(B\), velocity becomes zero. Hence at \(A\), velocity should be \(50 \mathrm{~ms}^{-1}\)
\(
\begin{array}{rlrl}
& \text { Now, } & (50)^2 & =\left(u^2\right)-2 \times 10 \times 10.2 \\
& \therefore & u & =52 \mathrm{~ms}^{-1}
\end{array}
\) -
Question 40 of 63
40. Question
A body is projected with a velocity \(u\). It passes through a certain point above the ground after \(t_1\) second. The time interval after which the body passes through the same point during the return journey is
CorrectIncorrectHint
\(
\text { (b) Velocity of particle of this instant will be } v=(u-g 4)
\)
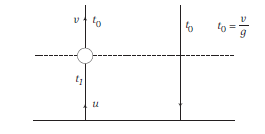
Now, the desired time interval will be \(\frac{2 v}{g}\). or \(\quad \frac{2\left(u-g t_1\right)}{g}=2\left(\frac{u}{g}-t_1\right)\)
-
Question 41 of 63
41. Question
A body is thrown vertically upwards from the top \(A\) of tower. It reaches the ground in \(t_1\) second. If it is thrown vertically downwards from \(A\) with the same speed, it reaches the ground in \(t_2\) second. If it is allowed to fall freely from \(A\), then the time it takes to reach the ground is given by
CorrectIncorrectHint
(c) Taking downward direction as the positive direction.
\(
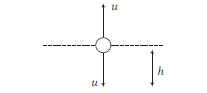
\begin{array}{l}
+h=-u t_1+\frac{1}{2} g t_1^2 \dots(i) \\
+h=u t_2+\frac{1}{2} g t_2^2 \dots(ii)
\end{array}
\)
Multiplying Eq. (i) by \(t_2\) and Eq. (ii) by \(t_1\) and adding, we get
\(
h\left(t_1+t_2\right)=\frac{1}{2} g t_2 t_2\left(t_1+t_2\right) \text { or } h=\frac{1}{2} g t_1 t_2
\)For free fall from rest, \(h=\frac{1}{2} g t^2\)
\(
\therefore \quad t^2=t_1 t_2 \Rightarrow t=\sqrt{t_1 t_2}
\) -
Question 42 of 63
42. Question
A man in a balloon rising vertically with an acceleration of \(4.9 \mathrm{~ms}^{-2}\) releases a ball \(2 \mathrm{~s}\) after the balloon is let go from the ground. The greatest height above the ground reached by the ball is (Take, \(g=9.8 \mathrm{~ms}^{-2}\) )
CorrectIncorrectHint
(a) After \(2 \mathrm{~s}\), velocity, \(v=4.9 \times 2=9.8\)
and
\(
h=\frac{1}{2} \times 4.9 \times(2)^2=98 \mathrm{~m}
\)Greatest height, \(h_{\max }=h+\frac{v^2}{2 g}=14.7 \mathrm{~m}\)
-
Question 43 of 63
43. Question
A stone falls freely under gravity. The total distance covered by it in the last second of its journey equals the distance covered by it in first \(3 \mathrm{~s}\) of its motion. The time for which stone remains in air, is
CorrectIncorrectHint
(a) Here, \(u=0\)
\(
\begin{aligned}
& S_3=0+\frac{1}{2} g t^2=\frac{1}{2} \times 10 \times 9=45 \\
S_{t \mathrm{th}} & =u+(2 t-1) \mathrm{g} / 2 \\
\Rightarrow S_{t \mathrm{th}} & =0+5(2 t-1) \\
45 & =5(2 t-1) \\
\Rightarrow 2 t-1 & =9 \Rightarrow t=5 \mathrm{~s}
\end{aligned}
\) -
Question 44 of 63
44. Question
A body falls from a height \(h=200 \mathrm{~m}\). The ratio of distance travelled in each \(2 \mathrm{~s}\), during \(t=0\) to \(t=6 \mathrm{~s}\) of the journey is
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (c) } \quad h_1=\frac{1}{2} \times g \times(2)^2=2 g \\
h_2=\frac{1}{2} \times g \times(4)^2-2 g=6 g \\
h_3=\frac{1}{2} \times g \times(6)^2-8 g=10 g \\
\therefore \quad h_1: h_2: h_3=1: 3: 5 \\
\end{array}
\) -
Question 45 of 63
45. Question
A ball is released from height \(h\) and another from \(2 h\). The ratio of time taken by the two balls to reach the ground is
CorrectIncorrectHint
\(
\text { (a) } t=\sqrt{\frac{2 h}{g}} \text { or } t \propto \sqrt{h} \Rightarrow \frac{t_1}{t_2}=\sqrt{\frac{h}{2 h}}=1: \sqrt{2}
\) -
Question 46 of 63
46. Question
A particle is dropped under gravity from rest from a height \(h\left(g=9.8 \mathrm{~ms}^{-2}\right)\) and it travels a distance \(9 h / 25\) in the last second, the height \(h\) is
CorrectIncorrectHint
\(
\text { (b) Let } h \text { be the distance covered in } t \text { second, } h=\frac{1}{2} g t^2 \quad \text {…(i) }
\)
\(
\begin{array}{l}
\text { Distance covered in } t \text { th second }=\frac{1}{2} g(2 t-1) \\
\Rightarrow \quad \frac{9 h}{25}=\frac{g}{2}(2 t-1) \dots(ii)
\end{array}
\)
From Eqs. (i) and (ii), we get
\(
h=122.5 \mathrm{~m}
\) -
Question 47 of 63
47. Question
A body dropped from the top of a tower covers a distance \(7 x\) in the last second of its journey, where \(x\) is the distance covered in first second. How much time does it take to reach the ground?
CorrectIncorrectHint
(b) In first second distance travelled, \(x=\frac{1}{2} \times g \times t^2=5 \mathrm{~m}\) and similarly, in last second distance travelled, \(7 x=35 \mathrm{~m}\) Now, \(s_t=\left(u+a t-\frac{1}{2} a\right)\)
\(
\Rightarrow \quad 35=0+10 \times t-\frac{1}{2} \times 10
\)
\(
\therefore \quad t=4 \mathrm{~s}
\) -
Question 48 of 63
48. Question
The displacement (in metre) of a particle moving along \(X\)-axis is given by \(x=18 t+5 t^2\). The average acceleration during the interval \(t_1=2 \mathrm{~s}\) and \(t_2=4 \mathrm{~s}\) is
CorrectIncorrectHint
\(
\begin{array}{l}
\text { (b) } x=18 t+5 t^2 \\
\quad v=\frac{d x}{d t}=\frac{d}{d t}\left(18 t+5 t^2\right)=18+10 t \\
\therefore \quad v=10 t+18 \\
\text { At } t_1=2 \mathrm{~s}, v_1=10(2)+18=38 \mathrm{~m} / \mathrm{s} \\
\text { At } t_2=4 \mathrm{~s}, v_2=10(4)+18=58 \mathrm{~m} / \mathrm{s} \\
\therefore \quad a=\frac{v_2-v_1}{t}=\frac{20}{2}=10 \mathrm{~m} / \mathrm{s}^2
\end{array}
\) -
Question 49 of 63
49. Question
The displacement of a particle moving in a straight line is described by the relation \(s=6+12 t-2 t^2\). Here, \(s\) is in metre and \(t\) is in second. The distance covered by particle in first 5 \(s\) is
CorrectIncorrectHint
(d) \(v=\frac{d s}{d t}=12-4 t\)
Comparing with \(v=u+a t, u=12 \mathrm{~ms}^{-1}\) and \(a=-4 \mathrm{~ms}^{-2}\)
Velocity will become zero at time \(t_0 \Rightarrow 0=12-4 t_0\) or \(t_0=3 \mathrm{~s}\).
Since, the given time \(t=5 \mathrm{~s}\) is greater than \(t_0=3 \mathrm{~s}\)distance \(>\mid\) displacement \(\mid\)
\(
\begin{array}{l}
\text { Distance, } d=\left|s_0-t_0\right|+\left|s_{t-t_0}\right|=\frac{u^2}{2|a|}+\frac{1}{2}|a|\left(t-t_0\right)^2 \\
=\frac{(12)^2}{8}+\frac{1}{2} \times 4 \times(2)^2=26 \mathrm{~m} \\
\end{array}
\) -
Question 50 of 63
50. Question
The displacement of a particle moving in a straight line depends on time as \(x=\alpha t^3+\beta t^2+\gamma t+\delta\). The ratio of initial acceleration to its initial velocity depends on
CorrectIncorrectHint
\(
\text { (b) } v=\frac{d x}{d t}=\frac{d}{d t}\left(\alpha t^3+\beta t^2+\gamma t+\delta\right)
\)
\(
v=3 \alpha t^2+2 \beta t+\gamma ; v_{t=0}=v_i=\gamma
\)
\(
a=6 \alpha t+2 \beta: a_{t=0}=a_i=2 \beta
\)
\(
\therefore \quad \frac{v_i}{a_i}=\frac{\gamma}{2 \beta}
\) -
Question 51 of 63
51. Question
The \(x\) and \(y\)-components of a position vector \(\mathbf{P}\) have numerical values 5 and 6, respectively. Direction and magnitude of vector \(\mathbf{P}\) are
CorrectIncorrectHint
(a) Vector \(\mathbf{P}\) is shown in the figure, then according to the given information,
\(
\begin{array}{cc}
& P_x=5, P_y=6 \\
\therefore & |\mathbf{P}|=\sqrt{P_x^2+P_y^2}=\sqrt{25+36} \\
\Rightarrow & |\mathbf{P}|=\sqrt{61} \\
\text { and } & \tan \theta=\frac{P_y}{P_x}=\frac{6}{5} \Rightarrow \theta=\tan ^{-1}\left(\frac{6}{5}\right)
\end{array}
\)
Thus, \(\mathbf{P}\) have magnitude of \(\sqrt{61}\) and lies in \(X Y\)-plane at an angle \(\tan ^{-1}\left(\frac{6}{5}\right)\) to the \(X\)-axis.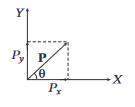
-
Question 52 of 63
52. Question
An object moves from positions \((6,8)\) to \((12,10)\) in the \(X Y\)-plane. Magnitude and direction of displacement is
CorrectIncorrectHint
(a) Positions of the object are
\(
\begin{aligned}
\mathbf{r}_1 & =6 \hat{\mathbf{i}}+8 \hat{\mathbf{j}} \text { and } \mathbf{r}_2=12 \hat{\mathbf{i}}+10 \hat{\mathbf{j}} \\
\therefore \Delta \mathbf{r} & =\mathbf{r}_2-\mathbf{r}_1=6 \hat{\mathbf{i}}+2 \hat{\mathbf{j}} \Rightarrow|\Delta \mathbf{r}|=\sqrt{40} \\
\theta & =\tan ^{-1}\left(\frac{\Delta y}{\Delta x}\right)=\tan ^{-1}\left(\frac{1}{3}\right)=1843^{\circ}
\end{aligned}
\) -
Question 53 of 63
53. Question
A particle moves in \(X Y\)-plane from positions \((2 \mathrm{~m}, 4 \mathrm{~m})\) to \((6 \mathrm{~m}, 8 \mathrm{~m})\) is \(2 \mathrm{~s}\). Magnitude and direction of average velocity is
CorrectIncorrectHint
(b) Displacement, \(\Delta \mathbf{r}=\mathbf{r}_2-\mathbf{r}_1=4 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}\)
\(
\therefore \quad \mathbf{v}_{\mathrm{av}}=\frac{\Delta \mathbf{r}}{\Delta t}=\frac{4 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}}{2}=2(\hat{\mathbf{i}}+\hat{\mathbf{j}}) \mathrm{ms}^{-1}
\)
\(\Rightarrow\) Magnitude of velocity,
\(
\left|\mathbf{v}_{\text {av }}\right|=2 \sqrt{1^2+1^2}=2 \sqrt{2} \mathrm{~ms}^{-1}
\)Direction, \(\theta=\tan ^{-1}\left(\frac{\Delta v_y}{\Delta v_x}\right)=\tan ^{-1}\left(\frac{2}{2}\right)=\tan ^{-1} 1=45^{\circ}\)
-
Question 54 of 63
54. Question
The displacement of an object along the three axes are given by, \(x=2 t^2, y=t^2-4 t\) and \(z=3 t-5\). The initial velocity of the particle is
CorrectIncorrectHint
\(
\begin{aligned}
(c) v_x & =4 t, v_y=2 t-4, v_z=3 \\
\text { At } t & =0, v_x=0, v_y=-4 \text { and } v_z=3 \\
\therefore \quad v & =\sqrt{v_y^2+v_z^2}=5 \text { units }
\end{aligned}
\) -
Question 55 of 63
55. Question
A particle moves along the positive branch of the curve \(y=\frac{x^2}{2}\), where \(x=\frac{t^2}{2}, x\) and \(y\) are measured in metres and \(t\) in second. At \(t=2 \mathrm{~s}\), the velocity of the particle is
CorrectIncorrectHint
(c) As, \(\quad v_x=\frac{d x}{d t}=\frac{2 t}{2}=t\)
At \(t=2 \mathrm{~s}, \quad v_x=2 \mathrm{~ms}^{-1}\)
Further, \(\quad y=\frac{x^2}{2}=\frac{\left(t^2 / 2\right)^2}{2}=\frac{t^4}{8} \Rightarrow v_y=\frac{d y}{d t}=\frac{t^3}{2}\)
At \(t=2 \mathrm{~s}, v_y=4 \mathrm{~ms}^{-1}\)
So, velocity of particle is \((2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}) \mathrm{ms}^{-1}\). -
Question 56 of 63
56. Question
The position vector of a particle is
\(
\mathbf{r}=a \sin \omega t \hat{\mathbf{i}}+a \cos \omega t \hat{\mathbf{j}}
\)
The velocity of the particle isCorrectIncorrectHint
\(
\begin{array}{l}
\text { (b) Given, } \mathbf{r}=(a \sin \omega t) \hat{\mathbf{i}}+(a \cos \omega t) \hat{\mathbf{j}} \\
\therefore \quad \mathbf{v}=\frac{d \mathbf{r}}{d t}=(-a \omega \sin \omega t) \hat{\mathbf{j}}+(a \omega \cos \omega t) \hat{\mathbf{i}} \\
\mathbf{r} \cdot \mathbf{v}=0 \Rightarrow \mathbf{r} \perp \mathbf{v} \\
\end{array}
\) -
Question 57 of 63
57. Question
The position vector of an object at any time \(t\) is given by \(3 t^2 \hat{\mathbf{i}}+6 \hat{\mathbf{j}}+\hat{\mathbf{k}}\). Its velocity (in \(\mathrm{m} / \mathrm{s}\) ) along \(Y\)-axis has the magnitude
CorrectIncorrectHint
(c) Position vector, \(\mathbf{r}=3 t^2 \hat{\mathbf{i}}+6 \hat{\mathbf{j}}+\hat{\mathbf{k}}\)
Velocity vector, \(\mathbf{v}=\frac{d \mathbf{r}}{d t}=6 \hat{\mathbf{i}}+6 \hat{\mathbf{j}}+0=6 \hat{\mathbf{i}}+6 \hat{\mathbf{j}}\)
\(
\therefore \text { Magnitude of the velocity of the object along } Y \text {-axis }=6 \mathrm{~m} / \mathrm{s}
\) -
Question 58 of 63
58. Question
The coordinates of a moving particle at any time \(t\) are given by, \(x=2 t^3\) and \(y=3 t^3\). Acceleration of the particle is given by
CorrectIncorrectHint
(b) Given, \(x=2 t^3\)
\(
\therefore \quad v_x=\frac{d x}{d t}=6 t^2 \Rightarrow a_x=\frac{d v_x}{d t}=12 t
\)
Also, \(y=3 t^3 \Rightarrow v_y=\frac{d y}{d t}=9 t^2 \Rightarrow a_y=\frac{d v_y}{d t}=18 t\)
\(\therefore\) Acceleration, \(a=\sqrt{a_x^2+a_y^2}=t \sqrt{468}\) -
Question 59 of 63
59. Question
The position of a particle moving in the \(X Y\)-plane at any time \(t\) is given by \(x=\left(3 t^2-6 t\right) \mathrm{m}, y=\left(t^2-2 t\right) \mathrm{m}\). Select the correct statement about the moving particle from the following.
CorrectIncorrectHint
\(
\begin{aligned}
\text { (c) } v_x & =\frac{d x}{d t}=6 t-6, a_x=\frac{d v_x}{d t}=6 \mathrm{~ms}^{-2} \\
v_y & =2 t-2, \quad a_y=\frac{d v_y}{d t}=2 \mathrm{~ms}^{-2}
\end{aligned}
\)
At \(t=1 \mathrm{~s}, v_x\) and \(v_y\) both are zero. Hence, net velocity is zero. -
Question 60 of 63
60. Question
A particle’s velocity changes from \((2 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}) \mathrm{ms}^{-1}\) to \((3 \hat{\mathbf{i}}-2 \hat{\mathbf{j}}) \mathrm{ms}^{-1}\) in \(2 \mathrm{~s}\). Its average acceleration \(\left(\right.\) in \(\mathrm{ms}^{-2}\) ) is
CorrectIncorrectHint
\(
\text { (d) } \mathbf{a}_{\mathrm{av}}=\frac{\Delta \mathbf{v}}{\Delta t}=\frac{3 \hat{\mathbf{i}}-2 \hat{\mathbf{j}}-2 \hat{\mathbf{i}}-3 \hat{\mathbf{j}}}{2}=\frac{\hat{\mathbf{i}}-5 \hat{\mathbf{j}}}{2}
\) -
Question 61 of 63
61. Question
A particle has an initial velocity of \(4 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}\) and an acceleration of \(0.4 \hat{\mathbf{i}}+0.3 \hat{\mathbf{j}}\). Its speed after \(10 \mathrm{~s}\) is
CorrectIncorrectHint
\(
\begin{array}{l}
(a) \mathbf{v}=\mathbf{u}+\mathbf{a} t=(4 \hat{\mathbf{i}}+3 \hat{\mathbf{j}})+(0.4 \hat{\mathbf{i}}+0.3 \hat{\mathbf{j}})(10)=(8 \hat{\mathbf{i}}+6 \hat{\mathbf{j}}) \\
\therefore \quad v=\sqrt{(8)^2+(6)^2}=10 \text { units }
\end{array}
\) -
Question 62 of 63
62. Question
A body lying initially at point \((3,7)\) starts moving with a constant acceleration of \(4 \hat{i}\). Its position after \(3 \mathrm{~s}\) is given by the coordinates
CorrectIncorrectHint
(c) Position vector of the body, \(\mathbf{r}=3 \hat{\mathbf{i}}+7 \hat{\mathbf{j}}\)
\(\because\) Acceleration of the body,
\(
\mathbf{a}=4 \hat{\mathbf{i}} \text { and } t=3 \mathrm{~s}
\)Using \(\mathbf{s}=\mathbf{u}_0 t+\frac{1}{2} \mathbf{a} t^2=0 \times 3+\frac{4 \hat{\mathbf{i}}}{2} \times 3 \times 3 \Rightarrow \mathbf{s}=18 \hat{\mathbf{i}}\)
\(\therefore\) New position vector of the body,
\(
\mathbf{r}_1=3 \hat{\mathbf{i}}+7 \hat{\mathbf{j}}+18 \hat{\mathbf{i}}=21 \hat{\mathbf{i}}+7 \hat{\mathbf{j}}
\)Coordinates becomes \((21,7)\)
-
Question 63 of 63
63. Question
The initial position of an object at rest is given by \(3 \hat{\mathbf{i}}-8 \hat{\mathbf{j}}\). It moves with constant acceleration and reaches to the position \(2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}\) after \(4 \mathrm{~s}\). What is its acceleration?
CorrectIncorrectHint
(a) Initial position vector, \(\mathbf{r}_1=3 \hat{\mathbf{i}}-8 \hat{\mathbf{j}}\)
Final position vector, \(\mathbf{r}_2=2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}\)
Change in position,
\(
\Delta \mathbf{r}=\mathbf{r}_2-\mathbf{r}_1=2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}-3 \hat{\mathbf{i}}+8 \hat{\mathbf{j}}=-\hat{\mathbf{i}}+12 \hat{\mathbf{j}}
\)
\(
\text { Using } \quad \mathbf{s}=\mathbf{u}_0 t+\frac{1}{2} \mathbf{a} t^2
\)
\(
\Rightarrow \quad-\hat{\mathbf{i}}+12 \hat{\mathbf{j}}=0+\frac{1}{2} \mathbf{a}(4)^2 \Rightarrow \mathbf{a}=\frac{-\hat{\mathbf{i}}+12 \hat{\mathbf{j}}}{8}=\frac{-\hat{\mathbf{i}}}{8}+\frac{3}{2} \hat{\mathbf{j}}
\)