Kinematics (Entrance Paper) Quiz-L3
Quiz Summary
0 of 51 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 51 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 51
1. Question
A vehicle travels half the distance with speed \(v\) and the remaining distance with speed \(2 v\). Its average speed is : [NEET 2023]
CorrectIncorrectHint
\(
V_{\text {avg }}=\frac{2 v_1 v_2}{v_1+v_2}=\frac{2(v)(2 v)}{v+2 v}=\frac{4 v^2}{3 v}=\frac{4 v}{3}
\) -
Question 2 of 51
2. Question
A football player is moving southward and suddenly turns eastward with the same speed to avoid an opponent. The force that acts on the player while turning is : [NEET 2023]
CorrectIncorrectHint
The centripetal force will exert itself in the north-east direction in order to maintain the player’s motion in a circular arc towards the east, while simultaneously avoiding contact with the opponent.
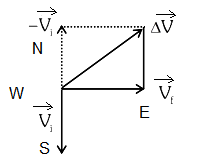
\(
\begin{array}{l}
\vec{V}_i=(V) \text { southward } \\
\vec{V}_F=(V) \text { Eastward } \\
\overrightarrow{\Delta V}=\vec{V}_F-\vec{V}_i \\
=\text { Along North – East }
\end{array}
\)When a football player is going south and then quickly turns east to dodge an opponent, they feel a force called the centripetal force. This force is aimed at the middle of the circle path that the person is following while turning. In this case, the centripetal force works toward the middle of the circular arc made by the player’s movement.
Since the player starts going south and then turns east, the centripetal force will act in the opposite direction of the player’s speed when the player turns. This is based on the basic rule that the centripetal force always points toward the center of curve of the path of motion.
-
Question 3 of 51
3. Question
A horizontal bridge is built across a river. A student standing on the bridge throws a small ball vertically upwards with a velocity \(4 \mathrm{~m} \mathrm{~s}^{-1}\). The ball strikes the water surface after \(4 \mathrm{~s}\). The height of bridge above water surface is (Take \(\mathrm{g}=10 \mathrm{~m} \mathrm{~s}^{-2}\) ) [NEET 2023]
CorrectIncorrectHint
\(
\mathrm{S}=\mathrm{ut}+\frac{1}{2} \mathrm{at}^2
\)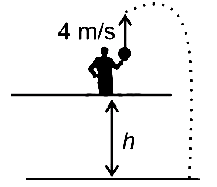
\(
\begin{aligned}
s & =u t-\frac{1}{2} g t^2 \\
& =16-\frac{1}{2} \times 10 \times 16 \\
& =-64 \mathrm{~m}
\end{aligned}
\)Height of bridge above water surface \(=64 \mathrm{~m}\)
-
Question 4 of 51
4. Question
A bullet from a gun is fired on a rectangular wooden block with velocity \(u\). When bullet travels \(24 \mathrm{~cm}\) through the block along its length horizontally, velocity of bullet becomes \(\frac{u}{3}\). Then it further penetrates into the block in the same direction before coming to rest exactly at the other end of the block. The total length of the block is : [NEET 2023]
CorrectIncorrectHint
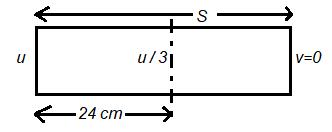
\(
v^2=u^2+2 a s
\)
\(
\begin{array}{c}
\frac{u^2}{9}=u^2+2 a(24) \\
\frac{-8 u^2}{9}=2 a(24) \dots(1)
\end{array}
\)
For the entire path
\(
v^2-u^2=2 a(s) \\
0-u^2=2 a(s) \\
-u^2=2 a(s) \dots(2)
\)
Dividing eqns (1) and (2)
\(
\frac{8}{9}=\frac{24}{s} \Rightarrow S=27 \mathrm{~cm}
\) -
Question 5 of 51
5. Question
The position-time (x – t) graph for positive acceleration is [NEET 2022]
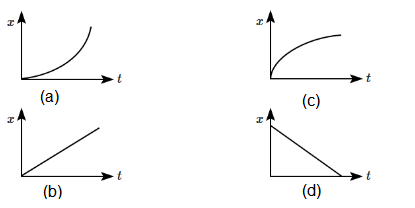 CorrectIncorrect
CorrectIncorrectHint
(a) Slope of position-time \((x-t)\) graph represents velocity.
In graph (a), the slope is increasing hence the velocity is increasing hence acceleration is positive.\(
s=\frac{1}{2} a t^2 \quad \text { (if coefficients of } t^2 \text { is positive }(a>0 \text { ) }
\) -
Question 6 of 51
6. Question
The ratio of the distances travelled by a freely falling body in the \(1^{\text {st }}, 2^{\text {nd }}, 3^{\text {rd }}\) and \(4^{\text {th }}\) second [NEET 2022]
CorrectIncorrectHint
\(
\begin{array}{l}
S_{n^{t h}}=u+\frac{1}{2} a(2 n-1) \\
S_{1^{s t}}=\frac{1}{2} g(2 \times 1-1)=\frac{g}{2} \\
S_{2^{n d}}=\frac{1}{2} g(2 \times 2-1)=3 \times\left(\frac{1}{2} g\right) \\
S_{3^{\text {rd }}}=\frac{1}{2} g(2 \times 3-1)=5 \times\left(\frac{1}{2} g\right) \\
S_{4^{t h}}=\frac{1}{2} g(2 \times 4-1)=7 \times\left(\frac{1}{2} g\right) \\
S_{1^{\text {st }}}: S_{2^{\text {nd }}}: S_{3^{\text {rd }}}: S_{4^{\text {th }}} \\
=1: 3: 5: 7 \\
\end{array}
\) -
Question 7 of 51
7. Question
The displacement-time graphs of two moving particles make angles of \(30^{\circ}\) and \(45^{\circ}\) with the \(x\)-axis as shown in the figure. The ratio of their respective velocity is: [NEET 2022]
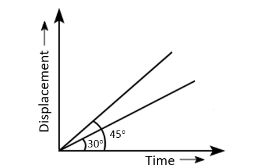 CorrectIncorrect
CorrectIncorrectHint
Slope of \(x\)-t curves gives the velocity
\(
\therefore \frac{v_1}{v_2}=\frac{\tan \theta_1}{\tan \theta_2}
\)
\(
=\frac{\tan 30^{\circ}}{\tan 45^{\circ}}=\frac{1}{\frac{\sqrt{3}}{1}}=1: \sqrt{3}
\) -
Question 8 of 51
8. Question
A small block slides down on a smooth inclined plane, starting from rest at time \(t=0\). Let \(S_n\) be the distance travelled by the block in the interval \(\mathrm{t}=\mathrm{n}-1\) to \(\mathrm{t}=\mathrm{n}\). The the ratio \(\frac{S_n}{S_{n+1}}\) is : [NEET 2022]
CorrectIncorrectHint
\(
\frac{S_n}{S_{n+1}}=\frac{\frac{a}{2}(2 n-1)}{\frac{a}{2}(2(n+1)-1)}=\frac{2 n-1}{2 n+2-1}=\frac{2 n-1}{2 n+1}
\) -
Question 9 of 51
9. Question
A ball is thrown vertically downward with a velocity of \(20 \mathrm{~m} / \mathrm{s}\) from the top of a tower. It hits the ground after some time with a velocity of \(80 \mathrm{~m} / \mathrm{s}\). The height of the tower is (Take, \(g=10 \mathrm{~m} / \mathrm{s}^2\) ) [NEET 2020]
CorrectIncorrectHint
(c) Given, \(u=20 \mathrm{~m} / \mathrm{s}, v=80 \mathrm{~m} / \mathrm{s}\) and \(h=\) ?
From kinematic equation of motion, \(v^2=u^2+2 g h\)
\(
\begin{aligned}
\Rightarrow h & =\frac{v^2-u^2}{2 g}=\frac{(80)^2-(20)^2}{2 \times 10} \quad\left(\because \text { Given, } g=10 \mathrm{~m} / \mathrm{s}^2\right) \\
& =300 \mathrm{~m}
\end{aligned}
\) -
Question 10 of 51
10. Question
A person sitting in the ground floor of a building notices through the window of height \(1.5 \mathrm{~m}\), a ball dropped from the roof of the building crosses the window in \(0.1 \mathrm{~s}\). What is the velocity of the ball when it is at the topmost point of the window? (Take, \(g=10 \mathrm{~m} / \mathrm{s}^2\) ) [NEET 2020]
CorrectIncorrectHint
(b) According to question, time taken by the ball to cross the window,
\(
t=0.1 \mathrm{~s}, h=1.5 \mathrm{~m}
\)
If \(u\) be the velocity at the top most point of the window, then from equation of motion,
\(
\begin{aligned}
& h=u t+\frac{1}{2} g t^2 \\
\Rightarrow & 1.5=u \times 0.1+\frac{1}{2} \times 10 \times(0.1)^2 \\
\Rightarrow & 1.5=0.1 u+0.05 \\
\Rightarrow & u=\frac{1.5-0.05}{0.1}=\frac{1.45}{0.1}=14.5 \mathrm{~m} / \mathrm{s}
\end{aligned}
\) -
Question 11 of 51
11. Question
A person travelling in a straight line moves with a constant velocity \(v_1\) for certain distance \(x\) and with a constant velocity \(v_2\) for next equal distance. The average velocity \(v\) is given by the relation [NEET 2019]
CorrectIncorrectHint
(b) For distance \(x\), the person moves with constant velocity \(v_1\) and for another \(x\) distance, he moves with constant velocity of \(v_2\), then
Total distance travelled by the person,
\(
D=x+x=2 x
\)
Total time taken to cover that distance,
\(
T=t_1+t_2=\frac{x}{v_1}+\frac{x}{v_2} \quad\left(\because t=\frac{\text { Distance }}{\text { Velocity }}\right)
\)
Average velocity,
\(
\begin{aligned}
v_{\mathrm{av}} & =\frac{\text { Total distance }}{\text { Total time }}=\frac{D}{T} \\
v & =\frac{2 x}{\frac{x}{v_1}+\frac{x}{v_2}}=\frac{2}{\frac{1}{v_1}+\frac{1}{v_2}} \\
\Rightarrow \quad \frac{2}{v} & =\frac{1}{v_1}+\frac{1}{v_2}
\end{aligned} \quad\left(\because v_{\mathrm{av}}=v\right)
\) -
Question 12 of 51
12. Question
The speed of a swimmer in still water is \(20 \mathrm{~ms}^{-1}\). The speed of river water is \(10 \mathrm{~ms}^{-1}\) and is flowing due east. If he is standing on the south bank and wishes to cross the river along the shortest path the angle at which he should make his strokes w.r.t. north is given by [NEET 2019]
CorrectIncorrectHint
Speed of swimmer w.r.t river, \(V_{S R}=20 \mathrm{~m} / \mathrm{s}\)
Speed of river flow, \(V_{R G}=10 \mathrm{~m} / \mathrm{s}\)
For the shortest path to cross the river, he should swim at an angle \(\left(90^{\circ}+\theta\right)\) with the stream flow. From the above figure,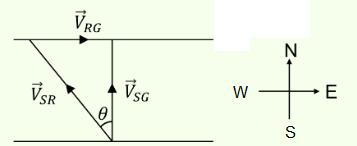
\(
\vec{V}_{S G}=\vec{V}_{S R}+\vec{V}_{R G}
\)
So,
\(
\begin{array}{l}
\sin \theta=\frac{\left|\overrightarrow{\mathrm{V}}_{\mathrm{RG}}\right|}{\left|\overrightarrow{\mathrm{V}}_{\mathrm{SR}}\right|} \\
\sin \theta=\frac{10}{20}=\frac{1}{2} \\
\therefore \theta=30^{\circ} \text { west }
\end{array}
\)As the river is flowing in east direction, so he should swim towards west.
-
Question 13 of 51
13. Question
Find the average velocity when a particle complete the circle of radius \(1 \mathrm{~m}\) in \(10 \mathrm{~s}\). [JIPMER 2019]
CorrectIncorrectHint
(d) When a particle completes one revolution in circular motion, then average displacement travelled by particle is zero.
Hence, average velocity
\(
=\frac{\text { average displacement }}{\Delta t}=\frac{0}{\Delta t}=0
\) -
Question 14 of 51
14. Question
Speed of a particle at 3rd and 8th second are \(20 \mathrm{~ms}^{-1}\) and zero respectively, then average acceleration between 3rd and 8th second will be [JIPMER 2019]
CorrectIncorrectHint
(b) Time interval between 8th and 3rd second,
\(
\Delta t=8-3=5 \mathrm{~s} \text {, i.e. } \Delta t=5 \mathrm{~s}
\)
Change in velocity,
\(
\Delta v=20-0=20 \mathrm{~ms}^{-1}
\)
\(\therefore\) Average acceleration \(=\frac{\Delta v}{\Delta t}=\frac{20}{5}=4 \mathrm{~ms}^{-2}\) -
Question 15 of 51
15. Question
A toy car with charge \(q\) moves on a frictionless horizontal plane surface under the influence of a uniform electric field \(\mathbf{E}\). Due to the force \(q \mathbf{E}\), its velocity increases from 0 to \(6 \mathrm{~ms}^{-1}\) in one second duration. At that instant, the direction of the field is reversed. The car continues to move for two more seconds under the influence of this field. The average velocity and the average speed of the toy car between 0 to \(3 \mathrm{~s}\) are respectively [NEET 2018]
CorrectIncorrectHint
Given condition can be represented through graph also as shown below.
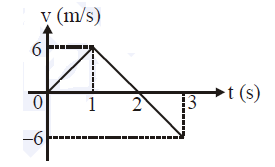
\(\therefore\) Displacement in three seconds
\(=\) Area under the graph
\(
=\frac{1}{2} \times 1 \times 6+\frac{1}{2} \times 1 \times 6-\frac{1}{2} \times 6 \times 1=3 \mathrm{~m}
\)
\(
\text { Average velocity }=\frac{\text { net displacement }}{\text { total time }}=\frac{3 \mathrm{~m}}{3 \mathrm{~s}}=1 \mathrm{~m} / \mathrm{s}
\)
Total distance travelled, \(d=9 \mathrm{~m}\)
Hence, average speed
\(
=\frac{\text { total distance }}{\text { total time }}=\frac{9}{3}=3 \mathrm{~ms}^{-1}
\) -
Question 16 of 51
16. Question
Assertion: A body is momentarily at rest at the instant, if it reverse the direction.
Reason: A body cannot have acceleration, if its velocity is zero at a given instant of time. [AIIMS 2018]CorrectIncorrectHint
(c) When a particle is released from rest position under gravity, then \(v=0\), but \(a \neq 0\).
Also, a body is momentarily at rest at the instant, if it reverse the direction.
Thus, Assertion is correct but Reason in incorrect. -
Question 17 of 51
17. Question
Velocity is given by \(v=4 t(1-2 t)\), then find the value of time at which velocity is maximum. [AIIMS 2018]
CorrectIncorrectHint
(a) To find value of time at which velocity is maximum, taking differentiation of \(v\) with respect to time
Given,
\(
\frac{d v}{d t}=0
\)
\(
\text { Given, } \begin{aligned}
v & =4 t(1-2 t) \\
v & =4 t-8 t^2 \Rightarrow \frac{d}{d t}\left(4 t-8 t^2\right)=0 \\
\Rightarrow \quad 4-16 t & =0 \Rightarrow t=\frac{1}{4} \mathrm{~s}=0.25 \mathrm{~s}
\end{aligned}
\)
Again, taking differentiation, we get
\(
\Rightarrow \quad \frac{d^2 v}{d t^2}=-16<0. \operatorname{maxima} \text { at } \mathrm{t}=1 / 4
\)So, at \(t=0.25 \mathrm{~s}\), velocity is maximum.
-
Question 18 of 51
18. Question
A runner starts from \(O\) and goes to \(O\) following path \(O Q R O\) in \(1 \mathrm{~h}\). What is net displacement and average speed? [JIPMER 2018]
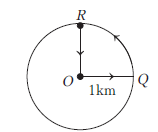 CorrectIncorrect
CorrectIncorrectHint
(a) Runner starts from \(O\) and goes to \(O\) following the path \(O Q R O\), so net displacement is zero.
\(
\begin{aligned}
\because \text { Average speed } & =\frac{\text { Total distance }}{\text { Total time }}=\frac{O Q+Q R+R O}{\text { Total time }} \\
& =\frac{1 \mathrm{~km}+(2 \pi r)(1 / 4)+1 \mathrm{~km}}{1 \mathrm{~h}} \\
& =2+\frac{\pi}{2}=3.57 \mathrm{~kmh}^{-1}
\end{aligned}
\) -
Question 19 of 51
19. Question
A ball is thrown upwards with a speed \(u\) from a height \(h\) above the ground. The time taken by the ball to hit the ground is [JIPMER 2018]
CorrectIncorrectHint
(c) Time taken to reach the highest point from the height \(h\) is obtained from equation, \(v=u-g t\)
\(
\therefore \quad 0=u-g t \text { or } t=\frac{u}{g}
\)
( \(\because\) At highest point, final velocity of ball \(=0\) )
Height attained above \(h\) is obtained from \(v^2-u^2=2(-g) h_1\)
or \(\quad 0-u^2=2(-g) h_1\) or \(h_1=\frac{u^2}{2 g}\)
Total height, \(h_2=\left(h_1+h=\frac{u^2}{2 g}+h\right)\)
Time taken to hit the ground is obtained from
\(
h_2=u t+\frac{1}{2} a t^2 \text { or } \frac{u^2}{2 g}+h=0+\frac{1}{2} g t^2
\)
\(\therefore\) Total time taken, \(t=\sqrt{\frac{\left(u^2+2 g h\right)}{g}}\) -
Question 20 of 51
20. Question
Preeti reached the metro station and found that the escalator was not working. She walked up the stationary escalator in time \(t_1\). On other days, if she remains stationary on the moving escalator, then the escalator takes her up in time \(t_2\). The time taken by her to walk up on the moving escalator will be [NEET 2017]
CorrectIncorrectHint
(c) Speed of walking, \(v_1=\frac{h}{t_1}\) Speed of escalator, \(v_2=\frac{h}{t_2}\)
Time taken when she walks over moving escalator,
\(
\begin{array}{ll}
& t=\frac{h}{v_1+v_2} \\
\Rightarrow & \frac{1}{t}=\frac{v_1}{h}+\frac{v_2}{h}=\frac{1}{t_1}+\frac{1}{t_2} \\
\Rightarrow \quad & t=\frac{t_1 \times t_2}{t_1+t_2}
\end{array}
\) -
Question 21 of 51
21. Question
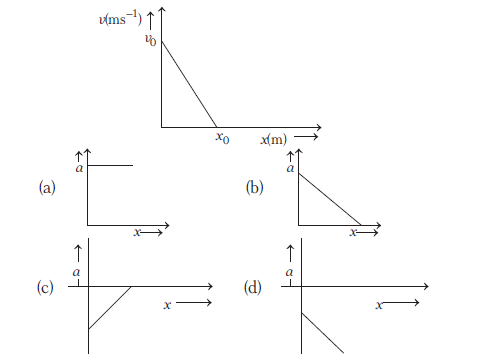
What will be the a versus \(x\) graph for the following graph? [AIIMS 2017]
 CorrectIncorrect
CorrectIncorrectHint
(c) For the given \(v-x\) graph,
Slope \(=-v_0 / x_0\)
and intercept \(=v_0\)
From the general equation of straight line, i.e.
\(
y=m x+c
\)
where, \(m\) is slope and \(c\) is the intercept.
The equation of motion of the \(v-x\) graph can be given as
\(
v=-\frac{v_0 x}{x_0}+v_0 \dots(i)
\)
(-ve sign signifies that the slope is decreasing)
On differentiating Eq. (i) with respect to \(t\), we get
\(
\frac{d v}{d t}=-\frac{v_0}{x_0} \frac{d x}{d t}+0 \text { or } a=-\frac{v_0}{x_0} v \dots(ii)
\)
Putting the value of \(v\) from Eq. (i) in Eq. (ii), we get
\(
a=-\frac{v_0}{x_0}\left[-\frac{v_0}{x_0} x+v_0\right]=\frac{v_0^2}{x_0^2} x-\frac{v_0^2}{x_0}
\)
This equation shows that at \(x=0\), \(a=-\frac{v_0^2}{x_0}=\) constant and at \(a=0, x=x_0\).
So, option (c) is correct. -
Question 22 of 51
22. Question
Which of the following statements is true for a car moving on the road? [Manipal 2017]
CorrectIncorrectHint
(b) For a car in motion, if we describe this event w.r.t. a frame of reference attached to the person sitting inside the car, the car will appear to be at rest as the person inside the car (i.e. observer) is also moving with same velocity and in the same direction as car.
-
Question 23 of 51
23. Question
If the velocity of a particle is \(v=A t+B t^2\), where \(A\) and \(B\) are constants, then the distance travelled by it between \(1 \mathrm{~s}\) and \(2 \mathrm{~s}\) is [NEET 2016]
CorrectIncorrectHint
(b) Velocity of the particle is given as \(v=A t+B t^2\) where, \(A\) and \(B\) are constants.
\(
\begin{aligned}
\Rightarrow & \frac{d x}{d t} =A t+B t^2 & \left(\because v=\frac{d x}{d t}\right) \\
\Rightarrow & d x =\left(A t+B t^2\right) d t &
\end{aligned}
\)
Integrating both sides, we get
\(
\begin{aligned}
\int_{x_1}^{x_2} d x & =\int_1^2\left(A t+B t^2\right) d t \\
\Rightarrow \quad \Delta x & =x_2-x_1=A \int_1^2 t d t+B \int_1^2 t^2 d t \\
& =A\left[\frac{t^2}{2}\right]_1^2+B\left[\frac{t^3}{3}\right]_1^2 \\
& =\frac{A}{2}\left(2^2-1^2\right)+\frac{B}{3}\left(2^3-1^3\right)
\end{aligned}
\)
\(\therefore\) Distance travelled by the particle between \(1 \mathrm{~s}\) and \(2 \mathrm{~s}\) is
\(
\Delta x=\frac{A}{2} \times(3)+\frac{B}{3}(7)=\frac{3 A}{2}+\frac{7 B}{3}
\) -
Question 24 of 51
24. Question
A particle of unit mass undergoes one dimensional motion such that its velocity varies according to \(v(x)=\beta x^{-2 n}\), where \(\beta\) and \(n\) are constants and \(x\) is the position of the particle. The acceleration of the particle as a function of \(x\), is given by [CBSE AIPMT 2015]
CorrectIncorrectHint
(b)
\(
\text { (b) Given, } \begin{aligned}
v & =\beta x^{-2 n} \\
a & =\frac{d v}{d t}=\frac{d x}{d t} \cdot \frac{d v}{d x}
\end{aligned}
\)
\(
\begin{array}{l}
a=v \frac{d v}{d x}=\left(\beta x^{-2 n}\right)\left(-2 n \beta x^{-2 n-1}\right) \\
a=-2 n \beta^2 x^{-4 n-1}
\end{array}
\) -
Question 25 of 51
25. Question
A ball is dropped from a bridge \(122.5 \mathrm{~m}\) above a river. After the ball has been falling for \(2 \mathrm{~s}\), a second ball is thrown straight down after it. What must be the initial velocity of the second ball, so that both ball hit the water at the same time? [AIIMS 2015]
CorrectIncorrectHint
(c) Let the ball hit water in \(t\) second.
For first ball, \(\quad s=u t+\frac{1}{2} a t^2\)
\(
\begin{aligned}
122.5 & =0+\frac{1}{2} \times 9.8 \times t^2=4.9 t^2 \\
\Rightarrow \quad t & =\sqrt{\frac{122.5}{4.9}}=\sqrt{25}=5 \mathrm{~s}
\end{aligned}
\)
\(
\begin{array}{l}
\text { For second ball, } \begin{aligned}
122.5 & =u(5-2)+\frac{1}{2} \times 9.8 \times(5-2)^2 \\
& =3 u+44.1 \\
3 u & =122.5-44.1 \\
3 u & =78.4 \Rightarrow u=26.1 \mathrm{~ms}^{-1}
\end{aligned}
\end{array}
\) -
Question 26 of 51
26. Question
A ball is thrown vertically upwards from the ground with a speed of \(25.2 \mathrm{~ms}^{-1}\). How long does it take to reach its highest point and how high does it rise? (Take, \(g=9.8 \mathrm{~ms}^{-2}\) ) [UK PMT 2015]
CorrectIncorrectHint
(c) Given, upward velocity of ball \(=25.2 \mathrm{~ms}^{-1}\)
Height attained by the ball,
\(
H=\frac{u^2}{2 g}=\frac{25.2 \times 25.2}{2 \times 9.8}=32.4 \mathrm{~m}
\)Now, time taken by the ball to attain \(32.4 \mathrm{~m}\) is
\(
t=\frac{u}{g}=\frac{25.2}{9.8}=2.57 \mathrm{~s}
\) -
Question 27 of 51
27. Question
A vehicle moving with a constant acceleration from \(A\) to \(B\) in a straight line \(A B\), has velocities \(u\) and \(v\) at \(A\) and \(B\), respectively. \(C\) is the mid-point of \(A B\). If time taken to travel from \(A\) to \(C\) is twice the time taken to travel from \(C\) to \(B\), then the velocity of the vehicle \(v\) at \(B\) is [EAMCET 2015]
CorrectIncorrectHint
(c) According to question, the given condition can be depicted as
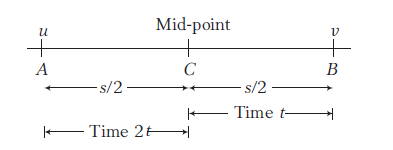
For motion from \(A\) to \(C\),
\(
\frac{s}{2}=2 u t+\frac{1}{2} a \times(2 t)^2=2 u t+2 a t^2 \dots(i)
\)
Also, for motion from \(C\) to \(B\),
\(
\frac{s}{2}=v^{\prime} t+\frac{1}{2} a t^2=(u+2 a t) t+\frac{1}{2} a t^2
\)
(Let initial velocity be \(v^{\prime}=u+2 a t\) )
\(
=u t+2 a t^2+\frac{1}{2} a t^2
\)
Now, from Eq. (i), we get
\(
2 u t+2 a t^2=u t+2 a t^2+\frac{1}{2} a t^2 \Rightarrow u=\frac{a t}{2}
\)
For overall motion,
\(
v=u+3 a t=\frac{a t}{2}+3 a t=\frac{7 a t}{2}=7 u \quad\left(\because u=\frac{a t}{2}\right)
\) -
Question 28 of 51
28. Question
The displacement of a particle as a function of time is shown in figure. It indicates that [Kerala CEE 2015]
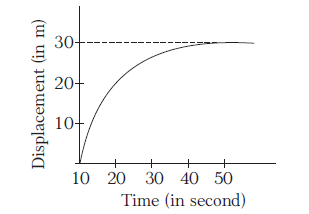 CorrectIncorrect
CorrectIncorrectHint
(d) At first, the slope is decreasing, therefore the motion is retarded. Finally, the displacement becomes constant, thus the particle stops.
-
Question 29 of 51
29. Question
A car starts from rest and accelerates uniformly to a speed of \(180 \mathrm{kmh}^{-1}\) in \(10 \mathrm{~s}\). The distance covered by the car in the time interval is [Manipal 2015]
CorrectIncorrectHint
(d) Given, \(u=0, v=180 \mathrm{kmh}^{-1}=50 \mathrm{~ms}^{-1}\)
Time taken, \(t=10 \mathrm{~s}, a=\frac{v-u}{t}=\frac{50}{10}=5 \mathrm{~ms}^{-2}\)
Distance covered by the car,
\(
\begin{aligned}
s & =u t+\frac{1}{2} a t^2=0+\frac{1}{2} \times 5 \times(10)^2 \\
& =\frac{500}{2}=250 \mathrm{~m}
\end{aligned}
\) -
Question 30 of 51
30. Question
The velocity-time graph for two bodies \(A\) and \(B\) are shown in figure. Then, the acceleration of \(A\) and \(B\) are in the ratio [KCET 2015]
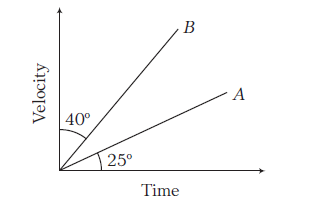 CorrectIncorrect
CorrectIncorrectHint
(d) The slope of velocity-time graph gives acceleration, i.e. \(\quad \frac{a_A}{a_B}=\frac{\tan \theta_1}{\tan \theta_2}\)
Here, \(\theta_1\) is the angle made by line \(A\) with time axis and \(\theta_2\) is the angle made by line \(B\) with time axis
\(
\Rightarrow \quad \frac{a_A}{a_B}=\frac{\tan 25^{\circ}}{\tan 50^{\circ}}
\) -
Question 31 of 51
31. Question
A ball thrown vertically upwards after reaching a maximum height \(h\) returns to the starting point after a time of \(10 \mathrm{~s}\). Its displacement after \(5 \mathrm{~s}\) is [Kerala CEE 2014]
CorrectIncorrectHint
(a) The position of an object is always expressed w.r.t. some reference point. If the initial position of an object w.r.t. a reference points is \(s_1\) and after sometime, it changes to \(s_2\), then the magnitude of the displacement of the object is \(s_2-s_1\). Since, the given ball returns to its starting point in \(10 \mathrm{~s}\). So, in \(5 \mathrm{~s}\), it reaches the highest point which is at \(s_2\).
Given, \(s_2\) is at a height \(h\) w.r.t. \(s_1\). Thus, the displacement after 5 s will be \(s_2-s_1=h\). -
Question 32 of 51
32. Question
A police jeep is chasing with velocity of \(45 \mathrm{kmh}^{-1}\), a thief in another jeep moving with velocity \(153 \mathrm{kmh}^{-1}\). Police fires a bullet with muzzle velocity of \(180 \mathrm{~ms}^{-1}\). The velocity with which it will strike the car of the thief is [EAMCET 2014]
CorrectIncorrectHint
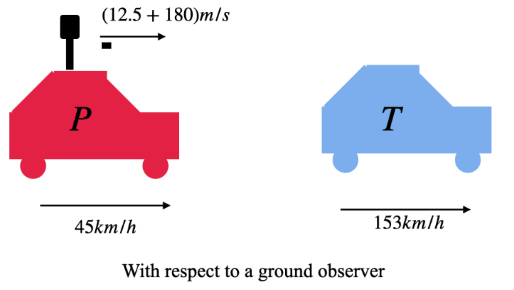
It is given that the velocity of the police jeep is \(45 \mathrm{~km} / \mathrm{h}\).
First, let us convert it to \(\mathrm{m} / \mathrm{s}\) as the options are in this unit.
\(
\begin{array}{l}
45 \mathrm{~km} / \mathrm{h}=45 \times \frac{1000}{3600} \mathrm{~m} / \mathrm{s} \\
=45 \times \frac{5}{18} \mathrm{~m} / \mathrm{s} =12.5 \mathrm{~m} / \mathrm{s}
\end{array}
\)
The muzzle velocity of the bullet is \(180 \mathrm{~m} / \mathrm{s}\). As the muzzle of the gun is also moving at a velocity of \(12.5 \mathrm{~m} / \mathrm{s}\), a ground observer will see the velocity of the bullet to be,
Observed bullet velocity = Muzzle velocity of the bullet + Muzzle’s velocity (Velocity of the police jeep).
\(
=(180+12.5)=192.5 \mathrm{~m} / \mathrm{s}
\)
Hence, the bullet velocity with respect to a ground observer is \(=192.5 \mathrm{~m} / \mathrm{s}\)
Now, let us convert the velocity of the thief’s jeep into \(\mathrm{m} / \mathrm{s}\),
\(
\begin{array}{l}
153 \mathrm{~km} / \mathrm{h}=153 \times \frac{5}{18} \mathrm{~m} / \mathrm{s} =42.5 \mathrm{~m} / \mathrm{s}
\end{array}
\)
Hence the relative velocity of the bullet with respect to the thief’s jeep is given by,
Relative velocity \(=(\) Velocity of bullet – Velocity of the thief’s jeep \()\).
Both these velocities are taken with respect to a ground observer.
So, the bullet will hit the thief’s jeep at a speed of,
\(
=(192.5-42.5)=150 \mathrm{~m} / \mathrm{s}
\) -
Question 33 of 51
33. Question
A particle moves with constant acceleration along a straight line starting from rest. The percentage increase in its displacement during the 4th second compared to that in the 3rd second is [WB JEE 2014]
CorrectIncorrectHint
\(
\begin{array}{c}
\text { (b) We know that, } s_{n \text {th }}=u+\frac{1}{2} a(2 n-1) \\
s_{3 \text { rd }}=0+\frac{1}{2} a(2 \times 3-1)=\frac{5}{2} a \text { (For } n=3 \mathrm{~s} \text { ) }
\end{array}
\)
\(
\left.s_{\text {th }}=0+\frac{1}{2} a(2 \times 4-1)=\frac{7}{2} a \quad \text { (For } n=4 \mathrm{~s}\right)
\)
\(
\begin{array}{l}
\text { So, the percentage increase }=\frac{s_{4 \text { th }}-s_{3 \text { rd }}}{s_{3 \text { rd }}} \times 100 \\
=\frac{\frac{7}{2} a-\frac{5}{2} a}{\frac{5}{2} a} \times 100=\frac{\frac{2 a}{2}}{\frac{5}{2} a} \times 100=2 \times 20=40 \%
\end{array}
\) -
Question 34 of 51
34. Question
A car covers the first half of the distance between the two places at \(40 \mathrm{kmh}^{-1}\) and another half at \(60 \mathrm{kmh}^{-1}\). The average speed of the car is [UK PMT 2014]
CorrectIncorrectHint
Average speed is \(\mathrm{V}=\frac{\text { distance }}{\text { time }}\)
if a car travels first half with \(V_1\) and second half of distance with \(V_2\) then formula of average velocity is given by
\(
\mathrm{V}=\frac{2 \mathrm{~V}_2 \mathrm{~V}_1}{\mathrm{~V}_1+\mathrm{V}_2}=\frac{2 \times 60 \times 40}{60+40}=48 \mathrm{~km} / \mathrm{h}
\) -
Question 35 of 51
35. Question
A particle starts moving from rest with uniform acceleration. It travels a distance \(x\) in first \(2 \mathrm{~s}\) and distance \(y\) in the next \(2 \mathrm{~s}\). Then, [EAMCET 2014]
CorrectIncorrectHint
(a) The distance covered in \(2 \mathrm{~s}, \quad x=\frac{1}{2} a(2)^2 \quad(\because u=0)\)
\(
=2 a
\)The distance covered in next \(2 \mathrm{~s}\),
\(
\begin{aligned}
y & =\frac{1}{2} a(4)^2-\frac{1}{2} a(2)^2=6 a \\
x / y & =\frac{2 a}{6 a}=\frac{1}{3} \Rightarrow y=3 x
\end{aligned}
\) -
Question 36 of 51
36. Question
At time \(t=0\), two bodies \(A\) and \(B\) are at the same point. \(A\) moves with constant velocity \(v\) and \(B\) starts from rest and moves with constant acceleration. Relative velocity of \(B\) w.r.t. \(A\) when the bodies meet each other is [EAMCET 2014]
CorrectIncorrectHint
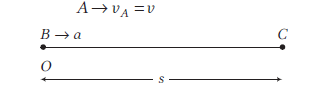
(c) \(A \rightarrow v_A\) (constant velocity)
\(B \rightarrow a\) (constant acceleration)
\(C\) be the fixed point at which both \(A\) and \(B\) meet in time \(t\).
Now, \(s=v_A t\) and \(v_B=a t\)
\(
\begin{array}{l}
s=\frac{1}{2} a t^2=v_A t \\
a=\frac{2 v_A}{t} \dots(i)
\end{array}
\)
\(
\begin{array}{rlr}
v_B & =u+a t & (\because v=0) \\
v_B & =a t=2 v_A & \text { [From Eq. (i)] } \\
v_{B A} & =\text { velocity of } B \text { w.r.t. } A & \\
v_{B A} & =v_B-v_A=2 v_A-v_A=v_A & \\
v_{B A} & =v & \left(\because v_A=v\right)
\end{array}
\) -
Question 37 of 51
37. Question
A car moves from \(A\) to \(B\) with a speed of \(30 \mathrm{kmh}^{-1}\) and from \(B\) to \(A\) with a speed of \(20 \mathrm{kmh}^{-1}\). What is the average speed of the car? [KCET 2014]
CorrectIncorrectHint
\(
v_{\mathrm{av}}=\frac{2 v_{A B} v_{B A}}{v_{A B}+v_{B A}}=24 \mathrm{kmh}^{-1}
\) -
Question 38 of 51
38. Question
A body starts from rest and moves with constant acceleration for \(t\) second. It travels a distance \(x_1\) in first half of time and \(x_2\) in next half of time, then [KCET 2014]
CorrectIncorrectHint
(c)
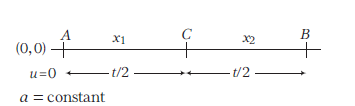
Let \(A\) be the original point.
From equation of motion,
\(
x=u t+\frac{1}{2} a t^2=\frac{1}{2} a t^2 \quad(\because u=0)
\)
For point \(C, \quad x_1=\frac{1}{2} a(t / 2)^2 \Rightarrow x_1=\frac{1}{8} a t^2\)
Distance travelled by the body in \(t\) second is
\(
\begin{aligned}
x_1+x_2 & =\frac{1}{2} a(t)^2=4 x_1 \\
x_2 & =4 x_1-x_1=3 x_1
\end{aligned}
\) -
Question 39 of 51
39. Question
The acceleration of a moving body is found from the [Kerala CEE 2014]
CorrectIncorrectHint
\(
a=\frac{d v}{d t}=\text { Slope of } v-t \text { curve }
\) -
Question 40 of 51
40. Question
A stone falls freely under gravity. It covers distances \(h_1, h_2\) and \(h_3\) in the first \(5 \mathrm{~s}\), the next \(5 \mathrm{~s}\) and the next \(5 \mathrm{~s}\), respectively. The relation between \(h_1, h_2\) and \(h_3\) is [NEET 2013]
CorrectIncorrectHint
(b) The distance \(h_1\) covers by stone,
\(
h_1=\frac{1}{2} g t^2 \times \frac{1}{2} 10 \times(5)^2=125
\)The distance \(h_2\) covers by stone,
\(
h_2=\frac{1}{2} \times 10 \times(10)^2-\frac{1}{2} \times 10 \times(5)^2=375
\)The distance \(h_3\) covers by stone,
\(
h_3=\frac{1}{2} \times 10 \times(15)^2-\frac{1}{2} \times 10 \times(10)^2=625
\)The relation between \(h_1, h_2\) and \(h_3\) is \(h_1=\frac{h_2}{3}=\frac{h_3}{5}\)
-
Question 41 of 51
41. Question
The motion of a particle in straight line is an example of [J & K CET 2013]
CorrectIncorrectHint
(b) When velocity of a body changes by equal amount in equal intervals of time, then the body is said to have uniform acceleration, this holds true for straight line motion.
-
Question 42 of 51
42. Question
The velocity-time graph of particle comes out to be a non-linear curve. The motion is [J & K CET 2013]
CorrectIncorrectHint
(c) Velocity-time graph gives the instantaneous value of acceleration at any instant. For non-uniformly accelerated motion, \(v-t\) graph is non-linear.
-
Question 43 of 51
43. Question
A body is thrown vertically upward from a point \(A\) \(125 \mathrm{~m}\) above the ground. It goes up to a maximum height of \(250 \mathrm{~m}\) above the ground and passes through \(A\) on its downward journey. The velocity of the body when it is at a height of \(70 \mathrm{~m}\) above the ground is (Take, \(g=10 \mathrm{~ms}^{-2}\) ) [EAMCET 2013]
CorrectIncorrectHint
(b) The initial velocity of the body, \(u^2=2 g h\)
\(
\Rightarrow \quad u=\sqrt{2 g h}=\sqrt{2 \times 10 \times 125}=\sqrt{2500}=50 \mathrm{~ms}^{-1}
\)The final velocity from equation of motion,
\(
\begin{aligned}
v^2 & =u^2+2 g h \\
v & =\sqrt{(50)^2+2 \times 10 \times 55} \\
v & =\sqrt{2500+1100} \\
& =\sqrt{3600}=60 \mathrm{~ms}^{-1}
\end{aligned}
\) -
Question 44 of 51
44. Question
A person reaches a point directly opposite on the other bank of a river. The velocity of the water in the river is \(4 \mathrm{~ms}^{-1}\) and the velocity of the person in still water is \(5 \mathrm{~ms}^{-1}\). If the width of the river is 84.6 \(\mathrm{m}\), time taken to cross the river (in seconds) is [EAMCET 2013]
CorrectIncorrectHint
(a) Given, velocity of water, \(v_w=4 \mathrm{~ms}^{-1}\)
Velocity of person, \(v_p=5 \mathrm{~ms}^{-1}\), width of the river \(=846 \mathrm{~m}\)
We know that, time taken, \(t=\frac{s}{\sqrt{v_p^2-v_W^2}}\)
\(
\begin{array}{ll}
\Rightarrow & t=\frac{846}{\sqrt{25-16}} \\
\Rightarrow & t=\frac{84.6}{3} \cong 28.2 \mathrm{~s}
\end{array}
\)Alternate: Let the angle between the path traversed by person and the direction in which he tries to swim with respect to river be \(\theta\).
Since the net path traveled is a straight line directly towards the opposite end, the component of net velocity does not exist in the direction of river’s flow.
Thus \(\operatorname{vin} \theta=v_{\text {river }}\)
\(
\Longrightarrow \sin \theta=\frac{4}{5}
\)
Thus net velocity of man in the direction of crossing=
\(
v \cos \theta=5 \mathrm{~m} / \mathrm{s} \times \frac{3}{5}=3 \mathrm{~m} / \mathrm{s}
\)
Thus total time taken to cross the river \(=\frac{84.6 \mathrm{~m}}{3 \mathrm{~m} / \mathrm{s}}=28.2 \mathrm{~s}\) -
Question 45 of 51
45. Question
The velocity-time graph of robber’s car and a chasing police car are shown in the following graph. Police car crosses the robber’s car in time [UP CPMT 2013]
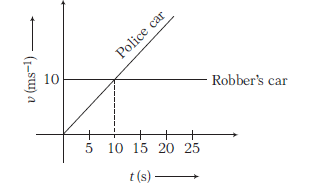 CorrectIncorrect
CorrectIncorrectHint
(c) From graph, velocity of robber’s car \(=10 \mathrm{~ms}^{-1}\)
Let police car crosses it after \(t\) second.
Distance travelled by robber’s car \(=10 t \mathrm{~m}\)
Police car is moving with a constant acceleration of \(1 \mathrm{~ms}^{-2}\) as it attains a velocity of \(10 \mathrm{~ms}^{-1}\) in \(10 \mathrm{~s}\) after starting from rest.
Distance travelled in \(t\) second \(=\frac{1}{2} \cdot a \cdot t^2=\frac{1}{2} t^2\)
When the police car crosses the robber’s car, distance travelled by the both cars should be same from the starting point of chase.
\(
\therefore \quad \frac{1}{2} t^2=10 t \Rightarrow t=20 \mathrm{~s}
\) -
Question 46 of 51
46. Question
Initial speed of an \(\alpha\)-particle inside a tube of length \(4 \mathrm{~m}\) is \(1 \mathrm{kms}^{-1}\), if it is accelerated in the tube and comes out with a speed of \(9 \mathrm{kms}^{-1}\), then the time for which the particle remains inside the tube is [BCECE 2013]
CorrectIncorrectHint
(b) Given, initial speed, \(u=1 \mathrm{kms}^{-1}=1000 \mathrm{~ms}^{-1}\)
Final speed, \(v=9 \mathrm{kms}^{-1}=9000 \mathrm{~ms}^{-1}\)
By using the relation, \(v^2=u^2+2 a s\)
\(
(9000)^2=(1000)^2+2 \times a \times 4 \Rightarrow a=10^7 \mathrm{~ms}^{-2}
\)
\(\therefore\) The time for which the particle remains in the tube
\(
\begin{aligned}
v & =u+a t \\
\Rightarrow \quad t & =\frac{v-u}{a}=\frac{9000-1000}{10^7}=8 \times 10^{-4} \mathrm{~s}
\end{aligned}
\) -
Question 47 of 51
47. Question
The motion of a particle along a straight line is described by equation
\(
x=8+12 t-t^3
\)
where, \(x\) is in metre and \(t\) in second. The retardation of the particle when its velocity becomes zero, is [CBSE AIPMT 2012]CorrectIncorrectHint
(d) Given, \(x=8+12 t-t^3\)
We know that , \(v=\frac{d x}{d t}[latex] and [latex]a=\frac{d v}{d t}\)
So,
\(v=12-3 t^2\)
and
\(t=2 \mathrm{~s}\),
\(v=0\)
and
\(a=-12 \mathrm{~ms}^{-2}\)So, retardation of the particle \(=12 \mathrm{~ms}^{-2}\).
-
Question 48 of 51
48. Question
A particle moves along with \(X\)-axis. The position \(x\) of particle with respect to time \(t\) from origin given by \(x=b_0+b_1 t+b_2 t^2\). The acceleration of particle is [AIIMS 2012]
CorrectIncorrectHint
(d) Distance, \(x=b_0+b_1 t+b_2 t^2\)
Velocity, \(v=\left(\frac{d x}{d t}\right)=b_1+2 b_2 t\)
Acceleration, \(a=\frac{d^2 x}{d t^2}=2 b_2\) -
Question 49 of 51
49. Question
A body \(X\) is projected upwards with a velocity of \(98 \mathrm{~ms}^{-1}\), after \(4 \mathrm{~s}\), a second body \(Y\) is also projected upwards with the same initial velocity. Two bodies will meet after [BCECE 2012]
CorrectIncorrectHint
(c) Let \(t\) second be the time of flight of the first body after meeting, then \((t-4)\) second will be the time of flight of the second body.
As the initial velocity at which the bodies \(A\) and \(B\) projected are same and also the position of meeting will be also same.
So, \(\quad h_x=h_y\)
\(
\therefore \quad 98 t-\frac{1}{2} g t^2=98(t-4)-\frac{1}{2} g(t-4)^2
\)
On solving, \(t=12 \mathrm{~s}\) -
Question 50 of 51
50. Question
A scooter starts from rest have an acceleration of \(1 \mathrm{~ms}^{-2}\) while a car \(150 \mathrm{~m}\) behind it starts from rest with an acceleration of \(2 \mathrm{~ms}^{-2}\). After how much time, the car catches up with the scooter? [BHU 2012]
CorrectIncorrectHint
(b) Let after time \(t\), car catches the scooter and the distance travelled by scooter in time \(t\),
\(
x=\frac{1}{2} \times(1) \times t^2=\frac{t^2}{2} \dots(i)
\)
The distance travelled by car in time \(t\)
\(
x+150=\frac{1}{2} \times 2 \times t^2=t^2 \dots(ii)
\)
Solving Eqs. (i) and (ii), we get
\(
t=\sqrt{300} \mathrm{~s}
\) -
Question 51 of 51
51. Question
Let
\(
\begin{array}{l}
\mathbf{r}_1(t)=3 t \hat{\mathbf{i}}+4 t^2 \hat{\mathbf{j}} \\
\text { and } \mathbf{r}_2(t)=4 t^2 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}
\end{array}
\)
represent the positions of particles 1 and 2 , respectively, as function of time \(t, \mathbf{r}_1(t)\) and \(\mathbf{r}_2(t)\) are in metre and \(t\) in second. The relative speed of the two particles at the instant \(t=1 \mathrm{~s}\), will be [AMU 2012]CorrectIncorrectHint
\(
\begin{array}{l}
\text { (c) Given, } \mathbf{r}_1(t)=3 t \hat{\mathbf{i}}+4 t^2 \hat{\mathbf{j}} \\
\therefore \quad \frac{d \mathbf{r}_1}{d t}=3 \hat{\mathbf{i}}+8 \hat{\mathbf{j}}
\end{array}
\)
\(
\begin{array}{l}
\text { At } t=1 \mathrm{~s} \text {, } \\
\mathbf{v}_1=\frac{d \mathbf{r}_1}{d t}=3 \hat{\mathbf{i}}+8 \hat{\mathbf{j}} \\
\text { Again, } \quad \mathbf{r}_2(t)=4 t^2 \hat{\mathbf{i}}+3 \hat{\mathbf{j}} \\
\Rightarrow \quad \frac{d \mathbf{r}_2}{d t}=8 \hat{\mathbf{i}}+3 \hat{\mathbf{j}} \\
\end{array}
\)
At
\(
\begin{aligned}
t & =1 \mathrm{~s}, \\
\mathbf{v}_2 & =\frac{d \mathbf{r}_2}{d t}=8 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}
\end{aligned}
\)
\(
\begin{aligned}
\text { Relative speed, } \mathbf{v}_{\text {rel }} & =\mathbf{v}_2-\mathbf{v}_1 \\
& =(8 \hat{\mathbf{i}}+3 \hat{\mathbf{j}})-(3 \hat{\mathbf{i}}+8 \hat{\mathbf{j}}) \\
& =5 \hat{\mathbf{i}}-5 \hat{\mathbf{j}} \\
\therefore \quad\left|\mathbf{v}_{\text {rel }}\right| & =\sqrt{(5)^2+(-5)^2} \\
& =5 \sqrt{2} \mathrm{~m} / \mathrm{s}
\end{aligned}
\)