JEE Physics Test Series Quiz-6
Quiz Summary
0 of 50 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 50 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 50
1. Question
1 point(s)A particle is dropped from a height \(H\). The de Broglie wavelength of the particle as a function of height is proportional to
CorrectIncorrect -
Question 2 of 50
2. Question
1 point(s)The wavelength of a photon needed to remove a proton from a nucleus which is bound to the nucleus with \(1 \mathrm{MeV}\) energy is nearly
CorrectIncorrect -
Question 3 of 50
3. Question
1 point(s)Consider a beam of electrons (each electron with energy \(E_0\) ) incident on a metal surface kept in an evacuated chamber. Then
CorrectIncorrect -
Question 4 of 50
4. Question
1 point(s)Consider the Figure below. Suppose the voltage applied to A is increased. The diffracted beam will have the maximum at a value of \(\theta\) that
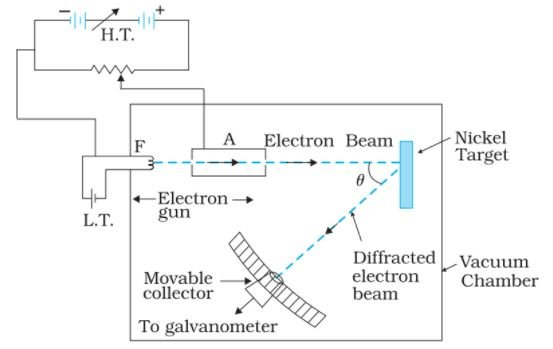 CorrectIncorrect
CorrectIncorrect -
Question 5 of 50
5. Question
1 point(s)A proton, a neutron, an electron and an \(\alpha\)-particle have same energy. Then their de Broglie wavelengths compare as
CorrectIncorrect -
Question 6 of 50
6. Question
1 point(s)An electron is moving with an initial velocity \(\mathbf{v}=v_0 \hat{\mathbf{i}}\) and is in a magnetic field \(\mathbf{B}=B_0 \hat{\mathbf{j}}\). Then it’s de Broglie wavelength
CorrectIncorrect -
Question 7 of 50
7. Question
1 point(s)An electron (mass \(m\) ) with an initial velocity \(\mathbf{v}=v_0 \hat{\mathbf{i}}\left(v_0>0\right.\) ) is in an electric field \(\mathbf{E}=-E_0 \hat{\mathbf{i}}\left(E_0=\right.\) constant \(\left.>0\right)\). It’s de Broglie wavelength at time \(t\) is given by
CorrectIncorrect -
Question 8 of 50
8. Question
1 point(s)n electron (mass \(m\) ) with an initial velocity \(\mathbf{v}=v_0 \hat{\mathbf{i}}\) is in an electric field \(\mathbf{E}=E_0 \hat{\mathbf{j}}\). If \(\lambda_0=h / m v_0\), it’s de Breoglie wavelength at time \(t\) is given by
CorrectIncorrect -
Question 9 of 50
9. Question
1 point(s)Monochromatic light of frequency \(6.0 \times 10^{14} \mathrm{~Hz}\) is produced by a laser. The power emitted is \(2.0 \times 10^{-3} \mathrm{~W}\). (a) What is the energy of a photon in the light beam? (b) How many photons per second, on an average, are emitted by the source?
CorrectIncorrect -
Question 10 of 50
10. Question
1 point(s)The work function of caesium is \(2.14 \mathrm{eV}\). Find the threshold frequency for caesium.
CorrectIncorrect -
Question 11 of 50
11. Question
1 point(s)What is the de Broglie wavelength associated with an electron moving with a speed of \(5.4 \times 10^6 \mathrm{~m} / \mathrm{s}\)
CorrectIncorrect -
Question 12 of 50
12. Question
1 point(s)What is the de Broglie wavelength associated with a ball of mass 150 \(\mathrm{g}\) travelling at \(30.0 \mathrm{~m} / \mathrm{s}\)?
CorrectIncorrect -
Question 13 of 50
13. Question
1 point(s)A particle is moving three times as fast as an electron. The ratio of the de Broglie wavelength of the particle to that of the electron is \(1.813 \times 10^{-4}\). Calculate the particle’s mass and identify the particle.
CorrectIncorrect -
Question 14 of 50
14. Question
1 point(s)What is the de Brogle wavelength associated with an electron, accelerated through a potential difference of 100 volts?
CorrectIncorrect -
Question 15 of 50
15. Question
1 point(s)It is found experimentally that \(13.6 \mathrm{~eV}\) energy is required to separate a hydrogen atom into a proton and an electron. Compute the orbital radius and the velocity of the electron in a hydrogen atom.
CorrectIncorrect -
Question 16 of 50
16. Question
1 point(s)\(\mathrm{~A} 10 \mathrm{~kg}\) satellite circles earth once every \(2 \mathrm{~h}\) in an orbit having a radius of \(8000 \mathrm{~km}\). Assuming that Bohr’s angular momentum postulate applies to satellites just as it does to an electron in the hydrogen atom, flnd the quantum number of the orbit of the satellite.
CorrectIncorrect -
Question 17 of 50
17. Question
1 point(s)Taking the Bohr radius as \(a_0=53 \mathrm{pm}\), the radius of \(\mathrm{Li}^{++}\)ion in its ground state, on the basis of Bohr’s model, will be about
CorrectIncorrect -
Question 18 of 50
18. Question
1 point(s)The binding energy of a \(\mathrm{H}\)-atom, considering an electron moving around a fixed nuclei (proton), is \(B=-\frac{m e^4}{8 n^2 \varepsilon_0^2 h^2} \cdot(m=\) electron mass).
If one decides to work in a frame of reference where the electron is at rest, the proton would be moving arround it. By similar arguments, the binding energy would be
\(
B=-\frac{M e^4}{8 n^2 \varepsilon_0^2 h^2}(M=\text { proton mass })
\)This last expression is not correct because
CorrectIncorrect -
Question 19 of 50
19. Question
1 point(s)The simple Bohr model cannot be directly applied to calculate the energy levels of an atom with many electrons. This is because
CorrectIncorrect -
Question 20 of 50
20. Question
1 point(s)For the ground state, the electron in the \(\mathrm{H}\)-atom has an angular momentum \(=h\), according to the simple Bohr model. Angular momentum is a vector and hence there will be infinitely many orbits with the vector pointing in all possible directions. In actuality, this is not true,
CorrectIncorrect -
Question 21 of 50
21. Question
1 point(s)\(\mathrm{O}_2\) molecule consists of two oxygen atoms. In the molecule, nuclear force between the nuclei of the two atoms
CorrectIncorrect -
Question 22 of 50
22. Question
1 point(s)Two \(\mathrm{H}\) atoms in the ground state collide inelastically. The maximum amount by which their combined kinetic energy is reduced is
CorrectIncorrect -
Question 23 of 50
23. Question
1 point(s)A set of atoms in an excited state decays.
CorrectIncorrect -
Question 24 of 50
24. Question
1 point(s)Given the mass of iron nucleus as \(55.85 \mathrm{u}\) and \(\mathrm{A}=56\), find the nuclear density.
CorrectIncorrect -
Question 25 of 50
25. Question
1 point(s)Calculate the energy equivalent of \(1 \mathrm{~g}\) of substance.
CorrectIncorrect -
Question 26 of 50
26. Question
1 point(s)Suppose we consider a large number of containers each containing initially 10000 atoms of a radioactive material with a half-life of 1 year. After 1 year,
CorrectIncorrect -
Question 27 of 50
27. Question
1 point(s)The gravitational force between a \(\mathrm{H}\)-atom and another particle of mass \(m\) will be given by Newton’s law:
\(F=G \frac{M \cdot m}{r^2}\), where \(r\) is in \(\mathrm{km}\) andCorrectIncorrect -
Question 28 of 50
28. Question
1 point(s)When a nucleus in an atom undergoes a radioactive decay, the electronic energy levels of the atom
CorrectIncorrect -
Question 29 of 50
29. Question
1 point(s)\(M_{\mathrm{x}}\) and \(M_{\mathrm{y}}\) denote the atomic masses of the parent and the daughter nuclei respectively in a radioactive decay. The \(Q\)-value for a \(\beta^{-}\) decay is \(Q_1\) and that for a \(\beta^{+}\)decay is \(Q_2\). If \(m_e\) denotes the mass of an electron, then which of the following statements is correct?
CorrectIncorrect -
Question 30 of 50
30. Question
1 point(s)Tritium is an isotope of hydrogen whose nucleus Triton contains 2 neutrons and 1 proton. Free neutrons decay into \(p+\overline{\mathrm{e}}+\bar{v}\). If one of the neutrons in Triton decays, it would transform into \(\mathrm{He}^3\) nucleus. This does not happen. This is because
CorrectIncorrect -
Question 31 of 50
31. Question
1 point(s)Heavy stable nuclei have more neutrons than protons. This is because of the fact that
CorrectIncorrect -
Question 32 of 50
32. Question
1 point(s)In a nuclear reactor, moderators slow down the neutrons which come out in a fission process. The moderator used have light nuclei. Heavy nuclei will not serve the purpose because
CorrectIncorrect -
Question 33 of 50
33. Question
1 point(s)A piece of wood from a recently cut tree shows 20 decays per minute. A wooden piece of the same size placed in a museum (obtained from a tree cut many years back) shows 2 decays per minute. If half-life of \(\mathrm{C}^{14}\) is 5730 years, then the age of the wooden piece placed in the museum is approximately:
CorrectIncorrect -
Question 34 of 50
34. Question
1 point(s)A radioactive sample \(S_1\) having an activity \(5 \mu \mathrm{Ci}\) has twice the number of nuclei as another sample \(\mathrm{S}_2\) which has an activity of \(10 \mu \mathrm{Ci}\). The half-lives of \(\mathrm{S}_1\) and \(\mathrm{S}_2\) can be
CorrectIncorrect -
Question 35 of 50
35. Question
1 point(s)\({ }_{87}^{221} \mathrm{Ra}\) is a radioactive substance having half-life of 4 days. Find the probability that a nucleus undergoes decay after two half-lives
CorrectIncorrect -
Question 36 of 50
36. Question
1 point(s)A nucleus with mass number 220 initially at rest emits an \(\alpha\)-particle. If the \(Q\) value of the reaction is \(5.5 \mathrm{MeV}\), calculate the kinetic energy of the \(\alpha\)-particle
CorrectIncorrect -
Question 37 of 50
37. Question
1 point(s)The half-life of \({ }^{215} \mathrm{At}\) is \(100 \mu \mathrm{s}\). The time taken for the radioactivity of a sample of \({ }^{215}\) At to decay to \(1 / 16^{\text {th }}\) of its initial value is
CorrectIncorrect -
Question 38 of 50
38. Question
1 point(s)The electron emitted in beta radiation originates from
CorrectIncorrect -
Question 39 of 50
39. Question
1 point(s)Two radioactive materials \(X_1\) and \(X_2\) have decay constants \(10 \lambda\) and \(\lambda\) respectively. If initially, they have the same number of nuclei, then the ratio of the number of nuclei of \(X_1\) to that of \(X_2\) will be \(1 / e\) after a time
CorrectIncorrect -
Question 40 of 50
40. Question
1 point(s)Which of the following is a correct statement?
CorrectIncorrect -
Question 41 of 50
41. Question
1 point(s)The energy required to ionise a hydrogen-like ion in its ground state is 9 Rydbergs. What is the wavelength of the radiation emitted when the electron in this ion jumps from the second excited state to the ground state?
CorrectIncorrect -
Question 42 of 50
42. Question
1 point(s)Taking the wavelength of first Balmer line in hydrogen spectrum \((\mathrm{n}=3\) to \(\mathrm{n}=2)\) as \(660 \mathrm{~nm}\), the wavelength of the \(2^{\text {nd }}\) Balmer line \((n=4\) to \(n=2)\) will be;
CorrectIncorrect -
Question 43 of 50
43. Question
1 point(s)A hydrogen atom, initially in the ground state is excited by absorbing a photon of wavelength \(980 Å\). The radius of the atom in the excited state, in terms of Bohr radius \(\mathrm{a}_0\). will be:
CorrectIncorrect -
Question 44 of 50
44. Question
1 point(s)In a hydrogen-like atom, when an electron jumps from the M-shell to the L-shell, the wavelength of emitted radiation is 1. If an electron jumps from \(\mathrm{N}\)-shell to the \(\mathrm{L}\) shell, the wavelength of emitted radiation will be:
CorrectIncorrect -
Question 45 of 50
45. Question
1 point(s)The energy required to remove the electron from a singly ionized Helium atom is 2.2 times the energy required to remove an electron from Helium atom. The total energy required to ionize the Helium atom completely is
CorrectIncorrect -
Question 46 of 50
46. Question
1 point(s)Some energy levels of a molecule are shown in the figure. The ratio of the wavelengths \(r=\lambda_1 / \lambda_2\), is given by
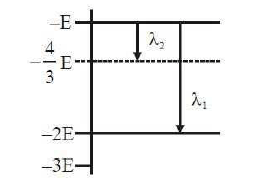 CorrectIncorrect
CorrectIncorrect -
Question 47 of 50
47. Question
1 point(s)A hydrogen atom makes a transition from \(n=2\) to \(n=1\) and emits a photon. This photon strikes a doubly ionized lithium atom \((z=3)\) in excited state and completely removes the orbiting electron. The least quantum number for the excited state of the ion for the process is:
CorrectIncorrect -
Question 48 of 50
48. Question
1 point(s)A particle A of mass ‘ \(\mathrm{m}\) ‘ and charge ‘ \(\mathrm{q}\) ‘ is accelerated by a potential difference of \(50 \mathrm{v}\) Another particle B of mass ‘ \(4 \mathrm{~m}\) ‘ and charge ‘q’ is accelerated by a potential differnce of \(2500 \mathrm{~V}\). The ratio of de-Broglie wavelength \(\frac{\lambda_A}{\lambda_B}\) is
CorrectIncorrect -
Question 49 of 50
49. Question
1 point(s)A proton has kinetic energy \(E=100 \mathrm{keV}\) which is equal to that of a photon. The wavelength of photon is \(\lambda_2\) and that of proton is \(\lambda_1\). The ration of \(\lambda_2 / \lambda_1\) is proportional to
CorrectIncorrect -
Question 50 of 50
50. Question
1 point(s)For which of the following particles will it be most difficult to experimentally verify the de-Broglie relationship?
CorrectIncorrect