JEE Physics Test Series Quiz-5
Quiz Summary
0 of 50 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 50 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 50
1. Question
1 point(s)An electron is moving along \(+x\) direction with a velocity of \(6 \times 10^6 \mathrm{~ms}^{-1}\). It enters a region of uniform electric field of \(300 \mathrm{~V} / \mathrm{cm}\) pointing along \(+y\) direction. The magnitude and direction of the magnetic field set up in this region such that the electron keeps moving along the \(x\) direction will be
CorrectIncorrect -
Question 2 of 50
2. Question
1 point(s)A particle of charge \(q\) and mass \(m\) is moving with a velocity \(-v \hat{i}(v \neq 0)\) towards a large screen placed in the \(\mathrm{Y}-\mathrm{Z}\) plane at a distance \(d\). If there is a magnetic field \(\vec{B}=B_0 \hat{k}\), the minimum value of \(v\) for which the particle wii not hit the screen is:
CorrectIncorrect -
Question 3 of 50
3. Question
1 point(s)A charged particle carrying charge \(1 \mu \mathrm{C}\) is moving with velocity \((2 \hat{i}+3 \hat{j}+4 \hat{k}) \mathrm{ms}^{-1}\). If an external magnetic field of \((5 \hat{i}+3 \hat{j}-6 \hat{k}) \times 10^{-3} \mathrm{~T}\) exists in the region where the particle is moving then the force on the particle is \(\vec{F} \times 10^{-9} \mathrm{~N} \text {. The vector } \vec{F} \text { is : }\)
CorrectIncorrect -
Question 4 of 50
4. Question
1 point(s)A beam of protons with speed \(4 \times 10^5 \mathrm{~ms}^{-1}\) enters a uniform magnetic field of \(0.3 \mathrm{~T}\) at an angle of \(60^{\circ}\) to the magnetic field. The pitch of the resulting helical path of protons is close to: (Mass of the proton \(=1.67 \times 10^{-27} \mathrm{~kg}\), the charge of the proton \(=1.69 \times 10^{-19} \mathrm{C}\) )
CorrectIncorrect -
Question 5 of 50
5. Question
1 point(s)The figure shows a region of length ‘ \(l\) ‘ with a uniform magnetic field of \(0.3 \mathrm{~T}\) in it and a proton entering the region with velocity \(4 \times 10^5 \mathrm{~ms}^{-1}\) making an angle \(60^{\circ}\) with the field. If the proton completes 10 revolution by the time it cross the region shown, ‘ \(l\) ‘ is close to (mass of proton \(=\) \(1.67 \times 10^{-27} \mathrm{~kg}\), charge of the proton \(=1.6 \times 10^{-19} \mathrm{C}\) )
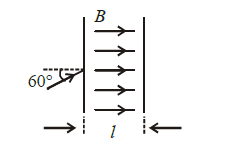 CorrectIncorrect
CorrectIncorrect -
Question 6 of 50
6. Question
1 point(s)A particle having the same charge as of electron moves in a circular path of radius \(0.5 \mathrm{~cm}\) under the influence of a magnetic field of \(0.5 \mathrm{~T}\). If an electric field of \(100 \mathrm{~V} / \mathrm{m}\) makes it to move in a straight path then the mass of the particle is (Given charge of electron \(=1.6 \times 10^{-19} \mathrm{C}\) )
CorrectIncorrect -
Question 7 of 50
7. Question
1 point(s)A proton, an electron, and a Helium nucleus, have the same energy. They are in circular orbits in a plane due to magnetic field perpendicular to the plane. Let \(r_p, r_e\) and \(r_{H e}\) be their respective radii, then,
CorrectIncorrect -
Question 8 of 50
8. Question
1 point(s)A proton and an \(\alpha\)-particle (with their masses in the ratio of \(1: 4\) and charges in the ratio \(1: 2\) ) are accelerated from rest through a potential difference \(V\). If a uniform magnetic field (B) is set up perpendicular to their velocities, the ratio of the radii \(r_p: r_\alpha\) of the circular paths described by them will be:
CorrectIncorrect -
Question 9 of 50
9. Question
1 point(s)In an experiment, electrons are accelerated, from rest, by applying a voltage of \(500 \mathrm{~V}\). Calculate the radius of the path if a magnetic field \(100 \mathrm{mT}\) is then applied. [Charge of the electron \(=1.6 \times 10^{-19} \mathrm{C}\) Mass of the electron \(\left.=9.1 \times 10^{-31} \mathrm{~kg}\right]\)
CorrectIncorrect -
Question 10 of 50
10. Question
1 point(s)The region between \(y=0\) and \(y=\mathrm{d}\) contains a magnetic field \(\vec{B}=B \hat{z}\). A particle of mass \(m\) and charge \(q\) enters the region with a velocity \(\vec{v}=v \hat{i}\). if \(\mathrm{d}=\frac{\mathrm{m} v}{2 \mathrm{qB}}\), the acceleration of the charged particle at the point of its emergence at the other side is:
CorrectIncorrect -
Question 11 of 50
11. Question
1 point(s)An electron, a proton and an alpha particle having the same kinetic energy are moving in circular orbits of radii \(r_{\mathrm{e}}\), \(r_{\mathrm{p}}, r_\alpha\) respectively in a uniform magnetic field \(\mathrm{B}\). The relation between \(r_e, r_p, r_\alpha\) is:
CorrectIncorrect -
Question 12 of 50
12. Question
1 point(s)A negative test charge is moving near a long straight wire carrying a current. The force acting on the test charge is parallel to the direction of the current. The motion of the charge is:
CorrectIncorrect -
Question 13 of 50
13. Question
1 point(s)Consider a thin metallic sheet perpendicular to the plane of the paper moving with speed ‘ \(v\) ‘ in a uniform magnetic field B going into the plane of the paper (See figure). If charge densities \(\sigma_1\) and \(\sigma_2\) are induced on the left and right surfaces, respectively, of the sheet then (ignore fringe effects):
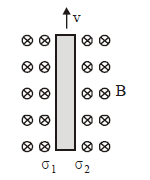 CorrectIncorrect
CorrectIncorrect -
Question 14 of 50
14. Question
1 point(s)A proton (mass \(\mathrm{m}\) ) accelerated by a potential difference \(\mathrm{V}\) flies through a uniform transverse magnetic field \(B\). The field occupies a region of space by width ‘ \(d\) ‘. If \(\alpha\) be the angle of deviation of proton from the initial direction of motion (see figure), the value of \(\sin \alpha\) will be:
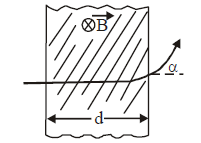 CorrectIncorrect
CorrectIncorrect -
Question 15 of 50
15. Question
1 point(s)A particle of charge \(16 \times 10^{-16} \mathrm{C}\) moving with velocity \(10 \mathrm{~ms}^{-1}\) along \(x\)-axis enters a region where magnetic field of induction \(\vec{B}\) is along the \(y\)-axis and an electric field of magnitude \(10^4 \mathrm{Vm}^{-1}\) is along the negative \(z\)-axis. If the charged particle continues moving along \(x\)-axis, the magnitude of \(\vec{B}\) is:
CorrectIncorrect -
Question 16 of 50
16. Question
1 point(s)A particle of mass \(m\) and charge \(q\) moves with a constant velocity \(\mathrm{v}\) along the positive \(x\)-direction. It enters a region containing a uniform magnetic field \(B\) directed along the negative \(z\)-direction, extending from \(x=a\) to \(x=b\). The minimum value of \(v\) required so that the particle can just enter the region \(x>b\) is
CorrectIncorrect -
Question 17 of 50
17. Question
1 point(s)An ionized gas contains both positive and negative ions. If it is subjected simultaneously to an electric field along the \(+\mathrm{x}\)-direction and a magnetic field along the \(+z\)-direction, then
CorrectIncorrect -
Question 18 of 50
18. Question
1 point(s)A particle of charge \(q\) and mass \(m\) moves in a circular orbit of radius \(r\) with angular speed \(\omega\). The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
CorrectIncorrect -
Question 19 of 50
19. Question
1 point(s)A charged particle is released from rest in a region of steady and uniform electric and magnetic fields which are parallel to each other. The particle will move in a
CorrectIncorrect -
Question 20 of 50
20. Question
1 point(s)A battery is connected between two points \(A\) and \(B\) on the circumference of a uniform conducting ring of radius \(r\) and resistance \(R\). One of the \(\operatorname{arcs} A B\) of the ring subtends an angle \(\theta\) at the centre. The value of the magnetic induction at the centre due to the current in the ring is
CorrectIncorrect -
Question 21 of 50
21. Question
1 point(s)Two particles \(X\) and \(Y\) having equal charges, after being accelerated through the same potential difference, enter a region of uniform magnetic field and describe circular paths of radii \(R_1\) and \(R_2\) respectively. The ratio of the mass of \(X\) to that of \(Y\) is
CorrectIncorrect -
Question 22 of 50
22. Question
1 point(s)Magnitude of magnetic field (in SI units) at the centre of a hexagonal shape coil of side \(10 \mathrm{~cm}, 50\) turns and carrying current \(I\) (Ampere) in units of \(\frac{\mu_0 I}{\pi}\) is:
CorrectIncorrect -
Question 23 of 50
23. Question
1 point(s)One of the two identical conducting wires of length \(\mathrm{L}\) is bent in the form of a circular loop and the other one into a circular coil of \(\mathrm{N}\) identical turns. If the same current is passed in both, the ratio of the magnetic field at the central of the loop \(\left(B_1\right)\) to that at the centre of the coil \(\left(\mathrm{B}_{\mathrm{C}}\right)\), i.e., \(\frac{\mathrm{B}_{\mathrm{L}}}{\mathrm{B}_{\mathrm{C}}}\) will be:
CorrectIncorrect -
Question 24 of 50
24. Question
1 point(s)The dipole moment of a circular loop carrying a current I, is \(\mathrm{m}\) and the magnetic field at the centre of the loop is \(B_1\). When the dipole moment is doubled by keeping the current constant, the magnetic field at the centre of the loop is \(B_2\). The ratio \(\frac{B_1}{B_2}\) is:
CorrectIncorrect -
Question 25 of 50
25. Question
1 point(s)Two identical wires A and B, each of length ‘ \(l\) ‘, carry the same current \(I\). Wire \(A\) is bent into a circle of radius \(R\) and wire \(B\) is bent to form a square of side ‘ \(a\) ‘. If \(B_A\) and \(B_B\) are the values of magnetic field at the centres of the circle and square respectively, then the ratio \(\frac{B_A}{B_B}\) is:
CorrectIncorrect -
Question 26 of 50
26. Question
1 point(s)Consider two thin identical conducting wires covered with very thin insulating material. One of the wires is bent into a loop and produces magnetic field \(B_1\), at its centre when a current \(I\) passes through it. The ratio \(B_1: B_2\) is:
CorrectIncorrect -
Question 27 of 50
27. Question
1 point(s)An electric current is flowing through a circular coil of radius \(R\). The ratio of the magnetic field at the centre of the coil and that at a distance \(2 \sqrt{2} R\) from the centre of the coil and on its axis is :
CorrectIncorrect -
Question 28 of 50
28. Question
1 point(s)A small circular loop of conducting wire has radius a and carries current \(I\). It is placed in a uniform magnetic field B perpendicular to its plane such that when rotated slightly about its diameter and released, it starts performing simple harmonic motion of time period T. If the mass of the loop is \(m\) then :
CorrectIncorrect -
Question 29 of 50
29. Question
1 point(s)A circular coil having \(N\) turns and radius \(r\) carries a current \(I\). It is held in the \(\mathrm{XZ}\) plane in a magnetic field \(\mathrm{B}\). The torque on the coil due to the magnetic field is:
CorrectIncorrect -
Question 30 of 50
30. Question
1 point(s)A charge \(\mathrm{q}\) is spread uniformly over an insulated loop of radius \(r\). If it is rotated with an angular velocity \(\omega\) with respect to normal axis then the magnetic moment of the loop is
CorrectIncorrect -
Question 31 of 50
31. Question
1 point(s)A moving coil galvanometer has resistance \(50 \Omega\) and it indicates full deflection at \(4 \mathrm{~mA}\) current. A voltmeter is made using this galvanometer and a \(5 \mathrm{k} \Omega\) resistance. The maximum voltage, that can be measured using this voltmeter, will be close to:
CorrectIncorrect -
Question 32 of 50
32. Question
1 point(s)A galvanometer, whose resistance is \(50 \mathrm{ohm}\), has 25 divisions in it. When a current of \(4 \times 10^{-4} \mathrm{~A}\) passes through it, its needle (pointer) deflects by one division. To use this galvanometer as a voltmeter of range \(2.5 \mathrm{~V}\), it should be connected to a resistance of :
CorrectIncorrect -
Question 33 of 50
33. Question
1 point(s)A small bar magnet placed with its axis at \(30^{\circ}\) with an external field of \(0.06 \mathrm{~T}\) experiences a torque of \(0.018 \mathrm{Nm}\). The minimum work required to rotate it from its stable to unstable equilibrium position is
CorrectIncorrect -
Question 34 of 50
34. Question
1 point(s)A circular coil has moment of inertia \(0.8 \mathrm{~kg} \mathrm{~m}^2\) around any diameter and is carrying current to produce a magnetic moment of \(20 \mathrm{Am}^2\). The coil is kept initially in a vertical position and it can rotate freely around a horizontal diameter. When a uniform magnetic field of \(4 \mathrm{~T}\) is applied along the vertical, it starts rotating around its horizontal diameter. The angular speed the coil acquires after rotating by \(60^{\circ}\) will be :
CorrectIncorrect -
Question 35 of 50
35. Question
1 point(s)A magnet of total magnetic moment \(10^{-2} \hat{i} \quad \mathrm{~A}-\mathrm{m}^2\) is placed in a time varying magnetic field, \(\mathrm{B} \hat{i}(\cos \omega \mathrm{t})\) where \(B=1\) Tesla and \(\omega=0.125 \mathrm{rad} / \mathrm{s}\). The work done for reversing the direction of the magnetic moment at \(\mathrm{t}=1\) second, is:
CorrectIncorrect -
Question 36 of 50
36. Question
1 point(s)A magnetic dipole is acted upon by two magnetic fields which are inclined to each other at an angle of \(75^{\circ}\). One of the fields has a magnitude of \(15 \mathrm{mT}\). The dipole attains stable equilibrium at an angle of \(30^{\circ}\) with this field. The magnitude of the other field (in \(\mathrm{mT}\) ) is close to:
CorrectIncorrect -
Question 37 of 50
37. Question
1 point(s)A \(25 \mathrm{~cm}\) long solenoid has radius \(2 \mathrm{~cm}\) and 500 total number of turns. It carries a current of \(15 \mathrm{~A}\). If it is equivalent to a magnet of the same size and magnetization \(\overrightarrow{\mathrm{M}}\) (magnetic moment/volume), then \(|\overrightarrow{\mathrm{M}}|\) is :
CorrectIncorrect -
Question 38 of 50
38. Question
1 point(s)The magnetic field lines due to a bar magnet are correctly shown in
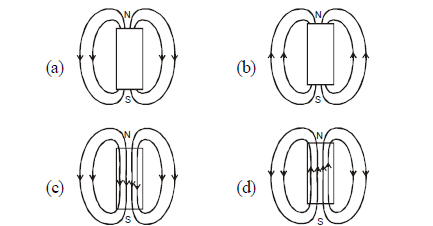 CorrectIncorrect
CorrectIncorrect -
Question 39 of 50
39. Question
1 point(s)A particle of charge \(q\) and mass \(m\) moves in a circular orbit of radius \(r\) with angular speed \(\omega\). The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
CorrectIncorrect -
Question 40 of 50
40. Question
1 point(s)A magnetic needle is kept in a non-uniform magnetic field. It experiences
CorrectIncorrect -
Question 41 of 50
41. Question
1 point(s)A paramagnetic material has \(10^{28}\) atoms \(/ \mathrm{m}^3\). Its magnetic susceptibility at temperature \(350 \mathrm{~K}\) is \(2.8 \times 10^{-4}\). Its susceptibility at \(300 \mathrm{~K}\) is:
CorrectIncorrect -
Question 42 of 50
42. Question
1 point(s)A bar magnet is demagnetized by inserting it inside a solenoid of length \(0.2 \mathrm{~m}, 100\) turns, and carrying a current of \(5.2 \mathrm{~A}\). The coercivity of the bar magnet is:
CorrectIncorrect -
Question 43 of 50
43. Question
1 point(s)Three identical bars A, B and C are made of different magnetic materials. When kept in a uniform magnetic field, the field lines around them look as follows:
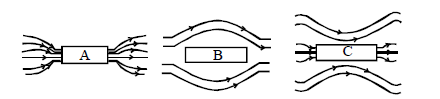
Make the correspondence of these bars with their material being diamagnetic (D), ferromagnetic (F) and paramagnetic (P):
CorrectIncorrect -
Question 44 of 50
44. Question
1 point(s)The earth’s magnetic field lines resemble that of a dipole at the centre of the earth. If the magnetic moment of this dipole is close to \(8 \times 10^{22} \mathrm{Am}^2\), the value of earth’s magnetic field near the equator is close to (radius of the earth \(=6.4 \times 10^6 \mathrm{~m}\) )
CorrectIncorrect -
Question 45 of 50
45. Question
1 point(s)A magnetic needle of magnetic moment \(6.7 \times 10^{-2} \mathrm{Am}^2\) and moment of inertia \(7.5 \times 10^{-6} \mathrm{~kg} \mathrm{~m}^2\) is performing simple harmonic oscillations in a magnetic field of \(0.01 \mathrm{~T}\). Time taken for 10 complete oscillations is :
CorrectIncorrect -
Question 46 of 50
46. Question
1 point(s)Four bulbs \(\mathrm{B}_1, \mathrm{~B}_2, \mathrm{~B}_3\) and \(\mathrm{B}_4\) of \(100 \mathrm{~W}\) each are connected to \(220 \mathrm{~V}\) main as shown in the figure.
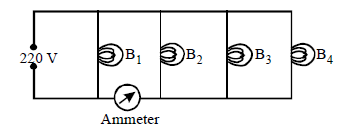
The reading in an ideal ammeter will be:
CorrectIncorrect -
Question 47 of 50
47. Question
1 point(s)In the circuit shown, the resistance \(\mathrm{r}\) is a variable resistance. If for \(r=f R\), the heat generation in \(r\) is maximum then the value of \(f\) is :
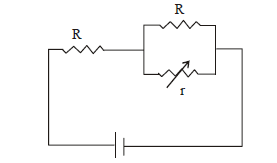 CorrectIncorrect
CorrectIncorrect -
Question 48 of 50
48. Question
1 point(s)The figure shows three circuits I, II and III which are connected to a \(3 \mathrm{~V}\) battery. If the powers dissipated by the configurations I, II and III are \(\mathrm{P}_1, \mathrm{P}_2\) and \(\mathrm{P}_3\) respectively, then:
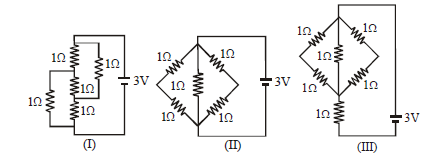 CorrectIncorrect
CorrectIncorrect -
Question 49 of 50
49. Question
1 point(s)Which of the four resistances \(P, Q, R\) and \(S\) generate the greatest amount of heat when a current flows from \(\mathrm{A}\) to \(\mathrm{B}\)?
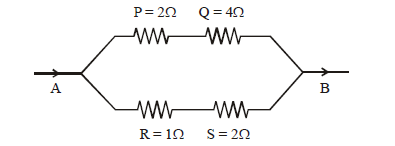 CorrectIncorrect
CorrectIncorrect -
Question 50 of 50
50. Question
1 point(s)Incandescent bulbs are designed by keeping in mind that the resistance of their filament increases with the increase in temperature. If at room temperature, \(100 \mathrm{~W}, 60 \mathrm{~W}\) and \(40 \mathrm{~W}\) bulbs have filament resistances \(R_{100}, R_{60}\) and \(R_{40}\), respectively the relation between these resistances is
CorrectIncorrect