JEE Physics Test Series Quiz-4
Quiz Summary
0 of 50 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 50 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 50
1. Question
1 point(s)An electron, a doubly ionized helium ion \(\left(\mathrm{He}^{++}\right)\)and a proton are having the same kinetic energy. The relation between their respective de-Broglie wavelengths \(\lambda_{\mathrm{e}}, \lambda_{\mathrm{He}++}\) and \(\lambda_{\mathrm{p}}\) is:
CorrectIncorrect -
Question 2 of 50
2. Question
1 point(s)A particle is moving 5 times as fast as an electron. The ratio of the de-Broglie wavelength of the particle to that of the electron is \(1.878 \times 10^{-4}\). The mass of the particle is close to:
CorrectIncorrect -
Question 3 of 50
3. Question
1 point(s)A particle moving with kinetic energy \(\mathrm{E}\) has de Broglie wavelength \(\lambda\). If energy \(\Delta \mathrm{E}\) is added to its energy, the wavelength become \(\frac{\lambda}{2}\). Value of \(\Delta \mathrm{E}\), is:
CorrectIncorrect -
Question 4 of 50
4. Question
1 point(s)A particle ‘ \(\mathrm{P}\) ‘ is formed due to a completely inelastic collision of particles ‘ \(x\) ‘ and ‘ \(y\) ‘ having de-Broglie wavelengths ‘ \(\gamma_x\) ‘ and ‘ \(\gamma_y\) ‘ respectively. If \(x\) and \(y\) were moving in opposite directions, then the de-Broglie wavelength of ‘ \(P\) ‘ is:
CorrectIncorrect -
Question 5 of 50
5. Question
1 point(s)A particle of mass \(M\) at rest decays into two particles of masses \(m_1\) and \(m_2\), having non-zero velocities. The ratio of the de Broglie wavelengths of the particles, \(\lambda_1 / \lambda_2\), is
CorrectIncorrect -
Question 6 of 50
6. Question
1 point(s)Two sources of light emit \(\mathrm{X}\)-rays of wavelength \(1 \mathrm{~nm}\) and visible light of wavelength \(500 \mathrm{~nm}\), respectively. Both the sources emit light of the same power \(200 \mathrm{~W}\). The ratio of the number density of photons of X-rays to the number density of photons of the visible light of the given wavelengths is:
CorrectIncorrect -
Question 7 of 50
7. Question
1 point(s)The stopping potential \(\mathrm{V}_0\) (in volt) as a function of frequency (v) for a sodium emitter, is shown in the figure. The work function of sodium, from the data plotted in the figure, will be: (Given : Planck’s constant \((h)=6.63 \times 10^{-34} \mathrm{Js}\), electron charge \(e=1.6 \times 10^{-19} \mathrm{C}\) )
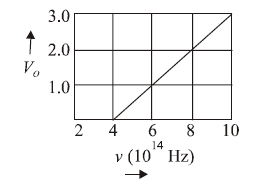 CorrectIncorrect
CorrectIncorrect -
Question 8 of 50
8. Question
1 point(s)A metal plate of area \(1 \times 10^{-4} \mathrm{~m}^2\) is illuminated by a radiation of intensity \(16 \mathrm{~mW} / \mathrm{m}^2\). The work function of the metal is \(5 \mathrm{eV}\). The energy of the incident photons is \(10 \mathrm{eV}\) and only \(10 \%\) of it produces photo electrons. The number of emitted photo electrons per second and their maximum energy, respectively, will be:
\(
\left[1 \mathrm{eV}=1.6 \times 10^{-19} \mathrm{~J}\right]
\)CorrectIncorrect -
Question 9 of 50
9. Question
1 point(s)A photoelectric surface is illuminated successively by monochromatic light of wavelengths \(\lambda\) and \(\frac{\lambda}{2}\). If the maximum kinetic energy of the emitted photoelectrons in the second case is 3 times that in the first case, the work function of the surface is :
CorrectIncorrect -
Question 10 of 50
10. Question
1 point(s)Match List – I (Fundamental Experiment) with List – II (its conclusion) and select the correct option from the choice given below the list:
\(
\begin{array}{|l|l|}
\hline {\text { List-I }} & {\text { List-II }} \\
\hline \begin{array}{l}
\text { A. Franck-Hertz } \\
\text { Experiment }
\end{array} & \text { (i) Particle nature of light } \\
\hline \begin{array}{l}
\text { B. Photo-electric } \\
\text { experiment }
\end{array} & \text { (ii) Discrete energy levels of atom } \\
\hline \begin{array}{l}
\text { C. Davison-Germer } \\
\text { experiment }
\end{array} & \text { (iii) Wave nature of electron } \\
\hline & \text { (iv) Structure of atom } \\
\hline
\end{array}
\)CorrectIncorrect -
Question 11 of 50
11. Question
1 point(s)The anode voltage of a photocell is kept fixed. The wavelength \(\lambda\) of the light falling on the cathode is gradually changed. The plate current I of the photocell varies as follows :
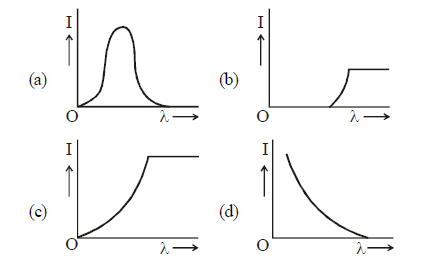 CorrectIncorrect
CorrectIncorrect -
Question 12 of 50
12. Question
1 point(s)A pulse of light of duration \(100 \mathrm{~ns}\) is absorbed completely by a small object initially at rest. Power of the pulse is 30 \(\mathrm{mW}\) and the speed of light is \(3 \times 10^8 \mathrm{~ms}^{-1}\). The final momentum of the object is
CorrectIncorrect -
Question 13 of 50
13. Question
1 point(s)\(K_\alpha\) wavelength emitted by an atom of atomic number \(Z=11\) is \(\lambda\). Find the atomic number for an atom that emits \(K_\alpha\) radiation with wavelength \(4 \lambda\).
CorrectIncorrect -
Question 14 of 50
14. Question
1 point(s)In a photoelectric experiment, anode potential is plotted against plate current.
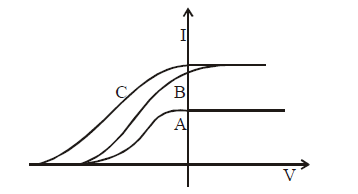 CorrectIncorrect
CorrectIncorrect -
Question 15 of 50
15. Question
1 point(s)The potential difference applied to an X-ray tube is \(5 \mathrm{kV}\) and the current through it is \(3.2 \mathrm{~mA}\). Then the number of electrons striking the target per second is
CorrectIncorrect -
Question 16 of 50
16. Question
1 point(s)The work function of a substance is \(4.0 \mathrm{eV}\). The longest wavelength of light that can cause photoelectron emission from this substance is approximately
CorrectIncorrect -
Question 17 of 50
17. Question
1 point(s)The X-ray beam coming from an X-ray tube will be
CorrectIncorrect -
Question 18 of 50
18. Question
1 point(s)The graph which depicts the results of Rutherford’s gold foil experiment with
\(\alpha\)-particles is:
\(\theta\) : Scattering angle
\(Y\): Number of scattered \(\alpha\)-particles detected (Plots are schematic and not to scale)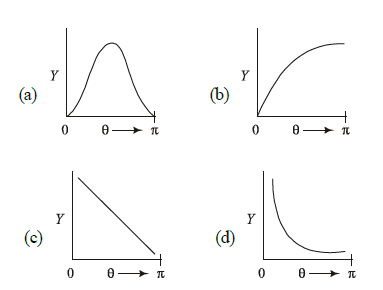 CorrectIncorrect
CorrectIncorrect -
Question 19 of 50
19. Question
1 point(s)In a hydrogen atom, the electron makes a transition from \((n+1)^{\text {th }}\) level to the \(n^{\text {th }}\) level. If \(n \gg 1\), the frequency of radiation emitted is proportional to:
CorrectIncorrect -
Question 20 of 50
20. Question
1 point(s)The time period of revolution of electron in its ground state orbit in a hydrogen atom is \(1.6 \times 10^{-16} \mathrm{~s}\). The frequency of revolution of the electron in its first excited state (in \(s^{-1}\) ) is:
CorrectIncorrect -
Question 21 of 50
21. Question
1 point(s)The electron in a hydrogen atom first jumps from the third excited state to the second excited state and subsequently to the first excited state. The ratio of the respective wavelengths, \(\lambda_1 / \lambda_2\), of the photons emitted in this process is:
CorrectIncorrect -
Question 22 of 50
22. Question
1 point(s)Radiation coming from transitions \(n=2\) to \(n=1\) of hydrogen atoms fall on \(\mathrm{He}^{+}\)ions in \(n=1\) and \(n=2\) states. The possible transition of helium ions as they absorb energy from the radiation is :
CorrectIncorrect -
Question 23 of 50
23. Question
1 point(s)If the series limit frequency of the Lyman series is \(\nu_1\), then the series limit frequency of the P-fund series is:
CorrectIncorrect -
Question 24 of 50
24. Question
1 point(s)According to Bohr’s theory, the time-averaged magnetic field at the centre (i.e. nucleus) of a hydrogen atom due to the motion of electrons in the \(\mathrm{n}^{\text {th }}\) orbit is proportional to : ( \(\mathrm{n}=\) principal quantum number)
CorrectIncorrect -
Question 25 of 50
25. Question
1 point(s)The binding energy of the electron in a hydrogen atom is \(13.6 \mathrm{eV}\), the energy required to remove the electron from the first excited state of \(\mathrm{Li}^{++}\)is:
CorrectIncorrect -
Question 26 of 50
26. Question
1 point(s)The largest wavelength in the ultraviolet region of the hydrogen spectrum is \(122 \mathrm{~nm}\). The smallest wavelength in the infrared region of the hydrogen spectrum (to the nearest integer) is
CorrectIncorrect -
Question 27 of 50
27. Question
1 point(s)If the atom \(100 \mathrm{Fm}^{257}\) follows the Bohr model and the radius of \({ }_{100} \mathrm{Fm}^{257}\) is \(n\) times the Bohr radius, then find \(n\).
CorrectIncorrect -
Question 28 of 50
28. Question
1 point(s)The transition from the state \(n=4\) to \(n=3\) in a hydrogenlike atom results in ultraviolet radiation. Infrared radiation will be obtained in the transition
CorrectIncorrect -
Question 29 of 50
29. Question
1 point(s)The electron in a hydrogen atom makes a transition from an excited state to the ground state. Which of the following statements is true?
CorrectIncorrect -
Question 30 of 50
30. Question
1 point(s)In hydrogen spectrum the wavelength of \(\mathrm{H}_\alpha\) line is 656 \(\mathrm{nm}\), whereas in the spectrum of a distant galaxy, \(\mathrm{H}_\alpha\) line wavelength is \(706 \mathrm{~nm}\). The estimated speed of the galaxy with respect to earth is,
CorrectIncorrect -
Question 31 of 50
31. Question
1 point(s)As per Bohr model, the minimum energy (in \(\mathrm{eV}\) ) required to remove an electron from the ground state of doubly ionized \(\mathrm{Li}\) atom \((Z=3)\) is
CorrectIncorrect -
Question 32 of 50
32. Question
1 point(s)Consider the spectral line resulting from the transition \(n=2 \rightarrow n=1\) in the atoms and ions given below. The shortest wavelength is produced by
CorrectIncorrect -
Question 33 of 50
33. Question
1 point(s)The radius \(R\) of a nucleus of mass number \(A\) can be estimated by the formula \(R=\left(1.3 \times 10^{-15}\right) A^{1 / 3} \mathrm{~m}\). It follows that the mass density of a nucleus is of the order of : \(\left(M_{\text {prot }} \cong M_{\text {neut }} \simeq 1.67 \times 10^{-27} \mathrm{~kg}\right)\)
CorrectIncorrect -
Question 34 of 50
34. Question
1 point(s)The ratio of the mass densities of nuclei of \({ }^{40} \mathrm{Ca}\) and \({ }^{16} \mathrm{O}\) is close to :
CorrectIncorrect -
Question 35 of 50
35. Question
1 point(s)An unstable heavy nucleus at rest breaks into two nuclei which move away with velocities in the ratio of \(8: 27\). The ratio of the radii of the nuclei (assumed to be spherical) is:
CorrectIncorrect -
Question 36 of 50
36. Question
1 point(s)For uranium nucleus how does its mass vary with volume?
CorrectIncorrect -
Question 37 of 50
37. Question
1 point(s)Order of magnitude of density of uranium nucleus is, \(\left[m_p=1.67 \times 10^{-27} \mathrm{~kg}\right.\) ]
CorrectIncorrect -
Question 38 of 50
38. Question
1 point(s)Find the Binding energy per neucleon for \({ }_{50}^{120} \mathrm{Sn}\). Mass of proton \(m_p=1.00783 \mathrm{U}\), mass of neutron \(m_n=1.00867 \mathrm{U}\) and mass of tin nucleus \(m_{\mathrm{Sn}}=119.902199 \mathrm{U}\). (take \(1 \mathrm{U}=931 \mathrm{MeV}\) )
CorrectIncorrect -
Question 39 of 50
39. Question
1 point(s)In a reactor, \(2 \mathrm{~kg}\) of \({ }_{92} \mathrm{U}^{235}\) fuel is fully used up in 30 days. The energy released per fission is \(200 \mathrm{MeV}\). Given that the Avogadro number, \(\mathrm{N}=6.023 \times 10^{26}\) per kilo mole and \(1 \mathrm{eV}\) \(=1.6 \times 10^{-19} \mathrm{~J}\). The power output of the reactor is close to:
CorrectIncorrect -
Question 40 of 50
40. Question
1 point(s)Imagine that a reactor converts all given mass into energy and that it operates at a power level of \(10^{\circ}\) watt. The mass of the fuel consumed per hour in the reactor will be : (velocity of light, c is \(3 \times 10^8 \mathrm{~m} / \mathrm{s}\) )
CorrectIncorrect -
Question 41 of 50
41. Question
1 point(s)When Uranium is bombarded with neutrons, it undergoes fission. The fission reaction can be written as : \({ }_{92} \mathrm{U}^{235}+{ }_0 n^1 \rightarrow{ }_{56} \mathrm{Ba}^{141}+{ }_{36} \mathrm{Kr}^{92}+3 x+\mathrm{Q}\) (energy) where three particles named \(x\) are produced and energy \(Q\) is released. What is the name of the particle \(x\) ?
CorrectIncorrect -
Question 42 of 50
42. Question
1 point(s)If a star can convert all the He nuclei completely into oxygen nuclei, the energy released per oxygen nuclei is [Mass of He nucleus is \(4.0026 \mathrm{amu}\) and mass of Oxygen nucleus is \(15.9994 \mathrm{~amu}\) ]
CorrectIncorrect -
Question 43 of 50
43. Question
1 point(s)Fast neutrons can easily be slowed down by
CorrectIncorrect -
Question 44 of 50
44. Question
1 point(s)During a nuclear fusion reaction
CorrectIncorrect -
Question 45 of 50
45. Question
1 point(s)A radioactive nucleus decays by two different processes. The half-life for the first process is \(10 \mathrm{~s}\) and that for the second is \(100 \mathrm{~s}\). The effective half-life of the nucleus is close to :
CorrectIncorrect -
Question 46 of 50
46. Question
1 point(s)In a radioactive material, fraction of active material remaining after time \(t\) is \(9 / 16\). The fraction that was remaining after \(t / 2\) is :
CorrectIncorrect -
Question 47 of 50
47. Question
1 point(s)Two radioactive substances \(A\) and \(B\) have decay constants \(5 \lambda\) and \(\lambda\) respectively. At \(t=0\), a sample has the same number of the two nuclei. The time taken for the ratio of the number of nuclei to become \(\left(\frac{1}{e}\right)^2\) will be:
CorrectIncorrect -
Question 48 of 50
48. Question
1 point(s)In a radioactive decay chain, the initial nucleus is \({ }_{90}^{232} \mathrm{Th}\). At the end there are \(6 \alpha\)-particles and \(4 \beta\)-particles which are emitted. If the end nucleus is \({ }_{\mathrm{Z}}^{\mathrm{A}} \mathrm{X}, \mathrm{A}\) and \(\mathrm{Z}\) are given by:
CorrectIncorrect -
Question 49 of 50
49. Question
1 point(s)Using a nuclear counter the count rate of emitted particles from a radioactive source is measured. At \(t=0\) it was 1600 counts per second and \(t=8\) seconds it was 100 counts per second. The count rate observed, as counts per second, at \(\mathrm{t}=6\) seconds is close to:
CorrectIncorrect -
Question 50 of 50
50. Question
1 point(s)Let \(N_\beta\) be the number of \(\beta\) particles emitted by 1 gram of \(\mathrm{Na}^{24}\) radioactive nuclei (half-life \(=15 \mathrm{hrs}\) ) in 7.5 hours, \(\mathrm{N}_\beta\) is close to (Avogadro number \(=6.023 \times 10^{23} / \mathrm{g}\). mole):
CorrectIncorrect