JEE Physics Test Series Quiz-3
Quiz Summary
0 of 50 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 50 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 50
1. Question
What is the force between two small charged spheres having charges of \(2 \times 10^{-7} \mathrm{C}\) and \(3 \times 10^{-7} \mathrm{C}\) placed \(30 \mathrm{~cm}\) apart in air?
CorrectIncorrect -
Question 2 of 50
2. Question
The electrostatic force on a small sphere of charge \(0.4 \mu \mathrm{C}\) due to another small sphere of charge \(-0.8 \mu \mathrm{C}\) in air is \(0.2 \mathrm{~N}\). (a) What is the distance between the two spheres? (b) What is the force on the second sphere due to the first?
CorrectIncorrect -
Question 3 of 50
3. Question
Four point charges \(q_{\mathrm{A}}=2 \mu \mathrm{C}, q_{\mathrm{B}}=-5 \mu \mathrm{C}, q_{\mathrm{C}}=2 \mu \mathrm{C}\), and \(q_{\mathrm{D}}=-5 \mu \mathrm{C}\) are located at the corners of a square \(\mathrm{ABCD}\) of side \(10 \mathrm{~cm}\). What is the force on a charge of \(1 \mu \mathrm{C}\) placed at the centre of the square?
CorrectIncorrect -
Question 4 of 50
4. Question
A system has two charges \(q_{\mathrm{A}}=2.5 \times 10^{-7} \mathrm{C}\) and \(q_{\mathrm{B}}=-2.5 \times 10^{-7} \mathrm{C}\) located at points \(A:(0,0,-15 \mathrm{~cm})\) and \(B:(0,0,+15 \mathrm{~cm})\), respectively. What are the total charge and electric dipole moment of the system?
CorrectIncorrect -
Question 5 of 50
5. Question
An electric dipole with dipole moment \(4 \times 10^{-9} \mathrm{C} \mathrm{m}\) is aligned at \(30^{\circ}\) with the direction of a uniform electric field of magnitude \(5 \times 10^4 \mathrm{~N} \mathrm{C}^{-1}\). Calculate the magnitude of the torque acting on the dipole.
CorrectIncorrect -
Question 6 of 50
6. Question
(a) Two insulated charged copper spheres A and B have their centers separated by a distance of \(50 \mathrm{~cm}\). What is the mutual force of electrostatic repulsion if the charge on each is \(6.5 \times 10^{-7} \mathrm{C}\)? The radii of \(\mathrm{A}\) and \(\mathrm{B}\) are negligible compared to the distance of separation.
(b) What is the force of repulsion if each sphere is charged double the above amount, and the distance between them is halved?CorrectIncorrect -
Question 7 of 50
7. Question
Consider a uniform electric fleld \(\mathbf{E}=3 \times 10^3 \hat{\mathbf{i}} \mathrm{N} / \mathrm{C}\). (a) What is the flux of this field through a square of \(10 \mathrm{~cm}\) on a side whose plane is parallel to the \(y z\) plane? (b) What is the flux through the same square if the normal to its plane makes a \(60^{\circ}\) angle with the \(x\)-axis?
CorrectIncorrect -
Question 8 of 50
8. Question
A uniformly charged conducting sphere of \(2.4 \mathrm{~m}\) diameter has a surface charge density of \(80.0 \mu \mathrm{C} / \mathrm{m}^2\). (a) Find the charge on the sphere. (b) What is the total electric flux leaving the surface of the sphere?
CorrectIncorrect -
Question 9 of 50
9. Question
A point charge \(+q\), is placed at a distance \(d\) from an isolated conducting plane. The field at a point \(\mathrm{P}\) on the other side of the plane is
CorrectIncorrect -
Question 10 of 50
10. Question
A hemisphere is uniformly charged positively. The electric field at a point on a diameter away from the centre is directed
CorrectIncorrect -
Question 11 of 50
11. Question
If \(\oint_{\mathrm{s}} \mathbf{E} \cdot \mathrm{d} \mathbf{S}=0\) over a surface, then
CorrectIncorrect -
Question 12 of 50
12. Question
The Electric field at a point is
CorrectIncorrect -
Question 13 of 50
13. Question
Three charges \(+\mathrm{Q}, \mathrm{q},+\mathrm{Q}\) are placed respectively, at distance, \(\mathrm{d} / 2\) and \(\mathrm{d}\) from the origin, on the \(x\)-axis. If the net force experienced by \(+Q\), placed at \(x=0\), is zero, then value of \(q\) is:
CorrectIncorrect -
Question 14 of 50
14. Question
Two identical conducting spheres \(\mathrm{A}\) and \(\mathrm{B}\), carry equal charge. They are separated by a distance much larger than their diameter, and the force between them is F. A third identical conducting sphere, \(C\), is uncharged. Sphere \(C\) is first touched to \(A\), then to \(B\), and then removed. As a result, the force between \(A\) and \(B\) would be equal to
CorrectIncorrect -
Question 15 of 50
15. Question
Shown in the figure are two point charges \(+Q\) and \(-Q\) inside the cavity of a spherical shell. The charges are kept near the surface of the cavity on opposite sides of the centre of the shell. If \(\sigma_1\) is the surface charge on the inner surface and \(Q_1\) net charge on it and \(\sigma_2\) the surface charge| on the outer surface and \(Q_2\) net charge on it then :
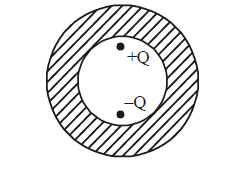 CorrectIncorrect
CorrectIncorrect -
Question 16 of 50
16. Question
Two charges, each equal to \(\mathrm{q}\), are kept at \(\mathrm{x}=-\mathrm{a}\) and \(\mathrm{x}=\mathrm{a}\) on the \(x\)-axis. A particle of mass \(m\) and charge \(q_0=\frac{q}{2}\) is placed at the origin. If charge \(q_0\) is given a small displacement \((y<<a)\) along the \(y\)-axis, the net force acting on the particle is proportional to
CorrectIncorrect -
Question 17 of 50
17. Question
Two balls of same mass and carrying equal charge are hung from a fixed support of length \(l\). At electrostatic equilibrium, assuming that angles made by each thread is small, the separation, \(x\) between the balls is proportional to :
CorrectIncorrect -
Question 18 of 50
18. Question
Consider a neutral conducting sphere. A positive point charge is placed outside the sphere. The net charge on the sphere is then
CorrectIncorrect -
Question 19 of 50
19. Question
Charge is distributed within a sphere of radius \(R\) with a volume charge density \(p(r)=\frac{A}{r^2} e^{-2 r / a}\) where \(A\) and a are constants. If \(\mathrm{Q}\) is the total charge of this charge distribution, the radius \(\mathrm{R}\) is:
CorrectIncorrect -
Question 20 of 50
20. Question
An electric dipole is formed by two equal and opposite charges \(q\) with separation \(d\). The charges have the same mass \(m\). It is kept in a uniform electric field \(E\). If it is slightly rotated from its equilibrium orientation, then its angular frequency \(\omega\) is:
CorrectIncorrect -
Question 21 of 50
21. Question
Ten charges are placed on the circumference of a circle of radius \(R\) with constant angular separation between successive charges. Alternate charges 1, 3, 5, 7, 9 have charge \((+q)\) each, while \(2,4,6,8,10\) have charge \((-q)\) each. The potential \(V\) and the electric field \(E\) at the centre of the circle are respectively: (Take \(V=0\) at infinity)
CorrectIncorrect -
Question 22 of 50
22. Question
Two isolated conducting spheres \(S_1\) and \(S_2\) of radius \(\frac{2}{3} R\) and \(\frac{1}{3} R\) have \(12 \mu \mathrm{C}\) and \(-3 \mu \mathrm{C}\) charges, respectively, and are at a large distance from each other. They are now connected by a conducting wire. Along time after this is done the charges on \(S_1\) and \(S_2\) are respectively:
CorrectIncorrect -
Question 23 of 50
23. Question
Concentric metallic hollow spheres of radii \(R\) and \(4 R\) hold charges \(Q_1\) and \(Q_2\) respectively. Given that surface charge densities of the concentric spheres are equal, the potential difference \(V(R)-V(4 R)\) is :
CorrectIncorrect -
Question 24 of 50
24. Question
A solid conducting sphere, having a charge \(Q\), is surrounded by an uncharged conducting hollow spherical shell. Let the potential difference between the surface of the solid sphere and that of the outer surface of the hollow shell be \(V\). If the shell is now given a charge of \(-4 Q\), the new potential difference between the same two surfaces is:
CorrectIncorrect -
Question 25 of 50
25. Question
The electric field in a region is given by \(\overrightarrow{\mathrm{E}}=(\mathrm{A} x+\mathrm{B}) \hat{i}\), where \(\mathrm{E}\) is in \(\mathrm{NC}^{-1}\) and \(x\) is in metres. The values of constants are \(\mathrm{A}=20 \mathrm{SI}\) unit and \(\mathrm{B}=10 \mathrm{SI}\) unit. If the potential at \(x=1\) is \(\mathrm{V}_1\) and that at \(x=-5\) is \(\mathrm{V}_2\), then \(\mathrm{V}_1-\mathrm{V}_2\) is:
CorrectIncorrect -
Question 26 of 50
26. Question
Two electric dipoles, A, B with respective dipole moments \(\overrightarrow{\mathrm{d}}_{\mathrm{A}}=-4 \mathrm{qa} \hat{i}\) and \(\overrightarrow{\mathrm{d}}_{\mathrm{B}}=-2\) qa \(\hat{i}\) are placed on the \(x\)-axis with a separation \(R\), as shown in the figure
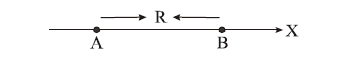
The distance from \(\mathrm{A}\) at which both of them produce the same potential is:CorrectIncorrect -
Question 27 of 50
27. Question
There is a uniform electrostatic field in a region. The potential at various points on a small sphere centred at \(P\), in the region, is found to vary between in the limits \(589.0 \mathrm{~V}\) to \(589.8 \mathrm{~V}\). What is the potential at a point on the sphere whose radius vector makes an angle of \(60^{\circ}\) with the direction of the field?
CorrectIncorrect -
Question 28 of 50
28. Question
An electric field \(\overrightarrow{\mathrm{E}}=(25 \hat{\mathrm{i}}+30 \hat{\mathrm{j}}) \mathrm{NC}^{-1}\) exists in a region of space. If the potential at the origin is taken to be zero then the potential at \(x=2 m, y=2 m\) is:
CorrectIncorrect -
Question 29 of 50
29. Question
For the circuit shown in Figure, which of the following statements is true?
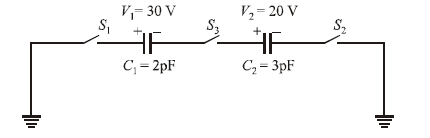 CorrectIncorrect
CorrectIncorrect -
Question 30 of 50
30. Question
Two capacitors of capacitances \(\mathrm{C}\) and \(2 \mathrm{C}\) are charged to potential differences \(\mathrm{V}\) and \(2 \mathrm{~V}\), respectively. These are then connected in parallel in such a manner that the positive terminal of one is connected to the negative terminal of the other. The final energy of this configuration is:
CorrectIncorrect -
Question 31 of 50
31. Question
In the circuit shown, the charge on the \(5 \mu \mathrm{F}\) capacitor is:
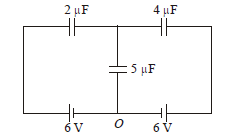 CorrectIncorrect
CorrectIncorrect -
Question 32 of 50
32. Question
A capacitor \(C\) is fully charged with voltage \(V_0\). After disconnecting the voltage source, it is connected in parallel with another uncharged capacitor of capacitance \(\frac{C}{2}\). The energy loss in the process after the charge is distributed between the two capacitors is:
CorrectIncorrect -
Question 33 of 50
33. Question
In the circuit shown in the figure, the total charge is \(750 \mu \mathrm{C}\) and the voltage across capacitor \(C_2\) is \(20 \mathrm{~V}\). Then the charge on capacitor \(C_2\) is :
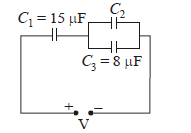 CorrectIncorrect
CorrectIncorrect -
Question 34 of 50
34. Question
The parallel combination of two air-filled parallel plate capacitors of capacitance \(\mathrm{C}\) and \(n \mathrm{C}\) is connected to a battery of voltage, V. When the capacitors are fully charged, the battery is removed and after that a dielectric material of dielectric constant \(\mathrm{K}\) is placed between the two plates of the first capacitor. The new potential difference of the combined system is:
CorrectIncorrect -
Question 35 of 50
35. Question
Figure shows charge \((q)\) versus voltage \((V)\) graph for series and parallel combination of two given capacitors. The capacitances are :
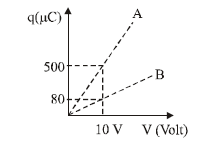 CorrectIncorrect
CorrectIncorrect -
Question 36 of 50
36. Question
In the figure shown, after the switch ‘ \(S\) ‘ is turned from position ‘ \(A\) ‘ to position ‘ \(B\) ‘, the energy dissipated in the circuit in terms of capacitance ‘ \(C\) ‘ and total charge ‘ \(Q\) ‘ is:
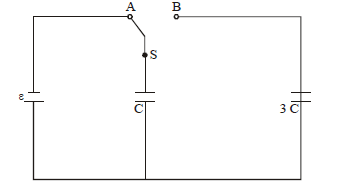 CorrectIncorrect
CorrectIncorrect -
Question 37 of 50
37. Question
A parallel plate capacitor with plates of area \(1 \mathrm{~m}^2\) each, are at a separation of \(0.1 \mathrm{~m}\). If the electric field between the plates is \(100 \mathrm{~N} / \mathrm{C}\), the magnitude of charge on each plate is: \(
\left(\text { Take } \epsilon_0=8.85 \times 10^{-12} \frac{\mathrm{C}^2}{\mathrm{~N}-\mathrm{M}^2}\right)
\)CorrectIncorrect -
Question 38 of 50
38. Question
In the circuit shown, find \(\mathrm{C}\) if the effective capacitance of the whole circuit is to be \(0.5 \mu \mathrm{F}\). All values in the circuit are in \(\mu \mathrm{F}\).
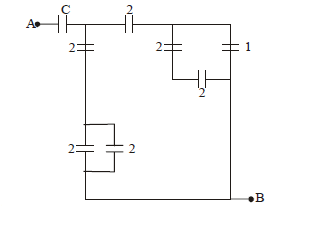 CorrectIncorrect
CorrectIncorrect -
Question 39 of 50
39. Question
In the figure shown below, the charge on the left plate of the \(10 \mu \mathrm{F}\) capacitor is \(-30 \mu \mathrm{C}\). The charge on the right plate of the \(6 \mu \mathrm{F}\) capacitor is :
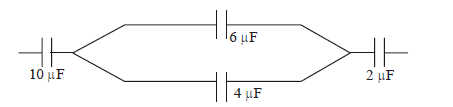 CorrectIncorrect
CorrectIncorrect -
Question 40 of 50
40. Question
A parallel plate capacitor having capacitance \(12 \mathrm{pF}\) is charged by a battery to a potential difference of \(10 \mathrm{~V}\) between its plates. The charging battery is now disconnected and a porcelain slab of dielectric constant 6.5 is slipped between the plates. The work done by the capacitor on the slab is:
CorrectIncorrect -
Question 41 of 50
41. Question
A capacitance of \(2 \mu \mathrm{F}\) is required in an electrical circuit across a potential difference of \(1.0 \mathrm{kV}\). A large number of \(1 \mu \mathrm{F}\) capacitors are available which can withstand a potential difference of not more than \(300 \mathrm{~V}\). The minimum number of capacitors required to achieve this is
CorrectIncorrect -
Question 42 of 50
42. Question
Three capacitors each of \(4 \mu \mathrm{F}\) are to be connected in such a way that the effective capacitance is \(6 \mu \mathrm{F}\). This can be done by connecting them :
CorrectIncorrect -
Question 43 of 50
43. Question
The value of current \(i_1\) flowing from \(A\) to \(C\) in the circuit diagram is :
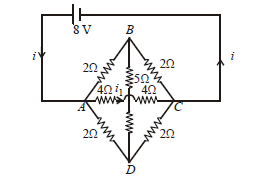 CorrectIncorrect
CorrectIncorrect -
Question 44 of 50
44. Question
A cell of internal resistance \(r\) drives current through an external resistance \(R\). The power delivered by the cell to the external resistance will be maximum when :
CorrectIncorrect -
Question 45 of 50
45. Question
In the circuit shown, the potential difference between A and B is :
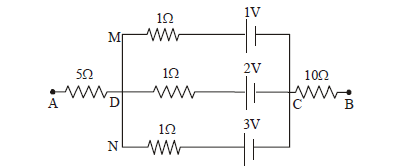 CorrectIncorrect
CorrectIncorrect -
Question 46 of 50
46. Question
Two batteries with e.m.f. \(12 \mathrm{~V}\) and \(13 \mathrm{~V}\) are connected in parallel across a load resistor of \(10 \Omega\). The internal resistances of the two batteries are \(1 \Omega\) and \(2 \Omega\) respectively. The voltage across the load lies between:
CorrectIncorrect -
Question 47 of 50
47. Question
A battery of internal resistance \(4 \Omega\) is connected to the network of resistances as shown. In order that the maximum power can be delivered to the network, the value of \(R\) in \(\Omega\) should be
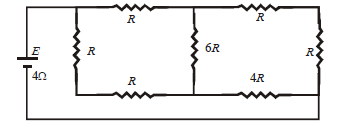 CorrectIncorrect
CorrectIncorrect -
Question 48 of 50
48. Question
For the resistance network shown in the figure, choose the correct option(s)
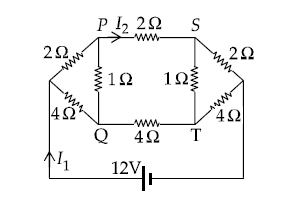 CorrectIncorrect
CorrectIncorrect -
Question 49 of 50
49. Question
For a common emitter configuration, if \(\alpha\) and \(\beta\) have their usual meanings, the incorrect relationship between \(\alpha\) and \(\beta\) is :
CorrectIncorrect -
Question 50 of 50
50. Question
An n-p-n transistor has three leads A, B and C. Connecting \(\mathrm{B}\) and \(\mathrm{C}\) by moist fingers, \(\mathrm{A}\) to the positive lead of an ammeter, and \(C\) to the negative lead of the ammeter, one finds large deflection. Then, \(A, B\) and \(C\) refer respectively to:
CorrectIncorrect