JEE Practice Questions:Trigonometric Equations (Single Choice Type)

Hint

(a) \(\sin \theta=1 / 2\) and \(\cos \theta=-\sqrt{3} / 2\)
\(\Rightarrow \theta\) lies in the second quadrant.
\(\Rightarrow \sin \theta=\sin 5 \pi / 6 ; \cos \theta=\cos 5 \pi / 6\);
\(\therefore \theta=2 n \pi+(5 \pi / 6)\)

Hint

(c) Since \(\tan \theta<0\) and \(\cos \theta>0, \theta\) lies in the fourth quadrant. Then \(\theta=7 \pi / 4\).
Hence, the general value of \(\theta\) is \(2 n \pi+7 \pi / 4, n \in Z\).

Hint

(c)

\(
\begin{aligned}
&\begin{aligned}
& \cos p \theta=-\cos q \theta=\cos (\pi-q \theta) \\
& \Rightarrow p \theta=2 n \pi \pm(\pi-q \theta) \\
& \Rightarrow \quad(p \mp q) \theta=(2 n \pm 1) \pi \\
& \Rightarrow \quad \theta=\frac{(2 n \pm 1) \pi}{(p \mp q)}, n \in Z \\
& \Rightarrow \quad \theta=\frac{r \pi}{p \pm q}, \text { where } r=-3,-1,1,3, \ldots \\
& \Rightarrow \quad \theta=\cdots, \frac{-3 \pi}{p \pm q}, \frac{-\pi}{p \pm q}, \frac{\pi}{p \pm q}, \frac{3 \pi}{p \pm q}, \cdots
\end{aligned}\\
&\text { Shown above is an A.P. of common difference } \frac{2 \pi}{p \pm q} \text {. }
\end{aligned}
\)

Hint

(d)

\(
\begin{aligned}
&\text { A. }\\
&\begin{aligned}
& (\cos \theta+\cos 7 \theta)+(\cos 3 \theta+\cos 5 \theta)=0 \\
& \Rightarrow 2 \cos 4 \theta(\cos 3 \theta+\cos \theta)=0 \\
& \Rightarrow 4 \cos 4 \theta \cos 2 \theta \cos \theta=0 \\
& \Rightarrow 4 \times \frac{1}{2^3 \sin \theta}\left(\sin 2^3 \theta\right)=0 \\
& \Rightarrow \sin 8 \theta=0 \text { or } \theta=n \pi / 8, n \in Z
\end{aligned}
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
& 3 \frac{\sin ^2 \theta}{\cos ^2 \theta}-2 \sin \theta=0, \cos \theta \neq 0 \\
& \Rightarrow 3 \sin ^2 \theta-2 \sin \theta\left(1-\sin ^2 \theta\right)=0 \\
& \Rightarrow \sin \theta\left(2 \sin ^2 \theta+3 \sin \theta-2\right)=0 \\
& \Rightarrow \sin \theta(2 \sin \theta-1)(\sin \theta+2)=0 \\
& \Rightarrow \sin \theta=0,1 \\
& \Rightarrow \theta=n \pi, n \pi+(-1)^n(\pi / 6), n \in Z
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
&\text { We have } 1^2=\sin \theta \cos 2 \theta\\
&\begin{aligned}
& \Rightarrow \quad 1-\sin \theta\left(1-2 \sin ^2 \theta\right)=0 \\
& \Rightarrow \quad 2 \sin ^3 \theta-\sin \theta+1=0 \\
& \Rightarrow \quad(\sin \theta+1)\left(2 \sin ^2 \theta-2 \sin \theta+1\right)=0 \\
& \Rightarrow \quad \sin \theta=-1
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
&\text { The other factor gives imaginary roots. }\\
&\Rightarrow \quad \theta=n \pi+(-1)^n\left(-\frac{\pi}{2}\right)=n \pi-(-1)^n \frac{\pi}{2}=n \pi+(-1)^{n-1} \frac{\pi}{2}, n \in Z .
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
& 2 \cos \theta\left[\cos 120^{\circ}+\cos 2 \theta\right]=1 \\
& \Rightarrow 2 \cos \theta\left(-\frac{1}{2}+2 \cos ^2 \theta-1\right)=1 \\
& \Rightarrow 4 \cos ^3 \theta-3 \cos \theta-1=0 \\
& \Rightarrow \cos 3 \theta=1=\cos 0 \\
& \Rightarrow 3 \theta=2 n \pi \text { or } \theta=\frac{2 n \pi}{3}, n \in Z
\end{aligned}
\)
Given the values so that \(2 n\) does not exceed 18 .
\(
\therefore \quad n=0,1,2,3, \ldots, 9
\)
Hence, the sum \(=\frac{2 \pi}{3} \sum_1^9 n=\frac{2 \pi}{3} \times \frac{9(9+1)}{2}=30 \pi\).

Hint

(b)

\(
\begin{aligned}
& \sec \theta-1=(\sqrt{2}-1) \tan \theta \Rightarrow \frac{1-\cos \theta}{\cos \theta}=\frac{(\sqrt{2}-1) \sin \theta}{\cos \theta} \\
& \Rightarrow 2 \sin ^2(\theta / 2)=(-\sqrt{2}-1) 2 \sin (\theta / 2) \cos (\theta / 2) \\
& \Rightarrow \sin (\theta / 2)=0 \text { or } \tan (\theta / 2)=(\sqrt{2}-1)=\tan (\pi / 8) \\
& \Rightarrow \theta / 2=n \pi \text { or } \theta / 2=n \pi+(\pi / 8), n \in Z \\
& \Rightarrow \theta=2 n \pi \text { or } \theta=2 n \pi+(\pi / 4), n \in Z
\end{aligned}
\)

Hint

(a)
\(
\begin{aligned}
& \sin ^4 x+\cos ^4 x=\sin x \cos x \\
& \Rightarrow\left(\sin ^2 x+\cos ^2 x\right)^2-2 \sin ^2 x \cos ^2 x=\sin x \cos x \\
& \Rightarrow 1-\frac{\sin ^2 2 x}{2}=\frac{\sin 2 x}{2} \\
& \Rightarrow \sin ^2 2 x+\sin 2 x-2=0 \\
& \Rightarrow(\sin 2 x+2)(\sin 2 x-1)=0 \\
& \Rightarrow \sin 2 x=1
\end{aligned}
\)
\(
\begin{aligned}
&\begin{aligned}
\Rightarrow \quad 2 x & =(4 n+1) \frac{\pi}{2}, n \in Z \\
\Rightarrow \quad x & =(4 n+1) \frac{\pi}{4}, n \in Z \\
& =\frac{\pi}{4}, \frac{5 \pi}{4}(\because x \in[0,2 \pi])
\end{aligned}\\
&\text { Thus, there are two solutions. }
\end{aligned}
\)

Hint

(c)

\(
\begin{aligned}
&\begin{aligned}
& \sin 3 x+(\sin 5 x+\sin x)=0 \\
& \Rightarrow \sin 3 x+(2 \sin 3 x \cos 2 x)=0 \\
& \Rightarrow \sin 3 x=0 \text { or } \cos 2 x=-\frac{1}{2}=\cos \frac{2 \pi}{3} \\
& \Rightarrow x=n \pi / 3 \text { or } x=n \pi \pm \pi / 3, n \in Z
\end{aligned}\\
&\text { Then } x=0, \pi / 3 \text {, and } 2 \pi / 3 \text {, Hence, there are three solutions. }
\end{aligned}
\)

Hint

(a) From the given relation
\(
\begin{aligned}
& \cos \theta=(2 \sin \theta \cos \theta) \sin \theta, \sin \theta \neq 0 \\
& \Rightarrow \sin \theta= \pm \frac{1}{\sqrt{2}} \text { or } \cos \theta=0 \\
& \Rightarrow \quad \theta=\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{\pi}{2}(\because \theta \in[0, \pi])
\end{aligned}
\)
Then the sum of roots is \(\frac{3 \pi}{2}\).

Hint

(c) The given equation is \((\cos x-1)\left(12 \cos ^2 x+5 \cos x+9\right)=0\) \(\Rightarrow \cos x=1\) only as the other factor gives imaginary roots
\(
=1 \Rightarrow x=2 n \pi, n \in Z
\)
Hence, it has infinite solutions as \(n \in Z\).

Hint

(d)

\(
\begin{aligned}
& \cos 2 x=1-2 \sin ^2 x \text { and put } 2^{-\sin ^2 x}=t \\
& \Rightarrow 2^{\cos 2 x}=2^{1-2 \sin ^2 x}=2\left(2^{-\sin ^2 x}\right)^2=2 t^2 \\
& \Rightarrow 2 t^2-3 t+1=0 \\
& \Rightarrow t=1,1 / 2 \\
& \Rightarrow 2^{-\sin ^2 x}=1=2^0 \\
& \Rightarrow \sin ^2 x=0 \text { or } x=n \pi, n \in Z \\
& \text { From } 2^{-\sin ^2 x}=\frac{1}{2}=2^{-1}, \text { we get } \\
& \sin ^2 x=1 \text { or } x=n \pi \pm \frac{\pi}{2}, n \in Z
\end{aligned}
\)

Hint

(a)
\(
\begin{aligned}
& \cos x \cos 6 x=-1 \\
& \Rightarrow 2 \cos x \cos 6 x=-2 \quad \Rightarrow \cos 7 x+\cos 5 x=-2 \quad \Rightarrow \cos 7 x=-1 \text { and } \cos 5 x=-1
\end{aligned}
\)
The value of \(x\) satisfying these two equations simultaneously and lying between 0 and \(2 \pi\) is \(\pi\). Therefore, the general solution is \(x=2 n \pi+\pi, n \in Z\).
\(
\Rightarrow \quad x=(2 n+1) \pi, n \in Z
\)

Hint

(c) This is possible only when \(\sin x=\cos x=1\), which does not hold simultaneously. Hence, there is no solution.

Hint

(a) The given equation is \(3(\sin x+\cos x)-2(\sin x+\cos x)(1-\sin x \cos x)=8\)
\(
\begin{aligned}
& \Rightarrow \quad(\sin x+\cos x)[3-2+2 \sin x \cos x]=8 \\
& \Rightarrow \quad(\sin x+\cos x)\left[\sin ^2 x+\cos ^2 x+2 \sin x \cos x\right]=8 \\
& \Rightarrow \quad(\sin x+\cos x)^3=8 \\
& \Rightarrow \quad \sin x+\cos x=2
\end{aligned}
\)
Above solution is not possible. Hence, the given equation has no solution.

Hint

(a)
\(
\begin{aligned}
& \cos ^2 \theta=\frac{1}{6} \sin \theta \tan \theta \\
& \Rightarrow 6 \cos ^3 \theta=1-\cos ^2 \theta \\
& \Rightarrow 6 \cos ^3 \theta+\cos ^2 \theta-1=0 \\
& \Rightarrow(2 \cos \theta-1)\left(3 \cos ^2 \theta+2 \cos \theta+1\right)=0
\end{aligned}
\)
\(
\begin{aligned}
&\Rightarrow \cos \theta=\frac{1}{2} \Rightarrow \theta=2 n \pi \pm \frac{\pi}{3}, n \in Z\\
&\text { The other factor gives imaginary roots. }
\end{aligned}
\)

Hint

(c)

\(
\begin{aligned}
&\begin{aligned}
& (1-\cos 2 x)+\left(1-\cos ^2 2 x\right)=2 \\
& \Rightarrow \cos 2 x(\cos 2 x+1)=0 \\
& \Rightarrow \cos 2 x=0 \text { or } \cos 2 x=-1 \\
& \Rightarrow 2 x=(2 n+1) \pi / 2 \text { or } 2 x=(2 n \pm 1) \pi, n \in Z \\
& \Rightarrow x=(2 n+1) \pi / 4 \text { or } x=(2 n \pm 1) \pi / 2, n \in Z
\end{aligned}\\
&\text { Hence, the solutions are } \pi / 4,3 \pi / 4,5 \pi / 4,7 \pi / 4, \pi / 2,3 \pi / 2 \text {. }
\end{aligned}
\)

Hint

(c) Dividing the given equation by \(\cos ^2 x\), as \(\cos x=0\) does not satisfy the equation, we have
\(
\begin{aligned}
& \tan ^2 x-5 \tan x-6=0 \\
& \Rightarrow(\tan x+1)(\tan x-6)=0 \\
& \Rightarrow \tan x=-1 \text { or } \tan x=6
\end{aligned}
\)
If \(\tan x=-1=\tan (-\pi / 4)\), then \(x=n \pi-\pi / 4, \forall n \in Z\)
and, if \(\tan x=6=\tan \alpha\) (say)
\(
\Rightarrow \quad \alpha=\tan ^{-1} 6, \text { then } x=n \pi+\alpha=n \pi+\tan ^{-1} 6, \forall n \in Z
\)
Hence, \(x=n \pi-(\pi / 4), n \pi+\tan ^{-1} 6, n \in Z\).

Hint

(d)

\(
\begin{aligned}
&\text { From the given equation, we have } \frac{\tan \theta+\tan 4 \theta}{1-\tan \theta \tan 4 \theta}=-\tan 7 \theta\\
&\begin{aligned}
& \Rightarrow \tan (\theta+4 \theta)=-\tan 7 \theta \\
& \Rightarrow \tan 5 \theta=\tan (-7 \theta) \\
& \Rightarrow 5 \theta=n \pi-7 \theta \\
& \Rightarrow \theta=n \pi / 12, \text { where } n \in Z, \text { but } n \neq 6,18,30, \ldots
\end{aligned}
\end{aligned}
\)

Hint

(d) We have \(\frac{1}{\sin ^2 \theta \cos ^2 \theta}+\frac{2}{\sin ^2 \theta}=8, \sin \theta \neq 0, \cos \theta \neq 0\)
\(
\begin{aligned}
& \Rightarrow 1+2 \cos ^2 \theta=8 \sin ^2 \theta \cos ^2 \theta=8 \cos ^2 \theta\left(1-\cos ^2 \theta\right) \\
& \Rightarrow 8 \cos ^4 \theta-6 \cos ^2 \theta+1=0 \\
& \Rightarrow\left(4 \cos ^2 \theta-1\right)\left(2 \cos ^2 \theta-1\right)=0 \\
& \Rightarrow \cos ^2 \theta=1 / 4=\cos ^2(\pi / 3) \text { or } \cos ^2 \theta=1 / 2=\cos ^2(\pi / 4) \\
& \Rightarrow \theta=n \pi \pm(\pi / 3) \text { or } \theta=n \pi \pm(\pi / 4), n \in Z
\end{aligned}
\)
Hence, for \(0 \leq \theta \leq \pi / 2, \theta=\pi / 3, \theta=\pi / 4\)

Hint

(b)
\(
\begin{aligned}
& \tan x+\cot x=2 \operatorname{cosec} x \\
& \Rightarrow \frac{\sin x}{\cos x}+\frac{\cos x}{\sin x}=\frac{2}{\sin x} \\
& \Rightarrow \frac{1}{\sin x \cos x}=\frac{2}{\sin x} \\
& \Rightarrow \cos x=\frac{1}{2}
\end{aligned}
\)
\(
\begin{aligned}
&\Rightarrow \quad x= \pm \frac{\pi}{3}, \pm \frac{5 \pi}{3}\\
&\text { Thus, there are four solutions. }
\end{aligned}
\)

Hint

(c)
\(
\text { Let } Z=\frac{3+2 i \sin \theta}{1-2 i \sin \theta}=\frac{(3+2 i \sin \theta)(1+2 i \sin \theta)}{(1-2 i \sin \theta)(1+2 i \sin \theta)}=\frac{\left(3-4 \sin ^2 \theta\right)+8 i \sin \theta}{1+4 \sin ^2 \theta}
\)
Therefore, the real part of \(Z=\frac{3-4 \sin ^2 \theta}{1+4 \sin ^2 \theta}\) and the imaginary part of \(Z=\frac{8 \sin \theta}{1+4 \sin ^2 \theta}\).
\(Z\) is real, if imaginary part \(=\frac{8 \sin \theta}{1+4 \sin ^2 \theta}=0\) or \(\sin \theta=0\) or \(\theta=n \pi, \forall n \in I\)
\(Z\) is purely imaginary, if real part \(\left(3-4 \sin ^2 \theta\right) /\left(1+4 \sin ^2 \theta\right)=0\)
or \(\sin ^2 \theta=3 / 4=\sin ^2(\pi / 3)\) or \(\theta=n \pi \pm \pi / 3, \forall n \in I\)

Hint

(b)

\(
\begin{aligned}
&\begin{aligned}
& 1-\sin ^2 x+\frac{\sqrt{3}+1}{2} \sin x-\frac{\sqrt{3}}{4}-1=0 \\
& \Rightarrow \sin ^2 x-\frac{\sqrt{3}+1}{2} \cdot \sin x+\frac{\sqrt{3}}{4}=0 \\
& \Rightarrow 4 \sin ^2 x-2 \sqrt{3} \sin x-2 \sin x+\sqrt{3}=0
\end{aligned}\\
&\text { On solving, we get } \sin x=1 / 2, \sqrt{3} / 2 \text {. }\\
&\Rightarrow x=\pi / 6,5 \pi / 6 ; \pi / 3,2 \pi / 3
\end{aligned}
\)

Hint

(d) Since, \(7 \cos ^2 x+\sin x \cos x-3=0\), Dividing the equation by \(\cos ^2 x\), we get
\(
\begin{aligned}
& 7+\tan x-3 \sec ^2 x=0 \\
& \Rightarrow \quad 7+\tan x-3\left(1+\tan ^2 x\right)=0 \\
& \Rightarrow \quad 3 \tan ^2 x-\tan x-4=0 \\
& \Rightarrow \quad(\tan x+1)(3 \tan x-4)=0 \\
& \Rightarrow \quad \tan x=-1 \text { or } \tan x=\frac{4}{3} \\
& \Rightarrow \quad x=n \pi+\frac{3 \pi}{4} \text { or } x=k \pi+\tan ^{-1}\left(\frac{4}{3}\right), \text { where }(k, n \in Z)
\end{aligned}
\)

Hint

(b)
\(
\begin{aligned}
& (\sin \theta+2)(\sin \theta+3)(\sin \theta+4)=6 \\
& \text { L.H.S. }>6 \text { and R.H.S. } 6
\end{aligned}
\)
Therefore, equality only holds if \(\sin \theta=-1 \Rightarrow \theta=3 \pi / 2,7 \pi / 2\)
Therefore, sum \(=5 \pi \Rightarrow k=5\)

Hint

(b)
\(
\begin{aligned}
& \sin ^2 x+a \cos x+a^2>1+\cos x \\
& \text { Putting } x=0, \text { we get } \\
& \Rightarrow a+a^2>2 \\
& \Rightarrow a^2+a-2>0 \\
& \Rightarrow(a+2)(a-1)>0 \\
& \Rightarrow a<-2 \text { or } a>1
\end{aligned}
\)
Therefore, we have the largest negative integral value of \(a=-3\).

Hint

(b)

\(
\begin{aligned}
&\begin{aligned}
& \sin ^4 x-\cos ^2 x \sin x+2 \sin ^2 x+\sin x=0 \\
& \Rightarrow \sin x\left[\sin ^3 x-\cos ^2 x+2 \sin x+1\right]=0 \\
& \Rightarrow \sin x\left[\sin ^3 x-1+\sin ^2 x+2 \sin x+1\right]=0 \\
& \Rightarrow \sin x\left[\sin ^3 x+\sin ^2 x+2 \sin x\right]=0 \\
& \Rightarrow \sin ^2 x=0 \text { or } \sin ^2 x+\sin x+2=0 \text { (not possible for real } x \text { ) } \\
& \Rightarrow \sin x=0
\end{aligned}\\
&\text { Hence, the solutions are } x=0, \pi, 2 \pi, 3 \pi \text {. }
\end{aligned}
\)

Hint

(a) Since, \(x \in[0,2 \pi]\) and \(y \in[0,2 \pi]\), and \(\sin x+\sin y=2\)
This is possible only, when \(\sin x=1\) and \(\sin y=1\) \(\Rightarrow x=\pi / 2\) and \(y=\pi / 2\)
Hence, \(x+y=\pi\).

Hint

(a)

\(
\begin{aligned}
& (\sqrt{3}-1) \sin \theta+(\sqrt{3}+1) \cos \theta=2 \\
& \Rightarrow \frac{(\sqrt{3}-1)}{2 \sqrt{2}} \sin \theta+\left(\frac{\sqrt{3}+1}{2 \sqrt{2}}\right) \cos \theta=\frac{1}{\sqrt{2}} \\
& \Rightarrow \sin \frac{\pi}{12} \sin \theta+\cos \frac{\pi}{12} \cos \theta=\cos \frac{\pi}{4} \\
& \Rightarrow \cos \left(\theta-\frac{\pi}{12}\right)=\cos \frac{\pi}{4} \\
& \Rightarrow \theta-\frac{\pi}{12}=2 n \pi \pm \frac{\pi}{4}, n \in Z \\
& =2 n \pi \pm \frac{\pi}{4}+\frac{\pi}{12}
\end{aligned}
\)

Hint

(a)

\(
\begin{aligned}
& \sin 6 \theta+\sin 4 \theta+\sin 2 \theta=0 \\
& \Rightarrow(\sin 6 \theta+\sin 2 \theta)+\sin 4 \theta=0 \\
& \Rightarrow 2 \sin 4 \theta \cos 2 \theta+\sin 4 \theta=0 \\
& \Rightarrow \sin 4 \theta(2 \cos 2 \theta+1)=0 \\
& \Rightarrow \sin 4 \theta=0 \text { or } \cos 2 \theta=-\frac{1}{2}=\cos \frac{2 \pi}{3} \\
& \Rightarrow 4 \theta=n \pi \text { or } 2 \theta=2 n \pi \pm \frac{2 \pi}{3}, n \in Z \\
& \Rightarrow \theta=\frac{n \pi}{4} \text { or } \theta=n \pi \pm \frac{\pi}{3}
\end{aligned}
\)

Hint

(d)
\(
\begin{aligned}
&\text { The given expression } \cos y \sin x-\sin y \cos x+\sin y \sin x+\cos x \cos y \text { is }\\
&\begin{aligned}
& \sin (x-y)+\cos (x-y) \\
& \therefore \sin (x-y)+\cos (x-y)=0 \\
& \Rightarrow \sqrt{2}\left(\frac{1}{\sqrt{2}} \sin (x-y)+\frac{1}{\sqrt{2}} \cos (x-y)\right)=0 \\
& \Rightarrow \sin \left(x-y+\frac{\pi}{4}\right)=0
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{\pi}{4}+x-y=n \pi, n \in Z \\
& \Rightarrow \quad x-y=n \pi-\frac{\pi}{4}, n \in Z \\
& \Rightarrow \quad x=n \pi-\frac{\pi}{4}+y \text { where } n \in Z
\end{aligned}
\)

Hint

(c)

\(
\begin{aligned}
&\begin{aligned}
& \tan x \tan 4 x=1 \\
& \Rightarrow \cos 4 x \cos x-\sin 4 x \sin x=0 \\
& \Rightarrow \cos 5 x=0 \\
& \Rightarrow 5 x=\left(n+\frac{1}{2}\right) \pi, n \in Z \\
& \Rightarrow x=\frac{(2 n+1)}{10} \pi ; 0<x<\pi \\
& \quad=\frac{\pi}{10}, \frac{3 \pi}{10}, \frac{5 \pi}{10}, \frac{7 \pi}{10}, \frac{9 \pi}{10}
\end{aligned}\\
&\text { Thus, there are only five solutions. }
\end{aligned}
\)

Hint

(a)

\(
\begin{aligned}
&\begin{aligned}
& \text { Let } f(x)=\cos x-x+\frac{1}{2} \\
& \qquad f(0)=1+\frac{1}{2}>0 \\
& f\left(\frac{\pi}{2}\right)=0-\frac{\pi}{2}+\frac{1}{2}=\frac{1-\pi}{2}<0
\end{aligned}\\
&\text { Therefore, one root lies in the interval }\left(0, \frac{\pi}{2}\right) \text {. }
\end{aligned}
\)

Hint

(d)

\(
\begin{aligned}
& \tan \left(\frac{p \pi}{4}\right)=\cot \left(\frac{q \pi}{4}\right)=\tan \left(\frac{\pi}{2}-\frac{q \pi}{4}\right) \\
& \Rightarrow \frac{p \pi}{4}=n \pi+\frac{\pi}{2}-\frac{q \pi}{4} \\
& \Rightarrow \frac{p}{4}=n+\frac{1}{2}-\frac{q}{4} \\
& \Rightarrow \frac{p+q}{4}=\frac{2 n+1}{2} \\
& \Rightarrow p+q=2(2 n+1)
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
y & =\sin x-\cos x=\sqrt{2}\left[\frac{1}{\sqrt{2}} \sin -\frac{1}{\sqrt{2}} \cos x\right] \\
& =\sqrt{2} \sin \left(x-\frac{\pi}{4}\right) \quad \Rightarrow-\sqrt{2} \leq y \leq \sqrt{2} \quad \Rightarrow \text { Range of } y \text { is }[-\sqrt{2}, \sqrt{2}] .
\end{aligned}
\)

Hint

(a)
\(
\begin{aligned}
& 4 \sin ^4 x+\cos ^4 x=1 \\
& \Rightarrow \quad\left(2 \sin ^2 x\right)^2+\frac{1}{4}\left(2 \cos ^2 x\right)^2=1
\end{aligned}
\)
\(
\begin{aligned}
& (1-\cos 2 x)^2+\frac{1}{4}(1+\cos 2 x)^2=i \\
& 5 \cos ^2 2 x-6 \cos 2 x+1=0 \\
& (\cos 2 x-1)(5 \cos 2 x-1)=0
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad \cos 2 x=1 \text { or } \cos 2 x=1 / 5 \\
& \Rightarrow \quad 2 x=2 n \pi \text { or } 2 x=2 n \pi \pm \alpha, \text { where } \alpha=\cos ^{-1}(1 / 5), \forall n \in Z
\end{aligned}
\)

Hint

(c)

\(
\begin{aligned}
& (1-\tan \theta)\left[1+2 \tan \theta /\left(1+\tan ^2 \theta\right)\right]=1+\tan \theta \\
& \Rightarrow(1-\tan \theta)(1+\tan \theta)^2=(1+\tan \theta)\left(1+\tan ^2 \theta\right) \\
& \Rightarrow(1+\tan \theta)\left[\left(1-\tan ^2 \theta\right)-\left(1+\tan ^2 \theta\right)\right]=0 \\
& \Rightarrow-2 \tan ^2 \theta=0,(1+\tan \theta)=0 \\
& \Rightarrow \tan \theta=0, \text { or } \tan \theta=-1 \\
& \Rightarrow \theta=n \pi \text { or } n \pi-\pi / 4, \forall n \in Z, \text { for } \theta \in[0,2 \pi] \theta=0, \pi, 2 \pi, 3 \pi / 4,7 \pi / 4
\end{aligned}
\)

Hint

(d) We have \((\sin x+\sin 3 x)+\sin 2 x=(\cos x+\cos 3 x)+\cos 2 x\)
\(
\begin{aligned}
& \Rightarrow \quad 2 \sin 2 x \cos x+\sin 2 x=2 \cos 2 x \cos x+\cos 2 x \\
& \Rightarrow \quad \sin 2 x(2 \cos x+1)=\cos 2 x(2 \cos x+1) \\
& \Rightarrow \quad(2 \cos x+1)(\sin 2 x-\cos 2 x)=0 \\
& \Rightarrow \quad \cos x=-1 / 2 \text { or } \sin 2 x-\cos 2 x=0 \\
& \Rightarrow \quad x=2 n \pi \pm(2 \pi / 3) \text { or } \tan 2 x=1=\tan (\pi / 4) \\
& \quad=2 n \pi \pm(2 \pi / 3) \text { or } x=(4 n+1) \pi / 8, n \in Z
\end{aligned}
\)
But here \(0 \leq x \leq 2 \pi\)
Hence, \(x=\pi / 8,5 \pi / 8,2 \pi / 3,9 \pi / 8,4 \pi / 3,13 \pi / 8\).

Hint

(b)
\(
\begin{aligned}
&\begin{aligned}
& 3 \sin \theta-4 \sin ^3 \theta-\sin \theta=2\left(2 \cos ^2 \theta-1\right) \\
& \Rightarrow 2 \sin \theta\left(1-2 \sin ^2 \theta\right)=2 \cos 2 \theta \\
& \Rightarrow 2 \cos 2 \theta(\sin \theta-1)=0 \\
& \Rightarrow \cos 2 \theta=0 \text { or } \sin \theta=1 \\
& \Rightarrow 2 \theta=(2 n+1) \pi / 2 \text { or } \theta=2 n \pi+\pi / 2, \forall n \in Z \\
& \Rightarrow \quad \theta=(2 n+1) \pi / 4, \text { or } \theta=(4 n+1) \pi / 2, \forall n \in Z
\end{aligned}\\
&\text { Hence, } \theta=\pi / 4,3 \pi / 4,5 \pi / 4,7 \pi / 4, \pi / 2 \text {. } (\because \theta \in[0,2 \pi])
\end{aligned}
\)

Hint

(c)

\(
\begin{aligned}
&\text { We have } 4 \sin \theta \sin 2 \theta \sin 4 \theta=3 \sin \theta-4 \sin ^3 \theta\\
&\begin{aligned}
& \Rightarrow \sin \theta\left[4 \sin 2 \theta \sin 4 \theta-3+4 \sin ^2 \theta\right]=0 \\
& \Rightarrow \sin \theta[2(\cos 2 \theta-\cos 6 \theta)-3+2(1-\cos 2 \theta)]=0 \\
& \Rightarrow \sin \theta(-2 \cos 6 \theta-1)=0 \\
& \Rightarrow \sin \theta=0 \text { or } \cos 6 \theta=-1 / 2 \\
& \Rightarrow \quad \theta=n \pi \text { or } 6 \theta=2 n \pi \pm 2 \pi / 3, \forall n \in Z \\
& \quad=n \pi \text { or } \theta=(3 n \pm 1) \pi / 9, \forall n \in Z
\end{aligned}
\end{aligned}
\)

Hint

(b)
\(
\begin{aligned}
&\text { From the given equation, we have } \tan \theta+\tan 2 \theta+\tan (\theta+2 \theta)=0\\
&\begin{aligned}
& \Rightarrow(\tan \theta+\tan 2 \theta)+\frac{\tan \theta+\tan 2 \theta}{1-\tan \theta \tan 2 \theta}=0 \\
& \Rightarrow(\tan \theta+\tan 2 \theta)\left[1+\frac{1}{1-\tan \theta \tan 2 \theta}\right]=0
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
&\begin{aligned}
& \Rightarrow \quad(\tan \theta+\tan 2 \theta)(2-\tan \theta \tan 2 \theta)=0 \\
& \Rightarrow \quad \tan \theta=\tan (-2 \theta) \text { or } 2-\tan \theta\left[(2 \tan \theta) /\left(1-\tan ^2 \theta\right)\right]=0 \\
& \Rightarrow \quad \theta=n \pi-2 \theta \text { or } 1-2 \tan ^2 \theta=0 \\
& \quad=n \pi / 3 \text { or } \tan ^2 \theta=1 / 2=\tan ^2 \alpha \text { (say) }
\end{aligned}\\
&\text { Therefore, } \theta=n \pi \pm \alpha \text {, where } \tan \alpha=1 / \sqrt{2} \text {; }
\end{aligned}
\)

Hint

(b)
\(
\begin{aligned}
&\text { We have } \sin 3 \alpha=4 \sin \alpha\left(\sin ^2 x-\sin ^2 \alpha\right)\\
&\begin{aligned}
& \Rightarrow 3 \sin \alpha-4 \sin ^3 \alpha=4 \sin \alpha \sin ^2 x-4 \sin ^3 \alpha \\
& \Rightarrow 3 \sin \alpha=4 \sin \alpha \sin ^2 x \text { or } \sin \alpha=0
\end{aligned}
\end{aligned}
\)
If \(\sin \alpha \neq 0, \sin ^2 x=3 / 4=(\sqrt{3} / 2)^2=\sin ^2(\pi / 3)\), therefore \(x=n \pi \pm \pi / 3, \forall n \in Z\)
If \(\sin \alpha=0\), i.e., \(\alpha=n \pi\), equation becomes an identity.

Hint

(c)

\(
\begin{aligned}
&\text { We have } \sqrt{3} \cos \theta-3 \sin \theta=2(\sin 5 \theta-\sin \theta) \text {. }\\
&\begin{aligned}
& \Rightarrow(\sqrt{3} / 2) \cos \theta-(1 / 2) \sin \theta=\sin 5 \theta \\
& \Rightarrow \cos (\theta+\pi / 6)=\sin 5 \theta=\cos (\pi / 2-5 \theta) \\
& \Rightarrow \theta+\pi / 6=2 n \pi \pm(\pi / 2-5 \theta) \\
& \Rightarrow \theta=(n \pi / 3)+(\pi / 18) \text { or } \theta=(-n \pi / 2)+(\pi / 6), \forall n \in Z
\end{aligned}
\end{aligned}
\)

Hint

(c)
\(
\begin{aligned}
& \sin ^4 x+\cos ^4 x+\sin 2 x+\alpha=0 \\
& \Rightarrow\left(\sin ^2 x+\cos ^2 x\right)^2-2 \sin ^2 x \cos ^2 x+\sin 2 x+\alpha=0 \\
& \Rightarrow \sin ^2 2 x-2 \sin 2 x-2-2 \alpha=0
\end{aligned}
\)
Let \(\sin 2 x=y\). Then the given equation becomes \(y^2-2 y-2(1+\alpha)=0\) where \(-1 \leq y \leq 1\),
\(
(\because-1 \leq \sin 2 x \leq 1)
\)
For real, discriminant \(\geq 0\)
\(
\begin{array}{ll}
\Rightarrow 3+2 \alpha \geq 0 & \Rightarrow \alpha \geq-\frac{3}{2} \\
\text { Also- } 1 \leq y \leq 1 & \Rightarrow-1 \leq 1-\sqrt{3+2 \alpha} \leq 1 . \\
\Rightarrow 3+2 \alpha \leq 4 & \Rightarrow \alpha \leq \frac{1}{2} . \text { Thus }-\frac{3}{2} \leq \alpha \leq \frac{1}{2}
\end{array}
\)

Hint

(a)

\(
\begin{aligned}
&\text { Since the system has a non-trivial solution, the determinant of coefficients }=0\\
&\begin{aligned}
& \Rightarrow\left|\begin{array}{crr}
\sin 3 \theta & -1 & 1 \\
\cos 2 \theta & 4 & 3 \\
2 & 7 & 7
\end{array}\right|=0 \\
& \Rightarrow \sin 3 \theta(28-21)-\cos 2 \theta(-7-7)+2(-3-4)=0 \\
& \Rightarrow \sin 3 \theta+2 \cos 2 \theta-2=0 \\
& \Rightarrow\left(3 \sin \theta-4 \sin ^3 \theta\right)+2\left(1-2 \sin ^2 \theta\right)-2=0 \\
& \Rightarrow 4 \sin \theta^3 \theta+4 \sin ^2 \theta-3 \sin \theta=0 \\
& \Rightarrow \sin \theta(2 \sin \theta-1)(2 \sin \theta+3)=0 \\
& \Rightarrow \sin \theta=0 \text { or } \theta=n \pi+(-1)^n \pi / 6, \forall n \in Z
\end{aligned}
\end{aligned}
\)

Hint

(c)
\(
\begin{aligned}
&\text { Let } \log _{\cos x} \sin x=t \text {, then the given equation is } t+\frac{1}{t}=2\\
&\begin{aligned}
& \Rightarrow(t-1)^2=0 \Rightarrow t=1 \Rightarrow \log _{\cos x} \sin x=1 \text { or } \sin x=\cos x \Rightarrow \tan x=1 \\
& \Rightarrow x=\pi / 4
\end{aligned}
\end{aligned}
\)

Hint

(b) Given \(x^2+2 x \sin (x y)+1=0\)
\(
\begin{aligned}
& \Rightarrow \quad[x+\sin (x y)]^2+\left[1-\sin ^2(x y)\right]=0 \\
& \Rightarrow \quad x+\sin (x y)=0 \text { and } \sin ^2(x y)=1 \\
& \sin ^2(x y)=1 \text { gives } \sin (x y)=1 \text { or }-1
\end{aligned}
\)
If \(\sin (x y)=1 \quad \Rightarrow \quad x=-1 \quad \Rightarrow \sin (-y)=1 \quad \Rightarrow \sin y=-1\), then the ordered pair is \((1,3 \pi / 2)\).
\(
\text { If } \sin (x y)=-1 \quad \Rightarrow \quad x=1 \quad \Rightarrow \quad \sin y=-1 \quad \Rightarrow \quad(-1,3 \pi / 2)
\)
Thus, there are two ordered pairs.

Hint

(c) The given equation is \(8 \sin x \cos x \cos 2 x \cos 4 x=\sin 6 x(\sin x \neq 0)\)
\(
\Rightarrow \sin 8 x=\sin 6 x \quad \Rightarrow 2 \cos 7 x \sin x=0
\)
As \(\sin x \neq 0, \cos 7 x=0\) or \(7 x=n \pi+\pi / 2, n \in Z\)
i.e., \(x=n \pi / 7+\pi / 14 ; n \in Z\)

Hint

(d) We have \(\cos 3 x+\sin \left(2 x-\frac{7 \pi}{6}\right)=-2\).
\(\Rightarrow 1+\cos 3 x+1+\sin \left(2 x-\frac{7 \pi}{6}\right)=0\)
\(\Rightarrow(1+\cos 3 x)+1-\cos \left(2 x-\frac{2 \pi}{3}\right)=0\)
\(\Rightarrow \quad 2 \cos ^2 \frac{3 x}{2}+2 \sin ^2\left(x-\frac{\pi}{3}\right)=0\)
\(\Rightarrow \quad \cos \frac{3 x}{2}=0\) and \(\sin \left(x-\frac{\pi}{3}\right)=0\)
\(\Rightarrow \quad \frac{3 x}{2}=\frac{\pi}{2}, \frac{3 \pi}{2}, \ldots\), and \(x-\frac{\pi}{3}=0, \pi, 2 \pi, \ldots \quad \Rightarrow \quad x=\frac{\pi}{3}\)
Therefore, the general solution of \(\cos \frac{3 x}{2}=0\) and \(\sin \left(x-\frac{\pi}{3}\right)=0\) is \(x=2 k \pi+\frac{\pi}{3}=\frac{\pi}{3}(6 k+1)\) where \(k \in Z\).

Hint

(b) \((1-\tan \theta)(1+\tan \theta) \sec ^2 \theta+2^{\tan ^2 \theta}=0\)
\(
\begin{aligned}
&\sec ^2 \theta=1+\tan ^2 \theta\\
&(1-\tan \theta)(1+\tan \theta)\left(1+\tan ^2 \theta\right)+2^{\tan ^2 \theta}=0
\end{aligned}
\)
Using the identity \(1-\tan ^2 \theta=\sec ^2 \theta-2 \tan ^2 \theta\), we can rewrite the equation as:
\(
1-\tan ^4 \theta+2^{\tan ^2 \theta}=0
\)
\(
\begin{aligned}
&\text { Let } t=\tan ^2 \theta \text {. The equation now becomes: }\\
&1-t^2+2^t=0
\end{aligned}
\)
\(
2^t=t^2-1
\)
We can test values for \(t\) :
For \(t=1\) :
\(
2^1=1-1 \Rightarrow 2 \neq 0
\)
For \(t=2\) :
\(
2^2=4-1 \Rightarrow 4 \neq 3
\)
For \(t=3\) :
\(2^3=9-1 \Rightarrow 8=8 \quad\) (equal)
After testing several values, we find that \(t=3\) satisfies the equation:
\(
1-9+8=0
\)
Since \(t=\tan ^2 \theta=3\), we have:
\(
\tan \theta= \pm \sqrt{3}
\)
The values of \(\theta\) corresponding to \(\tan \theta=\sqrt{3}\) and \(\tan \theta=-\sqrt{3}\) are:
\(
\theta=\frac{\pi}{3}, \quad \theta=-\frac{\pi}{3}
\)
Thus, the values of \(\theta\) in the interval \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) are:
\(
\theta=\frac{\pi}{3},-\frac{\pi}{3}
\)

Hint

(b)

\(
\begin{aligned}
& \tan \left(\frac{\pi}{2} \sin \theta\right)=\cot \left(\frac{\pi}{2} \cos \theta\right) \\
& \therefore \tan \left(\frac{\pi}{2} \sin \theta\right)=\tan \left(\frac{\pi}{2}-\frac{\pi}{2} \cos \theta\right) \\
& \therefore \frac{\pi}{2} \sin \theta=n \pi+\frac{\pi}{2}-\frac{\pi}{2} \cos \theta \\
& \sin \theta+\cos \theta=2 n+1 \\
& \Rightarrow \sin \theta+\cos \theta=1 \pm 1 \\
& \Rightarrow 1+\sin 2 \theta=1 \\
& \Rightarrow \sin 2 \theta=0 \\
& \Rightarrow \theta=n \pi
\end{aligned}
\)
\(
\theta \in[0,6 \pi] \text { (There are 7 different values possible) }
\)

Hint

(a)
\(
\begin{aligned}
& \cos x=\sqrt{1-\sin 2 x}=|\sin x-\cos x| \\
& \text { (i) } \sin x<\cos x \quad \Rightarrow x \in\left[0, \frac{\pi}{4}\right) \cup\left(\frac{5 \pi}{4}, 2 \pi\right] \dots(i)
\end{aligned}
\)
Then the given equation is \(\cos x=\cos x-\sin x \quad \Rightarrow \sin x=0 \quad \Rightarrow \quad x=\pi, 2 \pi\) \(\Rightarrow \quad x=2 \pi \text { [from Eq.(i)] }\)
\(
\begin{aligned}
&\begin{aligned}
& \text { (ii) } \sin x \geq \cos x \quad \Rightarrow x \in\left(\frac{\pi}{4}, \frac{5 \pi}{4}\right) \\
& \Rightarrow \cos x=\sin x-\cos x \\
& \Rightarrow \tan x=2 \\
& \Rightarrow x=\tan ^{-1} 2 \dots(ii)
\end{aligned}\\
&\text { Hence, there are two solutions. }
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
& \sum_{r=1}^5 \cos r x=5 \\
& \Rightarrow \cos x+\cos 2 x+\cos 3 x+\cos 4 x+\cos 5 x=5
\end{aligned}
\)
which is possible only, when \(\cos x=\cos 2 x=\cos 3 x=\cos 4 x=\cos 5 x=1\) and is satisfied by \(x=0\) and \(x=2 \pi\).

Hint

(a)

\(
\sin 2 x+\cos 4 x=2
\)
It is possible only, when \(\sin 2 x=1\) and \(\cos 4 x=1\)
\(
\begin{aligned}
& \Rightarrow \quad \sin 2 x=1 \text { and } 1-2 \sin ^2 2 x=1 \\
& \Rightarrow \quad \sin 2 x=1 \text { and } \sin 2 x=0
\end{aligned}
\)
Hence, there is no solution.

Hint

(d)

\(
\begin{aligned}
&\text { For a GP, } b^2=a c \text {. }\\
&\begin{aligned}
& (|\cos x|)^2=(2 \cos x)\left(1-3 \cos ^2 x\right) \\
& \cos ^2 x=2 \cos x-6 \cos ^3 x
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
&\begin{aligned}
& 6 \cos ^3 x+\cos ^2 x-2 \cos x=0 \\
& \cos x\left(6 \cos ^2 x+\cos x-2\right)=0 \\
& \cos x(3 \cos x+2)(2 \cos x-1)=0
\end{aligned}\\
&\text { Possible values for } \cos x \text { are } \cos x=0, \cos x=-\frac{2}{3} \text {, or } \cos x=\frac{1}{2} \text {. }
\end{aligned}
\)
\(
\Rightarrow \quad x=\frac{\pi}{2}, \frac{\pi}{3}, \cos ^{-1}\left(-\frac{2}{3}\right) \quad(\because \alpha, \beta \text { are }+\mathrm{ve})
\)\(
\text { If } \alpha=\frac{\pi}{2} ; \beta=\frac{\pi}{3} \text {, then we have }|\alpha-\beta|=\frac{\pi}{6} \text {. }
\)

Hint

(b) We have \(\sin ^{100} x-\cos ^{100} x=1\)
\(
\Rightarrow \sin ^{100} x=1+\cos ^{100} x
\)
Since the L.H.S. never exceeds 1, R.H.S. exceeds 1 unless \(\cos x=0\)
Then, \(x=n \pi+\frac{\pi}{2}, n \in I\)

Hint

(b) \(|\cot x|=\cot x+\frac{1}{\sin x}\)
If \(\cot x>0 \Rightarrow \cot x=\cot x+\frac{1}{\sin x}=0\).
\(\Rightarrow \frac{1}{\sin x}=0\), which is not possible.
If \(\cot x \leq 0 \Rightarrow-\cot x=\cot x+\frac{1}{\sin x}\)
\(\Rightarrow-2 \cot x=\frac{1}{\sin x}\)
\(\Rightarrow \cos x=-\frac{1}{2}\)
\(\Rightarrow \quad x=\frac{2 \pi}{3}, \frac{8 \pi}{3}\)

Hint

(a)
\(
\begin{aligned}
&\begin{aligned}
& \tan (A-B)=1 \\
& \Rightarrow A-B=n_1 \pi+\frac{\pi}{4}=\frac{\pi}{4}, \frac{3 \pi}{4},-\frac{3 \pi}{4}, \ldots \\
& \sec (A+B)=\frac{2}{\sqrt{3}} \Rightarrow A+B=2 n_2 \pi \pm \frac{\pi}{6}=\frac{\pi}{6}, \frac{11 \pi}{6}, \ldots
\end{aligned}\\
&\text { For the least positive values of } A \text { and } B \text {, }
\end{aligned}
\)
\(
A+B=\frac{11 \pi}{6}, A-B=\frac{\pi}{4} \quad \Rightarrow \quad B=\frac{19 \pi}{24}, A=\frac{25 \pi}{24}
\)

Hint

(a)
\(
\begin{aligned}
& \text { Let } A=\theta+15^{\circ}, B=\theta-15^{\circ} \\
& \Rightarrow A+B=2 \theta \text { and } A-B=30^{\circ} \\
& \text { Now } \frac{\tan A}{\tan B}=\frac{3}{1}
\end{aligned}
\)
\(
\Rightarrow \frac{\tan A+\tan B}{\tan A-\tan B}=\frac{3+1}{3-1} \text { (applying componendo and dividendo rule) }
\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{\sin (A+B)}{\sin (A-B)}=2 \\
& \Rightarrow \quad \sin 2 \theta=2 \sin 30^{\circ}=1 \\
& \Rightarrow \quad 2 \theta=2 n \pi+\frac{\pi}{2} \text { or } \theta=n \pi+\frac{\pi}{4} n \in Z
\end{aligned}
\)

Hint

(a)
\(
\begin{aligned}
& \tan 3 \theta+\tan \theta=2 \tan 2 \theta \\
& \Rightarrow \tan 3 \theta-\tan 2 \theta=\tan 2 \theta-\tan \theta \\
& \Rightarrow \frac{\sin (3 \theta-2 \theta)}{\cos 3 \theta \cos 2 \theta}=\frac{\sin (2 \theta-\theta)}{\cos 2 \theta \cos \theta} \\
& \Rightarrow \sin \theta(2 \sin \theta \sin 2 \theta)=0 \\
& \Rightarrow \sin \theta=0 \text { or } \sin 2 \theta=0 \\
& \Rightarrow \theta=n \pi \text { or } 2 \theta=n \pi, n \in Z
\end{aligned}
\)
But \(\theta=n \pi / 2\) is rejected as when \(n\) is odd, \(\tan \theta\) is not defined and when \(n\) is even, i.e., \(2 r\), then \(\theta=r \pi\).
Then \(\theta=n \pi, n \in I\) is the only solution.

Hint

(a)

\(
\begin{aligned}
& \text { We have }|4 \sin x-1|<\sqrt{5} \\
& \Rightarrow-\sqrt{5}<4 \sin x-1<\sqrt{5} \\
& \Rightarrow-\left(\frac{\sqrt{5}-1}{4}\right)<\sin x<\left(\frac{\sqrt{5}+1}{4}\right) \\
& \Rightarrow-\sin \frac{\pi}{10}<\sin x<\cos \frac{\pi}{5} \\
& \Rightarrow \sin \left(-\frac{\pi}{10}\right)<\sin x<\sin \left(\frac{\pi}{2}-\frac{\pi}{5}\right) \\
& \Rightarrow \sin \left(-\frac{\pi}{10}\right)<\sin x<\sin \frac{3 \pi}{10} \\
& \Rightarrow x \in\left(-\frac{\pi}{10}, \frac{3 \pi}{10}\right)
\end{aligned}
\)

Hint

(d)
\(
\begin{aligned}
&y^2-y+a=\left(y-\frac{1}{2}\right)^2+a-\frac{1}{4}\\
&\text { Since }-\sqrt{2} \leq \sin x+\cos x \leq \sqrt{2} \text {, the given equation will have no real value } x \text { for any } y \text { if } a-\frac{1}{4}>\sqrt{2}
\end{aligned}
\)
\(
\text { i.e., } a \in\left(\sqrt{2}+\frac{1}{4}, \infty\right) \quad \Rightarrow a \in(\sqrt{3}, \infty) \text { (as } \sqrt{2}+\frac{1}{4}<\sqrt{3} \text { ) }
\)

Hint

(a)

\(
\begin{aligned}
& (2 \sin x-\operatorname{cosec} x)^2+(\tan x-\cot x)^2=0 \\
& \Rightarrow \sin ^2 x=\frac{1}{2} \text { and } \tan ^2 x=1 \\
& \Rightarrow x=n \pi \pm \frac{\pi}{4}, n \in Z
\end{aligned}
\)

Hint

(a) \([\sin x+\cos x]=3+[-\sin x]+[-\cos x]\)
Maximum value of left-hand side is 1 and minimum of right hand side is also 1
\(
\begin{aligned}
& \Rightarrow \quad[\sin x+\cos x]=3+[-\sin x]+[-\cos x]=1 \Rightarrow x \in \pi \pm \frac{\pi}{4} \\
& \Rightarrow \quad[\sin x+\cos x]=1,[-\sin x]=-1,[-\cos x]=-1
\end{aligned}
\)
which is not possible.

Hint

(c)

\(
\begin{aligned}
& \cos ^8 x+b \cos ^4 x+1=0 \\
& \Rightarrow b=-\left(\cos ^4 x+\frac{1}{\cos ^4 x}\right) \leq-2 \forall x \in R \\
& \Rightarrow b \in(-\infty,-2]
\end{aligned}
\)

Hint

(b) Here \(1 \leq|\sin 2 x|+|\cos 2 x| \leq \sqrt{2}\) and \(|\sin y| \leq 1\) so solution is possible only when \(|\sin y|=1\)
\(
\Rightarrow \quad \sin y= \pm 1 \quad \Rightarrow \quad y= \pm \frac{\pi}{2}, \pm \frac{3 \pi}{2}
\)

Explanation: Let \(f(x)=|\sin 2 x|+|\cos 2 x|\).
Square both sides: \((|\sin 2 x|+|\cos 2 x|)^2=\sin ^2 2 x+\cos ^2 2 x+2|\sin 2 x \cos 2 x|\).
This simplifies to \(1+|\sin 4 x|\).
The minimum value of \(1+|\sin 4 x|\) is \(1+0=1\).
The maximum value of \(1+|\sin 4 x|\) is \(1+1=2\).
So, \(1 \leq(|\sin 2 x|+|\cos 2 x|)^2 \leq 2\).
Taking the square root, \(1 \leq|\sin 2 x|+|\cos 2 x| \leq \sqrt{2}\).
\(
\text { Since }|\sin y| \leq 1 \text {, the condition } 1 \leq|\sin y| \leq \sqrt{2} \text { simplifies to }|\sin y|=1 \text {. }
\)
This means \(\sin y=1[latex] or [latex]\sin y=-1\).
For \(\sin y=1, y=\frac{\pi}{2}, \frac{\pi}{2}-2 \pi=-\frac{3 \pi}{2}\).
For \(\sin y=-1, y=\frac{3 \pi}{2}, \frac{3 \pi}{2}-2 \pi=-\frac{\pi}{2}\).
The values of \(y\) in \([-2 \pi, 2 \pi]\) are \(-\frac{3 \pi}{2},-\frac{\pi}{2}, \frac{\pi}{2}, \frac{3 \pi}{2}\).

Hint

(b)

\(
\begin{aligned}
& \text { Given that }|\sin x|^2+|\sin x|+b=0 \\
& \Rightarrow|\sin x|=\frac{-1 \pm \sqrt{1-4 b}}{2} \Rightarrow 0 \leq \frac{-1 \pm \sqrt{1-4 b}}{2}<1 \quad \Rightarrow-2<b<0
\end{aligned}
\)

Hint

(a)
\(
\begin{aligned}
& |2 \sin \theta-\operatorname{cosec} \theta| \geq 1 \\
& \Rightarrow \quad\left|2 \sin ^2 \theta-1\right| \geq \mid \sin \theta \\
& \Rightarrow \quad\left|\cos 2 \theta_1 \geq\right| \sin \theta \\
& \Rightarrow \quad 2 \cos ^2 2 \theta \geq 1-\cos 2 \theta \\
& \Rightarrow \quad 2 \cos ^2 2 \theta+\cos 2 \theta-1 \geq 0 \\
& \Rightarrow \quad(2 \cos 2 \theta-1)(\cos 2 \theta+1) \geq 0 \\
& \Rightarrow \quad \cos 2 \theta \geq \frac{1}{2} [\text { as } \cos \theta \neq 0 \text {, i.e., } \cos 2 \theta \neq-1]
\end{aligned}
\)

Hint

(d) The given equation can be written as
\(
\begin{aligned}
& \sin x \cos x\left[\sin ^2 x+\sin x \cos x+\cos ^2 x\right]=1 \\
& \Rightarrow \sin x \cos x[1+\sin x \cos x]=1 \\
& \Rightarrow \sin 2 x[2+\sin 2 x]=4 \\
& \Rightarrow \sin 2 x=\frac{-2 \pm \sqrt{4+16}}{2}=-1 \pm \sqrt{5}
\end{aligned}
\)
which is not possible.

Hint

(d)
\(
\begin{aligned}
& e^{|\sin x|}+e^{-|\sin x|}+4 a=0, \text { let } t=e^{|\sin x|} \\
& \Rightarrow t \in[1, e] \\
& \Rightarrow t+\frac{1}{t}+4 a=0
\end{aligned}
\)
\(
\Rightarrow t^2+4 a t+1=0
\)
This quadratic expression should have two distinct roots in \([1, e]\)
\(
\begin{aligned}
& \Rightarrow \quad 16 a^2-4>0, f(1)=1+4 a+1 \geq 0, f(e)=e^2+4 a e+1 \geq 0,1<-2 a<e \\
& \Rightarrow \quad|a|>\frac{1}{2}, a \geq-\frac{1}{2}, a \geq \frac{-1-e^2}{4 e},-\frac{e}{2}<a<-\frac{1}{2}
\end{aligned}
\)
Clearly, there is no value of \(a\) satisfying the above inequalities simultaneously.

Hint

(d) For \(\ln |\sin x|\) to be defined, \(|\sin x|>0\).
This means \(\sin x \neq 0\).
In the interval \(\left[-\frac{\pi}{2}, \frac{3 \pi}{2}\right], x \neq 0, \pi\).
The maximum value of \(|\sin x|\) is 1.
So, the maximum value of \(\ln |\sin x|\) is \(\ln (1)=0\).
Thus, \(\ln |\sin x| \leq 0\).
Let \(f(x)=-x^2+2 x\).
This is a downward-opening parabola with vertex at \(x=-\frac{2}{2(-1)}=1\).
The maximum value of \(f(x)\) is \(f(1)=-(1)^2+2(1)=1\).
For a solution to exist, \(\ln |\sin x|=-x^2+2 x\) must be true.
This implies that both sides must be less than or equal to 0.
Since the maximum of \(\ln |\sin x|\) is 0 and the maximum of \(-x^2+2 x\) is 1, the only possible value for both sides to be equal is 0.
If \(\ln |\sin x|=0\), then \(|\sin x|=e^0=1\).
This means \(\sin x=1\) or \(\sin x=-1\).
In the interval \(\left[-\frac{\pi}{2}, \frac{3 \pi}{2}\right], x=-\frac{\pi}{2}, \frac{\pi}{2}\).
If \(-x^2+2 x=0\), then \(-x(x-2)=0\).
This means \(x=0\) or \(x=2\).
The values of \(x\) that make \(\ln |\sin x|=0\) are \(x=-\frac{\pi}{2}\) and \(x=\frac{\pi}{2}\).
The values of \(x\) that make \(-x^2+2 x=0\) are \(x=0\) and \(x=2\).
There are no common values of \(x\) that satisfy both conditions simultaneously.

Hint

(c)
\(
\begin{aligned}
& |x|+|y|=4, \sin \left(\frac{\pi x^2}{3}\right)=1 \\
& \Rightarrow \quad|x|,|y| \in[0,4], \frac{\pi x^2}{3}=(4 n+1) \frac{\pi}{2} \\
& \Rightarrow \quad x^2=\frac{(4 n+1) 3}{2}=\frac{3}{2}, \text { as }|x| \leq 4
\end{aligned}
\)
\(
\begin{aligned}
&\Rightarrow|x|=\sqrt{\frac{3}{2}},|y|=4-\sqrt{\frac{3}{2}} .\\
&\text { Thus, there are four ordered pairs. }
\end{aligned}
\)

Hint

(b)
\(
\begin{aligned}
& \sin \{x\}=\cos \{x\} \\
& \tan \{x\}=1 \\
& \tan (\pi / 4)=1<\tan 1
\end{aligned}
\)

\(
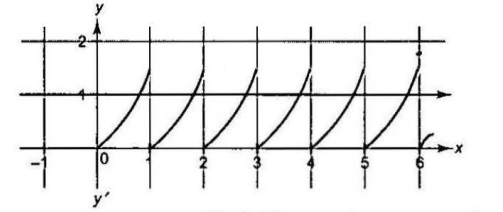
\text { Graphs of } y=\tan \{x\} \text { and } y=1 \text { meet exactly six times in }[0,2 \pi] \text {. }
\)

Hint

(a)

\(
\begin{aligned}
& x^2+4-2 x+3 \sin (a x+b)=0 \\
& (x-1)^2+3=-3 \sin (a x+b) \\
& \text { L.H.S. } \geq 3 \text { and R.H.S. } \leq 3 \\
& \Rightarrow \text { L.H.S }=\text { R.H.S }=3 \\
& (x-1)^2+3+3 \sin (a x+b)=0 \\
& \Rightarrow x=1, \sin (a x+b)=-1 \\
& \Rightarrow \sin (a+b)=-1 \\
& \Rightarrow a+b=(4 n-1) \frac{\pi}{2}, n \in I \Rightarrow a+b=\frac{7 \pi}{2}
\end{aligned}
\)

Hint

(c)

\(
\begin{aligned}
& \tan ^4 x-2 \sec ^2 x+a=0 \\
& \Rightarrow \tan ^4 x-2\left(1+\tan ^2 x\right)+a=0 \\
& \Rightarrow \tan ^4 x-2 \tan ^2 x+1=3-a \\
& \Rightarrow\left(\tan ^2 x-1\right)^2=3-a \\
& \Rightarrow 3-a \geq 0 \Rightarrow a \leq 3
\end{aligned}
\)

Hint

(a) \(1+\log _2 \sin x+\log _2 \sin 3 x \geq 0\)
(where \(\sin x, \sin 3 x>0\) )
\(
\begin{aligned}
& \Rightarrow \quad \log _2(2 \sin x \sin 3 x) \geq 0 \\
& \Rightarrow \quad 2 \sin x \sin 3 x \geq 1
\end{aligned}
\)
For \(\sin x>0\)
\(
\begin{aligned}
& \Rightarrow \quad x \in(0, \pi) \dots(i) \\
& \Rightarrow \quad \sin 3 x>0 \\
& \Rightarrow \quad 3 x \in(0, \pi) \cup(2 \pi, 3 \pi) . \\
& \Rightarrow \quad x \in\left(0, \frac{\pi}{3}\right) \cup\left(\frac{2 \pi}{3}, \pi\right) \dots(ii)
\end{aligned}
\)
For \(2 \sin x \sin 3 x \geq 1\)
\(
\begin{aligned}
& \Rightarrow \quad 2 \sin ^2 x\left(3-4 \sin ^2 x\right) \geq 1 \\
& \Rightarrow \quad 8 \sin ^4 x-6 \sin ^2+1 \leq 0 \\
& \Rightarrow \quad\left(2 \sin ^2 x-1\right)\left(4 \sin ^2 x-1\right) \leq 0 \\
& \Rightarrow \quad \frac{1}{2} \leq \sin x \leq \frac{1}{\sqrt{2}} \\
& \Rightarrow \quad x \in\left[\frac{\pi}{3}, \frac{\pi}{4}\right] \cup\left[\frac{2 \pi}{3}, \frac{3 \pi}{4}\right] \dots(ii)
\end{aligned}
\)
Thus, \(x \in\left(\frac{2 \pi}{3}, \frac{3 \pi}{4}\right] \text { [From Eqs. (i), (ii), (iii) ] }\).

Hint

(d)
\(
\sin ^2 \theta-\frac{4}{\sin ^3 \theta-1}=1-\frac{4}{\sin ^3 \theta-1}
\)
\(
\text { This yields } \sin ^2 \theta=1 \text {. }
\)
Take the square root of both sides: \(\sin \theta= \pm \sqrt{1}\). This gives \(\sin \theta=1\) or \(\sin \theta=-1\).
The original equation has a denominator \(\sin ^3 \theta-1\).
This denominator cannot be zero, so \(\sin ^3 \theta-1 \neq 0\).
Therefore, \(\sin ^3 \theta \neq 1\), which implies \(\sin \theta \neq 1\).
We found \(\sin \theta=1\) or \(\sin \theta=-1\).
The restriction states \(\sin \theta \neq 1\).
Thus, the only valid solution is \(\sin \theta=-1\).
The general solution for \(\sin \theta=-1\) is \(\theta=\frac{3 \pi}{2}+2 n \pi\), where \(n\) is an integer.
Since there are infinitely many integer values for \(n\), there are infinitely many roots.

Hint

(c)

\(
\begin{aligned}
&\begin{aligned}
& \pi \log _3\left(\frac{1}{x}\right)=k \pi, k \in I \\
& \log _3\left(\frac{1}{x}\right)=k \Rightarrow x=3^{-k}
\end{aligned}\\
&\text { The possible values of } k \text { are }-1,0,1,2,3, \ldots\\
&S=3+1+\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+\cdots \infty=\frac{3}{1-\frac{1}{3}}=\frac{9}{2}
\end{aligned}
\)

Hint

(a)

\(
\begin{aligned}
&\begin{aligned}
& \frac{\sin (x y)}{\cos (x y)}=y \\
& \Rightarrow \sin (x y)=x y \\
& \Rightarrow x y=0 \\
& \Rightarrow x=0 \text { or } y=0
\end{aligned}\\
&\text { But } x=0 \text { is not possible }\\
&\therefore y=0 \text { and } x=1 \text {, i.e., }(1,0)
\end{aligned}
\)

Hint

(c)

\(
\begin{aligned}
& \tan x+\cot x+1=\cos \left(x+\frac{\pi}{4}\right) \\
& \Rightarrow \tan x+\cot x=\cos \left(x+\frac{\pi}{4}\right)-1
\end{aligned}
\)
Now \(\tan x+\cot x \leq-2\) and \(\cos \left(x+\frac{\pi}{4}\right)-1 \geq-2\).
It implies that equality holds when both are -2.
\(
\begin{aligned}
& \Rightarrow \cos \left(x+\frac{\pi}{4}\right)=-1 \\
& \Rightarrow x+\frac{\pi}{4}=(2 m+1) \pi, m \in Z \\
& \Rightarrow x=\frac{3 \pi}{4} \text { or } \frac{11 \pi}{4}
\end{aligned}
\)
Therefore, the sum of the solutions is \(\frac{3 \pi}{4}+\frac{11 \pi}{4}=\frac{7 \pi}{2}\).

Hint

(c) \(\cos (\theta) \cos (\pi \theta)=1\)
\(\Rightarrow \cos (\theta)=1\) and \(\cos (\pi \theta)=1 \dots(i)\)
or \(\cos (\theta)=-1\) and \(\cos (\pi \theta)=-1 \dots(ii)\)
If \(\cos (\theta)=1 \Rightarrow \theta=2 m \pi\) and \(\cos (\pi \theta)=1 \Rightarrow \theta=2 \pi\) which is possible only when \(\theta=0\).
Equation (ii) is not possible for any \(\theta\) as for \(\cos (\theta)=-1, \theta\) should be odd multiple of \(\pi \Rightarrow\) irrational and for \(\cos (\pi \theta)=-1 \Rightarrow \theta\) should be odd integer \(\Rightarrow\) rational
Both the conditions cannot be satisfied.
Therefore, \(\theta=0\) is the only solution.

Hint

(c)

\(
\begin{aligned}
& (\cot x+\sqrt{3})^2+\cot ^2 x+4 \operatorname{cosec} x+5=0 \\
& \Rightarrow(\cot x+\sqrt{3})^2+\operatorname{cosec}^2 x+4 \operatorname{cosec} x+4=0 \\
& \Rightarrow(\cot x+\sqrt{3})^2+(\operatorname{cosec} x+2)^2=0 \\
& \Rightarrow \cot x=-\sqrt{3} \text { or } \operatorname{cosec} x=-2 \\
& \Rightarrow x=2 n \pi-\frac{\pi}{6}, n \in Z (\because x \in 4 \text { th quadrant })
\end{aligned}
\)

Hint

(c) \(\theta=k \pi, k=\frac{p}{q}, p, q \in I, q \neq 0\)
\(\cos k \pi\) is a rational
Hence, \(k=0,1,1 / 2,1 / 3,2 / 3\)
There are five values of \(\cos \theta\) for which \(\cos \theta\) is rational.

Explanation:
\(
\text { Let } \theta=\frac{p}{q} \pi \text {, where } p, q \text { are integers and } q \neq 0 \text {. }
\)
For \(\cos \theta\) to be rational, \(\theta\) must be a specific rational multiple of \(\pi\).
The only rational values of \(\cos \theta\) are \(\pm 1, \pm \frac{1}{2}\), and 0.
\(
\begin{aligned}
&\begin{aligned}
& \cos \theta=1 \Longrightarrow \theta=2 n \pi \\
& \cos \theta=-1 \Longrightarrow \theta=(2 n+1) \pi \\
& \cos \theta=0 \Longrightarrow \theta=\left(n+\frac{1}{2}\right) \pi \\
& \cos \theta=\frac{1}{2} \Longrightarrow \theta=\left(2 n \pm \frac{1}{3}\right) \pi \\
& \cos \theta=-\frac{1}{2} \Longrightarrow \theta=\left(2 n \pm \frac{2}{3}\right) \pi
\end{aligned}\\
&\text { All these } \theta \text { values are rational multiples of } \pi \text {. }
\end{aligned}
\)
The distinct rational values are \(\left\{1,-1,0, \frac{1}{2},-\frac{1}{2}\right\}\).
There are 5 distinct values.

Hint

(b)

\(
\text { The equation } a(\cos x-1)+b^2=\cos \left(a x+b^2\right)-1 \text { holds for all } x \in \mathbb{R} \text {. }
\)
Substitute \(x=0\) into the equation \(a(\cos x-1)+b^2=\cos \left(a x+b^2\right)-1\) :
\(a(\cos 0-1)+b^2=\cos \left(a \cdot 0+b^2\right)-1\)
\(a(1-1)+b^2=\cos \left(b^2\right)-1\)
\(b^2=\cos \left(b^2\right)-1\)
Rearrange the equation:
\(\cos \left(b^2\right)=1+b^2\)
Since \(\cos \left(b^2\right) \leq 1\) and \(1+b^2 \geq 1\), the only solution is when both sides are equal to 1.
\(\cos \left(b^2\right)=1\) and \(1+b^2=1\)
Therefore, \(b^2=0\), which implies \(b=0\).
Substitute \(b=0\) into the equation \(a(\cos x-1)+b^2=\cos \left(a x+b^2\right)-1\) :
\(a(\cos x-1)+0^2=\cos \left(a x+0^2\right)-1\)
\(a(\cos x-1)=\cos (a x)-1\)
Rewrite the equation using the double angle formula \(\cos (2 \theta)=1-2 \sin ^2(\theta)\) :
\(a(\cos x-1)=\cos (a x)-1\)
\(a\left(-2 \sin ^2\left(\frac{x}{2}\right)\right)=1-2 \sin ^2\left(\frac{a x}{2}\right)-1\)
\(-2 a \sin ^2\left(\frac{x}{2}\right)=-2 \sin ^2\left(\frac{a x}{2}\right)\)
\(a \sin ^2\left(\frac{x}{2}\right)=\sin ^2\left(\frac{a x}{2}\right)\)
For this equation to hold for all \(x\), we must have \(a=0\) or \(a=1\).
If \(a=0\), then \(0=0\), which is true.
If \(a=1\), then \(\sin ^2\left(\frac{x}{2}\right)=\sin ^2\left(\frac{x}{2}\right)\), which is also true.
Therefore, \(a\) can be 0 or 1.
The solutions for \((a, b)\) are \((0,0)\) and \((1,0)\). There are two ordered pairs.