JEE Practice Questions: Trigonometric Ratios and Identities (Single Choice Type)

Hint

(a)
\(
\text { We have } \frac{x^2+y^2}{2 x y}=\frac{1}{2}\left(\frac{x}{y}+\frac{y}{x}\right)
\)
\(
\begin{aligned}
&\text { Now, } \sin ^2 \theta=\frac{x^2+y^2}{2 x y} \quad \Rightarrow \frac{x^2+y^2}{2 x y} \geq 0\\
&\left[\because \sin ^2 \theta \geq 0\right]
\end{aligned}
\)
Therefore, \(x\) and \(y\) have the same sign.
Now, \(\frac{x^2+y^2}{2 x y}=\frac{1}{2}\left(\frac{x}{y}+\frac{y}{x}\right) \quad \Rightarrow \frac{x^2+y^2}{2 x y} \geq 1(\because[latex] A.M. [latex]\geq[latex] GM. \))\(
But [latex]\sin ^2 \theta \leq 1\). Therefore, \(\frac{x^2+y^2}{2 x y}=1 \Rightarrow x=y\).

Hint

(d) Since \(0<x<\pi\). Therefore, \(\sin x>0\)
We have \(1+\sin x+\sin ^2 x+\cdots \infty=4+2 \sqrt{3}\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{1}{1-\sin x}=4+2 \sqrt{3} \\
& \Rightarrow \quad \sin x=1-\frac{1}{4+2 \sqrt{3}} \\
& \quad=\frac{3+2 \sqrt{3}}{4+2 \sqrt{3}}=\frac{\sqrt{3}}{2} \\
& \Rightarrow \quad x=\frac{\pi}{3} \text { or } \frac{2 \pi}{3}
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
& \frac{\cos x \tan x}{k^2}+\frac{1}{\tan x}+\frac{\sin x}{1+\cos x} \\
& =\frac{\sin x}{k^2}+\frac{\cos x(1+\cos x)+\sin ^2 x}{\sin x(1+\cos x)}=\frac{\cos x(1+\cos x)+\left(1-\cos ^2 x\right)}{\sin x(1+\cos x)}=\frac{a}{k}+\frac{1}{\sin x}=\frac{a}{k}+\frac{1}{a k}
\end{aligned}
\)

Hint

(a)

\(
\begin{aligned}
& 2 \sin \frac{A}{2} \operatorname{cosec} \frac{B}{2}\left(\sin \frac{C}{2}-\cos \frac{A}{2} \cos \frac{B}{2}\right)-\cos A \\
& =2 \sin \frac{A}{2} \operatorname{cosec} \frac{B}{2}\left(\cos \frac{A+B}{2}-\cos \frac{A}{2} \cos \frac{B}{2}\right)-\cos A \\
& =2 \sin \frac{A}{2} \operatorname{cosec} \frac{B}{2}\left(-\sin \frac{A}{2} \sin \frac{B}{2}\right)-\cos A=-2 \sin ^2 \frac{A}{2}-\cos A=-1
\end{aligned}
\)

Hint

(b) Applying A.M. \(\geq\) G.M. in \(6 \tan ^2 \phi, 54 \cot ^2 \phi, 18\), we get
\(
\frac{6 \tan ^2 \phi+54 \cot ^2 \phi+18}{3} \geq(6 \times 54 \times 18)^{1 / 3} \geq 18
\)
This is true if \(6 \tan ^2 \phi=54 \cot ^2 \phi=18\)
\(
\Rightarrow \tan ^2 \phi=3 \text { and } \cot ^2 \phi=1 / 3
\)
Therefore, I and II are correct.

Hint

(c)

\(
\begin{aligned}
&5 \tan \theta=4 \Rightarrow \tan \theta=\frac{4}{5}\\
&\text { Now } \frac{5 \sin \theta-3 \cos \theta}{5 \sin \theta+2 \cos \theta}=\frac{5 \frac{\sin \theta}{\cos \theta}-3}{5 \frac{\sin \theta}{\cos \theta}+2}=\frac{5 \tan \theta-3}{5 \tan \theta+2}=\frac{5 \times \frac{4}{5}-3}{5 \times \frac{4}{5}+2}=\frac{1}{6}
\end{aligned}
\)

Hint

(b) \(2 \sec 2 \theta=\tan \phi+\cot \phi\)
\(
\begin{aligned}
& \Rightarrow \frac{2}{\cos 2 \theta}=\frac{\sin ^2 \phi+\cos ^2 \phi}{\sin \phi \cos \phi} \\
& \Rightarrow \frac{2}{\cos 2 \theta}=\frac{1}{\sin \phi \cos \phi} \\
& \Rightarrow \cos 2 \theta=\sin 2 \phi \\
& \Rightarrow 2 \theta=90^{\circ}-2 \phi \\
& \Rightarrow \theta+\phi=\frac{\pi}{4}
\end{aligned}
\)

Hint

(a)

\(
\begin{aligned}
& \sin x+\operatorname{cosec} x=2 \\
& \Rightarrow(\sin x-1)^2=0 \\
& \Rightarrow \sin x=1 \\
& \Rightarrow \sin ^n x+\operatorname{cosec}^n x=1+1=2
\end{aligned}
\)

Explanation:

\(
\sin x+\frac{1}{\sin x}=2
\)
Multiply by \(\sin x: \sin ^2 x+1=2 \sin x\)
Rearrange: \(\sin ^2 x-2 \sin x+1=0\)
This is a perfect square: \((\sin x-1)^2=0\)
\(
\begin{aligned}
& \sin x-1=0 \\
& \sin x=1
\end{aligned}
\)
\(
\text { Since } \sin x=1, \operatorname{cosec} x=\frac{1}{\sin x}=\frac{1}{1}=1 \text {. }
\)
\(
\begin{aligned}
& \sin ^n x+\operatorname{cosec}^n x=(1)^n+(1)^n \\
& (1)^n+(1)^n=1+1=2
\end{aligned}
\)

Hint

(c) Sum and Prodeuct of roots are
\(
\begin{aligned}
& \sec ^2 \theta+\operatorname{cosec}^2 \theta=\frac{1}{\cos ^2 \theta}+\frac{1}{\sin ^2 \theta}=\frac{4}{\sin ^2 2 \theta} \geq 4 \\
& \text { Also, } \sec ^2 \theta \operatorname{cosec}^2 \theta=\frac{4}{\sin ^2 2 \theta} \geq 4
\end{aligned}
\)
Both sum of roots and prouct of roots are equal.let it t.
Hence, equation will be \(x^2-t x+t=0\) ( \(t[latex] always greater or equals to 4)
Hence, the only equation which can have roots [latex]\operatorname{cosec}^2 \theta\) and \(\sec ^2 \theta\) is \(x^2-5 x+5=0\).

Hint

(b)

\(
\begin{aligned}
\sqrt{\frac{1-\cos \alpha}{1+\cos \alpha}}+\sqrt{\frac{1+\cos \alpha}{1-\cos \alpha}} & =\frac{1-\cos \alpha+1+\cos \alpha}{\sqrt{1-\cos ^2 \alpha}} \\
& =\frac{2}{|\sin \alpha|}=\frac{2}{-\sin \alpha}(\text { since } \pi<\alpha<3 \pi / 2)
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
& \text { We have } \cos \frac{\pi}{7}+\cos \frac{2 \pi}{7}+\cos \frac{3 \pi}{7}+\cos \frac{4 \pi}{7}+\cos \frac{5 \pi}{7}+\cos \frac{6 \pi}{7}+\cos \frac{7 \pi}{7} \\
& =\left(\cos \frac{\pi}{7}+\cos \frac{6 \pi}{7}\right)+\left(\cos \frac{2 \pi}{7}+\cos \frac{5 \pi}{7}\right)+\left(\cos \frac{3 \pi}{7}+\cos \frac{4 \pi}{7}\right)+\cos \pi \\
& =\left(\cos \frac{\pi}{7}-\cos \frac{\pi}{7}\right)+\left(\cos \frac{2 \pi}{7}-\cos \frac{2 \pi}{7}\right)+\left(\cos \frac{3 \pi}{7}-\cos \frac{3 \pi}{7}\right)+\cos \pi \\
& =\cos \pi=-1
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
& 2 \sin ^2 \theta+3 \cos ^2 \theta=2\left(\sin ^2 \theta+\cos ^2 \theta\right)+\cos ^2 \theta=2+\cos ^2 \theta \geq 2 \\
& {\left[\because \cos ^2 \theta>0\right]}
\end{aligned}
\)

Hint

(b)

\(
\sin ^4 \theta+\cos ^4 \theta=\left(\sin ^2 \theta+\cos ^2 \theta\right)^2-2 \sin ^2 \theta \cos ^2 \theta=1-2 \sin ^2 \theta \cos ^2 \theta \leq 1
\)

Hint

(d)

\(
\begin{aligned}
&\text { We have }\\
&f(x)=\cos ^2 \theta+\sec ^2 \theta=(\cos \theta-\sec \theta)^2+2 \cos \theta \sec \theta=2+(\cos \theta-\sec \theta)^2 \geq 2
\end{aligned}
\)

Hint

(a)

\(
\begin{aligned}
& f(x)=\cos ^6 x+\sin ^6 x \\
&=\left(\cos ^2 x+\sin ^2 x\right)\left(\sin ^4 x+\cos ^4 x-\cos ^2 x \sin ^2 x\right) \\
&=\left(\left(\sin ^2 x+\cos ^2 x\right)^2-3 \sin ^2 x \cos ^2 x\right) \\
&=1-\frac{3}{4} \sin ^2 2 x \\
& \Rightarrow f(x) \in\left[\frac{1}{4}, 1\right]
\end{aligned}
\)

Hint

(a)
\(
\begin{aligned}
f(x) & =3 \cos x+5 \sin (x-\pi / 6) \\
& =\frac{1}{2} \cos x+5 \times \frac{\sqrt{3}}{2} \sin x
\end{aligned}
\)
\(
\begin{aligned}
& \text { Then, }-\sqrt{\left(\frac{1}{2}\right)^2+\left(\frac{5 \sqrt{3}}{2}\right)^2} \leq f(x) \leq \sqrt{\left(\frac{1}{2}\right)^2+\left(\frac{5 \sqrt{3}}{2}\right)^2} \\
& \Rightarrow \quad-\sqrt{19} \leq f(x) \leq \sqrt{19}
\end{aligned}
\)

Hint

(d)

\(
\begin{aligned}
& 1-\cos 2 x+\sin 2 x=2 k \\
& \Rightarrow \quad \sin 2 x-\cos 2 x=2 k-1 \\
& \Rightarrow \quad \sin (2 x-\alpha)=\frac{2 k-1}{\sqrt{2}} \\
& \Rightarrow \quad-1 \leq \frac{2 k-1}{\sqrt{2}} \leq 1 \\
& \Rightarrow \quad \frac{1-\sqrt{2}}{2} \leq k \leq \frac{1+\sqrt{2}}{2}
\end{aligned}
\)

Hint

(d)

\(
\begin{aligned}
& \cot (\alpha+\beta)=0 \Rightarrow \alpha+\beta=\pi / 2+n \pi, n \in I \\
& \Rightarrow \sin (\alpha+2 \beta)=\sin \left(90^{\circ}+\beta\right)=\cos \beta(\text { for } n=0) .
\end{aligned}
\)

Hint

(b)

(b)
\(
\begin{aligned}
&\text { We have }\\
&\frac{x}{\cos \theta}=\frac{y}{\cos \left(\theta-\frac{2 \pi}{3}\right)}=\frac{z}{\cos \left(\theta+\frac{2 \pi}{3}\right)}
\end{aligned}
\)
\(
\begin{aligned}
&\text { Therefore, each ratio is equal to }\\
&\begin{aligned}
& \frac{x+y+z}{\cos \theta+\cos \left(\theta-\frac{2 \pi}{3}\right)+\cos \left(\theta+\frac{2 \pi}{3}\right)}=\frac{x+y+z}{0} \\
& \Rightarrow x+y+z=0
\end{aligned}
\end{aligned}
\)

Hint

(b) \(\text { Since } 0 \leq \sin ^{2 n} x \leq \sin ^2 x\)
\(
0 \leq \cos ^{2 n} x \leq \cos ^2 x \text { [as } \sin ^4 x=\sin ^2 x \sin ^2 x \leq \sin ^2 x, \sin ^4 x \leq \sin ^2 x \text { and so on] }
\)
\(
\begin{aligned}
& \Rightarrow \quad 0 \leq \sin ^{2 n} x+\cos ^{2 n} x \leq \sin ^2 x+\cos ^2 x=1 \\
& \Rightarrow \quad 0 \leq \sin ^{2 n} x+\cos ^{2 n} x \leq 1
\end{aligned}
\)

Hint

(b) \(4 x^2-2 \sqrt{5} x+1=0\)
Let \(\alpha\) and \(\beta\) be the roots, we have
\(
\alpha+\beta=\frac{2 \sqrt{5}}{4}=\frac{\sqrt{5}}{2}, \alpha \beta=\frac{1}{4}
\)
Since \(\sin 18^{\circ}=\frac{\sqrt{5}-1}{4}, \cos 36^{\circ}=\frac{\sqrt{5}+1}{4}\)
\(
\therefore \quad \sin 18^{\circ}+\cos 36^{\circ}=\frac{2 \sqrt{5}}{4}=\frac{\sqrt{5}}{2} \sin 18^{\circ} \cos 36^{\circ}=\frac{5-1}{16}=\frac{4}{16}=\frac{1}{4}
\)
Here the required roots are \(\sin 18^{\circ}, \cos 36^{\circ}\).

Hint

(b)

\(
\begin{aligned}
\sqrt{2 \cot \alpha+\frac{1}{\sin ^2 \alpha}}= & \sqrt{2 \cot \alpha+\operatorname{cosec}^2 \alpha} \\
= & \sqrt{2 \cot \alpha+1+\cot ^2 \alpha}=|1+\cot \alpha|=-1-\cot \alpha \\
& \quad[\text { since } \cot \alpha<-1 \text { when } 3 \pi / 4<\alpha<\pi,|1+\cot \alpha|=-1-\cot \alpha]
\end{aligned}
\)

Hint

(d)

\(
\begin{aligned}
f(\theta) & =5 \cos \theta+3 \cos \left(\theta+\frac{\pi}{3}\right)+3=5 \cos \theta+\frac{3}{2} \cos \theta-\frac{3 \sqrt{3}}{2} \sin \theta+3=\frac{13}{2} \cos \theta-\frac{3 \sqrt{3}}{2} \sin \theta+3 \\
& =\sqrt{\left(\frac{169}{4}+\frac{27}{4}\right)} \sin (\theta-\alpha)+3 . \text { Thus, the range of } f(\theta) \text { is }[-4,10] .
\end{aligned}
\)

Hint

(b) 

\(
\begin{aligned}
&\text { Since } \alpha<\beta<\gamma<\delta \text { and } \sin \alpha=\sin \beta=\sin \gamma=\sin \delta=K \text {, therefore } \beta=\pi-\alpha, \gamma=2 \pi+\alpha, \delta=3 \pi-\alpha\\
&\begin{aligned}
\Rightarrow 4 \sin \frac{\alpha}{2}+3 \sin \frac{\beta}{2}+2 \sin \frac{\gamma}{2}+\sin \frac{\delta}{2} & =4 \sin \frac{\alpha}{2}+3 \cos \frac{\alpha}{2}-2 \sin \frac{\alpha}{2}-\cos \frac{\alpha}{2} \\
& =2 \sin \frac{\alpha}{2}+2 \cos \frac{\alpha}{2}=2 \sqrt{1+\sin \alpha}=2 \sqrt{1+K}
\end{aligned}
\end{aligned}
\)

Hint

(c) Let \(O\) be the centre of the circle

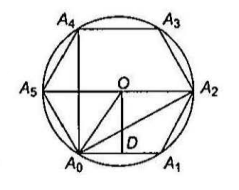
Since \(\angle A_0 O A_1=\frac{360^{\circ}}{6}=60^{\circ}\)
\(A_0 O A_1\) is an equilateral triangle, we get \(A_0 A_1=1\) [radius of circle \(=1\) ]
Also \(A_0 A_2=A_0 A_4=2 O D=2\left[O A_0\right] \sin 60^{\circ}=2(1) \frac{\sqrt{3}}{2}=\sqrt{3}\)

Hint

(d)

\(
\begin{aligned}
&\text { The given relation is satisfied only when } \sin \theta_1=\sin \theta_2=\sin \theta_3=1\\
&\begin{aligned}
& \Rightarrow \quad \cos \theta_1=\cos \theta_2=\cos \theta_3=0 \\
& \Rightarrow \quad \cos \theta_1+\cos \theta_2+\cos \theta_3=0
\end{aligned}
\end{aligned}
\)

Hint

(c)
\(
\begin{aligned}
&\begin{aligned}
& \sin ^2 \theta \leq 1 \\
& \Rightarrow \quad \frac{x^2+y^2+1}{2 x} \leq 1 \quad \Rightarrow x^2+y^2-2 x+1 \leq 0 [\operatorname{as} x>0]\\
& \Rightarrow \quad(x-1)^2+y^2 \leq 0
\end{aligned}\\
&\text { It is possible, iff } x-1 \text { and } y=0 \text {. }
\end{aligned}
\)

Hint

(a)

\(
\begin{aligned}
&\sin (\alpha+\beta)=1 \Rightarrow \alpha+\beta=\frac{\pi}{2} \sin (\alpha-\beta)=\frac{1}{2} \Rightarrow \alpha-\beta=\frac{\pi}{6}\\
&\text { Solving, we get } \alpha=\pi / 3 \text { and } \beta=\pi / 6\\
&\text { Now } \begin{aligned}
\tan (\alpha+2 \beta) \tan (2 \alpha+\beta)=\tan \left(\frac{\pi}{3}+\frac{\pi}{3}\right) \tan \left(\frac{2 \pi}{3}+\frac{\pi}{6}\right)=\tan \frac{2 \pi}{3} \tan \frac{5 \pi}{6} & =\left(-\cot \frac{\pi}{3}\right)\left(-\cot \frac{\pi}{6}\right) \\
& =\left(-\frac{1}{\sqrt{3}}\right)(-\sqrt{3})=1
\end{aligned}
\end{aligned}
\)

Hint

(a)

\(
\begin{aligned}
\sin 27^{\circ}-\sin 63^{\circ} & =-2 \cos 45^{\circ} \sin 18^{\circ} \\
& =-\sqrt{2}\left(\frac{\sqrt{5}-1}{4}\right)=-\frac{\sqrt{5}-1}{2 \sqrt{2}}=-\frac{\sqrt{3-\sqrt{5}}}{2}
\end{aligned}
\)

Hint

(c)

\(
\begin{aligned}
& \operatorname{cosec} \theta-\cot \theta=\dot{q} \\
& \therefore \operatorname{cosec} \theta+\cot \theta=\frac{1}{q} \\
& \therefore \operatorname{cosec} \theta=\frac{1}{2}[q+(1 / q)] \text { (on addition). }
\end{aligned}
\)

Hint

(a) Squaring both the sides, we get
\(
\begin{aligned}
& 1+\sin 2 \theta=\frac{1}{25} \\
& \Rightarrow \sin 2 \theta=-\frac{24}{25}
\end{aligned}
\)
Let \(t=\tan \theta\), we get \(\frac{2 t}{1+t^2}=-\frac{24}{25}\)
\(
\begin{aligned}
& \Rightarrow 50 t+24+24 t^2=0 \\
& \Rightarrow 12 t^2+25 t+12=0 \\
& \Rightarrow(4 t+3)(3 t+4)=0 \\
& \Rightarrow t=-4 / 3(\text { as for } t=-3 / 4(\text { rejected }) \text { as if } \tan \theta=-3 / 4, \text { then } \theta \in[\pi / 2, \pi) \text { and } \sin \theta+\cos \theta=-1 / 5)
\end{aligned}
\)

Hint

(c) Multiplying \(x\) above and below by \(1-\cos \theta+\sin \theta\), we get
\(
x=\frac{2 \sin \theta(1-\cos \theta+\sin \theta)}{(1+\sin \theta)^2-\cos ^2 \theta}=\frac{2 \sin \theta(1-\cos \theta+\sin \theta)}{(1+\sin \theta)^2-\left(1-\sin ^2 \theta\right)}
\)
Putting \(1-\sin ^2 \theta=(1+\sin \theta)(1-\sin \theta)\), we get \(\frac{2 \sin \theta}{2 \sin \theta} \frac{1-\cos \theta+\sin \theta}{1+\sin \theta}=x\).

Hint

(b)

\(
\begin{aligned}
&\begin{aligned}
& 2 n \theta=\pi / 2 \\
& \therefore \quad \theta,(2 n-1) \theta=(\pi / 2)-\theta ; 2 \theta,(2 n-2) \theta=(\pi / 2)-2 \theta, \ldots
\end{aligned}\\
&\text { They form complementary angles } A \text { and } B \text { so that } \tan A \tan B=\tan A \cot A=1 \text { for each pair. }
\end{aligned}
\)

Hint

(a)

\(
\begin{aligned}
& N^r=2\left[\left(\sin 1^{\circ}+\sin 89^{\circ}\right)+\left(\sin 2^{\circ}+\sin 88^{\circ}\right)+\cdots+\left(\sin 44^{\circ}+\sin 46^{\circ}\right)+\sin 45^{\circ}\right] \\
& \begin{aligned}
\Rightarrow \frac{\dot{N}^r}{D^r} & =2\left\{\sin 45^{\circ}\left[2\left(\cos 44^{\circ}+\cos 43^{\circ}+\cdots+\cos 1^{\circ}\right)\right]+1\right\} \\
& =2 \sin 45^{\circ} \\
& =\sqrt{2}
\end{aligned}
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
& \sec \alpha+\operatorname{cosec} \alpha=p, \sec \alpha \operatorname{cosec} \alpha=q \\
& \Rightarrow \frac{\sin \alpha+\cos \alpha}{\sin \alpha \cos \alpha}=p \text { and } \frac{1}{\sin \alpha \cos \alpha}=q \\
& \Rightarrow \frac{1+2 \sin \alpha \cos \alpha}{\sin ^2 \alpha \cos ^2 \alpha}=p^2 \\
& \Rightarrow \frac{1+\frac{2}{q}}{\frac{1}{q^2}}=p^2 \\
& \Rightarrow q^2\left(1+\frac{2}{q}\right)=p^2 \Rightarrow q(q+2)=p^2
\end{aligned}
\)

Hint

(c)

\(
\begin{aligned}
&\text { We have } \sin x+\sin ^2 x=1\\
&\begin{aligned}
& \Rightarrow \sin x=1-\sin ^2 x \Rightarrow \sin x=\cos ^2 x \\
& \text { Now } \cos ^{12} x+3 \cos ^{10} x+3 \cos ^8 x+\cos ^6 x-.2=\sin ^6 x+3 \sin ^5 x+3 \sin ^4 x+\sin ^3 x-2 \\
& =\left(\sin ^2 x\right)^3+3\left(\sin ^2 x\right)^2 \sin x+3\left(\sin ^2 x\right)(\sin x)^2+(\sin x)^3-2 \\
& =\left(\sin ^2 x+\sin x\right)^3-2=(1)^3-2=-1
\end{aligned}
\end{aligned}
\)

Hint

(a)
\(
\begin{aligned}
& \cos (A-B)=\frac{3}{5} \\
& \Rightarrow 5 \cos A \cos B+5 \sin A \sin B=3
\end{aligned}
\)
From 2nd relation, we have
\(\sin A \sin B=2 \cos A \cos B\)
\(\Rightarrow \quad \cos A \cos B=\frac{1}{5}\) and \(\sin A \sin B=\frac{2}{5}\)

Hint

(a)

\(
\begin{aligned}
& (1+\tan A)(1+\tan B)=2 \\
& \Rightarrow \tan A+\tan B=1-\tan A \tan B \\
& \Rightarrow \tan (A+B)=1, \text { i.e., } A+B=\frac{\pi}{4} \\
& \text { or } \alpha+4 \alpha=\frac{\pi}{4}, \text { i.e., } \alpha=\frac{\pi}{20}
\end{aligned}
\)

Hint

(a)

\(
\begin{aligned}
A & =\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2} \sin 90^{\circ} \\
B & =\sqrt{2}\left[\frac{1}{\sqrt{2}} \sin 44^{\circ}+\frac{1}{\sqrt{2}} \cos 44^{\circ}\right]=\sqrt{2} \sin \left(45^{\circ}+44^{\circ}\right) \\
& =\sqrt{2} \sin 89^{\circ}<\sqrt{2} \sin 90^{\circ}=\sqrt{2} \quad \therefore \dot{A}>B 
\end{aligned}
\)

Hint

(d)

\(
\frac{1}{4}\left(\sqrt{3} \cos 23^{\circ}-\sin 23^{\circ}\right)=\frac{1}{2}\left(\cos 30^{\circ} \cos 23^{\circ}-\sin 30^{\circ} \sin 23^{\circ}\right)=\frac{1}{2} \cos \left(30^{\circ}+23^{\circ}\right)=\frac{1}{2} \cos 53^{\circ}
\)

Hint

(b)

\(
\begin{aligned}
\tan \left(\frac{\theta_1-\theta_2}{2}\right) \tan \left(\frac{\theta_1+\theta_2}{2}\right) & =\frac{\sin \left(\frac{\theta_1+\theta_2}{2}\right) \sin \left(\frac{\theta_1-\theta_2}{2}\right)}{\cos \left(\frac{\theta_1+\theta_2}{2}\right) \cos \left(\frac{\theta_1-\theta_2}{2}\right)} \\
& =\frac{\cos \theta_2-\cos \theta_1}{\cos \theta_1+\cos \theta_2}=\frac{-1}{3}
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
\frac{3+\frac{\cos 80^{\circ} \cos 20^{\circ}}{\sin 80^{\circ} \sin 20^{\circ}}}{\frac{\cos 80^{\circ}}{\sin 80^{\circ}}+\frac{\cos 20^{\circ}}{\sin 20^{\circ}}} & =\frac{2 \sin 80^{\circ} \sin 20^{\circ}+\left(\cos 80^{\circ} \cos 20^{\circ}+\sin 80^{\circ} \sin 20^{\circ}\right)}{\sin 20^{\circ} \cos 80^{\circ}+\cos 20^{\circ} \sin 80^{\circ}} \\
& =\frac{-\cos 100^{\circ}+\cos 60^{\circ}+\cos 60^{\circ}}{\sin 100^{\circ}}=\frac{1-\cos 100^{\circ}}{\sin 100}=\tan 50^{\circ}
\end{aligned}
\)

Hint

(a)
\(
\begin{aligned}
& \tan \beta=2 \sin \alpha \sin \gamma \operatorname{cosec}(\alpha+\gamma)=\frac{2 \sin \alpha \sin \gamma}{\sin (\alpha+\gamma)} \\
& \Rightarrow \cot \beta=\frac{\sin (\alpha+\gamma)}{2 \sin \alpha \sin \gamma}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow 2 \cot \beta=\frac{\sin \alpha \cos \gamma+\cos \alpha \sin \gamma}{\sin \alpha \sin \gamma}=\cot \alpha+\cot \gamma \\
& \Rightarrow \cot \alpha, \cot \beta, \cot \gamma \text { are in A.P. }
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
& 3 \sin A \cos B=\sin B \cos A \\
& \Rightarrow \quad \cos A \sin B=\frac{3}{4} \\
& \Rightarrow \quad \sin (A+B)=1 \\
& \Rightarrow \quad C=\frac{\pi}{2}, B=\frac{\pi}{2}-A \\
& \Rightarrow \quad 3 \tan A=\tan \left(\frac{\pi}{2}-A\right) \\
& \Rightarrow \quad 3=\cot ^2 A
\end{aligned}
\)

Hint

(d)

\(
\begin{aligned}
&\begin{aligned}
& \tan \left(100^{\circ}+125^{\circ}\right)=\frac{\tan 100^{\circ}+\tan 125^{\circ}}{1-\tan 100^{\circ} \tan 125^{\circ}} \\
& \therefore \quad \tan 225^{\circ}=\frac{\tan 100^{\circ}+\tan 125^{\circ}}{1-\tan 100^{\circ} \tan 125^{\circ}}, \text { i.e., } 1=\frac{\tan 100^{\circ}+\tan 125^{\circ}}{1-\tan 100^{\circ} \tan 125^{\circ}}
\end{aligned}\\
&\text { i.e., } \tan 100^{\circ}+\tan 125^{\circ}+\tan 100^{\circ} \tan 125^{\circ}=1
\end{aligned}
\)

Hint

\(
\begin{aligned}
& \text { We know that } \tan \left(20^{\circ}+40^{\circ}\right)=\frac{\tan 20^{\circ}+\tan 40^{\circ}}{1-\tan 20^{\circ} \tan 40^{\circ}} \\
& \Rightarrow \sqrt{3}=\frac{\tan 20^{\circ}+\tan 40^{\circ}}{1-\tan 20^{\circ} \tan 40^{\circ}} \\
& \Rightarrow \sqrt{3}-\sqrt{3} \tan 20^{\circ} \tan 40^{\circ}=\tan 20^{\circ}+\tan 40^{\circ} \\
& \Rightarrow \tan 20^{\circ}+\tan 40^{\circ}+\sqrt{3} \tan 20^{\circ} \tan 40^{\circ}=\sqrt{3}
\end{aligned}
\)

Hint

(c)

\(
\begin{aligned}
& \frac{\sqrt{2}-\sin \alpha-\cos \alpha}{\sin \alpha-\cos \alpha} \\
& =\frac{\sqrt{2}-\sqrt{2}\left(\frac{1}{\sqrt{2}} \sin \alpha+\frac{1}{\sqrt{2}} \cos \alpha\right)}{\sqrt{2}\left(\frac{1}{\sqrt{2}} \sin \alpha-\frac{1}{\sqrt{2}} \cos \alpha\right)} \\
& =\frac{\sqrt{2}-\sqrt{2} \cos \left(\alpha-\frac{\pi}{4}\right)}{\sqrt{2} \sin \left(\alpha-\frac{\pi}{4}\right)} \\
& =\frac{\sqrt{2}(1-\cos \theta)}{\sqrt{2} \sin \theta}, \text { where } \theta=\alpha-\frac{\pi}{4}=\frac{2 \sin ^2(\theta / 2)}{2 \sin (\theta / 2) \cos (\theta / 2)}=\tan \frac{\theta}{2}=\tan \left(\frac{\alpha}{2}-\frac{\pi}{8}\right)
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
& \sin \theta_1-\sin \theta_2=a, \cos \theta_1+\cos \theta_2=b \\
& \Rightarrow \quad a^2+b^2=2+2 \cos \left(\theta_1+\theta_2\right) \\
& \Rightarrow \quad 0 \leq a^2+b^2 \leq 4
\end{aligned}
\)

Hint

(c)

\(
\begin{aligned}
\frac{1+\sin 2 x}{1-\sin 2 x} & =\frac{(\sin x+\cos x)^2}{(\sin x-\cos x)^2}=\left(\frac{1+\tan x}{1-\tan x}\right)^2=\left(\tan \left(\frac{\pi}{4}+x\right)\right)^2=\tan ^2\left(\frac{\pi}{4}+x\right) \\
& =\cot ^2\left(\frac{\pi}{2}+\frac{\pi}{4}+x\right)=\cot ^2\left(\frac{3 \pi}{4}+x\right) \\
\Rightarrow \quad a & =\frac{3 \pi}{4}
\end{aligned}
\)

Hint

(d) We have \(4 x^2-16 x+15<0 \Rightarrow \frac{3}{2}<x<\frac{5}{2}\)
Therefore, the integral solution of \(4 x^2-16 x+15<0[latex] is [latex]x=2\)
Thus, \(\tan \alpha=2\). It is given that \(\cos \beta=\tan 45^{\circ}=1\).
\(
\therefore \quad \sin (\alpha+\beta) \sin (\alpha-\beta)=\sin ^2 \alpha-\sin ^2 \beta=\frac{1}{1+\cot ^2 \alpha}-\left(1-\cos ^2 \beta\right)=\frac{1}{1+\frac{1}{4}}-0=\frac{4}{5}
\)

Hint

(b)

\(
\begin{aligned}
& \frac{\cos (x-y)}{\cos (x+y)}+\frac{\cos (z+t)}{\cos (z-t)}=0 \\
& \Rightarrow \frac{1+\tan x \tan y}{1-\tan x \tan y}+\frac{1-\tan z \tan t}{1+\tan z \tan t}=0 \\
& \Rightarrow 1+\tan z \tan t+\tan x \tan y+\tan x \tan y \tan z \tan t+1-\tan z \tan t-\tan x \tan y \\
& \quad+\tan x \tan y \tan z \tan t=0 \\
& \Rightarrow \tan x \tan y \tan z \tan t=-1 .
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
& f(n)=2 \cos n x \\
& \begin{aligned}
\Rightarrow \quad f(1) f(n+1)-f(n) & =4 \cos x \cos (n+1) x-2 \cos n x=2[2 \cos (n+1) x \cos x-\cos n x] \\
& =2[\cos (n+2) x+\cos n x-\cos n x]=2 \cos (n+2) x=f(n+2)
\end{aligned}
\end{aligned}
\)

Hint

(a)

\(
\begin{aligned}
& \frac{\tan A}{\tan B}=\frac{1}{3} \Rightarrow \frac{\sin A \cos B}{\cos A \sin B}=\frac{1}{3} \\
& \text { Put } \sin A \cos B=\frac{1}{4} \\
& \Rightarrow \cos A \sin B=\frac{3}{4} \\
& \Rightarrow \sin (A+B)=\frac{1}{4}+\frac{3}{4}=1 \\
& \Rightarrow \sin C=1=\sin \pi / 2 \\
& \Rightarrow C=\pi / 2 . \text { Hence, the triangle is right angled. }
\end{aligned}
\)

Hint

(b)
\(
\begin{aligned}
& 3 \sin ^2 A+2 \sin ^2 B=1 \\
& \Rightarrow \quad 3 \sin ^2 A=\cos 2 B \\
& \text { Also } 3 \sin 2 A-2 \sin 2 B=0 \\
& \Rightarrow \quad \sin 2 B=\frac{3}{2} \sin 2 A
\end{aligned}
\)
\(
\begin{aligned}
&\text { Now, } \cos (A+2 B)=\cos A \cos 2 B-\sin A \sin 2 B=\cos A 3 \sin ^2 A-\sin A \frac{3}{2} \sin 2 A\\
&=3 \sin ^2 A \cos A-3 \sin ^2 A \cos A=0\\
&\therefore A+2 B=\pi / 2
\end{aligned}
\)

Hint

\(
\begin{aligned}
&\text { (a) }\\
&\begin{aligned}
f(\beta)=f\left(\frac{5 \pi}{4}-\alpha\right) & =\frac{\cot \left(\frac{5 \pi}{4}-\alpha\right)}{1+\cot \left(\frac{5 \pi}{4}-\alpha\right)} \\
& =\frac{1}{1+\tan \left(\frac{5 \pi}{4}-\alpha\right)} \\
& =\frac{1}{1+\frac{1-\tan \alpha}{1+\tan \alpha}}=\frac{1+\tan \alpha}{2} \\
\text { As } f(\alpha)=\frac{\cot \alpha}{1+\cot \alpha} & =\frac{1}{1+\tan \alpha}, \text { we have } f(\alpha) f(\beta)=\frac{1}{2}
\end{aligned}
\end{aligned}
\)

Hint

(c) 

\(
\begin{aligned}
& A-B=\frac{\pi}{4} \Rightarrow \tan (A-B)=\tan \frac{\pi}{4} \\
& \Rightarrow \quad \frac{\tan A-\tan B}{1+\tan A \tan B} \\
& \Rightarrow \quad \tan A-\tan B-\tan A \tan B=1 \\
& \Rightarrow \quad \tan A-\tan B-\tan A \tan B+1=2 \\
& \Rightarrow \quad(1+\tan A)(1-\tan B)=2 \Rightarrow y=2 \\
& \text { Hence, }(y+1)^{y+1}=(2+1)^{2+1}=(3)^3=27
\end{aligned}
\)

Hint

(a) Applying \(b-a=c-b\) for A.P., we get \(2 \cos z \sin (x-y)=2 \cos x \sin (y-z)\)
Dividing by \(2 \cos x \cos y \cos z\), etc., we get \(\tan x-\tan y=\tan y-\tan z\).

Hint

(b)

\(
\begin{aligned}
(\cos \alpha+\cos \beta)^2-(\sin \alpha+\sin \beta)^2=0 \\
\Rightarrow \quad\left(\cos ^2 \alpha+\cos ^2 \beta+2 \cos \alpha \cos \beta\right)-\left(\sin ^2 \alpha+\sin ^2 \beta+2 \sin \alpha \sin \beta\right)=0 \\
\Rightarrow \quad \cos 2 \alpha+\cos 2 \beta=-2(\cos \alpha \cos \beta-\sin \alpha \sin \beta) \\
=-2 \cos (\alpha+\beta)
\end{aligned}
\)

Hint

(a)
\(
\begin{aligned}
&\text { We have }\\
&\begin{aligned}
& \sin \alpha \sec x_1 \sec x_2+\sin \alpha \sec x_2 \sec x_3+\cdots+\sin \alpha \sec x_{n-1} \sec x_n \\
& =\frac{\sin \left(x_2-x_1\right)}{\cos x_1 \cos x_2}+\frac{\sin \left(x_3-x_2\right)}{\cos x_2 \cos x_3}+\cdots+\frac{\sin \left(x_n-x_{n-1}\right)}{\cos x_{n-1} \cos x_n} \\
& =\left(\tan x_2-\tan x_1\right)+\left(\tan x_3-\tan x_2\right)+\cdots+\left(\tan x_n-\tan x_{n-1}\right) \\
& =\tan x_n-\tan x_1=\frac{\sin \left(x_n-x_1\right)}{\cos x_n \cos x_1}=\frac{\sin (n-1) \alpha}{\cos x_n \cos x_1} \left[\because x_n=x_1+(n-1) \alpha\right]
\end{aligned}
\end{aligned}
\)

Hint

(a)
\(
\begin{aligned}
&\text { By the given conditions } \tan \frac{\pi}{9}+\tan \frac{5 \pi}{18}=2 x\\
&\begin{aligned}
\tan \frac{\pi}{9}+ & \tan \frac{7 \pi}{18}=2 y \\
\Rightarrow 2 x & =\tan 20^{\circ}+\tan 50^{\circ} \\
& =\frac{\sin 20^{\circ}}{\cos 20^{\circ}}+\frac{\sin 50^{\circ}}{\cos 50^{\circ}} \\
& =\frac{\sin 20^{\circ} \cos 50^{\circ}+\cos 20^{\circ} \sin 50^{\circ}}{\cos 20^{\circ} \cos 50^{\circ}} \\
& =\frac{\sin 70^{\circ}}{\cos 20^{\circ} \cos 50^{\circ}}
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{\cos 20^{\circ}}{\cos 20^{\circ} \cos 50^{\circ}}=\frac{1}{\cos 50^{\circ}}=\frac{1}{\sin 40^{\circ}}=\operatorname{cosec} 40^{\circ} \\
2 y & =\tan 20^{\circ}+\tan 70^{\circ} \\
& =\frac{\sin 20^{\circ}}{\cos 20^{\circ}}+\frac{\sin 70^{\circ}}{\cos 70^{\circ}} \\
& =\frac{\sin 90^{\circ}}{\cos 20^{\circ} \cos 70^{\circ}} \\
& =\frac{1}{\cos 20^{\circ} \cos 70^{\circ}}=\frac{1}{\cos 20^{\circ} \sin 20^{\circ}} \\
& =\frac{2}{2 \sin 20^{\circ} \cos 20^{\circ}}=\frac{2}{\sin 40^{\circ}}=2 \operatorname{cosec} 40^{\circ} \\
\therefore 2 y & =2(2 x) \Rightarrow y=2 x
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
& \frac{1}{\sin 1^{\circ}}\left[\frac{\sin \left(1^{\circ}-0^{\circ}\right)}{\cos 0^{\circ} \cos 1^{\circ}}+\frac{\sin \left(2^{\circ}-1^{\circ}\right)}{\cos 1^{\circ} \cos 2^{\circ}}+\frac{\sin \left(3^{\circ}-2^{\circ}\right)}{\cos 2^{\circ} \cos 3^{\circ}}+\cdots+\frac{\sin \left(45^{\circ}-44^{\circ}\right)}{\cos 44^{\circ} \cos 45^{\circ}}\right] \\
& =\frac{1}{\sin 1^{\circ}}\left[\tan 1^{\circ}+\left(\tan 2^{\circ}-\tan 1^{\circ}\right)+\left(\tan 3^{\circ}-\tan 2^{\circ}\right)+\left(\tan 4^{\circ}-\tan 3^{\circ}\right)+\cdots+\left(\tan 45^{\circ}-\tan 44^{\circ}\right)\right] \\
& =\frac{1}{\sin 1^{\circ}}=\frac{1}{x}
\end{aligned}
\)

Hint

(a) We have \(\sin \alpha+\sin \beta=-\frac{21}{65} \dots(i)\)
\(
\cos \alpha+\cos \beta=-\frac{17}{65} \dots(ii)
\)
Squaring Eq. (i), we get \(\sin ^2 \alpha+\sin ^2 \beta+2 \sin \alpha \sin \beta=\left(\frac{21}{65}\right)^2 \dots(iii)\)
Squaring Eq. (ii), we get \(\cos ^2 \alpha+\cos ^2 \beta+2 \cos \alpha \cos \beta=\left(\frac{27}{65}\right)^2 \dots(iv)\).
\(
\begin{aligned}
& \text { Adding Eqs. (iii) and (iv), we get } 2+2 \cos (\alpha-\beta)=\frac{1}{(65)^2}\left[(27)^2+(21)^2\right]=\frac{1}{(65)^2}(729+441) \\
& \Rightarrow 2+2 \cos (\alpha-\beta)=\frac{1}{(65)^2}(1170)=\frac{18}{65} \\
& \Rightarrow 1+\cos (\alpha-\beta)=\frac{9}{65} \\
& \Rightarrow 2 \cos ^2 \frac{\alpha-\beta}{2}=\frac{9}{65}
\end{aligned}
\)
\(
\Rightarrow \cos \frac{\alpha-\beta}{2}=-\frac{3}{\sqrt{130}} \left[\because \pi<\alpha-\beta<3 \pi \Rightarrow \frac{\pi}{2}<\frac{\alpha-\beta}{2}<\frac{3 \pi}{2} \Rightarrow \cos \left(\frac{\alpha-\beta}{2}\right)<0\right]
\)

Hint

(b)

\(
\begin{aligned}
& \frac{\sin (x+y)}{\sin (x-y)}=\frac{a+b}{a-b} \\
& \Rightarrow \frac{\sin (x+y)+\sin (x-y)}{\sin (x+y)-\sin (x-y)}=\frac{(a+b)+(a-b)}{(a+b)-(a-b)} \\
& \Rightarrow \frac{2 \sin x \cos y}{2 \cos x \sin y}=\frac{2 a}{2 b} \\
& \Rightarrow \frac{\tan x}{\tan y}=\frac{a}{b}
\end{aligned}
\)

Hint

(c)

\(
\begin{aligned}
& \frac{\sin 3 \theta+\sin 5 \theta+\sin 7 \theta+\sin 9 \theta}{\cos 3 \theta+\cos 5 \theta+\cos 7 \theta+\cos 9 \theta}=\frac{(\sin 3 \theta+\sin 9 \theta)+(\sin 5 \theta+\sin 7 \theta)}{(\cos 3 \theta+\cos 9 \theta)+(\cos 5 \theta+\cos 7 \theta)} \\
& =\frac{2 \sin 6 \theta \cos 3 \theta+2 \sin 6 \theta \cos \theta}{2 \cos 6 \theta \cos 3 \theta+2 \cos 6 \theta \cos \theta}=\frac{2 \sin 6 \theta(\cos 3 \theta+\cos \theta)}{2 \cos 6 \theta(\cos 3 \theta+\cos \theta)}=\tan 6 \theta
\end{aligned}
\)

Hint

(b)

\(
\frac{\sin x-\sin z}{\cos z-\cos x}=\frac{2 \cos \left(\frac{x+z}{2}\right) \sin \left(\frac{x-z}{z}\right)}{2 \sin \left(\frac{x+z}{z}\right) \sin \left(\frac{x-z}{z}\right)}=\cot \left(\frac{x+z}{2}\right)=\cot (y)
\)

Hint

(c)
\(
\begin{aligned}
&\begin{aligned}
& \cos 50^{\circ}=\cos ^2 25^{\circ}-\sin ^2 25^{\circ}=\left(\cos 25^{\circ}+\sin 25^{\circ}\right)\left(\cos 25^{\circ}-\sin 25^{\circ}\right)=p\left(\cos 25^{\circ}-\sin 25^{\circ}\right) \dots(i) \\
& \text { Now }\left(\cos 25^{\circ}-\sin 25^{\circ}\right)^2+\left(\cos 25^{\circ}+\sin 25^{\circ}\right)^2=1+1 \\
& \therefore \quad \cos 25^{\circ}-\sin 25^{\circ}=\sqrt{2-p^2} \dots(ii)
\end{aligned}\\
&\text { We have taken }+ \text { ve sign as } \cos 25^{\circ}>\sin 25^{\circ} \text {, therefore } \cos 50^{\circ}=p \sqrt{2-p^2} \text {, by Eqs. (i) and (ii). }
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
\frac{\sin ^2 A-\sin ^2 B}{\sin A \cos A-\sin B \cos B}=\frac{2 \sin (A+B) \sin (A-B)}{\sin 2 A-\sin 2 B} & =\frac{2 \sin (A+B) \sin (A-B)}{2 \sin (A-B) \cos (A+B)} \\
& =\tan (A+B)
\end{aligned}
\)

Hint

(a)

\(
\tan A=\frac{1-\cos B}{\sin B}=\frac{2 \sin ^2(B / 2)}{2 \sin (B / 2) \cos (B / 2)}=\tan \frac{B}{2} \quad \Rightarrow \tan 2 A=\tan B
\)

Hint

(c)
\(
\begin{aligned}
& \cos ^2 10^{\circ}-\cos 10^{\circ} \cos 50^{\circ}+\cos ^2 50^{\circ} \\
& =\frac{1}{2}\left[1+\cos 20^{\circ}-\left(\cos 60^{\circ}+\cos 40^{\circ}\right)+\left(1+\cos 100^{\circ}\right)\right] \\
& =\frac{1}{2}\left[1+\cos 20^{\circ}-\frac{1}{2}-\cos 40^{\circ}+1-\cos 80^{\circ}\right] \\
& =\frac{1}{2}\left[\frac{3}{2}+\cos 20^{\circ}-\left(2 \cos 60^{\circ} \cos 20^{\circ}\right)\right]=\frac{3}{4} .
\end{aligned}
\)

Hint

(b) On adding, we get \(a=\frac{3-\cos 4 \theta+4 \sin 2 \theta}{2}=(1+\sin 2 \theta)^2\)
On subtracting, we get \(b=(1-\sin 2 \theta)^2 \Rightarrow a b=\cos ^4 2 \theta \leq 1\)

Hint

(a)

\(
\begin{aligned}
\tan 20^{\circ} \tan 80^{\circ} \cot 50^{\circ} & =\tan 20^{\circ} \tan 80^{\circ} \tan 40^{\circ} \\
& =\tan 20^{\circ} \tan \left(60^{\circ}-20^{\circ}\right) \tan \left(60^{\circ}+20^{\circ}\right)=\tan 60^{\circ}=\sqrt{3}
\end{aligned}
\)

Hint

(b)

\(
\begin{gathered}
\tan ^2 \theta=2 \tan ^2 \phi+1 \\
\Rightarrow \quad 1+\tan ^2 \theta=2\left(1+\tan ^2 \phi\right) \\
\Rightarrow \quad \sec ^2 \theta=2 \sec ^2 \phi \\
\Rightarrow \quad \cos ^2 \phi=2 \cos ^2 \theta \\
\quad=1+\cos 2 \theta \\
\Rightarrow \quad \cos 2 \theta=\cos ^2 \phi-1 \\
\quad=-\sin ^2 \phi \\
\Rightarrow \quad \sin ^2 \phi+\cos 2 \theta=0
\end{gathered}
\)

Hint

(b)

\(
\begin{aligned}
\cot 70^{\circ}+4 \cos 70^{\circ} & =\frac{\cos 70^{\circ}+4 \sin 70^{\circ} \cos 70^{\circ}}{\sin 70^{\circ}} \\
& =\frac{\cos 70^{\circ}+2 \sin 140^{\circ}}{\sin 70^{\circ}} \\
& =\frac{\cos 70^{\circ}+2 \sin \left(180^{\circ}-40^{\circ}\right)}{\sin 70^{\circ}} \\
& =\frac{\sin 20^{\circ}+\sin 40^{\circ}+\sin 40^{\circ}}{\sin 70^{\circ}} \\
& =\frac{2 \sin 30^{\circ} \cos 10^{\circ}+\sin 40^{\circ}}{\sin 70^{\circ}} \\
& =\frac{\sin 80^{\circ}+\sin 40^{\circ}}{\sin 70^{\circ}} \\
& =\frac{2 \sin 60^{\circ} \cos 20^{\circ}}{\sin 70^{\circ}}=\sqrt{3}
\end{aligned}
\)

Hint

(b)
\(
\begin{aligned}
& a \cos x+b \sin x=c \\
& \Rightarrow \frac{a\left(1-\tan ^2 \frac{x}{2}\right)}{1+\tan ^2 \frac{x}{2}}+\frac{2 b \tan \frac{x}{2}}{1+\tan ^2 \frac{x}{2}}=c
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad(c+a) \tan ^2 \frac{x}{2}-2 b \tan \frac{x}{2}+c-a=0 \\
& \Rightarrow \quad \tan \frac{x_1}{2}+\tan \frac{x_2}{2}=\frac{2 b}{c+a} \text { and } \tan \frac{x_1}{2} \tan \frac{x_2}{2}=\frac{c-a}{c+a} \\
& \Rightarrow \quad \tan \left(\frac{x_1+x_2}{2}\right)=\frac{\frac{2 b}{c+a}}{1-\frac{c-a}{c+a}}=\frac{2 b}{2 a}=\frac{b}{a}
\end{aligned}
\)

Hint

(c)

\(
\begin{aligned}
& \tan y=\frac{1+\sqrt{1-x}}{1+\sqrt{1+x}} \\
& \text { If } x=\cos \theta, \text { then } \sqrt{1-x}=\sqrt{2} \sin (\theta / 2), \sqrt{1+x}=\sqrt{2} \cos (\theta / 2) \\
& \Rightarrow \tan y=\frac{\sqrt{2}\left[\frac{1}{\sqrt{2}}+\sin \frac{\theta}{2}\right]}{\sqrt{2}\left[\frac{1}{\sqrt{2}}+\cos \frac{\theta}{2}\right]}=\frac{\sin \frac{\pi}{4}+\sin \frac{\theta}{2}}{\cos \frac{\pi}{4}+\cos \frac{\theta}{2}} \\
& \quad=\frac{2 \sin \left(\frac{\pi}{8}+\frac{\theta}{4}\right) \cos \left(\frac{\pi}{8}-\frac{\theta}{4}\right)}{2 \cos \left(\frac{\pi}{8}+\frac{\theta}{4}\right) \cos \left(\frac{\pi}{8}-\frac{\theta}{4}\right)} \\
& \quad=\tan \left(\frac{\pi}{8}+\frac{\theta}{4}\right) \\
& \Rightarrow 4 y=\frac{\pi}{2}+\theta \\
& \Rightarrow \sin 4 y=\cos \theta=x
\end{aligned}
\)

Hint

(d)
\(
\begin{aligned}
&\text { We have } \cos x=\tan y\\
&\begin{aligned}
\Rightarrow \quad \cos ^2 x & =\tan ^2 y \\
& =\sec ^2 y-1 \\
& =\cot ^2 z-1 [\because \cos y=\tan z, \sec y=\cot z]
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
\Rightarrow 1+\cos ^2 x & =\cot ^2 z \\
& =\frac{\tan ^2 x}{1-\tan ^2 x} [\because \cos z=\tan x]
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{\sin ^2 x}{\cos ^2 x-\sin ^2 x} \\
\Rightarrow \quad & 2 \sin ^4 x-6 \sin ^2 x+2=0 \\
\Rightarrow \quad & \sin ^2 x=\frac{3-\sqrt{5}}{2} .
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \sin ^2 x=\left(\frac{\sqrt{5}-1}{2}\right)^2 \\
& \Rightarrow \sin x=\frac{\sqrt{5}-1}{2}=2 \sin 18^{\circ}
\end{aligned}
\)

Hint

(a)

\(
\begin{aligned}
& \sin 2 \theta=\cos 3 \theta \quad \Rightarrow 2 \sin \theta \cos \theta=4 \cos ^3 \theta-3 \cos \theta \\
& \Rightarrow \quad 2 \sin \theta=4\left(1-\sin ^2 \theta\right)-3 \Rightarrow 4 \sin ^2 \theta+2 \sin \theta-1=0 \\
& \Rightarrow \quad \sin \theta=\frac{\sqrt{5}-1}{4}
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
& \tan \theta=\lambda, \text { we get } \frac{2 \tan \theta / 2}{1-\tan ^2 \theta / 2}=\lambda \\
& \Rightarrow \lambda \tan ^2 \frac{\theta}{2}+2 \tan \frac{\theta}{2}-\lambda=0 \\
& \Rightarrow \tan \frac{\theta_1}{2} \tan \frac{\theta_2}{2}=-1
\end{aligned}
\)

Hint

(a) \(\tan \theta=\sqrt{n} \quad \Rightarrow \cos 2 \theta=\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta}=\frac{1-n}{1+n}=\text { rational. }\)

Hint

(b)

\(
\begin{aligned}
& \sin x+\cos x=\frac{\sqrt{7}}{2} \\
& \Rightarrow \quad \frac{2 \tan \frac{x}{2}}{\left(1+\tan ^2 \frac{x}{2}\right)}+\frac{1-\tan ^2 \frac{x}{2}}{1+\tan ^2 \frac{x}{2}}=\frac{\sqrt{7}}{2} \\
& \Rightarrow \quad(\sqrt{7}+2) \tan ^2 \frac{x}{2}-4 \tan \frac{x}{2}+(\sqrt{7}-2)=0 \\
& \Rightarrow \quad \tan \frac{x}{2}=\frac{4 \pm \sqrt{16-4(7-4)}}{2(\sqrt{7}+2)}=\frac{1}{(\sqrt{7}+2)} \text { as } \frac{x}{2}<\frac{\pi}{8} \\
& \quad=\frac{\sqrt{7}-2}{3}
\end{aligned}
\)

Hint

(b)
\(
\begin{aligned}
& \sin \frac{7 \pi}{8}=\sin \left(\pi-\frac{\pi}{8}\right)=\sin \frac{\pi}{8} ; \sin \frac{5 \pi}{8}=\sin \left(\pi-\frac{3 \pi}{8}\right)=\sin \frac{3 \pi}{8} \\
& \text { Therefore, the given value }=2\left[\sin ^2 \frac{\pi}{8}+\sin ^2 \frac{3 \pi}{8}\right]=2\left[\sin ^2 \frac{\pi}{8}+\cos ^2 \frac{\pi}{8}\right]
\end{aligned}
\)
\(
=2(1)=2\left[\because \sin \frac{3 \pi}{8}=\sin \left(\frac{\pi}{2}-\frac{\pi}{8}\right)=\cos \frac{\pi}{8}\right]
\)

Hint

(b)

\(
\begin{aligned}
& 4 \cos ^2\left(\frac{\pi}{4}-\frac{x}{2}\right)+\sqrt{4 \sin ^4 x+\sin ^2 2 x}=4 \cos ^2\left(\frac{\pi}{4}-\frac{x}{2}\right)+\sqrt{4 \sin ^2 x\left(\cos ^2 x+\sin ^2 x\right)} \\
& =2\left(1+\cos \left(\frac{\pi}{2}-x\right)\right)+2|\sin x|=2+2 \sin x-2 \sin x \text { as } x \in\left(\pi, \frac{3 \pi}{2}\right)=2 .
\end{aligned}
\)

Hint

(b)
\(
\begin{aligned}
\cos ^3 x \sin 2 x & =\cos ^2 x \cos x \sin 2 x \\
& =\left(\frac{1-\cos 2 x}{2}\right)\left(\frac{2 \sin 2 x \cos x}{2}\right) \\
& =\frac{1}{4}(1-\cos 2 x)(\sin 3 x+\sin x) \\
& =\frac{1}{4}\left[\sin 3 x+\sin x-\frac{1}{2}(2 \sin 3 x \cdot \cos 2 x)-\frac{1}{2}(2 \cos 2 x \sin x)\right] \\
& =\frac{1}{4}\left[\sin 3 x+\sin x-\frac{1}{2}(\sin 5 x+\sin x)-\frac{1}{2}(\sin 3 x-\sin x)\right] \\
& =\frac{1}{4}\left[\sin x+\frac{1}{2} \sin 3 x-\frac{1}{2} \sin 5 x\right]
\end{aligned}
\)
\(
\Rightarrow \quad \dot{a}_1=1 / 4, a_3=1 / 8, n=5
\)

Hint

(b)

\(
\begin{aligned}
&\text { Given expression is } 2 \sin ^2 \phi+4 \cos (\theta+\phi) \sin \theta \sin \phi+\cos 2(\theta+\phi)\\
&\begin{aligned}
& =(1-\cos 2 \phi)+4 \cos (\theta+\phi) \sin \theta \sin \phi+2 \cos ^2(\theta+\phi)-1 \\
& =-\cos 2 \phi+4 \cos (\theta+\phi) \sin \theta \sin \phi+2 \cos ^2(\theta+\phi) \\
& =-\cos 2 \phi+2 \cos (\theta+\phi)[\cos (\theta+\phi)+2 \sin \theta \sin \phi] \\
& =-\cos 2 \phi+2 \cos (\theta+\phi)[\cos \theta \cos \phi+\sin \theta \sin \phi] \\
& =-\cos 2 \phi+2 \cos (\theta+\phi) \cos (\theta-\phi) \\
& =-\cos 2 \phi+\cos 2 \theta+\cos 2 \phi=\cos 2 \theta
\end{aligned}
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
&\frac{\cos 2 B}{1}=\frac{\cos (A+C)}{\cos (A-C)}\\
&\text { Applying componendo and dividendo, we get }\\
&\begin{aligned}
& \Rightarrow \frac{1-\cos 2 B}{1+\cos 2 B}=\frac{\cos (A-C)-\cos (A+C)}{\cos (A-C)+\cos (A+C)} \\
& \Rightarrow \frac{2 \sin ^2 B}{2 \cos ^2 B}=\frac{2 \sin A \sin C}{2 \cos A \cos C} \\
& \Rightarrow \tan { }^2 B=\tan A \tan C \\
& \Rightarrow \tan A, \tan B, \tan C \text { are in G.P. }
\end{aligned}
\end{aligned}
\)

Hint

(b)

(b)
\(
\begin{aligned}
&\cos x=\frac{2 \cos y-1}{2-\cos y}\\
&\Rightarrow \frac{1-\tan ^2 \frac{x}{2}}{1+\tan ^2 \frac{x}{2}}=\frac{\frac{2\left(1-\tan ^2 y / 2\right)}{1+\tan ^2 y / 2}-1}{2-\frac{1-\tan ^2 y / 2}{1+\tan ^2 y / 2}}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow 6 \tan ^2 y / 2=2 \tan ^2 \frac{x}{2} \\
& \Rightarrow \tan \frac{x}{2} \cot \frac{y}{2}=\sqrt{3}
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
&\text { We have }\\
&\begin{aligned}
\sqrt{\left(\frac{a+b}{a-b}\right)}+\sqrt{\left(\frac{a-b}{a+b}\right)} & =\frac{a+b+a-b}{\sqrt{\left(a^2-b^2\right)}} \\
& =\frac{2 a}{\sqrt{\left(a^2-b^2\right)}}=\frac{2}{\sqrt{\left[1-(b / a)^2\right]}} \\
& =\frac{2}{\sqrt{\left(1-\tan ^2 x\right)}}=\frac{2 \cos x}{\sqrt{\left(\cos ^2 x-\sin ^2 x\right)}} \\
& =\frac{2 \cos x}{\sqrt{(\cos 2 x)}}
\end{aligned}
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
&\text { Since } \alpha \text { is a root of } 25 \cos ^2 \theta+5 \cos \theta-12=0\\
&\begin{aligned}
& \therefore \quad 25 \cos ^2 \alpha+5 \cos \alpha-12=0 \quad \Rightarrow \cos \alpha=\frac{-5 \pm \sqrt{25+1200}}{50}=-\frac{4}{5}\left[\because \frac{\pi}{2}<\alpha<\pi\right] \\
& \text { and } \sin \alpha=\sqrt{1-\frac{16}{25}}=\frac{3}{5} \text {; therefore, } \sin 2 \alpha=2 \sin \alpha \cos \alpha=2\left(\frac{3}{5}\right)\left(\frac{-4}{5}\right)=\frac{-24}{25}
\end{aligned}
\end{aligned}
\)

Hint

(c)

\(
\begin{aligned}
&\text { We have } \tan 9^{\circ}-\tan 27^{\circ}-\tan 63^{\circ}+\tan 81^{\circ}=\left(\tan 9^{\circ}+\tan 81^{\circ}\right)-\left(\tan \cdot 27^{\circ}+\tan 63^{\circ}\right)\\
&\begin{aligned}
& =\frac{1}{\sin 9^{\circ} \cos 9^{\circ}}-\frac{1}{\sin 27^{\circ} \cos 27^{\circ}} \\
& =\frac{2}{\sin 18^{\circ}}-\frac{2}{\sin 54^{\circ}} \\
& =2\left[\frac{\sin 54^{\circ}-\sin 18^{\circ}}{\sin 54^{\circ} \sin 18^{\circ}}\right] \\
& =2\left[\frac{2 \cos 36^{\circ} \sin 18^{\circ}}{\sin 18^{\circ} \cos 36^{\circ}}\right]=4
\end{aligned}
\end{aligned}
\)

Hint

(c)
\(
\begin{aligned}
&\text { Let } A=\sin ^{-1} a, B=\sin ^{-1} b \text { and } C=\sin ^{-1} c \text {, we have } A+B+C=\pi \text {. }\\
&a \sqrt{1-a^2}+b \sqrt{1-b^2}+c \sqrt{1-c^2}=\frac{1}{2}(\sin 2 A+\sin 2 B+\sin 2 C)=\frac{1}{2}[4 \sin A \sin B \sin C]=2 a b c
\end{aligned}
\)

Hint

(d)
\(
\begin{aligned}
\cos 2 A+\cos 2 B+\cos 2 C & =2 \cos (A+B) \cos (A-B)+\cos 2 C \\
& =2 \cos \left(\frac{3 \pi}{2}-C\right) \cos (A-B)+\cos 2 C \\
& =-2 \sin C \cos (A-B)+1-2 \sin ^2 C \\
& =1-2 \sin C(\cos (A-B)+\sin C) \\
& =1-2 \sin C\{\cos (A-B)+\sin [3 \pi / 2-(A+B)]\} \\
& =1-2 \sin C[\cos (A-B)-\cos (A+B)]
\end{aligned}
\)
\(
=1-4 \sin A \sin B \sin C
\)

Hint

(c)

\(
\begin{aligned}
& \frac{2}{\tan \frac{B}{2}}=\frac{1}{\tan \frac{A}{2}}+\frac{1}{\tan \frac{C}{2}} \\
& \Rightarrow 2 \tan \frac{A}{2} \tan \frac{C}{2}=\tan \frac{B}{2} \tan \frac{C}{2}+\tan \frac{B}{2} \tan \frac{A}{2}=1-\tan \frac{A}{2} \tan \frac{C}{2} \\
& \Rightarrow \tan \frac{A}{2} \tan \frac{C}{2}=\frac{1}{3} \\
& \Rightarrow \cot \frac{A}{2} \cot \frac{C}{2}=3
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
\sin ^2 A-\sin ^2 B+\sin ^2 C & =\sin (A+B) \sin (A-B)+\sin ^2 C=\sin C(\sin (A-B)+\sin C) \\
& =\sin C(\sin (A-B)+\sin (A+B))=2 \sin A \cos B \sin C
\end{aligned}
\)

Hint

(c)
\(
\sin ^2 \alpha+\sin ^2 \beta+\sin ^2 \gamma=\frac{\tan ^2 \alpha}{1+\tan ^2 \alpha}+\frac{\tan ^2 \beta}{1+\tan ^2 \beta}+\frac{\tan ^2 \gamma}{1+\tan ^2 \gamma}
\)
\(
=\frac{x}{1+x}+\frac{y}{1+y}+\frac{z}{1+z} \quad\left[\text { where } x=\tan ^2 \alpha, y=\tan ^2 \beta, z=\tan ^2 \gamma\right]
\)
\(
=\frac{(x+y+z)+(x y+y z+z x+2 x y z)+x y+y z+z x+x y z}{(1+x)(1+y)(1+z)}
\)
\(
=\frac{1+x+y+z+x y+y z+z x+x y z}{(1+x)(1+y)(1+z)}=1 \quad[\because x y+y z+z x+2 x y z=\gamma]
\)

Hint

(c)

\(
\begin{aligned}
&\begin{aligned}
D^{r} & =\sin A+\sin B-\sin C \\
& =2 \sin \frac{A+B}{2} \cos \frac{A-B}{2}-2 \sin \frac{C}{2} \cos \frac{C}{2} \\
& =2 \cos \frac{C}{2}\left[\cos \left(\frac{A-B}{2}\right)-\sin \frac{C}{2}\right] \\
& =2 \cos \frac{C}{2}\left[\cos \frac{A-B}{2}-\cos \frac{A+B}{2}\right] \\
& =2 \cos \frac{C}{2}\left[2 \sin \frac{A}{2} \sin \frac{B}{2}\right] \\
& =4 \sin \frac{A}{2} \sin \frac{B}{2} \cos \frac{C}{2}
\end{aligned}\\
&\text { Also } \sin A+\sin B+\sin C=4 \cos \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2}\\
&\Rightarrow \frac{\sin A+\sin B+\sin C}{\sin A+\sin B-\sin C}=\cot \frac{A}{2} \cot \frac{B}{2}
\end{aligned}
\)

Hint

(a)

\(
\frac{\sin 2 A+\sin 2 B+\sin 2 C}{\sin \widetilde{A}+\sin B+\sin C}=\frac{4 \sin A \sin B \sin C}{4 \cos \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2}}=8 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2} \quad\left[\because \sin A=2 \sin \frac{A}{2} \cos \frac{A}{2}\right]
\)

Hint

(c) We have \(\cos ^2 A+\cos ^2 B-\left(1-\cos ^2 C\right)=0\)
\(
\begin{aligned}
& \Rightarrow \quad \cos ^2 A+\cos ^2 B-\sin ^2 C=0 \\
& \Rightarrow \quad \cos ^2 A+\cos (B+C) \cos (B-C)=0 \\
& \Rightarrow \quad 2 \cos A \cos B \cos C=0
\end{aligned}
\)
Hence, either \(A\) or \(B\) or \(C\) is \(90^{\circ}\).

Hint

(a) In a triangle, \(\tan A+\tan B+\tan C=\tan A \tan B \tan C \dots(i)\)
\(
\begin{aligned}
& \Rightarrow \quad 6=2 \tan C \\
& \Rightarrow \quad \tan C=3
\end{aligned}
\)
Also \(\tan A+\tan B=6-3=3 \dots(ii)\)
\(\Rightarrow \tan A\) and \(\tan B\) are roots \(x^2-3 x+2=0\) by Eqs. (i) and (ii).
\(\Rightarrow \tan A, \tan B=2,1\) or 1,2 and \(\tan C=3\).

Hint

(a)

\(
\begin{aligned}
&\text { We have } \tan 6^{\circ} \tan 42^{\circ} \tan 66^{\circ} \tan 78^{\circ}\\
&\begin{aligned}
& =\tan 6^{\circ} \tan \left(60^{\circ}-18^{\circ}\right) \tan \left(60^{\circ}+6^{\circ}\right) \tan \left(60^{\circ}+18^{\circ}\right) \\
& =\frac{\tan 6^{\circ} \tan \left(60^{\circ}+6^{\circ}\right) \tan 18^{\circ} \tan \left(60^{\circ}-18^{\circ}\right) \tan \left(60^{\circ}+18^{\circ}\right)}{\tan 18^{\circ}}=\frac{\tan 6^{\circ} \tan \left(60^{\circ}+6^{\circ}\right) \tan \left(3 \times 18^{\circ}\right)}{\tan 18^{\circ}} \\
& =\frac{\tan 6^{\circ} \tan \left(60^{\circ}-6\right) \tan \left(60^{\circ}+6\right)}{\tan 18^{\circ}}=\frac{\tan 18^{\circ}}{\tan 18^{\circ}}=1
\end{aligned}
\end{aligned}
\)

Hint

(c)
\(
\begin{aligned}
& \text { As } \alpha \rightarrow 0^{+}, \lim _{\alpha \rightarrow 0^{+}} \frac{\alpha}{\sin \alpha}=1 \\
& \text { At } \alpha=\frac{\pi}{6}, \frac{\frac{\pi}{6}}{\sin \left(\frac{\pi}{6}\right)}=\frac{\frac{\pi}{6}}{\frac{1}{2}}=\frac{2 \pi}{6}=\frac{\pi}{3}
\end{aligned}
\)
Since \(\frac{\alpha}{\sin \alpha}\) is increasing and its values are 1 at \(\alpha \rightarrow 0^{+}\)and \(\frac{\pi}{3}\)
at \(\alpha=\frac{\pi}{6}\), the range is \(1<\alpha(\operatorname{cosec} \alpha)<\frac{\pi}{3}\)

Hint

(d)
\(
\begin{aligned}
& (\alpha-\beta)=(\theta-\beta)-(\theta-\alpha) \\
& \Rightarrow \cos (\alpha-\beta)=\cos (\theta-\beta) \cos (\theta-\alpha)+\sin (\theta-\beta) \sin (\theta-\alpha) \\
& \quad=\frac{y}{b} \times \frac{x}{a}+\sqrt{1-\frac{x^2}{a^2}} \sqrt{1-\frac{y^2}{b^2}} \\
& \Rightarrow\left[\frac{x y}{a b}-\cos (\alpha-\beta)\right]^2=\left(1-\frac{x^2}{a^2}\right)\left(1-\frac{y^2}{b^2}\right)
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \frac{x^2 y^2}{a^2 b^2}+\cos ^2(\alpha-\beta)-\frac{2 x y}{a b} \cos (\alpha-\beta)=1-\frac{y^2}{b^2}-\frac{x^2}{a^2}+\frac{x^2 y^2}{a^2 b^2} \\
& \Rightarrow \frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{2 x y}{a b} \cos (\alpha-\beta)=\sin ^2(\alpha-\beta)
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
&\begin{aligned}
& \text { Let } u=\cos \theta\left\{\sin \theta+\sqrt{\sin ^2 \theta+\sin ^2 \alpha}\right\} \\
& \Rightarrow \quad(u-\sin \theta \cos \theta)^2=\cos ^2 \theta\left(\sin ^2 \theta+\sin ^2 \alpha\right) \\
& \Rightarrow \quad u^2 \tan ^2 \theta-2 u \tan \theta+u^2-\sin ^2 \alpha=0
\end{aligned}\\
&\text { Since } \tan \theta \text { is real, } 4 u^2-4 u^2\left(u^2-\sin ^2 \alpha\right) \geq 0 \text {. }\\
&\begin{aligned}
& \Rightarrow \quad u^2 \leq 1+\sin ^2 \alpha \\
& \Rightarrow \quad|u| \leq \sqrt{1+\sin ^2 \alpha}
\end{aligned}
\end{aligned}
\)

Hint

(a) 

\(
\begin{aligned}
&\begin{aligned}
& \sin \theta_1 \sin \theta_2-\cos \theta_1 \cos \theta_2=-1 \\
& \Rightarrow \cos \left(\theta_1+\theta_2\right)=1 \\
& \Rightarrow \theta_1+\theta_2=2 n \pi, n \in I \\
& \Rightarrow \frac{\theta_1}{2}+\frac{\theta_2}{2}=n \pi
\end{aligned}\\
&\text { Thus, } \tan \frac{\theta_1}{2} \cot \frac{\theta_2}{2}=\tan \frac{\theta_1}{2} \cot \left(n \pi-\frac{\theta_1}{2}\right)=-\tan \frac{\theta_1}{2} \cot \frac{\theta_1}{2}=-1
\end{aligned}
\)

Hint

(a)

\(
\begin{aligned}
& \tan \frac{\pi}{3}+2 \tan \frac{2 \pi}{3}+4 \tan \frac{4 \pi}{3}+8 \tan \frac{8 \pi}{3} \\
& =\tan \frac{\pi}{3}+2 \tan \left(\pi-\frac{\pi}{3}\right)+4 \tan \left(\pi+\frac{\pi}{3}\right)+8 \tan \left(3 \pi-\frac{\pi}{3}\right) \\
& =\tan \frac{\pi}{3}-2 \tan \frac{\pi}{3}+4 \tan \frac{\pi}{3}-8 \tan \frac{\pi}{3}=-5 \tan \frac{\pi}{3}=-5 \sqrt{3}
\end{aligned}
\)

Hint

(c) Since \(\tan 3 \theta=\frac{3 \tan \theta-\tan ^3 \theta}{1-3 \tan ^2 \theta}\)
Putting \(\theta=\frac{\pi}{9}\), we get \(\tan \frac{\pi}{3}=\frac{3 \tan \frac{\pi}{9}-\tan ^3 \frac{\pi}{9}}{1-3 \tan ^2 \frac{\pi}{9}}\)
\(
\begin{aligned}
& \Rightarrow \quad 3\left(1-3 \tan ^2 \frac{\pi}{9}\right)^2=\left(3 \tan \frac{\pi}{9}-\tan ^3 \frac{\pi}{9}\right)^2 \\
& \Rightarrow \quad \tan ^6 \frac{\pi}{9}-33 \tan ^4 \frac{\pi}{9}+27 \tan ^2 \frac{\pi}{9}=3
\end{aligned}
\)

Hint

(c)
\(
\begin{aligned}
& \cos x+\cos y-\cos (x+y)=\frac{3}{2} \\
& \Rightarrow 2 \cos \left(\frac{x+y}{2}\right) \cos \left(\frac{x-y}{2}\right)-2 \cos ^2\left(\frac{x+y}{2}\right)+1=\frac{3}{2}
\end{aligned}
\)
\(
\begin{aligned}
&\Rightarrow \quad 2 \cos ^2\left(\frac{x+y}{2}\right)-2 \cos \left(\frac{x+y}{2}\right) \cos \left(\frac{x-y}{2}\right)+\frac{1}{2}=0\\
&\text { Now } \cos \left(\frac{x+y}{2}\right) \text { is always real, then discriminant } \geq 0 \text {. }\\
&\begin{aligned}
& \Rightarrow \quad 4 \cos ^2\left(\frac{x-y}{2}\right)-4 \geq 0 \\
& \Rightarrow \quad \cos ^2\left(\frac{x-y}{2}\right) \geq 1 \\
& \Rightarrow \quad \cos ^2\left(\frac{x-y}{2}\right)=1 \\
& \Rightarrow \quad \frac{x-y}{2}=0 \Rightarrow x=y
\end{aligned}
\end{aligned}
\)

Hint

(a)

\(
\begin{aligned}
& a \sin x+b \cos (x+\theta)+b \cos (x-\theta)=d \\
& \Rightarrow \quad a \sin x+2 b \cos x \cos \theta=d \\
& \Rightarrow \quad|d| \leq \sqrt{a^2+4 b^2 \cos ^2 \theta} \\
& \Rightarrow \quad \frac{d^2-a^2}{4 b^2} \leq \cos ^2 \theta \\
& \Rightarrow \quad|\cos \theta| \geq \frac{\sqrt{d^2-a^2}}{2|b|}
\end{aligned}
\)

Hint

(d)

\(
\begin{aligned}
& \frac{\sin x}{\sin y}=\frac{1}{2}, \frac{\cos x}{\cos y}=\frac{3}{2} \Rightarrow \frac{\tan x}{\tan y}=\frac{1}{3} \Rightarrow \tan (x+y)=\frac{\tan x+\tan y}{1-\tan x \tan y}=\frac{4 \tan x}{1-3 \tan ^2 x} \\
& \text { Also } \sin y=2 \sin x, \cos y=\frac{2}{3} \cos x \\
& \Rightarrow \sin ^2 y+\cos ^2 y=4 \sin ^2 x+\frac{4 \cos ^2 x}{9}=1 \\
& \Rightarrow 36 \tan ^2 x+4=9 \sec ^2 x=9\left(1+\tan ^2 x\right) \\
& \Rightarrow 27 \tan ^2 x=5 \\
& \Rightarrow \tan x=\frac{\sqrt{5}}{3 \sqrt{3}} \\
& \Rightarrow \tan (x+y)=\frac{\frac{4 \sqrt{5}}{3 \sqrt{3}}}{1-\frac{15}{27}}=\frac{4 \sqrt{5} \times 27}{12 \times 3 \sqrt{3}}=\sqrt{15}
\end{aligned}
\)

Hint

(a)
\(
\begin{aligned}
& \sqrt{1+\cos x} \doteq \sqrt{2 \cos ^2 \frac{x}{2}}=\sqrt{2}\left|\cos \frac{x}{2}\right| \text { and } \sqrt{1-\cos x}=\sqrt{2 \sin ^2 \frac{x}{2}}=\sqrt{2}\left|\sin \frac{x}{2}\right| \\
& \Rightarrow \frac{\sqrt{1+\cos x}+\sqrt{1-\cos x}}{\sqrt{1+\cos x}-\sqrt{1-\cos x}}=\frac{\left|\cos \frac{x}{2}\right|+\left|\sin \frac{x}{2}\right|}{\left|\cos \frac{x}{2}\right|-\left|\sin \frac{x}{2}\right|}
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{-\cos \frac{x}{2}+\sin \frac{x}{2}}{-\cos \frac{x}{2}-\sin \frac{x}{2}} \quad\left(\because \frac{\pi}{2}<\frac{x}{2}<\pi\right) \\
& =\frac{\cos \frac{x}{2}-\sin \frac{x}{2}}{\cos \frac{x}{2}+\sin \frac{x}{2}} \\
& =\frac{1-\tan \frac{x}{2}}{1+\tan \frac{x}{2}} \\
& =\tan \left(\frac{\pi}{4}-\frac{x}{2}\right)=\cot \left(\frac{\pi}{2}-\left(\frac{\pi}{4}-\frac{x}{2}\right)\right)=\cot \left(\frac{\pi}{4}+\frac{x}{2}\right)
\end{aligned}
\)

Hint

(d)
\(
\begin{aligned}
& \tan x=n \tan y, \cos (x-y)=\cos x \cos y+\sin x \sin y \\
& \Rightarrow \quad \cos (x-y)=\cos x \cos y(1+\tan x \cdot \tan y)=\cos x \cos y\left(1+n \tan ^2 y\right)
\end{aligned}
\)
\(
\begin{aligned}
\Rightarrow \sec ^2(x-y) & =\frac{\sec ^2 x \sec ^2 y}{\left(1+n \tan ^2 y\right)^2} \\
& =\frac{\left(1+\tan ^2 x\right)\left(1+\tan ^2 y\right)}{\left(1+n \tan ^2 y\right)^2} \\
& =\frac{\left(1+n^2 \tan ^2 y\right)\left(1+\tan ^2 y\right)}{\left(1+n \tan ^2 y\right)^2} \\
& =1+\frac{(n-1)^2 \tan ^2 y}{\left(1+n \tan ^2 y\right)^2}
\end{aligned}
\)
\(
\text { Now, }\left(\frac{1+n \tan ^2 y}{2}\right)^2 \geq n \tan ^2 y \quad(\because \text { A.M. } \geq \text { G.M. })
\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{\tan ^2 y}{\left(1+n \tan ^2 y\right)^2} \leq \frac{1}{4 n} \\
& \Rightarrow \sec ^2(x-y) \leq 1+\frac{(n-1)^2}{4 n}=\frac{(n+1)^2}{4 n}
\end{aligned}
\)

Hint

(b)
\(
\begin{aligned}
& \cot ^2 x=\cot (x-y) \cot (x-z) \\
& \Rightarrow \cot ^2 x=\left(\frac{\cot x \cot y+1}{\cot y-\cot x}\right)\left(\frac{\cot x \cot z+1}{\cot z-\cot x}\right) \\
& \Rightarrow \cot ^2 x \cot y \cot z-\cot ^3 x \cot y-\cot ^3 x \cot z+\cot ^4 x
\end{aligned}
\)
\(
=\cot ^2 x \cot y \cot z+\cot x \cot y+\cot x \cot z+1
\)
\(
\begin{aligned}
& \Rightarrow \cot ^3 x(\cot y+\cot z)+\cot x(\cot y+\cot z)+1-\cot ^4 x=0 \\
& \Rightarrow \cot x(\cot y+\cot z)\left(1+\cot ^2 x\right)+\left(1-\cot ^2 x\right)\left(1+\cot ^2 x\right)=0 \\
& \Rightarrow\left[\cot x(\cot y+\cot z)+\left(1-\cot ^2 x\right)\right]=0 \\
& \Rightarrow \frac{\cot ^2 x-1}{2 \cot x}=\frac{1}{2}(\cot y+\cot z)=\cot 2 x
\end{aligned}
\)

Hint

(a)

\(
\begin{aligned}
&A+B+C=\pi \quad \Rightarrow \tan A+\tan B+\tan C=\tan A \tan B \tan C\\
&\text { Now, A.M. } \geq \text { G.M. }\\
&\begin{aligned}
& \Rightarrow \quad \frac{\tan A+\tan B+\tan C}{3} \geq(\tan A \tan B \tan C)^{1 / 3} \\
& \Rightarrow \quad \frac{\tan A+\tan B+\tan C}{3} \geq(\tan A \tan B \tan C)^{1 / 3} \\
& \Rightarrow \quad(\tan A \tan B \tan C)^{2 / 3} \geq 3 \\
& \Rightarrow \quad\left(\frac{1}{K}\right)^{2 / 3} \geq 3 \\
& \Rightarrow \quad K \leq \frac{1}{3 \sqrt{3}}
\end{aligned}
\end{aligned}
\)

Hint

(d)
\(
\begin{aligned}
& u^2=\left(a^2 \cos ^2 \theta+b^2 \sin ^2 \theta\right)+\left(a^2 \sin ^2 \theta+b^2 \sin ^2 \theta\right) \\
&=a^2+b^2+2 \sqrt{a^2 \cos ^2 \theta+b^2 \sin ^2 \theta} \sqrt{a^2 \sin ^2 \theta+b^2 \cos ^2 \theta} \\
&=a^2+b^2+2 \sqrt{\sin ^2 \theta \cos ^2 \theta\left(a^4+b^4\right)+a^2 b^2\left(\sin ^4 \theta+\cos ^4 \theta\right)} \\
&=a^2+b^2+2 \sqrt{a^2 b^2\left(1-2 \sin ^2 \theta \cos ^2 \theta\right)+\left(a^4+b^4\right) \sin ^2 \theta \cos ^2 \theta} \\
&=\left(a^2+b^2\right)+2 \sqrt{a^2 b^2+\left(a^2-b^2\right)^2 \sin ^2 \theta \cos ^2 \theta} \\
&=\left(a^2+b^2\right)+2 \sqrt{a^2 b^2+\frac{\left(a^2-b^2\right)^2}{4} \sin ^2 2 \theta} \\
& \text { Max. } u^2=\left(a^2+b^2\right)=2 \sqrt{a^2 b^2+\frac{\left(a^2-b^2\right)^2}{4}} \\
& \text { Min. } u^2=\left(a^2+b^2\right)+2 a b
\end{aligned}
\)
\(
\begin{aligned}
\text { Therefore, the difference } & =2 \sqrt{a^2 b^2+\frac{\left(a^2-b^2\right)^2}{4}}-2 a b=\sqrt{4 a^2 b^2+a^4+b^4-2 a^2 b^2}-2 a b \\
& =\sqrt{\left(a^2+b^2\right)^2}-2 a b=a^2+b^2-2 a b=(a-b)^2
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
&\begin{aligned}
& (\sin x+\cos x)^2+k \sin x \cos x=1 \\
& \Rightarrow 1+\sin 2 x+\frac{k}{2} \sin 2 x=1 \\
& \Rightarrow \sin 2 x\left[1+\frac{k}{2}\right]=0
\end{aligned}\\
&\text { For this to be an identity, } 1+\frac{k}{2}=0 \Rightarrow k=-2
\end{aligned}
\)

Hint

(b)
\(
\begin{aligned}
& k \cos ^2 x-k \cos x+1 \geq 0 \forall x \in(-\infty, \infty) \\
& \Rightarrow k\left(\cos ^2 x-\cos x\right)+1 \geq 0
\end{aligned}
\)
Now \(\cos ^2 x-\cos x=\left(\cos x-\frac{1}{2}\right)^2-\frac{1}{4}\)
\(
\Rightarrow-\frac{1}{4} \leq \cos ^2 x-\cos x \leq 2
\)
We have \(2 k+1 \geq 0\) and \(-\frac{k}{4}+1 \geq 0\)
Hence, \(-\frac{1}{2} \leq k \leq 4\).

Hint

(d)

\(
\min (2+\sin x-\cos x)=\min \left[2+\sqrt{2} \sin \left(x-\frac{\pi}{4}\right)\right]=2-\sqrt{2}
\)

Hint

(b)

\(
\begin{aligned}
& a \operatorname{cosec} \alpha-b \sec \alpha=\frac{a}{\sin \alpha}+\frac{b}{\cos \alpha} \\
& \qquad=\frac{\sqrt{a^2+b^2}}{\sin \alpha \cos \alpha}\left[\frac{a}{\sqrt{a^2+b^2}} \cos \alpha \frac{b}{\sqrt{a^2+b^2}} \sin \alpha\right] \\
& \text { Now } \sin 3 \alpha=\frac{a}{\sqrt{a^2+b^2}} \text { gives } \sqrt{a^2+b^2}\left[\frac{\sin 3 \alpha \cos \alpha-\cos 3 \alpha \sin \alpha}{\sin \alpha \cos \alpha}\right]=2 \sqrt{a^2+b^2}
\end{aligned}
\)

Hint

(d)

\(
\begin{aligned}
& \cot ^4 x-2\left(1+\cot ^2 x\right)+a^2=0 \\
& \Rightarrow \cot ^4 x-2 \cot ^2 x+a^2-2=0 \\
& \Rightarrow\left(\cot ^2 x-1\right)^2=3-a^2
\end{aligned}
\)
To have at least one solution, \(3-a^2 \geq 0\)
\(
\begin{aligned}
& \Rightarrow a^2-3 \leq 0 \\
& a \in[-\sqrt{3}, \sqrt{3}]
\end{aligned}
\)
Integral values are \(-1,0,1\); therefore, the sum is 0.

Hint

(b)

\(
\sin ^2 x+a \cos x+a^2>1+\cos x
\)
Putting \(x=0\), we have
\(
\begin{aligned}
& a+a^2>2 \\
& \Rightarrow a^2+a-2>0 \\
& \Rightarrow(a+2)(a-1)>0 \\
& \Rightarrow a<-2 \text { or } a>1
\end{aligned}
\)
Therefore, the largest negative integral value of ‘ \(a\) ‘ \(=-3\).

Hint

(d)

\(
\begin{aligned}
& \Delta=\frac{1}{2} a b \Rightarrow a b=60 \\
& b=c \cos \theta ; a=c \sin \theta \\
& \Rightarrow \Delta=\frac{1}{2} c^2 \sin \theta \cos \theta=\frac{c^2 \sin 2 \theta}{4}=30 \\
& \Rightarrow c^2=120 \operatorname{cosec} 2 \theta \\
& \Rightarrow c_{\min }^2=120 \\
& \Rightarrow c_{\min }=2 \sqrt{30}
\end{aligned}
\)

Hint

(b) From the figure,

\(
\begin{aligned}
& x \cos \left(\theta+30^{\circ}\right)=\theta \dots(i) \\
& \text { and } x \sin \theta=1-d \dots(ii)
\end{aligned}
\)
Dividing \(\sqrt{3} \cos \theta=\frac{1+d}{1-d}\), squaring Eq. (ii) and putting the value of \(\cot \theta\), we get \(x^2=\frac{1}{3}\left(4 d^2-4 d+4\right)\)
\(
\Rightarrow x=2 \frac{1}{2}
\)

Hint

(d)

\(
\begin{aligned}
& a=c \sin \theta, b=c \cos \theta \\
& \Rightarrow\left(\frac{c}{a}+\frac{c}{b}\right)^2=\left(\frac{1}{\sin \theta}+\frac{1}{\cos \theta}\right)^2=\frac{4(1+\sin 2 \theta)}{\sin ^2 2 \theta} \\
& =4\left(\frac{1}{\sin ^2 2 \theta}+\frac{1}{\sin 2 \theta}\right) \text { where } 0<\theta<\frac{\pi}{2} \\
& \Rightarrow\left(\frac{c}{a}+\frac{c}{b}\right)^2 \text { min. }=8 \text { when } 2 \theta=90^{\circ} . \\
& \Rightarrow \theta=45^{\circ}
\end{aligned}
\)

Hint

(c)
\(
y=\left(\sin ^2 x+\cos ^2 x\right)+2(\sin x \operatorname{cosec} x+\cos x \sec x)+\sec ^2 x+\operatorname{cosec}^2 x
\)
\(
\begin{aligned}
& =5+2+\tan ^2 x+\cot ^2 x \\
& =7+(\tan x-\cot x)^2+2 \\
& \therefore y_{\min }=9
\end{aligned}
\)

Hint

(c) We know that
\(
\begin{aligned}
& \quad|a \sin x+b \cos x| \leq \sqrt{a^2+b^2} \text { for all } x \in R \\
& \therefore \quad|c| \leq \sqrt{a^2+b^2} \\
& \text { But, }|c|>\sqrt{a^2+b^2} \text { [Given] }
\end{aligned}
\)
Hence, \(a \sin x+b \cos x=c\) does not hold for any \(x \in R\).

Hint

(a)

\(
\begin{aligned}
&\text { We have, }\\
&\begin{aligned}
& \sin \theta+\operatorname{cosec} \theta=2 \\
\Rightarrow \quad & \sin ^2 \theta-2 \sin \theta+1=0 \\
\Rightarrow \quad & \sin \theta=1 \\
\therefore \quad & \sin ^{10} \theta+\operatorname{cosec}^{10} \theta=1+1=2
\end{aligned}
\end{aligned}
\)

Hint

(d) We have,
\(
\begin{aligned}
& \cot \theta-\tan \theta=2 \cot 2 \theta \\
\therefore & \tan \alpha+2 \tan 2 \alpha+4 \tan 4 \alpha+\ldots+2^{n-1} \tan \left(2^{n-1} \alpha\right) \\
& +2^n \cot \left(2^n \alpha\right)
\end{aligned}
\)
\(
\begin{array}{r}
=-\left\{(\cot \alpha-\tan \alpha)-2 \tan 2 \alpha-4 \tan 4 \alpha \ldots-2^{n-1} \tan \left(2^{n-1} \alpha\right)\right. \\
\left.-2^n \cot \left(2^n \alpha\right)\right\}+\cot \alpha
\end{array}
\)
\(
\begin{aligned}
=\{-(2 \cot 2 \alpha-2 \tan 2 \alpha)-4 \tan 4 \alpha \ldots- & 2^{n-1} \tan \left(2^{n-1} \alpha\right) \\
& \left.-2^n \cot \left(2^n \alpha\right)\right\}+\cot \alpha
\end{aligned}
\)
\(
\begin{aligned}
=-\left\{\left(2^2 \cot 2^2 \alpha-2^2 \tan 2^2 \alpha\right)-2^3 \tan 2^3 \alpha\right. & \ldots-2^{n-1} \tan \left(2^{n-1} \alpha\right) \\
& \left.-2^n \cot \left(2^n \alpha\right)\right\}+\cot \alpha
\end{aligned}
\)
\(
\begin{array}{r}
=-\left\{\left(2^3 \cot 2^3 \alpha-2^3 \tan 2^3 \alpha\right)-2^4 \tan 2^4 \alpha \ldots-2^{n-1} \tan \left(2^{n-1} \alpha\right)\right. \\
\left.-2^n \cot \left(2^n \alpha\right)\right\}+\cot \alpha
\end{array}
\)
\(
\begin{aligned}
& =-\left\{2^{n-1} \cot \left(2^{n-1} \alpha\right)-2^{n-1} \tan \left(2^{n-1} \alpha\right)-2^n \cot \left(2^n \alpha\right)\right\}+\cot \alpha \\
& =-\left\{2^n{ }^1 \times 2 \cot \left(2^n \alpha\right)-2^n \cot \left(2^n \alpha\right)\right\}+\cot \alpha=\cot \alpha
\end{aligned}
\)

Hint

(a)

\(
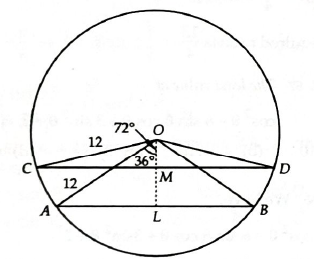
\begin{aligned}
& \text { We have, } \\
& \quad \text { Required distance }=L M \\
& \quad=O L-O M \\
& \quad=12 \cos 36^{\circ}-12 \cos 72^{\circ} \\
& \quad=12\left(\cos 36^{\circ}-\sin 18^{\circ}\right)=12\left(\frac{\sqrt{5}+1}{4}-\frac{\sqrt{5}-1}{4}\right)=6 \text { units. }
\end{aligned}
\)

Hint

(c) We have,
\(
\begin{aligned}
& \sqrt{1+\sin A}=\sqrt{\left(\cos \frac{A}{2}+\sin \frac{A}{2}\right)^2} \\
\Rightarrow & \sqrt{1+\sin A}=\left|\cos \frac{A}{2}+\sin \frac{A}{2}\right| \\
\Rightarrow & \sqrt{1+\sin A}=\cos \frac{A}{2}+\sin \frac{A}{2} \quad\left[\because \frac{A}{2} \text { is an acute angle }\right]
\end{aligned}
\)
and
\(
\begin{aligned}
& \sqrt{1-\sin A}=\sqrt{\left(\cos \frac{A}{2}-\sin \frac{A}{2}\right)^2} \\
\Rightarrow & \sqrt{1-\sin A}=\left|\cos \frac{A}{2}-\sin \frac{A}{2}\right| \\
\Rightarrow & \sqrt{1-\sin A}=-\left(\cos \frac{A}{2}-\sin \frac{A}{2}\right) \quad\left[\begin{array}{c}
\because \frac{A}{2}=66 \frac{1^{\circ}}{2} \\
\therefore \cos \frac{A}{2}<\sin \frac{A}{2}
\end{array}\right] \\
\Rightarrow & \sqrt{1-\sin A}=\sin \frac{A}{2}-\cos \frac{A}{2} \\
\therefore & 2 \cos \frac{A}{2}=\sqrt{1+\sin A}-\sqrt{1-\sin A}
\end{aligned}
\)

Hint

(b) We have,
\(
\frac{3 \sin A}{\sin B}=\frac{2 \cos B}{\cos A}
\)
\(
\begin{aligned}
& \Rightarrow \quad \frac{3 \sin A}{\cos A}=\frac{2 \cos B \sin B}{\cos ^2 A} \\
& \Rightarrow \quad \tan A=\frac{1}{3} \frac{\sin 2 B}{\cos ^2 A} \\
& \Rightarrow \quad \tan A=\frac{1}{3} \tan 2 B \cdot \frac{\cos 2 B}{\cos ^2 A} \\
& \Rightarrow \quad \tan A=\frac{1}{3} \frac{\tan 2 B}{\cos ^2 A}\left(2 \cos ^2 B-1\right)
\end{aligned}
\)
\(
\Rightarrow \quad \tan A=\frac{1}{3} \frac{\tan 2 B}{\cos ^2 A}\left(4-3 \cos ^2 A-1\right) \quad\left[\begin{array}{r}
\because 2 \cos ^2 B \\
=4-3 \cos ^2 A
\end{array}\right]
\)
\(
\begin{aligned}
& \Rightarrow \quad \tan A=\tan 2 B \tan ^2 A \\
& \Rightarrow \quad \tan A \tan 2 B=1 \\
& \Rightarrow \quad \tan A=\cot 2 B \\
& \Rightarrow \quad \tan A=\tan \left(\frac{\pi}{2}-2 B\right) \\
& \Rightarrow \quad A=\frac{\pi}{2}-2 B \Rightarrow A+2 B=\frac{\pi}{2}
\end{aligned}
\)

Hint

(d)

\(
\begin{aligned}
& \frac{\cos 6 x+6 \cos 4 x+15 \cos 2 x+10}{\cos 5 x+5 \cos 3 x+10 \cos x} \\
& =\frac{(\cos 6 x+\cos 4 x)+5(\cos 4 x+\cos 2 x)+10(\cos 2 x+1)}{\cos 5 x+5 \cos 3 x+10 \cos x} \\
& =\frac{2 \cos 5 x \cos x+10 \cos 3 x \cos x+20 \cos ^2 x}{\cos 5 x+5 \cos 3 x+10 \cos x} \\
& =2 \cos x .
\end{aligned}
\)

Hint

(c)
\(
8 \sin ^3 x \sin 3 x=2 \sin 3 x(3 \sin x-\sin 3 x)
\)
\(
\begin{aligned}
& \Rightarrow \quad 8 \sin ^3 x \sin 3 x=6 \sin 3 x \sin x-2 \sin ^2 3 x \\
& \Rightarrow \quad 8 \sin ^3 x \sin 3 x=3(\cos 2 x-\cos 4 x)-(1-\cos 6 x) \\
& \Rightarrow \quad 8 \sin ^3 x \sin 3 x=-1+3 \cos 2 x-3 \cos 4 x+\cos 6 x
\end{aligned}
\)
\(
\therefore \quad 8 \sin ^3 x \sin 3 x=\sum_{r=0}^n a_r \cos r x
\)
\(
\begin{aligned}
\Rightarrow \quad-1+3 \cos 2 x-3 \cos 4 x+\cos 6 x & \\
& =a_0+a_1 \cos x+\ldots+a_n \cos n x
\end{aligned}
\)
\(
\Rightarrow \quad n=6 .
\)

Hint

(b)
\(
\begin{aligned}
& \cos 2 A+\cos 2 B+\cos 2 C+4 \sin A \sin B \sin C \\
& =2 \cos (A+B) \cos (A-B)+\cos 2 C+4 \sin A \sin B \sin C \\
& =2 \cos \left(\frac{3 \pi}{2}-C\right) \cos (A-B)+\cos 2 C+4 \sin A \sin B \sin C \\
& =-2 \sin C \cos (A-B)+1-2 \sin ^2 C+4 \sin A \sin B \sin C \\
& =-2 \sin C|\cos (A-B)+\sin C|+4 \sin A \sin B \sin C+1
\end{aligned}
\)
\(
\begin{aligned}
= & -2 \sin C|\cos (A-B)-\cos (A+B)| \\
& +4 \sin A \sin B \sin C+1 \\
= & -4 \sin A \sin B \sin C+4 \sin A \sin B \sin C+1=1
\end{aligned}
\)

Hint

(a)
\(
\begin{aligned}
& \text { Use } \sin \left(180^{\circ}-\theta\right)=\sin \theta \\
& \sin 144^{\circ}=\sin \left(180^{\circ}-36^{\circ}\right)=\sin 36^{\circ} \\
& \sin 108^{\circ}=\sin \left(180^{\circ}-72^{\circ}\right)=\sin 72^{\circ}
\end{aligned}
\)
The expression becomes \(16 \sin 36^{\circ} \sin 72^{\circ} \sin 72^{\circ} \sin 36^{\circ}\). This simplifies to \(16 \sin ^2 36^{\circ} \sin ^2 72^{\circ}\).
\(
\begin{aligned}
& \sin 36^{\circ}=\frac{\sqrt{10-2 \sqrt{5}}}{4} . \\
& \sin 72^{\circ}=\frac{\sqrt{10+2 \sqrt{5}}}{4} .
\end{aligned}
\)
\(
\begin{aligned}
& \sin ^2 36^{\circ}=\left(\frac{\sqrt{10-2 \sqrt{5}}}{4}\right)^2=\frac{10-2 \sqrt{5}}{16} . \\
& \sin ^2 72^{\circ}=\left(\frac{\sqrt{10+2 \sqrt{5}}}{4}\right)^2=\frac{10+2 \sqrt{5}}{16} .
\end{aligned}
\)
The expression is \(16 \times \frac{10-2 \sqrt{5}}{16} \times \frac{10+2 \sqrt{5}}{16}\).
This simplifies to \(\frac{(10-2 \sqrt{5})(10+2 \sqrt{5})}{16}\).
Use the identity \((a-b)(a+b)=a^2-b^2\).
\(
(10-2 \sqrt{5})(10+2 \sqrt{5})=10^2-(2 \sqrt{5})^2=100-(4 \times 5)=100-20=80
\)
The final value is \(\frac{80}{16}=5\).

Hint

(c)
\(
\sqrt{3} \operatorname{cosec} 20^{\circ}-\sec 20^{\circ}=\frac{\sqrt{3}}{\sin 20^{\circ}}-\frac{1}{\cos 20^{\circ}}
\)
\(
\frac{\sqrt{3}}{\sin 20^{\circ}}-\frac{1}{\cos 20^{\circ}}=\frac{\sqrt{3} \cos 20^{\circ}-\sin 20^{\circ}}{\sin 20^{\circ} \cos 20^{\circ}}
\)
\(
\begin{aligned}
& \frac{2\left(\frac{\sqrt{3}}{2} \cos 20^{\circ}-\frac{1}{2} \sin 20^{\circ}\right)}{\sin 20^{\circ} \cos 20^{\circ}} \\
& \text { Recognize } \frac{\sqrt{3}}{2}=\sin 60^{\circ} \text { and } \frac{1}{2}=\cos 60^{\circ} \\
& \frac{2\left(\sin 60^{\circ} \cos 20^{\circ}-\cos 60^{\circ} \sin 20^{\circ}\right)}{\sin 20^{\circ} \cos 20^{\circ}}
\end{aligned}
\)
\(
\begin{aligned}
&\sin 60^{\circ} \cos 20^{\circ}-\cos 60^{\circ} \sin 20^{\circ}=\sin \left(60^{\circ}-20^{\circ}\right)=\sin 40^{\circ}\\
&\text { The expression becomes } \frac{2 \sin 40^{\circ}}{\sin 20^{\circ} \cos 20^{\circ}} \text {. }
\end{aligned}
\)
\(
\begin{aligned}
&\sin 40^{\circ}=\sin \left(2 \times 20^{\circ}\right)=2 \sin 20^{\circ} \cos 20^{\circ}\\
&\text { Substitute this into the expression: } \frac{2\left(2 \sin 20^{\circ} \cos 20^{\circ}\right)}{\sin 20^{\circ} \cos 20^{\circ}} \text {. }
\end{aligned}
\)
Cancel out \(\sin 20^{\circ} \cos 20^{\circ}\) from the numerator and denominator.
The result is \(2 \times 2=4\).

Hint

(d)
\(
y=\frac{1}{\cos ^2 \theta}+\cos ^2 \theta
\)
The Arithmetic Mean-Geometric Mean (AM-GM) inequality states that for non-negative numbers, the arithmetic mean is always greater than or equal to the geometric mean. In this case: \(\frac{a+b}{2} \geq \sqrt{a b}\), where \(a=\frac{1}{\cos ^2 \theta}\) and \(b=\cos ^2 \theta\).
\(
\begin{aligned}
&\text { Substituting the values, we get: }\\
&\begin{aligned}
& \frac{\frac{1}{\cos ^2 \theta}+\cos ^2 \theta}{2} \geq \sqrt{\frac{1}{\cos ^2 \theta} \cdot \cos ^2 \theta} \\
& \frac{y}{2} \geq \sqrt{1} \\
& \frac{y}{2} \geq 1 \\
& y \geq 2
\end{aligned}
\end{aligned}
\)
The inequality \(y \geq 2\) means that \(y\) can be any value greater than or equal to 2 , but it cannot be equal to 2 . For example, if \(\cos ^2 \theta=1\) (which occurs when \(\theta=0\), but we know \(\theta \neq 0\) ), then \(y=1+1=2\). However, if \(\cos ^2 \theta\) is any value other than \(1, y\) will be greater than 2.

Hint

(a)
\(
\begin{aligned}
& \cos (\theta-\alpha)=\cos \theta \cos \alpha+\sin \theta \sin \alpha=a \\
& \cos (\theta-\beta)=\cos \theta \cos \beta+\sin \theta \sin \beta=b
\end{aligned}
\)
\(
\begin{aligned}
& \cos (\alpha-\beta)=\cos ((\theta-\beta)-(\theta-\alpha)) \\
& \cos (\alpha-\beta)=\cos (\theta-\beta) \cos (\theta-\alpha)+\sin (\theta-\beta) \sin (\theta-\alpha) \\
& \cos (\alpha-\beta)=a b+\sin (\theta-\beta) \sin (\theta-\alpha)
\end{aligned}
\)
\(
\begin{aligned}
& \sin ^2(\theta-\alpha)=1-\cos ^2(\theta-\alpha)=1-a^2 \\
& \sin (\theta-\alpha)= \pm \sqrt{1-a^2} \\
& \sin ^2(\theta-\beta)=1-\cos ^2(\theta-\beta)=1-b^2 \\
& \sin (\theta-\beta)= \pm \sqrt{1-b^2}
\end{aligned}
\)
\(
\cos (\alpha-\beta)=a b \pm \sqrt{1-a^2} \sqrt{1-b^2}
\)
\(
\sin ^2(\alpha-\beta)+2 a b \cos (\alpha-\beta)=\left(1-\cos ^2(\alpha-\beta)\right)+2 a b \cos (\alpha-\beta)
\)
Let \(X=\cos (\alpha-\beta)\). The expression becomes \(1-X^2+2 a b X\).
Substitute \(X=a b \pm \sqrt{1-a^2} \sqrt{1-b^2}\).
This leads to \(a^2+b^2\).