JEE Practice Questions (Single Choice Type)
Operation on Sets
Like operations on real numbers such as addition, subtraction, multiplication, and division, we have some operations on the sets.
Union of Two Sets
The union of two sets \(A\) and \(B\) is the set of all those elements which are either in \(A\) or in \(B\) or in both.
This set is denoted by \(A \cup B\) (read as ‘ \(A\) union \(B\) ‘).
Symbolically, \(A \cup B=\{x \mid x \in A\) or \(x \in B\}\)
Clearly, \(x \in A \cup B \Leftrightarrow x \in A\) or \(x \in B\)
For example,
(i) \(A=\{1,2,3\}\) and \(B=\{2,1,5,6\}\)
Then \(A \cup B=\{1,2,3,5,6\}\)
(ii)
\(
\begin{aligned}
& A=\{x: x \text { is a prime number less than } 10\} \text { and } \\
& B=\{x: x \in Z,-5<x<5\} \\
& \text { Then } A=\{2,3,5,7\} \text { and } B=\{-4,-3,-2,-1,0,1,2,3,4\} \\
& \therefore \quad A \cup B=\{-4,-3,-2,-1,0,1,2,3,4,5,7\}
\end{aligned}
\)
(iii)
\(
\begin{aligned}
& A=\{1,2,3\}, B=\{3,5\}, C=\{4,7,8\} \\
& \text { Then } A \cup B \cup C=\{1,2,3,4,5,7,8\}
\end{aligned}
\)
Properties of the union of sets
If \(x \notin A \cup B\), then certainly \(x \notin A\) and \(x \notin B\).
If \(A \subseteq B\), then \(A \cup B=B\).
\(
A \cup B=B \cup A \quad \text { (commutative) }
\)
\(
A \cup B \cup C=(A \cup B) \cup C=A \cup(B \cup C) \quad \text { (Associative) }
\)
\(
\begin{aligned}
& \text { Also. } A \cup B \cup C=B \cup C \cup A=C \cup B \cup A \text { etc. } \\
& A \subseteq A \cup B \text { and } B \subseteq A \cup B \\
& \phi \cup A=A \cup \phi=A
\end{aligned}
\)
Union and the word ‘or’
The word ‘or’ tells us that there is a union of two sets.
For example,
{singers} \(\cup\{\) instrumentalists \(\} \equiv\{\) people who sing or play an instrument};
{vowels} \(\cup\{\) letters in word ARMED \(\} \equiv\{\) letters that are vowels or are in word ARMED};
Union and the word ‘at least’
The word ‘at least’ tells us that there is a union of two sets. Let sets \(A, B\) and \(C\) be the sets of students who play cricket, football and hockey, respectively.
Then set \(A \cup B\) is the set of students who play at least one of the sports cricket and football.
Similarly, \(B \cup C\) is the set of students who play at least one of the sports football and hockey.
Also, \(A \cup B \cup C\) is the set of students who play at least one of the sports, cricket, football and hockey.
Intersection of Two Sets
The intersection of two sets \(A\) and \(B\) is the set of all the elements which are common in \(A\) and \(B\). This set is denoted by \(A \cap B\) (read as ‘ \(A\) intersection \(B\) ‘).
Symbolically, \(A \cap B=\{x \mid x \in A\) and \(x \in D\}\) Clearly, \(x \in A \cap B \Leftrightarrow x \in A\) and \(x \in B\).
For example,
(i) Consider sets, \(A=\{1,2,3\}\) and \(B=\{1,2,5,6\}\)
Here, elements 1 and 2 are common in sets \(A\) and \(B\).
So, \(A \cap B=\{1,2\}\)
(ii) Consider sets \(A=\{1,2,3\}\) and \(B=\{5,6,7,8\}\). We observe that there is no element common in sets \(A\) and \(B\). So, \(A \cap B=\phi\)
(iii) Consider sets \(A=\{1,2,3\}\) and \(B=\{1,2,3,4,5,6\}\).
We observe that all the elements of set \(A\) are in set \(B\). In fact, set \(A\) is a subset of set \(B\).
So, \(A \cap B=\{1,2,3\}=A\)
(iv) Consider sets \(A=\{1,2,3\}, B=\{2,4,6\}\) and \(C=\{1,2\}\). Then \(A \cap B \cap C=\{2\}\)
Properties of the intersection of sets
\(x \notin A\) and \(x \notin B \Leftrightarrow x \notin A \cap B\)
If \(x \notin\left(A_1 \cap A_2 \cap A_3 \cap \ldots\right)\) then \(x\) is not the element of at least one of the sets.
If \(A \subseteq B\) then \(A \cap B=A\).
\(A \cap B=B \cap A\) (commutative)
\(A \cap B \cap C=(A \cap B) \cap C=A \cap(B \cap C)\) (associative)
Also, \(A \cap B \cap C=B \cap C \cap A=C \cap B \cap A\) etc.
\(A \cap B \subseteq A\) and \(A \cap B \subseteq B\)
\(\phi \cap A=A \cap \phi=\phi\)
\((A \cup B) \cap A=A\) and \((A \cup B) \cap B=B\)
\((A \cap B) \cup A=A\) and \((A \cap B) \cup B=B\)
\(A \cup(B \cap C)=(A \cup B) \cap(A \cup C) \quad \text { (Distributive law) }\)
\(A \cap(B \cup C)=(A \cap B) \cup(A \cap C) \quad \text { (Distributive law) }\)
Intersection and the word ‘and’
The word ‘and’ tells us that there is an intersection of two sets. For example,
{singers} \(\cap\) {instrumentalists} \(\equiv\) {people who sing and play an instrument}
{vowels} \(\cap\) {letters of word EXAMINATION} \(\equiv\) {letters that are vowels and are in word EXAMINATION}
Intersection and the word ‘both
The word ‘both’ tells us that there is an intersection of two sets.
Let sets \(A, B\) and \(C\) be the sets of students who play cricket, football and hockey, respectively.
Then set \(A \cap B\) is the set of students who play both the sports cricket and football.
Similarly, \(B \cap C\) is the set of students who play both the sports football and hockey.
Also, \(A \cap B \cap C\) is the set of students who play all the sports cricket, football and hockey.
Disjoint sets
If \(A \cap B=\phi\), then sets \(A\) and \(B\) are called disjoint sets.
Difference of Two Sets
The difference of two sets \(A\) and \(B\) (also called ‘relative complement’ of \(B\) in \(A\) ) is the set of all those elements of \(A\) which are not elements of \(B\). It is denoted by \(A-B\). Thus \(A-B\) can be obtained by discarding the elements of \(B\), present in \(A\).
Symbolically, \(A-B=\{x \mid x \in A\) and \(x \notin B\}\)
For example,
(i) Consider sets, \(A=\{1,3,5,6,7\}\) and \(B=\{2,3,4,5\}\).
Here, elements 3 and 5 are common in sets \(A\) and \(B\).
So, \(A-B=\{1,6,7\}\) and \(B-A=\{2,4\}\)
(ii) Consider sets \(A=\{1,2,3\}\) and \(B=\{5,6,7,8\}\).
We observe that there is no element common between sets \(A\) and \(B\).
So. \(A-B=\{1,2,3\}=A\) and \(B-A=\{5,6,7,8\}=B\)
(iii) Corsider sets \(A=\{1,2,3\}\) and \(B=\{1,2,3,4,5,6\}\).
We observe that all the elements of set \(A\) are in set \(B\). i.e., set \(A\) is subset of set \(B\).
So. \(A-B=\phi\) and \(B-A=\{4,5,6\}\)
Properties of the difference of sets
If \(A \cap B=\phi\) (i.e., sets \(A\) and \(B\) have no common elements), then \(A-B=A\) and \(B-A=B\).
If \(A \subseteq B\), then \(A-B=\phi\).
\(x\) is not the element of set \(A-B\) if \(x \in A\) and \(x \in B\).
\(A-B \neq B-A\)
Difference and the word ‘only’
Consider \(A=\) set of students who play cricket and \(B=\) set of students who play football.
Now, \(A-B=\) set of students who play cricket but not football \(=\) set of students who play cricket only
Similarly, \(B-A=\) set of students who play football only
COMPLEMENT OF A SET
The complement of a set \(A\) (also called ‘absolute complement’ of \(A\) ) is the set of all those elements of the universal set \(U\) which are not the elements of \(A\). It is denoted by \(A^c\) or \(A^{\prime}\).
For example, if set \(U=\{1,2,3,4,5,6,7,8,9,10\}\) and set \(A=\{1,2,5,7,9\}\) then set \(A^{\prime}=\{3,4,6,8,10\}\).
Clearly, \(A^{\prime}=U-A\).
Symbolically, set \(A^{\prime}=\{x \mid x \in U\) and \(x \notin A\}\)
Thus, if \(x \in A \Leftrightarrow x \notin A^{\prime}\).
Properties of complement of sets
\(A \cap A^{\prime}=\phi\) (as nothing is common between \(A\) and \(A^{\prime}\) )
\(A \cup A^{\prime}=U\)
\(U^{\prime}=\phi\)
\(\left(A^{\prime}\right)^{\prime}=A\)
\(A \subseteq B \Leftrightarrow B^{\prime} \subseteq A^{\prime}\)
\(A-B=B^{\prime}-A^{\prime}\)
\(A-B=A \cap B^{\prime}\)
\(B-A=A^{\prime} \cap B\)
Complement and the word ‘not’
The word ‘not’ corresponds to the complement of a set.
For example, let set \(V=\{\) letters that are vowel \(\}\)
Then complement of set \(V\) is \(V^{\prime}=\{\) letters that are not vowels \(\}\)
\(=\{\) letters that are consonants \(\}\)
De Morgan’s Laws
(i) \((A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}\)
(ii) \((A \cap B)^{\prime}=A^{\prime} \cup B^{\prime}\)
(iii) \(A-(B \cup C)=(A-B) \cap(A-C)\)
(iv) \(A-(B \cap C)=(A-B) \cup(A-C)\)
SOME IMPORTANT RESULTS
If \(A, B\) and \(C\) are finite sets, and \(U\) be the finite universal set, then
(i) \(n(A \cup B)=n(A)+n(B)-n(A \cap B)\)
(ii) \(n(A \cup B)=n(A)+n(B) \Leftrightarrow A, B\) are disjoint non-void sets.
(iii) \(n(A-B)=n(A)-n(A \cap B)\)
i.e. \(n(A-B)+n(A \cap B)=n(A)\)
(iv)
\(
\begin{aligned}
& n(A \Delta B) \\
& =\text { No. of elements which belong to exactly one of } A \text { or } B \\
& =n((A-B) \cup(B-A)) \\
& =n(A-B)+n(B-A)[\because(A-B) \text { and }(B-A) \text { are disjoint }] \\
& =n(A)-n(A \cap B)+n(B)-n(A \cap B) \\
& =n(A)+n(B)-2 n(A \cap B)
\end{aligned}
\)
\(\Delta:\) This symbol represents the symmetric difference of two sets. The symmetric difference of sets A and B, denoted \(A \Delta B\), is the set of elements that are in either A or \(B\), but not in their intersection.
(v)
\(
\begin{aligned}
& n(A \cup B \cup C) \\
& =n(A)+n(B)+n(C)-n(A \cap B)-n(B \cap C)-n(A \cap C) \\
& \quad+n(A \cap B \cap C)
\end{aligned}
\)
(vi) No. of elements in exactly two of the sets \(A, B, C\)
\(
=n(A \cap B)+n(B \cap C)+n(C \cap A)-3 n(A \cap B \cap C) .
\)
\(
\begin{aligned}
&\text { (vii) No. of elements in exactly one of the sets } A, B, C\\
&\begin{gathered}
=n(A)+n(B)+n(C)-2 n(A \cap B)-2 n(B \cap C) \\
-2 n(A \cap C)+3 n(A \cap B \cap C)
\end{gathered}
\end{aligned}
\)
(viii) \(n\left(A^{\prime} \cup B^{\prime}\right)=n\left((A \cap B)^{\prime}\right)=n(U)-n(A \cap B)\)
(ix) \(n\left(A^{\prime} \cap B^{\prime}\right)=n\left((A \cup B)^{\prime}\right)=n(U)-n(A \cup B)\).
Quiz Summary
0 of 123 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 123 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 123
1. Question
Let \(F_1\) be the set of parallelograms, \(F_2\) the set of rectangles, \(F_3\) be the set of rhombuses, \(F_4\) be the set of squares and \(\mathrm{F}_5\) be the set of trapeziums in a plane. Then \(F_1\) may be equal to
CorrectIncorrectHint
(d) Since every rectangle ( \(F_2\) ), rhombus ( \(F_3\) ), and square ( \(F_4\) ) is a type of parallelogram, we can say:
\(
F_2 \subseteq F_1, \quad F_3 \subseteq F_1, \quad F_4 \subseteq F_1
\)
However, not every trapezium is a parallelogram, hence:
\(
F_5 \nsubseteq F_1
\)
The union of the sets \(F_2, F_3\), and \(F_4\) can be expressed as:
\(
F_1=F_1 \cup F_2 \cup F_3 \cup F_4
\)
This indicates that all rectangles, rhombuses, and squares are included within the set of parallelograms.
From the analysis, we conclude that the set of all parallelograms ( \(F_1\) ) can indeed be represented as the union of itself and the other sets of quadrilaterals that are also parallelograms.
Thus, the correct answer is option (d): \(F_1=F_1 \cup F_2 \cup F_3 \cup F_4\) -
Question 2 of 123
2. Question
If \(n(A)=3, n(B)=6\) and \(A \subseteq B\). Then the number of elements in \(A \cup B\) is equal to
CorrectIncorrectHint
(c)
(c) Since \(A \subseteq B, A \cup B=B\)
So, \(n(A \cup B)=n(B)=6\)Explanation:
Since \(\boldsymbol{A} \subseteq \boldsymbol{B}\), every element in \(\boldsymbol{A}\) is also in \(\boldsymbol{B}\).
Because \(\boldsymbol{A}\) is a subset of \(\boldsymbol{B}\), the union of \(\boldsymbol{A}\) and \(\boldsymbol{B}\) is simply \(\boldsymbol{B}\). \(A \cup B=B\).
The number of elements in \(A \cup B\) is equal to the number of elements in \(B\).
\(
n(A \cup B)=n(B)
\)
Substitute the given value: \(n(A \cup B)=6\). -
Question 3 of 123
3. Question
If the sets \(A\) and \(B\) are defined as
\(
\begin{aligned}
& A=\{(x, y) \mid y=1 / x, x \neq 0, x \in R\}, \\
& B=\{(x, y) \mid y=-x, x \in R,\} . \text { Then }
\end{aligned}
\)CorrectIncorrectHint
(c) Set \(\boldsymbol{A}\) is defined by the equation \(\boldsymbol{y}=\frac{1}{\boldsymbol{x}}\), where \(\boldsymbol{x} \neq \mathbf{0}\).
Set \(\boldsymbol{B}\) is defined by the equation \(\boldsymbol{y}=-\boldsymbol{x}\).
The intersection \(\boldsymbol{A} \cap \boldsymbol{B}\) consists of the points that are in both sets.
\(
\begin{aligned}
&\text { For } A \cap B \text {, we have }\\
&\begin{array}{ll}
& -x=\frac{1}{x} \\
\Rightarrow & -x^2=1 \\
\Rightarrow & x^2=-1, \text { which is not possible } \\
\therefore & A \cap B=\phi
\end{array}
\end{aligned}
\)Note: To find the intersection \(A \cap B\), we need to determine if there are any points that satisfy both conditions:
From Set A: \(y=\frac{1}{x}\)
From Set B: \(y=-x\)
Setting these equal to each other: \(\frac{1}{x}=-x\)
\(x^2=-1\)
Since there are no real solutions to this equation, we conclude that:
\(A \cap B=\emptyset\) -
Question 4 of 123
4. Question
Two finite sets have \(m\) and \(n(m>n)\) elements. The number of subsets of the first set is 112 more than that of the second set. The value of \(m n\) is
CorrectIncorrectHint
(b) According to the question,
\(
\begin{aligned}
& 2^m-2^n=112 \\
\Rightarrow \quad & 2^n\left(2^{m-n}-1\right)=2^4 \times 7
\end{aligned}
\)
Comparing exponents on both sides, we get
\(
2^n=2^4 \text { and } 2^{m-n}-1=7
\)
Now, \(2^n=2^4\)
\(
\Rightarrow \quad n=4
\)
And \(2^{m-n}=8\)
\(
\begin{array}{ll}
\Rightarrow & 2^{m-n}=2^3 \\
\Rightarrow & m-n=3 \\
\Rightarrow & m-4=3 \\
\therefore & m=7
\end{array}
\)
\(
\text { The value of } m n \text { is }=28
\) -
Question 5 of 123
5. Question
Let \(A\) and \(B\) be two non-empty subsets of a set \(X\) such that \(A\) is not a subset of \(B\). Then
CorrectIncorrectHint
(d) Understanding the Given Information:
We have two non-empty subsets A and B of a set X.
It is stated that A is not a subset of B. This means there exists at least one element in A that is not in B.
Finding Elements in A and B :
Let’s assume some elements for A and B to illustrate the concept.
For example, let \(A=\{2,5,7\}\) and \(B=\{1,5,6\}\).
Here, we can see that \(A\) contains the elements 2 and 7 which are not in \(B\).
Checking Subset Relationships:
Since \(A\) is not a subset of \(B\), we confirm that there are elements in \(A\) that do not belong to B.
We also check if \(B\) is a subset of \(A\). In our example, \(B\) contains the element 1 which is not in \(A\), so \(B\) is also not a subset of \(A\).
Exploring the Complement of B :
The complement of B , denoted as \(B^{\prime}\), consists of all elements in X that are not in \(B\).If \(X=\{1,2,3,4,5,6,7\}\), then \(B^{\prime}=\{2,3,4,7\}\).
Analyzing the Relationship Between \(\mathbf{A}\) and \(\mathbf{B}^{\prime}\) :
We need to check if \(A\) is a subset of \(B^{\prime}\) or if \(A\) and \(B^{\prime}\) are disjoint.
In our example, \(A\) has elements 2 and 7 which are also in \(B^{\prime}\). Therefore, \(A\) is not a subset of \(B^{\prime}\) since it contains the element 5 which is not in \(B^{\prime}\).
Conclusion:
Since \(A\) is not a subset of \(B\) and we have found elements that are common between \(A\) and \(B^{\prime}\), we conclude that \(A\) and \(B^{\prime}\) are non-disjoint.
Thus, we can summarize that \(A\) and \(B\) have some common elements, and \(A\) is not a subset of \(B\).
The correct conclusion is that A and \(B^{\prime}\) are non-disjoint. -
Question 6 of 123
6. Question
If \(a N=\{a x: x \in N\}\), then the set \(4 N \cap 6 N\) is
CorrectIncorrectHint
(c)
\(
\begin{aligned}
&4 N=\{4,8,12,16,20,24, \ldots\} \text { and } 6 N=\{6,12,18,24, \ldots\}\\
&\text { Hence, } 4 N \cap 6 N=\{12,24,36, \ldots\}=12 N
\end{aligned}
\) -
Question 7 of 123
7. Question
The set \(\left(A \cap B^{\prime}\right)^{\prime} \cup(B \cap C)\) is equal to
CorrectIncorrectHint
(b)
\(
\begin{aligned}
\left(A \cap B^{\prime}\right)^{\prime} \cup(B \cap C) & =\left(\left(A^{\prime} \cup\left(B^{\prime}\right)^{\prime}\right) \cup(B \cap C)\right. \\
& =\left(A^{\prime} \cup B\right) \cup(C \cap B) \\
& =A^{\prime} \cup(B \cup(C \cap B)) \\
& =A^{\prime} \cup B
\end{aligned}
\) -
Question 8 of 123
8. Question
For sets \(A\) and \(B,(A \cup B)^{\prime} \cup\left(A^{\prime} \cap B\right)\) equals
CorrectIncorrectHint
(a)
\(
(A \cup B)^{\prime} \cup\left(A^{\prime} \cap B\right)
\)
\(
\begin{aligned}
& =\left(A^{\prime} \cap B^{\prime}\right) \cup\left(A^{\prime} \cap B\right) \\
& =\left(A^{\prime} \cup A^{\prime}\right) \cap\left(A^{\prime} \cup B\right) \cap\left(B^{\prime} \cup A^{\prime}\right) \cap\left(B^{\prime} \cup B\right) \\
& =A^{\prime} \cap\left\{A^{\prime} \cup\left(B \cap B^{\prime}\right)\right\} \cap U \\
& =A^{\prime} \cap\left\{A^{\prime} \cup \phi\right\} \cap U \\
& =A^{\prime} \cap A^{\prime} \cap U \\
& =A^{\prime} \cap U=A^{\prime}
\end{aligned}
\) -
Question 9 of 123
9. Question
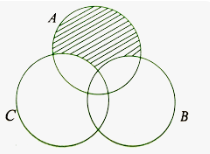
The shaded region in the given figure is
 CorrectIncorrect
CorrectIncorrectHint
(d) \(\text { Shaded region in the figure is clearly } A-(B \cup C) \text {. }\)
-
Question 10 of 123
10. Question
Which is the simplified representation of \(\left(A^{\prime} \cap B^{\prime} \cap C\right) \cup\) \((B \cap C) \cup(A \cap C)\) where \(A, B\) and \(C\) are subsets of set \(X\)?
CorrectIncorrectHint
(c)
\(
\begin{aligned}
{\left[\left(A^{\prime}\right.\right.} & \left.\left.\cap B^{\prime} \cap C\right)\right] \cup[(B \cap C) \cup(A \cap C)] \\
& \left.=\left[(A \cup B)^{\prime} \cap C\right)\right] \cup[(B \cup A) \cap C] \\
& =\left[(A \cup B)^{\prime} \cup(B \cup A)\right] \cap C \\
& =X \cap C \\
& =C
\end{aligned}
\) -
Question 11 of 123
11. Question
In statistical survey of 1003 families of Kolkata, it was found that 63 families has neither a radio nor a TV, 794 families has a radio and 187 has TV. The number of families in that group having both a radio and a TV is
CorrectIncorrectHint
(b) Families with at least one: 1003 (total) – 63 (neither) = 940 families have at least a radio or a TV.
Families with both: 794 (radio) + 187 (TV) – 940 (at least one) = 41 families have both. -
Question 12 of 123
12. Question
In a town of 10,000 families, it was found that \(40 \%\) families buy newspaper A, \(20 \%\) buy newspaper B and \(10 \%\) buy newspaper C. Also, \(5 \%\) families buy newspapers A and B, \(3 \%\) buy newspapers B and C and \(4 \%\) buy newspapers A and C. If \(2 \%\) families buy all the three newspapers, then number of families which buy newspaper A only is
CorrectIncorrectHint
(b)
\(
\begin{aligned}
&\begin{aligned}
& n(A)=40 \% \text { of } 10,000=4,000 \\
& n(B)=20 \% \text { of } 10,000=2,000 \\
& n(C)=10 \% \text { of } 10,000=1,000 \\
& n(A \cap B)=5 \% \text { of } 10,000=500 \\
& n(B \cap C)=3 \% \text { of } 10,000=300 \\
& n(C \cap A)=4 \% \text { of } 10,000=400 \\
& n(A \cap B \cap C)=2 \% \text { of } 10,000=200
\end{aligned}\\
&\text { Number of families which buy newspaper } A \text { only }\\
&\begin{aligned}
& =n\left(A \cap B^c \cap C^c\right) \\
& =n\left[A \cap(B \cup C)^c\right] \\
& =n(A)-n[A \cap(B \cup C)] \\
& =n(A)-n[(A \cap B) \cup(A \cap C)] \\
& =n(A)-[n(A \cap B)+n(A \cap C)-n(A \cap B \cap C)] \\
& =4000-[500+400-200] \\
& =4000-700 \\
& =3300
\end{aligned}
\end{aligned}
\) -
Question 13 of 123
13. Question
In a group of 500 people, 350 speak Hindi and 300 speak English. It is given that each person speaks at least one language.
(i) How many people can speak both Hindi and English?
(ii) How many people can speak Hindi only?
(iii) How many people can speak English only?CorrectIncorrectHint
(d) Let \(H\) be the set of people who speak Hind, and \(E\) be the set of people who speak English.
\(
\therefore \quad n(H \cup E)=500, n(H)=350, n(E)=300
\)
We have to find \(n(H \cap E)\).
Now, \(n(H \cup E)=n(H)+n(E)-n(H \cap E)\)
\(
\begin{array}{ll}
\therefore & 500=350+300-n(H \cap E) \\
\Rightarrow & 500=650-n(H \cap E) \\
\Rightarrow & n(H \cap E)=650-500 \\
\therefore & n(H \cap E)=150
\end{array}
\)
Thus, 150 people can speak both Hindi and English.
\(
\begin{aligned}
\text { Number of people who speak Hindi only } & =n(H)-n(H \cap E) \\
& =350-150=200
\end{aligned}
\)
\(
\begin{aligned}
\text { Number of people who speak English only } & =n(E)-n(H \cap E) \\
& =300-150=150
\end{aligned}
\) -
Question 14 of 123
14. Question
In a group of 50 students, the number of students learning French, English, Sanskrit were found to be as follows: French =17, English = 13, Sanskrit = 15, French and English = 09. English and Sanskrit =4, French and Sanskrit =5, English, French and Sanskrit =3. Find the number of students who are learning
(i) French only
(ii) English only
(iii) Sanskrit only
(iv) English and Sanskrit but not French
(v) French and Sanskrit but not English
(vi) French and English but not Sanskrit
(vii) at least one of the three languages
(viii) none of the three languages
(ix) exactly one language
(x) exactly two languagesCorrectIncorrectHint
(a)
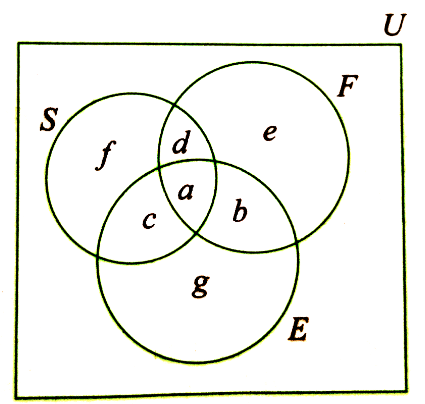
Let \(F, E\) and \(S\) be the sets of students who learn French, English and Sanskrit, respectively.
Then.
\(
\begin{aligned}
& n(U)=50, n(F)=17, n(E)=13, n(S)=15, \\
& n(F \cap E)=9, n(E \cap S)=4, n(F \cap S)=5, \\
& n(F \cap E \cap S)=3 .
\end{aligned}
\)
From the figure, we have
\(
\begin{aligned}
& a=n(E \cap F \cap S)=3 \text { and } a+d=n(F \cap S)=5 \Rightarrow d=2 \\
& a+b=n(F \cap E)=9 \Rightarrow b=6 \\
& a+c=n(E \cap S)=4 \Rightarrow c=1 \\
& a+b+d+e=n(F)=17 \Rightarrow 3+6+2+e=17 \Rightarrow e=6 \\
& a+b+c+g=n(E)=13 \Rightarrow 3+6+1+g=13 \Rightarrow g=3 \\
& a+c+d+f=n(S)=15 \Rightarrow 3+1+2+f=15 \Rightarrow f=9
\end{aligned}
\)
(i) Number of students learning French only \(=e=6\)
(ii) Number of students learning English only \(=g=3\)
(iii) Number of students learning Sanskrit only \(=f=9\)
(iv) Number of students learning English and Sanskrit but not French \(=c=1\)
(v) Number of students learning French and Sanskrit but not English \(=d=2\)
(vi) Number of students learning French and English but not Sanskrit \(=b=6\)
(vii) Number of students learning at least one of the three languages \(=a+b+c+d+e+f+g=30\)
(viii) Number of students learning none of the three languages \(=50-30=20\)
(ix) Number of students learning exactly one language \(=e+f+g=6+3+9=18\)
(x) Number of students learning exactly two languages \(=b+c+d=6+2+1=9\) -
Question 15 of 123
15. Question
If \(A, B\), and \(C\) are three sets such that \(A \cap B=A \cap C\) and \(A \cup B=A \cup C\), then
CorrectIncorrectHint
(c)
\(
\begin{array}{rlr}
B & =B \cap(A \cup B) & \\
& =B \cap(A \cup C) & (\because A \cup B=A \cup C) \\
& =(B \cap A) \cup(B \cap C) & \\
& =(A \cap B) \cup(B \cap C) & \\
& =(A \cap C) \cup(B \cap C) & (\because A \cap B=A \cap C) \\
& =(A \cup B) \cap C & \\
& =(A \cup C) \cap C & \\
& =C &
\end{array}
\) -
Question 16 of 123
16. Question
In a survey conducted on 800 students of a school, 250 students were found to like tea and 300 like coffee, 150 like both tea and coffee. Find how many students like neither tea nor coffee?
CorrectIncorrectHint
(d) Let \(U\) be the set of all students who took part in the survey, \(T\) be the set of students who like tea, and \(C\) be the set of students who like coffee.
According to the question,
\(
n(U)=800, n(T)=250, n(C)=300, n(T \cap C)=150
\)
To find the number of students taking neither tea nor coffee i.e., we have to find \(n\left(T^{\prime} \cap C^{\prime}\right)\)
\(
\begin{aligned}
n\left(T^{\prime} \cap C^{\prime}\right) & =n\left((T \cup C)^{\prime}\right) \\
& =n(U)-n(T \cup C) \\
& =n(U)-[n(T)+n(C)-n(T \cap C)] \\
& =800-[250+300-150]=400
\end{aligned}
\)
Hence, 400 students like neither tea nor coffee.Alternate Method:
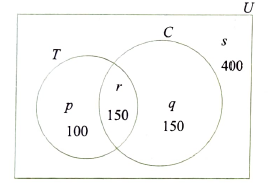
We can use Venn diagram as shown in the figure.
In the above figure regions are
\(r \rightarrow\) students liking tea and coffee both \(=n(T \cap C)\)
\(p \rightarrow\) students liking tea only \(=n(T)-n(T \cap C)\)
\(q \rightarrow\) students liking coffee only \(=n(C)-n(T \cap C)\)
\(s \rightarrow\) students liking neither tea nor coffee \(=n\left(T^{\prime} \cap C^{\prime}\right)\)
Here, \(r=150\) (given)
Now, \(p+r=\) students liking tea \(=250\) (given)
\(
\Rightarrow \quad p=250-150=100
\)
\(q+r=\) students liking coffee \(=300\) (given)
\(
\begin{aligned}
\Rightarrow \quad q & =300-150=150 \\
p+q+r & =\text { students liking at least one of tea and coffee } \\
& =100+150+150=400
\end{aligned}
\)
\(s=\) students liking neither tea nor coffee \(=800-400=400\) -
Question 17 of 123
17. Question
Out of 100 students; 15 passed in English, 12 in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science, 4 in English and Science and 4 in all the three. Find how many students passed
(a) in English and Mathematics but not in Science
(b) in Mathematics and Science but not in English
(c) in Mathematics only
(d) in more than one subjectsCorrectIncorrectHint
(c) Let \(M\) be the set of students who passed in Mathematics, \(E\) be the set of students who passed in English and \(S\) be the set of students who passed in Science.
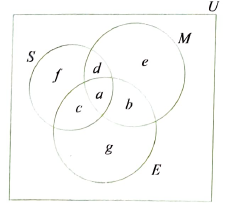
\(
\begin{aligned}
&\text { Given }\\
&\begin{aligned}
& n(U)=100 \\
& n(E)=15, n(M)=12, n(S)=8 \\
& n(E \cap M)=6, n(M \cap S)=7 \\
& n(E \cap S)=4, \text { and } n(E \cap M \cap S)=4
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
&\text { From the Venn diagram, we have }\\
&\begin{array}{ll}
a=n(E \cap M \cap S)=4 \text { and } & a+d=n(M \cap S)=7 \Rightarrow d=3 \\
a+b=n(M \cap E)=6 & \Rightarrow b=2 \\
a+c=n(S \cap E)=4 & \Rightarrow c=0 \\
a+b+d+e=n(M)=12 &
\end{array}
\end{aligned}
\)
\(
\begin{array}{lll}
\Rightarrow & 4+2+3+\mathrm{e}=12 & \Rightarrow e=3 \\
& a+b+c+g=15 & \\
\Rightarrow & 4+2+0+g=n(E)=15 & \Rightarrow g=9 \\
& a+c+d+f=n(S)=8 & \\
\Rightarrow & 4+0+3+f=8 & \Rightarrow f=1
\end{array}
\)
Number of students passed in
(a) English and Mathematics but not in Science \(=b=2\)
(b) Mathematics and Science but not in English \(=d=3\)
(c) Mathematics only \(=e=3\)
(d) more than one subject \(=a+b+c+d=4+2+0+3=9\) -
Question 18 of 123
18. Question
State which of the following statements are true and which ones are false. Justify your answer.
(i) \(21 \in\{x \mid x\) has exactly four positive factors \(\}\)
(ii) \(64 \in\{y \mid\) the sum of all the positive factors of \(y\) is \(2 y\}\)
(iii) \(2 \notin\left\{x \mid x^4-3 x^3+4 x^2-5 x+6=0\right\}\)
(iv) \(23562 \notin\{y \mid y\) is divisible by 9\(\}\)CorrectIncorrectHint
(b)
(i) The factors of 21 are \(1,3,7\) and 21. So, 21 is an element of the set.
Hence, the given statement is true.
(ii) The factors of 64 are \(1,2,4,8,16,32\) and 64.
\(\therefore\) Sum of factors \(=1+2+4+8+16+32+64\) \(=127 \neq 2 \times 64\)
So, 64 is not an element of the set.
Hence, the given statement is false.
(iii) We have, \(x^4-3 x^3+4 x^2-5 x+6=0\) For \(x=2,(2)^4-3(2)^3+4(2)^2-5(2)+6=0\)
\(\Rightarrow 16-24+16-10+6=0\) \(\Rightarrow 4=0\); which is not true.
So, 2 is not an element of the set.
Hence, the given statement is true.
(iv) We have number, 23562
Sum of the digits of the number is \(2+3+5+6+2=18\); which is divisible by 9.
So, 23562 is an element of the set.
Hence, the given statement is false. -
Question 19 of 123
19. Question
Are the following pairs of sets equal?
(i) \(A=\{x \mid x\) is prime factor of 6\(\}\);
\(B=\left\{x \mid x\right.\) is a solution of \(\left.x^2-5 x+6=0\right\}\)
(ii) \(A=\{x \mid x\) is a letter in the word REPLACED \(\}\);
\(B=\{y \mid y\) is a letter in the word PARCELED \(\}\)
(iii) \(A=\{x \mid x\) is a natural number, \(x>1\}\);
\(B=\{x \mid x\) is natural number, \(x \geq 1\}\)CorrectIncorrectHint
(d)
(i)
\(
\begin{aligned}
A= & \{x \mid x \text { is prime factor of } 6\}=\{2,3\} \\
B= & \left\{x \mid x \text { is solution of } x^2-5 x+6=0\right\} \\
& x^2-5 x+6=0 \\
\text { or } & (x-2)(x-3)=0 \\
\text { or } & x=2,3 \\
\therefore & B=\{2,3\}
\end{aligned}
\)
Therefore, \(A=B\).
(ii)
\(
\begin{aligned}
A & =\{x \mid x \text { is a letter in the word REPLACED }\} \\
& =\{\mathrm{R}, \mathrm{E}, \mathrm{P}, \mathrm{~L}, \mathrm{~A}, \mathrm{C}, \mathrm{D}\} \\
B & =\{y \mid y \text { is a letter in the word PARCELED }\} \\
& =\{\mathrm{P}, \mathrm{~A}, \mathrm{R}, \mathrm{C}, \mathrm{E}, \mathrm{~L}, \mathrm{D}\}
\end{aligned}
\)
Therefore, \(A=B\).
(iii)
\(
\begin{aligned}
& A=\{x \mid x \text { is natural number, } x>1\}=\{2,3,4, \ldots\} \\
& B=\{x \mid x \text { is natural number, } x \geq 1\}=\{1,2,3, \ldots\}
\end{aligned}
\)
We observe that \(1 \in B\) but \(1 \notin A\). Therefore, \(A \neq B\). -
Question 20 of 123
20. Question
If \(A \not \subset B\) and \(B \not \subset C\) then \(A \not \subset C\). Is this statement true?
CorrectIncorrectHint
(b) Let \(A=\{1,2\}, B=\{0,6,8\}\), and \(C=\{0,1,2,6,9\}\)
Here, \(A \not \subset B\) and \(B \not \subset C\), but \(A \subset C\). So, the given statement is false. -
Question 21 of 123
21. Question
If \(x \in A\) and \(A \not \subset B\), then \(x \in B\). Is this statement true?
CorrectIncorrectHint
(b) Let \(A=\{3,5,7\}\) and \(B=\{3,4,6\}\)
Now, \(5 \in A\) and \(A \not \subset B\)
However, \(5 \notin B\)
So, the given statement is false. -
Question 22 of 123
22. Question
If \(A\) and \(B\) be two sets containing 6 and 3 elements respectively, what can be the minimum number of elements in \(A \cup B\) ? Also, find the maximum number of elements in \(A \cup B\).
CorrectIncorrectHint
(a) We have, \(\quad n(A \cup B)=n(A)+n(B)-n(A \cap B)\), \(n(A \cup B)\) is minimum or maximum according as \(n(A \cap B)\) is maximum or minimum, respectively.
Case I: If \(n(A \cap B)\) is minimum i.e., \(n(A \cap B)=0\) such that
\(
\begin{aligned}
A & =\{a, b, c, d, e, f\} \text { and } B=\{g, h, i\} \\
\therefore \quad n(A \cup B) & =n(A)+n(B)=6+3=9
\end{aligned}
\)\(
Case II: If [latex]n(A \cap B)\) is maximum i.e., \(n(A \cap B)=3\), such that
\(
\begin{aligned}
A & =\{a, b, c, d, e, f\} \text { and } B=\{d, a, c\} \\
\therefore n(A \cup B) & =n(A)+n(B)-n(A \cap B)=6+3-3=6
\end{aligned}
\) -
Question 23 of 123
23. Question
In a pollution study of 1500 Indian rivers the following data were reported. 520 were polluted by sulphur compounds, 335 were polluted by phosphates, 425 were polluted by crude oil, 100 were polluted by both crude oil and sulphur compounds, 180 were polluted by both sulphur compounds and phosphates, 150 were polluted by both phosphates and crude oil and 28 were polluted by sulphur compounds, phosphates and crude oil. How many of the rivers were polluted by atleast one of the three impurities? How many of the rivers were polluted by exactly one of the three impurities?
CorrectIncorrectHint
(c) Let \(S, P\) and \(C\) denote the sets of rivers polluted by sulphur compounds, by phosphates and by crude oil respectively, and let \(a, b, c, d, e, f, g\) denote the elements (impurities) contained in the bounded region as shown in the diagram.
\(
\begin{aligned}
&\text { Then, }\\
&\begin{aligned}
& a+d+e+g=520 \\
& c+d+f+g=425 \\
& b+e+f+g=335 \Rightarrow d+g=100
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
e+g & =180 \Rightarrow f+g=150 \\
g & =28
\end{aligned}
\)
After solving, we get
\(
g=28, f=122, e=152, b=33, d=72, c=203 \text { and } a=268
\)
The number of rivers were polluted by atleast one of the three impurities
\(
=(a+b+c+d+e+f+g)=878
\)
and the number of rivers were polluted by exactly one of the three impurities,
\(
a+b+c=268+33+203=504
\) -
Question 24 of 123
24. Question
In a group of 1000 people, there are 750 who can speak Hindi and 400 who can speak Bengali. How many can speak Hindi only? How many can speak Bengali only? How many can speak both Hindi and Bengali?
CorrectIncorrectHint
(b) Let \(H\) and \(B\) be the set of those people who can speak Hindi and Bengali respectively, then according to the problem, we have
\(
\begin{aligned}
n(H \cup B) & =1000, \\
n(H) & =750, n(B)=400
\end{aligned}
\)
We know that,
\(
\begin{aligned}
n(H \cup B) & =n(H)+n(B)-n(H \cap B) \\
1000 & =750+400-n(H \cap B) \\
\therefore \quad n(H \cap B) & =150
\end{aligned}
\)
\(\therefore\) Number of people speaking Hindi and Bengali both is 150.
Also, \(\quad n\left(H \cap B^{\prime}\right)=n(H)-n(H \cap B)\)
\(
\begin{aligned}
& =750-150 \\
& =600
\end{aligned}
\)
Thus, number of people speaking Hindi only is 600.
Again, \(n\left(B \cap H^{\prime}\right)=n(B)-n(B \cap H)=400-150=250\)
Thus, number of people speaking Bengali only is 250. -
Question 25 of 123
25. Question
A survey of 500 television watchers produced the following information, 285 watch football, 195 watch hockey, 115 watch basketball, 45 watch football and basketball, 70 watch football and hockey, 50 watch hockey and basketball, 50 do not watch any of the three games. How many watch all the three games? How many watch exactly one of the three games?
CorrectIncorrectHint
(c) Let \(F, H\) and \(B\) be the sets of television watchers who watch Football, Hockey and Basketball, respectively.
Then, according to the problem, we have
\(
\begin{aligned}
& \qquad \begin{aligned}
n(U) & =500, n(F)=285, n(H)=195, \\
n(B) & =115, n(F \cap B)=45, \\
n(F \cap H) & =70, n(H \cap B)=50 \\
\text { and } \quad n\left(F^{\prime}\right. & \left.\cup H^{\prime} \cup B^{\prime}\right)=50,
\end{aligned}
\end{aligned}
\)
where \(U\) is the set of all the television watchers.
Since, \(n\left(F^{\prime} \cup H^{\prime} \cup B^{\prime}\right)=n(U)-n(F \cup H \cup B)\)
\(
\begin{array}{lrl}
\Rightarrow & & 50=500-n(F \cup H \cup B) \\
\Rightarrow & & n(F \cup H \cup B)=450
\end{array}
\)
\(
\begin{aligned}
&\text { We know that, }\\
&\begin{aligned}
& n(F \cup H \cup B)=n(F)+n(H)+n(B)-n(F \cap H) \\
&-n(H \cap B)-n(B \cap F)+n(F \cap H \cap B)
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
450= & 285+195+115-70-50-45+n(F \cap H \cap B) \\
& n(F \cap H \cap B)=20
\end{aligned}
\)
which is the number of those who watch all the three games. Also, number of persons who watch football only
\(
\begin{aligned}
& =n\left(F \cap H^{\prime} \cap B^{\prime}\right) \\
& =n(F)-n(F \cap H)-n(F \cap B)+n(F \cap H \cap B) \\
& =285-70-45+20=190
\end{aligned}
\)
The number of persons who watch hockey only
\(
\begin{aligned}
& =n\left(H \cap F^{\prime} \cap B^{\prime}\right) \\
& =n(H)-n(H \cap F)-n(H \cap B)+n(H \cap F \cap B) \\
& =195-70-50+20=95
\end{aligned}
\)
and the number of persons who watch basketball only
\(
\begin{aligned}
& =n\left(B \cap H^{\prime} \cap F^{\prime}\right) \\
& =n(B)-n(B \cap H)-n(B \cap F)+n(H \cap F \cap B) \\
& =115-50-45+20=40
\end{aligned}
\)
Hence, required number of those who watch exactly one of the three games
\(
=190+95+40=325
\) -
Question 26 of 123
26. Question
A class has 175 students. The following table shows the number of students studying one or more of the following subjects in this case.
\(
\begin{array}{ll}
\hline \text { Subjects } & \text { Number of students } \\
\hline \text { Mathematics } & 100 \\
\hline \text { Physics } & 70 \\
\hline \text { Chemistry } & 46 \\
\hline \text { Mathematics and Physics } & 30 \\
\hline \text { Mathematics and Chemistry } & 28 \\
\hline \text { Physics and Chemistry } & 23 \\
\hline \text { Mathematics, Physics and Chemistry } & 18 \\
\hline
\end{array}
\)
How many students are enrolled in Mathematics alone, Physics alone and Chemistry alone? Are there students who have not offered any one of these subjects?CorrectIncorrectHint
(a) Let \(P, C\) and \(M\) denotes the sets of students studying Physics, Chemistry and Mathematics, respectively.
Let \(a, b, c, d, e, f, g\) denote the elements (students) contained in the bounded region as shown in the diagram.
Then,
\(
\begin{aligned}
a+d+e+g & =170 \\
c+d+f+g & =100 \\
b+e+f+g & =46 \\
d+g & =30 \\
e+g & =23 \\
f+g & =28 \\
g & =18
\end{aligned}
\)
After solving, we get \(g=18, f=10, e=5, d=12, a=35\), \(b=13\) and \(c=60\)
\(
\therefore \quad a+b+c+d+e+f+g=153
\)
So, the number of students who have not offered any of these three subjects \(=175-153=22\)
Number of students studying Mathematics only, \(c=60\)
Number of students studying Physics only, \(a=35\)
Number of students studying Chemistry only, \(b=13\) -
Question 27 of 123
27. Question
If \(X=\left\{4^n-3n-1: n \in N\right\}\) and \(y=\{9(n-1): n \in N\}\), then \(X \cup Y\) equals
CorrectIncorrectHint
(b) Given, \(X=\left\{4^n-3 n-1: n \in N\right\}\), where \(N\) is the set of natural numbers so \(N=1,2,3, \ldots\).
After putting all these values of N, we will get the elements of X.
\(
\Rightarrow X=\{0,9,54, \ldots .\}
\)
Similarly, \(Y=\{9(n-1): n \in N\}\), where \(N\) is the set of natural numbers,
\(
\Rightarrow \mathrm{Y}=\{0,9,18,27, \ldots .\}
\)
Here, all elements of X is contained in set Y.
Since \(X\) is a subset of \(Y\), the union of the two sets is simply:
\(
X \cup Y=Y
\) -
Question 28 of 123
28. Question
If \(N_a=\{a n: n \in N\}\), then \(N_5 \cap N_7\) equals
CorrectIncorrectHint
(d) The intersection of \(N_5\) and \(N_7\), denoted as \(N_5 \cap N_7\), is equal to \(N_{35}\).
Explanation:
Definition of \(N_a\) :
The set \(N_a\) is defined as the set of all multiples of the number ‘ a ‘, where ‘ a ‘ is a positive integer. So, \(N_5=\{5 n \mid n \in N\}=\{5,10,15,20, \ldots\}\) and
\(
N_7=\{7 n \mid n \in N\}=\{7,14,21,28, \ldots\}
\)
Intersection: The intersection of two sets contains only the elements that are common to both sets. Therefore, \(N_5 \cap N_7\) will contain all numbers that are multiples of both 5 and 7.
Common Multiples: The numbers that are multiples of both 5 and 7 are multiples of the least common multiple (LCM) of 5 and 7 , which is 35.
Result: Therefore, \(N_5 \cap N_7\) is the set of all multiples of 35 , which is
\(
N_{35}=\{35 n \mid n \in N\}=\{35,70,105, \ldots\}
\) -
Question 29 of 123
29. Question
If \(A\) and \(B\) are two sets, then \(A \cap(A \cup B)^{\prime}\) equals
CorrectIncorrectHint
(c) \(\phi\).
We need to find \(A \cap(A \cup B)^{\prime}\).
Using De Morgan’s laws, \((A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}\).
Therefore, \(A \cap\) \((A \cup B)^{\prime}=A \cap\left(A^{\prime} \cap B^{\prime}\right)=\left(A \cap A^{\prime}\right) \cap B^{\prime}=\phi \cap B^{\prime}=\phi\). -
Question 30 of 123
30. Question
If \(U\) be the universal set and \(A \cup B \cup C=U\), then \([(A-B) \cup(B-C) \cup(C-A)]^{\prime}\) equals
CorrectIncorrectHint
(b)
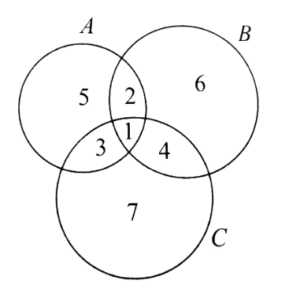
\(A-B \rightarrow\) Regions 3 and 5
\(B-C \rightarrow\) Regions 2 and 6
\(C-A \rightarrow\) Regions 4 and 7
\(\therefore(A-B) \cup(B-C) \cup(C-A) \rightarrow\) Regions 2,3,4,5,6,7
\(\therefore [(A-B) \cup(B-C) \cup(C-A)]^{\prime}\) Region 1 which is \(A \cap B \cap C\) -
Question 31 of 123
31. Question
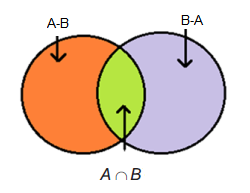
If \(A\) and \(B\) are two sets, then \((A-B) \cup(B-A) \cup(A \cap B)\) equals
CorrectIncorrectHint
(a)
-
Question 32 of 123
32. Question
If \(A=\{x: x\) is a multiple of 4\(\}\) and \(B=\{x: x\) is a multiple of 6\(\}\), then \(A \subset B\) consists of all multiple of
CorrectIncorrectHint
(c) The intersection of two sets, \(\boldsymbol{A} \cap \boldsymbol{B}\), contains elements present in both sets.
The least common multiple (LCM) of two numbers is the smallest positive integer that is a multiple of both numbers.
Find the least common multiple (LCM) of 4 and 6.
Find the prime factorization of each number.
Prime factorization of 4 is \(2^2\).
Prime factorization of 6 is \(2 \times 3\).
Calculate the LCM:
The LCM is found by taking the highest power of each prime factor present in either factorization.
\(
\operatorname{LCM}(4,6)=2^2 \times 3^1=4 \times 3=12 .
\)
Determine the elements of \(A \cap B\).
\(A \cap B\) consists of all multiples of the \(\operatorname{LCM}(4,6)\).
Therefore, \(A \cap B\) consists of all multiples of 12. -
Question 33 of 123
33. Question
A set contains \(2 n+1\) elements. The number of subsets of this set containing more than \(n\) elements equals
CorrectIncorrectHint
(d) Let the original set contain \((2 n+1)\) elements, then the number of subsets containing more than \(n\) elements, that is, subsets containing ( \(n+1\) ) elements, ( \(n+2\) ) elements, \(\ldots,(2 n+1)\) elements will be required to be computed.
\(\therefore\) Required number of subsets
\(
\begin{aligned}
& ={ }^{2 n+1} C_{n+1}+{ }^{2 n+1} C_{n+2}+\cdots+{ }^{2 n+1} C_{2 n}+{ }^{2 n+1} C_{2 n+1} \\
= & { }^{2 n+1} C_n+{ }^{2 n+1} C_{n+1}+\cdots+{ }^{2 n+1} C_1+{ }^{2 n+1} C_0 \\
= & { }^{2 n+1} C_0+{ }^{2 n+1} C_1+{ }^{2 n+1} C_2+\cdots+{ }^{2 n+1} C_{n-1}+{ }^{2 n+1} C_n \\
= & \frac{1}{2}\left[(1+1)^{2 n+1}\right]=\frac{1}{2}\left[2^{2 n+1}\right]=2^{2 n}
\end{aligned}
\) -
Question 34 of 123
34. Question
If \(A=\{\phi,\{\phi\}\}\), then the power set of \(A\) is
CorrectIncorrectHint
(c) Key Concept:
If \(A=\{a, b\}\)
\(\Rightarrow P(A)=\{\phi\},\{a\},\{b\},\{a, b\}\)In the given case, we get \(P(A)=\{\phi,\{\phi,\{\{\phi\}\}, A\}\)
-
Question 35 of 123
35. Question
Given \(n(U)=20, n(A)=12, n(B)=9, n(A \cap B)=4\), where \(U\) is the universal set, \(A\) and \(B\) are subsets of \(U\), then \(n\left((A \cup B)^{\prime}\right)\) equals
CorrectIncorrectHint
(a) The number of elements in the universal set \(U\) is \(n(U)=20\).
The number of elements in set \(A\) is \(n(A)=12\).
The number of elements in set \(\boldsymbol{B}\) is \(\boldsymbol{n}(\boldsymbol{B})=9\).
The number of elements in the intersection of \(A\) and \(B\) is \(n(A \cap B)=4\).
The Principle of Inclusion-Exclusion for two sets states
\(
n(A \cup B)=n(A)+n(B)-n(A \cap B)
\)
The complement of a set \(X\) in a universal set \(U\) is given by \(n\left(X^{\prime}\right)=n(U)-n(X)\).
Use the formula: \(n(A \cup B)=n(A)+n(B)-n(A \cap B)\).
Substitute the given values: \(n(A \cup B)=12+9-4\).
Calculate the sum: \(n(A \cup B)=21-4\).
\(
n(A \cup B)=17
\)
Use the formula for the complement: \(n\left((A \cup B)^{\prime}\right)=n(U)-n(A \cup B)\).
Substitute the values: \(n\left((A \cup B)^{\prime}\right)=20-17\).
\(
n\left((A \cup B)^{\prime}\right)=3
\) -
Question 36 of 123
36. Question
A survey shows that \(63 \%\) of the Indians like cheese, whereas \(76 \%\) like apples. If \(x \%\) of the Indians like both cheese and apples, then \(x\) can be
CorrectIncorrectHint
(c) The percentage of Indians who like cheese is 63%.
The percentage of Indians who like apples is \(76 \%\).
The percentage of Indians who like both cheese and apples is \(x \%\).
The total percentage of people cannot exceed \(100 \%\).
The percentage of people liking both cannot exceed the percentage of people liking either item individually.
Let C denote the percentage of people who like cheese and and A denote the percentage of people who like apples.
Given, \(\mathrm{n}(\mathrm{C})=63, \mathrm{n}(\mathrm{A})=76\) and \(\mathrm{n}(\mathrm{C} \cap \mathrm{A})={x}\).
We know that,
\(
\begin{aligned}
& n(C \cup A)=n(C)+n(A)-n(C \cap A) \\
& \Rightarrow n(C \cup A)=63+76-x
\end{aligned}
\)
\(
\Rightarrow x=139-n(C \cup A) \dots(i)
\)
\(
\begin{aligned}
&\text { Now, } n(C \cup A) \leq 100 \text { [Since, total people surveyed is 100] }\\
&\begin{aligned}
& \Rightarrow 139-n(C \cup A) \geq 139-100=39[\text { From }(\mathrm{i})] \\
& \Rightarrow x \geq 39
\end{aligned}
\end{aligned}
\)
\(
\begin{aligned}
&\begin{aligned}
& \text { Also, } n(C \cap A) \leq n(C) \text { and } n(C \cap A) \leq n(A) \\
& \Rightarrow x \leq 63 \\
& \therefore 39 \leq x \leq 63 \text {. }
\end{aligned}\\
&\text { Thus, the value of } x \text { lies between } 39 \text { and } 63 \text { also; the value of } x \text { can be } 39 \text { or } 63 \text {. }
\end{aligned}
\) -
Question 37 of 123
37. Question
In a class of 55 students, the number of students studying different subjects are 23 in Mathematics, 24 in Physics, 19 in Chemistry, 12 in Mathematics and Physics, 9 in Mathematics and Chemistry, 7 in Physics and Chemistry and 4 in all the three subjects. The number of students who have taken exactly one subject is
CorrectIncorrectHint
(d)
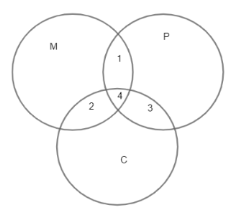
Here, region 1 represents \(M \cap P\) which means students studying Mathematics and Physics.
Region 2 represents \(M \cap C\) which means students studying Mathematics and Chemistry.
Region 3 represents \(P \cap C\) which means students studying Physics and Chemistry.
Region 4 represents \(M \cap P \cap C\) which means students studying Mathematics, Physics as well as Chemistry.
First of all we will find the number of students studying only mathematics, which is given as:
\(
n(M)-n(M \cap P)-n(M \cap C)+n(M \cap P \cap C) \dots(1)
\)
Here, \(n(M)=\) total number of students studying mathematics = 23
\(n(M \cap P)=\) number of students studying Mathematics and Physics = 12
\(n(M \cap C)=\) number of students studying Mathematics and Chemistry = 9
\(n(M \cap P \cap C)=\) number of students studying Mathematics, Physics as well as Chemistry = 4
We have to add \(n(M \cap P \cap C)\) once because ( \(M \cap P \cap C\) ) is contained in ( \(M \cap P\) ) as well as in \((M \cap C)\) and thus it gets subtracted twice.
On putting the respective values in equation (1), we get:
Number of students studying only Mathematics \(=23-12-9+4=6\)
Similarly, number of students studying only Chemistry is given as:
\(
\begin{aligned}
& =n(C)-n(C \cap M)-n(C \cap P)+n(M \cap P \cap C) \\
& =19-9-7+4=7
\end{aligned}
\)
And, the number of students studying only Physics is given as:
\(
\begin{aligned}
& =n(P)-n(P \cap C)-n(P \cap M)+n(M \cap P \cap C) \\
& =24-7-12+4=9
\end{aligned}
\)
So, the number of students who study exactly one subject is \(=6+7+9=22\). -
Question 38 of 123
38. Question
Two finite sets have \(m\) and \(n\) elements. The total number of subsets of the first set is 56 more than the total number of subsets of the second set. The values of \(m\) and \(n\) are
CorrectIncorrectHint
(b) The first set has \(m\) elements.
The second set has \(n\) elements.
The total number of subsets of the first set is 56 more than the total number of subsets of the second set.
The number of subsets of a set with \(x\) elements is \(2^x\).
The number of subsets of the first set is \(2^m\).
The number of subsets of the second set is \(2^n\).
The given condition is \(2^m-2^n=56\).
Factor out \(2^n\) from the left side: \(2^n\left(2^{m-n}-1\right)=56=2^3 \times 7\).
\(
\text { This implies } 2^n=2^3 \text { and } 2^{m-n}-1=7 \text {. }
\)
\(
\text { From } 2^n=2^3 \text {, we get } n=3 \text {. }
\)
From \(2^{m-n}-1=7\), we get \(2^{m-n}=8\).
Since \(8=2^3\), we have \(2^{m-n}=2^3\).
This implies \(m-n=3\).
Substitute \(n=3\) : \(m-3=3\).
Therefore, \(m=6\).
The values of \(m\) and \(n\) are 6 and 3 respectively. -
Question 39 of 123
39. Question
If \(a N=\{a x: x \in N\}\) and \(b N \cap c N=d N\), where \(b\), \(c \in N\) are relatively prime, then
CorrectIncorrectHint
(a) \(a N=\{a x: x \in N\}\) represents the set of multiples of \(a\).
\(b N \cap c N=d N\) means the intersection of multiples of \(b\) and \(c\) is the set of multiples of \(d\).
\(b, c \in N\) are relatively prime.
The intersection of two sets of multiples, \(b N \cap c N\), represents the set of common multiples of \(b\) and \(c\).
If \(b\) and \(c\) are relatively prime, their least common multiple (LCM) is their product, \(b c\).
\(b N\) is the set of all multiples of \(b\). \(c N\) is the set of all multiples of \(c\). \(b N \cap c N\) is the set of common multiples of \(b\) and \(c\).
Since \(b N \cap c N=d N, d N\) represents the set of common multiples of \(b\) and \(c\).
The smallest positive common multiple is the least common multiple (LCM).
Therefore, \(d\) must be the LCM of \(b\) and \(c\).
Given that \(b\) and \(c\) are relatively prime, their LCM is their product.
\(
\operatorname{LCM}(b, c)=b c
\)
Since \(d=\operatorname{LCM}(b, c)\), and \(\operatorname{LCM}(b, c)=b c\), then \(d=b c\). -
Question 40 of 123
40. Question
In a town of 10000 families, it was found that \(40 \%\) families buy newspaper A, 20% families buy newspaper B and 10% families buy newspaper C, 5% families buy newspapers \(A\) and \(B, 3 \%\) buy newspapers \(B\) and \(C\) and \(4 \%\) buy newspapers \(A\) and \(C\). If \(2 \%\) families buy all the three newspapers, then number of families which buy \(A\) only is
CorrectIncorrectHint
(b)
\(
\begin{gathered}
n(A)=40 \% \text { of } 10000=4000 \\
n(B)=20 \% \text { of } 10000=2000 \\
n(C)=10 \% \text { of } 10000=1000
\end{gathered}
\)
\(
\begin{aligned}
& n(A \cap B)=5 \% \text { of } 10000=500 \\
& n(B \cap C)=3 \% \text { of } 10000=300 \\
& n(C \cap A)=4 \% \text { of } 10000=400 \\
& n(A \cap B \cap C)=2 \% \text { of } 10000=200
\end{aligned}
\)
\(
\begin{aligned}
&\text { We want to find } n\left(A \cap B^c \cap C^c\right)=n\left[A \cap(B \cup C)^c\right]\\
&\begin{aligned}
& =n(A)-n[A \cap(B \cup C)]=n(A)-n[(A \cap B) \cup(A \cap C)] \\
& =n(A)-[n(A \cap B)+n(A \cap C)-n(A \cap B \cap C)] \\
& =4000-[500+400-200]=4000-700=3300
\end{aligned}
\end{aligned}
\) -
Question 41 of 123
41. Question
If \(A=\{2,3\}, B=\{4,5\}\) and \(C=\{5,6\}\), then \(n\{(A \times B) \cup(B \times C)\}\) is
CorrectIncorrectHint
(c)
\(
\begin{aligned}
\begin{aligned}
A \times B =\{2,3\} \times\{4,5\} \\
=\{(2,4),(2,5),(3,4),(3,5)\}
\end{aligned} \\
\text { and } \begin{aligned}
B \times C =\{4,5\} \times\{5,6\} \\
=\{(4,5),(4,6),(5,5),(5,6)\}
\end{aligned} \\
\begin{aligned}
\therefore(A \times B) & \cup(B \times C)=\{(2,4),(2,5),(3,4),(3,5), \\
& (4,5),(4,6),(5,5),(56)\}
\end{aligned} \\
\text { Now, } n\{(A \times B) \cup(B \times C)\}=8
\end{aligned}
\) -
Question 42 of 123
42. Question
Find the smallest and largest sets of Ysuch that \(Y \cup\{1,2\}=\{1,2,3,5,9\}.\)
CorrectIncorrectHint
(a) The union of set \(Y\) and set \(\{1,2\}\) is \(\{1,2,3,5,9\}\) This can be written as \(Y \cup\{1,2\}=\{1,2,3,5,9\}\).
The elements \(\{3,5,9\}\) are in \(\{1,2,3,5,9\}\) but not in \(\{1,2\}\). Therefore, \(Y\) must contain \(\{3,5,9\}\).
The smallest set \(Y\) contains only the necessary elements. So, the smallest set \(Y\) is \(\{3,5,9\}\).
The largest set \(Y\) can include elements from \(\{1,2\}\) without changing the union.
If \(Y\) contains \(\{1,2,3,5,9\}\), then \(Y \cup\{1,2\}=\{1,2,3,5,9\}\).
So, the largest set \(Y\) is \(\{1,2,3,5,9\}\).
The smallest set \(Y\) is \(\{3,5,9\}\) and the largest set \(Y\) is \(\{1,2,3,5,9\}\). -
Question 43 of 123
43. Question
Let \(A=\left\{\theta: 2 \cos ^2 \theta+\sin \theta \leq 2\right\}\) and \(B=\{\theta: \pi / 2 \leq \theta \leq 3 \pi / 2\}\). Then find \(A \cap B\).
CorrectIncorrectHint
(b)
\(
\begin{aligned}
2 \cos ^2 \theta+\sin \theta & \leq 2 \\
2\left(1-\sin ^2 \theta\right)+\sin \theta & \leq 2 \\
2 \sin ^2 \theta-\sin \theta & \geq 0 \\
\sin \theta(2 \sin \theta-1) & \geq 0
\end{aligned}
\)
\(
\begin{aligned}
&\begin{array}{ll}
\Rightarrow & \sin \theta\left(\sin \theta-\frac{1}{2}\right) \geq 0 \\
\therefore & \sin \theta \leq 0 \text { and } \sin \theta \geq \frac{1}{2}
\end{array}\\
&\text { Now, the values of } \theta \text { which lie in the interval } \frac{\pi}{2} \leq \theta \leq \frac{3 \pi}{2} \text {. }\\
&\left[\because B=\left\{\theta: \frac{\pi}{2} \leq \theta \leq \frac{3 \pi}{2}\right\}\right]
\end{aligned}
\)
So, \(\theta\) satisfy \(\sin \theta \leq 0\) in the interval \(\pi \leq \theta \leq \frac{3 \pi}{2}\) and \(\theta\) satisfy \(\sin \theta \geq \frac{1}{2}\) in the interval \(\frac{\pi}{2} \leq \theta \leq \frac{5 \pi}{6}\).
\(
\begin{aligned}
& \therefore \quad A \cap B=\left\{\theta: \pi \leq \theta \leq \frac{3 \pi}{2}\right\} \\
& \text { and } \quad \begin{aligned}
A \cap B & =\left\{\theta: \frac{\pi}{2} \leq \theta \leq \frac{5 \pi}{6}\right\} \\
\text { Hence, } A \cap B & =\left\{\theta: \frac{\pi}{2} \leq \theta \leq \frac{5 \pi}{6} \text { or } \pi \leq \theta \leq \frac{3 \pi}{2}\right\} \\
& =\left\{\theta: \theta \in\left[\frac{\pi,}{2} \frac{5 \pi}{6}\right] \cup\left[\pi, \frac{3 \pi}{2}\right]\right\}
\end{aligned}
\end{aligned}
\) -
Question 44 of 123
44. Question
An investigator interviewed 100 students to determine their preferences for the three drinks; milk \((M)\), coffee \((C)\) and tea \((T)\). He reported the following: 10 students has all the three drinks \(M, C, T ; 20\) had \(M\) and \(C ; 30\) had \(C\) and \(T\), 25 had \(M\) and \(T ; 12\) had \(M\) only; 5 had \(C\) only and 8 had \(T\) only. Using a Venn diagram, find how many did not take any of the three drinks?
CorrectIncorrectHint
(d) Given, \(M, C\) and \(T\) are the sets of drinks; milk, coffee and tea, respectively. Let us denote the number of drinks (students) contained in the bounded region as shown in the diagram by \(a, b, c, d, e, f\) and \(g\), respectively.
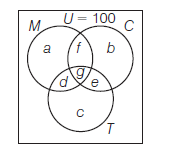
Then,
\(
\begin{aligned}
g & =10 \\
g+f & =20 \Rightarrow f=10 \quad[\because g=10] \\
g+e & =30 \Rightarrow e=20 \\
d+g & =25 \Rightarrow d=15 \\
a=12, b & =5, c=8
\end{aligned}
\)
Thus, total number of students taking drinks \(M\) or \(C\) or \(T\)
\(
\begin{aligned}
& =a+b+c+d+e+f+g \\
& =12+5+8+15+20+10+10=80
\end{aligned}
\)
Hence, the number of students taking none of them drinks
\(
=100-80=20
\) -
Question 45 of 123
45. Question
In a certain city, only two newspapers \(A\) and \(B\) are published. It is known that \(25 \%\) of the city population reads \(A\) and \(20 \%\) reads \(B\), while \(8 \%\) reads \(A\) and \(B\). It is also known that \(30 \%\) of those who read \(A\) but not \(B\), look into advertisements and \(40 \%\) of those who read \(B\) but not \(A\), look into advertisements while \(50 \%\) of those who read both \(A\) and \(B\), look into advertisements. What per cent of the population read on advertisement?
CorrectIncorrectHint
(a) Let \(C=\) Set of people who read paper \(A\)
and \(D=\) Set of people who read paper \(B\)
Given, \(\quad n(C)=25, n(D)=20, n(C \cap D)=8\)
\(
\begin{aligned}
\therefore \quad n\left(C \cap D^{\prime}\right) & =n(C)-n(C \cap D) \\
& =25-8=17
\end{aligned}
\)
But total number of people who read \(A\) but not \(B=30 \%\)
\(\therefore\) Percentage of people reading \(A\) but not \(B=30 \%\) of 17
\(
=\frac{30 \times 17}{100}=\frac{51}{10}
\)
and \(n\left(C^{\prime} \cap D\right)=n(D)-n(C \cap D)=20-8=12\)
Also, total number of people who read \(B\) but not \(A=40 \%\)
\(\therefore\) Percentage of people reading \(B\) but not \(A=40 \%\) of 12
\(
=\frac{40 \times 12}{100}=\frac{24}{5}
\)
and given total people who read \(A\) and \(B=50 \%\)
\(\therefore\) Total number of people who read \(A\) and \(B=50 \%\) of 8
\(
=\frac{50 \times 8}{100}=4
\)
\(\therefore\) Percentage of people reading an advertisement
\(
=\frac{51}{10}+\frac{24}{5}+4=13.9 \%
\) -
Question 46 of 123
46. Question
An analysis of 100 personal injury claims made upon a motor insurance company revealed that loss or injury in respect of an eye, an arm, a leg occurred in 30, 50 and 70 cases, respectively. Claims involving this loss or injury to two of these members numbered 44. How many claims involved loss or injury to all the three, we must assume that one or another of three members was mentioned in each of the 100 claims?
CorrectIncorrectHint
(c)
\(
\begin{aligned}
\text { Let } \quad E & =\text { Set of people having injuries in eyes } \\
\therefore \quad n(E) & =30 \\
A & =\text { Set of people having injuries in arms } \\
\therefore n(A) & =50 \\
\text { and } \quad L & =\text { Set of people having injuries in legs } \\
\therefore \quad n(L) & =70
\end{aligned}
\)
Let us denote the number of injuries contained in the bounded region as shown in the diagram by \(a, b, c, d, e, f\) and \(g\), respectively.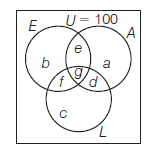
Then,
\(
\begin{array}{r}
b+e+f+g=30 \dots(i) \\
a+d+e+g=50 \dots(ii) \\
c+d+f+g=70 \dots(iii) \\
d+e+f=44 \dots(iv)
\end{array}
\)
and \(a+b+c+d+e+f+g=100 \dots(v)\)
On adding Eqs. (i), (ii) and (iii), we get
\(
\begin{aligned}
a+b+c+2(d+e+f)+3 g & =150 \\
\Rightarrow 100-d-e-f-g+2(d+e+f)+3 g & =150 \text { [from Eq. (v)] }
\end{aligned}
\)
\(
\begin{aligned}
\Rightarrow & d+e+f+2 g & =50 & \\
\Rightarrow & 44+2 g & =50 & \text { [from Eq. (iv)] } \\
\therefore & g & =3 &
\end{aligned}
\)
Hence, there are three claims involved loss or injury to all the three. -
Question 47 of 123
47. Question
If \(A\) and \(B\) are two sets, then \(A \cap(A \cup B)\) equals
CorrectIncorrectHint
(a) By Venn diagram
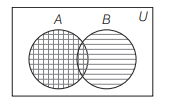
\(
\text { It is clear that } A \cap(A \cup B)=A
\)Example: Let’s say \(A=\{1,2,3\}\) and \(B=\{3,4,5\}\).
\(A \cup B=\{1,2,3,4,5\}\)
\(A \cap(A \cup B)=\{1,2,3\} \cap\{1,2,3,4,5\}=\{1,2,3\}=A\) -
Question 48 of 123
48. Question
If \(X\) and \(Y\) are two sets, then \(X \cap(Y \cap X)^{\prime}\) equals
CorrectIncorrectHint
(d) De Morgan’s Law: The complement of an intersection of two sets equals the union of their complements. Therefore, \((\mathbf{Y} \cap \mathbf{X})^{\prime}\) is equivalent to \(\mathbf{Y}^{\prime} \cup \mathbf{X}^{\prime}\). Substituting this into the original expression gives: \(\mathbf{X} \cap\left(\mathbf{Y}^{\prime} \cup \mathbf{X}^{\prime}\right)\)
Distributive Law: The distributive law for sets is similar to the distributive property in algebra. The intersection of a set with the union of two other sets is equal to the union of the intersections. Applying this to the expression: \(\left(\mathbf{X} \cap \mathbf{Y}^{\prime}\right) \cup\left(\mathbf{X} \cap \mathbf{X}^{\prime}\right)\)
Complement Law: The intersection of a set with its complement results in the empty set. \(\mathbf{X} \cap \mathbf{X}^{\prime}\) equals the empty set, denoted by \(\phi\). Substituting this into the expression: \(\left(\mathbf{X} \cap \mathbf{Y}^{\prime}\right) \cup \phi\)
Identity Law: The union of a set with the empty set is the set itself. Therefore: \(X \cap Y^{\prime}\) -
Question 49 of 123
49. Question
The number of elements of the power set of a set containing \(n\) elements is
CorrectIncorrectHint
(b) The number of elements in the power set is equal to the total number of subsets.
Therefore, the number of elements in the power set is \(2^n\).Let set \(A\) contains \(n\) elements.
Power set of \(A\) is the set of all subsets.
\(\therefore\) Number of subsets of \(A={ }^n C_o+{ }^n C_1+{ }^n C_2+\ldots+{ }^n C_n=2^n\)
\(\therefore\) Power set of \(A\) contains \(2^n\) elements. -
Question 50 of 123
50. Question
Which one of the following is not true?
CorrectIncorrectHint
(c)
(a) \(A-B \subseteq A\)
If an element \(\boldsymbol{x}\) is in \(\boldsymbol{A}-\boldsymbol{B}\), it means \(\boldsymbol{x}\) is in \(\boldsymbol{A}\) and not in \(\boldsymbol{B}\). Therefore, \(\boldsymbol{x}\) is in \(\boldsymbol{A}\). So, \(\boldsymbol{A}-\boldsymbol{B}\) is a subset of \(\boldsymbol{A}\). This statement is true.(b) \(B^{\prime}-A^{\prime} \subseteq A\)
Using the property \(\boldsymbol{X}-\boldsymbol{Y}=\boldsymbol{X} \cap \boldsymbol{Y}^{\prime}\), this statement can be rewritten as: \(B^{\prime}-A^{\prime}=B^{\prime} \cap\left(A^{\prime}\right)^{\prime}=B^{\prime} \cap A\).
So, the statement becomes \(\boldsymbol{B}^{\prime} \cap \boldsymbol{A} \subseteq \boldsymbol{A}\). If an element \(\boldsymbol{x}\) is in \(\boldsymbol{B}^{\prime} \cap \boldsymbol{A}\), it means \(\boldsymbol{x}\) is in \(\boldsymbol{B}^{\prime}\) and \(\boldsymbol{x}\) is in \(\boldsymbol{A}\). Therefore, \(\boldsymbol{x}\) is in \(\boldsymbol{A}\). So, \(\boldsymbol{B}^{\prime} \cap \boldsymbol{A}\) is a subset of \(\boldsymbol{A}\). This statement is true.(c) \(A \subseteq A-B\)
For \(\boldsymbol{A}\) to be a subset of \(\boldsymbol{A}-\boldsymbol{B}\), every element in \(\boldsymbol{A}\) must also be in \(\boldsymbol{A}-\boldsymbol{B}\). This means that for every \(\boldsymbol{x} \in \boldsymbol{A}, \boldsymbol{x}\) must not be in \(\boldsymbol{B}\). This implies that the intersection of \(\boldsymbol{A}\) and \(\boldsymbol{B}\) must be empty, i.e., \(\boldsymbol{A} \cap \boldsymbol{B}=\phi\). However, this is not always true for any sets \(A\) and \(B\). For example, if \(\boldsymbol{A}=\{1,2\}\) and \(\boldsymbol{B}=\{2,3\}\), then \(\boldsymbol{A}-\boldsymbol{B}=\{1\}\). In this case, \(\boldsymbol{A}=\{1,2\}\) is not a subset of \(\boldsymbol{A}-\boldsymbol{B}=\{1\}\) because \(2 \in A\) but \(2 \notin A-B\). Therefore, this statement is not true.(d) \(A \cap B^{\prime} \subseteq A\)
If an element \(\boldsymbol{x}\) is in \(\boldsymbol{A} \cap \boldsymbol{B}^{\prime}\), it means \(\boldsymbol{x}\) is in \(\boldsymbol{A}\) and \(\boldsymbol{x}\) is in \(\boldsymbol{B}^{\prime}\). Therefore, \(\boldsymbol{x}\) is in \(\boldsymbol{A}\). So, \(\boldsymbol{A} \cap \boldsymbol{B}^{\prime}\) is a subset of \(\boldsymbol{A}\). This statement is true.
Therefore, the statement that is not true is (c) \(\boldsymbol{A} \subseteq \boldsymbol{A}-\boldsymbol{B}\). -
Question 51 of 123
51. Question
If \(A=\{1,2,3\}\) and \(B=\{3,8\}\), then \((A \cup B) \times(A \cap B)\) is
CorrectIncorrectHint
(b)
\(
\begin{aligned}
A=\{1,2,3\} & \\
B & =\{3,8\} \\
A \cup B & =\{1,2,3,8\} \\
A \cap B & =\{3\} \\
(A \cup B) \times(A \cap B) & =\{1,2,3,8\} \times\{3\} \\
& =\{(1,3),(2,3),(3,3)(8,3)\}
\end{aligned}
\) -
Question 52 of 123
52. Question
Let \(A=\{x: x\) is a multiple of 3\(\}\) and \(B=\{x: x\) is a multiple of 5\(\}\), then \(A \cap B\) is given by
CorrectIncorrectHint
(c)
\(
\begin{aligned}
A & =\{x: x \text { is a multiple of } 3\} \\
A & =\{x: x=3 m, m \in N\} \\
B & =\{x: x \text { is a multiple of } 5\} \\
B & =\{x: x=5 n, n \in N\}
\end{aligned}
\)
The intersection of two sets, \(\boldsymbol{A} \cap \boldsymbol{B}\), contains elements common to both sets. A number that is a multiple of both 3 and 5 is a multiple of their least common multiple.
The LCM of 3 and 5 is \(3 \times 5=15\).
Elements in \(A \cap B\) are multiples of the LCM, which is 15 . So, \(A \cap B=\{15,30,45, \ldots\}\).
\(
\begin{gathered}
A \cap B=\{x: x \text { is a multiple of both } 3 \text { and } 5\} \\
=\{15,30,45, \ldots\}
\end{gathered}
\) -
Question 53 of 123
53. Question
Which of the following is the empty set?
CorrectIncorrectHint
(b) We observe that there is no real number \(x\) such that \(x^2+1=0\)
\(
x= \pm i
\)
\(\therefore \quad\left\{x: x\right.\) is a real number and \(\left.x^2+1=0\right\}=\phi\) -
Question 54 of 123
54. Question
Let \(A\) and \(B\) be two non-empty subsets of set \(X\) such that \(A\) is not a subset of \(B\), then
CorrectIncorrectHint
(d) Understand the definitions. A set \(A\) is said to be a subset of another set \(B\) (denoted \(A \subseteq B\) ) if every element of \(A\) is also an element of \(B\). The complement of \(B\), denoted \(B^{\prime}\), consists of all elements in the universal set \(X\) that are not in \(B\)
Given that \(A\) is not a subset of \(B\) (i.e., \(A \nsubseteq B\) ), this means there exists at least one element in \(A\) that is not in \(B\). Therefore, this element must belong to the complement of \(B\)
Since there is at least one element in \(A\) that is also in \(B^{\prime}\) (the complement of \(B\) ), it follows that \(A\) and \(B^{\prime}\) share at least one common element. This implies that \(A\) and \(B^{\prime}\) are not disjoint, as disjoint sets have no elements in common.
Consequently, we can conclude that the statement ” A and the complement of B are non-disjoint” is always true when \(A\) is not a subset of \(B\)
Thus, the correct choice is that \(A\) and the complement of \(B\) are non-disjoint.
-
Question 55 of 123
55. Question
In a group of children, 35 play football out of which 20 play football only, 22 play hockey; 25 play cricket out of which 11 play cricket only. Out of these 7 play cricket and football but not hockey, 3 play football and hockey but not cricket and 12 play football and cricket both. How many play all the three games? How many play cricket and hockey but not football, how many play hockey only? What is the total number of children in the group?
CorrectIncorrectHint
(b)
\(
\begin{aligned}
&\text { Given, }\\
&\begin{array}{r}
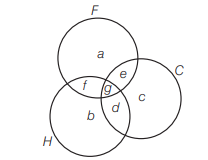
a=20 \dots(i) \\
e+f+g=15 \dots(ii) \\
b+d+f+g=22 \dots(iii) \\
c=11 \dots(iv)
\end{array}
\end{aligned}
\)
\(
\begin{aligned}
&\Rightarrow \quad \begin{aligned}
c+d+e+g & =25 \dots(v) \\
d+e+g & =14 \dots(vi) \\
e & =7 \dots(vii) \\
f & =3 \dots(viii)
\end{aligned}\\
&\text { From Eqs. (vii), (viii) and (ix), }\\
&\begin{aligned}
e+g & =12 \dots(ix) \\
e & =7, f=3, g=5
\end{aligned}
\end{aligned}
\)
From Eq. (vi), \(d=2\)
From Eq. (iii) \(b+2+3+5=22\)
\(
\therefore \quad b=12
\)
Hence, \(\quad a=20, b=12, c=11, d=2, e=7, f=3, g=5\)
Number of children play all the three games \(=g=5\)
Number of children play cricket and hockey but not football
\(
=d=2
\)
Number of children play hockey only \(=b=12\)
Total number of children in the group
\(
=a+b+c+d+e+f+g=60
\) -
Question 56 of 123
56. Question
Of the members of three athletic team in a certain school, 21 are on the basketball team, 26 on the hockey team and 29 on the football team. 14 play hockey and basketball, 15 play hockey and football, 12 play football and basketball and 8 play all the three games. How many members are there in all?
CorrectIncorrectHint
(d)
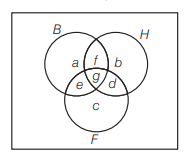
\(
\begin{aligned}
a+f+e+g & =21 \dots(i) \\
b+d+f+g & =26 \dots(ii) \\
c+d+e+g & =29 \dots(iii) \\
f+g & =14 \dots(iv)\\
g+d & =15 \dots(v) \\
e+g & =12 \dots(vi) \\
g & =8 \dots(vii)
\end{aligned}
\)
From Eqs. (vii) and (vi), \(e=4\)
Form Eqs. (vii) and (v), \(d=7\)
From Eqs. (vii) and (iv), \(f=6\)
From Eq. (iii), \(c+7+4+8=29 \Rightarrow c=29-19=10=c\)
From Eq. (ii), \(b+7+6+8=26 \Rightarrow b=26-21 \Rightarrow b=5\)
From Eq. (i), \(a+6+4+8=21 \Rightarrow a=21-18 \Rightarrow a=3\)
\(
\begin{aligned}
n(B)+n(H)+n(F) & =a+b+c+d+e+f+g \\
& =3+5+10+7+4+6+8=43
\end{aligned}
\) -
Question 57 of 123
57. Question
In a survey of 200 students of higher secondary school, it was found that 120 studied Mathematics; 90 studies Physics and 70 studied Chemistry; 40 studied Mathematics and Physics; 3 studied Physics and Chemistry; 50 studied Chemistry and Mathematics and 20 studied none of these subjects. Find the number of students who studied all the three subjects.
CorrectIncorrectHint
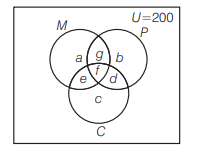
(b)
\(
\begin{aligned}
a+e+f+g & =120 \dots(i) \\
b+d+f+g & =90 \dots(ii) \\
e+f+c+d & =70 \dots(iii) \\
g+f & =40 \dots(iv) \\
f+d & =30 \dots(v) \\
e+f & =50 \dots(vi)
\end{aligned}
\)
\(
\begin{aligned}
& & U-(a+b+c+d+e+f+g) & =20 \\
\Rightarrow & & a+b+c+d+e+f+g & =180 \dots(vii)
\end{aligned}
\)
From Eqs. (i) and (iv), \(\quad a+e=80 \dots(viii)\)
From Eqs. (ii) and (iv), \(\quad b+d=50 \dots(ix)\)
\(
\begin{aligned}
& \text { From Eqs. (iii) and (v), } \quad e+c=40 \dots(x) \\
& \text { from Eqs (viii), (ix) \& (x), } a+b+c+d+e+e=197 \dots(xi) \\
& \text { from (xi), (vii) and (iv), } \begin{aligned}
197-e+40 & =180 \\
170-e+40 & =180 \\
e & =210-180=30
\end{aligned} \\
& \text { From Eq. (vi), } e+f=50 \\
& \Rightarrow \quad 30+f=50 \\
& \Rightarrow \quad f=20
\end{aligned}
\) -
Question 58 of 123
58. Question
In a survey of population of 450 people, it is found that 205 can speak English, 210 can speak Hindi and 120 people can speak Tamil. If 100 people can speak both Hindi and English; 80 people can speak both English and Tamil, 35 people can speak Hindi and Tamil and 20 people can speak all the three languages, find the number of people who can speak English but not a Hindi or Tamil. Find also the number of people who can speak neither English nor Hindi nor Tamil.
CorrectIncorrectHint
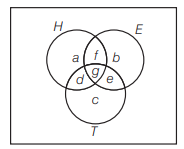
(c)
\(
\begin{aligned}
b+e+f+g & =205 \dots(i) \\
a+d+f+g & =210 \dots(ii) \\
c+d+e+g & =120 \dots(iii) \\
f+g & =100 \dots(iv) \\
e+g & =800 \dots(v) \\
d+g & =35 \dots(vi) \\
g & =20 \dots(vii)
\end{aligned}
\)
From Eqs. (vi) and (vii), \(d=15\)
From Eqs. (vii) and (v), \(e=60\)
From Eqs. (vii) and (iv), \(f=80\)
From Eq. (i), \(b+60+80+20=205 \Rightarrow b=205-160\)
\(\Rightarrow b=45=\) Can speak English but not Hindi or Tamil.
From Eq. (ii) \(a+15+80+20=210\)
\(
\Rightarrow \quad a+115=210 \Rightarrow a=95
\)
From Eq. (iii),
\(
\begin{aligned}
c+15+60+20 & =120 \\
c & =120-95 \Rightarrow c=25
\end{aligned}
\)
People who can speak neither \(E\) nor \(H\) nor \(T\)
\(
\begin{aligned}
& =450-(95+45+25+15+60+80+20) \\
& =450-340=110
\end{aligned}
\) -
Question 59 of 123
59. Question
A group of 123 workers went to a canteen for cold drinks, ice-cream and tea, 42 workers took ice-cream, 36 tea and 30 cold drinks. 15 workers purchased ice-cream and tea, 10 ice-cream and cold drinks, and 4 cold drinks and tea but not ice-cream, 11 took ice-cream and tea but not cold drinks. Determine how many workers did not purchase anything?
CorrectIncorrectHint
(d)
A\(
c+f+g+e=42 \dots(i)
\)
\(
\begin{aligned}
b+d+g+e & =36 \dots(ii) \\
a+f+d+g & =30 \dots(iii) \\
g+e & =15 \dots(iv) \\
f+g & =10 \dots(v) \\
d & =4 \dots(vi) \\
e & =11 \dots(vii)
\end{aligned}
\)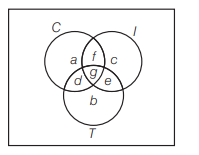
From (iv) and (vii), \(g+11=15 \Rightarrow g=4 \dots(viii)\)
From (v) and (viii), \(f+4=10 \Rightarrow f=6 \dots(ix) \)
From (i), \(c+6+4+11=42 \Rightarrow c=21 \dots(x) \)
From (ii), \(b+4+4+11=36 \Rightarrow b=17 \dots(xi) \)
From (iii), \(a+6+4+4=30 \Rightarrow a=16 \dots(xii)\)
Number of required persons
\(
\begin{aligned}
& =123-(16+17+21+4+11+6+4) \\
& =123-79 \\
& =44
\end{aligned}
\) -
Question 60 of 123
60. Question
Which of the following collection is a set?
CorrectIncorrectHint
(a) The collection of all girls in your class.
Explanation:
A set is a well-defined collection of distinct objects. This means that we can determine with certainty whether or not an object belongs to the set. “Girl” is a clearly defined term. We can identify all the girls in a class with certainty. Therefore, (a) represents a set.Why other options are incorrect:
(b), (c), and (d) are not sets because the terms “intelligent,” “beautiful,” and “tall” are subjective. What one person considers intelligent, beautiful, or tall may not be the same for another. There is no objective, universally accepted measure for these qualities. Therefore, these collections are not well-defined and do not form sets. -
Question 61 of 123
61. Question
Which of the following sets is not finite?
CorrectIncorrectHint
(a) The set is \(\left\{(x, y): x^2+y^2 \leq 1 \leq x+y, x, y \in \mathbb{R}\right\}\). \(x, y \in \mathbb{R}\) means \(x\) and \(y\) can be any real numbers.
The conditions define a region within the unit circle, which contains infinitely many real points.
Therefore, set (a) is infinite.
The set is \(\left\{(x, y): x^2+y^2 \leq 1 \leq x+y, x, y \in \mathbb{Z}\right\}\).
\(x, y \in \mathbb{Z}\) means \(x\) and \(y\) must be integers.
Integer pairs satisfying \(x^2+y^2 \leq 1\) are limited to \(( \pm 1,0),(0, \pm 1),(0,0)\).
Checking \(x+y \geq 1:(1,0)\) satisfies \(1 \geq 1,(0,1)\) satisfies \(1 \geq 1\).
Other pairs like \((-1,0),(0,-1),(0,0)\) do not satisfy \(x+y \geq 1\).
Thus, set (b) contains only two elements: \((1,0)\) and \((0,1)\), making it finite.
The set is \(\left\{(x, y): x^2 \leq y \leq|x|, x, y \in \mathbb{Z}\right\}\). \(x, y \in \mathbb{Z}\) means \(x\) and \(y\) must be integers.
If \(x=0\), then \(0 \leq y \leq 0\), so \(y=0\). Pair: \((0,0)\).
If \(x=1\), then \(1 \leq y \leq 1\), so \(y=1\). Pair: \((1,1)\).
If \(x=-1\), then \(1 \leq y \leq 1\), so \(y=1\). Pair: \((-1,1)\).
For \(|x|>1, x^2>|x|\), so no integer \(y\) can satisfy \(x^2 \leq y \leq|x|\).
Thus, set (c) contains only three elements: \((0,0),(1,1),(-1,1)\), making it finite.
The set is \(\left\{(x, y): x^2+y^2=1, x, y \in \mathbb{Z}\right\}\). \(x, y \in \mathbb{Z}\) means \(x\) and \(y\) must be integers.
Integer pairs satisfying \(x^2+y^2=1\) are \(( \pm 1,0)\) and \((0, \pm 1)\).
Thus, set (d) contains only four elements: \((1,0),(-1,0),(0,1),(0,-1)\), making it finite. -
Question 62 of 123
62. Question
The collection of intelligent students in a class is:
CorrectIncorrectHint
(d) The term “intelligent” is not a well-defined term. So, the given collection does not form a set.
-
Question 63 of 123
63. Question
If \(X=\left\{8^n-7 n-1: n \in N\right\}\) and \(Y=\{49(n-1): n \in N\}\), then
CorrectIncorrectHint
(a)
\(
\begin{aligned}
& n=1.2,3 \ldots .(n \in N) \\
& X(\text { at } n=1)=8-7-1=0 \\
& X(\text { at } n=2)=64-14-1=49 \\
& X(\text { at } n=3)=512-21-1=490 \\
& X=\{0,49,490 \ldots \ldots .\}
\end{aligned}
\)
\(
\begin{aligned}
& Y(\text { at } n=1)=49-49=0 \\
& Y(\text { at } n=2)=98-49=49 \\
& Y(\text { at } n=3)=147-49=98 \\
& Y=\{0,49,98,147 \ldots . .490 \ldots\}
\end{aligned}
\)
Here we can conclude that every element of X can be found in Y but vice versa is not true.
So, \(X \subset Y\).Explanation: We have,
\(
\begin{aligned}
8^n-7 n-1 & =(1+7)^n-7 n-1 \\
& =\left({ }^n C_0+{ }^n C_1 \times 7+{ }^n C_2 \times 7^2+\ldots+{ }^n C_n \times 7^n\right)-(7 n+1) \\
& =7^2\left({ }^n C_2+{ }^n C_3 \times 7+\ldots+{ }^n C_n \times 7^{n-2}\right)
\end{aligned}
\)
\(\therefore \quad X\) contains some multiples of 49.
Clearly, \(Y\) contains all multiples of 49 including 0.
\(
\therefore \quad X \subset Y
\) -
Question 64 of 123
64. Question
If \(A=(x: x=2 n+1, n \in Z)\) and \(B=\{x: x=2 n, n \in Z\}\), then \(A \cup B=\)
CorrectIncorrectHint
(b) Set \(A=\{x: x=2 n+1, n \in Z\}\).
Set \(B=\{x: x=2 n, n \in Z\}\).
\(Z\) represents the set of all integers.
Set \(A\) consists of all numbers of the form \(2 n+1\) where \(n\) is an integer. These are all odd integers: \(\ldots,-3,-1,1,3, \ldots\).
Set \(\boldsymbol{B}\) consists of all numbers of the form \(2 \boldsymbol{n}\) where \(\boldsymbol{n}\) is an integer. These are all even integers: \(\ldots,-4,-2,0,2,4, \ldots\).
The union \(\boldsymbol{A} \cup \boldsymbol{B}\) includes all elements present in either \(\boldsymbol{A}\) or \(\boldsymbol{B}\).
Combining all odd and even integers results in the set of all integers.
\(
A \cup B=\{\ldots,-4,-3,-2,-1,0,1,2,3,4, \ldots\}
\)
The set of all integers is denoted by \(\boldsymbol{Z}\).
The union of set \(\boldsymbol{A}\) (odd integers) and set \(\boldsymbol{B}\) (even integers) is the set of all integers, \(\boldsymbol{Z}\). -
Question 65 of 123
65. Question
If \(A=\{x: x=4 n, n \in Z\}\) and \(B=\{x: x=6 n, n \in Z\}\), then \(A \cap B=\)
CorrectIncorrectHint
(c) Set \(A\) is defined as \(\{x: x=4 n, n \in Z\}\).
Set \(B\) is defined as \(\{x: x=6 n, n \in Z\}\).
The intersection of two sets contains elements common to both sets.
The least common multiple (LCM) is the smallest positive integer divisible by both numbers.
Set \(A\) contains all multiples of 4.
Set \(B\) contains all multiples of 6.
The intersection \(A \cap B\) consists of elements that are multiples of both 4 and 6. This means \(x\) must be a common multiple of 4 and 6.
Find the LCM of 4 and 6.
Multiples of \(4: 4,8,12,16, \ldots\)
Multiples of 6: 6, 12, 18, 24, …
The LCM of 4 and 6 is 12.
Since \(x\) must be a multiple of 12 , the intersection is \(\{x: x=12 n, n \in Z\}\).
The intersection \(A \cap B\) is the set of all multiples of 12. -
Question 66 of 123
66. Question
Which one of the following is \((A-B) \cup(B-A)\)? [CEE (Delhi) 1998]
CorrectIncorrectHint
(c) It is evident from the Venn-diagram that
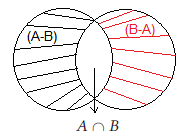
\(
(A-B) \cup(B-A)=(A \cup B)-(A \cap B)
\) -
Question 67 of 123
67. Question
If \(A\) and \(B\) are two sets, then \((A-B) \cup(B-A) \cup(A \cap B)\) is equal to
CorrectIncorrectHint
(a) It is evident from the Venn-diagram that
\(
\begin{array}{ll}
& (A-B) \cup(B-A)=(A \cup B)-(A \cap B) \\
\therefore \quad & ((A-B) \cup(B-A)) \cup(A \cap B) \\
& =((A \cup B)-(A \cap B)) \cup(A \cap B)=A \cup B .
\end{array}
\) -
Question 68 of 123
68. Question
Let \(A\) and \(B\) be two sets that \(A \cap X=B \cap X=\phi\) and \(A \cup X=B \cup X\) for some set \(X\). Then,
CorrectIncorrectHint
(a) We have
\(
\begin{aligned}
& A \cup X=B \cup X \text { for some set } X \\
& A \cap(A \cup X)=A \cap(B \cup X) \\
& A=(A \cap B) \cup(A \cap X) [\because A \cap(A \cup X)=A] \\
& A=(A \cap B) \cup \emptyset [\because A \cap X=\phi] \\
& A=A \cap B \dots(i)
\end{aligned}
\)
Again
\(
\begin{aligned}
& A \cup X=B \cup X \\
& B \cup(A \cup X)=B \cap(B \cup X) \\
& (B \cap A) \cup(B \cap X)=B \\
& (B \cap A) \cup \emptyset=B \\
& A \cap B=B \dots(ii)
\end{aligned}
\)
\(
\begin{aligned}
&\text { From (i) and (ii), we have }\\
&A=B
\end{aligned}
\) -
Question 69 of 123
69. Question
Let \(A\) and \(B\) be two sets defined as given below:
\(
\begin{aligned}
& A=\{(x, y):|x-3|<1 \text { and }|y-3|<1\} \\
& B=\left\{(x, y): 4 x^2+9 y^2-32 x-54 y+109 \leq 0\right\}
\end{aligned}
\)
Then,CorrectIncorrectHint
(a) Set \(A\) is defined by \(|x-3|<1\) and \(|y-3|<1\).
Set \(B\) is defined by \(4 x^2+9 y^2-32 x-54 y+109 \leq 0\).
The condition \(|x-3|<1\) implies \(-1<x-3<1\).
This simplifies to \(2<x<4\).
The condition \(|y-3|<1\) implies \(-1<y-3<1\).
This simplifies to \(2<y<4\).
Set \(A\) represents the interior of a square with vertices at \((2,2),(4,2),(4,4)\), and \((2,4)\). Thus, \(A\) is the set of all points \((x, y)\) lying inside the square formed by the lines \(x=2, x=4, y=2\) and \(y=4\).
We have,
\(
\begin{aligned}
& 4 x^2+9 y^2-32 x-54 y+109 \leq 0 \\
& 4\left(x^2-8 x\right)+9\left(y^2-6 y\right)+109 \leq 0 \\
& 4(x-4)^2+9(y-3)^2 \leq 36 \\
& \frac{(x-4)^2}{3^2}+\frac{(y-3)^2}{2^2} \leq 1
\end{aligned}
\)
Thus, \(B\) is the set of all points lying inside the ellipse having its centre at \((4,3)\) and major and minor axes of lengths 3 and 2 units.
The square \(A\) has corners \((2,2),(4,2),(4,4),(2,4)\).
The ellipse \(\boldsymbol{B}\) is centered at \((4,3)\).
The ellipse extends from \(4-3=1\) to \(4+3=7\) in \(x\) and \(3-2=1\) to \(3+2=5\) in \(y\).
The square \(A\) is entirely contained within the ellipse \(B\).
For example, the point \((2,2)\) is in \(\boldsymbol{A}\).
For \(\boldsymbol{B}\) : \(\frac{(2-4)^2}{9}+\frac{(2-3)^2}{4}=\frac{4}{9}+\frac{1}{4}=\frac{16+9}{36}=\frac{25}{36} \leq 1\), so \((2,2)\) is in \(\boldsymbol{B}\).
The point \((4,4)\) is in \(A\). For \(B: \frac{(4-4)^2}{9}+\frac{(4-3)^2}{4}=0+\frac{1}{4}=\frac{1}{4} \leq 1\), so \((4,4)\) is in B.
Since all points in \(\boldsymbol{A}\) satisfy the condition for \(\boldsymbol{B}, \boldsymbol{A} \subset \boldsymbol{B}\).
Set \(A\) is a square region, and set \(B\) is an elliptical region, with \(A\) being a subset of \(B\). -
Question 70 of 123
70. Question
If \(A=\left\{(x, y): x^2+y^2 \leq 1, x, y \in R\right\}\) and \(B=\left\{(x, y): x^2+y^2 \leq 4 ; x, y \in R\right\}\), then
CorrectIncorrectHint
(c)
\(
\text { The expression } x^2+y^2 \leq r^2 \text { represents points inside or on a circle with radius } r \text {. }
\)
Clearly, \(A\) is the set of all points lying inside or on the circle with centre at the origin and radius 1 and \(B\) is the set of all points lying inside or on the circle with centre at the origin and radius 2 units. Clearly, \(A \subset B\). Therefore, \(A-B=\phi\) and \(B-A \neq \phi\) -
Question 71 of 123
71. Question
20 teachers of a school either teach Mathematics or Physics. 12 of them teach Mathematics while 4 teach both the subjects. The number of teachers teaching Physics only is
CorrectIncorrectHint
(b)
Let M = Set of teachers teaching Mathematics.
\(
P=\text { Set of teachers teaching Physics. }
\)
We have,
\(
\begin{array}{ll}
& n(M \cup P)=20, n(M)=12 \text { and } n(M \cap P)=4 \\
\therefore & n(M \cup P)=n(M)+n(P)-n(M \cap P) \\
\Rightarrow & 20=12+n(P)-4 \\
\Rightarrow & n(P)=12
\end{array}
\)
So, the required number \(=n(P)-n(M \cap P)\)
\(
=12-4=8
\) -
Question 72 of 123
72. Question
A market research group conducted a survey of 2000 consumers and reported that 1720 consumers liked product \(P_1\) and 1450 consumers liked product \(P_2\). The least number of consumers who must have liked both the products is
CorrectIncorrectHint
(a) Let \(U\) be the set of all consumers who were questioned, \(A\) be the set of consumers who lied product \(P_1\) and \(B\) be the set of consumers who liked product \(P_2\). It is given that
\(
\begin{array}{ll}
& n(U)=2000, n(A)=1720 \text { and } n(B)=1450 \\
\therefore & n(A \cup B)=n(A)+n(B)-n(A \cap B) \\
\Rightarrow & n(A \cup B)=1720+1450-n(A \cap B) \\
\Rightarrow & n(A \cup B)=3170-n(A \cap B)
\end{array}
\)
Now,
\(
\begin{array}{ll}
& A \cup B \subset U \\
\Rightarrow & n(A \cup B) \leq n(U) \\
\Rightarrow & 3170-n(A \cap B) \leq 2000 \\
\Rightarrow & n(A \cap B) \geq 1170
\end{array}
\)
Hence, the least number of consumers who like both the products is 1170. -
Question 73 of 123
73. Question
A college awarded 38 medals in Football, 15 in Basketball and 20 to Cricket. If these medals went to a total of 58 men and only three men got medals in all the three sports. The number of students who received medals in exactly two of the three sports is
CorrectIncorrectHint
Let \(F, B\) and \(C\) denote the sets of students who received medals in Football, Basketball and Cricket respectively. Then, we have
\(
\begin{aligned}
& n(F)=37, n(B)=15, n(C)=20 \\
& n(F \cup B \cup C)=58 \text { and } n(F \cap B \cap C)=3
\end{aligned}
\)
Now,
\(
\begin{aligned}
& n(F \cup B \cup C)=n(F)+n(B)+n(C)-n(F \cap B)-n(B \cap C) \\
& -n(C \cap F)+n(F \cap D \cap C) \\
\Rightarrow \quad & 58=38+15+20-{n(F \cap B)+n(B \cap C)+n(C \cap F)}+3 \\
\Rightarrow \quad & n(F \cap B)+n(B \cap C)+n(C \cap F)=18
\end{aligned}
\)
Hence, the number of students who received medals in exactly two of the three sports
\(
\begin{aligned}
& =n(F \cap B)+n(B \cap C)+n(C \cap F)-3 n(F \cap B \cap C) \\
& =18-3 \times 3=9
\end{aligned}
\) -
Question 74 of 123
74. Question
If \(A=\left\{(x, y): x^2+y^2=25\right\}\) and \(B=\left\{(x, y): x^2+9 y^2=144\right\}\), then \(A \cap B\) contains
CorrectIncorrectHint
(d) Clearly, \(A\) is the set of all points on the circle \(x^2+y^2=25\) and \(B\) is the set of all points on the ellipse \(x^2+9 y^2=144\). These two intersect at four points \(P, Q, R\) and \(S\). Hence, \(A \cap B\) contains four points.
Explanation:
From \(x^2+y^2=25\), we get \(x^2=25-y^2\).
Substitute this into \(x^2+9 y^2=144\).
\(
\left(25-y^2\right)+9 y^2=144
\)
\(
\begin{aligned}
& 25+8 y^2=144 \\
& 8 y^2=144-25 \\
& 8 y^2=119 \\
& y^2=\frac{119}{8} \\
& y= \pm \sqrt{\frac{119}{8}}
\end{aligned}
\)
\(
\begin{aligned}
&\text { Substitute } y^2=\frac{119}{8} \text { into } x^2=25-y^2 \text {. }\\
&\begin{aligned}
& x^2=25-\frac{119}{8} \\
& x^2=\frac{200-119}{8} \\
& x^2=\frac{81}{8} \\
& x= \pm \sqrt{\frac{81}{8}}
\end{aligned}
\end{aligned}
\)
Since there are two possible values for \(x\) (positive and negative) and two possible values for \(y\) (positive and negative), there are \(2 \times 2=4\) distinct intersection points.
The intersection \(\boldsymbol{A} \cap \boldsymbol{B}\) contains four points. -
Question 75 of 123
75. Question
If \(n(A)=10, n(B)=6\) and \(n(C)=5\) for three disjoint sets \(A, B, C\), then \(n(A \cup B \cup C)\) equals
CorrectIncorrectHint
(a) since \(A, B, C\) are disjoint sets.
\(
\begin{array}{ll}
\therefore & n(A \cup B \cup C)=n(A)+n(B)+n(C) \\
\Rightarrow & n(A \cup B \cup C)=10+6+5=21
\end{array}
\) -
Question 76 of 123
76. Question
In a certain town 25% families own a phone and 15% own a car, 65% families own neither a phone nor a car. 2000 families own both a car and a phone.
Consider the following statements in this regard:
1. \(10 \%\) families own both a car and a phone
2. \(35 \%\) families own either a car or a phone
3. 40,000 families live in the town
Which of the following statements are correct?CorrectIncorrectHint
(c) Let there be \(x\) families in the town. Let \(P\) and \(C\) denote the set of families using phone and car respectively. Then,
\(
n(P)=\frac{25 x}{100}=\frac{x}{4}, n(C)=\frac{15 x}{100}=\frac{3 x}{20}
\)
and, \(n(\bar{P} \cap \bar{C})=\frac{65 x}{100}=\frac{13 x}{20}\)
Also, \(n(P \cap C)=2000\).
Now,
\(
\begin{aligned}
& n(\bar{P} \cap \bar{C})=\frac{13 x}{20} \\
& n(\overline{P \cup C})=\frac{13 x}{20} \\
& n(U)-n(P \cup C)=\frac{13 x}{20} \\
& x-{n(P)+n(C)-n(P \cap C)}=\frac{13 x}{20} \\
& x-\left(\frac{x}{4}+\frac{3 x}{20}-2000\right)=\frac{13 x}{20} \\
& \frac{x}{20}=2000 \Rightarrow x=40000
\end{aligned}
\)
Thus, statement 3 is true.
\(10 \%\) of the total families in the town is 4000 and it is given that 2000 families own both a car and a phone. So, statement 1 is not true.
Now,
\(
\begin{array}{ll}
& n(P \cup C)=n(P)+n(C)-n(P \cap C) \\
\Rightarrow & n(P \cup C)=\frac{x}{4}+\frac{3 x}{20}-2000 \\
\Rightarrow & n(P \cup C)=10000+6000-2000=14000 \\
\Rightarrow & n(P \cup C)=35 \% \text { of } 40000
\end{array}
\)
Thus, statement 2 is correct. -
Question 77 of 123
77. Question
Three sets \(A, B, C\) are such that \(A=B \cap C\) and \(B=C \cap A\), then [JEE (WB) 2008]
CorrectIncorrectHint
(c)
We have,
\(
\begin{aligned}
A & =B \cap C \text { and } B=C \cap A \\
\Rightarrow \quad A & =(C \cap A) \cap C \Rightarrow A=C \cap A=B
\end{aligned}
\) -
Question 78 of 123
78. Question
For any three sets \(A, B\) and \(C\) the set \((A \cup B \cup C) \cap\left(A \cap B^{\prime} \cap C^{\prime}\right)^{\prime} \cap C^{\prime}\) is equal to [CEE (Delhi) 2007]
CorrectIncorrectHint
(a) We have,
\(
\begin{aligned}
& \left(A \cap B^{\prime} \cap C^{\prime}\right)^{\prime}=A^{\prime} \cup B \cup C \\
& (A \cup B \cup C) \cap\left(A \cap B^{\prime} \cap C^{\prime}\right)^{\prime} \\
& =(A \cup B \cup C) \cap\left(A^{\prime} \cup B \cup C\right)
\end{aligned}
\)
\(
=\left(A \cap A^{\prime}\right) \cup(B \cup C) \quad[\text { By distributivity of } \cup \text { over } \cap]
\)
\(
=\phi \cup(B \cup C)=B \cup C
\)
\(
\begin{aligned}
&\text { Hence, }\\
&\begin{aligned}
& (A \cup B \cup C) \cap\left(A \cap B^{\prime} \cap C^{\prime}\right)^{\prime} \cup C^{\prime} \\
& =(B \cup C) \cap C^{\prime} \\
& =\left(B \cap C^{\prime}\right) \cup\left(C \cap C^{\prime}\right) \\
& =B \cap C^{\prime}
\end{aligned}
\end{aligned}
\) -
Question 79 of 123
79. Question
In a battle \(70 \%\) of the combatants lost one eye, \(80 \%\) an ear, \(75 \%\) an arm, \(85 \%\) a leg, \(x \%\) lost all the four limbs. The minimum value of \(x\) is
CorrectIncorrectHint
a) Given: We have given the percentage of combatants who lost at least one limb which are \(70 \%\) lost their one eye, \(80 \%\) lost their an ear, \(75 \%\) lost their an arm, \(85 \%\) lost their a leg and we have to find the percentage of combatants who lost all the four limbs.
First, we will consider that there are a total of 100 combatants.
Then, if 70% combatants lost one eye which implies that 30 do not lose any eye.
If \(80 \%\) combatants lost any ear which implies that 20 do not lose any ear.
If \(75 \%\) combatants lost any arm which implies that 25 do not lose any arm.
If \(85 \%\) combatants lost any leg which implies that 15 do not lose any leg.
Now, we will add up the number of combatants which lost at least one limb.
Now, Number of combatants who do not lost any limb \(=30+20+25+15=90\)
Now, to find the number of combatants who lost their all four limbs, we will subtract the number of combatants from the total which is 100.
Number of combatants who lost all the four limbs is equal to \(100-90=10\)
Which means the value of \(x\) is 10.
Therefore, the minimum percentage of combatants who lost all their 4 limbs is \(10 \%\). -
Question 80 of 123
80. Question
If \(A=\{1,3,5,7,9,11,13,15,17\}, B=\{2,4, \ldots, 18\}\) and \(N\) is the universal set, then \(A^{\prime} \cup\left((A \cup B) \cap B^{\prime}\right)\) is
CorrectIncorrectHint
(b)
\(
\begin{aligned}
&\text { We have, }\\
&\begin{aligned}
& (A \cup B) \cap B^{\prime}=A \\
& \therefore\left((A \cup B) \cap B^{\prime}\right) \cup A^{\prime}=A \cup A^{\prime}=N
\end{aligned}
\end{aligned}
\) -
Question 81 of 123
81. Question
If sets \(A\) and \(B\) are defined as
\(
\begin{aligned}
& A=\left\{(x, y): y=\epsilon^x, x \in R\right\} \\
& B=\{(x, y): y=x, x \in R\}, \text { then }
\end{aligned}
\)CorrectIncorrectHint
(c) Let \(A=\left\{(x, y): y=e^x, x \in R\right\}\)
i.e., A denotes the set of exponential function.
Graph of exponential function is given by and \(B=\{(x, y): y=x, x \in R\}\)
i.e. \(B\) denotes the set of identity function (equation is a straight line).
Graph of identity function is given by
Then, there is nothing common between the sets A and B.
\(
\therefore A \cap B=\phi
\)
-
Question 82 of 123
82. Question
Consider the set \(A\) of all determinants of order 3 with entries 0 or 1 only. Let \(B\) be the subset of \(A\) consisting of all determinants with value 1. Let \(C\) be the subset of the set of all determinants with value -1. Then
CorrectIncorrectHint
(b) Given: Set A of all matrices of order \(3 \times 3\) with entries 0 or 1 only.
Let \(B\) be the subset of \(A\) consisting of all matrices whose determinant is 1. \(\Rightarrow B \in(0,1)\) and \(|B|=1\)
Assume \(B=\left|\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right|\)
Now, \(|B|=1(1-0)-0+0\)
\(
\therefore|B|=1
\)
Let \(C\) be the subset of \(A\) consisting of all matrices whose determinant is -1.
\(
\Rightarrow C \in(0,1) \text { and }|C|=-1
\)
Assume \(C=\left|\begin{array}{lll}1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0\end{array}\right|\)
Now, \(|\mathrm{C}|=1(0-1)-0+0\)
\(
\therefore|C|=-1
\)
Here, number of elements in \(B\) and \(C\) are equal. -
Question 83 of 123
83. Question
Let \(U\) be the universal set for sets \(A\) and \(B\) such that \(n(A)=200, n(B)=300\) and \(n(A \cap B)=100\). Then, \(n\left(A^{\prime} \cap B^{\prime}\right)\) is equal to 300, provided that \(n(U)\) is equal to
CorrectIncorrectHint
(b) The cardinality of set \(A\) is \(n(A)=200\).
The cardinality of set \(\boldsymbol{B}\) is \(\boldsymbol{n}(\boldsymbol{B})=300\).
The cardinality of the intersection of \(A\) and \(B\) is \(n(A \cap B)=100\).
The cardinality of the intersection of the complements of \(A\) and \(B\) is \(n\left(A^{\prime} \cap B^{\prime}\right)=300\)
De Morgan’s Law states that \((A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}\).
The cardinality of the complement of a set \(X\) is \(n\left(X^{\prime}\right)=n(U)-n(X)\).
Use the formula: \(n(A \cup B)=n(A)+n(B)-n(A \cap B)\).
Substitute the given values: \(n(A \cup B)=200+300-100\).
Calculate the result: \(n(A \cup B)=400\).
Apply De Morgan’s Law: \(\boldsymbol{A}^{\prime} \cap \boldsymbol{B}^{\prime}=(A \cup \boldsymbol{B})^{\prime}\).
Use the complement rule: \(n\left((A \cup B)^{\prime}\right)=n(U)-n(A \cup B)\). So, \(n\left(A^{\prime} \cap B^{\prime}\right)=n(U)-n(A \cup B)\).
Substitute the known values into the equation from Step 2: \(300=n(U)-400\).
Rearrange the equation to find \(n(U): n(U)=300+400\).
Calculate the final value: \(n(U)=700\).
\(
\text { The cardinality of the universal set } n(U) \text { is } 700 \text {. }
\) -
Question 84 of 123
84. Question
Out of 800 boys in a school 224 played cricket, 240 played hockey and 336 played basketball. Of the total, 64 played both basketball and hockey; 80 played cricket and basketball and 40 played cricket and hockey; 24 played all the three games. The number of boys who did not play any game is
CorrectIncorrectHint
(a) Total number of boys: 800
Boys who played cricket: 224
Boys who played hockey: 240
Boys who played basketball: 336
Boys who played both basketball and hockey: 64
Boys who played both cricket and basketball: 80
Boys who played both cricket and hockey: 40
Boys who played all three games: 24
Calculate the number of boys who played at least one game:
Use the formula:
\(
n(C \cup H \cup B)=n(C)+n(H)+n(B)-n(C \cap H)-n(C \cap B)-n(H \cap B)+n(C \cap H \cap B)
\)
Substitute the given values:
\(n(C \cup H \cup B)=224+240+336-40-80-64+24\)
\(n(C \cup H \cup B)=800-184+24\)
\(n(C \cup H \cup B)=640\)
Calculate the number of boys who did not play any game.
Subtract the number of boys who played at least one game from the total number of boys:
Number of boys not playing any game \(=800-n(C \cup H \cup B)\)
Number of boys not playing any game \(=800-640\)
Number of boys not playing any game \(=160\) -
Question 85 of 123
85. Question
Let Z be the set of all integers and \(A=\left\{(a, b): a^2+3 b^2=28, a, b \in Z\right\}\) and
\(B=\{(a, b): a>b, a, b \in Z\}\). Then, the number of elements in \(A \cap B\), isCorrectIncorrectHint
(c) Set \(A\) is defined by the equation \(a^2+3 b^2=28\), where \(a\) and \(b\) are integers.
Set \(B\) is defined by the condition \(a>b\), where \(a\) and \(b\) are integers.
First, find all integer pairs \((a, b)\) that satisfy the equation for set \(A\), then filter these pairs to satisfy the condition for set \(\boldsymbol{B}\).
Since \(3 b^2 \leq 28\), we have \(b^2 \leq \frac{28}{3} \approx 9.33\).
Possible integer values for \(b\) are \(0, \pm 1, \pm 2, \pm 3\).
If \(b=0, a^2=28\), so \(a= \pm \sqrt{28}\), which is not an integer.
If \(b= \pm 1, a^2+3( \pm 1)^2=28 \Longrightarrow a^2=25\), so \(a= \pm 5\).
If \(b= \pm 2, a^2+3( \pm 2)^2=28 \Longrightarrow a^2=16\), so \(a= \pm 4\).
If \(b= \pm 3, a^2+3( \pm 3)^2=28 \Longrightarrow a^2=1\), so \(a= \pm 1\).
\(
A=\{(5,1),(-5,1),(5,-1),(-5,-1),(4,2),(-4,2),(4,-2),(-4,-2),(1,3),(-1,3),(1,-3),(-1,-3)\}
\)
\(
\begin{aligned}
&\text { Filter elements of } A \text { that satisfy } a>b \text { (elements of } A \cap B \text { ). }\\
&\begin{aligned}
& (5,1) \text { since } 5>1 \\
& (5,-1) \text { since } 5>-1 \\
& (4,2) \text { since } 4>2 \\
& (4,-2) \text { since } 4>-2 \\
& (1,-3) \text { since } 1>-3 \\
& (-1,-3) \text { since }-1>-3
\end{aligned}
\end{aligned}
\)
There are 6 elements in \(A \cap B\). -
Question 86 of 123
86. Question
If \(A=\left\{(x, y): y=\frac{4}{x}, x \neq 0\right\}\) and \(B=\left\{(x, y): x^2+y^2=8, x, y \in R\right\}\), then
CorrectIncorrectHint
(c) You are determining the number of intersection points between a hyperbola and a circle.
Set \(A\) is defined by the equation \(y=\frac{4}{x}\), where \(x \neq 0\).
Set \(B\) is defined by the equation \(x^2+y^2=8\).
Substitute the equation for \(y\) from set \(A\) into the equation for set \(B\) and solve for \(x\).
Substitute \(y\) into the circle equation.
Substitute \(y=\frac{4}{x}\) into \(x^2+y^2=8\).
\(
\begin{aligned}
& x^2+\left(\frac{4}{x}\right)^2=8 \\
& x^2+\frac{16}{x^2}=8
\end{aligned}
\)
Multiply by \(x^2\) to clear the denominator.
\(
x^4+16=8 x^2
\)
Rearrange into a quadratic form in terms of \(x^2\).
\(
x^4-8 x^2+16=0
\)
Factor the quadratic.
\(
\left(x^2-4\right)^2=0
\)
Solve for \(x^2\).
\(
x^2=4
\)
Solve for \(x\).
\(
x= \pm 2
\)
For \(x=2\) :
\(
y=\frac{4}{2}=2
\)
For \(x=-2\) :
\(
y=\frac{4}{-2}=-2
\)
The intersection points are \((2,2)\) and \((-2,-2)\).
\(A \cap B\) contains 2 points only. -
Question 87 of 123
87. Question
If \(A=\left\{(x, y): x^2+y^2=4 ; x, y \in R\right\}\) and \(B=\left\{(x, y): x^2+y^2=9 ; x, y \in R\right\}\), then
CorrectIncorrectHint
(b) You are determining the correct set relationship between two circles defined by their equations.
Set \(A\) represents a circle centered at the origin with radius \(\sqrt{4}=2\).
Set \(B\) represents a circle centered at the origin with radius \(\sqrt{9}=3\).
For a point ( \(x, y\) ) to be in \(A \cap B\), it must satisfy both \(x^2+y^2=4\) and \(x^2+y^2=9\). Since \(4 \neq 9\), no point can satisfy both equations simultaneously.
Therefore, \(A \cap B=\phi\).
(a) \(A-B=\phi\) : This is incorrect because \(A-B=A\) since \(A \cap B=\phi\).
(b) \(\boldsymbol{B}-\boldsymbol{A}=\boldsymbol{B}\) : This is correct because \(\boldsymbol{B}-\boldsymbol{A}=\boldsymbol{B}\) since \(\boldsymbol{A} \cap \boldsymbol{B}=\phi\).
(c) \(A \cap B \neq \phi\) : This is incorrect because \(A \cap B=\phi\).
(d) \(A \cap B=A\) : This is incorrect because \(A \cap B=\phi \neq A\).
The correct statement is \(B-A=B\). -
Question 88 of 123
88. Question
If \(A=\left\{(x, y): y^2=x ; x, y \in R\right\}\) and \(B=\{(x, y): y=|x| ; x, y \in R\}\), then
CorrectIncorrectHint
(c) Set \(A\) is defined by the equation \(y^2=x\).
Set \(\boldsymbol{B}\) is defined by the equation \(y=|x|\).
Substitute \(y=|x|\) into \(y^2=x\).
This yields \((|x|)^2=x\).
\((|x|)^2=x\) simplifies to \(x^2=x\).
Rearrange to \(x^2-x=0\).
Factor out \(x: x(x-1)=0\).
This gives two possible values for \(x\) : \(x=0\) or \(x=1\).
For \(x=0, y=|0|=0\).
For \(x=1, y=|1|=1\).
The intersection points of sets \(A\) and \(B\) are \((0,0)\) and \((1,1)\). -
Question 89 of 123
89. Question
If \(A=\left\{\theta: \cos \theta>-\frac{1}{2}, 0 \leq \theta \leq \pi\right\}\) and \(B=\left\{\theta: \sin \theta>\frac{1}{2}, \frac{\pi}{3} \leq \theta \leq \pi\right\}\), then
CorrectIncorrectHint
(a) Set \(A=\left\{\theta: \cos \theta>-\frac{1}{2}, 0 \leq \theta \leq \pi\right\}\).
Set \(B=\left\{\theta: \sin \theta>\frac{1}{2}, \frac{\pi}{3} \leq \theta \leq \pi\right\}\).
Determine the intervals for \(\theta\) for each set and then find their intersection and union.
\(\cos \theta>-\frac{1}{2}\) in the interval \(0 \leq \theta \leq \pi\).
The value \(\cos \theta=-\frac{1}{2}\) occurs at \(\theta=\frac{2 \pi}{3}\).
Since \(\cos \theta\) is decreasing in \(0 \leq \theta \leq \pi, \cos \theta>-\frac{1}{2}\) implies \(\theta<\frac{2 \pi}{3}\).
So, \(A=\left\{\theta: 0 \leq \theta<\frac{2 \pi}{3}\right\}\).
\(\sin \theta>\frac{1}{2}\) in the interval \(\frac{\pi}{3} \leq \theta \leq \pi\).
The value \(\sin \theta=\frac{1}{2}\) occurs at \(\theta=\frac{\pi}{6}\) and \(\theta=\frac{5 \pi}{6}\).
In the given range, \(\sin \theta>\frac{1}{2}\) implies \(\frac{\pi}{6}<\theta<\frac{5 \pi}{6}\).
Considering the given domain for \(\boldsymbol{B}, \frac{\pi}{3} \leq \theta \leq \pi\), the interval for \(\boldsymbol{B}\) is \(\left\{\theta: \frac{\pi}{3} \leq \theta<\frac{5 \pi}{6}\right\}\).
\(
\begin{aligned}
&A \cap B=\left\{\theta: 0 \leq \theta<\frac{2 \pi}{3}\right\} \cap\left\{\theta: \frac{\pi}{3} \leq \theta<\frac{5 \pi}{6}\right\} .\\
&\text { The intersection is the common interval: }\left\{\theta: \frac{\pi}{3} \leq \theta<\frac{2 \pi}{3}\right\} \text {. }
\end{aligned}
\)
\(
\begin{aligned}
&A \cup B=\left\{\theta: 0 \leq \theta<\frac{2 \pi}{3}\right\} \cup\left\{\theta: \frac{\pi}{3} \leq \theta<\frac{5 \pi}{6}\right\}\\
&\text { The union is the combined interval: }\left\{\theta: 0 \leq \theta<\frac{5 \pi}{6}\right\} \text {. }
\end{aligned}
\)
\(
\text { The correct option is (a) } A \cap B=\{\theta: \pi / 3 \leq \theta \leq 2 \pi / 3\} \text {. }
\) -
Question 90 of 123
90. Question
In rule method the null set is represented by
CorrectIncorrectHint
(c) The rule method, or set-builder notation, is used to describe a property that no element can satisfy when representing the null set.
\(\{x: x \neq x\}\) This reads as “the set of all x such that x is not equal to x “. Since no element can be not equal to itself, this set will have no elements, thus representing the null set. This is the correct representation using the rule method. -
Question 91 of 123
91. Question
Let \(n(U)=700, \quad n(A)=200, \quad n(B)=300 \quad\) and \(n(A \cap B)=100\). Then, \(n\left(A^c \cap B^c\right)=\)
CorrectIncorrectHint
(c)
\(
\begin{aligned}
& n\left(A^{\prime} \cap B^{\prime}\right)=n(A \cup B)^{\prime}=n(U)-n(A \cup B) \\
& =n(U)-[n(A)+n(B)-n(A \cap B)] \\
& =700-[200+300-100]=300
\end{aligned}
\) -
Question 92 of 123
92. Question
In a class of 35 students, 17 have taken Mathematics, 10 have taken Mathematics but not Economics. If each student has taken either Mathematics or Economics or both, then the number of students who have taken Economics but not Mathematics is
CorrectIncorrectHint
(c) Let \(M\) and \(E\) denote the sets of students who have taken Mathematics and Economics respectively. Then, we have
\(
n(M \cup E)=35, n(M)=17 \text { and } n\left(M \cap E^{\prime}\right)=10
\)
Now,
\(
\begin{aligned}
& n\left(M \cap E^{\prime}\right)=n(M)-n(M \cap E) \\
& \Rightarrow 10=17-n(M \cap E) \Rightarrow n(M \cap E)=7
\end{aligned}
\)
Now,
\(
\begin{aligned}
& n(M \cup E)=n(M)+n(E)-n(M \cap E) \\
& \Rightarrow 35=17+n(E)-7 \Rightarrow n(E)=25 \\
& \therefore n\left(E \cap M^{\prime}\right)=n(E)-n(E \cap M)=25-7=18
\end{aligned}
\) -
Question 93 of 123
93. Question
In a city \(20 \%\) of the population travels by car, \(50 \%\) travels by bus and \(10 \%\) travels by both car and bus. Then, persons travelling by car or bus is
CorrectIncorrectHint
(c) Let \(c\) be the event of traveling by car.
Let \(B\) be the event of traveling by bus.
\(
\begin{aligned}
& P(C)=20 \% \\
& P(B)=50 \% \\
& P(C \cap B)=10 \%
\end{aligned}
\)
The percentage of people traveling by car or bus is \(P(C \cup B)\).
\(
P(C \cup B)=P(C)+P(B)-P(C \cap B)
\)
\(
\begin{aligned}
& P(C \cup B)=20 \%+50 \%-10 \% \\
& P(C \cup B)=70 \%-10 \% \\
& P(C \cup B)=60 \%
\end{aligned}
\) -
Question 94 of 123
94. Question
In a class of 45 students, 22 can speak Hindi and 12 can speak English only. The number of students, who can speak both Hindi and English, is
CorrectIncorrectHint
(b) It is given that; the total number of students in the class is 45.
The number of students who can speak Hindi is 22.
The number of students who can speak English is 12.
We have to find the number of students who can speak both Hindi and English.
So, as per the given information
\(\)
\begin{aligned}
& n(H \cup E)=45 \\
& n(H)=22 \\
& n(E)=12
\end{aligned}
latex]
Let us consider the number of students who can speak both Hindi and English is \(\)xlatex] that is
\(\)
n(H \cap E)=x
latex]
We have to find the value of \(\)n(H \cap E)latex].
We know that,
\(\)
\Rightarrow n(H \cup E)=n(H)+n(E)+n(H \cap E)
latex]
Substitute the values in the above formula we get,
\(\)
\Rightarrow 45=22+12+x
latex]
Simplifying we get,
\(\)
\Rightarrow x=11
latex]
Hence, the number of students who can speak both Hindi and English is 11. -
Question 95 of 123
95. Question
In a certain town \(25 \%\) families own a cell phone, \(15 \%\) families own a scooter and \(65 \%\) families own neither a cell phone nor a scooter. If 500 families own both a cell phone and a scooter, then the total number of families in the town is
CorrectIncorrectHint
(c) Let’s say the number of families that own a cell phone is \(A\), number of families that own a scooter \(B\), the number of families that own neither of them is \(C\) and the total number of families in that town is \(x\).
According to set theory we can equate an equation as
\(
A+B-(A \cap B)+C=x
\)
Here, \(A=\frac{25 x}{100}, B=\frac{15 x}{100}, C=\frac{65 x}{100}\) and \((A \cap B)=1500\)
Substituting the above values in the formed equation we get
\(
\Rightarrow \frac{25 x}{100}+\frac{15 x}{100}-1500+\frac{65 x}{100}=x
\)
Subtracting \(x\) from both the sides of the above equation we get
\(
\Rightarrow \frac{25 x}{100}+\frac{15 x}{100}-1500+\frac{65 x}{100}-x=0
\)
Adding 1500 to both the sides of the above equation we get
\(
\Rightarrow \frac{25 x}{100}+\frac{15 x}{100}+\frac{65 x}{100}-x=1500
\)
Further simplifying the above equation, we get
\(
\begin{aligned}
& \Rightarrow \frac{105 x}{100}-x=1500 \\
& \Rightarrow \frac{105 x-100 x}{100}=1500 \\
& \Rightarrow \frac{5 x}{100}=1500
\end{aligned}
\)
Multiplying both the sides of the above equation to 100 we get
\(
\Rightarrow 5 x=150000
\)
Dividing both the sides of the above equation by 5 we get
\(
\Rightarrow x=30000
\)
Therefore, we conclude that the total number of families in that town is 30000. -
Question 96 of 123
96. Question
If \(A=\{1,2,3,4\}\), then the number of subsets of set \(A\) containing element 3, is
CorrectIncorrectHint
(c) The number of subsets of a set with \(n\) elements is \(2^n\).
We need to find the number of subsets of the remaining elements after fixing 3 as an element in the subset.
Since element 3 must be in every subset, consider the remaining elements in set \(A\).
The number of remaining elements is \(n^{\prime}=3\).
The number of subsets formed by these \(n^{\prime}\) elements is \(2^{n^{\prime}}\).
\(
2^3=8
\)
Each of these 8 subsets, when combined with element 3 , forms a unique subset of \(A\) containing 3.
Thus, the number of subsets of set \(A\) containing element 3 is 8. -
Question 97 of 123
97. Question
If \(n(u)=100, n(A)=50, n(B)=20\) and \(n(A \cap B)=10\), then \(n\left\{(A \cup B)^{\prime}\right\}\)
CorrectIncorrectHint
(c) The total number of elements in the universal set is \(n(U)=100\).
The number of elements in set \(A\) is \(n(A)=50\).
The number of elements in set \(\boldsymbol{B}\) is \(\boldsymbol{n}(\boldsymbol{B})=20\).
The number of elements in the intersection of sets \(A\) and \(B\) is \(n(A \cap B)=10\).
The number of elements in the union of two sets is
\(
n(A \cup B)=n(A)+n(B)-n(A \cap B)
\)
The number of elements in the complement of a set \(X\) is \(n\left(X^C\right)=n(U)-n(X)\).
First, calculate the number of elements in the union of sets \(A\) and \(B\), then subtract this value from the total number of elements in the universal set.
Use the formula: \(n(A \cup B)=n(A)+n(B)-n(A \cap B)\).
Substitute the given values: \(n(A \cup B)=50+20-10\).
Calculate the result: \(n(A \cup B)=60\).
Use the complement formula: \(n\left\{(A \cup B)^C\right\}=n(U)-n(A \cup B)\).
Substitute the values: \(n\left\{(A \cup B)^C\right\}=100-60\).
Calculate the final answer: \(n\left\{(A \cup B)^C\right\}=40\). -
Question 98 of 123
98. Question
Let \(Z\) denote the set of integers, then \({x \in Z:|x-3|<4} \cap {x \in Z:|x-4|<5}=\)
CorrectIncorrectHint
(c) The inequality \(|x-3|<4\) can be written as \(-4<x-3<4\).
Add 3 to all parts: \(-4+3<x<4+3\).
This simplifies to \(-1<x<7\).
Since \(x \in Z\), the first set is \(\{0,1,2,3,4,5,6\}\).
The inequality \(|x-4|<5\) can be written as \(-5<x-4<5\).
Add 4 to all parts: \(-5+4<x<5+4\).
This simplifies to \(-1<x<9\).
Since \(x \in Z\), the second set is \(\{0,1,2,3,4,5,6,7,8\}\).
The intersection of \(\{0,1,2,3,4,5,6\}\) and \(\{0,1,2,3,4,5,6,7,8\}\) is the set of common elements.
The common elements are \(\{0,1,2,3,4,5,6\}\). -
Question 99 of 123
99. Question
If \(A_n\) is the set of first \(n\) prime numbers, then \(\bigcup_{n=2}^{10} A_n=\)
CorrectIncorrectHint
(b) List the sets \(A_n\) for \(n\) from 2 to 10 and then find their union.
The first 10 prime numbers are \(2,3,5,7,11,13,17,19,23,29\).
Define the sets \(A_n\).
\(
\begin{aligned}
& A_2=\{2,3\} \\
& A_3=\{2,3,5\} \\
& A_4=\{2,3,5,7\} \\
& A_5=\{2,3,5,7,11\} \\
& A_6=\{2,3,5,7,11,13\} \\
& A_7=\{2,3,5,7,11,13,17\} \\
& A_8=\{2,3,5,7,11,13,17,19\} \\
& A_9=\{2,3,5,7,11,13,17,19,23\} \\
& A_{10}=\{2,3,5,7,11,13,17,19,23,29\}
\end{aligned}
\)
Since \(A_2 \subset A_3 \subset \ldots \subset A_{10}\), the union is the largest set.
\(
\begin{aligned}
& \bigcup_{n=2}^{10} A_n=A_{10} \\
& A_{10}=\{2,3,5,7,11,13,17,19,23,29\}
\end{aligned}
\)
The union of the sets \(A_n\) from \(n=2\) to \(n=10\) is the set of the first 10 prime numbers. -
Question 100 of 123
100. Question
If \(A_n\) is the set of first \(n\) prime numbers, then \(\bigcap_{n=3}^{10} A_n=\)
CorrectIncorrectHint
(b) List the sets \(A_n\) for \(n\) from 2 to 10 and then find their intersection.
The first 10 prime numbers are \(2,3,5,7,11,13,17,19,23,29\).
Define the sets \(A_n\).
\(
\begin{aligned}
& A_3=\{2,3,5\} \\
& A_4=\{2,3,5,7\} \\
& A_5=\{2,3,5,7,11\} \\
& A_6=\{2,3,5,7,11,13\} \\
& A_7=\{2,3,5,7,11,13,17\} \\
& A_8=\{2,3,5,7,11,13,17,19\} \\
& A_9=\{2,3,5,7,11,13,17,19,23\} \\
& A_{10}=\{2,3,5,7,11,13,17,19,23,29\}
\end{aligned}
\)
Since \(A_3 \subset \ldots \subset A_{10}\), the intersection is the smallest set.
\(
\begin{aligned}
& \bigcap_{n=3}^{10} A_n=A_{3} \\
& A_{3}=\{2,3,5\}
\end{aligned}
\) -
Question 101 of 123
101. Question
Let \(A_1, A_2, A_3, \ldots, A_{100}\) be 100 sets such that \(n\left(A_i\right)=i+1\) and \(A_1 \subset A_2 \subset A_3 \subset \ldots \subset A_{100}\), then \(\bigcup_{i=1}^{100} A_i\) contains …….. elements
CorrectIncorrectHint
(c) Understand the Subset Relationship: The condition \(A_1 \subset A_2 \subset A_3 \subset \ldots \subset A_{100}\) means each set is contained within the next set in the sequence. \(\boldsymbol{A}_1\) is a subset of \(\boldsymbol{A}_2, \boldsymbol{A}_2\) is a subset of \(\boldsymbol{A}_3\), and so on, up to \(\boldsymbol{A}_{100}\).
The Union of Nested Sets: When sets are nested in this way, the union of all the sets is the largest set in the sequence. The largest set \(\left(\boldsymbol{A}_{100}\right)\) contains all the elements present in all preceding sets ( \(\boldsymbol{A}_1\) through \(\boldsymbol{A}_{99}\) ).
Determine the Number of Elements in the Union: Since \(\bigcup_{i=1}^{100} A_i=A_{100}\), the number of elements in the union equals the number of elements in \(\boldsymbol{A}_{100}\), which is \(\boldsymbol{n}\left(\boldsymbol{A}_{100}\right)\).
Calculate \(\boldsymbol{n}\left(\boldsymbol{A}_{100}\right)\) : The formula \(\boldsymbol{n}\left(\boldsymbol{A}_{\boldsymbol{i}}\right)=\boldsymbol{i}+\mathbf{1}\) is given. Substituting \(\boldsymbol{i}=\mathbf{1 0 0}\) into this formula gives:
\(
n\left(A_{100}\right)=100+1=101
\) -
Question 102 of 123
102. Question
If \(A\) and \(B\) are two sets such that \(n(A)=7, n(B)=6\) and \((A \cap B) \neq \phi\). Then the greatest possible value of \(n(A \Delta B)\), is
CorrectIncorrectHint
(a) You are solving for the greatest possible value of the symmetric difference of two sets, \(n(A \Delta B)\).
What’s given in the problem
The cardinality of set \(A\) is \(n(A)=7\).
The cardinality of set \(\boldsymbol{B}\) is \(\boldsymbol{n}(\boldsymbol{B})=6\).
The intersection of sets \(\boldsymbol{A}\) and \(\boldsymbol{B}\) is not empty, \((\boldsymbol{A} \cap \boldsymbol{B}) \neq \phi\).
The formula for the cardinality of the symmetric difference is \(n(A \Delta B)=n(A)+n(B)-2 n(A \cap B)\).
To maximize \(n(A \Delta B)\), we need to minimize \(n(A \cap B)\).
Minimize the intersection of the sets to maximize the symmetric difference.
Determine the minimum possible value of \(n(A \cap B)\).
Since \((A \cap B) \neq \phi\), the minimum value for \(n(A \cap B)\) is 1.
So, \(n(A \cap B)_{\text {min }}=1\).
Calculate the greatest possible value of \(n(A \Delta B)\).
Substitute the values into the formula: \(n(A \Delta B)=n(A)+n(B)-2 n(A \cap B)\).
\(
\begin{aligned}
& n(A \Delta B)_{\max }=7+6-2(1) \\
& n(A \Delta B)_{\max }=13-2 \\
& n(A \Delta B)_{\max }=11
\end{aligned}
\)
The greatest possible value of \(n(A \Delta B)\) is 11. -
Question 103 of 123
103. Question
If \(A\) and \(B\) are two sets such that \(n(A)=7, n(B)=6\) and \(n(A \cap B) \neq \phi\). The least possible value of \(n(A \Delta B)\), is
CorrectIncorrectHint
(a) You are finding the least possible value of the symmetric difference of two sets, \(n(A \Delta B)\).
What’s given in the problem
The number of elements in set \(A\) is \(n(A)=7\).
The number of elements in set \(\boldsymbol{B}\) is \(\boldsymbol{n}(\boldsymbol{B})=6\).
The intersection of sets \(A[latex] and [latex]B\) is not empty, \(n(A \cap B) \neq \phi\).
The formula for the symmetric difference of two sets is
\(
n(A \Delta B)=n(A)+n(B)-2 n(A \cap B)
\)
To minimize \(n(A \Delta B)\), we need to maximize \(n(A \cap B)\).
How to solve
Determine the maximum possible value of the intersection and substitute it into the symmetric difference formula.
Determine the maximum possible value of \(n(A \cap B)\).
Since \(n(A \cap B) \neq \phi, n(A \cap B) \geq 1\).
The maximum number of common elements is limited by the smaller set.
So, \(n(A \cap B) \leq \min (n(A), n(B))\).
\(
n(A \cap B) \leq \min (7,6)
\)
Thus, the maximum value of \(n(A \cap B)\) is 6.
Use the formula: \(n(A \Delta B)=n(A)+n(B)-2 n(A \cap B)\).
Substitute the given values and the maximum \(n(A \cap B)\) :
\(
\begin{aligned}
& n(A \Delta B)=7+6-2 \times 6 \\
& n(A \Delta B)=13-12 \\
& n(A \Delta B)=1
\end{aligned}
\)
Calculate the least possible value of \(n(A \Delta B)\).
The least possible value of \(n(A \Delta B)\) is 1. -
Question 104 of 123
104. Question
If \(A_1, A_2, \ldots, A_{100}\) are sets such that \(n\left(A_i\right)=i+2\), \(A_1 \subset A_2 \subset A_3 \ldots \subset A_{100}\) and \(\bigcap_{n=3}^{100} A_i=A\), then \(n(A)=\)
CorrectIncorrectHint
(c) We have \(n\left(A_i\right)=i+2\)
\(
\therefore \mathrm{n}\left(\mathrm{~A}_1\right)=3, \mathrm{n}\left(\mathrm{~A}_2\right)=4, \mathrm{n}\left(\mathrm{~A}_3\right)=5
\)
Similarly \(n\left(A_{100}\right)=102\)
given \(\mathrm{A}_1 \subset \mathrm{~A}_2 \subset \mathrm{~A}_3 \ldots \ldots \ldots \subset \mathrm{~A}_{100}\)
As \(A_3\) is a subset of all the successive sets
\(
\begin{aligned}
& \therefore \mathrm{A}_3 \cap \mathrm{~A}_4 \cap \mathrm{~A}_5 \cap \ldots \ldots \ldots \cap \mathrm{~A}_{100}=\mathrm{A}_3 \\
& \therefore \mathrm{~A}_3=\mathrm{A} \\
& \therefore \mathrm{n}(\mathrm{~A})=\mathrm{n}\left(\mathrm{~A}_3\right)=5
\end{aligned}
\) -
Question 105 of 123
105. Question
If \(A, B\) and \(C\) are three non-empty sets such that \(A\) and \(B\) are disjoint and the number of elements contained in \(A\) is equal to those contained in the set of elements common to the sets \(A\) and \(C\), then \(n(A \cup B \cup C)\) is necessarily equal to
CorrectIncorrectHint
(a) The formula for the number of elements in the union of three sets is:
\(
n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A \cap B)-n(A \cap C)-n(B \cap C)+n(A \cap B \cap C)
\)
Apply the given condition: \(A\) and \(B\) are disjoint
Disjoint sets have no common elements, which means their intersection is the empty set. Therefore:
\(
n(A \cap B)=0
\)
Substituting this into the formula from step 1:
\(
n(A \cup B \cup C)=n(A)+n(B)+n(C)-0-n(A \cap C)-n(B \cap C)+n(A \cap B \cap C)
\)
Simplifying:
\(
n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A \cap C)-n(B \cap C)+n(A \cap B \cap C)
\)
Apply the given condition: \(n(A)=n(A \cap C)\)
This condition implies that all elements of \(\boldsymbol{A}\) are also elements of \(\boldsymbol{C}\). If \(\boldsymbol{n}(\boldsymbol{A})=\boldsymbol{n}(\boldsymbol{A} \cap \boldsymbol{C})\), then \(\boldsymbol{A}\) must be a subset of \(\boldsymbol{C}\), i.e., \(\boldsymbol{A} \subseteq \boldsymbol{C}\).
If \(A \subseteq C\), then:
\(A \cap C=A\)
\(\boldsymbol{A} \cap \boldsymbol{B} \cap \boldsymbol{C}=(\boldsymbol{A} \cap \boldsymbol{B}) \cap \boldsymbol{C}=\varnothing \cap \boldsymbol{C}=\varnothing\) (since \(\boldsymbol{A}\) and \(\boldsymbol{B}\) are disjoint, \(\boldsymbol{A} \cap \boldsymbol{B}=\varnothing\) )
Substitute these into the formula:
Replace \(\boldsymbol{n}(\boldsymbol{A} \cap \boldsymbol{C})\) with \(\boldsymbol{n}(\boldsymbol{A})\) and \(\boldsymbol{n}(\boldsymbol{A} \cap \boldsymbol{B} \cap \boldsymbol{C})\) with 0 in the simplified formula
\(
n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A)-n(B \cap C)+0
\)
Simplify the expression:
The \(\boldsymbol{n}(\boldsymbol{A})\) terms cancel out:
\(
n(A \cup B \cup C)=n(B)+n(C)-n(B \cap C)
\)
Conclusion
Given the conditions, \(\boldsymbol{n}(\boldsymbol{A} \cup \boldsymbol{B} \cup \boldsymbol{C})\) is necessarily equal to \(\boldsymbol{n}(\boldsymbol{B})+\boldsymbol{n}(\boldsymbol{C})-\boldsymbol{n}(\boldsymbol{B} \cap \boldsymbol{C})\) . This can be further simplified to \(\boldsymbol{n}(\boldsymbol{B} \cup \boldsymbol{C})\), as the formula for the union of two sets is \(n(B \cup C)=n(B)+n(C)-n(B \cap C)\).
The final answer is \(\boldsymbol{n}(\boldsymbol{B} \cup \boldsymbol{C})\). -
Question 106 of 123
106. Question
If \(A=\left\{n: \frac{n^3+5 n^2+2}{n} \text { is an integer and itself is an integer }\right\}\), then the number of elements in the set \(A\), is
CorrectIncorrectHint
(d) We have,
\(
\frac{n^3+5 n^2+2}{n}=n^2+5 n+\frac{2}{n}
\)
\(\therefore \frac{n^3+5 n^2+2}{n}\) is an integer, if \(\frac{2}{n}\) is an integer
\(
\Rightarrow n= \pm 1, \pm 2
\)
\(\Rightarrow\) A consists of four elements viz. \(-1,1,-2,2\)
The number of elements in set \(A\) is 4. -
Question 107 of 123
107. Question
If \(A=\left\{p \in N: p\right.\) is a prime and \(p=\frac{7 n^2+3 n+3}{n}\) for some \(\left.n \in N\right\}\), then the number of elements in the set \(A\) is
CorrectIncorrectHint
(a)
\(
\begin{aligned}
& p=\frac{7 n^2+3 n+3}{n} \\
& p=\frac{7 n^2}{n}+\frac{3 n}{n}+\frac{3}{n} \\
& p=7 n+3+\frac{3}{n}
\end{aligned}
\)
Since \(p\) must be a natural number, \(\frac{3}{n}\) must be an integer.
This implies that \(n\) must be a divisor of 3.
As \(n \in N\), possible values for \(n[latex] are 1 and 3.
[latex]
\begin{aligned}
&\text { For } n=1 \text { : }\\
&p=7(1)+3+\frac{3}{1} =13
\end{aligned}
\)
\(
\begin{aligned}
&\text { For } n=3 \text { : }\\
&p=7(3)+3+\frac{3}{3}=25
\end{aligned}
\)
For \(p=13: 13\) is a prime number.
For \(p=25: 25\) is not a prime number since \(25=5 \times 5\).
The only prime number found is 13. So, \(A=\{13\}\).
The number of elements in the set \(A\) is 1. -
Question 108 of 123
108. Question
\(A, B\) and \(C\) are three non-empty sets. If \(A \subset B\) and \(B \subset C\), then which of the following is true?
CorrectIncorrectHint
(c) If \(A \subset B\) and \(B \subset C\), then these sets is represented in Venn diagram as
Clearly,
\(
A \cup B=B
\)
and \(B \cap C=B\)
Hence, \(A \cup B=B \cap C\) -
Question 109 of 123
109. Question
If \(A=\{1,2,3,4,5,6\}\), then how many subsets of \(A\) contain the elements 2,3 and 5?
CorrectIncorrectHint
(b)
\(
\begin{aligned}
&\text { The number of subsets containing } 2,3 \text {, and } 5 \text { is } 2^n \text {. }\\
&2^3=8
\end{aligned}
\) -
Question 110 of 123
110. Question
If \(S\) is the set of squares and \(R\) is the set of rectangles, then \((S \cup R)-(S \cap S)\) is
CorrectIncorrectHint
(d)
\(
\begin{aligned}
&\text { Clearly, } S \subset R\\
&\begin{aligned}
& \therefore S \cup R=R \text { and } S \cap R=S \\
& \Rightarrow(S \cup R)-(S \cap R)=\text { Set of rectangles which are not squares }
\end{aligned}
\end{aligned}
\) -
Question 111 of 123
111. Question
If \(P\) is the set of all parallelograms, and \(T\) is the set of all trapeziums, then \(P \cap T\) is
CorrectIncorrectHint
(a)
\(
\begin{aligned}
&\text { Clearly, } P \subset T\\
&\therefore P \cap T=P
\end{aligned}
\) -
Question 112 of 123
112. Question
If \(n(A \cap B)=10, n(B \cap C)=20\) and \(n(A \cap C)=30\), then the greatest possible value of \(n(A \cap B \cap C)\) is
CorrectIncorrectHint
(c) The greatest possible value of \(n(A \cap B \cap C)\) is the least amongst the values \(n(A \cap B), n(B \cap C)\) and \(n(A \cap C)=\min (10,20,30)=10\) i.e. 10.
-
Question 113 of 123
113. Question
If \(n(A \cap B)=5, n(A \cap C)=7\) and \(n(A \cap B \cap C)=3\), then the minimum possible value of \(n(B \cap C)\) is
CorrectIncorrectHint
(c) The number of elements in the intersection of sets \(A\) and \(B\) is \(n(A \cap B)=5\).
The number of elements in the intersection of sets \(A\) and \(C\) is \(n(A \cap C)=7\).
The number of elements in the intersection of sets \(\boldsymbol{A}, \boldsymbol{B}\), and \(\boldsymbol{C}\) is \(n(A \cap B \cap C)=3\).
The intersection of three sets \(A \cap B \cap C\) is a subset of any pairwise intersection, e.g., \(A \cap B \cap C \subseteq B \cap C\).
The number of elements in a subset cannot be greater than the number of elements in the superset.
To find the minimum value of \(n(B \cap C)\), we use the property that \(A \cap B \cap C\) is a subset of \(B \cap C\).
The set \(A \cap B \cap C\) represents elements common to all three sets.
The set \(\boldsymbol{B} \cap \boldsymbol{C}\) represents elements common to sets \(\boldsymbol{B}\) and \(\boldsymbol{C}\).
Any element in \(A \cap B \cap C\) must also be in \(B \cap C\).
This implies \(A \cap B \cap C \subseteq B \cap C\).
Since \(A \cap B \cap C \subseteq B \cap C\), it follows that \(n(A \cap B \cap C) \leq n(B \cap C)\).
We are given \(n(A \cap B \cap C)=3\).
Therefore, \(3 \leq n(B \cap C)\).
Determine the minimum value.
The inequality \(3 \leq n(B \cap C)\) means that \(n(B \cap C)\) must be at least 3.
The minimum possible value for \(n(B \cap C)\) is thus 3. -
Question 114 of 123
114. Question
If \(A, B\) and \(C\) are three non-empty sets such that any two of them are disjoint, then \((A \cup B \cup C) \cap(A \cap B \cap C)=\)
CorrectIncorrectHint
(d) \(A, B, C\) are three non-empty sets.
Any two of these sets are disjoint, meaning \(A \cap B=\phi, A \cap C=\phi\), and \(B \cap C=\phi\).
The intersection of disjoint sets is the empty set.
Since \(\boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C}\) are pairwise disjoint, their common intersection is the empty set. \(A \cap B \cap C=\phi\)
The union \(A \cup B \cup C\) contains all elements from \(A, B\), and \(C\).
We have \((A \cup B \cup C) \cap(A \cap B \cap C)\).
Substitute the result: \((A \cup B \cup C) \cap \phi\).
The intersection of any set with the empty set is the empty set.
\((A \cup B \cup C) \cap \phi=\phi\) -
Question 115 of 123
115. Question
\(A\) and \(B\) are any two non-empty sets and \(A\) is proper subset of \(B\). If \(n(A)=5\), then find the minimum possible value of \(n(A \Delta B)\)
CorrectIncorrectHint
(a) It is given that \(A\) is a proper subset of \(B\)
\(
\therefore A-B=\phi \Rightarrow n(A-B)=0
\)
We have, \(n(A)=5\). So, minimum number of elements in \(B\) is 6
Hence, the minimum possible value of \(n(A \Delta B)\) is \(n(B)-n(A)=6-5=1\)Explanation:
\(A\) and \(B\) are non-empty sets.
\(A\) is a proper subset of \(B\).
\(
n(A)=5
\)
The symmetric difference \(A \Delta B\) is defined as \((A-B) \cup(B-A)\).
If \(\boldsymbol{A}\) is a proper subset of \(\boldsymbol{B}\), then \(\boldsymbol{A}-\boldsymbol{B}=\phi\).
How to solve?
Determine the minimum size of \(\boldsymbol{B}\) and then calculate the symmetric difference.
Determine the minimum size of set \(\boldsymbol{B}\):
Since \(A\) is a proper subset of \(B, B\) must contain all elements of \(A\) and at least one additional element not in \(A\).
The minimum number of elements in \(\boldsymbol{B}\) is \(\boldsymbol{n}(\boldsymbol{A})+1\).
\(
n(B)_{\min }=n(A)+1=5+1=6
\)
Calculate the symmetric difference \(n(A \Delta B)\):
Since \(A\) is a proper subset of \(B, A-B=\phi\).
Therefore, \(A \Delta B=(A-B) \cup(B-A)=\phi \cup(B-A)=B-A\).
The number of elements in \(A \Delta B\) is \(n(B-A)\).
\(
n(A \Delta B)=n(B)-n(A)
\)
Substitute the minimum value of \(n(\boldsymbol{B})\) :
\(
n(A \Delta B)_{\min }=n(B)_{\min }-n(A)=6-5=1
\)
The minimum possible value of \(n(A \Delta B)\) is 1. -
Question 116 of 123
116. Question
If \(A=\left\{p: p=\frac{(n+2)\left(2 n^5+3 n^4+4 n^3+5 n^2+6\right)}{n^2+2 n}, n, p \in Z^{+}\right\}\) then the number of elements in the set \(A\), is
CorrectIncorrectHint
(c) Factor the denominator: \(n^2+2 n=n(n+2)\).
Substitute into the expression for \(p: p=\frac{(n+2)\left(2 n^5+3 n^4+4 n^3+5 n^2+6\right)}{n(n+2)}\).
Cancel out the common term ( \(n+2\) ) since \(n \in Z^{+}\)implies \(n+2 \neq 0\) :
\(
p=\frac{2 n^5+3 n^4+4 n^3+5 n^2+6}{n}
\)
Divide each term in the numerator by \(n: p=2 n^4+3 n^3+4 n^2+5 n+\frac{6}{n}\).
For \(p\) to be an integer, \(\frac{6}{n}\) must be an integer.
Since \(n \in Z^{+}, n\) must be a positive divisor of 6.
The positive divisors of 6 are \(1,2,3,6\).
\(
\text { For } n=1: p=2(1)^4+3(1)^3+4(1)^2+5(1)+\frac{6}{1}=2+3+4+5+6=20 \text {. }
\)
\(
\begin{aligned}
&\text { For } n=2 \text { : }\\
&p=2(2)^4+3(2)^3+4(2)^2+5(2)+\frac{6}{2}=2(16)+3(8)+4(4)+10+3=32+24+16+10+3=85
\end{aligned}
\)
\(
\begin{aligned}
&\text { For } n=3 \text { : }\\
&p=2(3)^4+3(3)^3+4(3)^2+5(3)+\frac{6}{3}=2(81)+3(27)+4(9)+15+2=162+81+36+15+2=296
\end{aligned}
\)
\(
\begin{aligned}
&\text { For } n=6 \text { : }\\
&p=2(6)^4+3(6)^3+4(6)^2+5(6)+\frac{6}{6}=2(1296)+3(216)+4(36)+30+1=2592+648+144+30+1=3415
\end{aligned}
\)
The calculated values of \(p\) are \(20,85,296,3415\).
All these values are distinct positive integers.
The number of elements in the set \(A\) is 4. -
Question 117 of 123
117. Question
If \(A, B\) and \(C\) are three sets such that \(A \supset B \supset C\), then \((A \cup B \cup C)-(A \cap B \cap C)=\)
CorrectIncorrectHint
(c) \(A, B\), and \(C\) are three sets.
The relationship between the sets is \(A \supset B \supset C\).
If \(X \supset Y[latex], then [latex]X \cup Y=X\).
If \(X \supset Y[latex], then [latex]X \cap Y=Y\).
Given \(A \supset B \supset C\).
This implies \(\boldsymbol{A} \supset \boldsymbol{B}\) and \(\boldsymbol{B} \supset \boldsymbol{C}\).
Therefore, \(A \cup B=A\).
Also, \((A \cup B) \cup C=A \cup C\).
Since \(A \supset C, A \cup C=A\).
So, \(A \cup B \cup C=A\).
Given \(A \supset B \supset C\).
This implies \(A \cap B=B\).
Also, \((A \cap B) \cap C=B \cap C\).
Since \(\boldsymbol{B} \supset \boldsymbol{C}, \boldsymbol{B} \cap \boldsymbol{C}=\boldsymbol{C}\).
So, \(A \cap B \cap C=C\).
The expression becomes \((A \cup B \cup C)-(A \cap B \cap C)=A-C\).Note:
PROPER SUBSET OF A SET
Set \(A\) is said to be a proper subset of set \(B\) if \(A\) is a subset of \(B\) and \(A \neq B\).
This fact is expressed by writing \(A \subset B\) or \(B \supset A\) (read as ‘ \(A\) is a proper subset of \(B\) ).
Thus, the number of elements in \(B\) is greater than that in \(A\). For example,
Let \(A=\{1,2,3\}, B=\{2,3,4,1,5\}\). Then \(A \subset B\) or \(B \supset A\). -
Question 118 of 123
118. Question
If \(A_1 \subset A_2 \subset A_3 \subset \ldots \subset A_{50}\) and \(n\left(A_i\right)=i-1\), then \(n\left(\underset{i=11}{\stackrel{50}{\cap} A_i}\right)=\)
CorrectIncorrectHint
(d) The sets are nested: \(A_1 \subset A_2 \subset \ldots \subset A_{50}\).
The cardinality of each set \(A_i\) is given by \(n\left(A_i\right)=i-1\).
For nested sets \(\boldsymbol{B}_1 \subset \boldsymbol{B}_2 \subset \ldots \subset \boldsymbol{B}_k\), their intersection is the smallest set: \(\cap_{j=1}^k B_j=B_1\).
Determine the smallest set in the intersection and find its cardinality.
Identify the intersection of the sets.
Given \(A_{11} \subset A_{12} \subset \ldots \subset A_{50}\).
The intersection \(\cap_{i=11}^{50} A_i\) is the smallest set in this sequence.
So, \(\cap_{i=11}^{50} A_i=A_{11}\).
Find the cardinality of the resulting set.
The cardinality of \(A_i\) is \(n\left(A_i\right)=i-1\).
For \(A_{11}\), substitute \(i=11\) into the formula.
\(
\begin{aligned}
& n\left(A_{11}\right)=11-1 \\
& n\left(A_{11}\right)=10
\end{aligned}
\)
The cardinality of the intersection is 10. -
Question 119 of 123
119. Question
If \(n\left(A_i\right)=i+1\) and \(A_1 \subset A_2 \subset A_3 \subset \ldots \subset A_{99}\), then \(n\left(\bigcup_{i=1}^{99} A_i\right)=\)
CorrectIncorrectHint
(c) You are solving for the cardinality of the union of a sequence of nested sets.
What’s given in the problem
The cardinality of each set \(A_i\) is given by \(n\left(A_i\right)=i+1\).
The sets are nested: \(A_1 \subset A_2 \subset A_3 \subset \ldots \subset A_{99}\).
How to solve
Determine the cardinality of the union by identifying the largest set in the nested sequence.
Identify the union of nested sets.
Given \(A_1 \subset A_2 \subset A_3 \subset \ldots \subset A_{99}\).
The union \(\bigcup_{i=1}^{99} A_i\) is equal to the largest set in the sequence.
This means \(\bigcup_{i=1}^{99} A_i=A_{99}\).
Find the cardinality of the union.
The cardinality of the union is \(n\left(\bigcup_{i=1}^{99} A_i\right)=n\left(A_{99}\right)\).
Use the given formula \(n\left(A_i\right)=i+1\).
Substitute \(i=99\) into the formula: \(n\left(A_{99}\right)=99+1\).
Calculate the result: \(n\left(A_{99}\right)=100\).
The cardinality of the union is 100. -
Question 120 of 123
120. Question
In a class, 70 students wrote two tests viz; test-I and test-II. 50% of the students failed in test-I and 40% of the students in test-II. How many students passed in both tests?
CorrectIncorrectHint
(b) Calculate the number of students who passed both tests.
What’s given in the problem
Total number of students: 70
Percentage of students who failed test-I: 50%
Percentage of students who failed test-II: \(\mathbf{4 0 \%}\)
How to solve
Calculate the number of students who failed each test, subtract the sum of these from the total number of students, and then assume that students who failed both tests are negligible.
Step 1: Calculate the number of students who failed test-1
Convert the percentage to a decimal: \(\frac{50}{100}=0.5\)
Multiply the decimal by the total number of students: \(0.5 \times 70=35\)
Number of students who failed test-I: 35
Step 2: Calculate the number of students who failed test-II
Convert the percentage to a decimal: \(\frac{40}{100}=0.4\)
Multiply the decimal by the total number of students: \(0.4 \times 70=28\)
Number of students who failed test-II: 28
Step 3: Calculate the number of students who passed both tests
Calculate the total number of students who failed at least one test: \(35+28=63\)
Calculate the number of students who passed both tests by assuming those who failed both tests are negligible, and subtracting the students who failed at least one test from the total number of students: \(70-(35+28)=7\)
Number of students who passed both tests: 7 -
Question 121 of 123
121. Question
In an election, two contestants \(A\) and \(B\) contested \(x \%\) of the total voters voted for \(A\) and \((x+20) \%\) for \(B\). If \(20 \%\) of the voters did not vote, then \(x=\)
CorrectIncorrectHint
(a) Understanding the percentages: The percentages given relate to the total number of voters.
Setting up the equation: The sum of the percentages for A, B, and those who did not vote must equal \(100 \%\). So, the equation is:
\(
x+(x+20)+20=100
\)
Simplifying the equation: Combine the terms:
\(
2 x+40=100
\)
\(
x=30
\) -
Question 122 of 123
122. Question
In a rehabilitation programme, a group of 50 families were assured new houses and compensation by the government. Number of families who got both is equal to the number of families who got neither of the two. The number of families who got new houses is 6 greater than the number of families who got compensation. How many families got houses?
CorrectIncorrectHint
(b) Let \(x=\) number of families who got compensation
\(y=\) number of families who got new houses
\(z=\) number of families who got both
\(n=\) number of families who got neither
From the problem, we have the following relationships:
Total families: \(x+y-z+n=50\) (since families who got both are counted in both \(x\) and \(y\) )
\(z=n\) (the number of families who got both is equal to the number of families who got neither)
\(y=x+6\) (the number of families who got new houses is 6 greater than those who got compensation)
Substituting \(n\) with \(z\) in the first equation gives us:
\(
x+y-z+z=50
\)
This simplifies to:
\(
x+y=50
\)
Now substituting \(y\) with \(x+6\) :
\(
x+(x+6)=50
\)
This simplifies to:
\(
2 x+6=50
\)
\(
2 x=44
\)
\(
x=22
\)
Now substituting \(x\) back to find \(y\) :
\(
y=x+6=22+6=28
\)
Thus, the number of families who got houses is 28. -
Question 123 of 123
123. Question
In an office, every employee likes at least one of tea, coffee and milk. The number of employees who like only tea, only coffee, only milk and all the three are all equal. The number of employees who like only tea and coffee, only coffee and milk and only tea and milk are equal and each is equal to the number of employees who like all the three. Then a possible value of the number of employees in the office is
CorrectIncorrectHint
(c)
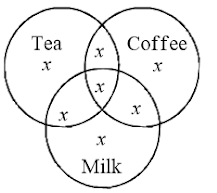
The total number of employees can be expressed as:
Number who like only tea: \(x\)
Number who like only coffee: \(x\)
Number who like only milk: \(x\)
Number who like tea and coffee: \(x\)
Number who like coffee and milk: \(x\)
Number who like tea and milk: \(x\)
Number who like all three: \(x\)
Total number of employees \(=7 x\) i.e., a multiple of 7.