JEE Practice Questions (Single Choice Type)
Quiz Summary
0 of 122 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 122 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 122
1. Question
The function \(f: N \rightarrow N(N\) is the set of natural numbers) defined by \(f(n)=2 n+3\) is
Hint
(b) \(f: N \rightarrow N, f(n)=2 n+3\)
Here, the range of the function is \(\{5,6,7, \ldots\}\) or \(N-\{1,2\), \(3,4\}\)
which is a subset of \(N\) (co-domain).
Hence, function is into.
Also, it is clear that \(f(n)\) is one-one or injective.
Hence. \(f(n)\) is iniective only. -
Question 2 of 122
2. Question
The function \(f(x)=\sin \left(\log \left(x+\sqrt{1+x^2}\right)\right)\) is
Hint
(b)
\(
\begin{aligned}
& f(x)=\sin \left(\log \left(x+\sqrt{1+x^2}\right)\right) \\
\Rightarrow & f(-x)=\sin \left[\log \left(-x+\sqrt{1+x^2}\right)\right] \\
\Rightarrow & f(-x)=\sin \log \left(\left(\sqrt{1+x^2}-x\right) \frac{\left(\sqrt{1+x^2}+x\right)}{\left(\sqrt{1+x^2}+x\right)}\right) \\
\Rightarrow & f(-x)=\sin \log \left[\frac{1}{\left(x+\sqrt{1+x^2}\right)}\right]
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow f(-x)=\sin \left[-\log \left(x+\sqrt{1+x^2}\right)\right] \\
& \Rightarrow f(-x)=-\sin \left[\log \left(x+\sqrt{1+x^2}\right)\right] \\
& \Rightarrow f(-x)=-f(x) \\
& \Rightarrow f(x) \text { is an odd function. }
\end{aligned}
\) -
Question 3 of 122
3. Question
If \(x\) is real, then the value of the expression \(\frac{x^2+14 x+9}{x^2+2 x+3}\) lies between
Hint
(c)
\(
\begin{aligned}
&\begin{aligned}
& \frac{x^2+14 x+9}{x^2+2 x+3}=y \\
& \Rightarrow x^2+14 x+9=x^2 y+2 x y+3 y \\
& \Rightarrow x^2(y-1)+2 x(y-7)+(3 y-9)=0
\end{aligned}\\
&\text { Since } x \text { is real, }\\
&\begin{aligned}
& \therefore \quad 4(y-7)^2-4(3 y-9)(y-1)>0 \\
& \Rightarrow \quad 4\left(y^2+49-14 y\right)-4\left(3 y^2+9-12 y\right)>0 \\
& \Rightarrow \quad(y+5)(y-4)<0 ; \\
& \therefore \quad y \text { lies between }-5 \text { and } 4 .
\end{aligned}
\end{aligned}
\) -
Question 4 of 122
4. Question
The function \(f: R \rightarrow R\) is defined by \(f(x)=\cos ^2 x+\sin ^4 x\) for \(x \in R\), then the range of \(f(x)\) is
Hint
(c)
\(
\begin{aligned}
& y=f(x)=\cos ^2 x+\sin ^4 x \\
\Rightarrow \quad & y=f(x)=\cos ^2 x+\sin ^2 x\left(1-\cos ^2 x\right) \\
\Rightarrow \quad & y=\cos ^2 x+\sin ^2 x-\sin ^2 x \cos ^2 x \\
\Rightarrow \quad & y=1-\sin ^2 x \cos ^2 x \\
\Rightarrow \quad & y=1-\frac{1}{4} \sin ^2 2 x
\end{aligned}
\)
\(
\therefore \frac{3}{4} \leq f(x) \leq 1 \quad\left(\because 0 \leq \sin ^2 2 x \leq 1\right)
\)
\(
\Rightarrow f(x) \in[3 / 4,1]
\) -
Question 5 of 122
5. Question
The domain of the function \(f(x)=\log _{3+x}\left(x^2-1\right)\) is
Hint
(c)
\(
\begin{aligned}
&f(x) \text { is to be defined when } x^2-1>0 \text { and } 3+x>0 \text { and }\\
&\begin{aligned}
& 3+x \neq 1 \\
& \Rightarrow \quad x^2>1 \text { and } x>-3 \text { and } x \neq-2 \\
& \Rightarrow \quad x<-1 \text { or } x>1 \text { and } x>-3 \text { and } x \neq-2 \\
& \therefore \quad D_f=(-3,-2) \cup(-2,-1) \cup(1, \infty)
\end{aligned}
\end{aligned}
\) -
Question 6 of 122
6. Question
The domain of the function \(f(x)=\left[\log _{10}\left(\frac{5 x-x^2}{4}\right)\right]^{1 / 2}\) is
Hint
(b) We have \(f(x)=\left[\log _{10}\left(\frac{5 x-x^2}{4}\right)\right]^{1 / 2} \dots(1)[latex]
From (1), clearly [latex]f(x)\) is defined for those values of \(x\) for
\(
\begin{aligned}
& \text { which } \log _{10}\left[\frac{5 x-x^2}{4}\right] \geq 0 \\
& \Rightarrow\left(\frac{5 x-x^2}{4}\right) \geq 10^0 \\
& \Rightarrow\left(\frac{5 x-x^2}{4}\right) \geq 1 \\
& \Rightarrow x^2-5 x+4 \leq 0 \\
& \Rightarrow(x-1)(x-4) \leq 0
\end{aligned}
\)
Hence, the domain of the function is \([1,4]\). -
Question 7 of 122
7. Question
The domain of the function \(f(x)=\frac{\sin ^{-1}(3-x)}{\ln (|x|-2)}\) is
Hint
(b) \(f(x)=\frac{\sin ^{-1}(3-x)}{\log (|x|-2)}\)
Let \(g(x)=\sin ^{-1}(3-x)\)
\(
\Rightarrow-1 \leq 3-x \leq 1
\)
The domain of \(g(x)\) is \([2,4]\)
and let \(h(x)=\log (|x|-2)\)
\(
\begin{aligned}
& \Rightarrow \quad|x|-2>0 \text { or }|x|>2 \\
& \Rightarrow \quad x<-2 \text { or } x>2 \\
& \Rightarrow \quad(-\infty,-2) \cup(2, \infty)
\end{aligned}
\)
We know that
\(
(f / g)(x)=\frac{f(x)}{g(x)} \forall x \in D_1 \cap D_2-\{x \in R: g(x)=0\}
\)
\(\therefore\) the domain of \(f(x)=(2,4]-\{3\}=(2,3) \cup(3,4]\). -
Question 8 of 122
8. Question
The domain of \(f(x)=\log |\log x|\) is
Hint
(c)
\(
\begin{aligned}
& f(x)=\log |\log x|, f(x) \text { is defined if }|\log x|>0 \text { and } x>0, \text { i.e., } \\
& \text { if } x>0 \text { and } x \neq 1 \\
& \Rightarrow x \in(0,1) \cup(1, \infty) .
\end{aligned}
\) -
Question 9 of 122
9. Question
The domain of \(f(x)=\frac{\log _2(x+3)}{x^2+3 x+2}\) is
Hint
(d)
\(
\begin{aligned}
& \text { Here } x+3>0 \text { and } x^2+3 x+2 \neq 0 \\
& \therefore \quad x>-3 \text { and }(x+1)(x+2) \neq 0, \text { i.e., } x \neq-1,-2 \\
& \therefore \quad \text { The domain }=(-3, \infty)-\{-1,-2\} .
\end{aligned}
\) -
Question 10 of 122
10. Question
Let \(f:\left[-\frac{\pi}{3}, \frac{2 \pi}{3}\right] \rightarrow[0,4]\) be a function defined as \(f(x) =\sqrt{3} \sin x-\cos x+2\). Then \(f^{-1}(x)\) is given by
Hint
(b) \(y=f(x)=\sqrt{3} \sin x-\cos x+2=2 \sin \left(x-\frac{\pi}{6}\right)+2 \dots(1)\)
Since \(f(x)\) is one-one and onto, \(f\) is invertible.
From (1) \(\sin \left(x-\frac{\pi}{6}\right)=\frac{y-2}{2}\)
\(
\Rightarrow \quad x=\sin ^{-1} \frac{y-2}{2}+\frac{\pi}{6}
\)
\(
\Rightarrow f^{-1}(x)=\sin ^{-1}\left(\frac{x-2}{2}\right)+\frac{\pi}{6}
\) -
Question 11 of 122
11. Question
If \(F(n+1)=\frac{2 F(n)+1}{2} n=1,2, \ldots\) and \(F(1)=2\), then \(F(101)\) equals
Hint
(a)
\(
\begin{aligned}
&F(n+1)=\frac{2 F(n)+1}{2} \Rightarrow F(n+1)-F(n)=\frac{1}{2}\\
&\text { Put } n=1,2,3, \ldots, 100 \text { and add, we get }\\
&\begin{aligned}
& F(101)-F(1)=100 \times \frac{1}{2} \\
& \Rightarrow \quad F(101)=52
\end{aligned} \quad[\because F(1)=2]
\end{aligned}
\) -
Question 12 of 122
12. Question
The domain of the function \(f(x)=\frac{1}{\sqrt{{ }^{10} C_{x-1}-3 \times{ }^{10} C_x}}\) contains the points
Hint
(d)
\(
\begin{aligned}
&\text { Given function is defined if }{ }^{10} C_{x-1}>3{ }^{10} C_x\\
&\begin{aligned}
& \Rightarrow \frac{1}{11-x}>\frac{3}{x} \Rightarrow 4 x>33 \\
& \Rightarrow x \geq 9 \text { but } x \leq 10 \Rightarrow x=9,10 .
\end{aligned}
\end{aligned}
\) -
Question 13 of 122
13. Question
The domain of the function \(f(x)=\frac{x}{\sqrt{\sin (\ln x)-\cos (\ln x)}} (n \in Z)\) is
Hint
(b)
\(
\begin{aligned}
&\text { For the domain } \sin (\ln x)>\cos (\ln x) \text { and } x>0\\
&2 n \pi+\frac{\pi}{4}<\ln x<2 n \pi+\frac{5 \pi}{4}, n \in N \cup\{0\}
\end{aligned}
\) -
Question 14 of 122
14. Question
If \(f\) is a function such that \(f(0)=2, f(1)=3\) and \(f(x+2) =2 f(x)-f(x+1)\) for every real \(x\), then \(f(5)\) is
Hint
(b)
\(
\begin{aligned}
& \text { Put } x=0 \Rightarrow f(2)=2 f(0)-f(1)=2 \times 2-3=1 \\
& \text { Put } x=1 \Rightarrow f(3)=6-1=5 \\
& \text { Put } x=2 \Rightarrow f(4)=2 f(2)-f(3)=2 \times 1-5=-3 \\
& \text { Put } x=3 \Rightarrow f(5)=2 f(3)-f(4)=2(5)-(-3)=13 \text {. }
\end{aligned}
\) -
Question 15 of 122
15. Question
The range of \(f(x)=\sin ^{-1}\left(\frac{x^2+1}{x^2+2}\right)\) is
Hint
(c)
\(
\text { Here, } \frac{x^2+1}{x^2+2}=1-\frac{1}{x^2+2}
\)
\(
\begin{aligned}
&\text { Now, } 2 \leq x^2+2<\infty \text { for all } x \in R\\
&\begin{aligned}
& \Rightarrow \frac{1}{2} \geq \frac{1}{x^2+2}>0 \\
& \Rightarrow-\frac{1}{2} \leq \frac{-1}{x^2+2}<0 \\
& \Rightarrow \frac{1}{2} \leq 1-\frac{1}{x^2+2}<1 \\
& \Rightarrow \frac{\pi}{6} \leq \sin ^{-1}\left(1-\frac{1}{x^2+2}\right)<\frac{\pi}{2}
\end{aligned}
\end{aligned}
\) -
Question 16 of 122
16. Question
The function \(f(x)=\frac{\sec ^{-1} x}{\sqrt{x-[x]}}\), where \([x]\) denotes the greatest integer less than or equal to \(x\), is defined for all \(x \in\)
Hint
(b) The function \(\sec ^{-1} x\) is defined for all \(x \in R-(-1,1)\) and the function \(\frac{1}{\sqrt{x-[x]}}\) is defined for all \(x \in R-Z\)
So the given function is defined for all \(x \in R-\{(-1,1) \cup\{n \mid n \in Z\}\}\). -
Question 17 of 122
17. Question
The domain of \(f(x)=\cos ^{-1}\left(\frac{2-|x|}{4}\right)+[\log (3-x)]^{-1}\) is
Hint
(b)
\(
\begin{aligned}
& \cos ^{-1}\left(\frac{2-|x|}{4}\right) \text { exists if }-1 \leq \frac{2-|x|}{4} \leq 1 \\
& \Rightarrow-6 \leq-|x| \leq 2 \\
& \Rightarrow-2 \leq|x| \leq 6 \\
& \Rightarrow|x| \leq 6 \\
& \Rightarrow-6 \leq x \leq 6
\end{aligned}
\)
The function \([\log (3-x)]^{-1}=\frac{1}{\log (3-x)}\) is defined if \(3-x>0\) and \(x \neq 2\), i.e., if \(x \neq 2\) and \(x<3\).
Thus, the domain of the given function is
\(
\{x \mid-6 \leq x \leq 6\} \cap\{x \mid x \neq 2, x<3\}=[-6,2) \cup(2,3) .
\) -
Question 18 of 122
18. Question
The domain of the function \(f(x)=\sqrt{\log \left(\frac{1}{|\sin x|}\right)}\) is
Hint
(b)
\(
\begin{aligned}
& f(x) \text { is defined for } \log \left(\frac{1}{|\sin x|}\right) \geq 0 \\
& \Rightarrow \frac{1}{|\sin x|} \geq 1 \text { and }|\sin x| \neq 0
\end{aligned}
\)
\(
\Rightarrow \quad|\sin x| \neq 0 \quad\left[\because \frac{1}{|\sin x|} \geq 1 \text { for all } x\right]
\)
\(
\begin{aligned}
&\Rightarrow \quad x \neq n \pi, n \in Z\\
&\text { Hence, the domain of } f(x)=R-\{n \pi: n \in Z\} \text {. }
\end{aligned}
\) -
Question 19 of 122
19. Question
The domain of the function \(f(x)=\log _2\left(-\log _{1 / 2}\left(1+\frac{1}{x^{1 / 4}}\right)-1\right)\) is
Hint
(a)
\(
\begin{aligned}
& f(x) \text { is defined if }-\log _{1 / 2}\left(1+\frac{1}{x^{1 / 4}}\right)-1>0 \\
& \Rightarrow \quad \log _{1 / 2}\left(1+\frac{1}{x^{1 / 4}}\right)<-1 \\
& \Rightarrow \quad 1+\frac{1}{x^{1 / 4}}>\left(\frac{1}{2}\right)^{-1} \\
& \Rightarrow \quad \frac{1}{x^{1 / 4}}>1 \\
& \Rightarrow \quad 0<x<1
\end{aligned}
\) -
Question 20 of 122
20. Question
The range of \(f(x)=\sin ^{-1}\left(\sqrt{x^2+x+1}\right)\) is
Hint
(c)
\(
\begin{aligned}
&\text { For the function to get defined } 0 \leq x^2+x+1 \leq 1 \text {, }\\
&\text { but } x^2+x+1 \geq \frac{3}{4} \Rightarrow \frac{\sqrt{3}}{2} \leq \sqrt{x^2+x+1} \leq 1
\end{aligned}
\)
\(
\Rightarrow \quad \frac{\pi}{3} \leq \sin ^{-1}\left(\sqrt{x^2+x+1}\right) \leq \frac{\pi}{2} .
\) -
Question 21 of 122
21. Question
If \(f(x)=\) maximum \(\left\{x^3, x^2, \frac{1}{64}\right\} \forall x \in[0, \infty)\), then
Hint
(c)
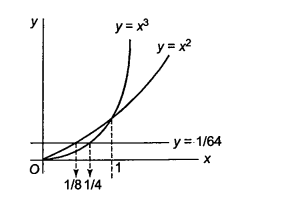
\(
\text { Clearly, from the graph } f(x)=\left\{\begin{array}{cc}
\frac{1}{64}, & 0 \leq x \leq \frac{1}{8} \\
x^2, & \frac{1}{8}<x \leq 1 \\
x^3, & x>1
\end{array}\right.
\) -
Question 22 of 122
22. Question
If the period of \(\frac{\cos (\sin (n x))}{\tan (x / n)}, n \in N\), is \(6 \pi\), then \(n\) is equal to
Hint
(c) The period of \(\cos (\sin n x)\) is \(\frac{\pi}{n}\) and the period of \(\tan \left(\frac{x}{n}\right)\) is \(\pi n\).
Thus, \(6 \pi=\operatorname{LCM}\left(\frac{\pi}{n}, \pi n\right)\).
By checking for the different values of \(n, n=6\). -
Question 23 of 122
23. Question
The number of real solutions of the equation \(\log _{0.5}|x|=2|x|\) is
Hint
(b) \(\text { Draw the graph of } y=\log _{0.5}|x| \text { and } y=2|x|\)
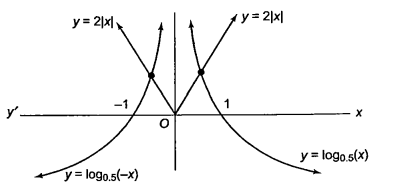
Clearly, from the graph, there are two solutions.
-
Question 24 of 122
24. Question
The period of the function \(\left|\sin ^3 \frac{x}{2}\right|+\left|\cos ^5 \frac{x}{5}\right|\) is
Hint
(b) \(f(x)=\left|\sin ^3 \frac{x}{2}\right|+\left|\cos ^5 \frac{x}{5}\right|\)
The period of \(\sin ^3 x\) is \(2 \pi\)
\(\Rightarrow\) The period of \(\sin ^3 \frac{x}{2}\) is \(\frac{2 \pi}{1 / 2}=4 \pi\)
\(\Rightarrow\) The period of \(\left|\sin ^3 \frac{x}{2}\right|\) is \(2 \pi\)
The period of \(\cos ^5 x\) is \(2 \pi\)
\(\Rightarrow\) The period of \(\cos ^5 \frac{x}{5}\) is \(\frac{2 \pi}{\left(\frac{1}{5}\right)}=10 \pi\)
\(\Rightarrow\) The period of \(\left|\cos ^5 \frac{x}{2}\right|\) is \(5 \pi\)
\(
\text { Now the period of } f(x)=\operatorname{LCM} \text { of }\{2 \pi, 10 \pi\}=10 \pi \text {. }
\) -
Question 25 of 122
25. Question
If \(f(x)=\sqrt[n]{x^m}, n \in N\), is an even function, then \(m\) is
Hint
(a)
\(
\begin{aligned}
&\text { Given } f(x)=\sqrt[n]{x^m}, n \in N \text { is an even function where } m \in I .\\
&\begin{aligned}
& \Rightarrow f(x)=f(-x) \\
& \Rightarrow \sqrt[n]{x^m}=\sqrt[n]{(-x)^m} \\
& \Rightarrow x^m=(-x)^m \\
& \Rightarrow m \text { is an even integer } \\
& \Rightarrow m=2 k, k \in I
\end{aligned}
\end{aligned}
\) -
Question 26 of 122
26. Question
If \(f\) is periodic, \(g\) is polynomial function and \(f(g(x))\) is periodic and \(g(2)=3, g(4)=7\) then \(g(6)\) is
Hint
(c) From the given data \(g(x)\) must be linear function
Hence, \(g(x)=a x+b\)
Also \(g(2)=2 a+b=3\) and \(g(4)=4 a+b=7\)
Solving, we get \(a=2\) and \(b=-1\)
Hence, \(g(x)=2 x-1\)
Then, \(g(6)=11\). -
Question 27 of 122
27. Question
The period of function \(2^{\{x\}}+\sin \pi x+3^{\{x / 2\}}+\cos 2 \pi x\) (where \(\{x\}\) denotes the fractional part of \(x\) ) is
Hint
(b) The period of \(\sin \pi x\) and \(\cos 2 \pi x\) is 2 and 1 , respectively
The period of \(2^{\{x\}}\) is 1
The period of \(3^{\{x / 2\}}\) is 2
Hence, the period of \(f(x)\) is LCM of 1 and \(2=2\). -
Question 28 of 122
28. Question
The equation \(||x-2|+a|=4\) can have four distinct real solutions for \(x\) if \(a\) belongs to the interval
Hint
(a)
\(
\begin{aligned}
&\begin{aligned}
& |x-2|+a= \pm 4 \\
& \Rightarrow \quad|x-2|= \pm 4-a
\end{aligned}\\
&\text { for } 4 \text { real roots, } 4-a>0 \text { and }-4-a>0\\
&\Rightarrow \quad a \in(-\infty,-4)
\end{aligned}
\) -
Question 29 of 122
29. Question
Given the function \(f(x)=\frac{a^x+a^{-x}}{2}\) (where \(\left.a>2\right)\). Then \(f(x+y)+f(x-y)=\)
Hint
(a)
\(
\begin{aligned}
&\text { We have } f(x+y)+f(x-y)\\
&\begin{aligned}
& =\frac{1}{2}\left[a^{x+y}+a^{-x-y}+a^{x-y}+a^{-x+y}\right] \\
& =\frac{1}{2}\left[a^x\left(a^y+a^{-y}\right)+a^{-x}\left(a^y+a^{-y}\right)\right] \\
& =\frac{1}{2}\left(a^x+a^{-x}\right)\left(a^y+a^{-y}\right)=2 f(x) f(y)
\end{aligned}
\end{aligned}
\) -
Question 30 of 122
30. Question
If \(\log _3\left(x^2-6 x+11\right) \leq 1\), then exhaustive range of values of \(x\) is
Hint
(d)
\begin{aligned}
& \log _3\left(x^2-6 x+11\right) \leq 1 \\
& \Rightarrow \quad 0<x^2-6 x+11 \leq 3 \\
& \Rightarrow \quad x \in[2,4]
\end{aligned} -
Question 31 of 122
31. Question
The domain of the function \(f(x)=\sqrt{x^2-[x]^2}\), where \([x]=\) the greatest integer less than or equal to \(x\), is
Hint
(d) \(x^2-[x]^2 \geq 0 \Rightarrow x^2 \geq[x]^2\)
This is true for all positive values of \(x\) and all negative integer \(x\). -
Question 32 of 122
32. Question
The range of the function \(f(x)=|x-1|+|x-2|\), \(-1 \leq x \leq 3\), is
Hint
(b)
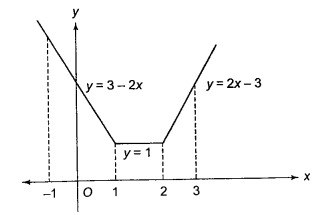
Clearly, from the graph, the range is \([1, f(-1)] \equiv[1,5]\) If \(x<1, f(x)=-(x-1)-(x-2)=-2 x+3\).
In this interval, \(f(x)\) is decreasing.
If \(1 \leq x<2, f(x)=x-1-(x-2)=1\)
In this interval, \(f(x)\) is constant.
\(
\text { If } 2 \leq x \leq 3, f(x)=x-1+x-2=2 x-3
\)
In this interval, \(f(x)\) is increasing.
\(\therefore \max f(x)=\) the greatest among \(f(-1)\) and \(f(3)=5, \min f(x)\)
\(
=f(1)=1
\)
So, the range \(=[1,5]\). -
Question 33 of 122
33. Question
Which of the following functions is inverse to itself?
Hint
(a) By checking for different function, we find that for \(f(x)=\frac{1-x}{1+x}, f^{-1}(x)=f(x)\).
-
Question 34 of 122
34. Question
A function \(F(x)\) satisfies the functional equation \(x^2 F(x) +F(1-x)=2 x-\mathrm{x}^4\) for all real \(x . F(x)\) must be
Hint
(b) \(x^2 F(x)+F(1-x)=2 x-x^4 \dots(1)\)
\(
\begin{aligned}
&\text { Replacing } x \text { by } 1-x \text {, we get }\\
&\Rightarrow \quad(1-x)^2 F(1-x)+F(x)=2(1-x)-(1-x)^4 \dots(2)
\end{aligned}
\)
\(
\text { Eliminating } F(1-x) \text { from (1) and (2), we get } F(x)=1-x^2 \text {. }
\) -
Question 35 of 122
35. Question
If \(f(x)=\left\{\begin{array}{cc}x^2 \sin \frac{\pi x}{2}, & |x|<1 \\ x|x|, & |x| \geq 1\end{array}\right.\) then \(f(x)\) is
Hint
(b)
\(
f(-x)=\left\{\begin{array}{cc}
(-x)^2 \sin \frac{\pi(-x)}{2}, & |-x|<1 \\
(-x)|-x|, & |-x| \geq 1
\end{array}\right.
\)
\(
=\left\{\begin{array}{cc}
-x^2 \sin \frac{\pi x}{2}, & |x|<1 \\
-x|x|, & |x| \geq 1
\end{array}\right.
\)
\(
=-f(x)
\) -
Question 36 of 122
36. Question
Function \(f:(-\infty,-1) \rightarrow\left(0, e^5\right]\) defined by \(f(x)=e^{x^3-3 x+2}\) is
Hint
(d)
\(
\begin{aligned}
& f(x)=e^{x^3-3 x+2} \\
& \text { Let } g(x)=x^3-3 x+2 ; g^{\prime}(x) \\
& \quad=3 x^2-3=3\left(x^2-1\right)
\end{aligned}
\)
\(g^{\prime}(x) \geq 0\) for \(x \in(-\infty,-1]\)
\(\therefore f(x)\) is increasing function
\(\therefore f(x)\) is one-one
Now, the range of \(f(x)=\left(0, e^4\right]\)
But co-domain is \(\left(0, e^5\right] . \quad \therefore f(x)\) is an into function. -
Question 37 of 122
37. Question
If \(f(x)=\frac{1}{x}, g(x)=\frac{1}{x^2}\) and \(h(x)=x^2\)
Hint
(c)
\(
\begin{aligned}
f(x) & =\frac{1}{x}, g(x)=\frac{1}{x^2} \text { and } h(x)=x^2 \\
f(g(x)) & =x^2 ; x \neq 0 \\
h(g(x)) & =\frac{1}{x^4}=(g(x))^2, x \neq 0
\end{aligned}
\) -
Question 38 of 122
38. Question
If \([x]\) and \(\{x\}\) represent the integral and fractional parts of \(x\), respectively, then the value of \(\sum_{r=1}^{2000} \frac{\{x+r\}}{2000}\) is
Hint
(c)
\(
\sum_{r=1}^{2000} \frac{\{x+r\}}{2000}=\sum_{r=1}^{2000} \frac{\{x\}}{2000}=2000 \frac{\{x\}}{2000}=\{x\}
\) -
Question 39 of 122
39. Question
If \(f(x)\) is a polynomial satisfying \(f(x) f(1 / x)=f(x) +f(1 / x)\) and \(f(3)=28\), then \(f(4)\) is equal to
Hint
(b)
\(
\begin{aligned}
f(x) & =x^n+1 \\
f(3) & =3^n+1=28 \\
3^n & =27 \\
n & =3 \\
f(4) & =4^3+1=65 .
\end{aligned}
\) -
Question 40 of 122
40. Question
The values of \(b\) and \(c\) for which the identity \(f(x+1) -f(x)=8 x+3\) is satisfied, where \(f(x)=b x^2+c x+d\), are
Hint
(b)
\(
\begin{aligned}
& \because f(x+1)-f(x)=8 x+3 \\
& \Rightarrow\left\{b(x+1)^2+c(x+1)+d\right\}-\left\{b x^2+c x+d\right\}=8 x+3 \\
& \Rightarrow b\left\{(x+1)^2-x^2\right\}+c=8 x+3 \\
& \Rightarrow b(2 x+1)+c=8 x+3
\end{aligned}
\)
On comparing co-efficient of \(x\) and constant term, we get \(2 b=8\) and \(b+c=3\) then \(b=4\) and \(c=-1\). -
Question 41 of 122
41. Question
Let \(f: R \rightarrow R, g: R \rightarrow R\) be two given functions such that \(f\) is injective and \(g\) is surjective, then which of the following is injective?
Hint
(d) If \(f\) is injective and \(g\) is surjective
\(\Rightarrow f o g\) is injective
\(\Rightarrow f o f\) is injective. -
Question 42 of 122
42. Question
\(f: N \rightarrow N\) where \(f(x)=x-(-1)^x\) then \(f\) is
Hint
(c) \(f(x)=\left\{\begin{array}{ll}x-1, & x \text { is even } \\ x+1, & x \text { is odd }\end{array}\right.\), which is clearly are one-one and onto.
-
Question 43 of 122
43. Question
If \(g(x)=x^2+x-2\) and \(\frac{1}{2} g \circ f(x)=2 x^2-5 x+2\), then which is not a possible \(f(x)\) ?
Hint
(c)
\(
\begin{aligned}
& \frac{1}{2}(g \circ f)(x)=2 x^2-5 x+2 \text { or } \frac{1}{2} g[f(x)]=2 x^2-5 x+2 \\
& \therefore\left[\{f(x)\}^2+\{f(x)\}-2\right]=2\left[2 x^2-5 x+2\right] \\
& \Rightarrow f(x)^2+f(x)-\left(4 x^2-10 x+6\right)=0 \\
& \therefore f(x)=\frac{-1 \pm \sqrt{1+4\left(4 x^2-10 x+6\right)}}{2} \\
& =\frac{-1 \pm \sqrt{\left(16 x^2-40 x+25\right.}}{2}=\frac{-1 \pm(4 x-5)}{2}=2 x-3 \text { or }-2 x+2
\end{aligned}
\) -
Question 44 of 122
44. Question
If \(f: R \rightarrow R\) is an invertible function such that \(f(x)\) and \(f^{-1}(x)\) are symmetric about the line \(y=-x\), then
Hint
(a)
\(
\begin{aligned}
& \text { Since } f(x) \text { and } f^{-1}(x) \text { are symmetric about the line } y=-x \text {. } \\
& \text { If }(\alpha, \beta) \text { lies on } y=f(x) \text { then }(-\beta,-\alpha) \text { on } y=f^{-1}(x) \\
& \Rightarrow \quad(-\alpha,-\beta) \text { lies on } y=f(x) \\
& \Rightarrow \quad y=f(x) \text { is odd. }
\end{aligned}
\) -
Question 45 of 122
45. Question
Let \(f: N \rightarrow N\) defined by \(f(x)=x^2+x+1, x \in N\), then \(f\) is
Hint
(c) Let \(x, y \in N\) such that \(f(x)=f(y)\)
\(
\begin{aligned}
& \text { Then } f(x)=f(y) \\
& \Rightarrow \quad x^2+x+1=y^2+y+1 \\
& \Rightarrow \quad(x-y)(x+y+1)=0 \\
& \Rightarrow \quad x=y \text { or } x=(-y-1) \notin N
\end{aligned}
\)
\(\therefore \quad f\) is one-one.
Also, \(f(x)\) does not take all positive integral values. Hence \(f\) is into. -
Question 46 of 122
46. Question
Let \(f: X \rightarrow y f(x)=\sin x+\cos x+2 \sqrt{2}\) is invertible. Then which \(X \rightarrow Y\) is not possible?
Hint
(c)
\(
\begin{aligned}
f(x) & =\sqrt{2} \sin \left(x+\frac{\pi}{4}\right)+2 \sqrt{2} \\
f(x) & =\sqrt{2} \cos \left(x-\frac{\pi}{4}\right)+2 \sqrt{2} \\
Y & =[\sqrt{2}, 3 \sqrt{2}] \text { and } X=\left[-\frac{3 \pi}{4}, \frac{\pi}{4}\right] \text { or }\left[\frac{\pi}{4}, \frac{5 \pi}{4}\right]
\end{aligned}
\) -
Question 47 of 122
47. Question
If \(f(x)=a x^7+b x^3+c x-5, a, b, c\) are real constants and \(f(-7)=7\), then the range of \(f(7)+17 \cos x\) is
Hint
(a)
\(
\begin{aligned}
& f(7)+f(-7)=-10 \\
& \Rightarrow f(7)=-17 \\
& \Rightarrow f(7)+17 \cos x=-17+17 \cos x \text { which has the range } \\
& {[-34,0] .}
\end{aligned}
\) -
Question 48 of 122
48. Question
If \(f(x)=\frac{\sin ([x] \pi)}{x^2+x+1}\), where [.] denotes the greatest integer function, then
Hint
(c) \(f(x)=\frac{\sin [x] \pi}{x^2+x+1}\)
Let \([x]=n \in\) integer
\(
\begin{aligned}
& \Rightarrow \quad \sin [x] \pi=0 \\
& \Rightarrow \quad f(x)=0
\end{aligned}
\)
\(\Rightarrow f(x)\) is constant function. -
Question 49 of 122
49. Question
Let \(S\) be the set of all triangles and \(R^{+}\)be the set of positive real numbers. Then the function \(f: S \rightarrow R^{+}, f(\Delta)=\) area of \(\Delta\), where \(\Delta \in S\) is
Hint
(b) Two triangles may have equal areas
\(\therefore f\) is not one-one.
Since each positive real number can represent area of a triangle.
\(\therefore f\) is onto. -
Question 50 of 122
50. Question
The graph of \((y-x)\) against \((y+x)\) is shown
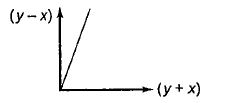
Which one of the following shows the graph of \(y\) against \(x\) ?
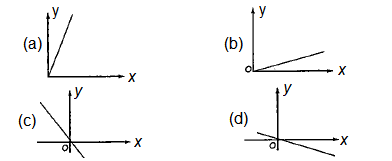
Hint
(c)
\(
\begin{aligned}
& \frac{y-x}{y+x}=k(k>1) ; \quad y-x=k(y+x) \\
& \Rightarrow \quad y(1+k)=x(1+k) \\
& \Rightarrow \quad y=\left(\frac{1+k}{1-k}\right) x, \text { where } \frac{1+k}{1-k}<-1
\end{aligned}
\) -
Question 51 of 122
51. Question
If \(g:[-2,2] \rightarrow R\) where \(f(x)=x^3+\tan x+\left[\frac{x^2+1}{P}\right]\) is a odd function, then the value of parametric \(P\) where \([\).\(] denotes\) the greatest integer function is
Hint
(c)
\(
\begin{aligned}
& g(x)=x^3+\tan x+\left[\frac{x^2+1}{P}\right] \\
& \Rightarrow g(-x)=(-x)^3+\tan (-x)+\left[\frac{(-x)^2+1}{P}\right] \\
& \Rightarrow g(-x)=-x^3-\tan x+\left[\frac{x^2+1}{P}\right] \\
& \Rightarrow g(x)+g(-x)=0
\end{aligned}
\)
because \(g(x)\) is a odd function
\(
\begin{aligned}
& \therefore\left(-x^3-\tan x+\left[\frac{x^2+1}{P}\right]\right)+\left(-x^3-\tan x\right) \\
& \left.\Rightarrow 2\left[\frac{x^2+1}{P}\right]\right)=0 \\
& \Rightarrow\left[\frac{\left(x^2+1\right)}{P}\right]=0 \Rightarrow 0 \leq \frac{x^2+1}{P}<1
\end{aligned}
\)
Now \(x \in[-2,2]\)
\(
\Rightarrow 0 \leq \frac{5}{P}<1 \Rightarrow P>5
\) -
Question 52 of 122
52. Question
If \(f\left(2 x+\frac{y}{8}, 2 x-\frac{y}{8}\right)=x y\), then \(f(m, n)+f(n, m)=0\)
Hint
(d) Let \(2 x+\frac{y}{8}=\alpha\) and \(2 x-\frac{y}{8}=\beta\), then \(x=\frac{\alpha+\beta}{4}\) and \(y=4(\alpha-\beta)\).
Given, \(f\left(2 x+\frac{y}{8}, 2 x-\frac{y}{8}\right)=x y\)
\(
\begin{aligned}
& \Rightarrow f(\alpha, \beta)=\alpha^2-\beta^2 \\
& \Rightarrow f(m, n)+f(n, m)=m^2-n^2+n^2-m^2=0 \text { for all } m, n
\end{aligned}
\) -
Question 53 of 122
53. Question
If \(f(x+y)=f(x)+f(y)-x y-1 \forall x, y \in R\) and \(f(1)=1\), then the number of solutions of \(f(n)=n, n \in N\) is
Hint
(b)
\(
\begin{aligned}
& \text { Given } f(x+y)=f(x)+f(y)-x y-1 \forall x, y \in R \\
& f(1)=1 \\
& f(2)=f(1+1)=f(1)+f(1)-1-1=0 \\
& f(3)=f(2+1)=f(2)+f(1)-2 \cdot 1-1=-2 \\
& f(n+1)=f(n)+f(1)-n-1=f(n)-n<f(n)
\end{aligned}
\)
\(
\begin{aligned}
& \text { Thus, } f(1)>f(2)>f(3)>\ldots \text { and } f(1)=1 . \\
& \therefore \quad f(1)=1 \text { and } f(n)<1, \text { for } n>1 . \\
& \text { Hence, } f(n)=n, n \in N \text { has only one solution } n=1 .
\end{aligned}
\) -
Question 54 of 122
54. Question
The range of the function \(f(x)=\frac{e^x-e^{|x|}}{e^x+e^{|x|}}\)
Hint
(c)
\(
f(x)=\frac{e^x-e^{|x|}}{e^x+e^{|x|}}=\left\{\begin{array}{cc}
0, & x \geq 0 \\
\frac{e^x-e^{-x}}{e^x+e^{-x}}, & x<0
\end{array}\right.
\)
Clearly, \(f(x)\) is identically zero if \(x \geq 0 \dots(1)\)
\(
\begin{aligned}
& \text { If } x<0, \text { let } y=f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} \Rightarrow e^{2 x}=\frac{1+y}{1-y} \\
& \because \quad x<0 \Rightarrow e^{2 x}<1 \Rightarrow 0<e^{2 x}<1 \\
& \therefore \quad 0<\frac{1+y}{1-y}<1
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \frac{1+y}{1-y}>0 \text { and } \frac{1+y}{1-y}<1 \\
& \Rightarrow(y+1)(y-1)<0 \text { and } \frac{2 y}{1-y}<0 \\
& \Rightarrow-1<y<1 \text { and } y<0 \text { or } y>1 \\
& \Rightarrow-1<y<0 \dots(2)
\end{aligned}
\)
Combining (1) and (2), we get \(-1<y \leq 0 \Rightarrow\) Range \(=(-1,0]\). -
Question 55 of 122
55. Question
If \(f: R \rightarrow R\) is a function satisfying the property \(f(2 x+3)+ f(2 x+7)=2, \forall x \in R\), then the fundamental period of \(f(x)\) is
Hint
(c)
\(
\begin{aligned}
& f(2 x+3)+f(2 x+7)=2 \dots(1) \\
& \text { Replace } x \text { by } x+2, f(2 x+7)+f(2 x+11)=2 \dots(2) \\
& \text { from }(1)-(2) \text { we get } f(2 x+3)-f(2 x+11)=0 \\
& \Rightarrow f(2 x+3)=f(2 x+11) \\
& \Rightarrow f(2 x+3)=f(2(x+4)+3) \\
& \Rightarrow \text { Period of } f(x) \text { is } 8
\end{aligned}
\) -
Question 56 of 122
56. Question
Let \(f: R \rightarrow\left[0, \frac{\pi}{2}\right)\) defined by \(f(x)=\tan ^{-1}\left(x^2+x+a\right)\), then the set of values of \(a\) for which \(f\) is onto is
Hint
(c) \(\text { Since co-domain }=\left[0, \frac{\pi}{2}\right)\)
\(\therefore\) for \(f\) to be onto, the range \(=\left[0, \frac{\pi}{2}\right)\)
This is possible only when \(x^2+x+a \geq 0 \quad \forall x \in R\)
\(
\therefore 1^2-4 a \leq 0 \Rightarrow a \geq \frac{1}{4}
\) -
Question 57 of 122
57. Question
The domain of the function \(f(x)=\frac{1}{\sqrt{\{\sin x\}+\{\sin (\pi+x)\}}}\), where \(\{\cdot\}\) denotes the fractional part, is
Hint
(d)
\(
\begin{aligned}
& f(x)=\frac{1}{\sqrt{\{\sin x\}+\{\sin (\pi+x)\}}}=\frac{1}{\sqrt{\{\sin x\}+\{-\sin x\}}} \\
& \text { Now }\{\sin x\}+\{-\sin x\}=\left\{\begin{array}{lc}
0, & \sin x \text { is an integer } \\
1, & \sin x \text { is not an integer }
\end{array}\right.
\end{aligned}
\)
For \(f(x)\) to get defined \(\{\sin x\}+\{-\sin x\} \neq 0\)
\(
\begin{aligned}
& \Rightarrow \quad \sin x \neq \text { integer } \\
& \Rightarrow \quad \sin x \neq \pm 1,0 \\
& \Rightarrow \quad x \neq \frac{n \pi}{2}, n \in I
\end{aligned}
\)
Hence, the domain is \(R-\left\{\frac{n \pi}{2} / n \in I\right\}\). -
Question 58 of 122
58. Question
\(f(x)=\frac{\cos x}{\left[\frac{2 x}{\pi}\right]+\frac{1}{2}}\), where \(x\) is not an integral multiple of \(\pi\) and [.] denotes the greatest integer function is
Hint
(a)
\(
\begin{aligned}
&f(-x)=\frac{\cos (-x)}{\left[-\frac{2 x}{\pi}\right]+\frac{1}{2}}=\frac{\cos x}{-1-\left[\frac{2 x}{\pi}\right]+\frac{1}{2}}\\
&\text { (as } x \text { is not an integral multiple of } \pi \text { ) }
\end{aligned}
\)
\(
\begin{aligned}
&\Rightarrow f(-x)=-\frac{\cos x}{\left[\frac{2 x}{\pi}\right]+\frac{1}{2}}=-f(x)\\
&\Rightarrow f(x) \text { is an odd function. }
\end{aligned}
\) -
Question 59 of 122
59. Question
Let \(f(x)=\left([a]^2-5[a]+4\right) x^3-\left(6\{a\}^2-5\{a\}+1\right) x-(\tan x) \times \operatorname{sgn} x\) be an even function for all \(x \in R\), then the sum of all possible values of ‘ \(a\) ‘ is (where \([\cdot]\) and \(\{\cdot\}\) denote greatest integer function and fractional part functions, respectively)
Hint
(d)
\(
\begin{aligned}
& f(x)=\alpha x^3-\beta x-(\tan x) \operatorname{sgn} x \\
& f(-x)=f(x) \\
& \Rightarrow-\alpha x^3+\beta x-\tan x \operatorname{sgn} x=\alpha x^3-\beta x-(\tan x)(\operatorname{sgn} x) \\
& \Rightarrow 2\left(-\alpha x^2-\beta\right) x=0 \forall x \in R \\
& \Rightarrow \alpha=0 \text { and } \beta=0 \\
& \therefore[a]^2-5[a]+4=0 \text { and } 6\{a\}^2-5\{a\}+1=0 \\
& \Rightarrow(3\{x\}-1)(2\{x\}-1)=0 \\
& \therefore a=1+\frac{1}{3}, 1+\frac{1}{2}, 4+\frac{1}{3}, 4+\frac{1}{2}
\end{aligned}
\)
\(
\text { Sum of values of } a=\frac{35}{3}
\) -
Question 60 of 122
60. Question
Let \(f:[-10,10] \rightarrow R\), where \(f(x)=\sin x+\left[x^2 / a\right]\) be an odd function. Then the set of values of parameter \(a\) is/are
Hint
(d) Since \(f(x)\) is an odd function, \(\left[\frac{x^2}{a}\right]=0\) for all \(x \in [-10,10]\)
\(\Rightarrow 0 \leq \frac{x^2}{a}<1\) for all \(x \in[-10,10] \Rightarrow a>100\). -
Question 61 of 122
61. Question
The function \(f\) satisfies the functional equation \(3 f(x) +2 f\left(\frac{x+59}{x-1}\right)=10 x+30\) for all real \(x \neq 1\). The value of \(f(7)\) is
Hint
(b)
\(
\begin{aligned}
& 3 f(x)+2 f\left(\frac{x+59}{x-1}\right)=10 x+30 \\
& \text { For } x=7,3 f(7)+2 f(11)=70+30=100 \text {. } \\
& \text { For } x=11,3 f(11)+2 f(7)=140 \text {. }
\end{aligned}
\)
\(
\frac{f(7)}{-20}=\frac{f(11)}{-220}=\frac{-1}{9-4} \Rightarrow f(7)=4
\) -
Question 62 of 122
62. Question
The period of the function \(f(x)=[6 x+7]+\cos \pi x-6 x\), where [.] denotes the greatest integer function, is
Hint
(c)
\(
\begin{aligned}
f(x) & =[6 x+7]+\cos \pi x-6 x \\
& =[6 x]+7+\cos \pi x-6 x \\
& =7+\cos \pi x-\{6 x\}
\end{aligned}
\)
\(\{6 x\}\) has the period \(1 / 6\) and \(\cos \pi x\) has the period 2, then the period of \(f(x)=\mathrm{LCM}\) of 2 and \(1 / 6\) which is 2. Hence, the period is 2. -
Question 63 of 122
63. Question
If the graph of the function \(f(x)=\frac{a^x-1}{x^n\left(a^x+1\right)}\) is symmetrical about \(y\)-axis, then \(n\) equals
Hint
(d) \(f(x)=\frac{a^x-1}{x^n\left(a^x+1\right)}\)
\(f(x)\) is symmetrical about \(y\)-axis
\(
\begin{aligned}
& \Rightarrow f(x)=f(-x) \\
& \Rightarrow \frac{a^x-1}{x^n\left(a^x+1\right)}=\frac{a^{-x}-1}{(-x)^n\left(a^{-x}+1\right)} \\
& \Rightarrow \frac{a^x-1}{x^n\left(a^x+1\right)}=\frac{1-a^x}{(-x)^n\left(1+a^x\right)} \Rightarrow x^n=-(-x)^n
\end{aligned}
\)
\(\Rightarrow\) the value of \(n\) which satisfy this relation is \(-\frac{1}{3}\). -
Question 64 of 122
64. Question
If \(f(x)\) is an even function and satisfies the relation \(x^2 f(x) -2 f\left(\frac{1}{x}\right)=g(x)\) where \(g(x)\) is an odd function, then \(f(5)\) equals
Hint
(a)
\(
\begin{aligned}
& x^2 f(x)-2 f\left(\frac{1}{x}\right)=g(x) \text { and } 2 f\left(\frac{1}{x}\right)-4 x^2 f(x)=2 x^2 g\left(\frac{1}{x}\right) \\
& \text { (Replacing } x \text { by } \frac{1}{x} \text { ) } \\
& \Rightarrow-3 x^2 f(x)=g(x)+2 x^2 g\left(\frac{1}{x}\right) \\
& \text { (Eliminating } f\left(\frac{1}{x}\right) \text { ) } \\
& \Rightarrow f(x)=-\left(\frac{g(x)+2 x^2 g\left(\frac{1}{x}\right)}{3 x^2}\right)
\end{aligned}
\)
\(\because g(x)\) and \(x^2\) are odd and even functions, respectively.
So, \(f(x)\) is an odd function. But \(f(x)\) is given even
\(\Rightarrow f(x)=0 \forall x\). Hence, \(f(5)=0\). -
Question 65 of 122
65. Question
If \(f(x+y)=f(x) \cdot f(y)\) for all real \(x, y\) and \(f(0) \neq 0\), then the function \(g(x)=\frac{f(x)}{1+\{f(x)\}^2}\) is
Hint
(a) Given \(f(x+y)=f(x) f(y)\). Put \(x=y=0\), then \(f(0)=1\).
Put \(y=-x\), then \(f(0)=f(x) f(-x) \Rightarrow f(-x)=\frac{1}{f(x)}\)
Now, \(g(x)=\frac{f(x)}{1+\{f(x)\}^2}\)
\(
\begin{aligned}
g(-x) & =\frac{f(-x)}{1+\{f(-x)\}^2}=\frac{\frac{1}{f(x)}}{1+\frac{1}{\{f(x)\}^2}} \\
& =\frac{f(x)}{1+\{f(x)\}^2}=g(x)
\end{aligned}
\) -
Question 66 of 122
66. Question
Possible values of \(a\) such that the equation \(x^2+2 a x+a= \sqrt{a^2+x-\frac{1}{16}}-\frac{1}{16}, x \geq-a\), has two distinct real roots are given by
Hint
(d) The equation is \(x^2+2 a x+\frac{1}{16}=-a+\sqrt{a^2+x-\frac{1}{16}}\), \(\Rightarrow f(x)=f^{-1}(x)\) which has the solution if \(x^2+2 a x+\frac{1}{16}=x\)
\(
\Rightarrow \quad x^2+(2 a-1) x+\frac{1}{16}=0
\)
\(
\begin{aligned}
& \text { For real and distinct roots }(2 a-1)^2-4 \frac{1}{16} \geq 0 \\
& \Rightarrow 2 a-1 \leq \frac{-1}{2} \text { or } 2 a-1 \geq \frac{1}{2} \Rightarrow a \leq \frac{1}{4} \text { or } a \geq \frac{3}{4} .
\end{aligned}
\) -
Question 67 of 122
67. Question
Let \(g(x)=f(x)-1\). If \(f(x)+f(1-x)=2 \forall x \in R\), then \(g(x)\) is symmetrical about
Hint
(d)
\(
\begin{aligned}
&\begin{aligned}
& f(x)-1+f(1-x)-1=0 ; \text { so } g(x)+g(1-x)=0 \\
& \text { Replacing } x \text { by } x+\frac{1}{2}, \text { we get } g\left(\frac{1}{2}+x\right)+g\left(\frac{1}{2}-x\right)=0 .
\end{aligned}\\
&\text { So, it is symmetrical about }\left(\frac{1}{2}, 0\right) \text {. }
\end{aligned}
\) -
Question 68 of 122
68. Question
Domain \((D)\) and range \((R)\) of \(f(x)=\sin ^{-1}\left(\cos ^{-1}[x]\right)\) where [.] denotes the greatest integer function is
Hint
(a) When \([x]=0\) we have \(\sin ^{-1}\left(\cos ^{-1} 0\right)=\sin ^{-1}(\pi / 2)\), not defined.
When \([x]=-1\) we have \(\sin ^{-1}\left(\cos ^{-1}-1\right)=\sin ^{-1}(\pi)\), not defined.
When \([x]=1\) we have \(\sin ^{-1}\left(\cos ^{-1} 1\right)=\sin ^{-1}(0)=0\).
Hence, \(x \in[1,2)\) and the range of function is \(\{0\}\). -
Question 69 of 122
69. Question
If \(f(x+1)+f(x-1)=2 f(x)\) and \(f(0)=0\), then \(f(n)\), \(n \in N\), is
Hint
(a)
\(
\begin{aligned}
& \text { Putting } x=1, f(2)+f(0)=2 f(1) \Rightarrow f(2)=2 f(1) \\
& \text { Putting } x=2, f(3)+f(1)=2 f(2) \\
& \Rightarrow \quad f(3)=2 \times 2 f(1)-f(1)=3 f(1), \text { and so on. } \\
& \therefore \quad f(n)=n f(1), \text { for } n=1,2, \ldots, n \\
& \quad f(n+1)+f(n-1)=2 f(n) \\
& \Rightarrow \quad f(n+1)+(n-1) f(1)=2 n f(1) \\
& \Rightarrow \quad f(n+1)=(n+1) f(1)
\end{aligned}
\) -
Question 70 of 122
70. Question
The range of the function \(f\) defined by \(f(x)=\left[\frac{1}{\sin \{x\}}\right]\) (where [.] and \(\{\).\(\} \text { respectively denote the greatest integer }\text { and the fractional part functions) is }\)
Hint
(d) \(\because\{x\} \in[0,1)\)
\(\sin \{x\} \in(0, \sin 1)\) as \(f(x)\) is defined if \(\sin \{x\} \neq 0\)
\(
\Rightarrow \frac{1}{\sin \{x\}} \in\left(\frac{1}{\sin 1}, \infty\right) \Rightarrow\left[\frac{1}{\sin \{x\}}\right] \in\{1,2,3, \ldots\}
\)
Note that \(1<\frac{\pi}{3} \Rightarrow \sin 1<\sin \frac{\pi}{3}=0.866 \Rightarrow \frac{1}{\sin 1}>1.155\). -
Question 71 of 122
71. Question
If \(\left[\cos ^{-1} x\right]+\left[\cot ^{-1} x\right]=0\), where \([\).\(] \text { denotes the greatest integer function, then the complete set of values of }\) \(x\) is
Hint
(c)
\(
\begin{aligned}
& \text { We have }\left[\cos ^{-1} x\right] \geq 0 \forall x \in[-1,1] \\
& \text { and }\left[\cot ^{-1} x\right] \geq 0 \forall x \in R \\
& \text { Hence, }\left[\cot ^{-1} x\right]+\left[\cot ^{-1} x\right]=0 \\
& \Rightarrow \quad\left[\cot ^{-1} x\right]=\left[\cot ^{-1} x\right]=0 \\
& \text { If }\left[\cos ^{-1} x\right]=0 \Rightarrow x \in(\cos 1,1]
\end{aligned}
\)
\(
\begin{aligned}
& \text { If }\left[\cot ^{-1} x\right]=0 \Rightarrow x \in(\cot 1, \infty) \\
& \Rightarrow x \in(\cot 1,1]
\end{aligned}
\) -
Question 72 of 122
72. Question
If \(f(x)\) and \(g(x)\) are periodic functions with period 7 and 11, respectively. Then the period of \(F(x)=f(x) g\left(\frac{x}{5}\right)-g(x) f\left(\frac{x}{3}\right)\) is
Hint
(d) The period of \(f(x)\) is \(7 \Rightarrow\) The period of \(f\left(\frac{x}{3}\right)\) is \(\frac{7}{1 / 3}=21\)
The period of \(g(x)\) is \(11 \Rightarrow\) The period of \(g\left(\frac{x}{5}\right)\) is \(\frac{11}{1 / 5}=55\)
Hence, \(T_1=\) period of \(f(x) g\left(\frac{x}{5}\right)=7 \times 55=385\) and
\(
\begin{aligned}
& T_2=\text { period of } g(x) f\left(\frac{x}{3}\right)=11 \times 21=231 \\
& \begin{aligned}
\therefore \text { Period of } F(x) & =\operatorname{LCM}\left\{T_1, T_2\right\} \\
& =\operatorname{LCM}\{385,231\} \\
& =7 \times 11 \times 3 \times 5 \\
& =1155
\end{aligned}
\end{aligned}
\) -
Question 73 of 122
73. Question
The period of the function
\(
f(x)=c^{\sin ^2 x+\sin ^2\left(x+\frac{\pi}{3}\right)+\cos x \cos \left(x+\frac{\pi}{3}\right)}
\)
is (where \(c\) is constant)Hint
(d)
\(
\begin{aligned}
& \sin ^2 x+\sin ^2\left(x+\frac{\pi}{3}\right)+\cos x \cos \left(x+\frac{\pi}{3}\right) \\
& =\sin ^2 x+\left(\frac{\sin x}{2}+\frac{\sqrt{3} \cos x}{2}\right)^2+\cos x\left(\frac{\cos x}{2}-\frac{\sqrt{3} \sin x}{2}\right) \\
& =\sin ^2 x+\frac{\sin ^2 x}{4}+\frac{3 \cos ^2 x}{4}+\frac{\cos ^2 x}{2} \\
& =\frac{5 \sin ^2 x}{4}+\frac{5 \cos ^2 x}{4}=5 / 4
\end{aligned}
\)
Hence, \(f(x)=c^{5 / 4}=\) constant, which is periodic whose period cannot be determined. -
Question 74 of 122
74. Question
If \(f(x+f(y))=f(x)+y \forall x, y \in R\) and \(f(0)=1\), then the value of \(f(7)\) is
Hint
(a)
\(
\begin{aligned}
&\begin{aligned}
& f(x+f(y))=f(x)+y, f(0)=1 \\
& \text { Putting } y=0 \text {, we get } f(x+f(0))=f(x)+0 \\
& \Rightarrow f(x+1)=f(x) \forall x \in R
\end{aligned}\\
&\text { Thus, } f(x) \text { is the period with } 1 \text { as one of its period. }\\
&\Rightarrow \quad f(7)=f(6)=f(5)=\cdots=f(1)=(0)=1
\end{aligned}
\) -
Question 75 of 122
75. Question
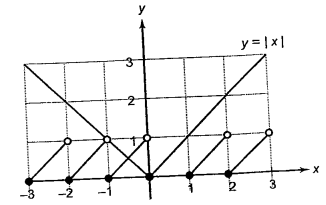
Let \(f(x)=\sqrt{|x|-\{x\}}\) (where \(\{\).\(\} \text { denotes the fractional part of }\) \(x\) ) and \(X, Y\) are its domain and range, respectively, then
Hint
(c)
\(
\begin{aligned}
&f(x)=\sqrt{|x|-\{x\}} \text { is defined if }|x| \geq\{x\}\\
&\Rightarrow \quad x \in\left(-\infty-\frac{1}{2}\right] \cup[0, \infty) \Rightarrow Y \in[0, \infty)
\end{aligned}
\)
-
Question 76 of 122
76. Question
Let \(f\) be a function satisfying of \(x\) then \(f(x y)=\frac{f(x)}{y}\) for all positive real numbers \(x\) and \(y\) if \(f(30)=20\), then the value of \(f(40)\) is
Hint
(a)
\(
\begin{aligned}
f(x y) & =\frac{f(x)}{y} \\
f(y) & =\frac{f(1)}{y} \quad \text { (putting } x=1 \text { ) }
\end{aligned}
\)
\(
\begin{aligned}
&\Rightarrow \quad f(30)=\frac{f(1)}{30} \text { or } f(1)=30 \times f(30)=30 \times 20=600 .\\
&\text { Now, } f(40)=\frac{f(1)}{40}=\frac{600}{40}=15 \text {. }
\end{aligned}
\) -
Question 77 of 122
77. Question
The domain of the function \(f(x)=\sqrt{\ln _{(|x|-1)}\left(x^2+4 x+4\right)}\) is
Hint
(c) Case I:
\(
\begin{aligned}
& 0<|x|-1<1 \Rightarrow 1<|x|<2, \text { then } \\
& x^2+4 x+4 \leq 1 \\
& \Rightarrow x^2+4 x+3 \leq 0 \\
& \Rightarrow-3 \leq x \leq-1 \dots(1)
\end{aligned}
\)
So \(x \in(-2,-1)\)
Case II:
\(
\begin{aligned}
& |x|-1>1 \Rightarrow|x|>2, \text { then } x^2+4 x+4 \geq 1 \\
& \Rightarrow x^2+4 x+3 \geq 0 \\
& \Rightarrow x \geq-1 \text { or } x \leq-3
\end{aligned}
\)
So, \(x \in(-\infty,-3] \cup(2, \infty) \dots(2)\)
\(
\text { From (1) and (2), } x \in(-\infty,-3] \cup(-2,-1) \cup(2, \infty) \text {. }
\) -
Question 78 of 122
78. Question
The range of \(f(x)=[1+\sin x]+\left[2+\sin \frac{x}{2}\right]+\left[3+\sin \frac{x}{3}\right]+ \cdots+\left[n+\sin \frac{x}{n}\right], \forall x \in[0, \pi]\), where [.] denotes the greatest integer function, is
Hint
(d) \(f(x)=\frac{n(n+1)}{2}+[\sin x]+\left[\sin \frac{x}{2}\right]+\cdots+\left[\sin \frac{x}{n}\right]\)
Thus, the range of \(f(x)=\left\{\frac{n(n+1)}{2}, \frac{n(n+1)}{2}+1\right\}\) as \(x \in[0, \pi]\). -
Question 79 of 122
79. Question
The total number of solutions of \([x]^2=x + 2\{x\}\), where [.] and {.} denote the greatest integer function and fractional part, respectively, is equal to
Hint
(b)
\(
\begin{aligned}
& {[x]^2=x+2\{x\} } \\
\Rightarrow & {[x]^2=[x]+3\{x\} } \\
\Rightarrow & \{x\}=\frac{[x]^2-[x]}{3} \\
\Rightarrow & 0 \leq \frac{[x]^2-[x]}{3}<1 \\
\Rightarrow & 0 \leq[x]^2-[x]<3
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad[x] \in\left(\frac{1-\sqrt{3}}{2}, 0\right] \cup\left[1, \frac{1+\sqrt{3}}{2}\right) \\
& \Rightarrow \quad[x]=-1,0,1,2 \\
& \Rightarrow \quad\{x\}=\frac{2}{3}, 0,0, \frac{2}{3}, \text { (respectively) } \\
& \Rightarrow \quad x=-\frac{1}{3}, 0,1, \frac{8}{3}
\end{aligned}
\) -
Question 80 of 122
80. Question
The domain of \(f(x)=\sqrt{2\{x\}^2-3\{x\}+1}\), where \(\{.\}\) denotes the fractional part in \([-1,1]\), is
Hint
(b) We must have
\(
2\{x\}^2-3\{x\}+1 \geq 0 \Rightarrow\{x\} \geq 1 \text { or }\{x\} \leq 1 / 2
\)
Thus, we have \(0 \leq\{x\} \leq 1 / 2 \Rightarrow x \in\left[n, n+\frac{1}{2}\right], n \in I\). -
Question 81 of 122
81. Question
The range of \(\sin ^{-1}\left[x^2+\frac{1}{2}\right]+\cos ^{-1}\left[x^2-\frac{1}{2}\right]\), where [.] denotes the greatest integer function, is
Hint
(b)
\(
\begin{aligned}
&\left[x^2+\frac{1}{2}\right]=\left[x^2-\frac{1}{2}+1\right]=1+\left[x^2-\frac{1}{2}\right] .\\
&\text { Thus, from domain point of view, }
\end{aligned}
\)
\(
\begin{aligned}
& {\left[x^2-\frac{1}{2}\right]=0,-1 \Rightarrow\left[x^2+\frac{1}{2}\right]=1,0} \\
& \Rightarrow f(x)=\sin ^{-1}(1)+\cos ^{-1}(0) \text { or } \sin ^{-1}(0)+\cos ^{-1}(-1) \\
& \Rightarrow f(x)=\{\pi\}
\end{aligned}
\) -
Question 82 of 122
82. Question
If the period of \(\frac{\cos (\sin (n x))}{\tan \left(\frac{x}{n}\right)}, n \in N\) is \(6 \pi\) then \(n=\)
Hint
(c) The period of \(\cos (\sin n x)\) is \(\frac{\pi}{n}\) and the period of \(\tan \left(\frac{x}{n}\right)\) is \(\pi n\).
Thus, \(6 \pi=\operatorname{LCM}\left(\frac{\pi}{n}, \pi n\right)\)
\(
\Rightarrow 6 \pi=\frac{\pi}{n} \lambda_1 \Rightarrow n=\frac{\lambda_1}{6}, \text { and } 6 \pi=\lambda_2 \pi n \Rightarrow n=\frac{6}{\lambda_2}, \lambda_1,
\)
\(\lambda_2 \in I^{+}\)
\(
\begin{aligned}
&\text { From } n=\frac{6}{\lambda_2} \Rightarrow n=6,3,2,1 .\\
&\text { Clearly, for } n=6 \text {, we get the period of } f(x) \text { to be } 6 \pi \text {. }
\end{aligned}
\) -
Question 83 of 122
83. Question
The domain of \(f(x)=\ln \left(a x^3+(a+b) x^2+(b+c) x+c\right)\), where \(a>0, b^2-4 a c=0\), is (where [.] represents greatest integer function).
Hint
(a)
\(
\begin{aligned}
&\text { We must have } a x^3+(a+b) x^2+(b+c) x+c>0\\
&\begin{aligned}
& \Rightarrow a x^2(x+1)+b x(x+1)+c(x+1)>0 \\
& \Rightarrow(x+1)\left(a x^2+b x+c\right)>0 \\
& \Rightarrow a(x+1)\left(x+\frac{b}{2 a}\right)^2>0 \text { as } b^2=4 a c \\
& \Rightarrow x>-1 \text { and } \neq-\frac{b}{2 a}
\end{aligned}
\end{aligned}
\) -
Question 84 of 122
84. Question
The period of \(f(x)=[x]+[2 x]+[3 x]+[4 x]+\cdots[n x]- \frac{n(n+1)}{2} x\), where \(n \in N\), is (where \([\cdot]\) represents greatest integer function)
Hint
(b)
\(
\begin{aligned}
&\begin{aligned}
f(x) & =[x]+[2 x]+[3 x]+\cdots+[n x]-(x+2 x+3 x+\cdots+n x) \\
& =-(\{x\}+\{2 x\}+\{3 x\}+\cdots+\{n x\})
\end{aligned}\\
&\text { The period of } f(x)=\operatorname{LCM}\left(1, \frac{1}{2}, \frac{1}{3}, \ldots, \frac{1}{n}\right)=1 \text {. }
\end{aligned}
\) -
Question 85 of 122
85. Question
If \(f\left(x+\frac{1}{2}\right)+f\left(x-\frac{1}{2}\right)=f(x)\) for all \(x \in R\), then the period of \(f(x)\) is
Hint
(c)
\(
\begin{aligned}
&\begin{aligned}
& f\left(x+\frac{1}{2}\right)+f\left(x-\frac{1}{2}\right)=f(x) \\
& \Rightarrow f(x+1)+f(x)=f\left(x+\frac{1}{2}\right) \\
& \Rightarrow f(x+1)+f\left(x-\frac{1}{2}\right)=0 \\
& \Rightarrow f\left(x+\frac{3}{2}\right)=-f(x) \\
& \Rightarrow f(x+3)=-f\left(x+\frac{3}{2}\right)=f(x)
\end{aligned}\\
&\therefore f(x) \text { is periodic with period } 3 .
\end{aligned}
\) -
Question 86 of 122
86. Question
If \(f: R^{+} \rightarrow R, f(x)+3 x f\left(\frac{1}{x}\right)=2(x+1)\), then \(f(99)\) is equal to
Hint
(c) \(f(x)+3 x f\left(\frac{1}{x}\right)=2(x+1) \dots(1)\)
Replacing \(x\) by \(\frac{1}{x}\), we get
\(
\begin{aligned}
& f\left(\frac{1}{x}\right)+3 \frac{1}{x} f(x)=2\left(\frac{1}{x}+1\right) \\
& \Rightarrow x f\left(\frac{1}{x}\right)+3 f(x)=2(x+1) \dots(2)
\end{aligned}
\)
From (1) and (2), we have \(f(x)=\frac{x+1}{2} \Rightarrow f(99)=50\) -
Question 87 of 122
87. Question
If \(f: X \rightarrow Y\), where \(X\) and \(Y\) are sets containing natural numbers, \(f(x)=\frac{x+5}{x+2}\) then the number of elements in the domain and range of \(f(x)\) are respectively
Hint
(a) Let \(y=\frac{x+5}{x+2}=1+\frac{3}{x+2} \Rightarrow x=1\)
Also, \(y-1=\frac{3}{x+2} \Rightarrow x+2=\frac{3}{y-1}\)
\(
\Rightarrow \quad x=-2+\frac{3}{y-1}
\)
\(\Rightarrow y=2\) only as \(x\) and \(y\) are natural numbers. -
Question 88 of 122
88. Question
If \(f(x)=\left\{\begin{array}{ll}x^2 & \text { for } x \geq 0 \\ x & \text { for } x<0\end{array}\right.\) then \(f \circ f(x)\) is given by
Hint
(d)
\(
f(f(x))= \begin{cases}(f(x))^2, & \text { for } f(x) \geq 0 \\ f(x), & \text { for } f(x)<0\end{cases}
\)
\(
=\left\{\begin{array}{l}
\left(x^2\right)^2, x^2 \geq 0, x \geq 0 \\
x^2, x \geq 0, x<0 \\
x^2, x^2<0, x \geq 0 \\
x, x<0, x<0
\end{array}\right.
\)
\(
=\left\{\begin{array}{l}
x^4, x \geq 0 \\
x, x<0
\end{array}\right.
\) -
Question 89 of 122
89. Question
If the graph of \(y=f(x)\) is symmetrical about lines \(x=1\) and \(x=2\), then which of the following is true?
Hint
(c) From the given data
\(
\begin{aligned}
& f(1-x)=f(1+x) \dots(1) \\
& \text { and } f(2-x)=f(2+x) \dots(2)
\end{aligned}
\)
In (2) replacing \(x\) by \(1+x\), we have
\(
\begin{aligned}
& & f(1-x) & =f(3+x) \\
\Rightarrow & & f(1+x) & =f(3+x) [\text { from (1) }]\\
\Rightarrow & & f(x) & =f(2+x)
\end{aligned}
\) -
Question 90 of 122
90. Question
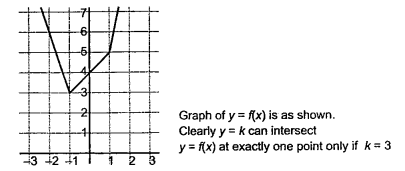
Let \(f(x)=x+2|x+1|+2|x-1|\). If \(f(x)={k}\) has exactly one real solution, then the value of \(k\) is
Hint
(a)
\(
\begin{aligned}
& \text { Let } f(x)=x+2|x+1|+2|x-1| \\
& \Rightarrow f(x)= \begin{cases}x-2(x+1)-2(x-1), & x<-1 \\
x+2(x+1)-2(x-1), & -1 \leq x \leq 1 \\
x+2(x+1)+2(x-1), & x>1\end{cases} \\
& \text { or } f(x)= \begin{cases}-3 x, & x<-1 \\
x+4, & -1 \leq x \leq 1 \\
5 x, & x>1\end{cases}
\end{aligned}
\)
-
Question 91 of 122
91. Question
The domain of \(f(x)=\sin ^{-1}\left[2 x^2-3\right]\), where [.] denotes the greatest integer function, is
Hint
(d)
\(
\begin{aligned}
&\text { We must have }-1 \leq\left[2 x^2-3\right] \leq 1\\
&\begin{aligned}
& \Rightarrow \quad-1 \leq 2 x^2-3<2 \Rightarrow 1 \leq x^2<\frac{5}{2} \\
& \Rightarrow \quad x \in\left(-\sqrt{\frac{5}{2}},-1\right] \cup\left[1, \sqrt{\frac{5}{2}}\right)^2
\end{aligned}
\end{aligned}
\) -
Question 92 of 122
92. Question
The range of \(f(x)=\cos ^{-1}\left(\frac{1+x^2}{2 x}\right)+\sqrt{2-x^2}\) is
Hint
(c)
\(
\cos ^{-1}\left(\frac{1+x^2}{2 x}\right) \text { is defined if }\left|\frac{1+x^2}{2 x}\right| \leq 1 \text { and } x \neq 0
\)
\(
\begin{aligned}
& \Rightarrow \quad 1+x^2-2|x| \leq 0 \\
& \Rightarrow \quad(|x|-1)^2 \leq 0 \\
& \Rightarrow \quad x=1,-1
\end{aligned}
\)
Thus, the domain of \(f(x)\) is \(\{1,-1\}\). Hence, the range is \(\{1,1+\pi\}\). -
Question 93 of 122
93. Question
If \(f(x)=\left\{\begin{array}{l}x, x \text { is rational } \\ 1-x, x \text { is irrational }\end{array}\right.\) then \(f(f(x))\) is
Hint
(a)
\(
\begin{aligned}
& f(f(x))=\left\{\begin{array}{cc}
f(x), & f(x) \text { is rational } \\
1-f(x), & f(x) \text { is irrational }
\end{array}\right. \\
& f(f(x))=\left\{\begin{array}{cc}
x, & x \text { is rational } \\
1-(1-x)=x, & x \text { is irrational }
\end{array}\right.
\end{aligned}
\) -
Question 94 of 122
94. Question
The range of \(f(x)=[|\sin x|+|\cos x|]\), where [.] denotes the greatest integer function, is
Hint
(c)
\(
\begin{aligned}
& y=|\sin x|+|\cos x| \\
& \Rightarrow y^2=1+|\sin 2 x| \\
& \Rightarrow 1 \leq y^2 \leq 2 \\
& \Rightarrow y \in[1, \sqrt{2}] \\
& \Rightarrow f(x)=1 \forall x \in R
\end{aligned}
\) -
Question 95 of 122
95. Question
If \(f(x)=\log _e\left(\frac{x^2+e}{x^2+1}\right)\), then the range of \(f(x)\) is
Hint
(d) \(f(x)=\ln \left(\frac{x^2+e}{x^2+1}\right)=\ln \left(\frac{x^2+1+e-1}{x^2+1}\right)=\ln \left(1+\frac{e-1}{x^2+1}\right)\)
Now, \(1 \leq x^2+1<\infty\)
\(
\begin{aligned}
& \Rightarrow 0<\frac{1}{x^2+1} \leq 1 \Rightarrow 0<\frac{e-1}{x^2+1} \leq e-1 \\
& \Rightarrow 1<1+\frac{e-1}{x^2+1} \leq e \Rightarrow 0<\ln \left(1+\frac{e-1}{x^2+1}\right) \leq 1
\end{aligned}
\)
Hence, the range is \((0,1]\). -
Question 96 of 122
96. Question
The domain of the function \(f(x)=\frac{1}{\sqrt{4 x-\left|x^2-10 x+9\right|}}\) is
Hint
(d)
\(
\begin{aligned}
&f(x)=\frac{1}{\sqrt{4 x-\left|x^2-10 x+9\right|}}\\
&\text { For } f(x) \text { to be defined }\left|x^2-10 x+9\right|<4 x\\
&\begin{aligned}
& \Rightarrow \quad x^2-10 x+9<4 x \text { and } x^2-10 x+9>-4 x \\
& \Rightarrow \quad x^2-14 x+9<0 \text { and } x^2-6 x+9>0 \\
& \Rightarrow \quad x \in(7-\sqrt{40}, 7+\sqrt{40}) \text { and } x \in R-\{-3\} \\
& \Rightarrow \quad x \in(7-\sqrt{40},-3) \cup(-3,7+\sqrt{40})
\end{aligned}
\end{aligned}
\) -
Question 97 of 122
97. Question
If the function \(f:[1, \infty) \rightarrow[1, \infty)\) is defined by \(f(x)=2^{x(x-1)}\), then \(f^{-1}(x)\) is
Hint
(b)
\(
\begin{aligned}
&\text { Given } y=2^{x(x-1)}\\
&\begin{aligned}
& \Rightarrow x(x-1)=\log _2 y \\
& \Rightarrow x^2-x-\log _2 y=0 \\
& \Rightarrow x=\frac{1 \pm \sqrt{1+4 \log _2 y}}{2}
\end{aligned}\\
&\text { Only } x=\frac{1+\sqrt{1+4 \log _2 y}}{2} \text { lies in the domain. }\\
&\Rightarrow f^{-1}(x)=\frac{1}{2}\left[1+\sqrt{1+4 \log _2 x}\right]
\end{aligned}
\) -
Question 98 of 122
98. Question
The number of roots of the equation \(x \sin x=1\), \(x \in[-2 \pi, 0) \cup(0,2 \pi]\), is
Hint
(c)
\(
\begin{aligned}
& x \sin x=1 \dots(1) \\
& \Rightarrow \quad y=\sin x=\frac{1}{x}
\end{aligned}
\)
Root of equation (1) will be given by the point(s) of intersection of the graphs \(y=\sin x\) and \(y=\frac{1}{x}\). Graphically, it is clear that we get four roots.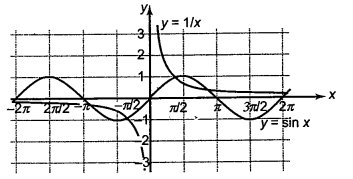
-
Question 99 of 122
99. Question
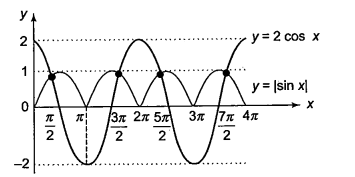
The number of solutions of \(2 \cos x=|\sin x|, 0 \leq x \leq 4 \pi\), is
Hint
(c) See the graph of \(y=2 \cos x\) and \(y=|\sin x|\). Their points of intersection represent the solution of the given equation.
-
Question 100 of 122
100. Question
If \(a f(x+1)+b f\left(\frac{1}{x+1}\right)=x, x \neq-1, a \neq b\), then \(f(2)\) is equal to
Hint
(a)
\(
\begin{aligned}
&a f(x+1)+b f\left(\frac{1}{x+1}\right)=(x+1)-1 \dots(1)\\
&\text { Replacing } x+1 \text { by } \frac{1}{x+1} \text {, we get }\\
&\therefore a f\left(\frac{1}{x+1}\right)+b f(x+1)=\frac{1}{x+1}-1 \dots(2)
\end{aligned}
\)
\(
\begin{aligned}
& \text { (1) } \times a-(2) \times b \Rightarrow\left(a^2-b^2\right) f(x+1)=a(x+1) \\
& -a-\frac{b}{x+1}+b \\
& \text { Putting } x=1,\left(a^2-b^2\right) f(2)=2 a-a-\frac{b}{2}+b=a+\frac{b}{2} \\
& \qquad=\frac{2 a+b}{2}
\end{aligned}
\) -
Question 101 of 122
101. Question
The number of solutions of \(\tan x-m x=0, m>1\) in \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) is
Hint
(c)
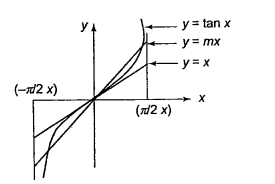
In \(\left(-\frac{\pi}{2}, 0\right)\), the graph of \(y=\tan x\) lies below the line \(y=x\) which is the tangent at \(x=0\) and in \(\left(0, \frac{\pi}{2}\right)\) it lies above the lies \(y=x\).
For \(m>1\), the line \(y=m x\) lies below \(y=x\) in \(\left(-\frac{\pi}{2}, 0\right)\) and above \(y=x\) in \(\left(0, \frac{\pi}{2}\right)\). Thus graphs of \(y=\tan x\) and \(y=m x, m>1\), meet at three points including \(x=0\) in \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) independent of \(m\). -
Question 102 of 122
102. Question
The range of \(f(x)=[\sin x+[\cos x+[\tan x+[\sec x]]]], x \in (0, \pi / 4)\), where [.] denotes the greatest integer function \(\leq x\), is
Hint
(c)
\(
\text { Given } \begin{aligned}
f(x) & =[\sin x+[\cos x+[\tan x+[\sec x]]]] \\
& =[\sin +p], \text { where } p=[\cos x+[\tan x+[\sec x]]] \\
& =[\sin x]+p,(\operatorname{as} p \text { is an integer }) \\
& =[\sin x]+[\cos x+[\tan x+[\sec x]]] \\
& =[\sin x]+[\cos x]+[\tan x]+[\sec x]
\end{aligned}
\)
\(
\begin{aligned}
&\text { Now, for } x \in(0, \pi / 4), \sin x \in\left(0, \frac{1}{\sqrt{2}}\right), \cos x \in\left(\frac{1}{\sqrt{2}}, 1\right) \text {, }\\
&\begin{aligned}
& \tan x \in(0,1), \sec x \in(1, \sqrt{2}) \\
& \Rightarrow \quad[\sin x]=0,[\cos x]=0,[\tan x]=0 \text { and }[\sec x]=1 \\
& \Rightarrow \quad \text { The range of } f(x) \text { is } 1 .
\end{aligned}
\end{aligned}
\) -
Question 103 of 122
103. Question
If \(f(3 x+2)+f(3 x+29)=0~ \forall ~x \in R\), then the period of \(f(x)\) is
Hint
(d)
\(
f(3 x+2)+f(3 x+29)=0 \dots(1)
\)
Replacing \(x\) by \(x+9\), we get
\(
\begin{aligned}
& f(3(x+9)+2)+f(3(x+9)+29)=0 \\
& \Rightarrow f(3 x+29)+f(3 x+56)=0 \dots(2)
\end{aligned}
\)
From (1) and (2), we get
\(
\begin{aligned}
& f(3 x+2)=f(3 x+56) \\
& \Rightarrow \quad f(3 x+2)=f(3(x+18)+2)
\end{aligned}
\)
\(\Rightarrow f(x)\) is periodic with period 54. -
Question 104 of 122
104. Question
If \(f\) and \(g\) are one-one function, then
Hint
(c)
(a) \(f(x)=\sin x[latex] and [latex]g(x)=\cos x, x \in[0, \pi / 2]\)
Here, both \(f(x)\) and \(g(x)\) are one-one functions, but \(h(x)=f(x)+g(x)=\sin x+\cos x\) is many-one as \(h(0)=h(\pi / 2)=1\).
(b) \(h(x)=f(x) g(x)=\sin x \cos x=\frac{\sin 2 x}{2}\) is many-one, as \(h(0)=h(\pi / 2)=0\).
(c) It is a fundamental property. -
Question 105 of 122
105. Question
The domain of \(f(x)\) is \((0,1)\), then, domain of \(f\left(e^x\right)+f(\ln |x|)\) is
Hint
(c)
\(
\begin{aligned}
& f(x) \text { is definea for } x \in(0,1) \\
& \Rightarrow \quad f\left(e^x\right)+f(\ln |x|) \text { is defined for, } \\
& \quad 0<e^x<1 \text { and } 0<\ln |x|<1 \\
& \Rightarrow \quad-\infty<x<0 \text { and } 1<|x|<e \\
& \Rightarrow \quad x \in(-\infty, 0) \text { and } x \in(-e,-1) \cup(1, e) \\
& \Rightarrow \quad x \in(-e,-1)
\end{aligned}
\) -
Question 106 of 122
106. Question
The domain of \(f(x)=\frac{1}{\sqrt{|\cos x|+\cos x}}\) is
Hint
(d)
\(
\begin{aligned}
&|\cos x|+\cos x= \begin{cases}0, & \cos x \leq 0 \\ 2 \cos x & , \cos x>0\end{cases}\\
&\text { For } f(x) \text { to defined } \cos x>0\\
&\Rightarrow x \in\left(\frac{(4 n-1) \pi}{2}, \frac{(4 n+1) \pi}{2}\right) n \in Z(1 \text { st and } 4 \text { th quadrant }) .
\end{aligned}
\) -
Question 107 of 122
107. Question
If \(f(2 x+3 y, 2 x-7 y)=20 x\), then \(f(x, y)\) equals
Hint
(b)
\(
\begin{aligned}
&\text { Let } 2 x+3 y=m \text { and } 2 x-7 y=n\\
&\begin{aligned}
& \Rightarrow y=\frac{m-n}{10} \text { and } x=\frac{7 m+3 n}{20} \\
& \Rightarrow f(m, n)=7 m+3 n \\
& \Rightarrow f(x, y)=7 x+3 y
\end{aligned}
\end{aligned}
\) -
Question 108 of 122
108. Question
Let \(X=\left\{a_1, a_2, \ldots, a_6\right\}\) and \(Y=\left\{b_1, b_2, b_3\right\}\). The number of functions \(f\) from \(x\) to \(y\) such that it is onto and there are exactly three elements \(x\) in \(X\) such that \(f(x)=b_1\) is
Hint
(d) Image \(b_1\) is assigned to any three of the six pre-images in \({ }^6 C_3\) ways.
Rest two images can be assigned to remaining three preimages in \(2^3-2\) ways (as function is onto).
Hence number of functions are \({ }^6 C_3 \times\left(2^3-2\right)=20 \times 6=120\) -
Question 109 of 122
109. Question
Let \(f: R \rightarrow R\) and \(g: R \rightarrow R\) be two one-one and onto functions such that they are the mirror images of each other about the line \(y=a\). If \(h(x)=f(x)+g(x)\), then \(h(x)\) is
Hint
(d) \(y=f(x)\) and \(y=g(x)\) are mirror image of each other about line \(y=a\)
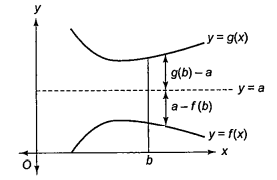
\(
\begin{aligned}
& \Rightarrow \text { for some } x=b, g(b)-a=a-f(b) \\
& \Rightarrow f(b)+g(b)=2 a \\
& \Rightarrow h(b)=f(b)+g(b)=2 a \text { ( constant) }
\end{aligned}
\)
Hence \(h(x)\) is constant function. Thus it is neither oneone nor onto. -
Question 110 of 122
110. Question
If \(f(x)=(-1)^{\left[\frac{2 x}{\pi}\right]}, g(x)=|\sin x|-|\cos x|\) and \(\phi(x)=f(x) g(x)\) (where [.] denotes the greatest integer function) then the respective fundamental periods of \(f(x), g(x)\) and \(\phi(x)\) are
Hint
(c) Clearly \(f(x+\pi)=f(x), g(x+\pi)=g(x)\) and \(\phi\left(x+\frac{\pi}{2}\right) =\{(-1) f(x)\}\{(-1) g(x)\}=\phi(x)\).
-
Question 111 of 122
111. Question
Let \(f(n)=1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}\), then \(f(1)+f(2)+f(3)+\cdots+f(n)\) is equal to.
Hint
(b) In the sum, \(f(1)+f(2)+f(3)+\cdots+f(n), 1\) occurs \(n\) times, \(\frac{1}{2}\) occurs \((n-1)\) times, \(\frac{1}{3}\) occurs \((n-2)\) times and so on
\(
\begin{aligned}
& \therefore f(1)+f(2)+f(3)+\cdots+f(n) \\
& =n \cdot 1+(n-1) \cdot \frac{1}{2}+(n-2) \cdot \frac{1}{3}+\cdots+1 \cdot \frac{1}{n} \\
& =n\left(1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}\right)-\left(\frac{1}{2}+\frac{2}{3}+\frac{3}{4}+\cdots+\frac{n-1}{n}\right) \\
& =n f(n)-\left[\left(1-\frac{1}{2}\right)+\left(1-\frac{1}{3}\right)+\left(1-\frac{1}{4}\right)+\cdots+\left(1-\frac{1}{n}\right)\right]
\end{aligned}
\)
\(
\begin{aligned}
& =n f(n)-[n-f(n)] \\
& =(n+1) f(n)-n
\end{aligned}
\) -
Question 112 of 122
112. Question
Let \(f(x)=e^{\left\{e^{|x|} \operatorname{sgn} x\right\}}\) and \(g(x)=e^{\left[e^{|x|} \operatorname{sgn} x\right]}, x \in R\) where \(\}\) and [ ] denotes the fractional and integral part functions, respectively. Also \(h(x)=\log (f(x))+\log (g(x))\) then for real \(x, h(x)\) is
Hint
(a)
\(
\begin{aligned}
& h(x)=\log (f(x) \cdot g(x))=\log e^{\{y\}+[y]}=\{y\}+[y]=e^{|x|} \operatorname{sgn} x \\
& \therefore h(x)=e^{|x|} \operatorname{sgn} x= \begin{cases}e^x, & x>0 \\
0, & x=0 \\
-e^{-x}, & x<0\end{cases} \\
& \Rightarrow h(-x)=\left\{\begin{array}{ll}
e^{-x}, & x<0 \\
0, & x=0 \\
-e^x, & x>0
\end{array} \Rightarrow h(x)+\dot{h}(-x)=0 \text { for all } x .\right.
\end{aligned}
\) -
Question 113 of 122
113. Question
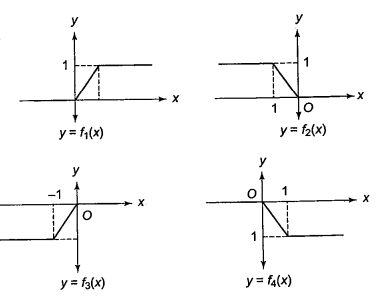
Let \(f_1(x)=\left\{\begin{array}{cc}x, & 0 \leq x \leq 1 \\ 1, & x>1 \\ 0, & \text { otherwise }\end{array}\right.\) and \(f_2(x)=f_1(-x)\) for all \(x f_3(x)=-f_2(x)\) for all \(x f_4(x)=f_3(-x)\) for all \(x\) Which of the following is necessarily true?
Hint
(b)
-
Question 114 of 122
114. Question
The number of solutions of the equation \([y+[y]]=2 \cos x\), where \(y=\frac{1}{3}[\sin x+[\sin x+[\sin x]]]\) (where [.] denotes the greatest integer function) is
Hint
(d)
\(
\begin{aligned}
& \text { d. }[y+[y]]=2 \cos x \\
& \quad \Rightarrow \quad[y]+[y]=2 \cos x \quad(\because[x+n]=[x]+n \text { if } n \in I) \\
& \Rightarrow \quad 2[y]=2 \cos x \Rightarrow[y]=\cos x \dots(1)
\end{aligned}
\)
\(
\begin{aligned}
&\text { Also } \begin{aligned}
y & =\frac{1}{3}[\sin x+[\sin x+[\sin x]]] \\
& =\frac{1}{3}(3[\sin x]) \\
& =[\sin x] \dots(2)
\end{aligned}\\
&\text { From (1) and (2) }\\
&\begin{aligned}
& {[[\sin x]]=\cos x} \\
& \Rightarrow[\sin x]=\cos x
\end{aligned}
\end{aligned}
\)
The number of solutions is 0.
-
Question 115 of 122
115. Question
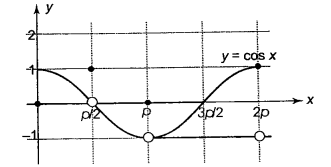
The sum of roots of the equation \(\cos ^{-1}(\cos x)=[x]\), [.] denotes the greatest integer function is
Hint
(a) \(\cos ^{-1}(\cos x)=[x]\)
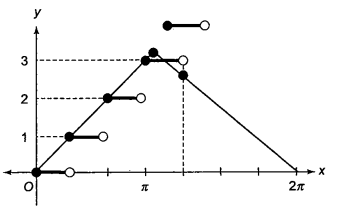
The solutions are clearly \(0,1,2,3\) and \(3=2 \pi-x\) or \(x=2 \pi-3\).
-
Question 116 of 122
116. Question
The range of
\(
f(x)=\sqrt{(1-\cos x) \sqrt{(1-\cos x) \sqrt{(1-\cos x) \sqrt{\ldots \infty}}}}
\)
isHint
(c)
\(
\begin{aligned}
& \text { Given } f(x)=\sqrt{(1-\cos x) \sqrt{(1-\cos x) \sqrt{(1-\cos x) \sqrt{\ldots \infty}}}} \\
& \Rightarrow f(x)=(1-\cos x)^{\frac{1}{2}}(1-\cos x)^{\frac{1}{4}}(1-\cos x)^{\frac{1}{8}} \ldots \infty \\
& \Rightarrow f(x)=(1-\cos x)^{\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots \infty} \\
& \Rightarrow f(x)=(1-\cos x)^{\frac{\frac{1}{2}}{1-\frac{1}{2}}} \\
& \Rightarrow f(x)=1-\cos x \\
& \Rightarrow \text { The range of } f(x) \text { is }[0,2)
\end{aligned}
\) -
Question 117 of 122
117. Question
Let \(h(x)=|k x+5|\), the domain of \(f(x)\) is \([-5,7]\), the domain of \(f(h(x))\) is \([-6,1]\) and the range of \(h(x)\) is the same as the domain of \(f(x)\), then the value of \(k\) is
Hint
(b)
\(
\begin{aligned}
& -5 \leq|k x+5| \leq 7 \\
& \Rightarrow \quad-12 \leq k x \leq 2 \text { where }-6 \leq x \leq 1 \\
& \Rightarrow \quad-6 \leq \frac{k}{2} x \leq 1 \text { where }-6 \leq x \leq 1 \\
& \therefore k=2 . \quad[\because \text { the range of } h(x)=\text { the domain of } f(x)]
\end{aligned}
\) -
Question 118 of 122
118. Question
The range of \(f(x)=(x+1)(x+2)(x+3)(x+4)+5\) for \(x \in[-6,6]\) is
Hint
(a) Let \(g(x)=(x+1)(x+2)(x+3)(x+4)\)
The rough graph of \(g(x)\) is given as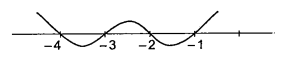
\(
\begin{aligned}
\therefore g(x) & =(x+1)(x+2)(x+3)(x+4) \\
& =(x+1)(x+4)(x+2)(x+3) \\
& =\left(x^2+5 x+4\right)\left(x^2+5 x+6\right) \\
& =t(t+2)=(t+1)^2-1,
\end{aligned}
\)
where \(t=x^2+5 x\)
Now \(g_{\min }=-1\), for which \(x^2+5 x=-1\) has real roots in [-6, 6]
Also \(g(6)=7 \times 8 \times 9 \times 10=5040\)
Hence, the range of \(g(x)\) is \([-1,5040]\) for \(x \in[-6,6]\).
Then, the range of \(f(x)\) is \([4,5045]\). -
Question 119 of 122
119. Question
The exhaustive domain of
\(
f(x)=\sqrt{x^{12}-x^9+x^4-x+1}
\)
isHint
(d) \(f(x)=\sqrt{x^{12}-x^9+x^4-x+1}\)
We must have \(x^{12}-x^9+x^4-x+1 \geq 0 \dots(1)\)
Obviously (1) is satisfied by \(x \in(-\infty, 0]\)
Also, \(x^9\left(x^3-1\right)+x\left(x^3-1\right)+1 \geq 0 \forall x \in[1, \infty)\)
Further, \(x^{12}-x^9+x^4-x+1=(1-x)+x^4\left(1-x^5\right)+x^{12}\) is also satisfied by \(x \in(0,1)\).
Hence, the domain is \(R\). -
Question 120 of 122
120. Question
The range of \(f(x)=\sec ^{-1}\left(\log _3 \tan x+\log _{\tan x} 3\right)\) is
Hint
(a)
\(
\begin{aligned}
& f(x)=\sec ^{-1}\left(\log _3 \tan x+\log _{\tan x} 3\right) . \\
& f(x)=\sec ^{-1}\left(\log _3 \tan x+\frac{1}{\log _3 \tan x}\right)
\end{aligned}
\)
Now for \(\log _3 \tan x\) to get defined, \(\tan x \in(0, \infty)\)
\(\Rightarrow \log _3 \tan x \in(-\infty, \infty)\) or \(\log _3 \tan x \in R\)
Also \(x+\frac{1}{x} \leq-2\) or \(x+\frac{1}{x} \geq 2\)
\(
\begin{aligned}
\Rightarrow & \log _3 \tan x+\frac{1}{\log _3 \tan x} \leq-2 \text { or } \\
& \log _3 \tan x+\frac{1}{\log _3 \tan x} \geq 2 \\
\Rightarrow & \sec ^{-1}\left(\log _3 \tan x+\frac{1}{\log _3 \tan x}\right) \leq \sec ^{-1}(-2) \text { or } \\
& \sec ^{-1}\left(\log _3 \tan x+\frac{1}{\log _3 \tan x}\right) \geq \sec ^{-1} 2 \\
\Rightarrow & f(x) \leq \frac{2 \pi}{3} \text { or } f(x) \geq \frac{\pi}{3} \\
\Rightarrow & f(x) \in\left[\frac{\pi}{3}, \frac{\pi}{2}\right) \cup\left(\frac{\pi}{2}, \frac{2 \pi}{3}\right]
\end{aligned}
\) -
Question 121 of 122
121. Question
The range of the function \(f(x)={ }^{7-x} P_{x-3}\) is
Hint
(a)
We have \(f(x)={ }^{7-x} P_{x-3}=\frac{(7-x)!}{(10-2 x)!}\)
We must have \(7-x>0, x \geq 3\) and \(7-x \geq x-3\)
\(
\begin{aligned}
& \Rightarrow \quad x<7, x \geq 3 \text { and } x \leq 5 \\
& \Rightarrow \quad 3 \leq x \leq 5 \\
& \Rightarrow \quad x=3,4,5 \\
& \text { Now, } f(3)=\frac{4!}{4!}=1, f(4)=\frac{3!}{2!}=3, f(5)=\frac{2!}{0!}=2 . \\
& \text { Hence, } R_f=\{1,2,3\} .
\end{aligned}
\) -
Question 122 of 122
122. Question
A real-valued function \(f(x)\) satisfies the functional equation \(f(x-y)=f(x) f(y)-f(a-x) f(a+y)\), where \(a\) is a given constant and \(f(0)=1 . f(2 a-x)\) is equal to
Hint
(b) We have \(f(x-y)=f(x) f(y)-f(a-x) f(a+y)\)
Putting \(x=a\) and \(y=a-x\), we get
\(
\begin{aligned}
& \quad f(a-(x-a))=f(a) f(x-a)-f(0) f(x) \\
& \text { Putting } x=0, y=0, \text { we get } \\
& \quad f(0)=f(0)(f(0))-f(a) f(a) \\
& \Rightarrow \quad f(0)=(f(0))^2-(f(a))^2 \\
& \Rightarrow \quad 1=(1)^2-(f(a))^2 \\
& \Rightarrow \quad f(a)=0 \\
& \Rightarrow \quad f(2 a-x)=-f(x)
\end{aligned}
\)