JEE Practice Questions (NAT)
Quiz Summary
0 of 18 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 18 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 18
1. Question
The area of the triangular region in the first quadrant bounded on the left by the \(y\)-axis, bounded above by the line \(7 x+4 y=168\) and bounded below by the line \(5 x+3 y =121\) is \(A\), then the value of \(3 A / 10\) is
CorrectIncorrectHint
(a) The given lines \(7 x+4 y=168\) and \(5 x+3 y=121\) intersect at \(P(20,7)\)
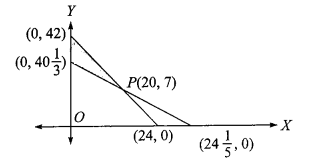
\(
\begin{aligned}
&\therefore \text { Area of shaded region }\\
&\begin{aligned}
A & =\frac{1}{2}\left(42-40 \frac{1}{3}\right) 20 \\
& =\frac{1}{2}\left(\frac{5}{3}\right) 20=\frac{50}{3} \text { (square units) }
\end{aligned}
\end{aligned}
\)
\(
3 A / 10=5
\) -
Question 2 of 18
2. Question
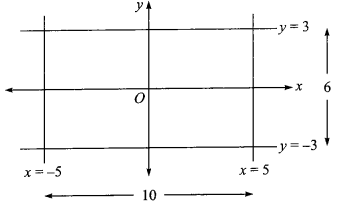
If the area enclosed by the graph of \(x^2 y^2-9 x^2-25 y^2+ 225=0\) is \(A\) if then value of \(A / 10\) is
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (b) } x^2 y^2-9 x^2-25 y^2+225=0 \\
& \Rightarrow x^2\left(y^2-9\right)-25\left(y^2-9\right)=0 \\
& \Rightarrow \quad\left(y^2-9\right)\left(x^2-25\right)=0
\end{aligned}
\)
\(
\therefore \quad \text { Area } A=10 \times 6=60 \text { sq. units. }
\)
\(
A / 10=6
\) -
Question 3 of 18
3. Question
The number of values of \(k\) for which the lines \((k+1) x+ 8 y=4 k\) and \(k x+(k+3) y=3 k-1\) are coincident
CorrectIncorrectHint
(c) Lines \((k+1) x+8 y=4 k\) and \(k x+(k+3) y=3 k-1\) are coincident then we can compare ratio of coefficients
\(
\begin{aligned}
& \Rightarrow \frac{k+1}{k}=\frac{8}{k+3}=\frac{4 k}{3 k-1} \\
& \Rightarrow k^2+4 k+3=8 k \text { and } 24 k-8=4 k^2+12 k \\
& \Rightarrow(k-3)(k-1)=0 \text { and }(k-2)(k-1)=0 \\
& \Rightarrow k=1
\end{aligned}
\) -
Question 4 of 18
4. Question
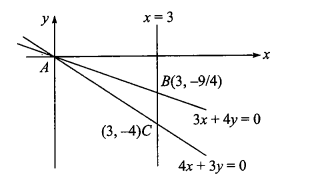
The sides of a triangle \(A B C\) lie on the lines \(3 x+4 y=0\), \(4 x+3 y=0\) and \(x=3\). Let \((h, k)\) be the centre of the circle inscribed in \(\triangle A B C\). The value of \((h+k)\) equals
CorrectIncorrectHint
(d) Equation of angle bisector of angle \(A\)
\(
\frac{3 x+4 y}{5}= \pm \frac{4 x+3 y}{5} \Rightarrow x= \pm y
\)
equation of internal bisector is \(x=-y\)
since \(h\) and \(k\) lie on the line \(x=-y\)
\(
\Rightarrow h+k=0
\)
-
Question 5 of 18
5. Question
Number of value of \(b\) for which in an acute triangle \(A B C\), if the coordinates of orthocentre ‘ \(H\) ‘ are \((4, b)\), centroid ‘ \(G\) ‘ are \((b, 2 b-8)\) and circumcentre ‘ \(S\) ‘ are \((-4,8)\), is
CorrectIncorrectHint
(a) As \(H, G\) and \(S\) are collinear
\(
\begin{aligned}
& \therefore\left|\begin{array}{ccc}
4 & b & 1 \\
b & 2 b-8 & 1 \\
-4 & 8 & 1
\end{array}\right|=0 \\
& \Rightarrow\left|\begin{array}{ccc}
4 & b & 1 \\
b-4 & b-8 & 0 \\
-(b+4) & 16-2 b & 0
\end{array}\right|=0 \\
& \Rightarrow(b-4)(16-2 b)+(b+4)(b-8)=0 \\
& \Rightarrow 2(b-4)(8-b)+(b+4)(b-8)=0 \\
& \Rightarrow(8-b)[(2 b-8)-(b+4)]=0 \\
& \Rightarrow(8-b)(b-12)=0
\end{aligned}
\)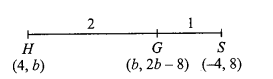
Also
\(
\therefore \quad \frac{-8+4}{3}=b \quad \Rightarrow b=\frac{-4}{3}
\)
And \(\frac{16+b}{3}=2 b-8 \Rightarrow b=8\)
But no common value of ‘ \(b\) ‘ is possible -
Question 6 of 18
6. Question
The piont \(A\) divided the join of \(P(-5,1), Q(3,5)\) in the ratio \(k: 1\), then the integral value of \(k[latex] for which the area of [latex]\triangle A B C\) where \(B\) is \((1,5)\) and \(C\) is \((7,-2)\) is equal to 2 units in magnitude is
CorrectIncorrectHint
(d) Using section formula \(A\left(\frac{3 k-5}{k+1}, \frac{5 k+1}{k+1}\right)\)
Area of triangle \(A B C\) is 2 sq. units
\(
\begin{aligned}
& \Rightarrow \frac{1}{2}\left|\begin{array}{ccc}
1 & 5 & 1 \\
7 & -2 & 1 \\
\frac{3 k-5}{k+1} & \frac{5 k+1}{k+1} & 1
\end{array}\right|= \pm 2 \\
& \text { Operating } R_2 \rightarrow R_2-R_1 ; R_3 \rightarrow R_3-R_1 \\
& \Rightarrow\left|\begin{array}{ccc}
1 & 5 & 1 \\
6 & -7 & 0 \\
\frac{3 k-5}{k+1}-1 & \frac{5 k+1}{k+1}-5 & 0
\end{array}\right|= \pm 4 \\
& \Rightarrow 6\left(\frac{5 k+1-5 k-5}{k+1}\right)+7\left(\frac{3 k-5-k-1}{k+1}\right)= \pm 4 \\
& \Rightarrow-24+7(2 k-6)= \pm 4(k+1) \\
& \Rightarrow k=7 \text { or } k=\frac{31}{9}
\end{aligned}
\) -
Question 7 of 18
7. Question
The sides of a triangle have the combined equation \(x^2- 3 y^2-2 x y+8 y-4=0\). The third side, which is variable always passes through the point \((-5,-1)\). If the range of values of the slope of the third line is such that the origin is an interior point of the triangle is \((a, b)\) then the value of \(\left(a+\frac{1}{b}\right)\) is
CorrectIncorrectHint
(b) \(x^2-3 y^2-2 x y+8 y-4 \equiv(x-3 y+2)(x+y-2)\)
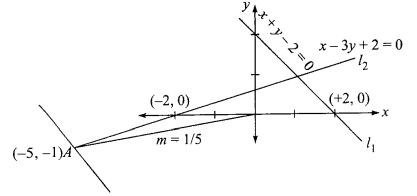
Now \((-5,-1)\) lies on \(x-3 y+2=0\)
In limiting case line passing through \((-5,-1)\) can be parallel to \(x+y-2=0\)
i.e. \(m>-1\)
and maximum slope can occur if it passes through \((0,0)\)
i.e. \(m<\frac{1}{5} \Rightarrow m \in\left(-1, \frac{1}{5}\right)\)
\(\Rightarrow a=-1\) and \(b=\frac{1}{5}\)
\(\Rightarrow\left(a+\frac{1}{b}\right)=-1+5=4\) -
Question 8 of 18
8. Question
If area of the triangle formed by the line \(x+y=3\) and the angle bisectors of the pair of lines \(x^2-y^2+4 y-4=0\) is \(A\), then the value of \(16 A\) is
CorrectIncorrectHint
\(
\begin{aligned}
&\text { (b) Given pair of lines } x^2-\left(y^2-4 y+4\right)=0\\
&\begin{aligned}
& \Rightarrow x^2-(y-2)=0 \\
& \Rightarrow(x+y-2)(x-y+2)=0
\end{aligned}
\end{aligned}
\)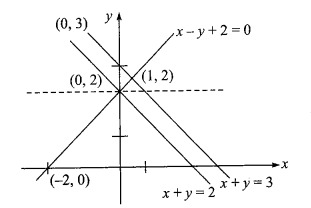
\(
\text { Required area is } A=\frac{1 \cdot 1}{2}=\frac{1}{2}
\)
\(
16 A=8
\) -
Question 9 of 18
9. Question
The points \((x, y)\) lies on the line \(2 x+3 y=6\). The smallest value of the quantity \(\sqrt{x^2+y^2}\) is \(m\) then the value of \(\sqrt{13} \mathrm{~m}\) is
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (d) Let } x=r \cos \theta ; y=r \sin \theta \\
& \Rightarrow 2 r \cos \theta+3 r \sin \theta=6 \\
& \Rightarrow r=\frac{6}{2 \cos \theta+3 \sin \theta} ; \text { and } r=\sqrt{x^2+y^2}
\end{aligned}
\)
for \(r\) to be minimum \(2 \cos \theta+3 \sin \theta\) must be maximum i.e. \(\sqrt{13}\)
\(
\therefore \quad r_{\min }=\frac{6}{\sqrt{13}}
\)
\(
\sqrt{13} \mathrm{~m}=6
\) -
Question 10 of 18
10. Question
The distance between the circumcnetre and orthocenter of the triangle whose vertices are \((0,0),(6,8)\) and \((-4,3)\) is \(L\), then the value of \(\frac{2}{\sqrt{5}} L\) is
CorrectIncorrectHint
(c) Given vertices of triangle are \(O(0,0), B(6,8)\) and \(C(-4,3)\)
Slope of \(O B=\frac{8}{6}\)
Slope of \(O C=-\frac{3}{4}\)
\(
\therefore \quad \angle B O C=\frac{\pi}{2}
\)
\(\triangle \mathrm{OBC}\) is right angled at \(O\)
Circumcentre \(=\) midpoint of hypotenuse \(B C=\left(1, \frac{11}{2}\right)\)
Orthocentre = vertex \(O(0,0)\)
Required distance \(=\sqrt{\left(1+\frac{121}{4}\right)}=\frac{5 \sqrt{5}}{2}\) unit
\(
\frac{2}{\sqrt{5}} L=5
\) -
Question 11 of 18
11. Question
Absolute value of the sum of the abscissas of all the points on the line \(x+y=4\) that lie at a unit distance from the line \(4 x+3 y-10=0\) is
CorrectIncorrectHint
(b) Any point on the line \(x+y=4\) is \((t, 4-4)\) where \(t \in R\)
Now distance of this point from the line \(4 x+3 y-10=0\) is 1
\(
\begin{array}{cc}
\Rightarrow & \frac{|4 t+3(4-t)-10|}{5}=1 \\
\Rightarrow & |t+2|=5 \\
\Rightarrow & t=3 \text { or } t=-7 \\
\Rightarrow & \text { sum of values is }-4
\end{array}
\) -
Question 12 of 18
12. Question
The line \(x=C\) cuts the triangle with vertices \((0,0),(1,1)\) and \((9,1)\) into two regions. For the area of the two regions to be the same, \(C\) must be equal to
CorrectIncorrectHint
(c) \(\text { Area of } \triangle O A B=\frac{1}{2}(1)(8)=4 \text { sq. units }\)
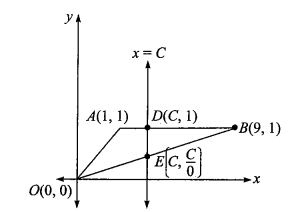
Equation of \(O B\) is \(y=\frac{1}{9} x\)
Hence point \(E\) is \(\left(C, \frac{C}{9}\right)\)
Now area of \(\triangle B D E\) is 2 square units.
\(
\begin{aligned}
& \Rightarrow \frac{1}{2}\left(1-\frac{C}{9}\right)(9-C)=2 \\
& \Rightarrow(9-C)^2=36 \\
& \Rightarrow 9-C= \pm 6 \\
& \Rightarrow C=3
\end{aligned}
\) -
Question 13 of 18
13. Question
A man starts from the point \(P(-3,4)\) and reaches point \(Q(0,1)\) touching \(x\)-axis at \(R(\alpha, 0)\) such that \(P R+R Q\) is minimum, then \(5|\alpha|=\)
CorrectIncorrectHint
(b) For \(P R=R Q\) to be minimum it should be the path of light
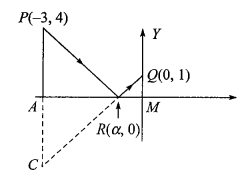
\(
\begin{aligned}
&\therefore \quad \angle P R A=\angle Q R M\\
&\text { From similar } \triangle P A R \text { and } \triangle Q M R\\
&\begin{aligned}
& \frac{A R}{R M}=\frac{P A}{Q M} \\
& \Rightarrow \frac{\alpha+3}{0-\alpha}=\frac{4}{1} \Rightarrow \alpha=-\frac{3}{5}
\end{aligned}
\end{aligned}
\)
\(
5|\alpha|=3
\) -
Question 14 of 18
14. Question
If the area of triangle formed by the points \((2 a, b)(a+ b, 2 b+a)\) and ( \(2 b, 2 a\) ) be 2 sq. units, then the area of the triangle whose vertices are \((a+b, a-b),(3 b-a, b+3 a)\) and \((3 a-b, 3 b-a)\) will be
CorrectIncorrectHint
(d) We know that the area of the triangle formed by joining the mid points of any triangle is one fourth of that triangle. Therefore required area is 8 .
-
Question 15 of 18
15. Question
For all real values of \(a\) and \(b\), lines \((2 a+b) x+(a+3 b) y+(b-3 a)=0\) and \(m x+2 y+6=0\) are concurrent, then \(|m|\) is equal to
CorrectIncorrectHint
(a) Lines \((2 a+b) \mathrm{x}+(a+3 b) y+(b-3 a)=0\) or \(a(2 x+ y-3)+b(x+3 y+1)=0\) are concurrent at point of intersection of lines \(2 x+y-3=0\) and \(x+3 y+1=0\) which is \((2,-1)\).
Now line \(m x+2 y+6=0\) must pass through this point \(\Rightarrow 2 m-2+6=0\) or \(m=-2\)
\(
|m|=2
\) -
Question 16 of 18
16. Question
The line \(3 x+2 y=24\) meets the \(y\)-axis at \(A\) and the \(x\) axis at \(B\). The perpendicular bisector of \(A B\) meets the line through \((0,-1)\) parallel to \(x\)-axis at \(C\). If the area of the triangle \(A B C\) is \(A\) then the value of \(A / 13\) is
CorrectIncorrectHint
(c) Line \(3 x+2 y=24\) meets the axis at \(B(8,0)\) and \(A(0\), 12). Midpoint of \(A B\) is \(D(4,6)\)
Equation of perpendicular bisector of \(A B\) is
\(
2 x-3 y+10=0 \dots(1)
\)
Now line through \((0,-1)\) and parallel to \(x\)-axis is \(y=-1\)
Co-ordinates of \(C\) where line (1) meets \(y=-1\) is \(C\left(-\frac{13}{2},-1\right)\)
Now the area of triangle \(A B C\)
\(
\begin{aligned}
& \Delta=\frac{1}{2}\left|\begin{array}{ccc}
0 & 12 & 1 \\
8 & 0 & 1 \\
-\frac{13}{2} & -1 & 1
\end{array}\right| \\
& =\frac{1}{2}\left[0-12\left(8+\frac{13}{2}\right)+1(-8)\right] \\
& =\frac{1}{2}[-6(29)-8]=91
\end{aligned}
\)
\(
A / 13=7
\) -
Question 17 of 18
17. Question
Consider a \(\triangle A B C\) whose sides \(A B, B C\) and \(C A\) are represented by the straight lines \(2 x+y=0, x+p y=q\) and \(x-y =3\), respectively. The point \(P\) is \((2,3)\) is orthocenter then the value of \((p+q) / 10\) is
CorrectIncorrectHint
(b)
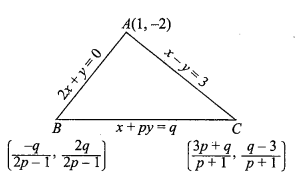
\(
\begin{aligned}
&P \text { is orthocenter }\\
&\begin{aligned}
& \Rightarrow A P \perp B C \\
& \Rightarrow\left(-\frac{1}{p}\right)\left(\frac{3+2}{2-1}\right)=-1 \\
& \Rightarrow \frac{5}{p} \Rightarrow p=5 \\
& \because B P \perp A C \\
& \Rightarrow \frac{27-2 q}{18+q}=-1 \Rightarrow q=27+18 \\
& \Rightarrow q=45 \\
& \therefore p+q=5+45=50
\end{aligned}
\end{aligned}
\)
\(
(p+q) / 10=5
\)Note: The orthocenter of a triangle is the point where its three altitudes intersect. An altitude is a line segment drawn from a vertex perpendicular to the opposite side. The location of the orthocenter depends on the triangle’s type: it lies inside an acute triangle, coincides with the right-angle vertex in a right triangle, and is located outside an obtuse triangle.
-
Question 18 of 18
18. Question
Triangle \(A B C\) with \(A B=13, B C=5\) and \(A C=12\) slides on the coordinates axis with \(A\) and \(B\) on the positive \(x\)-axis and positive \(y\)-axis respectively, the locus of vertex \(C\) is a line \(12 x-k y=0\), then the value of \(k\) is
CorrectIncorrectHint
(d)
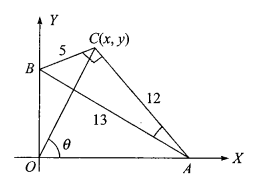
Since \(\angle B C A=90^{\circ}\)
Points \(A, O, B, C\) are concyclic
Let \(\angle A O C=\theta\)
\(\angle B O C=\angle B A C\)
\(\tan \left(\frac{\pi}{2}-\theta\right)=\frac{5}{12}\)
\(\frac{x}{y}=\frac{5}{12} \Rightarrow 12 x-5 y=0\)
Comparing with \(12 x-k y=0\), we get \(k=5\)