JEE Practice Questions (NAT)

Hint

(c) We have \(f\left(\frac{2 x-3}{x-2}\right)=5 x-2 \Rightarrow f^{-1}(5 x-2)=\frac{2 x-3}{x-2}\) Let \(5 x-2=13\), then \(x=3\)
Hence \(f^{-1}(13)=\frac{2(3)-3}{3-2}=3\)

Hint

(a)
\(
\left|\left|\left|x^2-x+4\right|-2\right|-3\right|=x^2+x-12
\)
\(
\begin{aligned}
& \Rightarrow\left|\left|x^2-x+2\right|-3\right|=x^2+x-12 \\
& \Rightarrow\left|x^2-x-1\right|=x^2+x-12 \\
& \Rightarrow 2 x=11 \\
& \Rightarrow x=11 / 2
\end{aligned}
\)

Hint

(b) For \(f(x)\) to touch \(f^{-1}(x)\), there must be exactly one point of intersection, which means the quadratic equation \(3 x^2-8 x+c=0\) must have exactly one solution. This occurs when the discriminant of the quadratic equation is equal to zero.
The discriminant \(\Delta\) of a quadratic equation \(a x^2+b x+c=0\) is given by \(\Delta=b^2-4 a c\). In this case, \(a=3, b=-8\), and the constant term is \(c\).
Setting the discriminant to zero: \((-8)^2-4(3)(c)=0\).
Simplifying the equation: \(64-12 c=0\).
Solving for \(c: 12 c=64\), which gives \(c=\frac{64}{12}=\frac{16}{3}\).
The value of \(c\) is \(\frac{16}{3}\). The greatest integer function \([c]\) is required.
Calculating the value of \([c]:\left[\frac{16}{3}\right]=[5.333 \ldots]=5\).

Hint

(d)

\(
\begin{aligned}
& x!-(x-1)!\neq 0 \Rightarrow x \in I^{+}-\{1\} \\
& 2^{\frac{\pi}{\tan ^{-1} x}}>4 \text { as } \tan ^{-1} x<\frac{\pi}{2} \\
& \frac{(x-4)(x-10)}{(x-1)!(x-1)}<0 \\
& x \in\{5,6, \ldots, 9\}
\end{aligned}
\)

Hint

(b)
\(
\begin{aligned}
& \text { Put } x=1 \text { and } y=1 \text {, } \\
& f^2(1)-f(1)-6=0 \\
& f(1)=3 \text { or } f(1)=-2 \\
& \text { Now put } y=1
\end{aligned}
\)
\(
f(x) \cdot f(1)=f(x)+2\left(\frac{1}{x}+2\right)=f(x)+2\left(\frac{2 x+1}{x}\right)
\)
\(
f(x)[f(1)-1]=\frac{2(2 x+1)}{2}
\)
\(
f(x)=\frac{2(2 x+1)}{x[f(1)-1]}
\)
\(
\begin{aligned}
& \text { For } f(1)=3, f(x)=\frac{2 x+1}{x} \\
& \text { and for } x=-2, f(x)=\frac{2(2 x+1)}{-3 x} \\
& f(1 / 2)=4
\end{aligned}
\)

Hint

\(
\begin{aligned}
& \text { (c) } \text { Let } 2 x+y=3 x-y \Rightarrow 2 y=x \Rightarrow y=\frac{x}{2} \\
& \therefore \text { Put } y=\frac{x}{2} \\
& \Rightarrow f(x)+f\left(\frac{5 x}{2}\right)+\frac{5 x^2}{2}=f\left(\frac{5 x}{2}\right)+2 x^2+1 \\
& \Rightarrow f(x)=1-\frac{x^2}{2} \\
& \Rightarrow f(4)=-7
\end{aligned}
\)
\(
|f(4)|=7
\)

Hint

(a) As \(a>2\), hence
\(
\begin{aligned}
& a^2>2 a>a>2 \\
& \text { now }(x-a)(x-2 a)\left(x-a^2\right)<0
\end{aligned}
\)
the solution set is as shown

between \((0, a)\) there are \((a-1)\) positive integers and between ( \(2 a, a^2\) ) there are \(a^2-2 a-1\) integer
\(
\begin{aligned}
& \therefore a^2-2 a-1+a-1=18 \Rightarrow a^2-a-20=0 \\
& \quad(a-5)(a+4)=0 \\
& \therefore a=5
\end{aligned}
\)

Hint

(b)
\(
\begin{aligned}
& f(x)+f\left(\frac{1}{x}\right)=x^2+\frac{1}{x} \\
& \text { replacing } x \rightarrow \frac{1}{x} ; f\left(\frac{1}{x}\right)+f(x)=\frac{1}{x^2}+x \\
\Rightarrow & \frac{1}{x^2}+x=x^2+\frac{1}{x} \\
\Rightarrow & x-\frac{1}{x}=x^2-\frac{1}{x^2} \\
\Rightarrow & \left(x-\frac{1}{x}\right)=\left(x-\frac{1}{x}\right)\left(x+\frac{1}{x}\right) \\
\Rightarrow & \left(x-\frac{1}{x}\right)\left(x+\frac{1}{x}-1\right)=0
\end{aligned}
\)
\(
\begin{aligned}
&x=\frac{1}{x} ; x+\frac{1}{x}=1(\text { rejected })\\
&\text { Hence } x=1 \text { or }-1
\end{aligned}
\)

Hint

(c) Obviously \(f\) is a linear polynomial
\(
\begin{aligned}
& \text { Let } f(x)=a x+b \text { hence } f\left(x^2+x+3\right)+2 f\left(x^2-3 x+5\right) \equiv 6 x^2- \\
& 10 x+17 \\
& \Rightarrow\left[a\left(x^2+x+3\right)+b\right]+2\left[a\left(x^2-3 x+5\right)+b\right] \equiv 6 x^2-10 x+17 \\
& \Rightarrow a+2 a=6 \dots(1) \\
& \Rightarrow a-6 a=-10 \dots(2)
\end{aligned}
\)
(comparing coeff. of \(x^2\) and coeff. of \(x\) on both sides)
\(
\begin{aligned}
& a \Rightarrow 2 \\
& \text { Again, } 3 a+b+10 a+2 b=17 \text { (Comparing constant term) } \\
\Rightarrow & 6+b+20+2 b=17 \\
\therefore & f(x)=2 x-3 \\
\Rightarrow & f(5)=7
\end{aligned}
\)

Hint

(a) Given \(f(x+2)=f(x)+f(2)\)
Put \(x=-1\), we have \(f(1)=f(-1)+f(2)\)
\(f(1)=-f(1)+f(2)\) (as \(f(x)\) is an odd function)
\(f(2)=2 f(1)=6\)
Now put \(x=1\),
We have \(f(3)=f(1)+f(2)=3+6=9\)

Hint

(a) \(f(x)+f(-x)=0\)
\(f(x)\) is an odd function.
Since points \((-3,2)\) and \((5,4)\) lie on the curve, therefore \((3,-2)\) and \((-5,-4)\) will also lie on the curve. For minimum number of roots, graph of continuous function \(f(x)\) is as follows: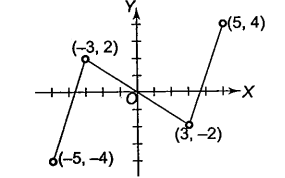

From the above graph of \(f(x)\), it is clear that equation \(f(x) =0\) has at least three real roots.

Hint

(d)
\(
\begin{aligned}
&\begin{aligned}
f(x) & =\sqrt{\sin x+\cos x}+\sqrt{7 x-x^2-6} \\
& =\sqrt{\sqrt{2} \sin \left(x+\frac{\pi}{4}\right)}+\sqrt{(x-6)(1-x)}
\end{aligned}\\
&\text { Now } f(x) \text { is defined if } \sin \left(x+\frac{\pi}{4}\right) \geq 0 \text { and }(x-6)(1-x) \geq 0
\end{aligned}
\)
\(
\begin{aligned}
&\begin{aligned}
& \Rightarrow 0 \leq x+\frac{\pi}{4} \leq \pi \text { or } 2 \pi \leq x+\frac{\pi}{4} \leq 3 \pi \text { and } 1 \leq x \leq 6 \\
& \Rightarrow-\frac{\pi}{4} \leq x \leq \frac{3 \pi}{4} \text { or } \frac{7 \pi}{4} \leq x \leq \frac{11 \pi}{4} \text { and } 1 \leq x \leq 6 \\
& \Rightarrow x \in\left[1, \frac{3 \pi}{4}\right] \cup\left[\frac{7 \pi}{4}, 6\right]
\end{aligned}\\
&\text { Integral values of } x \text { are } x=1,2 \text { and } 6
\end{aligned}
\)

Hint

(b) Since \(f\) is periodic with period 2 and \(f(x)=x \quad \forall x \in[0,1]\) also \(f(x)\) is even
symmetry about \(y\)-axis
graph of \(f(x)\) is as shown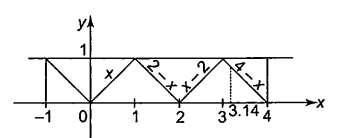

\(
f(3.14)=4-3.14=0.86
\)

Hint

(a) Let \(x^2=4 \cos ^2 \theta+\sin ^2 \theta\)
then \(\left(4-x^2\right)=3 \sin ^2 \theta\) and \(\left(x^2-1\right)=3 \cos ^2 \theta\)
\(
\begin{aligned}
& f(x)=\sqrt{3}|\sin \theta|+\sqrt{3}|\cos \theta| \\
& y_{\min }=\sqrt{3} \text { and } \\
& y_{\max }=\sqrt{3}\left(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\right)=\sqrt{6}
\end{aligned}
\)
Hence range of \(f(x)\) is \([\sqrt{3}, \sqrt{6}]\)
Hence maximum value of \((f(x))^2\) is 6

Hint

(a)
\(
\begin{aligned}
g(x) & =\frac{f(x)+f(-x)}{2} \\
& =\frac{1}{2}\left[\frac{x+1}{x^3+1}+\frac{1-x}{1-x^3}\right] \\
& =\frac{1}{2}\left[\frac{1}{x^2-x+1}+\frac{1}{1+x+x^2}\right] \\
& =\frac{1}{2}\left[\frac{2\left(x^2+1\right)}{\left(x^2+1\right)^2-x^2}\right] \\
& =\frac{x^2+1}{x^4+x^2+1} \\
& =\frac{x^4-1}{x^6+1} \Rightarrow |g(0)|=1
\end{aligned}
\)

Hint

(c)

\(
\begin{aligned}
f(x) & =[8 x+7]+|\tan 2 \pi x+\cot 2 \pi x|-8 x \\
& =[8 x]-8 x-7+|\tan 2 \pi x+\cot 2 \pi x| \\
& =-\{8 x\}+|\tan 2 \pi x+\cot 2 \pi x|+7
\end{aligned}
\)
Period of \(\{8 x\}\) is \(1 / 8\)
Also, \(|\tan 2 \pi x+\cot 2 \pi x|\)
\(
=\left|\frac{\sin 2 \pi x}{\cos 2 \pi x}+\frac{\cos 2 \pi x}{\sin 2 \pi x}\right|=\left|\frac{1}{\sin 2 \pi x \cos 2 \pi x}\right|=|2 \operatorname{cosec} 4 \pi x|
\)
Now period of \(2 \operatorname{cosec} 4 \pi x\) is \(1 / 2\), then period of \(\mid 2 \operatorname{cosec} 4 \pi x\) | is \(1 / 4\)
Period is L.C.M. of \(\frac{1}{8}\) and \(\frac{1}{4}\) which is \(\frac{1}{4}\)

Hint

(a) Let \(x=\frac{|a|}{a}+\frac{|b|}{b}+\frac{|c|}{c}\)
If exactly one-ve, then \(x=1\)
Exactly two-ve, then \(x=-1\)
All three -ve , then \(x=-3\)
All three +ve , then \(x=3\)
Then the required sum is 0.

Hint

(b) We have \(f(2 x)-f(2 x) f\left(\frac{1}{2 x}\right)+f\left(16 x^2 y\right)=f(-2)-f(4 x y)\)
Replacing \(y\) by \(\frac{1}{8 x^2}\), we get
\(
\begin{aligned}
& f(2 x)-f(2 x)\left(\frac{1}{2 x}\right)+f(2)=f(-2)-f\left(\frac{1}{2 x}\right) \\
& f(2 x)+f\left(\frac{1}{2 x}\right)=f(2 x) f\left(\frac{1}{2 x}\right) \quad[\text { As } f(x) \text { is even }] \\
& f(2 x)=1 \pm(2 x)^n \\
& f(x)=1 \pm x^n
\end{aligned}
\)
Now \(f(4)=1 \pm 4^n=-255 \quad\) (Given)
Taking negative sign, we get \(256=4^n \Rightarrow n=4\)
Hence \(f(x)=1-x^4\), which is an even function.
\(
f(2)=-15
\)
\(
|(f(2)+1) / 2|=7
\)

Hint

(c)

\(
\begin{aligned}
& f(x)=\sin ^2 x+\sin ^2\left(x+\frac{\pi}{3}\right)+\cos x \cos \left(x+\frac{\pi}{3}\right) \\
& =\sin ^2 x+\frac{1}{4}(\sin x+\sqrt{3} \cos x)^2+\frac{1}{2} \cos x(\cos x-\sqrt{3} \sin x) \\
& =\frac{5}{4}\left(\sin ^2 x+\cos ^2 x\right)=\frac{5}{4} \\
& (g \circ f) x=g[f(x)]=g(5 / 4)=1
\end{aligned}
\)

Hint

(a) From \(E\) to \(F\) we can define, in all, \(2 \times 2 \times 2 \times 2=16\) functions ( 2 options for each elements of \(E\) ) out of which 2 are into, when all the elements of \(E\) either map to 1 or to 2 \(\therefore\) Number of onto function \(=16-2=14\)
\(
N / 2=7
\)

Hint

(d)

\(
\begin{aligned}
& \text { Given } f(f(x))=-x+1 \\
& \text { replacing } x \rightarrow f(x) \\
& \qquad \begin{array}{r}
f(f(f(x)))=-f(x)+1 \\
f(1-x)=-f(x)+1 \\
f(x)+f(1-x)=1 \\
f\left(\frac{1}{4}\right)+f\left(\frac{3}{4}\right)=1
\end{array}
\end{aligned}
\)

Hint

\(
\begin{aligned}
& \text { (c) }\left(\frac{3}{4}\right)^{6 x+10-x^2}<\frac{27}{64} \\
& \Rightarrow 6 x+10-x^2>3 \\
& \therefore x^2-6 x-7<0 \\
& \therefore(x+1)(x-7)<0 \\
& \Rightarrow 0,1,2,3,4,5,6
\end{aligned}
\)

Hint

(a)
\(
\begin{aligned}
\because \quad k & \in \text { odd } \\
f(k) & =k+3 \\
f(f(k)) & =\frac{k+3}{2}
\end{aligned}
\)
If \(\frac{k+3}{2}\) is odd \(\Rightarrow 27=\frac{k+3}{2}+3 \Rightarrow k=45\) not possible \(\frac{k+3}{2}\) is even
\(
\begin{aligned}
& 27=f(f(f(k)))=f\left(\frac{k+3}{2}\right)=\frac{k+3}{4} \\
& k=105
\end{aligned}
\)
\(
\begin{array}{ll}
& \text { verifying } f(f(f(105)))=f(f(108))=f(54)=27 \\
\therefore & k=105
\end{array}
\)

Hint

(c) Clearly fundamental period is \(\frac{4 \pi}{3}\), then \(z\) lies in the third quadrant.

Hint

(d)

\(
\begin{aligned}
& \log _a\left(x^2-x+2\right)>\log _a\left(-x^2+2 x+3\right) \\
& \text { Put } x=\frac{4}{9}, \log _a\left(\frac{142}{81}\right)>\log _a\left(\frac{299}{81}\right) \\
& \frac{142}{81}<\frac{299}{81} \Rightarrow 0<a<1 \\
& \log _a\left(x^2-x+2\right)>\log _2\left(-x^2+2 x+3\right) \\
& \operatorname{gives}^2 0<x^2-x+2<-x^2+2 x+3 \\
& x^2-x+2>0 \text { and } 2 x^2-3 x-1<0 \\
& \frac{3-\sqrt{17}}{4}<x<\frac{3+\sqrt{17}}{4}
\end{aligned}
\)

Hint

(c)

\(
\begin{aligned}
&\begin{aligned}
& \left(2^{2 x}-4 \cdot 2^x+4\right)+1+||b-1|-3|=|\sin y| \\
& \left(2^x-2\right)^2+1+||b-1|-3|=|\sin y| \\
& \left(2^x-2\right)^2+1+||b-1|-3|=|\sin y|
\end{aligned}\\
&\text { LHS } \geq 1 \text { and RHS } \leq 1\\
&\begin{aligned}
& 2^x=2,|b-1|-3=0 \\
& (b-1)= \pm 3 \\
& b=4,-2
\end{aligned}
\end{aligned}
\)

Hint

(d)

\(
\begin{aligned}
& f(3 n)=f(f(f(n)))=3 f(n), \forall n \in N \\
& \text { Put } n=1, f(3)=3 f(1) \\
& \text { If } f(1)=1, \text { then } f(f(1))=f(1)=1, \text { but } f(f(n))=3 n \\
& f(f(1))=3 \text { giving } 1=3 \text { which is absurd. } \\
& f(1) \neq 1 \\
& 3=f(f(1))>f(1)>1 \\
& \text { So } f(1)=2 \\
& f(2)=f(f(1))=3
\end{aligned}
\)

Hint

(b)

\(
\begin{aligned}
& \log _{1 / 3} \log _7(\sin x+a)>0 \\
& 0<\log _7(\sin x+a)<1 \\
& 1<(\sin x+a)<7 \quad \forall x \in R[\text { ‘ } a \text { ‘ should be less than the } \\
& \text { minimum value of } 7-\sin x \text { and ‘ } a \text { ‘ must be greater than } \\
& \text { maximum value of } 1-\sin x] \\
& 1-\sin x<a<7-\sin x \forall x \in R \\
& 2<a<6
\end{aligned}
\)

Hint

(d)

\(
\begin{aligned}
& g(x)=\frac{1}{2} \tan ^{-1}|x|+1 \Rightarrow-\operatorname{sgn}(g(x))=1 \\
& \sin ^{23} x-\cos ^{22} x=1 \\
& \sin ^{23} x=1+\cos ^{22} x \text { which is possible if } \sin x=1 \text { and } \cos x=0 \\
& \sin x=1, x=2 n \pi+\frac{\pi}{2} \\
& \text { hence }-10 \pi \leq 2 n \pi+\frac{\pi}{2} \leq 8 \pi \Rightarrow-\frac{21}{4} \leq n \leq \frac{15}{4} \\
& -5 \leq n \leq 3 \\
& \text { Hence, number of values of } x=9
\end{aligned}
\)

Hint

(a) \(f(x)=\frac{a x^8+b x^6+c x^4+d x^2+15 x+1}{x}\)
\(
=\underbrace{a x^7+b x^5+c x^3+d x+\frac{1}{x}}_{\text {odd function }}+15
\)
\(
\begin{aligned}
& \text { Now } f(x)+f(-x)=30 \\
\Rightarrow \quad & f(-5)=30-f(5)=28
\end{aligned}
\)
\(
|f(-5)| / 4=7
\)