JEE Physics Test Series Quiz-9
Quiz Summary
0 of 50 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 50 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 50
1. Question
1 point(s)A spherical mirror is obtained as shown in the figure from a hollow glass sphere. If an object is positioned in front of the mirror, what will be the nature and magnification of the image of the object? (Figure drawn as schematic and not to scale)
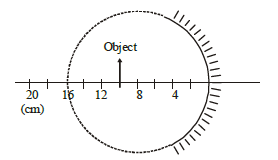 CorrectIncorrect
CorrectIncorrect -
Question 2 of 50
2. Question
1 point(s)A concave mirror for face viewing has focal length of \(0.4 \mathrm{~m}\). The distance at which you hold the mirror from your face in order to see your image upright with a magnification of 5 is:
CorrectIncorrect -
Question 3 of 50
3. Question
1 point(s)A point source of light, \(S\) is placed at a distance \(L\) in front of the centre of plane mirror of width \(\mathrm{d}\) which is hanging vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror, at a distance \(2 \mathrm{~L}\) as shown below. The distance over which the man can see the image of the light source in the mirror is:
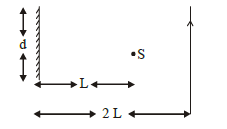 CorrectIncorrect
CorrectIncorrect -
Question 4 of 50
4. Question
1 point(s)Two plane mirrors are inclined to each other such that a ray of light incident on the first mirror \(\left(M_1\right)\) and parallel to the second mirror \(\left(\mathrm{M}_2\right)\) is finally reflected from the second mirror \(\left(\mathrm{M}_2\right)\) parallel to the first mirror \(\left(\mathrm{M}_1\right)\). The angle between the two mirrors will be:
CorrectIncorrect -
Question 5 of 50
5. Question
1 point(s)An object is gradually moving away from the focal point of a concave mirror along the axis of the mirror. The graphical representation of the magnitude of linear magnification \((m)\) versus the distance of the object from the mirror \((x)\) is correctly given by (Graphs are drawn schematically and are not to scale)
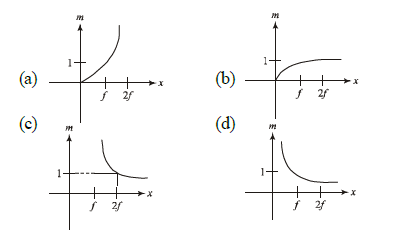 CorrectIncorrect
CorrectIncorrect -
Question 6 of 50
6. Question
1 point(s)A particle is oscillating on the \(\mathrm{X}\)-axis with an amplitude \(2 \mathrm{~cm}\) about the point \(x_0=10 \mathrm{~cm}\) with a frequency \(\omega\). A concave mirror of focal length \(5 \mathrm{~cm}\) is placed at the origin (see figure) Identify the correct statements:
(A) The image executes periodic motion
(B) The image executes non-periodic motion
(C) The turning points of the image are asymmetric w.r.t the image of the point at \(x=10 \mathrm{~cm}\)
(D) The distance between the turning points of the oscillation of the image is \(\frac{100}{21}\)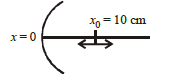 CorrectIncorrect
CorrectIncorrect -
Question 7 of 50
7. Question
1 point(s)You are asked to design a shaving mirror assuming that a person keeps it \(10 \mathrm{~cm}\) from his face and views the magnified image of the face at the closest comfortable distance of \(25 \mathrm{~cm}\). The radius of curvature of the mirror would then be:
CorrectIncorrect -
Question 8 of 50
8. Question
1 point(s)A ray of light travelling in the direction \(\frac{1}{2}(\hat{i}+\sqrt{3} \hat{j})\) is incident on a plane mirror. After reflection, it travels along the direction \(\frac{1}{2}(\hat{i}-\sqrt{3} \hat{j})\). The angle of incidence is
CorrectIncorrect -
Question 9 of 50
9. Question
1 point(s)In an experiment to determine the focal length \((f)\) of a concave mirror by the \(\mathrm{u}-\mathrm{v}\) method, a student places the object pin A on the principal axis at a distance \(x\) from the pole \(P\). The student looks at the pin and its inverted image from a distance keeping his/her eye in line with \(P A\). When the student shifts his/her eye towards left, the image appears to the right of the object pin. Then,
CorrectIncorrect -
Question 10 of 50
10. Question
1 point(s)A point source of light \(B\) is placed at a distance \(L\) in front of the centre of a mirror of width ‘ \(d\) ‘ hung vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror at a distance \(2 L\) from it as shown in figure. The greatest distance over which he can see the image of the light source in the mirror is
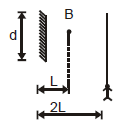 CorrectIncorrect
CorrectIncorrect -
Question 11 of 50
11. Question
1 point(s)A short linear object of length \(b\) lies along the axis of a concave mirror of focal length \(f\) at a distanee \(u\) from the pole of the mirror. The size of the image is approximately equal to
CorrectIncorrect -
Question 12 of 50
12. Question
1 point(s)Image of an object approaching a convex mirror of radius of curvature \(20 \mathrm{~m}\) along its optical axis is observed to move from \(\frac{25}{3} \mathrm{~m}\) to \(\frac{50}{7} \mathrm{~m}\) in 30 seconds. What is the speed of the object in \(\mathrm{km}\) per hour?
CorrectIncorrect -
Question 13 of 50
13. Question
1 point(s)When an object is kept at a distance of \(30 \mathrm{~cm}\) from a concave mirror, the image is formed at a distance of \(10 \mathrm{~cm}\) from the mirror. If the object is moved with a speed of 9 \(\mathrm{cms}^{-1}\), the speed (in \(\mathrm{cms}^{-1}\) ) with which image moves at that instant is
CorrectIncorrect -
Question 14 of 50
14. Question
1 point(s)A thin rod of length \(\frac{f}{3}\) is placed along the optic axis of a concave mirror of focal length \(f\) such that its image which is real and elongated, just touches the rod. The magnification is
CorrectIncorrect -
Question 15 of 50
15. Question
1 point(s)STATEMENT-1: The formula connecting \(u, v\) and \(f\) for a spherical mirror is valid for mirrors whose sizes are very small compared to their radii of curvature.
STATEMENT-2: Laws of reflection are strictly valid for plane surfaces, but not for large spherical surfaces.CorrectIncorrect -
Question 16 of 50
16. Question
1 point(s)A vessel of depth \(2 \mathrm{~h}\) is half filled with a liquid of refractive index \(2 \sqrt{2}\) and the upper half with another liquid of refractive index \(\sqrt{2}\). The liquids are immiscible. The apparent depth of the inner surface of the bottom of vessel will be:
CorrectIncorrect -
Question 17 of 50
17. Question
1 point(s)There is a small source of light at some depth below the surface of water (refractive index \(=\frac{4}{3}\) ) in a tank of large cross-sectional surface area. Neglecting any reflection from the bottom and absorption by water, the percentage of light that emerges out of the surface is (nearly):
[Use the fact that the surface area of a spherical cap of height \(h\) and radius of curvature \(r\) is \(2 \pi r h\) ]CorrectIncorrect -
Question 18 of 50
18. Question
1 point(s)The critical angle of a medium for a specific wavelength, if the medium has relative permittivity 3 and relative permeability \(\frac{4}{3}\) for this wavelength, will be:
CorrectIncorrect -
Question 19 of 50
19. Question
1 point(s)A transparent cube of side \(\mathrm{d}\), made of a material of refractive index \(\mu_2\), is immersed in a liquid of refractive index \(\mu_1\left(\mu_1<\mu_2\right)\). A ray is incident on the face \(A B\) at an angle \(\theta\) (shown in the figure). Total internal reflection takes place at point \(E\) on the face \(B C\).
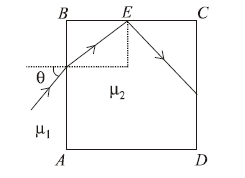
Then \(\theta\) must satisfy :
CorrectIncorrect -
Question 20 of 50
20. Question
1 point(s)A ray of light \(\mathrm{AO}\) in vacuum is incident on a glass slab at angle \(60^{\circ}\) and refracted at angle \(30^{\circ}\) along \(O B\) as shown in the figure. The optical path length of light ray from A to \(\mathrm{B}\) is:
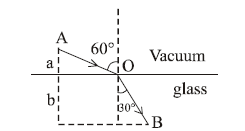 CorrectIncorrect
CorrectIncorrect -
Question 21 of 50
21. Question
1 point(s)In the figure, the optical fiber is \(l=2 \mathrm{~m}\) long and has a diameter of \(d=20 \mu \mathrm{m}\). If a ray of light is incident on one end of the fiber at angle \(\theta_1=40^{\circ}\), the number of reflections it makes before emerging from the other end is close to :
(refractive index of fiber is 1.31 and \(\sin 40^{\circ}=0.64\) )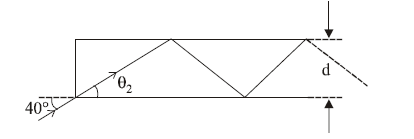 CorrectIncorrect
CorrectIncorrect -
Question 22 of 50
22. Question
1 point(s)A light wave is incident normally on a glass slab of refractive index 1.5 . If \(4 \%\) of light gets reflected and the amplitude of the electric field of the incident light is \(30 \mathrm{~V} /\) \(\mathrm{m}\), then the amplitude of the electric field for the wave propagating in the glass medium will be:
CorrectIncorrect -
Question 23 of 50
23. Question
1 point(s)Let the refractive index of a denser medium with respect to a rarer medium be \(n_{12}\) and its critical angle be \(\theta_C\). At an angle of incidence A when light is travelling from denser medium to rarer medium, a part of the light is reflected and the rest is refracted and the angle between reflected and refracted rays is \(90^{\circ}\). Angle \(\mathrm{A}\) is given by:
CorrectIncorrect -
Question 24 of 50
24. Question
1 point(s)A diver looking up through the water sees the outside world contained in a circular horizon. The refractive index of water is \(\frac{4}{3}\), and the diver’s eyes are \(15 \mathrm{~cm}\) below the surface of water. Then the radius of the circle is:
CorrectIncorrect -
Question 25 of 50
25. Question
1 point(s)A light ray falls on a square glass slab as shown in the diagram. The index of refraction of the glass, if total internal reflection is to occur at the vertical face, is equal to:
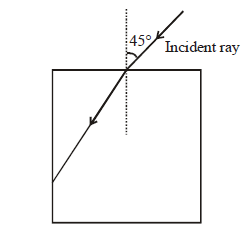 CorrectIncorrect
CorrectIncorrect -
Question 26 of 50
26. Question
1 point(s)A ball is dropped from a height of \(20 \mathrm{~m}\) above the surface of water in a lake. The refractive index of water is 4.3. A fish inside the lake, in the line of fall of the ball, is looking at the ball. At an instant, when the ball is \(12.8 \mathrm{~m}\) above the water surface, the fish sees the speed of ball as [Take \(g=\) \(10 \mathrm{~m} / \mathrm{s}^2\).]
CorrectIncorrect -
Question 27 of 50
27. Question
1 point(s)A ray of light traveling in water is incident on its surface open to air. The angle of incidence is \(\theta\), which is less than the critical angle. Then there will be
CorrectIncorrect -
Question 28 of 50
28. Question
1 point(s)A point object is placed at the centre of a glass sphere of radius \(6 \mathrm{~cm}\) and refractive index 1.5. The distance of virtual image from the surface is
CorrectIncorrect -
Question 29 of 50
29. Question
1 point(s)A ray of light is incident at the glass-water interface at an angle \(i\), it emerges finally parallel to the surface of the water, then the value of \(\mu_{\mathrm{g}}\) would be
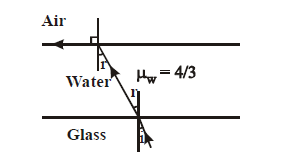 CorrectIncorrect
CorrectIncorrect -
Question 30 of 50
30. Question
1 point(s)Two plane mirrors A and B are aligned parallel to each other, as shown in the figure. A light ray is incident at an angle \(30^{\circ}\) at a point just inside one end of \(A\). The plane of incidence coincides with the plane of the figure. The maximum number of times the ray undergoes reflections (including the first one) before it emerges out is
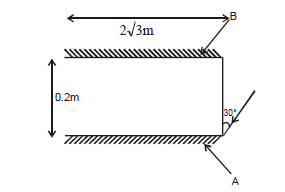 CorrectIncorrect
CorrectIncorrect -
Question 31 of 50
31. Question
1 point(s)An observer can see through a pinhole the top end of a thin rod of height \(h\), placed as shown in the figure. The beaker height is \(3 \mathrm{~h}\) and its radius \(\mathrm{h}\). When the beaker is filled with a liquid up to a height \(2 \mathrm{~h}\), he can see the lower end of the rod. Then the refractive index of the liquid is
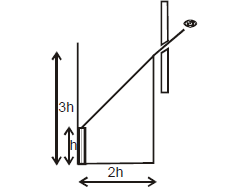 CorrectIncorrect
CorrectIncorrect -
Question 32 of 50
32. Question
1 point(s)A ray of light passes through four transparent media with refractive indices \(\mu_1, \mu_2, \mu_3\) and \(\mu_4\) as shown in the figure. The surfaces of all media are parallel. If the emergent ray \(C D\) is parallel to the incident ray \(A B\), we must have
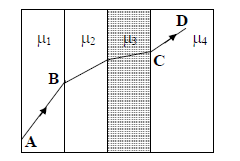 CorrectIncorrect
CorrectIncorrect -
Question 33 of 50
33. Question
1 point(s)A rectangular glass slab \(A B C D\) of refractive index \(n_1\) is immersed in water of refractive index \(n_2\left(n_1>n_2\right)\). A ray of light is incident at the surface \(A B\) of the slab as shown. The maximum value of the angle of incidence \(\alpha_{\max }\) such that the ray comes out only from the other surface \(C D\) is given by
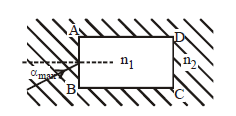 CorrectIncorrect
CorrectIncorrect -
Question 34 of 50
34. Question
1 point(s)A diverging beam of light from a point source \(S\) having divergence angle \(\alpha\), falls symmetrically on a glass slab as shown. The angles of incidence of the two extreme rays are equal. If the thickness of the glass slab is \(t\) and the refractive index \(n\), then the divergence angle of the emergent beam is
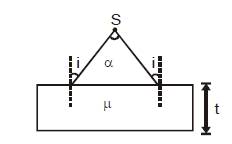 CorrectIncorrect
CorrectIncorrect -
Question 35 of 50
35. Question
1 point(s)A ray of light from a denser medium strike a rarer medium at an angle of incidence \(i\) (see Fig). The reflected and refracted rays make an angle of \(90^{\circ}\) with each other. The angles of reflection and refraction are \(r\) and \(r\prime\) The critical angle is
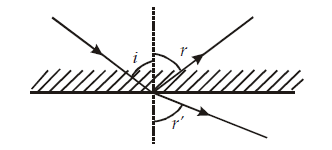 CorrectIncorrect
CorrectIncorrect -
Question 36 of 50
36. Question
1 point(s)When a ray of light enters a glass slab from air
CorrectIncorrect -
Question 37 of 50
37. Question
1 point(s)A point like object is placed at a distance of \(1 \mathrm{~m}\) in front of a convex lens of focal length \(0.5 \mathrm{~m}\). A plane mirror is placed at a distance of \(2 \mathrm{~m}\) behind the lens. The position and nature of the final image formed by the system is:
CorrectIncorrect -
Question 38 of 50
38. Question
1 point(s)A double convex lens has power \(P\) and same radii of curvature \(R\) of both the surfaces. The radius of curvature of a surface of a plano-convex lens made of the same material with power \(1.5 \mathrm{P}\) is :
CorrectIncorrect -
Question 39 of 50
39. Question
1 point(s)For a concave lens of focal length \(f\), the relation between object and image distances \(u\) and \(v\), respectively, from its pole can best be represented by \((u=v\) is the reference line) :
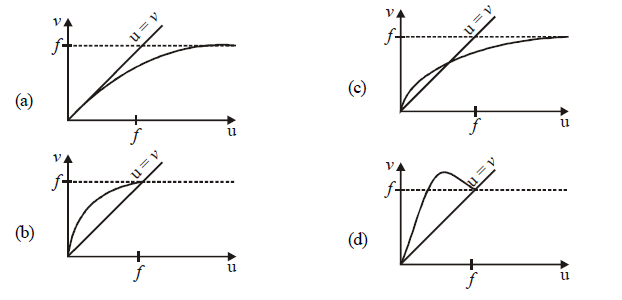 CorrectIncorrect
CorrectIncorrect -
Question 40 of 50
40. Question
1 point(s)A thin lens made of glass (refractive index \(=1.5\) ) of focal length \(f=16 \mathrm{~cm}\) is immersed in a liquid of refractive index 1.42. If its focal length in liquid is \(f_l\), then the ratio \(f_l / f\) is closest to the integer:
CorrectIncorrect -
Question 41 of 50
41. Question
1 point(s)One plano-convex and one plano-concave lens of same radius of curvature ‘ \(R\) ‘ but of different materials are joined side by side as shown in the figure. If the refractive index of the material of 1 is \(\mu_1\) and that of 2 is \(\mu_2\), then the focal length of the combination is :
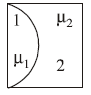 CorrectIncorrect
CorrectIncorrect -
Question 42 of 50
42. Question
1 point(s)The graph shows how the magnification \(m\) produced by a thin lens varies with image distance \(v\). What is the focal length of the lens used?
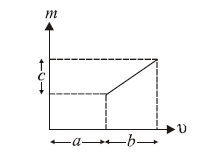 CorrectIncorrect
CorrectIncorrect -
Question 43 of 50
43. Question
1 point(s)A thin convex lens \(L\) (refractive index \(=1.5\) ) is placed on a plane mirror \(M\). When a pin is placed at \(A\), such that \(O A\) \(=18 \mathrm{~cm}\), its real inverted image is formed at A itself, as shown in the figure. When a liquid of refractive index \(\mu_{\mathrm{i}}\) is put between the lens and the mirror, the pin has to be moved to \(A^{\prime}\), such that \(\mathrm{OA}^{\prime}=27 \mathrm{~cm}\), to get its inverted real image at A’ itself. The value of \(\mu_{\mathrm{i}}\) will be:
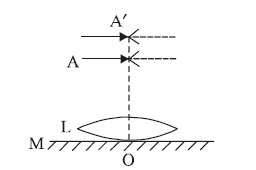 CorrectIncorrect
CorrectIncorrect -
Question 44 of 50
44. Question
1 point(s)An upright object is placed at a distance of \(40 \mathrm{~cm}\) in front of a convergent lens of focal length \(20 \mathrm{~cm}\). A convergent mirror of focal length \(10 \mathrm{~cm}\) is placed at a distance of 60 \(\mathrm{cm}\) on the other side of the lens. The position and size of the final image will be :
CorrectIncorrect -
Question 45 of 50
45. Question
1 point(s)A convex lens (of focal length \(20 \mathrm{~cm}\) ) and a concave mirror, having their principal axes along the same lines, are kept \(80 \mathrm{~cm}\) apart from each other. The concave mirror is to the right of the convex lens. When an object is kept at a distance of \(30 \mathrm{~cm}\) to the left of the convex lens, its image remains at the same position even if the concave mirror is removed. The maximum distance of the object for which this concave mirror, by itself would produce a virtual image would be :
CorrectIncorrect -
Question 46 of 50
46. Question
1 point(s)What is the position and nature of the image formed by the lens combination shown in the figure? \(\left(f_1, f_2\right.\) are focal lengths)
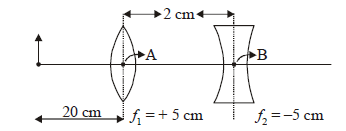 CorrectIncorrect
CorrectIncorrect -
Question 47 of 50
47. Question
1 point(s)The formation of real image using a biconvex lens is shown below:
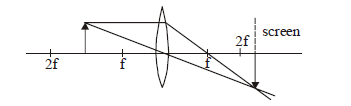
If the whole setup is immersed in water without disturbing the object and the screen positions, what will one observe on the screen?
CorrectIncorrect -
Question 48 of 50
48. Question
1 point(s)An object is at a distance of \(20 \mathrm{~m}\) from a convex lens of focal length \(0.3 \mathrm{~m}\). The lens forms an image of the object. If the object moves away from the lens at a speed of \(5 \mathrm{~m} / \mathrm{s}\), the speed and direction of the image will be:
CorrectIncorrect -
Question 49 of 50
49. Question
1 point(s)A plano convex lens of refractive index \(\mu_1\) and focal length \(f_1\) is kept in contact with another plano concave lens of refractive index \(\mu_2\) and focal length \(f_2\) If the radius of curvature of their spherical faces is \(\mathrm{R}\) each and \(f_1=2 f_2\), then \(\mu_1\) and \(\mu_2\) are related as:
CorrectIncorrect -
Question 50 of 50
50. Question
1 point(s)The eye can be regarded as a single refracting surface. The radius of curvature of this surface is equal to that of the cornea \((7.8 \mathrm{~mm})\). This surface separates two media of refractive indices 1 and 1.34. Calculate the distance from the refracting surface at which a parallel beam of light will come to focus.
CorrectIncorrect