JEE Physics Test Series Quiz-8
Quiz Summary
0 of 50 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 50 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 50
1. Question
1 point(s)In the figure below, P and Q are two equally intense coherent sources emitting radiation of wavelength \(20 \mathrm{~m}\). The separation between P and Q is \(5 \mathrm{~m}\) and the phase of P is ahead of that of Q by \(90^{\circ}\). A, B and C are three distinct points of observation, each equidistant from the midpoint of PQ. The intensities of radiation at A, B, C will be in the ratio:
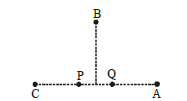 CorrectIncorrect
CorrectIncorrect -
Question 2 of 50
2. Question
1 point(s)Two coherent sources of sound, \(S_1\) and \(S_2\), produce sound waves of the same wavelength, \(\lambda=1 \mathrm{~m}\), in phase. \(S_1\) and \(S_2\) are placed \(1.5 \mathrm{~m}\) apart (see fig.). A listener, located at \(L\), directly in front of \(S_2\) finds that the intensity is at a minimum when he is \(2 \mathrm{~m}\) away from \(S_2[latex]. The listener moves away from [latex]S_1\), keeping his distance from \(S_2\) fixed. The adjacent maximum of intensity is observed when the listener is at a distance \(d\) from \(S_1\). Then, \(d\) is :
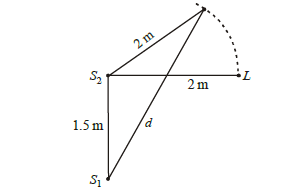 CorrectIncorrect
CorrectIncorrect -
Question 3 of 50
3. Question
1 point(s)Two light waves having the same wavelength \(\lambda\) in vacuum are in phase initially. Then the first wave travels a path \(L_1\) through a medium of refractive index \(n_1\) while the second wave travels a path of length \(L_2\) through a medium of refractive index \(n_2\). After this the phase difference between the two waves is:
CorrectIncorrect -
Question 4 of 50
4. Question
1 point(s)In an interference experiment the ratio of amplitudes of coherent waves is \(\frac{a_1}{a_2}=\frac{1}{3}\). The ratio of maximum and minimum intensities of fringes will be:
CorrectIncorrect -
Question 5 of 50
5. Question
1 point(s)Two coherent sources produce waves of different intensities which interfere. After interference, the ratio of the maximum intensity to the minimum intensity is 16. The intensity of the waves are in the ratio:
CorrectIncorrect -
Question 6 of 50
6. Question
1 point(s)On a hot summer night, the refractive index of air is smallest near the ground and increases with height from the ground. When a light beam is directed horizontally, the Huygens’ principle leads us to conclude that as it travels, the light beam:
CorrectIncorrect -
Question 7 of 50
7. Question
1 point(s)An interference pattern is observed at ‘ \(\mathrm{P}\) ‘ due to the superimposition of two rays coming out from a source ‘ \(\mathrm{S}\) ‘ as shown in the figure. The value of ‘ \(l\) ‘ for which maxima is obtained at ‘ \(P\) ‘ is:
( \(R\) is perfect reflecting surface)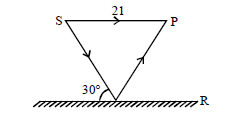 CorrectIncorrect
CorrectIncorrect -
Question 8 of 50
8. Question
1 point(s)In the adjacent diagram, \(C P\) represents a wavefront and \(A O \& B P\), the corresponding two rays. Find the condition on \(\theta\) for constructive interference at \(P\) between the ray \(B P\) and reflected ray \(O P\)
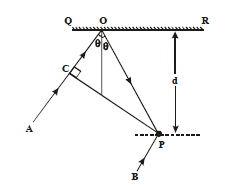 CorrectIncorrect
CorrectIncorrect -
Question 9 of 50
9. Question
1 point(s)Two beams of light having intensities \(I\) and \(4 I\) interfere to produce a fringe pattern on a screen. The phase difference between the beams is \(\pi / 2\) at point \(A\) and \(\pi\) at point \(B\). Then the difference between the resultant intensities at \(A\) and \(B\) is
CorrectIncorrect -
Question 10 of 50
10. Question
1 point(s)A thin slice is cut out of a glass cylinder along a plane parallel to its axis. The slice is placed on a flat glass plate as shown in Figure. The observed interference fringes from this combination shall be
 CorrectIncorrect
CorrectIncorrect -
Question 11 of 50
11. Question
1 point(s)Two coherent monochromatic light beams of intensities \(I\) and \(4 I\) are superposed. The maximum and minimum possible intensities in the resulting beam are
CorrectIncorrect -
Question 12 of 50
12. Question
1 point(s)In a Young’s double slit experiment, light of \(500 \mathrm{~nm}\) is used to produce an interference pattern. When the distance between the slits is \(0.05 \mathrm{~mm}\), the angular width (in degree) of the fringes formed on the distance screen is close to :
CorrectIncorrect -
Question 13 of 50
13. Question
1 point(s)Interference fringes are observed on a screen by illuminating two thin slits \(1 \mathrm{~mm}\) apart with a light source \((\lambda\) \(=632.8 \mathrm{~nm}\) ). The distance between the screen and the slits is \(100 \mathrm{~cm}\). If a bright fringe is observed on a screen at a distance of \(1.27 \mathrm{~mm}\) from the central bright fringe, then the path difference between the waves, which are reaching this point from the slits is close to :
CorrectIncorrect -
Question 14 of 50
14. Question
1 point(s)In a Young’s double slit experiment, 16 fringes are observed in a certain segment of the screen when light of wavelength \(700 \mathrm{~nm}\) is used. If the wavelength of light is changed to \(400 \mathrm{~nm}\), the number of fringes observed in the same segment of the screen would be :
CorrectIncorrect -
Question 15 of 50
15. Question
1 point(s)In a double-slit experiment, at a certain point on the screen the path difference between the two interfering waves is \(\frac{1}{8}\) th of a wavelength. The ratio of the intensity of light at that point to that at the centre of a bright fringe is:
CorrectIncorrect -
Question 16 of 50
16. Question
1 point(s)In a Young’s double slit experiment, the separation between the slits is \(0.15 \mathrm{~mm}\). In the experiment, a source of light of wavelength \(589 \mathrm{~nm}\) is used and the interference pattern is observed on a screen kept \(1.5 \mathrm{~m}\) away. The separation between the successive bright fringes on the screen is:
CorrectIncorrect -
Question 17 of 50
17. Question
1 point(s)In a double slit experiment, when a thin film of thickness \(t\) having refractive index \(\mu\) is introduced in front of one of the slits, the maximum at the centre of the fringe pattern shifts by one fringe width. The value of \(t\) is \((\approx\) is the wavelength of the light used) :
CorrectIncorrect -
Question 18 of 50
18. Question
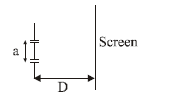
1 point(s)The figure shows a Young’s double slit experimental setup. It is observed that when a thin transparent sheet of thickness \(t\) and refractive index \(1 / 4\) is put in front of one of the slits, the central maximum gets shifted by a distance equal to \(\mathrm{n}\) fringe widths. If the wavelength of light used is \(», \mathrm{t}\) will be:
 CorrectIncorrect
CorrectIncorrect -
Question 19 of 50
19. Question
1 point(s)In a Young’s double slit experiment, the path difference, at a certain point on the screen, betwen two interfering waves is \(\frac{1}{8}\) th of wavelength. The ratio of the intensity at this point to that at the centre of a bright fringe is close to:
CorrectIncorrect -
Question 20 of 50
20. Question
1 point(s)In a Young’s double slit experiment with slit separation \(0.1 \mathrm{~mm}\), one observes a bright fringe at angle \(\frac{1}{40} \mathrm{rad}\) by using light of wavelength \(\lambda_1\) When the light of wavelength \(\lambda_2\) is used a bright fringe is seen at the same angle in the same setup. Given that \(\lambda_1\) and \(\lambda_2\) are in visible range ( \(380 \mathrm{~nm}\) to \(740 \mathrm{~nm}\) ), their values are:
CorrectIncorrect -
Question 21 of 50
21. Question
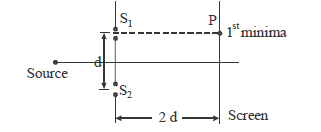
1 point(s)Consider a Young’s double slit experiment as shown in the figure. What should be the slit separation \(d\) in terms of wavelength \(\lambda\) such that the first minima occurs directly in front of the slit \(\left(\mathrm{S}_1\right)\)?
 CorrectIncorrect
CorrectIncorrect -
Question 22 of 50
22. Question
1 point(s)In a Young’s double slit experiment, the slits are placed \(0.320 \mathrm{~mm}\) apart. Light of wavelength \(\lambda=500 \mathrm{~nm}\) is incident on the slits. The total number of bright fringes that are observed in the angular range \(-30^{\circ} \leq \theta \leq 30^{\circ}\) is
CorrectIncorrect -
Question 23 of 50
23. Question
1 point(s)In a Young’s double slit experiment, slits are separated by \(0.5 \mathrm{~mm}\), and the screen is placed \(150 \mathrm{~cm}\) away. A beam of light consisting of two wavelengths, \(650 \mathrm{~nm}\) and \(520 \mathrm{~nm}\), is used to obtain interference fringes on the screen. The least distance from the common central maximum to the point where the bright fringes due to both the wavelengths coincide is :
CorrectIncorrect -
Question 24 of 50
24. Question
1 point(s)In a Young’s double slit experiment with light of wavelength \(\lambda\) the separation of slits is \(d\) and distance of screen is \(D\) such that \(D \gg d \gg \lambda\). If the fringe width is \(\beta\), the distance from point of maximum intensity to the point where intensity falls to half of maximum intensity on either side is:
CorrectIncorrect -
Question 25 of 50
25. Question
1 point(s)In Young’s double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
CorrectIncorrect -
Question 26 of 50
26. Question
1 point(s)For a plane electromagnetic wave, the magnetic field at a point \(x\) and time \(t\) is
\(
\overrightarrow{\mathrm{B}}(x, t)=\left\lceil 1.2 \times 10^{-7} \sin \left(0.5 \times 10^3 x+1.5 \times 10^{11} t\right) \hat{k}\right\rceil \mathrm{T}
\)
The instantaneous electric field \(\vec{E}\) corresponding to \(\vec{B}\) is:
\(
\text { (speed of light } \mathrm{c}=3 \times 10^8 \mathrm{~ms}^{-1} \text { ) }
\)CorrectIncorrect -
Question 27 of 50
27. Question
1 point(s)An electron is constrained to move along the \(y\)-axis with a speed of \(0.1 c\) ( \(c\) is the speed of light) in the presence of electromagnetic wave, whose electric field is \(\vec{E}=30 \hat{\mathrm{j}}\) \(\sin \left(1.5 \times 10^7 t-5 \times 10^{-2} x\right) \mathrm{V} / \mathrm{m}\). The maximum magnetic force experienced by the electron will be :
(given \(c=3 \times 10^8 \mathrm{~ms}^{-1} \&\) electron charge \(=1.6 \times 10^{-19} \mathrm{C}\) )CorrectIncorrect -
Question 28 of 50
28. Question
1 point(s)The electric field of a plane electromagnetic wave is given by \(\vec{E}=E_0(\hat{x}+\hat{y}) \sin (k z-\omega t)\)
Its magnetic field will be given by:CorrectIncorrect -
Question 29 of 50
29. Question
1 point(s)The magnetic field of a plane electromagnetic wave is
\(
\vec{B}=3 \times 10^{-8} \sin [200 \pi(y+c t)] \hat{i} T
\)
where \(c=3 \times 10^8 \mathrm{~ms}^{-1}\) is the speed of light.
The corresponding electric field is :CorrectIncorrect -
Question 30 of 50
30. Question
1 point(s)The electric field of a plane electromagnetic wave propagating along the \(x\) direction in vacuum is \(\vec{E}=E_0 \hat{j} \cos (\omega t-k x)\). The magnetic field \(\vec{B}\), at the moment \(t=0\) is :
CorrectIncorrect -
Question 31 of 50
31. Question
1 point(s)A plane electromagnetic wave, has frequency of \(2.0 \times 10^{10}\) \(\mathrm{Hz}\) and its energy density is \(1.02 \times 10^{-8} \mathrm{~J} / \mathrm{m}^3\) in vacuum. The amplitude of the magnetic field of the wave is close to \(\left(\frac{1}{4 \pi \varepsilon_0}=9 \times 10^9 \frac{\mathrm{Nm}^2}{\mathrm{C}^2}\right.\) and speed of light \(\left.=3 \times 10^8 \mathrm{~ms}^{-1}\right)\) :
CorrectIncorrect -
Question 32 of 50
32. Question
1 point(s)In a plane electromagnetic wave, the directions of electric field and magnetic field are represented by \(\hat{k}\) and \(2 \hat{i}-2 \hat{j}\), respectively. What is the unit vector along direction of propagation of the wave.
CorrectIncorrect -
Question 33 of 50
33. Question
1 point(s)A plane electromagnetic wave is propagating along the direction \(\frac{\hat{i}+\hat{j}}{\sqrt{2}}\), with its polarization along the direction \(\hat{k}\). The correct form of the magnetic field of the wave would be (here \(\mathrm{B}_0\) is an appropriate constant):
CorrectIncorrect -
Question 34 of 50
34. Question
1 point(s)A plane electromagnetic wave of frequency \(25 \mathrm{GHz}\) is propagating in vacuum along the \(z\)-direction. At a particular point in space and time, the magnetic field is given by \(\vec{B}=5 \times 10^{-8} \hat{j} T\). The corresponding electric field \(\vec{E}\) is (speed of light \(c=3 \times 10^8 \mathrm{~ms}^{-1}\) )
CorrectIncorrect -
Question 35 of 50
35. Question
1 point(s)If the magnetic field in a plane electromagnetic wave is given by \(\vec{B}=3 \times 10^{-8} \sin \left(1.6 \times 10^3 x+48 \times 10^{10} \mathrm{t}\right) \hat{j} \mathrm{~T}\), then what will be expression for electric field?
CorrectIncorrect -
Question 36 of 50
36. Question
1 point(s)The electric field of a plane electromagnetic wave is given by
\(
\vec{E}=E_0 \frac{\hat{i}+\hat{j}}{\sqrt{2}} \cos (k z+\omega t)
\)
At \(t=0\), a positively charged particle is at the point \((x, y, z)=\left(0,0, \frac{\pi}{k}\right)\). If its instantaneous velocity at \((t=0)\)
is \(v_0 \hat{k}\), the force acting on it due to the wave is:CorrectIncorrect -
Question 37 of 50
37. Question
1 point(s)An electromagnetic wave is represented by the electric field \(\vec{E}=E_0 \hat{n} \sin [\omega \mathrm{t}+(6 \mathrm{y}-8 \mathrm{z})]\). Taking unit vectors in \(x, y\) and \(z\) directions to be \(\hat{i}, \hat{j}, \hat{k}\), the direction of propagation \(\hat{s}\) is :
CorrectIncorrect -
Question 38 of 50
38. Question
1 point(s)A plane electromagnetic wave having a frequency \(y=23.9 \mathrm{GHz}\) propagates along the positive \(z\)-direction in free space. The peak value of the Electric Field is \(60 \mathrm{~V} / \mathrm{m}\). Which among the following is the acceptable magnetic field component in the electromagnetic wave?
CorrectIncorrect -
Question 39 of 50
39. Question
1 point(s)The electric field of a plane electromagnetic wave is given by \(\overrightarrow{\mathrm{E}}=\mathrm{E}_0 \hat{\mathrm{i}} \cos (\mathrm{kz}) \cos (\omega \mathrm{t})\)
The corresponding magnetic field is then given by:CorrectIncorrect -
Question 40 of 50
40. Question
1 point(s)Light is incident normally on a completely absorbing surface with an energy flux of \(25 \mathrm{Wcm}^{-2}\). If the surface has an area of \(25 \mathrm{~cm}^2\), the momentum transferred to the surface in \(40 \mathrm{~min}\) time duration will be:
CorrectIncorrect -
Question 41 of 50
41. Question
1 point(s)A plane electromagnetic wave of frequency \(50 \mathrm{MHz}\) travels in free space along the positive \(x\)-direction. At a particular point in space and time, \(\overrightarrow{\mathrm{E}}=6.3 \hat{j} \mathrm{~V} / \mathrm{m}\). The corresponding magnetic field \(\overrightarrow{\mathrm{B}}\), at that point will be:
CorrectIncorrect -
Question 42 of 50
42. Question
1 point(s)\(50 \mathrm{~W} / \mathrm{m}^2\) energy density of sunlight is normally incident on the surface of a solar panel. Some part of incident energy \((25 \%)\) is reflected from the surface and the rest is absorbed. The force exerted on \(1 \mathrm{~m}^2\) surface area will be close to \(\left(\mathrm{c}=3 \times 10^8 \mathrm{~m} / \mathrm{s}\right)\) :
CorrectIncorrect -
Question 43 of 50
43. Question
1 point(s)A plane electromagnetic wave travels in free space along the \(x\)-direction. The electric field component of the wave at a particular point of space and time is \(\mathrm{E}=6 \mathrm{Vm}^{-1}\) along \(y\)-direction. Its corresponding magnetic field component, B would be:
CorrectIncorrect -
Question 44 of 50
44. Question
1 point(s)The magnetic field of an electromagnetic wave is given by: \(\overrightarrow{\mathrm{B}}=1.6 \times 10^{-6} \cos \left(2 \times 10^7 z+6 \times 10^{15} t\right)(2 \hat{i}+\hat{j}) \frac{\mathrm{Wb}}{\mathrm{m}^2}\)
The associated electric field will be :CorrectIncorrect -
Question 45 of 50
45. Question
1 point(s)The mean intensity of radiation on the surface of the Sun is about \(10^8 \mathrm{~W} / \mathrm{m}^2\). The rms value of the corresponding magnetic field is closest to :
CorrectIncorrect -
Question 46 of 50
46. Question
1 point(s)An electromagnetic wave of intensity \(50 \mathrm{Wm}^{-2}\) enters in a medium of refractive index ‘ \(n\) ‘ without any loss. The ratio of the magnitudes of electric fields, and the ratio of the magnitudes of magnetic fields of the wave before and after entering into the medium are respectively, given by:
CorrectIncorrect -
Question 47 of 50
47. Question
1 point(s)A \(27 \mathrm{~mW}\) laser beam has a cross-sectional area of \(10 \mathrm{~mm}^2\). The magnitude of the maximum electric field in this electromagnetic wave is given by:
[Given permittivity of space \(\epsilon_0=9 \times 10^{-12}\) SI units, Speed of light \(\mathrm{c}=3 \times 10^8 \mathrm{~m} / \mathrm{s}\) ]CorrectIncorrect -
Question 48 of 50
48. Question
1 point(s)If the magnetic field of a plane electromagnetic wave is given by (The speed of light \(=3 \times 10^8 \mathrm{~m} / \mathrm{s}\) )
\(
B=100 \times 10^{-6} \sin \left[2 \pi \times 2 \times 10^{15}\left(t-\frac{x}{c}\right)\right]
\)
then the maximum electric field associated with it is:CorrectIncorrect -
Question 49 of 50
49. Question
1 point(s)The electric field of a plane polarized electromagnetic wave in free space at time \(t=0\) is given by an expression \(\overrightarrow{\mathrm{E}}(x, y)=10 \mathrm{j} \cos [(6 x+8 z)]\)
The magnetic field \(\overrightarrow{\mathrm{B}}(x, z, t)\) is given by: (c is the velocity of light)CorrectIncorrect -
Question 50 of 50
50. Question
1 point(s)An EM wave from air enters a medium. The electric fields are \(\vec{E}_1=E_{01} \hat{x} \cos \left[2 \pi v\left(\frac{z}{c}-t\right)\right]\) in air and \(\vec{E}_2=E_{02} \hat{x} \cos [k(2 z-c t)]\) in medium, where the wave number \(k\) and frequency \(v\) refer to their values in air. The medium is nonmagnetic. If \(\epsilon_{r_1}\) and \(\epsilon_{r_2}\) refer to relative permittivities of air and medium respectively, which of the following options is correct?
CorrectIncorrect