Jee Math Test Series Quiz-5
Multiple choice questions with one correct answer
Quiz Summary
0 of 50 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 50 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 50
1. Question
If the system of linear equations,
\(
\begin{gathered}
x+y+z=6 \\
x+2 y+3 z=10 \\
3 x+2 y+\lambda z=\mu
\end{gathered}
\)
has more two solutions, then \(\mu-\lambda^2\) is equal toCorrectIncorrectHint
System has intfinitely many solution
\(
\begin{aligned}
& \Rightarrow\left|\begin{array}{lll}
1 & 1 & 1 \\
1 & 2 & 3 \\
3 & 2 & \lambda
\end{array}\right|=0 \\
& \Rightarrow \lambda=1 \\
& D_1=\left|\begin{array}{ccc}
6 & 1 & 1 \\
10 & 2 & 3 \\
\mu & 2 & 1
\end{array}\right|=0 \\
& \mu=14 \\
& \mu-\lambda^2=13
\end{aligned}
\) -
Question 2 of 50
2. Question
If the system of linear equations
\(
\begin{aligned}
& 2 x+2 a y+a z=0 \\
& 2 x+3 b y+b z=0 \\
& 2 x+4 c y+c z=0
\end{aligned}
\)
where \(\mathrm{a}, \mathrm{b}, \mathrm{c} \in \mathrm{R}\) are non-zero and distinct; has a non-zero solution, then :CorrectIncorrectHint
For non-zero solution
\(
\left|\begin{array}{ccc}
2 & 2 \mathrm{a} & \mathrm{a} \\
2 & 3 \mathrm{~b} & \mathrm{~b} \\
2 & 4 \mathrm{c} & \mathrm{c}
\end{array}\right|=0, \Rightarrow\left|\begin{array}{ccc}
1 & 2 \mathrm{a} & \mathrm{a} \\
0 & 3 \mathrm{~b}-2 \mathrm{a} & \mathrm{b}-\mathrm{a} \\
0 & 4 \mathrm{c}-2 \mathrm{a} & \mathrm{c}-\mathrm{a}
\end{array}\right|=0
\)
\(
\begin{aligned}
& \Rightarrow(3 \mathrm{~b}-2 \mathrm{a})(\mathrm{c}-\mathrm{a})-(\mathrm{b}-\mathrm{a})(4 \mathrm{c}-2 \mathrm{a})=0 \\
& \Rightarrow 2 \mathrm{ac}=\mathrm{bc}+\mathrm{ab} \\
& \Rightarrow \frac{2}{\mathrm{~b}}=\frac{1}{\mathrm{a}}+\frac{1}{\mathrm{c}} \text { Hence } \frac{1}{\mathrm{a}}, \frac{1}{\mathrm{~b}}, \frac{1}{\mathrm{c}} \text { are in A.P. }
\end{aligned}
\) -
Question 3 of 50
3. Question
The system of linear equations
\(
\begin{aligned}
& \lambda x+2 y+2 z=5 \\
& 2 \lambda x+3 y+5 z=8 \\
& 4 x+\lambda y+6 z=10 \text { has }
\end{aligned}
\)CorrectIncorrectHint
\(
\begin{aligned}
& \mathrm{D}=\left|\begin{array}{ccc}
\lambda & 3 & 2 \\
2 \lambda & 3 & 5 \\
4 & \lambda & 6
\end{array}\right|=(\lambda+8)(2-\lambda) \\
& \text { for } \lambda=2 ; \mathrm{D}_1 \neq 0
\end{aligned}
\)Hence, no solution for \(\lambda=2\)
-
Question 4 of 50
4. Question
For which of the following ordered pairs \((\mu, \delta)\), the system of linear equations
\(
\begin{aligned}
& x+2 y+3 z=1 \\
& 3 x+4 y+5 z=\mu \\
& 4 x+4 y+4 z=\delta
\end{aligned}
\)
is inconsistent?CorrectIncorrectHint
\(
\begin{aligned}
& 2 \times(\mathrm{ii})-2 \times(\mathrm{i})-(\mathrm{iii}): \\
& 0=2 \mu-2-\delta \\
& \Rightarrow \delta=2(\mu-1)
\end{aligned}
\) -
Question 5 of 50
5. Question
The following system of linear equations
\(
\begin{aligned}
& 7 x+6 y-2 z=0 \\
& 3 x+4 y+2 z=0 \\
& x-2 y-6 z=0, \text { has }
\end{aligned}
\)CorrectIncorrectHint
\(
\begin{aligned}
& 7 x+6 y-2 z=0 \\
& 3 x+4 y+2 z=0 \\
& x-2 y-6 z=0
\end{aligned}
\)
\(
\Delta=\left|\begin{array}{ccc}
7 & 6 & -2 \\
3 & 4 & 2 \\
1 & -2 & -6
\end{array}\right|=0 \Rightarrow \text { infinite solutions }
\)
Now (1) \(+(2) \Rightarrow y=-x\) put in (1), (2) & (3) all will lead to \(x=2 z\) -
Question 6 of 50
6. Question
Let \(S\) be the set of all \(\lambda \in R\) for which the system of linear equations
\(
\begin{aligned}
& 2 x-y+2 z=2 \\
& x-2 y+\lambda z=-4 \\
& x+\lambda y+z=4
\end{aligned}
\)
has no solution. Then the set \(\mathrm{S}\)CorrectIncorrectHint
\(
\begin{aligned}
& 2 x-y+2 z=2 \\
& x-2 y+\lambda z=-4 \\
& x+\lambda y+z=4
\end{aligned}
\)
For no solution :
\(
\begin{aligned}
& \mathrm{D}=\left|\begin{array}{ccc}
2 & -1 & 2 \\
1 & -2 & \lambda \\
1 & \lambda & 1
\end{array}\right|=0 \\
& \Rightarrow 2\left(-2-\lambda^2\right)+1(1-\lambda)+2(\lambda+2)=0 \\
& \Rightarrow-2 \lambda^2+\lambda+1=0 \\
& \Rightarrow \lambda=1,-\frac{1}{2} \\
& \mathrm{D}_{\mathrm{x}}=\left|\begin{array}{ccc}
2 & -1 & 2 \\
-4 & 2 & \lambda \\
4 & \lambda & 1
\end{array}\right|=2\left|\begin{array}{ccc}
1 & -1 & 2 \\
-2 & -2 & \lambda \\
\lambda & \lambda & 1
\end{array}\right| \\
& =2(1+\lambda)
\end{aligned}
\)
whichis not equal to zero for
\(
\lambda=1,-\frac{1}{2}
\) -
Question 7 of 50
7. Question
Let \(\mathrm{S}\) be the set of all integer solutions, \((x, y, z)\), of the system of equations
\(
\begin{aligned}
& x-2 y+5 z=0 \\
& -2 x+4 y+z=0 \\
& -7 x+14 y+9 z=0
\end{aligned}
\)
such that \(15 \leq x^2+y^2+z^2 \leq 150\). Then, the number of elements in the set \(\mathrm{S}\) is equal toCorrectIncorrectHint
\(
\Delta=\left|\begin{array}{ccc}
1 & -2 & 5 \\
-2 & 4 & 1 \\
-7 & 14 & 9
\end{array}\right|=0
\)
Let \(\mathrm{x}=\mathrm{k}\)
\(
\begin{aligned}
& \Rightarrow \text { Put in (1) \& (2) } \\
& k-2 y+5 z=0 \\
& -2 k+4 y+z=0
\end{aligned}
\)
\(
\mathrm{z}=0, \mathrm{y}=\frac{\mathrm{k}}{2}
\)
\(\therefore \mathrm{x}, \mathrm{y}, \mathrm{z}\) are integer
\(\Rightarrow \mathrm{k}\) is even integer
Now \(x=k, y=\frac{k}{2}, z=0\) put in condition
\(
\begin{aligned}
& 15 \leq \mathrm{k}^2+\left(\frac{\mathrm{k}}{2}\right)^2+0 \leq 150 \\
& 12 \leq \mathrm{k}^2 \leq 120 \\
& \Rightarrow \mathrm{k}= \pm 4, \pm 6, \pm 8, \pm 10 \\
& \Rightarrow \text { Number of element in } \mathrm{S}=8 .
\end{aligned}
\) -
Question 8 of 50
8. Question
If the system of equations
\(
\begin{aligned}
& x-2 y+3 z=9 \\
& 2 x+y+z=b \\
& x-7 y+a z=24
\end{aligned}
\)
has infinitely many solutions, then \(a-b\) is equal toCorrectIncorrectHint
\(\mathrm{D}=\left|\begin{array}{ccc}1 & -2 & 3 \\ 2 & 1 & 1 \\ 1 & -7 & \mathrm{a}\end{array}\right|=0 \Rightarrow \mathrm{a}=8\)
also, \(D_1=\left|\begin{array}{ccc}9 & -2 & 3 \\ b & 1 & 1 \\ 24 & -7 & 8\end{array}\right|=0 \Rightarrow b=3\)
hence, \(a-b=8-3=5\) -
Question 9 of 50
9. Question
If the system of equations
\(
\begin{aligned}
& x+y+z=2 \\
& 2 x+4 y-z=6 \\
& 3 x+2 y+\lambda z=\mu
\end{aligned}
\)
has infinitely many solutions, then :CorrectIncorrectHint
For infinite solutions
\(
\Delta=\Delta_{\mathrm{x}}=\Delta_{\mathrm{y}}=\Delta_{\mathrm{z}} \quad=0
\)
Now \(\Delta=0 \Rightarrow\left|\begin{array}{ccc}1 & 1 & 1 \\ 2 & 4 & -1 \\ 3 & 2 & \lambda\end{array}\right|=0\)
\(
\begin{aligned}
& \Rightarrow \lambda=\frac{9}{2} \\
& \Delta_{x=0} \Rightarrow\left|\begin{array}{rrr}
2 & 1 & 1 \\
6 & 4 & -1 \\
\mu & 2 & -\frac{9}{2}
\end{array}\right|=0 \\
& \Rightarrow \mu=5
\end{aligned}
\)
For \(\lambda=\frac{9}{2} \& \mu=5, \Delta_y=\Delta_z=0\)
Now check option \(2 \lambda+\mu=14\) -
Question 10 of 50
10. Question
If the minimum and the maximum values of the function \(\mathrm{f}:\left[\frac{\pi}{4}, \frac{\pi}{2}\right] \rightarrow \mathrm{R}\), defined by : \(f(\theta)=\left|\begin{array}{ccc}-\sin ^2 \theta & -1-\sin ^2 \theta & 1 \\ -\cos ^2 \theta & -1-\cos ^2 \theta & 1 \\ 12 & 10 & -2\end{array}\right|\) are \(m\) and \(M\) respectively, then the ordered pair \((\mathrm{m}, \mathrm{M})\) is equal to:
CorrectIncorrectHint
\(
\begin{aligned}
&\mathrm{C}_3 \rightarrow \mathrm{C}_3-\left(\mathrm{C}_1-\mathrm{C}_2\right)\\
&f(\theta)=\left|\begin{array}{ccc}
-\sin ^2 \theta & -1-\sin ^2 \theta & 0 \\
-\cos ^2 \theta & -1-\cos ^2 \theta & 0 \\
12 & 10 & -4
\end{array}\right|
\end{aligned}
\)
\(
\begin{aligned}
& =-4\left[\left(1+\cos ^2 \theta\right) \sin ^2 \theta-\cos ^2 \theta\left(1+\sin ^2 \theta\right)\right] \\
& =-4\left[\sin ^2 \theta+\sin ^2 \theta \cos ^2 \theta-\cos ^2 \theta-\cos ^2 \theta \sin ^2 \theta \right.
\end{aligned}
\)
\(
\begin{aligned}
& \mathrm{f}(\theta)=4 \cos 2 \theta \\
& \theta \in\left[\frac{\pi}{4}, \frac{\pi}{2}\right] \\
& 2 \theta \in\left[\frac{\pi}{2}, \pi\right] \\
& f(\theta) \in[-4,0] \\
& (\mathrm{m}, \mathrm{M})=(-4,0)
\end{aligned}
\) -
Question 11 of 50
11. Question
Let \(\lambda \in \mathrm{R}\). The system of linear equations
\(
\begin{aligned}
& 2 \mathrm{x}_1-4 \mathrm{x}_2+\lambda \mathrm{x}_3=1 \\
& \mathrm{x}_1-6 \mathrm{x}_2+\mathrm{x}_3=2 \\
& \lambda \mathrm{x}_1-10 \mathrm{x}_2+4 \mathrm{x}_3=3
\end{aligned}
\)
is inconsistent for :CorrectIncorrectHint
\(
\mathrm{D}=\left|\begin{array}{ccc}
2 & -4 & \lambda \\
1 & -6 & 1 \\
\lambda & -10 & 4
\end{array}\right|
\)
\(
\begin{aligned}
& =2(3 \lambda+2)(\lambda-3) \\
& D_1=-2(\lambda-3) \\
& D_2=-2(\lambda+1)(\lambda-3) \\
& D_3=-2(\lambda-3)
\end{aligned}
\)
When \(\lambda=3\), then
\(
\mathrm{D}=\mathrm{D}_1=\mathrm{D}_2=\mathrm{D}_3=0
\)
\(\Rightarrow\) Infinite many solution
when \(\lambda=-\frac{2}{3}\) then \(D_1, D_2, D_3\) none of them is zero so equations are inconsistant
\(
\therefore \lambda=-\frac{2}{3}
\) -
Question 12 of 50
12. Question
If the system of linear equations
\(
\begin{aligned}
& x+y+3 z=0 \\
& x+3 y+k^2 z=0 \\
& 3 x+y+3 z=0
\end{aligned}
\)
has a non-zero solution \((x, y, z)\) for some \(k \in R\), then \(x+\left(\frac{y}{z}\right)\) is equal to :CorrectIncorrectHint
\(
\begin{aligned}
& x+y+3 z=0 \dots(i) \\
& x+3 y+k^2 z=0 \dots(ii) \\
& 3 x+y+3 z=0 \dots(iii)
\end{aligned}
\)
\(
\begin{aligned}
& \left|\begin{array}{ccc}
1 & 1 & 3 \\
1 & 3 & \mathrm{k}^2 \\
3 & 1 & 3
\end{array}\right|=0 \\
& \Rightarrow 9+3+3 \mathrm{k}^2-27-\mathrm{k}^2-3=0 \\
& \Rightarrow \mathrm{k}^2=9
\end{aligned}
\)
(i) – (iii) \(\Rightarrow-2 \mathrm{x}=0 \Rightarrow \mathrm{x}=0\)Now from (i) \(\Rightarrow y+3 z=0\)
\(
\begin{aligned}
& \Rightarrow \frac{y}{z}=-3 \\
& x+\frac{y}{z}=-3
\end{aligned}
\) -
Question 13 of 50
13. Question
If \(\mathrm{a}+\mathrm{x}=\mathrm{b}+\mathrm{y}=\mathrm{c}+\mathrm{z}+1\), where \(\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{x}\), \(y, z\) are non-zero distinct real numbers, then \(\left|\begin{array}{lll}x & a+y & x+a \\ y & b+y & y+b \\ z & c+y & z+c\end{array}\right|\) is equal to :
CorrectIncorrectHint
\(
a+x=b+y=c+z+1
\)
\(
\left|\begin{array}{lll}
x & a+y & x+a \\
y & b+y & y+b \\
z & c+y & z+c
\end{array}\right| \quad C_3 \rightarrow C_3-C_1
\)
\(
\left|\begin{array}{lll}
x & a+y & a \\
y & b+y & b \\
z & c+y & c
\end{array}\right| \quad \quad C_2 \rightarrow C_2-C_3
\)
\(
\left|\begin{array}{ccc}
x & y & a \\
y & y & b \\
z & y & c
\end{array}\right| \quad R_3 \rightarrow R_3-R_1, R_2 \rightarrow R_2-R_1
\)
\(
\left|\begin{array}{ccc}
x & y & a \\
y-x & 0 & b-a \\
z-x & 0 & c-a
\end{array}\right|
\)
\(
\begin{aligned}
& =(-y)[(y-x)(c-a)-(b-a)(z-x)] \\
& =(-y)[(a-b)(c-a)+(a-b)(a-c-1)] \\
& =(-y)[(a-b)(c-a)+(a-b)(a-c)+b-a) \\
& =-y(b-a)=y(a-b)
\end{aligned}
\) -
Question 14 of 50
14. Question
The values of \(\lambda\) and \(\mu\) for which the system of linear equations
\(
\begin{aligned}
& x+y+z=2 \\
& x+2 y+3 z=5 \\
& x+3 y+\lambda z=\mu
\end{aligned}
\)
has infinitely many solutions are, respectivelyCorrectIncorrectHint
For infinite many solutions
\(
\mathrm{D}=\mathrm{D}_1=\mathrm{D}_2=\mathrm{D}_3=0
\)
Now \(D=\left|\begin{array}{lll}1 & 1 & 1 \\ 1 & 2 & 3 \\ 1 & 3 & \lambda\end{array}\right|=0\)
\(
\begin{aligned}
& 1 .(2 \lambda-9)-1 .(\lambda-3)+1 .(3-2)=0 \\
& \therefore \lambda=5
\end{aligned}
\)
Now \(D_1=\left|\begin{array}{lll}2 & 1 & 1 \\ 5 & 2 & 3 \\ \mu & 3 & 5\end{array}\right|=0\)
\(
\begin{aligned}
& 2(10-9)-1(25-3 \mu)+1(15-2 \mu)=0 \\
& \mu=8
\end{aligned}
\) -
Question 15 of 50
15. Question
Let \(\mathrm{m}\) and \(\mathrm{M}\) be respectively the minimum and maximum values of
\(
\left|\begin{array}{ccc}
\cos ^2 x & 1+\sin ^2 x & \sin 2 x \\
1+\cos ^2 x & \sin ^2 x & \sin 2 x \\
\cos ^2 x & \sin ^2 x & 1+\sin 2 x
\end{array}\right|
\)
Then the ordered pair \((\mathrm{m}, \mathrm{M})\) is equal toCorrectIncorrectHint
\(
\left|\begin{array}{ccc}
\cos ^2 x & 1+\sin ^2 x & \sin 2 x \\
1+\cos ^2 x & \sin ^2 x & \sin 2 x \\
\cos ^2 x & \sin ^2 x & 1+\sin 2 x
\end{array}\right|
\)
\(
\mathrm{R}_1 \rightarrow \mathrm{R}_1-\mathrm{R}_2, \mathrm{R}_2 \rightarrow \mathrm{R}_2-\mathrm{R}_3
\)
\(
\left|\begin{array}{ccc}
-1 & 1 & 0 \\
1 & 0 & -1 \\
\cos ^2 x & \sin ^2 x & 1+\sin 2 x
\end{array}\right|
\)
\(
\begin{aligned}
& =-1\left(\sin ^2 \mathrm{x}\right)-1\left(1+\sin 2 \mathrm{x}+\cos ^2 \mathrm{x}\right) \\
& =-\sin 2 \mathrm{x}-2 \\
& \mathrm{~m}=-3, \mathrm{M}=-1
\end{aligned}
\) -
Question 16 of 50
16. Question
The sum of distinct values of \(\lambda\) for which the system of equations
\(
\begin{aligned}
& (\lambda-1) \mathrm{x}+(3 \lambda+1) \mathrm{y}+2 \lambda \mathrm{z}=0 \\
& (\lambda-1) \mathrm{x}+(4 \lambda-2) \mathrm{y}+(\lambda+3) \mathrm{z}=0 \\
& 2 \mathrm{x}+(3 \lambda+1) \mathrm{y}+3(\lambda-1) \mathrm{z}=0,
\end{aligned}
\)
has non-zero solutions, isCorrectIncorrectHint
\(
\begin{aligned}
& (\lambda-1) \mathrm{x}+(3 \lambda+1) \mathrm{y}+2 \lambda \mathrm{z}=0 \\
& (\lambda-1) \mathrm{x}+(4 \lambda-2) \mathrm{y}+(\lambda+3) \mathrm{z}=0 \\
& 2 \mathrm{x}+(3 \lambda+1) \mathrm{y}+(3 \lambda-3) \mathrm{z}=0 \\
& \left|\begin{array}{ccc}
\lambda-1 & 3 \lambda+1 & 2 \lambda \\
\lambda-1 & 4 \lambda-2 & \lambda+3 \\
2 & 3 \lambda+1 & 3 \lambda-3
\end{array}\right|=0 \\
& \mathrm{R}_1 \rightarrow \mathrm{R}_1-\mathrm{R}_2 \& \mathrm{R}_2 \rightarrow \mathrm{R}_2-\mathrm{R}_3 \\
& \left|\begin{array}{ccc}
0 & 3-\lambda & \lambda-3 \\
\lambda-3 & \lambda-3 & -2(\lambda-3) \\
2 & 3 \lambda+1 & 3 \lambda-3
\end{array}\right|=0 \\
& (\lambda-3)^2\left|\begin{array}{ccc}
0 & -1 & 1 \\
1 & 1 & -2 \\
2 & 3 \lambda+1 & 3 \lambda-3
\end{array}\right|=0 \\
& (\lambda-3)^2[(3 \lambda+1)+(3 \lambda-1)]=0 \\
& 6 \lambda(\lambda-3)^2=0 \Rightarrow \lambda=0,3 \\
& \text { Sum }=3 \\
&
\end{aligned}
\) -
Question 17 of 50
17. Question
The least value of the product \(x y z\) for which the determinant \(\left|\begin{array}{ccc}\mathrm{x} & 1 & 1 \\ 1 & \mathrm{y} & 1 \\ 1 & 1 & \mathrm{z}\end{array}\right|\) is non-negative, is :
CorrectIncorrectHint
\(
\begin{aligned}
& \left|\begin{array}{ccc}
x & 1 & 1 \\
1 & y & 1 \\
1 & 1 & z
\end{array}\right| \geq 0 \\
& x y z-x-y-z+2 \geq 0
\end{aligned}
\)
\(
\begin{aligned}
& x y z+2 \geq x+y+z \geq 3(x y z)^{1 / 3} \\
& x y z+2-3(x y z)^{1 / 3} \geq 0 \\
& u t(x y z)=t^3 \\
& t^3-3 t+2 \geq 0 \\
& (t+2)(t-1)^2 \geq 0 \\
& {[t=-2] t^3=-8}
\end{aligned}
\) -
Question 18 of 50
18. Question
\(
\text { If } f(\theta)=\left|\begin{array}{ccc}
1 & \cos \theta & 1 \\
-\sin \theta & 1 & -\cos \theta \\
-1 & \sin \theta & 1
\end{array}\right| \text { and }
\)
\(A\) and \(B\) are respectively the maximum and the minimum values of \(f(\theta)\), then (A, B) is equal to:CorrectIncorrectHint
Let \(f(\theta)=\left|\begin{array}{ccc}1 & \cos \theta & 1 \\ -\sin \theta & 1 & -\cos \theta \\ -1 & \sin \theta & 1\end{array}\right|\)
\(
\begin{aligned}
& =(1+\sin \theta \cos \theta)-\cos \theta(-\sin \theta-\cos \theta)+1\left(-\sin ^2 \theta+1\right) \\
& =1+\sin \theta \cos \theta+\sin \theta \cos \theta+\cos ^2 \theta-\sin ^2 \theta+1 \\
& =2+2 \sin \theta \cos \theta+\cos 2 \theta \\
& =2+\sin 2 \theta+\cos 2 \theta \dots(1)
\end{aligned}
\)
Now, the maximum value of (1) is \(2+\sqrt{1^2+1^2}=2+\sqrt{2}\) and the minimum value of (1) is
\(
2-\sqrt{1^2+1^2}=2-\sqrt{2} \text {. }
\) -
Question 19 of 50
19. Question
If \(B\) is a \(3 \times 3\) matrix such that \(B^2=0\), then det. \(\left[(I+B)^{50}-50 B\right]\) is equal to:
CorrectIncorrectHint
\(
\begin{aligned}
& \operatorname{det}\left[(\mathrm{I}+\mathrm{B})^{50}-50 \mathrm{~B}\right] \\
& =\operatorname{det}\left[{ }^{50} \mathrm{C}_0 \mathrm{I}+{ }^{50} \mathrm{C}_1 \mathrm{~B}+{ }^{50} \mathrm{C}_2 \mathrm{~B}^2+{ }^{50} \mathrm{C}_3 \mathrm{~B}^3+\ldots\right. \\
& \left.\quad+{ }^{50} \mathrm{C}_{50} \mathrm{~B}^{50} \mathrm{~B}^{50}-50 \mathrm{~B}\right]
\end{aligned}
\)
{All terms having \(\mathrm{B}^{\mathrm{n}}, 2 \leq n \leq 50\)
will be zero because given that \(\mathrm{B}^2=0\) \}
\(
=\operatorname{det}[\mathrm{I}+50 \mathrm{~B}-50 \mathrm{~B}]=\operatorname{det}[\mathrm{I}]=1
\) -
Question 20 of 50
20. Question
Let \(S=\left\{\left(\begin{array}{ll}a_{11} & a_{12} \\ a_{21} & a_{22}\end{array}\right): a_{i j} \in\{0,1,2\}, a_{11}=a_{22}\right\}\)
Then the number of non-singular matrices in the set \(\mathrm{S}\) is:CorrectIncorrectHint
(d) The matrices in the form
\(
\left[\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right], a_{i j} \in\{0,1,2\}, a_{11}=a_{12} \text { are }
\)
\(
\left[\begin{array}{cc}
0 & 0 / 1 / 2 \\
0 / 1 / 2 & 0
\end{array}\right],\left[\begin{array}{cc}
1 & 0 / 1 / 2 \\
0 / 1 / 2 & 1
\end{array}\right],\left[\begin{array}{cc}
2 & 0 / 1 / 2 \\
0 / 1 / 2 & 2
\end{array}\right]
\)
At any place, \(0 / 1 / 2\) means 0,1 or 2 will be the element at that place.Hence there aretotal \(27=3 \times 3+3 \times 3+3 \times 3\) ) matrices of the above form. Out of which the matrices which are singular are
\(
\left[\begin{array}{cc}
0 & 0 / 1 / 2 \\
0 & 0
\end{array}\right],\left[\begin{array}{cc}
0 & 0 \\
1 / 2 & 0
\end{array}\right],\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right],\left[\begin{array}{ll}
2 & 2 \\
2 & 2
\end{array}\right]
\)
Hence there are total \(7(=3+2+1+1)\) singular matrices. Therefore number of all non-singular matrices in the given form \(=27-7=20\) -
Question 21 of 50
21. Question
Let \(A\), other than \(I\) or \(-I\), be a \(2 \times 2\) real matrix such that \(A^2=I\), \(I\) being the unit matrix. Let \(\operatorname{Tr}(A)\) be the sum of diagonal elements of \(A\).
Statement-1: \(\operatorname{Tr}(A)=0\)
Statement-2: \(\operatorname{det}(A)=-1\)CorrectIncorrectHint
\(
\begin{aligned}
& {\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]=\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]} \\
& {\left[\begin{array}{ll}
a^2+b c & a b+b d \\
a c+c d & b c+d^2
\end{array}\right]=\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]}
\end{aligned}
\)
\(
\begin{aligned}
& b(a+d)=0, b=0 \text { or } a=-d \dots(1)\\
& c(a+d)=0, c=0 \text { or } a=-d \dots(2) \\
& a^2+b c=1, b c+d^2=1 \dots(3)
\end{aligned}
\)
‘ \(a\) ‘ and ‘ \(d\) ‘ are diagonal elements \(a+d=0\) statement- 1 is correct.Now, \(\operatorname{det}(A)=a d – b c\)
Now, from (3) \(a^2+b c=1\) and \(d^2+b c=1\)
So, \(a^2-d^2=0\)
Adding \(a^2+d^2+2 b c=2\)
\(\Rightarrow(a+d)^2-2 a d+2 b c=2\)
or \(0-2(a d-b c)=2\)
So, \(a d-b c=1 \Rightarrow \operatorname{det}(A)=-1\)
So, statement -2 is also true.
But statement -2 is not the correct explanation of statement-1. -
Question 22 of 50
22. Question
Statement-1: Determinant of a skew-symmetric matrix of order 3 is zero.
Statement-2 : For any matrix \(A, \operatorname{det}(A)^T=\operatorname{det}(A)\) and \(\operatorname{det}(-A)=-\operatorname{det}(A)\).
Where det (B) denotes the determinant of matrix B. Then:CorrectIncorrectHint
(d) Statement-1: Determinant of skew symmetric matrix of odd order is zero.
Statement-2 \(: \operatorname{det}\left(A^T\right)=\operatorname{det}(\mathrm{A})\).
\(\operatorname{det}(-\mathrm{A})=-(-1)^{\mathrm{n}} \operatorname{det}(\mathrm{A})\).
where \(\mathrm{A}\) is a \(n \times n\) order matrix. -
Question 23 of 50
23. Question
Let \(A\) be a \(2 \times 2\) matrix with non-zero entries and let \(A^2=I\), where \(I\) is \(2 \times 2\) identity matrix. Define \(\operatorname{Tr}(A)=\) sum of diagonal elements of \(A\) and \(|A|=\) determinant of matrix \(A\).
Statement – 1: \(\operatorname{Tr}(A)=0\).
Statement -2: \(|A|=1\).CorrectIncorrectHint
\(
\text { (b) Let } A=\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right) \text { where a, b, c, d } \neq 0
\)
\(
A^2=\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)
\)
\(
\Rightarrow A^2=\left(\begin{array}{ll}
a^2+b c & a b+b d \\
a c+c d & b c+d^2
\end{array}\right)
\)
\(
\begin{aligned}
& \Rightarrow a^2+b c=1, b c+d^2=1 \\
& a b+b d=a c+c d=0 \\
& c \neq 0 \text { and } b \neq 0 \Rightarrow a+d=0 \\
& |A|=a d-b c=-a^2-b c=-1
\end{aligned}
\) -
Question 24 of 50
24. Question
Let \(A\) be \(a 2 \times 2\) matrix with real entries. Let \(I\) be the \(2 \times 2\) identity matrix. Denote by \(\operatorname{tr}(A)\), the sum of diagonal entries of \(a\). Assume that \(A^2=I\).
Statement-1: If \(A \neq I\) and \(A \neq-I\), then \(\operatorname{det}(A)=-1\)
Statement-2 : If \(A \neq I\) and \(A \neq-I\), then \(\operatorname{tr}(A) \neq 0\).CorrectIncorrectHint
(d) Let \(A=\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]\) then \(A^2=\mathrm{I}\)
\(
\Rightarrow a^2+b c=1 \text { and } a b+b d=0
\)
\(a c+c d=0\) and \(b c+d^2=1\)
From these four relations,
\(
a^2+b c=b c+d^2 \Rightarrow a^2=d^2
\)
and
\(
b(a+d)=0=c(a+d) \Rightarrow a=-d
\)
We can take \(a=1, b=0, c=0, d=-1\) as one possible set of values, then \(A=\left[\begin{array}{cc}1 & 0 \\ 0 & -1\end{array}\right]\)
Clearly \(A \neq I\) and \(A \neq-I\) and \(\operatorname{det} A=-1\)
\(\therefore\) Statement 1 is true.
Also if \(A \neq I\) then \(\operatorname{tr}(A)=0\)
\(\therefore\) Statement 2 is false. -
Question 25 of 50
25. Question
Let \(A=\left|\begin{array}{ccc}5 & 5 \alpha & \alpha \\ 0 & \alpha & 5 \alpha \\ 0 & 0 & 5\end{array}\right|\). If \(\left|A^2\right|=25\), then \(|\alpha|\) equals
CorrectIncorrectHint
(a) Given \(A=\left[\begin{array}{ccc}5 & 5 \alpha & \alpha \\ 0 & \alpha & 5 \alpha \\ 0 & 0 & 5\end{array}\right]\) and \(\left|A^2\right|=25\)
\(
\begin{aligned}
& \therefore A^2=\left[\begin{array}{ccc}
5 & 5 \alpha & \alpha \\
0 & \alpha & 5 \alpha \\
0 & 0 & 5
\end{array}\right]\left[\begin{array}{ccc}
5 & 5 \alpha & \alpha \\
0 & \alpha & 5 \alpha \\
0 & 0 & 5
\end{array}\right] \\
& =\left[\begin{array}{ccc}
25 & 25 \alpha+5 \alpha^2 & 5 \alpha+25 \alpha^2+5 \alpha \\
0 & \alpha^2 & 5 \alpha^2+25 \alpha \\
0 & 0 & 25
\end{array}\right] \\
& \therefore\left|A^2\right|=25\left(25 \alpha^2\right) \\
& \therefore 25=25\left(25 \alpha^2\right) \Rightarrow|\alpha|=\frac{1}{5}
\end{aligned}
\) -
Question 26 of 50
26. Question
If \(1, \omega, \omega^2\) are the cube roots of unity, then \(\Delta=\left|\begin{array}{ccc}1 & \omega^n & \omega^{2 n} \\ \omega^n & \omega^{2 n} & 1 \\ \omega^{2 n} & 1 & \omega^n\end{array}\right|\) is equal to
CorrectIncorrectHint
\(
\begin{aligned}
\Delta & =\left|\begin{array}{ccc}
1 & \omega^n & \omega^{2 n} \\
\omega^n & \omega^{2 n} & 1 \\
\omega^{2 n} & 1 & \omega^n
\end{array}\right| \\
& =1\left(\omega^{3 n}-1\right)-\omega^n\left(\omega^{2 n}-\omega^{2 n}\right)+\omega^{2 n}\left(\omega^n-\omega^{4 n}\right) \\
& =\omega^{3 n}-1-0+\omega^{3 n}-\omega^{6 n} \\
& =1-1+1-1=0\left[\because \omega^{3 n}=1\right]
\end{aligned}
\) -
Question 27 of 50
27. Question
Let \(\mathrm{k}\) be an integer such that triangle with vertices \((\mathrm{k},-3 \mathrm{k}),(5, \mathrm{k})\) and \((-\mathrm{k}, 2)\) has area 28 sq. units. Then the orthocentre of this triangle is at the point :
CorrectIncorrectHint
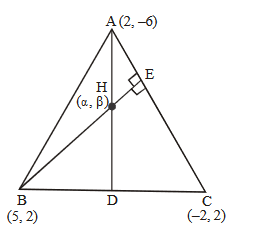
(a) We have
\(
\begin{aligned}
& \quad \frac{1}{2}\left|\begin{array}{ccc}
\mathrm{k} & -3 \mathrm{k} & 1 \\
5 & \mathrm{k} & 1 \\
-\mathrm{k} & 2 & 1
\end{array}\right|=28 \\
& \Rightarrow 5 \mathrm{k}^2+13 \mathrm{k}-46=0 \\
& \text { or } 5 \mathrm{k}^2+13 \mathrm{k}+66=0 \\
& \text { Now, } 5 \mathrm{k}^2+13 \mathrm{k}-46=0 \\
& \Rightarrow \quad \mathrm{k}=\frac{-13 \pm \sqrt{1089}}{10} \\
& \therefore \quad \mathrm{k}=\frac{-23}{5} ; \mathrm{k}=2
\end{aligned}
\)
since \(\mathrm{k}\) is an integer, \(\therefore \mathrm{k}=2\)
Also \(5 k^2+13 k+66=0\)
\(
\Rightarrow \mathrm{k}=\frac{-13 \pm \sqrt{-1151}}{10}
\)
So no real solution exist
For orthocentre
\(
\begin{aligned}
& \mathrm{BH} \perp \mathrm{AC} \\
& \therefore \quad\left(\frac{\beta-2}{\alpha-5}\right)\left(\frac{8}{-4}\right)=-1 \\
& \Rightarrow \quad \alpha-2 \beta=1 \dots(a)
\end{aligned}
\)
Also \(\mathrm{CH} \perp \mathrm{AB}\)
\(
\begin{aligned}
& \therefore \quad\left(\frac{\beta-2}{\alpha+2}\right)\left(\frac{8}{3}\right)=-1 \\
& \Rightarrow \quad 3 \alpha+8 \beta=10 \dots(b)
\end{aligned}
\)
Solving (a) and (b), we get
\(
\alpha=2, \beta=\frac{1}{2}
\)
orthocentre is \(\left(2, \frac{1}{2}\right)\) -
Question 28 of 50
28. Question
Let \(\omega\) be a complex number such that \(2 \omega+1=z\) where \(z=\) \(\sqrt{-3}\). If \(\left|\begin{array}{ccc}1 & 1 & 1 \\ 1 & -\omega^2-1 & \omega^2 \\ 1 & \omega^2 & \omega^7\end{array}\right|=3 \mathrm{k}\), then \(\mathrm{k}\) is equal to :
CorrectIncorrectHint
(b) Given \(2 \omega+1=\mathrm{z}\);
\(
\begin{aligned}
& z=\sqrt{3} i \\
& \Rightarrow \omega=\frac{\sqrt{3} i-1}{2}
\end{aligned}
\)
\(\Rightarrow \omega\) is complex cube root of unity Applying \(\mathrm{R}_1 \rightarrow \mathrm{R}_1+\mathrm{R}_2+\mathrm{R}_3\)
\(
\begin{aligned}
& =\left|\begin{array}{ccc}
3 & 0 & 0 \\
1 & -\omega^2-1 & \omega^2 \\
1 & \omega^2 & \omega
\end{array}\right| \\
& =3(-1-\omega-\omega)=-3(1+2 \omega)=-3 \mathrm{z} \\
& \Rightarrow \mathrm{k}=-\mathrm{z}
\end{aligned}
\) -
Question 29 of 50
29. Question
The number of distinct real roots of the equation, \(\left|\begin{array}{ccc}\cos x & \sin x & \sin x \\ \sin x & \cos x & \sin x \\ \sin x & \sin x & \cos x\end{array}\right|=0\) in the interval \(\left[-\frac{\pi}{4}, \frac{\pi}{4}\right]\) is :
CorrectIncorrectHint
(c)
\(
\begin{aligned}
& \left|\begin{array}{lll}
\cos x & \sin x & \sin x \\
\sin x & \cos x & \sin x \\
\sin x & \sin x & \cos x
\end{array}\right|=0 \\
& R_1 \rightarrow R_1-R_2 \\
& R_2 \rightarrow R_2-R_3
\end{aligned}
\)
\(
\begin{aligned}
& \left|\begin{array}{ccc}
\cos x-\sin x & \sin x-\cos x & 0 \\
0 & \cos x-\sin x & \sin x-\cos x \\
\sin x & \sin x & \cos x
\end{array}\right|=0 \\
& C_2 \rightarrow C_2+C_3 \\
& \left|\begin{array}{ccc}
\cos x-\sin x & \sin x-\cos x & 0 \\
0 & 0 & \sin x-\cos x \\
\sin x & \sin x & \cos x
\end{array}\right|=0 \\
& \text { Expanding using second row }
\end{aligned}
\)
\(
\begin{aligned}
& 2 \sin x(\sin x-\cos x)^2=0 \\
& \sin x=0 \text { or } \sin x=\cos x \\
& x=0 \text { or } x=\frac{\pi}{4}
\end{aligned}
\) -
Question 30 of 50
30. Question
If \(\alpha, \beta \neq 0\), and \(f(n)=\alpha^n+\beta^n\) and
\(
\left|\begin{array}{ccc}
3 & 1+f(1) & 1+f(2) \\
1+f(1) & 1+f(2) & 1+f(3) \\
1+f(2) & 1+f(3) & 1+f(4)
\end{array}\right|=K(1-\alpha)^2(1-\beta)^2(\alpha-\beta)^2
\)
then \(K\) is equal to:CorrectIncorrectHint
\(
\begin{aligned}
& \left|\begin{array}{ccc}
3 & 1+f(1) & 1+f(2) \\
1+f(1) & 1+f(2) & 1+f(3) \\
1+f(2) & 1+f(3) & 1+f(4)
\end{array}\right| \\
& =\left|\begin{array}{ccc}
1+1+1 & 1+\alpha+\beta & 1+\alpha^2+\beta^2 \\
1+\alpha+\beta & 1+\alpha^2+\beta^2 & 1+\alpha^3+\beta^3 \\
1+\alpha^2+\beta^2 & 1+\alpha^3+\beta^3 & 1+\alpha^4+\beta^4
\end{array}\right| \\
& =\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & \alpha & \beta \\
1 & \alpha^2 & \beta^2
\end{array}\right| \times\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & \alpha & \beta \\
1 & \alpha^2 & \beta^2
\end{array}\right| \\
& =\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & \alpha & \beta \\
1 & \alpha^2 & \beta^2
\end{array}\right|=[(1-\alpha)(1-\beta)(\alpha-\beta)]^2
\end{aligned}
\)
\(
\text { So, } K=1
\) -
Question 31 of 50
31. Question
If \(\Delta_{\mathrm{r}}=\left|\begin{array}{ccc}\mathrm{r} & 2 \mathrm{r}-1 & 3 \mathrm{r}-2 \\ \frac{\mathrm{n}}{2} & \mathrm{n}-1 & \mathrm{a} \\ \frac{1}{2} \mathrm{n}(\mathrm{n}-1) & (\mathrm{n}-1)^2 & \frac{1}{2}(\mathrm{n}-1)(3 \mathrm{n}-4)\end{array}\right|\) then the value of \(\sum_{\mathrm{r}=1}^{\mathrm{n}-1} \Delta_{\mathrm{r}}\)
CorrectIncorrectHint
\(
\sum_{r=1}^{n-1} r=1+2+3+\ldots+(n-1)=\frac{n(n-1)}{2}
\)
\(
\sum_{r=1}^{n-1}(2 r-1)=1+3+5+\ldots+[2(n-1)-2]=(n-1)^2
\)
\(
\sum_{r=1}^{n-1}(3 r-2)=1+4+7+\ldots+(3 n-3-2)=\frac{(n-1)(3 n-4)}{2}
\)
\(
\therefore \sum_{r=1}^{n-1} \Delta_r=\left|\begin{array}{ccc}
\Sigma r & \Sigma(2 r-1) & \Sigma(3 r-2) \\
\frac{n}{2} & n-1 & a \\
\frac{n(n-1)}{2} & (n-1)^2 & \frac{(n-1)(3 n-4)}{2}
\end{array}\right|
\)
\(\sum_{r=1}^{n-1} \Delta_r\) consists of \((n-1)\) determinants in L.H.S. and in R.H.S every constituent of first row consists of \((n-1)\) elements and hence it can be splitted into sum of \((n-1)\) determinants.
\(
\therefore \sum_{r=1}^{n-1} \Delta_r=\left|\begin{array}{ccc}
\frac{n(n-1)}{2} & (n-1)^2 & \frac{(n-1)(3 n-4)}{2} \\
\frac{n}{2} & n-1 & a \\
\frac{n(n-1)}{2} & (n-1)^2 & \frac{(n-1)(3 n-4)}{2}=0
\end{array}\right|
\)
\(\left(\because \mathrm{R}_1\right.\) and \(\mathrm{R}_3\) are identical)
Hence, value of \(\sum_{r=1}^{n-1} \Delta_{\mathrm{r}}\) is independent of both ‘ \(a\) ‘ and ‘ \(n\) ‘. -
Question 32 of 50
32. Question
If
\(
\left|\begin{array}{ccc}
\mathrm{a}^2 & \mathrm{~b}^2 & \mathrm{c}^2 \\
(\mathrm{a}+\lambda)^2 & (\mathrm{~b}+\lambda)^2 & (\mathrm{c}+\lambda)^2 \\
(\mathrm{a}-\lambda)^2 & (\mathrm{~b}-\lambda)^2 & (\mathrm{c}-\lambda)^2
\end{array}\right|=\mathrm{k} \lambda\left|\begin{array}{ccc}
\mathrm{a}^2 & \mathrm{~b}^2 & \mathrm{c}^2 \\
\mathrm{a} & \mathrm{b} & \mathrm{c} \\
1 & 1 & 1
\end{array}\right|, \lambda \neq 0
\)
then \(\mathrm{k}\) is equal to:CorrectIncorrectHint
\(
\text { Let } \Delta=\left|\begin{array}{ccc}
a^2 & b^2 & c^2 \\
(a+\lambda)^2 & (b+\lambda)^2 & (c+\lambda)^2 \\
(a-\lambda)^2 & (b-\lambda)^2 & (c-\lambda)^2
\end{array}\right|
\)
\(
\text { Apply } R_2 \rightarrow R_2-R_3
\)
\(
\Delta=\left|\begin{array}{ccc}
a^2 & b^2 & c^2 \\
(a+\lambda)^2-(a-\lambda)^2 & (b+\lambda)^2-(b-\lambda)^2 & (c+\lambda)^2-(c-\lambda)^2 \\
(a-\lambda)^2 & (b-\lambda)^2 & (c-\lambda)^2
\end{array}\right|
\)
\(
=\left|\begin{array}{ccc}
a^2 & b^2 & c^2 \\
4 a \lambda & 4 b \lambda & 4 c \lambda \\
(a-\lambda)^2 & (b-\lambda)^2 & (c-\lambda)^2
\end{array}\right|
\)
\(
\left(\because(x+y)^2-(x-y)^2=4 x y\right)
\)
Taking out 4 common from \(\mathrm{R}_2\)
\(
=4\left|\begin{array}{ccc}
a^2 & b^2 & c^2 \\
a \lambda & b \lambda & c \lambda \\
a^2+\lambda^2-2 a \lambda & b^2+\lambda^2-2 b \lambda & c^2+\lambda^2-2 c \lambda
\end{array}\right|
\)
Apply \(R_3 \rightarrow\left[R_3-\left(R_1-2 R_2\right)\right]\)
\(
=4\left|\begin{array}{lll}
a^2 & b^2 & c^2 \\
a \lambda & b \lambda & c \lambda \\
\lambda^2 & \lambda^2 & \lambda^2
\end{array}\right|
\)
Taking out \(\lambda\) common from \(\mathrm{R}_2\) and \(\lambda^2\) from \(\mathrm{R}_3\).
\(
=4 \lambda\left(\lambda^2\right)\left|\begin{array}{ccc}
a^2 & b^2 & c^2 \\
a & b & c \\
1 & 1 & 1
\end{array}\right|
\)
\(
\begin{aligned}
& =k \lambda\left|\begin{array}{lll}
a^2 & b^2 & c^2 \\
a & b & c \\
1 & 1 & 1
\end{array}\right| \\
& \Rightarrow k=4 \lambda^2
\end{aligned}
\) -
Question 33 of 50
33. Question
If \(a, b, c\) are sides of a scalene triangle, then the value of \(\left|\begin{array}{lll}a & b & c \\ b & c & a \\ c & a & b\end{array}\right|\) is :
CorrectIncorrectHint
\(
\begin{aligned}
& \left|\begin{array}{ccc}
a & b & c \\
b & c & a \\
c & a & b
\end{array}\right|=\left|\begin{array}{ccc}
a+b+c & a+b+c & a+b+c \\
b & c & a \\
c & a & b
\end{array}\right| \\
= & (a+b+c)\left|\begin{array}{ccc}
1 & 1 & 1 \\
b & c & a \\
c & a & b
\end{array}\right| \\
= & (a+b+c)\left|\begin{array}{ccc}
0 & 0 & 1 \\
b-c & c-a & a \\
c-a & a-b & b
\end{array}\right| \\
= & (a+b+c)\left[a b+b c+c a-a^2-b^2-c^2\right] \\
= & -(a+b+c)\left[(a-b)^2+(b-c)^2+(c-a)^2\right]
\end{aligned}
\)
Since \(a, b, c\) are sides of \(a\) scalene triangle, therefore at least two of the \(a, b, c\) will be unequal.
\(
(a-b)^2+(b-c)^2+(c-a)^2>0
\)
Also \(a+b+c>0\)
\(
-(a+b+c)\left[(a-b)^2+(b-c)^2+(c-a)^2\right]<0
\) -
Question 34 of 50
34. Question
If \(a, b, c\), are non zero complex numbers satisfying \(a^2+b^2+c^2=0\) and
\(\left|\begin{array}{ccc}b^2+c^2 & a b & a c \\ a b & c^2+a^2 & b c \\ a c & b c & a^2+b^2\end{array}\right|=k a^2 b^2 c^2\), then \(k\) is equal toCorrectIncorrectHint
Let \(\Delta=\left|\begin{array}{ccc}b^2+c^2 & a b & a c \\ a b & c^2+a^2 & b c \\ a c & b c & a^2+b^2\end{array}\right|\)
Multiply \(C_1\) by \(a, C_2\) by b and \(C_3\) by \(\mathrm{c}\) and hence divide by \(a b c\).
\(
=\frac{1}{a b c}\left|\begin{array}{ccc}
a\left(b^2+c^2\right) & a b^2 & a c^2 \\
a^2 b & b\left(c^2+a^2\right) & b c^2 \\
a^2 c & b^2 c & c\left(a^2+b^2\right)
\end{array}\right|
\)
Take out \(a, b, c\) common from \(R_1, R_2\) and \(R_3\) respectively.
\(
\Delta=\frac{a b c}{a b c}\left|\begin{array}{ccc}
b^2+c^2 & b^2 & c^2 \\
a^2 & c^2+a^2 & c^2 \\
a^2 & b^2 & a^2+b^2
\end{array}\right|
\)
Apply \(C_1 \rightarrow C_1-C_2-C_3\)
\(
\begin{aligned}
& \Delta=\left|\begin{array}{ccc}
0 & b^2 & c^2 \\
-2 c^2 & c^2+a^2 & c^2 \\
-2 b^2 & b^2 & a^2+b^2
\end{array}\right| \\
& =-2\left|\begin{array}{ccc}
0 & b^2 & c^2 \\
c^2 & c^2+a^2 & c^2 \\
b^2 & b^2 & a^2+b^2
\end{array}\right|
\end{aligned}
\)
Apply \(C_2-C_1\) and \(C_3-C_1\)
\(
\begin{aligned}
& =-2\left|\begin{array}{ccc}
0 & b^2 & c^2 \\
c^2 & a^2 & 0 \\
b^2 & 0 & a^2
\end{array}\right| \\
& =-2\left[-b^2\left(c^2 a^2\right)+c^2\left(-a^2 b^2\right)\right] \\
& =2 a^2 b^2 c^2+2 a^2 b^2 c^2=4 a^2 b^2 c^2 \\
& \text { But } \Delta=k a^2 b^2 c^2 \therefore k=4
\end{aligned}
\) -
Question 35 of 50
35. Question
If \(\left|\begin{array}{ccc}-2 a & a+b & a+c \\ b+a & -2 b & b+c \\ c+a & b+c & -2 c\end{array}\right|=\alpha(a+b)(b+c)(c+a) \neq 0\) then \(\alpha\) is equal to
CorrectIncorrectHint
Let \(\Delta=\left|\begin{array}{ccc}-2 a & a+b & a+c \\ b+a & -2 b & b+c \\ c+a & b+c & -2 c\end{array}\right|\) Applying \(C_1+C_3\) and \(C_2+C_3\) \(\Delta=\left|\begin{array}{ccc}-a+c & 2 a+b+c & a+c \\ 2 b+a+c & -b+c & b+c \\ a-c & b-c & -2 c\end{array}\right|\) Now, applying \(R_1+R_3\) and \(R_2+R_3\)
\(
\Delta=\left|\begin{array}{ccc}
0 & 2(a+b) & a-c \\
2(a+b) & 0 & b-c \\
a-c & b-c & -2 c
\end{array}\right|
\)
On expanding, we get
\(
\begin{aligned}
\Delta= & -2(a+b)\{-2 c[2(a+b)] \\
& \quad-(a-c)(b-c)\} \\
& +(a-c)[2(a+b)(b-c)] \\
\Delta= & 8 \mathrm{c}(a+b)(a+b) \\
& \quad+4(a+b)(a-c)(b-c) \\
= & 4(a+b)\left[2 a c+2 b c+a b-b c-a c+c^2\right] \\
= & 4(a+b)\left[a c+b c+a b+c^2\right] \\
= & 4(a+b)[c(a+c)+b(a+c)] \\
= & 4(a+b)(b+c)(c+a) \\
= & \alpha(a+b)(b+c)(c+a)
\end{aligned}
\)
Hence, \(\alpha=4\) -
Question 36 of 50
36. Question
The area of the triangle whose vertices are complex numbers \(z, i z, z+i z\) in the Argand diagram is
CorrectIncorrectHint
(b) Vertices of triangle in complex form is \(z, i z, z+i z\)
In cartesian form vertices are \((x, y),(-y, x)\) and \((x-y, x+y)\)
\(
\begin{aligned}
& \therefore \text { Area of triangle }=\frac{1}{2}\left|\begin{array}{ccc}
x & y & 1 \\
-y & x & 1 \\
x-y & x+y & 1
\end{array}\right| \\
& =\frac{1}{2}[x(x-x-y)-y(-y-x+y)+1 \\
& \left.\left(-y x-y^2-x^2+x y\right)\right]
\end{aligned}
\)
\(
=\frac{1}{2}\left[-x y+x y-y^2-x^2\right]=\frac{1}{2}\left(x^2+y^2\right)
\)
( \(\because\) Area can not be negative)
\(
=\frac{1}{2}|z|^2 \quad\left(\because z=x+i y,|z|^2=x^2+y^2\right)
\) -
Question 37 of 50
37. Question
The area of the triangle formed by the lines joining the vertex of the parabola, \(x^2=8 y\), to the extremities of its latus rectum is
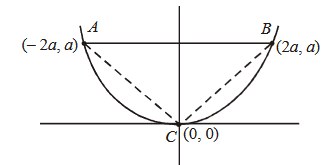
CorrectIncorrectHint
(b) Given parabola is \(x^2=8 y\)
\(
\Rightarrow 4 a=8 \Rightarrow a=2
\)
To find: Area of \(\triangle A B C\)
\(
\begin{aligned}
& A=(-2 a, a)=(-4,2) \\
& B=(2 a, a)=(4,2) \\
& \mathrm{C}=(0,0)
\end{aligned}
\)
\(
\therefore \text { Area }=\frac{1}{2}\left|\begin{array}{ccc}
-4 & 2 & 1 \\
4 & 2 & 1 \\
0 & 0 & 1
\end{array}\right|
\)
\(
\begin{aligned}
& =\frac{1}{2}[-4(2)-2(4)+1(0)] \\
& =\frac{-16}{2}=-8 \approx 8 \text { sq. unit } \\
& (\because \text { area cannot be negative) }
\end{aligned}
\) -
Question 38 of 50
38. Question
Let \(a, b, c\) be such that \(b(a+c) \neq 0\) if
\(
\left|\begin{array}{ccc}
a & a+1 & a-1 \\
-b & b+1 & b-1 \\
c & c-1 & c+1
\end{array}\right|+\left|\begin{array}{ccc}
a+1 & b+1 & c-1 \\
a-1 & b-1 & c+1 \\
(-1)^{n+2} a & (-1)^{n+1} b & (-1)^n c
\end{array}\right|=0
\)
then the value of \(n\) is:CorrectIncorrectHint
\(
\left|\begin{array}{ccc}
a & a+1 & a-1 \\
-b & b+1 & b-1 \\
c & c-1 & c+1
\end{array}\right|+
\)
\(
\left|\begin{array}{ccc}
a+1 & b+1 & c-1 \\
a-1 & b-1 & c+1 \\
(-1)^{n+2} a & (-1)^{n+1} b & (-1)^n c
\end{array}\right|=0
\)
\(
\Rightarrow\left|\begin{array}{ccc}
a & a+1 & a-1 \\
-b & b+1 & b-1 \\
c & c-1 & c+1
\end{array}\right|+\left|\begin{array}{ccc}
a+1 & a-1 & (-1)^{n+2} a \\
b+1 & b-1 & (-1)^{n+1} b \\
c-1 & c+1 & (-1)^n c
\end{array}\right|=0
\)
(Taking transpose of second determinant)
\(
C_1 \Leftrightarrow C_3
\)
\(
\Rightarrow\left|\begin{array}{ccc}
a & a+1 & a-1 \\
-b & b+1 & b-1 \\
c & c-1 & c+1
\end{array}\right|-\left|\begin{array}{ccc}
(-1)^{n+2} a & a-1 & a+1 \\
(-1)^{n+2}(-b) & b-1 & b+1 \\
(-1)^{n+2} c & c+1 & c-1
\end{array}\right|=0
\)
\(
C_2 \Leftrightarrow C_3
\)
\(
\Rightarrow\left|\begin{array}{ccc}
a & a+1 & a-1 \\
-b & b+1 & b-1 \\
c & c-1 & c+1
\end{array}\right|+(-1)^{n+2}\left|\begin{array}{ccc}
a & a+1 & a-1 \\
-b & b+1 & b-1 \\
c & c-1 & c+1
\end{array}\right|=0
\)
\(
\Rightarrow\left[1+(-1)^{n+2}\right]\left|\begin{array}{ccc}
a & a+1 & a-1 \\
-b & b+1 & b-1 \\
c & c-1 & c+1
\end{array}\right|=0
\)
\(
C_2-C_1, C_3-C_1
\)
\(
\Rightarrow\left[1+(-1)^{n+2}\right]\left|\begin{array}{ccc}
a & 1 & -1 \\
-b & 2 b+1 & 2 b-1 \\
c & -1 & 1
\end{array}\right|=0; R_1+R_3
\)
\(
\begin{aligned}
& \Rightarrow\left[1+(-1)^{n+2}\right]\left|\begin{array}{ccc}
a+c & 0 & 0 \\
-b & 2 b+1 & 2 b-1 \\
c & -1 & 1
\end{array}\right|=0 \\
& \Rightarrow\left[1+(-1)^{n+2}\right](a+c)(2 b+1+2 b-1)=0 \\
& \Rightarrow 4 b(a+c)\left[1+(-1)^{n+2}\right]=0 \\
& \Rightarrow 1+(-1)^{n+2}=0 \text { as } b(a+c) \neq 0
\end{aligned}
\)
\(\Rightarrow n\) should be an odd integer. -
Question 39 of 50
39. Question
If \(D=\left|\begin{array}{ccc}1 & 1 & 1 \\ 1 & 1+x & 1 \\ 1 & 1 & 1+y\end{array}\right|\) for \(x \neq 0, y \neq 0\), then \(\mathrm{D}\) is
CorrectIncorrectHint
(d) Given, \(D=\left|\begin{array}{ccc}1 & 1 & 1 \\ 1 & 1+x & 1 \\ 1 & 1 & 1+y\end{array}\right|\)
Apply \(R_2 \rightarrow R_2-R_1\) and \(R \rightarrow R_3-R_1\)
\(
\therefore D=\left|\begin{array}{lll}
1 & 1 & 1 \\
0 & x & 0 \\
0 & 0 & y
\end{array}\right|=x y
\)
Hence, \(D\) is divisible by both \(x\) and \(y\) -
Question 40 of 50
40. Question
If \(a_1, a_2, a_3, \ldots \ldots \ldots, a_n, \ldots \ldots\) are in G. P., then the determinant
\(
\Delta=\left|\begin{array}{ccc}
\log a_n & \log a_{n+1} & \log a_{n+2} \\
\log a_{n+3} & \log a_{n+4} & \log a_{n+5} \\
\log a_{n+6} & \log a_{n+7} & \log a_{n+8}
\end{array}\right|
\)
is equal toCorrectIncorrectHint
\(\because a_1, a_2, a_3, \ldots \ldots\) are in G.P.
\(\therefore\) Using \(a_n=a r^{n-1}\), we get the given determinant, as
\(
\left|\begin{array}{ccc}
\log a r^{n-1} & \log a r^n & \log a r^{n+1} \\
\log a r^{n+2} & \log a r^{n+3} & \log a r^{n+4} \\
\log a r^{n+5} & \log a r^{n+6} & \log a r^{n+7}
\end{array}\right|
\)
Operating \(C_3-C_2\) and \(C_2-C_1\) and using
\(
\log m-\log n=\log \frac{m}{n} \text { we get }
\)
\(
=\left|\begin{array}{lll}
\log a r^{n-1} & \log r & \log r \\
\log a r^{n+2} & \log r & \log r \\
\log a r^{n+5} & \log r & \log r
\end{array}\right|
\)
\(=0\) (two columns being identical) -
Question 41 of 50
41. Question
If \(a^2+b^2+c^2=-2\) and
\(
\mathbf{f}(\mathrm{x})=\left|\begin{array}{ccc}
1+a^2 x & \left(1+b^2\right) x & \left(1+c^2\right) x \\
\left(1+a^2\right) x & 1+b^2 x & \left(1+c^2\right) x \\
\left(1+a^2\right) x & \left(1+b^2\right) x & 1+c^2 x
\end{array}\right|
\)
then \(f(x)\) is a polynomial of degreeCorrectIncorrectHint
\(
\text { Applying, } C_1 \rightarrow C_1+C_2+C_3 \text { we get }
\)
\(
f(x)=\left|\begin{array}{ccc}
1+\left(a^2+b^2+c^2+2\right) x & \left(1+b^2\right) x & \left(1+c^2\right) x \\
1+\left(a^2+b^2+c^2+2\right) x & 1+b^2 x & \left(1+c^2 x\right) \\
1+\left(a^2+b^2+c^2+2\right) x & \left(1+b^2\right) x & 1+c^2 x
\end{array}\right|
\)
\(
=\left|\begin{array}{ccc}
1 & \left(1+b^2\right) x & \left(1+c^2\right) x \\
1 & 1+b^2 x & \left(1+c^2 x\right) \\
1 & \left(1+b^2\right) x & 1+c^2 x
\end{array}\right|
\)
[As given that \(a^2+b^2+c^2=-2\) ]
\(
\therefore a^2+b^2+c^2+2=0
\)
Applying \(R_1 \rightarrow R_1-R_2, R_2 \rightarrow R_2-R_3\)
\(
\therefore f(x)=\left|\begin{array}{ccc}
0 & x-1 & 0 \\
0 & 1-x & x-1 \\
1 & \left(1+b^2\right) x & 1+c^2 x
\end{array}\right|
\)
\(
f(x)=(x-1)^2
\)
Hence degree \(=2\). -
Question 42 of 50
42. Question
If \(a_1, a_2, a_3, \ldots \ldots, a_n, \ldots\). are in G.P., then the value of the determinant
\(
\left|\begin{array}{ccc}
\log a_n & \log a_{n+1} & \log a_{n+2} \\
\log a_{n+3} & \log a_{n+4} & \log a_{n+5} \\
\log a_{n+6} & \log a_{n+7} & \log a_{n+8}
\end{array}\right|
\)
isCorrectIncorrectHint
(d) Let \(r\) be the common ratio, then
\(
\left|\begin{array}{ccc}
\log a_n & \log a_{n+1} & \log a_{n+2} \\
\log a_{n+3} & \log a_{n+4} & \log a_{n+5} \\
\log a_{n+6} & \log a_{n+7} & \log a_{n+8}
\end{array}\right|
\)
\(
=\left|\begin{array}{ccc}
\log a_1 r^{n-1} & \log a_1 r^n & \log a_1 r^{n+1} \\
\log a_1 r^{n+2} & \log a_1 r^{n+3} & \log a_1 r^{n+4} \\
\log a_1 r^{n+5} & \log a_1 r^{n+6} & \log a_1 r^{n+7}
\end{array}\right|
\)
\(
=\left|\begin{array}{lll}
\log a_1+(n-1) \log r & \log a_1+n \log r & \log a_1+(n+1) \log r \\
\log a_1+(n+2) \log r & \log a_1+(n+3) \log r & \log a_1+(n+4) \log r \\
\log a_1+(n+5) \log r & \log a_1+(n+6) \log r & \log a_2+(n+7) \log r
\end{array}\right|
\)
\(
\left.=0 \quad \text { Apply } c_2 \rightarrow c_2-\frac{1}{2} c_1-\frac{1}{2} c_3\right]
\) -
Question 43 of 50
43. Question
If \(a>0\) and discriminant of \(a x^2+2 b x+c\) is \(-\mathrm{ve}\), then
\(
\left|\begin{array}{ccc}
a & b & a x+b \\
b & c & b x+c \\
a x+b & b x+c & 0
\end{array}\right|
\)
is equal toCorrectIncorrectHint
\(
\text { We have }\left|\begin{array}{ccc}
a & b & a x+b \\
b & c & b x+c \\
a x+b & b x+c & 0
\end{array}\right|
\)
\(
\begin{aligned}
& \text { By } R_3 \rightarrow R_3-\left(x R_1+R_2\right) \\
& =\left|\begin{array}{ccc}
a & b & a x+b \\
b & c & b x+c \\
0 & 0 & -\left(a x^2+2 b x+c\right)
\end{array}\right| \\
& =\left(a x^2+2 b x+c\right)\left(b^2-a c\right)=(+)(-)=-\mathrm{ve} .
\end{aligned}
\) -
Question 44 of 50
44. Question
\(l, m, n\) are the \(p^{t h}, q^{\text {th }}\) and \(r^{\text {th }}\) term of a G. P. all positive,
\(
\text { then }\left|\begin{array}{lll}
\log l & p & 1 \\
\log m & q & 1 \\
\log n & r & 1
\end{array}\right| \text { equals }
\)CorrectIncorrectHint
(d)
\(
\begin{aligned}
& l=\mathrm{AR}^{p-1} \Rightarrow \log 1=\log A+(p-1) \log R \\
& m=\mathrm{AR}^{q-1} \Rightarrow \log m=\log A+(q-1) \log \mathrm{R} \\
& n=\mathrm{AR}^{r-1} \Rightarrow \log n=\log A+(r-1) \log \mathrm{R}
\end{aligned}
\)Now,
\(
\left|\begin{array}{lll}
\log l & p & 1 \\
\log m & q & 1 \\
\log n & r & 1
\end{array}\right|=\left|\begin{array}{lll}
\log A+(p-1) \log R & p & 1 \\
\log A+(q-1) \log R & q & 1 \\
\log A+(r-1) \log R & r & 1
\end{array}\right|
\)Operating
\(
\begin{aligned}
& \mathrm{C}_1-(\log \mathrm{R}) \mathrm{C}_2+(\log \mathrm{R}-\log \mathrm{A}) \mathrm{C}_3 \\
& =\left|\begin{array}{lll}
0 & p & 1 \\
0 & q & 1 \\
0 & r & 1
\end{array}\right|=0
\end{aligned}
\) -
Question 45 of 50
45. Question
If \(A=\left[\begin{array}{cc}2 & -3 \\ -4 & 1\end{array}\right]\), then \(\operatorname{adj}\left(3 A^2+12 A\right)\) is equal to :
CorrectIncorrectHint
(c)
\(
\begin{aligned}
& \text { We have } A=\left[\begin{array}{cc}
2 & -3 \\
-4 & 1
\end{array}\right] \\
& \Rightarrow A^2=\left[\begin{array}{cc}
16 & -9 \\
-12 & 13
\end{array}\right] \\
& \Rightarrow 3 A^2=\left[\begin{array}{cc}
48 & -27 \\
-36 & 39
\end{array}\right] \\
& \text { Also } 12 A=\left[\begin{array}{cc}
24 & -36 \\
-48 & 12
\end{array}\right] \\
& \therefore 3 A^2+12 A=\left[\begin{array}{cc}
48 & -27 \\
-36 & 39
\end{array}\right]+\left[\begin{array}{cc}
24 & -36 \\
-48 & 12
\end{array}\right]=\left[\begin{array}{cc}
72 & -63 \\
-84 & 51
\end{array}\right] \\
& \operatorname{adj}\left(3 A^2+12 A\right)=\left[\begin{array}{ll}
51 & 63 \\
84 & 72
\end{array}\right]
\end{aligned}
\) -
Question 46 of 50
46. Question
Let \(A\) be any \(3 \times 3\) invertible matrix. Then which one of the following is not always true?
CorrectIncorrectHint
Consider the properties of matrices.
\(
\begin{aligned}
A^{-1} & =\frac{1}{|A|} \cdot \operatorname{adj}(A) \\
\operatorname{adj}(A) & =|A| A^{-1} \dots(1)
\end{aligned}
\)
Also,
\(
|\operatorname{adj}(A)|=|A|^{n-1}=|A|^2 \dots(2)
\)
From equations (1) and (2).
\(
\operatorname{adj}(\operatorname{adj}(A))=|A|^2(\operatorname{adj}(A))^{-1}
\)
So, 1,2 and 3 are correct option and option 4 occurs only when \(|A|=1\).
Hence, the question is asking for the relation which is not true, so option 4 is correct. -
Question 47 of 50
47. Question
If \(\mathrm{A}=\left[\begin{array}{cc}5 \mathrm{a} & -\mathrm{b} \\ 3 & 2\end{array}\right]\) and \(\mathrm{A}\) adj \(\mathrm{A}=\mathrm{AA}^{\mathrm{T}}\), then \(5 \mathrm{a}+\mathrm{b}\) is equal to:
CorrectIncorrectHint
(d)
\(
\begin{aligned}
& \mathrm{A}(\operatorname{adj} \mathrm{A})=\mathrm{AA}^{\mathrm{T}} \\
& \Rightarrow \mathrm{A}^{-1} \mathrm{~A}(\operatorname{adj} \mathrm{A})=\mathrm{A}^{-1} \mathrm{AA}^{\mathrm{T}}
\end{aligned}
\)
\(
\operatorname{adj} A=A^T
\)
\(
\Rightarrow\left\lfloor\begin{array}{cc}
2 & b \\
-3 & 5 a
\end{array}\right\rfloor=\left\lfloor\begin{array}{cc}
5 a & 3 \\
-b & 2
\end{array}\right\rfloor
\)
\(
\begin{aligned}
& \Rightarrow \mathrm{a}=\frac{2}{5} \text { and } \mathrm{b}=3 \\
& \Rightarrow 5 \mathrm{a}+\mathrm{b}=5
\end{aligned}
\) -
Question 48 of 50
48. Question
Let \(A\) be a \(3 \times 3\) matrix such that \(A^2-5 A+71=0\).
Statement-I: \(\mathrm{A}^{-1}=\frac{1}{7}(51-\mathrm{A})\).
Statement II : the polynomial \(\mathrm{A}^3-2 \mathrm{~A}^2-3 \mathrm{~A}+1\) can be reduced to \(5(\mathrm{~A}-4 \mathrm{I})\).
Then:CorrectIncorrectHint
(a)
\(
\begin{aligned}
& A^2-5 A=-7 I \\
& A A A^{-1}-5 A A^{-1}=-7 I A^{-1} \\
& A I-5 I=-7 A^{-1} \\
& A-5 I=-7 A^{-1} \\
& A^{-1}=\frac{1}{7}(5 I-A) \\
& A^3-2 A^2-3 A+I \\
& =A(5 A-7 I)-2 A^2-3 A+I \\
& =5 A^2-7 A-2 A^2-3 A+I \\
& =3 A^2-10 A+I \\
& =3(5 A-7 I)-10 A+I \\
& =5 A-20 I \\
& =5(A-4 I)
\end{aligned}
\) -
Question 49 of 50
49. Question
If \(A\) is a \(3 \times 3\) matrix such that \(|5 \cdot \operatorname{adj} A|=5\), then \(|A|\) is equal to:
CorrectIncorrectHint
\(
|5 \cdot \operatorname{adj} A|=5 \Rightarrow 5^3 \cdot|A|^{3-1}=5
\)
\(
\Rightarrow 125|\mathrm{~A}|^2=5 \Rightarrow|\mathrm{A}|= \pm \frac{1}{5}
\) -
Question 50 of 50
50. Question
If \(A\) is an \(3 \times 3\) non-singular matrix such that \(A A^{\prime}=A^{\prime} A\) and \(B=A^{-1} A^{\prime}\), then BB’ equals:
CorrectIncorrectHint
(d)
\(
B B^{\prime}=B\left(A^{-1} A^{\prime}\right)^{\prime}=B\left(A^{\prime}\right)^{\prime}\left(A^{-1}\right)^{\prime}
\)
\(
\begin{aligned}
& =B A\left(A^{-1}\right)^{\prime} \\
& =\left(A^{-1} A^{\prime}\right)\left(A\left(A^{-1}\right)^{\prime}\right) \\
& =A^{-1} A \cdot A^{\prime} \cdot\left(A^{-1}\right)^{\prime} \quad\left\{\text { as } A A^{\prime}=A^{\prime} A\right\} \\
& =I\left(A^{-1} A\right)^{\prime}=I \cdot I=I^2=I
\end{aligned}
\)