Jee Math Test Series Complex Numbers Quiz-1

Hint

\(
\begin{aligned}
& \text { In }(1+i)^{2 n}+(1-i)^{2 n} \\
& =\left\{(1+i)^2\right\}^n+\left\{(1-i)^2\right\}^n \\
& =\left(1+i^2+2 i\right)^n+\left(1+i^2-2 i\right)^n \\
& =(1-1+2 i)^n+(1-1-2 i)^n
\end{aligned}
\)
\(
=2^n i^n+i^n(-2)^n=\mathrm{i}^n
\)
For all values of n the given equation does not satisfy.

Hint

We have,
\(
i^n+i^{n+1}+i^{n+2}+i^{n+3}=i^n\left(1+i+i^2+i^3\right)=i^n(1+i-1-i)=0
\)

Hint

We have the following cases:
CASEI
When \(n=4 m, m \in Z\)
In this case, we have
\(
\begin{aligned}
& i^n=i^{4 m}=\left(i^4\right)^m=1 \text { and } i^{-n}=\frac{1}{i^n}=\frac{1}{1}=1 \\
\therefore \quad & i^n+i^{-n}=2
\end{aligned}
\)
CASE II
When \(n=4 m+1, m \in Z\) In this case, we have
\(
\begin{aligned}
& i^n=i^{4 m+1}=\left(i^4\right)^m i^1=i \text { and, } i^{-n}=\frac{1}{i^n}=\frac{1}{i}=-i \\
\therefore \quad & i^n+i^{-n}=i-i=0
\end{aligned}
\)
CASE III
When \(n=4 m+2, m \in Z\)
In this case, we have
\(
\begin{aligned}
& i^n=i^{4 m+2}=\left(i^4\right)^m i^2=i^2=-1 \\
\therefore \quad & i^n+i^n=(-1)+(-1)=-2
\end{aligned}
\)
CASE IV
When \(n=4 m+3, m \in Z\)
In this case, we have
\(
\begin{aligned}
& \quad i^n=i^{4 m+3}=\left(i^4\right)^m i^3=i^3=-i \text { and, } i^{-n}=\frac{1}{i^n}=\frac{1}{i^3}=i \\
& \therefore \quad i^n+i^{-n}=(-i)+(i)=0 \\
& \text { Hence, } S=(-2,0,2)
\end{aligned}
\)

Hint

We have,
\(
\begin{aligned}
& \sum_{n=1}^{13}\left(i^n+i^{n+1}\right) \\
& =\sum_{n=1}^{13} i^n+\sum_{n=1}^{13} i^{n+1} \\
& =i\left(\frac{1-i^{13}}{1-i}\right)+i^2\left(\frac{1-i^{13}}{1-i}\right)=i \frac{(1-i)}{1-i}-\left(\frac{1-i}{1-i}\right)=i-1
\end{aligned}
\)

Hint

We have,
\(
\begin{aligned}
& (1+i)^{6 n}+(1-i)^{6 n}=\left\{(1+i)^2\right\}^{3 n}+\left\{(1-i)^2\right\}^{3 n} \\
& =(2 i)^{3 n}+(-2 i)^{3 n}=2^{3 n}\left\{i^{3 n}+(-i)^{3 n}\right\} \\
& =2^{3 n}\left\{i^{3 n}-i^{3 n}\right\}=0
\end{aligned}
\)

Hint

The notion of linear ordering, greater than or less than, does not apply to complex numbers.

Thus the statement \(Z_1<Z_2\) and \(Z_1>Z_2\) have no meaning unless \(Z_1\) and \(Z_2\) are both real.

Hint

Given, \(z_1+z_2\) and \(z_1 z_2\) are real.
Let, \(z_1=a+i b, z_2=c+i d\)
Since, \(z_1+z_2\) is real,
\(
\begin{array}{lll}
\Rightarrow & (a+c)+i(b+d) \text { is real } & \\
\Rightarrow b+d & =0 & \left[\mathrm{z}_1+\mathrm{z}_2 \text { is real }\right] \\
\Rightarrow \quad b & =-d & \ldots \ldots(1)
\end{array}
\)
Also, \(z_1 z_2\) is real,
\(
\begin{aligned}
& =(a+i b) \cdot(c+i d) \text { is real } \\
& =a c+i a d+i b c+i^2 b d \text { is real } \\
& =a c+i(a d+b c)-b d \text { is real } \\
& =(a c-b d)+i(a d+b c) \text { is real } \\
& \Rightarrow \quad a d+b c=0 \\
& \Rightarrow a(-b)+b c=0 \\
& \Rightarrow \quad a=c \dots(2)
\end{aligned}
\)
Therefore,
\(
\begin{aligned}
z_1 & =a+i b & & \\
& =c-i d & & {[\text { From }(1) \text { and }(2)] } \\
& =\overline{z_2} & & {\left[\because z_2=c+i d\right] }
\end{aligned}
\)

Hint

By definition of the arithmetic progression we know that if \(a, b, c\) are in A.P then, \(2 b=a+c\).
So, if \(z_1, z_2, z_3\) are in A.P then,
\(
\begin{gathered}
2 z_2=z_1+z_3 \\
z_2=\frac{z_1+z_3}{2}
\end{gathered}
\)
It means that \(z_2\) is the mid point of \(z_1, z_3\).
Therefore, \(z_1, z_2, z_3\) lie on a straight line.

Hint

Given,
\(
\left(\frac{1+i}{1-i}\right)^n=1
\)
Multiply and divide numerator by \((1+i)^n\) we get
\(
\begin{aligned}
& \left(\frac{(1+i)(1+i)}{(1+i)(1-i)}\right)^n=1 \\
& \Rightarrow\left(\frac{1+i^2+2 i}{1-i^2}\right)^n=1\left(\because i^2=-1\right) \\
& \Rightarrow\left(\frac{2 i}{2}\right)^n=1 \\
& \Rightarrow i^n=1
\end{aligned}
\)
Hence, the smallest value of \(n\) for this is 4 .

Hint

We have, \(\arg \left(\frac{z-1}{z+1}\right)=k,(k \neq 0)\)
Put \(z=x+i y\), we get
\(
\begin{aligned}
& \arg \left(\frac{x-1+i y}{x+1+i y}\right)=k \\
& \Rightarrow \arg \left[\frac{(x-1+i y)(x+1-i y)}{(x+1+i y)(x+1-i y)}\right]=k \\
& \Rightarrow \arg \left[\frac{\left(x^2-1\right)+i y(2)+y^2}{(x+1)^2+y^2}\right]=k \\
& \Rightarrow \arg \left[\frac{x^2+y^2-1+2 i y}{(x+1)^2+y^2}\right]=k \\
& \Rightarrow \arg \left[\frac{x^2+y^2-1+2 i y}{(x+1)^2+y^2}\right]=k \\
& \Rightarrow \frac{2 y}{x^2+y^2-1}=k \\
& {\left[\because \arg (z)=\tan ^{-1} \frac{y}{x}\right]} \\
& \Rightarrow\left(x^2+y^2\right) k-k-2 y=0 \\
& \Rightarrow k x^2+k y^2-2 y-k=0 \\
& \Rightarrow x^2+y^2-\frac{2 y}{k}-1=0
\end{aligned}
\)
Which represent a circle of centre \(\left(0, \frac{1}{k}\right)\) i.e. on \(y\)-axis.

Hint

\(
\begin{aligned}
& \sqrt{x+i y}=a+i b \\
& \Rightarrow x=a^2-b^2 \\
& y=2 a b \\
& \sqrt{-x-i y} \\
& =\sqrt{b^2-a^2-2 a b i} \\
& =\sqrt{(b-i a)^2}= \pm(b-i a)
\end{aligned}
\)

Hint

Given, \(\arg \left(\frac{z-1}{z+1}\right)=\frac{\pi}{3}\)
\(
\begin{aligned}
& \text { Let } z=x+i y \therefore \frac{z-1}{z+1}=\frac{x+i y-1}{x+i y+1} \\
& =\frac{x^2+y^2-1+2 i y}{(x+1)^2+y^2} \\
& \therefore \arg \left(\frac{z-1}{z+1}\right)=\tan ^{-1} \frac{2 y}{x^2+y^2-1}=\frac{\pi}{3} \\
& \Rightarrow \frac{2 y}{x^2+y^2-1}=\tan \frac{\pi}{3}=\sqrt{3} \\
& \Rightarrow x^2+y^2-1=\frac{2}{\sqrt{3}} y \\
& \Rightarrow x^2+y^2-\frac{2}{\sqrt{3}} y-1=0
\end{aligned}
\)
Which is the equation of circle.

Hint

We have,
\(
\begin{aligned}
& (\sqrt{3}+i)^{10}=a+i b \\
& \Rightarrow i^{10}(1-i \sqrt{3})^{10}=a+i b \\
& \Rightarrow-(-2 \omega)^{10}=a+i b \quad\left[\because \omega=-\frac{1}{2}+i \frac{\sqrt{3}}{2}\right] \\
& \Rightarrow-2^{10} \omega^{10}=a+i b \\
& \Rightarrow-2^{10} \omega=a+i b \\
& \Rightarrow-2^{10}\left(\frac{-1}{2}+i \frac{\sqrt{3}}{2}\right)=a+i b \\
& \Rightarrow 2^9-2^9 \sqrt{3} i=a+i b \Rightarrow a=2^9 \text { and } \\
& b=-2^9 \sqrt{3}
\end{aligned}
\)

Hint

If \(z\) is a complex number then
\(
2+\bar{z}=2 \operatorname{Re}(z)
\)
Eqn of a circle in complex form \(\quad|z|^2+\alpha \bar{z}+\bar{\alpha} z+k=0\)
center \(=-\alpha\), radius \(\sqrt{|\alpha|^2-k}\)
\(
2 \operatorname{Re}\left(\frac{z-8 i}{z+6}\right)=0
\)
\(
\frac{z-8 i}{z+6}+\overline {\left(\frac{z-8 i}{z+6}\right)}
\)
\(
\frac{z-8 i}{z+6}+\frac{\bar{z}+8 i}{\bar{z}+6}=0
\)
\(
\frac{2 z \bar{z}-8 i \bar{z}-48 i+8 i z+6 \bar{z}+48 i}{(z+6)(\bar{z}+6)}=0
\)
\(
\begin{aligned}
& z \bar{z}=|z|^2 \\
& 2|z|^2+z(6+8 i)+\bar{z}(6-8 i)=0 \\
& |z|^2+(3+4 i) z+(3-4 i) \bar{z}=0 \\
& 3-4 i=\alpha \\
& |z|^2+\bar{\alpha} z+\alpha \bar{z}=0
\end{aligned}
\)
\(
\begin{aligned}
\text { center }= & -\alpha, \quad-3+4 i \\
& \text { point form } (-3,4)
\end{aligned}
\)
\(
\gamma=\sqrt{|\alpha|^2}=\sqrt{3^2+4^2}=5
\)
\(
(x+3)^2+(y-4)^2=25 \Rightarrow x^2+y^2+6 x-8 y+25=25
\)
\(
x^2+y^2+6 x-8 y=0
\)

Hint

\(
\begin{aligned}
& z=\left(\frac{\sqrt{3}}{2}+\frac{i}{2}\right)^5+\left(\frac{\sqrt{3}}{2}-\frac{i}{2}\right)^5 \\
& z=\left(e^{\frac{i \pi}{6}}\right)^5+\left(e^{\frac{-i \pi}{6}}\right)^5 \\
&=e^{i \frac{5 \pi}{6}}+e^{-\frac{5 \pi}{6}} \\
&=\cos \frac{5 \pi}{6}+i \sin \frac{5 \pi}{6}+\cos \frac{5 \pi}{6}-i \sin \frac{5 \pi}{6} \\
& z=2 \cos \frac{5 \pi}{6} \\
& \operatorname{Im}(z)=0~ \& \operatorname{Re}(z)<0
\end{aligned}
\)

Hint

We have,
\(
|\mathrm{w}|=1 \Longrightarrow\left|\frac{1-\mathrm{iz}}{\mathrm{z}-\mathrm{i}}\right|=1
\)
\(
\begin{aligned}
& |1-i z|=|z-i|(1) \\
& |1-i(x+i y)|=|x+i y-i|, \text { where } z=x+i y
\end{aligned}
\)
\(
|1+y-i x|=|x+i(y-1)|
\)
\(
\begin{aligned}
& \sqrt{(1+y)^2+(-x)^2}=\sqrt{x^2+(y-1)^1} \\
& (1+y)^2+x^2=x^2+(y-1)^2 \\
& y=0
\end{aligned}
\)
\(
\Longrightarrow \mathrm{z}={x}+{i \times 0}={x} \text {, which is purely real. }
\)

Hint

We have a complex number \(z=x+i y\)
\(
\begin{aligned}
& \text { and }|z-3+i|=|z-2-i| \\
& \Rightarrow|x+i y-3+i|=|x+i y-2-i| \\
& \Rightarrow(x-3)^2+(y+1)^2=(x-2)^2+(y-1)^2 \\
& \Rightarrow x^3-6 x+9+y^2+2 y+1 \\
& =x^2-4 x+4+y^2-2 y+1 \\
& \Rightarrow-2 x+4 y+5=0 \ldots(i)
\end{aligned}
\)
So, it represent a line
Point \(A(3,-1)\) and \(B(2,1)\)
So, mid-point of \(A B=\left(\frac{5}{2}, 0\right)\)
\(
m_1=\text { slope of } A B=\frac{1-(-1)}{2-3}=-2
\)
Point \(\left(\frac{5}{2}, 0\right)\) satisfies the equation \(-2 x+4 y+5=0\)
and slope of line \(=m_2=\frac{1}{2}\)
Now, \(m_1 m_2=-2 \times \frac{1}{2}=-1\)
So, line \(-2 x+4 y+5\) is perpendicular to \(A B\). Hence, locus of point \(p\) is the perpendicular bisector of \(A B\)

Hint

\(
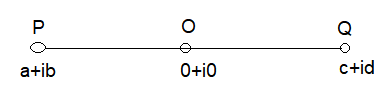
a+i b=c+i d
\)
\(
\frac{a+c}{2}=0
\)
\(
\frac{b+d}{2}=0
\)
\(
a+c=b+d
\)
\(
\begin{aligned}
& \arg (c+i d)=0 \\
& \arg (a+i b)=\pi
\end{aligned}
\)
\(
\arg (a+i b)-\arg (c+i d)=\pi
\)
\(
|a+i b|=|c+i d|
\)

Hint

Since, \(z_1=a+i b\) and \(z_2=c+i d\)
\(
\Rightarrow\left|z_1\right|^2=a^2+b^2=1 \text { and }\left|z_2\right|^2=c^2+d^2=1 \dots(i)
\)
Also, \(\operatorname{Re}\left(z_1 \overline{z_2}\right)=0 \Rightarrow a c+b d=0\)
\(
\Rightarrow \quad \frac{a}{b}=-\frac{d}{c}=\lambda \dots(ii)
\)
From Eqs. (i) and (ii), \(b^2 \lambda^2+b^2=c^2+\lambda^2 c^2\)
\(
\Rightarrow b^2=c^2 \text { and } a^2=d^2
\)
Also, given \(w_1=a+i c\) and \(w_2=b+i d\)
Now,
\(
\begin{aligned}
& \left|w_1\right|=\sqrt{a^2+c^2}=\sqrt{a^2+b^2}=1 \\
& \left|w_2\right|=\sqrt{b^2+d^2}=\sqrt{a^2+b^2}=1
\end{aligned}
\)
and
\(
\begin{aligned}
& \operatorname{Re}\left(w_1 \overline{w_2}\right)=a b+c d=(b \lambda) b+c(-\lambda c) \\
& =\lambda\left(b^2-c^2\right)=0 \quad \text { [from Eq. (i)] }
\end{aligned}
\)

Hint

Given, \(\left|z_1\right|=\left|z_2\right|\),
Now, \(\quad \frac{z_1+z_2}{z_1-z_2} \times \frac{\overline{z_1}-\overline{z_2}}{\overline{z_1}-\overline{z_2}}\)
\(
=\frac{z_1 \overline{z_1}-z_1 \overline{z_2}+z_2 \overline{z_1}-z_2 \overline{z_2}}{\left|z_1-z_2\right|^2}
\)
\(
=\frac{\left|z_1\right|^2+\left(z_2 \overline{z_1}-z_1 \overline{z_2}\right)-\left|z_2\right|^2}{\left|z_1-z_2\right|^2}
\)
\(
=\frac{z_2 \overline{z_1}-z_1 \overline{z_2}}{\left|z_1-z_2\right|^2} \quad\left(\because\left|z_1\right|^2=\left|z_2\right|^2\right)
\)
As, we know \(z-\bar{z}=2 i \operatorname{Im}(z)\)
\(
\begin{aligned}
& \therefore \quad z_2 \overline{z_1}-z_1 \overline{z_2}=2 i \operatorname{Im}\left(z_2 \overline{z_1}\right) \\
& \therefore \quad \frac{z_1+z_2}{z_1-z_2}=\frac{2 i \operatorname{Im}\left(z_2 \overline{z_1}\right)}{\left|z_1-z_2\right|^2} \\
&
\end{aligned}
\)
Which is purely imaginary

Hint

\(
\sin \frac{2 \pi k}{7}-i \cos \frac{2 \pi k}{7}
\)
\(
=-\mathrm{i}\left(\cos \frac{2 \pi \mathrm{k}}{7}+\mathrm{i} \sin \frac{2 \pi \mathrm{k}}{7}\right)
\)
\(
=-\mathrm{ie}^{2 \pi \mathrm{k} / 7 \mathrm{i}}
\)
\(
\begin{aligned}
& \Rightarrow \mathrm{S}=\sum_{\mathrm{k}=1}^6-\mathrm{i}\left(\mathrm{e}^{2 \pi \mathrm{k} / \mathrm{i}}\right) \\
& =-\mathrm{i}\left(\sum_{\mathrm{k}=1}^6 \mathrm{e}^{\mathrm{i} 2 \pi \mathrm{k} / 7}\right)
\end{aligned}
\)
\(
=-\mathrm{i} \text { [sum of roots of the equation }\left.x^6+x^5+x^4+x^3+x^2+1=0\right]
\)
\(
\begin{aligned}
& =-\mathrm{i}(-1) \\
& =\mathrm{i}
\end{aligned}
\)

Hint

Key concept:- If \(z=a+i b\).
\(
\bar{z}=a-i b . \quad \text { \{conjugate }\}
\)
\(
\begin{aligned}
& \bar{b} z+b \bar{z}=c . \\
& b=u+i v, \bar{b}=u-i v . \\
& z=x+i y, \bar{z}=x-i y . \\
&(u-i v)(x+i y)+(u+i v)(x-i y)=0 .
\end{aligned}
\)
\(
\begin{aligned}
& 2 u x+2 v y=c \\
& u x+v y=\frac{c}{2} .
\end{aligned}
\)
This is in the form of
\(
a x+b y=c .
\)
is a straight line

Hint

\(
\left|a_i\right|<1 \text { and } \lambda_i \geqslant 0 \text {, and } \lambda_1+\lambda_2+\cdots+\lambda_n=1
\)
\(
\left|\lambda_1 a_1+\lambda_2 a_2+\cdots+\lambda_n a_n\right| \leqslant\left|\lambda_1 a_1\right|+\left|\lambda_2 a_2\right|+\cdots+\left|\lambda_n a_n\right|
\)
\(
\begin{aligned}
& \leqslant\left|\lambda_1\right|\left|a_1\right|+\left|\lambda_2\right|\left|a_2\right|+\cdots+\left|\lambda_n\right|\left|a_n\right| \\
& \leqslant\left|\lambda_1\right|(1)+\left|\lambda_2\right|(1)+\cdots+\left|\lambda_n\right|(1) \\
& =\left|\lambda_1\right|+\left|\lambda_2\right|+\cdots+\left|\lambda_n\right| \\
& =\left|\lambda_1+\lambda_2+\cdots+\lambda_n\right|, \lambda_i ‘s \text { are +ve } \\
& =|1|=1
\end{aligned}
\)
\(
\text { so, }\left|\lambda a_1+\lambda_2 a_2+\cdots+\lambda_n a_n\right| \leqslant 1
\)

Hint

\(
\begin{aligned}
& \left|a z_1-b z_2\right|^2+\left|b z_1+a z_2\right|^2=\left(a z_1-b z_2\right)\left(a \overline{z_1}-b \overline{z_2}\right)+\left(a z_1+b z_2\right)\left(a \overline{z_1}+b \overline{z_2}\right) \\
& =a^2\left|z_1\right|^2-a b z_1 \overline{z_2}-a b z_2 \overline{z_1}+b^2\left|z_2\right|^2+a^2\left|z_1\right|^2+a b z_1 \overline{z_2}+a b z_2 \overline{z_2}+b^2\left|z_2\right|^2 \\
& \Rightarrow\left|a z_1-b z_2\right|^2+\left|b z_1+a z_2\right|^2=\left(a^2+b^2\right)\left(\left|z_1\right|^2+\left|z_2\right|^2\right)
\end{aligned}
\)

Hint

If \(\mathrm{n}=0\) we get the answer as 2 .
If \(\mathrm{n}\) is even and \(\mathrm{n}\) is simply a multiple of 2 but not a multiple of 4 , we get the answer as -2 . if \(\mathrm{n}\) is odd,
Let \(\mathrm{n}=3\) we get
\(
\begin{aligned}
& -\mathrm{i}-\frac{1}{\mathrm{i}} \\
& =\frac{1-1}{\mathrm{i}} \\
& =0 \\
& \mathrm{n}=5 \text { we get } \\
& \mathrm{i}+\frac{1}{\mathrm{i}} \\
& =0
\end{aligned}
\)
Hence in total there are only 3 values,
\(
-2,0,2
\)

Hint

In this question we have been given two conditions \(a>0\) and \(b<0\).
Hence we need to find \(\sqrt{a} \sqrt{b}\).
Now \(b<0\), which means that the values are negative, hence we can write \(\sqrt{b}\) as \(\sqrt{|b| \cdot i}\).
i.e. \(\sqrt{(-b)}=\sqrt{|b|(-1)}=i \sqrt{|b|}\), this is formed because \(\mathrm{b}\) is negative.

We know that \(\mathrm{a}>0\). Hence, \(\sqrt{a}\) can be written as such. Thus, we can write \(\sqrt{a} \sqrt{b}\) as,
\(
\sqrt{a} \sqrt{b}=\sqrt{a} \sqrt{|b|} \cdot i
\)

We got, \(\sqrt{b}=\sqrt{|b|} \cdot i\)
Thus simplifying the above expression we get,
\(
\sqrt{a} \sqrt{b}=\sqrt{a|b|} \cdot i
\)

Thus we got the value of \(\sqrt{a} \sqrt{b}\) as \(\sqrt{a|b|} \cdot i\).

Hint

\(
\begin{aligned}
& \mathrm{S}_1=\sqrt{-4} \times \sqrt{-9} \\
& =\sqrt{-1} \times \sqrt{4} \times \sqrt{-1} \times \sqrt{9} \\
& =\sqrt{-1} \times 2 \times \mathrm{i} \times 3 \\
& =2 \mathrm{i} \times 3 \mathrm{i} \\
& =6 \mathrm{i}^2=-6 \text { is true } \\
& \mathrm{S}_2=\sqrt{(-4) \times(-9)} \\
& =\sqrt{36}=\sqrt{4 \times 9} \neq \sqrt{4} \times \sqrt{9} \neq \sqrt{-4} \times \sqrt{-9} \text { since } \\
& \sqrt{-4} \times \sqrt{-9}=2 \mathrm{i} \times 3 \mathrm{i}=6 \mathrm{i}^2=-6
\end{aligned}
\)
Hence \(\mathrm{S}_2\) is not true.
\(S_3=\sqrt{(-4) \times(-9)}=\sqrt{36}\) is true.
\(S_4=\sqrt{36}=\sqrt{6 \times 6}=6\) is true

Hint

\(
\begin{aligned}
& \sum_{n=0}^{50} i^{(2 n+1) !}=i^{1 !}+i^{3 !}+i^{5 !}+\ldots . i^{101 !} \\
& \quad=i+i^6+\left(i^{4 m}+i^{4 m}+\ldots .49 \text { times }\right) \\
& \quad=i-1+49 \\
& \quad=48+i
\end{aligned}
\)

Hint

\(
\begin{gathered}
\sum_{r=-3}^{1003} i^r=i^{-3}+i^{-2}+i^{-1}+i^0+i^{1}+i^2+i^3+i^4+\cdots +i^{1003} \\
\end{gathered}
\)
\(
=\frac{1}{i^3}+\frac{1}{i^2}+\frac{1}{i}+1+i-1-i+1+\ldots . .+i^{1003}
\)
\(
\begin{aligned}
& \Rightarrow-\frac{1}{i}+(-1)+\frac{1}{i}+1+i-1-i+1+\ldots i^{1001}+i^{1002}+i^{1003} \\
&
\end{aligned}
\)
\(
\Rightarrow \quad\left(i^4\right)^{250} \cdot i+\left(i^4\right)^{250} \cdot i^2+\left(i^4\right)^{250} \cdot i^3
\)
\(
\Rightarrow \quad i+i^2+i^3 \Rightarrow i-1-i=-1
\)

Hint

153 has 3 in the unit’s place.
\(153^2\) has 9 in the unit’s place.
\(153^3\) has 7 in the unit’s place.
\(153^4\) has 1 in the unit’s place.
\(154^5\) has 3 in the unit’s place.
From next, the digit in the unit’s place gets repeated. So the unit’s place can be either 3 or 9 or 7 or 1 .
\(
(153)^{98}=(153)^{(4 \times 24)+2}=(153)^{(4 \times 24)} \times(153)^2 .
\)
The digit in the unit’s place of \((153)^{(4 \times 24)}\) is 1 and that in \(\left(153^2\right)\) is 9 .
Therefore the digit in the unit’s place of \((153)^{(4 \times 24)} \times(153)^2\) is 9 .
Therefore, the digit in the unit’s place of \((153)^{98}\) is 9 .

Hint

We are required to find the digit in unit’s place of \((141414)^{12121}\)
Since the unit digit of 141414 is 4 , we will divide the index with 4 for the remainder.
Upon dividing 12121 with 4, we get quotient as 303 and the remainder is 1.
Now, we can write the index using the division algorithm as: dividend = quotient \(\times\) divisor + remainder (i.e., \(a=\) bq + r) as: \(12121=303(4)+1\)
Therefore, \((141414)^{12121}=(141414)^{303(4)+1}\)
It can also be written as: \((141414)^{303(4)+1}=\left(141414^4\right)^{303}(141414)^1\)
Now, we only need the unit place of 141414 , therefore, we can write the above equation as: \(\left(4^4\right)^{303}(4)^1\)
Now, the unit digits in various powers of 4 can be written as: \(4^1=4,4^2=6,4^3=4,4^4=6\) and so on. Hence, we can write the equation \(\left(4^4\right)^{303}(4)^1\) as \((6)^{303}(4)\).
Now, we know that for every power of 6 , the unit digit is always 6 . Hence, we can write \((6)^{303}(4)\) as \(6 \times 4=24\) and the digit at unit place is 4 .

Hint

\(\because 1+i^2+i^4+i^6+\ldots+i^{2 n}=1-1+1-1+\ldots+(-1)^n\)
Case I: If \(n\) is odd, then
\(
1+i^2+i^4+i^6+\ldots+i^{2 n}=1-1+1-1+\ldots+1-1=0
\)

Case II: If \(n\) is even, then
\(
1+i^2+i^4+i^6+\ldots+i^{2 n}=1-1+1-1+\ldots+1=1
\)

Hint

\(
\begin{aligned}
a^2=\left(\frac{1+i}{\sqrt{2}}\right)^2 & =\left(\frac{1+i^2+2 i}{2}\right) \\
& =\left(\frac{1-1+2 i}{2}\right)=i \\
a^{1929} & =a \cdot a^{1928}=a \cdot\left(a^2\right)^{964}=a(i)^{964} \\
& =a(i)^{4 \times 241}=a \cdot\left(i^4\right)^{241}=a
\end{aligned}
\)

Hint

\(
\sum_{n=1}^{13}\left(i^n+i^{n+1}\right)=\sum_{n=1}^{13} i^n+\sum_{n=1}^{13} i^{n+1}=(i+0)+\left(i^2+0\right)
\)
\(=i-1 \left[\begin{array}{l}
\because \sum_{n=2}^{13} i^n=0 \text { and } \sum_{n=2}^{13} i^{n+1}=0 \\
\text { (three sets of four consecutive powers of } i \text { ) }
\end{array}\right]
\)

Hint

\(n !\) is divisible by \(4, \forall n \geq 4\).
\(
\begin{aligned}
\therefore \sum_{n=4}^{100} i^{n !} & =\sum_{n=1}^{97} i^{(n+3) !} \\
& =i^0+i^0+i^0+\ldots 97 \text { times }=97 \dots(i)
\end{aligned}
\)
\(
\begin{aligned}
\therefore \sum_{n=0}^{100} i^{n !} & =\sum_{n=0}^3 i^{n !}+\sum_{n=4}^{100} i^{n !} \\
& =i^{0 !}+i^{1 !}+i^{2 !}+i^{3 !}+97
\end{aligned}
\)
[from Eq. (i)]
\(
\begin{aligned}
& =i^1+i^1+i^2+i^6+97=i+i-1-1+97 \\
& =95+2 i
\end{aligned}
\)

Hint

The first equation may be written as
\(
(z+1)(z+z+1)=0:
\)
its roots are \(-1, \omega\) and \(\omega^2\).
The root \(z=-1\) does not satisfy the second equation but \(z=\omega\) and \(z=\omega^2\) satisfy it as \(\omega^{3 n}=1\) Hence and \(\omega\) and \(\omega^2\) are the common roots.

Explanation;

\(
\begin{aligned}
& z^3+2 z^2+2 z+1=0 \\
& z^{1985}+z^{100}+1=0
\end{aligned}
\)
We know that \(1+\omega+\omega^2=0, \omega^3=1\) check to be root,
\(
\begin{aligned}
& \text { (1) } \omega^3+2 \omega^2+2 \omega+1 \\
& =1+\omega+\omega^2+1+\omega+\omega^2=0+0=0 \\
& \text { (2) } \omega^{1985}+\omega^{100}+1 \\
& \omega^2+\omega+1=0
\end{aligned}
\)
\(\omega\) is a common root check \(\omega^2\) to be a root
\(
\begin{aligned}
& \text { (1) } \omega^6+2 \omega^4+2 \omega^2+1 \\
& =\left(\omega^3\right)^2+2 \omega\left(\omega^3\right)+2 \omega^2+1 \\
& =1+\omega+\omega^2+1+\omega+\omega^2=0 \\
& \text { (2) }=\omega^{3970}+\omega^{200}+1 \\
& =\omega+\omega^2+1=0
\end{aligned}
\)
\(\omega^2\) is a common root

Hint

\(
\text { Given: }\left|\frac{z_1-z_2}{1-\bar{z}_1 z_2}\right|=1 \Rightarrow \frac{\left|z_1-z_2\right|}{1-\bar{z}_1 z_2 \mid}=1 \Rightarrow\left|z_1-z_2\right|=\left|1-\bar{z}_1 z_2\right|
\)
\(
\text { Squaring both sides }\left|z_1-z_2\right|^2=\left|1-\bar{z}_1 z_2\right|^2
\)
\(
\left(z_1-z_2\right)\left(\bar{z}_1-\bar{z}_2\right)=\left(1-\overline{z_1} z_2\right)\left(1-z_1 \bar{z}_2\right)\left[\because(z)^2=z \cdot \bar{z}\right]
\)
\(
\begin{aligned}
& \Rightarrow\left|z_1\right|^2+\left|z_2\right|^2=1+\left|z_1\right|^2\left|z_2\right|^2 \\
& \Rightarrow 1-\left|z_1\right|^2-\left|z_2\right|^2+\left|z_1\right|^2\left|z_2\right|^2=0 \\
& \Rightarrow\left(1-\left|z_1\right|^2\right)\left(1-\left|z_2\right|^2\right)=0 \Rightarrow\left|z_1\right|=1,\left|z_2\right|=1
\end{aligned}
\)

Hint

The cube roots of unity are given by \(A(1,0), B(-1 / 2,\sqrt{3} / 2, C(-1 / 2,-\sqrt{3} / 2)\)

The value for each of \(A B, B C\) and \(C A\) is \(\sqrt{3}\) Hence these points represent an equilateral triangle

Hint

\(
\left|\frac{z_1-z_2}{z_1+z_2}\right|
\)
Replace \(z_1=i k z_2\) in the above equation and solve it you will get 1.

Hint

\(
\text { Given: }\left|\frac{z_1-z_2}{z_1+z_2}\right|=1
\)
\(
\Rightarrow \frac{\left|z_1-z_2\right|}{\left|z_1+z_2\right|}=1 \Rightarrow\left|z_1-z_2\right|=\left|z_1+z_2\right|
\)
\(
\Rightarrow\left|\frac{z_1}{z_2}-1\right|=\left|\frac{z_1}{z_2}+1\right|
\)
\(
\text { squaring: }\left|\frac{z_1}{z_2}-1\right|^2=\left|\frac{z_1}{z_2}+1\right|^2
\)
\(
\Rightarrow\left|\frac{z_1}{z_2}\right|^2+1-2 \operatorname{Re}\left(\frac{z_1}{z_2}\right)=\left|\frac{z_1}{z_2}\right|^2+1+2 \operatorname{Re}\left(\frac{z_1}{z_2}\right)
\)
\(
\Rightarrow 4 \operatorname{Re}\left(\frac{z_1}{z_2}\right)=0 \Rightarrow \frac{z_1}{z_2} \text { is purely imagnary } \Rightarrow \frac{i z_1}{z_2}=k, k \in \mathbb{R}
\)
\(
\text { let } \theta \text { be the angle between } z_1-z_2 \text { and } z_1+z_2
\)
\(
\theta=\operatorname{Arg}\left(\frac{z_1-z_2}{z_1+z_2}\right)=\operatorname{Arg}\left(\frac{\frac{z_1}{z_2}-1}{\frac{z_1}{z_2}+1}\right)
\)
\(
=\operatorname{Arg}\left(\frac{-i k-1}{-i k+1}\right)=\operatorname{Arg}\left(\frac{1+i k}{-1+i k}\right)
\)
\(
=\operatorname{Arg}\left(\frac{(1+i k)(1+i k)}{(-1+i k)(1+i k)}\right)=\operatorname{Arg}\left(\frac{1-k^2+2 i k}{-k^2-1}\right)=\operatorname{Arg}\left(\frac{k^2-1-2 i k}{k^2+1}\right)
\)
\(
\text { so, } \theta=\tan ^{-1}\left(\frac{-2 k}{k^2-1}\right)=\tan ^{-1}\left(\frac{2 k}{1-k^2}\right)
\)

Hint

\(
\begin{aligned}
& z^n=(z+1)^n \\
& \frac{z^n}{(z+1)^n}=1 \\
& \left(\frac{z}{z+1}\right)^n=1 \\
& \left(\frac{z}{z+1}\right)=(1)^{1 / n}{\text {th }} \text { root of unity }
\end{aligned}
\)

\(
\begin{gathered}
\frac{|z|}{|z+1|}=1 \Rightarrow \quad|z|^2=|z+1|^2 \\
(z \bar{z}=(z+1)(\overline{z+1}) \\
(x+i y)(x-i y)=((x+1)+i y) \cdot((x+1)-i y)
\end{gathered}
\)
\(
x=-\frac{1}{2}
\)
Let
\(
\begin{aligned}
z & =x+i y \\
\bar{z} & =x-i y
\end{aligned}
\)
\(
\operatorname{Re}(z)<0
\)

as \(x=-\frac{1}{2}\)

Hint

\(
\begin{aligned}
\frac{z}{1+z}=1^{1 / n} \Rightarrow\left|\frac{z}{1+z}\right|=1 & \Rightarrow|z|^2=|1+z|^2 \\
& \Rightarrow|z|^2=1+|z|^2+2 \operatorname{Re}(z)
\end{aligned}
\)
let \(z=x+i y \Rightarrow 2 x+1=0 \Rightarrow x=-\frac{1}{2}\) \(y\) can take any real value. So, none of the options is correct.

Hint

Let \(\mathrm{z}=\mathrm{x}+\) iy be a complex number satisfying the given condition. then \(\mathrm{a}^2-3 \mathrm{a}+2=|\mathrm{z}+\sqrt{2}|=|\mathrm{z}+\mathrm{i} \sqrt{2}-\mathrm{i} \sqrt{2}+\sqrt{2}|\) \(\Rightarrow \mathrm{a}^2-3 \mathrm{a}+2 \leq|\mathrm{z}+\mathrm{i} \sqrt{2}|+\sqrt{2}|1-\mathrm{i}|<\mathrm{a}^2+2 \Rightarrow \mathrm{a}>0\)
Since \(\mathrm{a}^2-3 \mathrm{a}+2=|\mathrm{z}+\sqrt{2}|\) represents a circle with center at \(\mathrm{A}(-\sqrt{2}, 0)\) and radius \(\sqrt{a^2-3 a+2}\)
and \(|z+i \sqrt{2}|<a^2\) represents the interior of the circle with center at \(B(0, \sqrt{2})\) and radius \(a\).
Thus there will be a complex number satisfying the given condition and the given inequality if the distance \(A B\) is less than the sum or difference of the two radii of 2 circles. i.e.
\(
\Rightarrow \sqrt{(-\sqrt{2}-0)^2+(0+\sqrt{2})^2}<\sqrt{a^2-3 a+2} \pm a \Rightarrow 2 \pm a<\sqrt{a^2-3 a+2}
\)
Square both sides to get, \(-\mathrm{a}<-2\) or \(7 \mathrm{a}<-2 \Rightarrow \mathrm{a}>2, \quad \mathrm{a}<\frac{-2}{7}\)
But \(\mathrm{a}>0\) thus \(\mathrm{a}>2\)

Hint

\(
\begin{aligned}
& \left(\frac{1+i a}{1-i a}\right)^4=z \\
& \left(\frac{-i(i-a)}{-i(i+a)}\right)^4=z \\
& \left(\frac{a-i}{a+i}\right)^4=z \\
& \left|\frac{a-i}{a+i}\right|^4=|z|=1 \\
& |a-i|^4=|a+i|^4 \\
& |a-i|=|a+i|
\end{aligned}
\)
\(\therefore\) a lies on the perpendicular bisector of \(\mathrm{i}\) and \(-\mathrm{i}\). a lies on real axis. Hence the roots all are real and distinct.

Hint

Concept:
If the centre of a regular polygon of \(n\) sides is located at the point \(z=0\) and one of its vertex \(z_1\) is known, then the adjecent vertex \(z_2\) can be obtained by rotating \(z 1\) by an angle \(\frac{2 \pi}{\mathrm{n}}\) either in clockwise or anticlockwise direction.
\(
\mathrm{e}^{ \pm} \frac{2 \pi \mathrm{i}}{\mathrm{n}}=\cos \frac{2 \pi}{\mathrm{n}} \pm \mathrm{i} \sin \frac{2 \pi}{\mathrm{n}}
\)
Calculations:
Given, the centre of a regular polygon of \(n\) sides is located at the point \(z=0\) and one of its vertex \(z_1\) is known.
\(\Rightarrow z_2\) be the vertex adjacent to \(z_1\).
\(\Rightarrow z_2\) can be obtained by rotating \(z_1\) by an angle \(\frac{2 \pi}{n}\) either in clockwise or anticlockwise direction.
\(
\begin{aligned}
& \Rightarrow \mathrm{z}_2=\mathrm{z}_1 \mathrm{e}^{ \pm} \frac{2 \pi \mathrm{i}}{\mathrm{n}} \\
& \Rightarrow\left|\mathrm{z}_2\right|=\left|\mathrm{z}_1\right| \mathrm{e}^{ \pm} \frac{2 \pi \mathrm{i}}{\mathrm{n}} \\
& \Rightarrow \mathrm{z}_2=z_1\left(\cos \frac{2 \pi}{n} \pm i \sin \frac{2 \pi}{n}\right)
\end{aligned}
\)
Hence, the centre of a regular polygon of \(n\) sides is located at the point \(z=0\) and one of its vertex \(z_1\) is known. If \(z_2\) be the vertex adjacent to \(z_1\), then \(z_2\) is equal to
\(
z_1\left(\cos \frac{2 \pi}{n} \pm i \sin \frac{2 \pi}{n}\right)
\)

Hint

Let \(z=x+i y\) with \(x, y\) real.
\(
|z|+|z-1|=\sqrt{x^2+y^2}+\sqrt{(x-1)^2+y^2}
\)
Clearly if this has minimum value, then \(y=0\), since any other value of \(y\) would make it larger.
So we must find the minimum value of
\(
\begin{aligned}
& \sqrt{x^2}+\sqrt{(x-1)^2} \\
& |x|+|x-1|
\end{aligned}
\)
Consider the function:
\(
f(x)=|x|+|x-1|
\)
We consider six cases:
Case 1: \(x=0\) Then \(f(x)=f(0)=0+1=1\)
Case 2: \(x=1\) Then \(f(x)=f(1)=1+0=1\)
Case 3: \(x>0\) and \(x-1>0\) which implies \(x>1\)
Then \(f(x)=x+x=1=2 x-1\)
Case 4: \(x>0\) and \(x-1<0\) which implies 00 which is impossible
Then \(f(x)=x+x=1=2 x-1\)
Case 5: \(x<0\) and \(x-1>0\) which is impossible
Case 6: \(x<0\) and \(x-1<0\) which implies \(x<0\)
Then \(f(x)=-x-(x-1)=x-x+1=-2 x+1\)
So \(f(x)=|x|+|x-1|\) is the piecewise function:
\(
f(x)=\left\{\begin{array}{cl}
-2 x+1 & \text { if } x<0 \\
1 & \text { if } 0 \leqslant x<1 \\
2 x-1 & \text { if } x \geqslant 1
\end{array}\right.
\)
Thus the minimum value is of \(|z|+|z-1|\) is 1 .

Hint

Let, \(\mathrm{z}=\mathrm{x}+\mathrm{iy}\)
Putting in the given inequality,
\(
\begin{aligned}
& |(x-4)-i y|<|(x-2)+i y| \\
& \Rightarrow \sqrt{(x-4)^2+y^2}<\sqrt{(x-2)^2+y^2}
\end{aligned}
\)
squaring both sides,
\(
\begin{aligned}
& \Rightarrow(\mathrm{x}-4)^2+\mathrm{y}^2<(\mathrm{x}-2)^2+\mathrm{y}^2 \\
& \Rightarrow-8 \mathrm{x}+16<-4 \mathrm{x}+4 \\
& \Rightarrow 4 \mathrm{x}>12 \Rightarrow \mathrm{x}>3 \Rightarrow \operatorname{Re}(\mathrm{z})>3
\end{aligned}
\)

Hint

Lets first find the value of \(|1-i|\)
Complex number is of the form \(x+i y\)
Where \(x=1\)
\(
\begin{aligned}
y & =-1 \\
|1-i| & =\sqrt{x^2+y^2}=\sqrt{2}
\end{aligned}
\)
\(
\text { Hence, }|1-i|=\sqrt{2}
\)
\(
\text { Given }|1-i|^n=2^n
\)
\(
\begin{aligned}
& \text { Putting }|1-i|=\sqrt{2} \\
& \qquad \begin{aligned}
(\sqrt{2})^n=2^n \\
(\sqrt{2})^n=(\sqrt{2} \times \sqrt{2})^n \\
(\sqrt{2})^n=(\sqrt{2})^{2 \times n} \\
(\sqrt{2})^n=\sqrt{2}^{2 n}
\end{aligned}
\end{aligned}
\)
Comparing Powers
\(
\begin{aligned}
& n=2 n \\
& n-2 n=0 \\
& -n=0 \\
& n=0
\end{aligned}
\)
Hence, There is no non-zero integral solution

Hint

\(
\begin{aligned}
& z=x+i y \\
& \frac{2(x+i y)+1}{i(x+i y)+1}=-2 \\
= & \frac{2(x+i y)+1}{i x-y+1}
\end{aligned}
\)
\(
=\frac{(2 x+1)+2 i y}{(1-y)+i x} \times \frac{(1-y)-i x}{(1-y)-i x}
\)
\(
=\frac{[(2 x+1)+2 i y][(1-y)-i x]}{(1-y)^2+x^2}
\)
\(
-2 x^2-x+2 y-2 y^2=\left[x^2+(1-y)^2\right](-2)
\)
\(
\begin{aligned}
-x-2 y & =-2 \\
x+2 y & =2 \rightarrow \text { a straight line }
\end{aligned}
\)

Hint

\(
\begin{aligned}
& (1-\sqrt{3} i)^{200}=2^{199}(p+i q) \\
& 2^{200}\left(\cos \frac{\pi}{3}-i \sin \frac{\pi}{3}\right)^{200}=2^{199}(p+i q)
\end{aligned}
\)
\(
\begin{aligned}
& 2\left(-\frac{1}{2}-\mathrm{i} \frac{\sqrt{3}}{2}\right)=\mathrm{p}+\mathrm{iq} \\
& \mathrm{p}=-1, \mathrm{q}=-\sqrt{3} \\
& \alpha=\mathrm{p}+\mathrm{q}+\mathrm{q}^2=2-\sqrt{3} \\
& \beta=\mathrm{p}-\mathrm{q}+\mathrm{q}^2=2+\sqrt{3} \\
& \alpha+\beta=4 \\
& \alpha \cdot \beta=1 \\
& \text { equation } \mathrm{x}^2-4 \mathrm{x}+1=0
\end{aligned}
\)