2D Quiz
Quiz Summary
0 of 50 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 50 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 50
1. Question
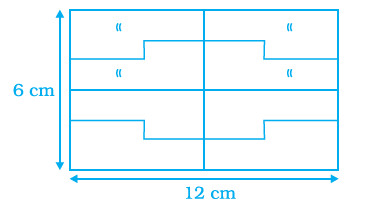
The following rectangle is composed of 8 congruent parts. Area of each part is
 CorrectIncorrect
CorrectIncorrectHint
It is given that
Length \(=12 \mathrm{~cm}\)
Breadth \(=6 \mathrm{~cm}\)
We know that
Area of a rectangle \(=\) Length \(\times\) Breadth
Substituting the values
Area of a rectangle \(=12 \times 6=72 \mathrm{~cm}^2\)
As there are 8 congruent parts
Area of each part \(=72 / 8=9 \mathrm{~cm}^2\)
Therefore, the area of each part is \(9 \mathrm{~cm}^2\). -
Question 2 of 50
2. Question
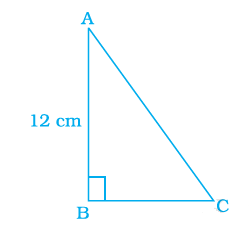
Area of a right triangle is \(54 \mathrm{~cm}^2\). If one of its legs is \(12 \mathrm{~cm}\) long, its perimeter is
 CorrectIncorrect
CorrectIncorrectHint
It is given that
Area of a right triangle \(=54 \mathrm{~cm}^2\)
We know that
Area \(=1 / 2 \times\) base \(\times\) height \(=1 / 2 a b\)
Here
Perimeter \(=a+b+\sqrt{a^2}+b^2\)
\(
P=a+\sqrt{a^2}+4(A / a)^2+2 A / a
\)
Substituting the values
\(
\begin{aligned}
& P=12+\sqrt{12^2}+4(54 / 12)^2+2(54 / 12) \\
& P=36 \mathrm{~cm}
\end{aligned}
\) -
Question 3 of 50
3. Question
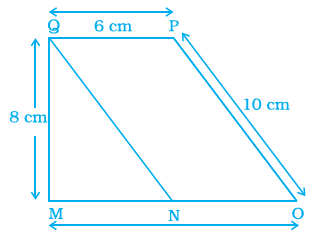
Find the Area of parallelogram QPON shown in the figure below.
 CorrectIncorrect
CorrectIncorrectHint
We know that
Area of a parallelogram \(=\) base \(\times\) height
Substituting the values from the figure
Area of a parallelogram \(=6 \times 8=48 \mathrm{~cm}^2\)
Therefore, the area of parallelogram QPON is \(48 \mathrm{~cm}^2\). -
Question 4 of 50
4. Question
All the congruent triangles have equal area. Is this statement true?
CorrectIncorrectHint
Two triangles are said to be congruent if their corresponding sides and angles are equal.
We know that the Congruent triangle have equal area.
Therefore, all the congruent triangles have equal area. -
Question 5 of 50
5. Question
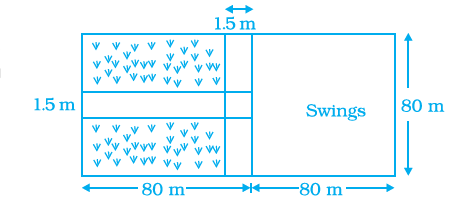
A nursery school play ground is \(160 \mathrm{~m}\) long and \(80 \mathrm{~m}\) wide. In it \(80 \mathrm{~m} \times 80 \mathrm{~m}\) is kept for swings and in the remaining portion, there is \(1.5 \mathrm{~m}\) wide path parallel to its width and parallel to its remaining length as shown in Figure below. The remaining area is covered by grass. Find the area covered by grass.
 CorrectIncorrect
CorrectIncorrectHint
Area of the school playground is \(160 \mathrm{~m} \times 80 \mathrm{~m}=12800 \mathrm{~m}^2\)
Area kept for swings \(=80 \mathrm{~m} \times 80 \mathrm{~m}=6400 \mathrm{~m}^2\)
Area of path parallel to the width of playground
\(
=80 \mathrm{~m} \times 1.5 \mathrm{~m}=120 \mathrm{~m}^2
\)
Area of path parallel to the remaining length of
playground
\(
=80 \mathrm{~m} \times 1.5 \mathrm{~m}=120 \mathrm{~m}^2 .
\)
Area common to both paths \(=1.5 \mathrm{~m} \times 1.5 \mathrm{~m}=2.25 \mathrm{~m}^2\).
[since it is taken twice for measurement it is to be subtracted from the area of paths]
Total area covered by both the paths
\(
\begin{aligned}
& =(120+120-2.25) \mathrm{m}^2 \\
& =237.75 \mathrm{~m}^2 .
\end{aligned}
\)
Area covered by grass = Area of school playground \(–\) (Area
kept for swings + Area covered by paths)
\(
\begin{aligned}
& =12800 \mathrm{~m}^2-[6400+237.75] \mathrm{m}^2 \\
& =(12800-6637.75) \mathrm{m}^2 \\
& =6162.25 \mathrm{~m}^2 .
\end{aligned}
\) -
Question 6 of 50
6. Question
In Figure below, \(\mathrm{ABCD}\) is a parallelogram, in which \(\mathrm{AB}=8 \mathrm{~cm}, \mathrm{AD}=6 \mathrm{~cm}\) and altitude \(\mathrm{AE}=4 \mathrm{~cm}\). Find the altitude corresponding to side \(\mathrm{AD}\).
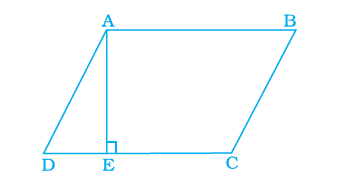 CorrectIncorrect
CorrectIncorrectHint
Area of parallelogram \(\mathrm{ABCD}=\mathrm{AB} \times \mathrm{AE}=8 \times 4 \mathrm{~cm}^2\) \(=32 \mathrm{~cm}^2\)
Let altitude corresponding to \(\mathrm{AD}\) be \(h\). Then,
\(
\begin{array}{ll}
& h \times \mathrm{AD}=32 \\
\text { or } & h \times 6=32 \\
\text { or } & h=\frac{32}{6}=\frac{16}{3}
\end{array}
\)
Thus, altitude corresponding to \(\mathrm{AD}\) is \(\frac{16}{3} \mathrm{~cm}\). -
Question 7 of 50
7. Question
A rectangular-shaped swimming pool with dimensions \(30 \mathrm{~m} \times 20 \mathrm{~m}\) has \(5 \mathrm{~m}\) wide cemented path along its length and \(8 \mathrm{~m}\) wide path along its width (as shown in Figure below). Find the cost of cementing the path at the rate of Rs 200 per \(\mathrm{m}^2\).
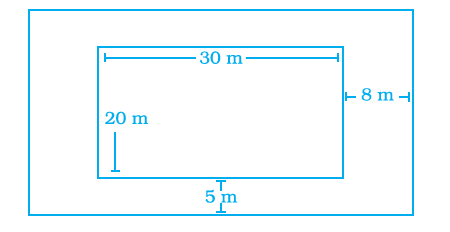 CorrectIncorrect
CorrectIncorrectHint
Area covered by swimming pool \(=30 \mathrm{~m} \times 20 \mathrm{~m}=600 \mathrm{~m}^2\).
Length of outer rectangle \(=(30+8+8) \mathrm{m}=46 \mathrm{~m}\)
and its breadth \(=(20+5+5) m=30 \mathrm{~m}\)
So, the area of outer rectangle
\(
=46 \mathrm{~m} \times 30 \mathrm{~m}=1380 \mathrm{~m}^2 \text {. }
\)
Area of cemented path \(=\)
Area of outer rectangle – Area of swimming pool
\(
=(1380-600) \mathrm{m}^2=780 \mathrm{~m}^2 .
\)
Cost of cementing \(1 \mathrm{~m}^2\) path \(=₹ 200\)
So, total cost of cementing the path
\(
\begin{aligned}
& =₹ 780 \times 200 \\
& =₹ 156000
\end{aligned}
\) -
Question 8 of 50
8. Question
The Circumference of a circle is 33 cm. Find its area.
CorrectIncorrectHint
Let the radius of the circle be \(r\). Then, \(\quad 2 \pi r=33\)
i.e., \(\quad r=\frac{33}{2 \pi}=\frac{33}{2} \times \frac{7}{22}=\frac{21}{4}\)
Thus, radius is \(\frac{21}{4} \mathrm{~cm}\)
So, area of the circle \(=\pi r^2=\frac{22}{7} \cdot \frac{21}{4} \cdot \frac{21}{4}=\frac{693}{8}\)
Thus, area of the circle is \(\frac{693}{8} \mathrm{~cm}^2\). -
Question 9 of 50
9. Question
Rectangle \(\mathrm{ABCD}\) is formed in a circle as shown in Figure below. If AE \(=8 \mathrm{~cm}\) and \(\mathrm{AD}=5 \mathrm{~cm}\), find the perimeter of the rectangle.
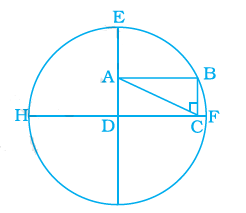 CorrectIncorrect
CorrectIncorrectHint
\(
\mathrm{DE}=\mathrm{EA}+\mathrm{AD}=(8+5) \mathrm{cm}=13 \mathrm{~cm}
\)
\(\mathrm{DE}\) is the radius of the circle.
Also, DB is the radius of the circle.
Next, AC \(=\) DB [Since diagonals of a rectangle are equal in length]
Therefore, \(\mathrm{AC}=13 \mathrm{~cm}\).
From \(\triangle \mathrm{ADC}, \mathrm{DC}^2=\mathrm{AC}^2-\mathrm{AD}^2=13^2-5^2=169-25=\) \(144=12^2\)
So, \(\mathrm{DC}=12\)
Thus, length of DC is \(12 \mathrm{~cm}\).
Hence, perimeter of the rectangle ABCD
\(=2(12+5) \mathrm{cm}=34 \mathrm{~cm}\) -
Question 10 of 50
10. Question
Observe the shapes 1, 2, 3, and 4 in the figure below. Which of the following statements is not correct?
 CorrectIncorrect
CorrectIncorrectHint
Trick: Count the number of squares around the shape.
Shape 1:
We know that
Perimeter \(=1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1\) \(+1+1\) \(=22\) units
Here
Area \(=18 \times 1=18 \mathrm{sq}\) units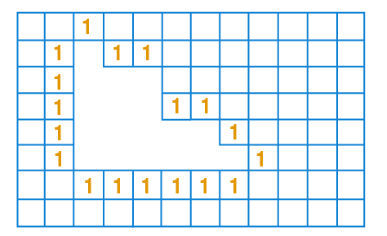
Shape 2:
We know that
Perimeter \(=1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1\) \(=18\) units
Here
Area \(=18 \times 1=18 \mathrm{sq}\) units
Shape 3:
We know that
Perimeter \(=1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1\) \(+1+1\) \(=22\) units
Area \(=16 \times 1=16\) sq units
Shape 4:
We know that
Perimeter \(=1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1\) \(+1+1\) \(=22\) units
Here
Area \(=18 \times 1=18 \mathrm{sq}\) units -
Question 11 of 50
11. Question
36 unit squares are joined to form a rectangle with the least perimeter. Perimeter of the rectangle is
CorrectIncorrectHint
It is given that
Area of rectangle \(=36\) unit squares
We know that
\(
36=6 \times 6
\)
It can be written as
\(
36=2 \times 3 \times 2 \times 3
\)
So we get
\(
\begin{aligned}
& 36=2^2 \times 3^2 \\
& 36=4 \times 9
\end{aligned}
\)
Here the sides of a rectangle are \(4 \mathrm{~cm}\) and \(9 \mathrm{~cm}\)
Perimeter \(=2(l+b)\)
Substituting the values
\(
\begin{aligned}
& =2(4+9) \\
& =2(13) \\
& =26 \text { units }
\end{aligned}
\)
Therefore, the perimeter of the rectangle is 26 units. -
Question 12 of 50
12. Question
A wire is bent to form a square of side 22 cm. If the wire is rebent to form a circle, its radius is
CorrectIncorrectHint
It is given that
Side of a square \(=22 \mathrm{~cm}\)
Perimeter of square and circumference of circle are equal as the length of wire is same. Based on the question
Perimeter of square \(=\) Circumference of circle
\(4 \times\) side \(=2 \pi r\)
We know that \(\pi=22 / 7\)
Substituting the values
\(
4 \times 22=2 \times 22 / 7 \times r
\)
By further calculation
\(
\begin{aligned}
& r=(4 \times 22 \times 7) /(2 \times 22) \\
& r=14 \mathrm{~cm}
\end{aligned}
\)
Therefore, its radius is \(14 \mathrm{~cm}\). -
Question 13 of 50
13. Question
Area of a rectangle and the area of a circle are equal. If the dimensions of the rectangle are 14cm × 11 cm, then radius of the circle is
CorrectIncorrectHint
It is given that
Dimensions of the rectangle \(=14 \times 11 \mathrm{~cm}\)
From the question
Area of rectangle \(=\) Area of circle
\(1 \times b=\pi r^2\)
Substituting the values
\(
14 \times 11=22 / 7 \times r^2
\)
By further calculation
\(
\begin{aligned}
& r^2=(14 \times 11 \times 7) / 22 \\
& r^2=49 \\
& r=7 \mathrm{~cm}
\end{aligned}
\)
Therefore, the radius of the circle is \(7 \mathrm{~cm}\). -
Question 14 of 50
14. Question
Area of the shaded portion in the figure below is
 CorrectIncorrect
CorrectIncorrectHint
From the figure
Length of rectangle \(=5 \mathrm{~cm}\)
Breadth of rectangle \(=3+1=4 \mathrm{~cm}\)
We know that
Area of shaded portion \(=1 / 2 \times\) Area of rectangle \(=1 / 2 \times(l \times b)\)
Substituting the values
\(
\begin{aligned}
& =1 / 2 \times(5 \times 4) \\
& =1 / 2 \times 20
\end{aligned}
\)
So we get
\(
=10 \mathrm{~cm}^2
\)
Therefore, the area of the shaded portion is \(10 \mathrm{~cm}^2\). -
Question 15 of 50
15. Question
Area of parallelogram ABCD (Figure below) is not equal to
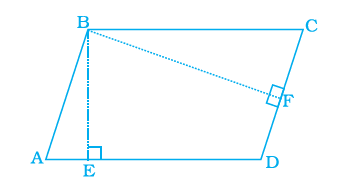 CorrectIncorrect
CorrectIncorrectHint
A parallelogram is defined as a quadrilateral in which both pairs of opposite sides are parallel and equal.
We know that
Area of parallelogram \(=\) base \(\times\) height
From the figure
Area of parallelogram \(A B C D=A D \times B E\)
As \(A D=B C\)
Area of parallelogram \(A B C D=B C \times B E\)
Or
Area of parallelogram \(A B C D=D C \times B F\)
Therefore, the area of the parallelogram is not equal to DE \(\times D C\). -
Question 16 of 50
16. Question
Area of triangle MNO of the figure below is
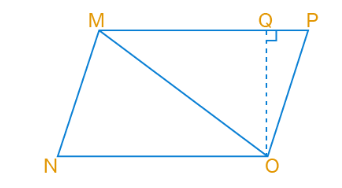 CorrectIncorrect
CorrectIncorrectHint
We know that
Area of triangle \(=1 / 2 \times b \times h\)
From the figure
Area of triangle \(=1 / 2 \times \mathrm{NO} \times \mathrm{OQ}\)
Therefore, the area of the triangle MNO is \(1 / 2 \times N O \times O Q\). -
Question 17 of 50
17. Question
Ratio of area of \(\triangle M N O\) to the area of parallelogram MNOP in the same figure below is
CorrectIncorrectHint
We know that
Area of \(\triangle M N O:\) Area of parallelogram \(M N O P=1 / 2 \times b \times h: b \times h\)
It can be written as
\(
=1 / 2 \times N O \times O Q: M P \times O Q
\)
So we get
\(
\begin{aligned}
& =1 / 2 \times N O: N O[\text { As } N O=M P] \\
& =1: 2
\end{aligned}
\)
Therefore, the ratio is \(1: 2\) -
Question 18 of 50
18. Question
Ratio of areas of \(\Delta\) MNO, \(\Delta \mathrm{MOP}\) and \(\Delta \mathrm{MPQ}\) in the figure below is
 CorrectIncorrect
CorrectIncorrectHint
Using the figure
Area of \(\Delta \mathrm{MNO}=1 / 2 \times \mathrm{NO} \times \mathrm{MO}\)
Substituting the values
\(
\begin{aligned}
& =1 / 2 \times 4 \times 5 \\
& =10 \mathrm{~cm}^2
\end{aligned}
\)
Area of \(\triangle M O P=1 / 2 \times O P \times M O\)
Substituting the values
\(
\begin{aligned}
& =1 / 2 \times 2 \times 5 \\
& =5 \mathrm{~cm}^2
\end{aligned}
\)
Area of \(\triangle M P Q=1 / 2 \times P Q \times M O\)
Substituting the values
\(
\begin{aligned}
& =1 / 2 \times 6 \times 5 \\
& =15 \mathrm{~cm}^2
\end{aligned}
\)
We know that
Required ratio \(=10: 5: 15=2: 1: 3\)
Therefore, the ratio of areas is \(2: 1: 3\). -
Question 19 of 50
19. Question
In the figure below, EFGH is a parallelogram, and altitudes FK and FI are \(8 \mathrm{~cm}\) and \(4 \mathrm{~cm}\) respectively. If \(\mathrm{EF}=10 \mathrm{~cm}\), then area of EFGH is
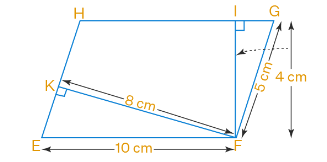 CorrectIncorrect
CorrectIncorrectHint
A parallelogram is defined as a quadrilateral in which both pairs of opposite sides are parallel and equal.
In parallelogram EFGH,
\(
\mathrm{EF}=\mathrm{HG}=10 \mathrm{~cm}
\)
We know that
Area of parallelogram \(\mathrm{EFGH}=\) Base \(\times\) Corresponding height
Substituting the values
\(
\begin{aligned}
& =10 \times 4 \\
& =40 \mathrm{~cm}^2
\end{aligned}
\)
Therefore, the area of EFGH is \(40 \mathrm{~cm}^2\). -
Question 20 of 50
20. Question
In the figure below, if \(\mathrm{PR}=12 \mathrm{~cm}, \mathrm{QR}=6 \mathrm{~cm} \text { and } \mathrm{PL}=8 \mathrm{~cm} \text {, then } \mathrm{QM} \text { is }\)
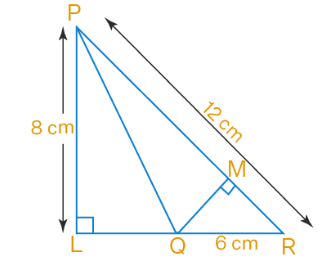 CorrectIncorrect
CorrectIncorrectHint
It is given that
\(
\begin{aligned}
& P R=12 \mathrm{~cm} \\
& \mathrm{QR}=6 \mathrm{~cm} \\
& \mathrm{PL}=8 \mathrm{~cm}
\end{aligned}
\)
In right angled triangle PLR, Using the Pythagoras theorem
\(
\begin{aligned}
& P R^2=P L^2+L R^2 \\
& L R^2=P R^2-P L^2
\end{aligned}
\)
Substituting the values
\(
\begin{aligned}
& \mathrm{LR}^2=144-64 \\
& \mathrm{LR}^2=80 \\
& \mathrm{LR}=\sqrt{ } 80=4 \sqrt{5} \mathrm{~cm}
\end{aligned}
\)
Here
\(
\begin{aligned}
& \mathrm{LR}=\mathrm{LQ}+\mathrm{QR} \\
& \mathrm{LQ}=\mathrm{LR}-\mathrm{QR}
\end{aligned}
\)
Substituting the values \(L Q=4 \sqrt{5}-6 \mathrm{~cm}\)
Area of triangle PLR \(\mathrm{A} 1=1 / 2 \times \mathrm{LR} \times \mathrm{PL}\)
Substituting the values \(L Q=4 \sqrt{5}-6 \mathrm{~cm}\)
Area of triangle PLR \(\mathrm{A} 1=1 / 2 \times \mathrm{LR} \times \mathrm{PL}\)
Substituting the values \(\mathrm{A} 1=1 / 2 \times 4 \sqrt{5} \times 8=16 \sqrt{5} \mathrm{~cm}^2\)
Area of triangle PLQ \(\mathrm{A} 2=1 / 2 \times \mathrm{LQ} \times \mathrm{PL}\)
Substituting the values \(\begin{aligned}& A_2=1 / 2 \times(4 \sqrt{5}-6) \times 8 \\& A 2=16 \sqrt{5}-24 \mathrm{~cm}^2\end{aligned}\)
We know that
Area of triangle PLR = Area of triangle \(\mathrm{PLQ}+\) Area of triangle PQR
Substituting the values \(16 \sqrt{5}=16 \sqrt{5}-24+\) Area of triangle PQR
Area of triangle \(\mathrm{PQR}=24 \mathrm{~cm}^2\)
\(
\begin{aligned}
& 1 / 2 \times P R \times Q M=24 \\
& 1 / 2 \times 12 \times Q M=24 \\
& Q M=4 \mathrm{~cm}
\end{aligned}
\)
Therefore, \(\mathrm{QM}\) is \(4 \mathrm{~cm}\). -
Question 21 of 50
21. Question
In Figure below, \(\Delta \mathrm{MNO}\) is a right-angled triangle. Its legs are \(6 \mathrm{~cm}\) and \(8 \mathrm{~cm}\) long. Length of perpendicular NP on the side MO is
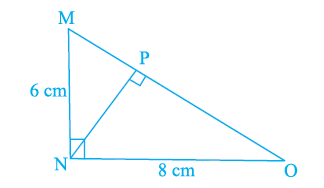 CorrectIncorrect
CorrectIncorrectHint
Given, MNO is a right-angled triangle
The legs are \(6 \mathrm{~cm}\) and \(8 \mathrm{~cm}\) long
We have to find the length of perpendicular NP on the side MO.
By using Pythagoras theorem,
\(
\begin{aligned}
& M O^2=M N^2+M O^2 \\
& M O^2=(6)^2+(8)^2 \\
& M O^2=36+64 \\
& M O^2=100
\end{aligned}
\)
Taking square root,
\(
M O=10 \mathrm{~cm}
\)
Area of triangle \(=1 / 2 \times\) base \(\times\) height
\(
\begin{aligned}
& 1 / 2 \times M N \times N O=1 / 2 \times M O \times N P \\
& 6 \times 8=10 \times N P \\
& N P=48 / 10 \\
& N P=4.8 \mathrm{~cm}
\end{aligned}
\)
Therefore, the value of NP is \(4.8 \mathrm{~cm}\) -
Question 22 of 50
22. Question
Area of a right-angled triangle is \(30 \mathrm{~cm}^2\). If its smallest side is \(5 \mathrm{~cm}\), then its hypotenuse is
CorrectIncorrectHint
Given, area of a right-angled triangle is \(30 \mathrm{~cm}^2\)
The length of the smallest side is \(5 \mathrm{~cm}\)
We have to find the length of the hypotenuse.
Area of triangle \(=1 / 2 \times\) base \(\times\) height
\(30=1 / 2 \times 5 \times \&\) height
Height \(=30(2) / 5\)
Height \(=6(2)\)
Height \(=12 \mathrm{~cm}\)
By using Pythagoras theorem,
\((\text { Hypotenuse })^2=(\text { height })^2+(\text { base })^2\)
\(\&(\text { Hypotenuse })^2=(12)^2+(5)^2\)
\((\text { Hypotenuse })^2=144+25\)
\((\text { Hypotenuse })^2=169\)
Taking square root,
Hypotenuse \(=13 \mathrm{~cm}\)
Therefore, the hypotenuse is \(13 \mathrm{~cm}\). -
Question 23 of 50
23. Question
Length of tape required to cover the edges of a semicircular disc of radius 10 cm is
CorrectIncorrectHint
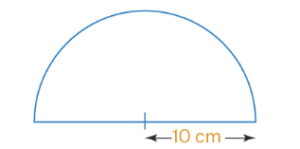
Perimeter of semicircle \(=\) circumference of semicircle \(+\) diameter
Circumference of semicircle \(=\pi r\)
Where, \(r\) is the radius of circle
\(
\begin{aligned}
& =22 / 7 \times 10 \\
& =22(10) / 7 \\
& =220 / 7 \\
& =31.4 \mathrm{~cm} \\
& \text { Perimeter of semicircle }=31.4+10(2) \\
& =31.4+20 \\
& =51.4 \mathrm{~cm}
\end{aligned}
\)
Therefore, the perimeter of semicircle is \(51.4 \mathrm{~cm}\) -
Question 24 of 50
24. Question
If \(p\) squares of each side \(1 \mathrm{~mm}\) makes a square of side \(1 \mathrm{~cm}\), then \(p\) is equal to
CorrectIncorrectHint
Given, \(p\) squares of each side \(1 \mathrm{~mm}\) makes a square of side \(1 \mathrm{~cm}\)
We have to find the value of \(p\).
Area of square \(=(\text { side })^2\)
Area of square with side \(1 \mathrm{~cm}=(1)^2=1 \mathrm{~cm}^2\)
Area of square with side \(1 \mathrm{~mm}=(1)^2=1 \mathrm{~mm}^2\)
Given, \(p \times\) area of square with side \(1 \mathrm{~mm}=\) area of square of side \(1 \mathrm{~cm}\)
We know, \(1 \mathrm{~cm}=10 \mathrm{~mm}\)
So, \(\mathrm{p} \times 1 \mathrm{~mm}^2\left(10^2\right) \mathrm{mm}^2\)
\(p=100 / 1\)
Therefore, \(p=100\) -
Question 25 of 50
25. Question
If each side of a rhombus is doubled, how much will its area increase?
CorrectIncorrectHint
Given, each side of a rhombus is doubled.
We have to find the increase in its area.
Area of rhombus \(=\) base \(\times\) corresponding height
Let the side of rhombus be \(b\)
Since the side is doubled, side \(=2 b\)
Old Area \(=b h\)
New area \(=2 b h\)
Therefore, the area has increased by 2 times. -
Question 26 of 50
26. Question
If the sides of a parallelogram are increased to twice its original lengths, how much will the perimeter of the new parallelogram?
CorrectIncorrectHint
Given, the sides of a parallelogram are increased to twice its original lengths.
We have to find the increase in perimeter of the new parallelogram
Perimeter of parallelogram \(=2\) (length \(+\) breadth)
Let the length be \(l\)
Let the breadth be \(b\)
So, perimeter \(=2(l+b)\)
Now, length \(=2l\)
Breadth \(=2 b\)
New perimeter \(=2(2 {l}+2 {b})\)
\(=2[2(l+b)]\)
Therefore, the new perimeter is increased by 2 times. -
Question 27 of 50
27. Question
If the radius of a circle is increased to twice its original length, how much will the area of the circle increase?
CorrectIncorrectHint
Given, the radius of a circle is increased to twice its original length
We have to find the increase in area of the circle
Area of circle \(=\pi r^2\)
Where, \(r\) is the radius of the circle
Now, \(r=2 r\)
Area of circle \(=\pi(2 r)^2\)
\(=4 \pi r^2\)
Therefore, the area of the circle will be increased by 4 times. -
Question 28 of 50
28. Question
What will be the area of the largest square that can be cut out of a circle of radius 10 cm?
CorrectIncorrectHint
Given, radius of circle is \(10 \mathrm{~cm}\)
We have to find the area of the largest square that can be cut out of the circle.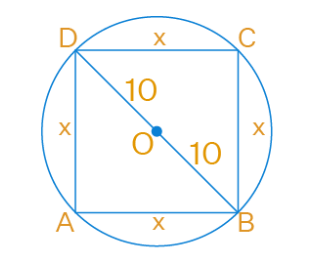
The diagonal of the largest square will be equal to the diameter of the circle.
Let the side of the square be \(b\).
Area of square \(=(\text { side })^2=b^2\)
Considering right-angled triangle DAB,
By using Pythagoras theorem,
\(
\begin{aligned}
& B D^2=A D^2+A B^2 \\
& (20)^2=b^2+b^2 \\
& 2 b^2=400 \\
& b^2=200 \\
&
\end{aligned}
\)
Area of square \(=200 \mathrm{~cm}^2\)
Therefore, area of the largest square is \(200 \mathrm{~cm}^2\) -
Question 29 of 50
29. Question
What is the radius of the largest circle that can be cut out of the rectangle measuring 10 cm in length and 8 cm in breadth?
CorrectIncorrectHint
Given, the dimension of the rectangle is \(10 \mathrm{~cm}\) in length and \(8 \mathrm{~cm}\) in breadth
We have to find the radius of the largest circle that can be cut out of the rectangle.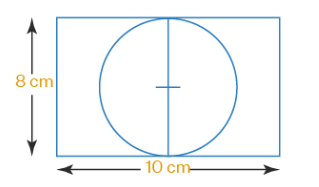
From the figure, we observe that the diameter of the largest circle will be equal to the breadth of the rectangle.
So, diameter of circle \(=8 \mathrm{~cm}\)
Radius \(=\) diameter \(/ 2\)
\(=8 / 2\)
\(=4 \mathrm{~cm}\)
Therefore, the radius is \(4 \mathrm{~cm}\) -
Question 30 of 50
30. Question
The area of a square is \(100 \mathrm{~cm}^2\). The circumference (in \(\mathrm{cm}\) ) of the largest circle cut of it is
CorrectIncorrectHint
Given, area of square is \(100 \mathrm{~cm}^2\)
We have to find the circumference of the largest circle cut out of the square.
Area of square \(=(\text { side })^2\)
side \(^2=100\)
Taking square root,
side \(=10 \mathrm{~cm}\)
The diameter of the circle will be equal to the side of the square.
Diameter of circle \(=10 \mathrm{~cm}\)
Radius \(=10 / 2=5 \mathrm{~cm}\)
Circumference of circle \(=2 \pi r\)
Where, \(r\) is the radius of circle
\(
\begin{aligned}
& =2 \pi(5) \\
& =10 \pi \mathrm{cm}
\end{aligned}
\)
Therefore, the circumference of the circle is \(10 \pi \mathrm{cm}\). -
Question 31 of 50
31. Question
The area of a semicircle of radius \(4 r\) is
CorrectIncorrectHint
Given, radius of semicircle is \(4 r\)
We have to find the area of the semicircle
Area of semicircle \(=\pi r^2 / 2\)
Where, \(r\) is the radius of the circle
Given, \(r=4 r\)
Area \(=\pi(4 r)^2 / 2\)
\(=16 \pi r^2 / 2\)
\(=8 \pi r^2\)
Therefore, the area of the semicircle is \(8 \pi r^2\) square units. -
Question 32 of 50
32. Question
A hedge boundary needs to be planted around a rectangular lawn of size 72 m × 18 m. If 3 shrubs can be planted in a metre of hedge, how many shrubs will be planted in all?
CorrectIncorrectHint
Given, a hedge boundary needs to be planted around a rectangular lawn
of size \(72 \mathrm{~m} \times 18 \mathrm{~m}\).
3 shrubs can be planted in a metre of hedge.
We have to find the number of shrubs that can be planted in all.
Perimeter of rectangle \(=2\) (length \(\times\) breadth \()\)
Length of rectangular lawn \(=72 \mathrm{~m}\)
Breadth of rectangular lawn \(=18 \mathrm{~m}\)
Perimeter of rectangular lawn \(=2(72+18)\)
\(=2(90)\)
\(=180 \mathrm{~m}\)
In one meter 3 shrubs can be planted.
Number of shrubs that can be planted in rectangular lawn \(=3 \times\)
perimeter of lawn
\(=3(180)\)
\(=540\) shrubs
Therefore, the number of shrubs that can be planted is 540. -
Question 33 of 50
33. Question
In the Figure below, area of \(\triangle \mathrm{AFB}\) is equal to the area of parallelogram ABCD. If altitude \(\mathrm{EF}\) is \(16 \mathrm{~cm}\) long, find the altitude of the parallelogram to the base \(\mathrm{AB}\) of length \(10 \mathrm{~cm}\). What is the area of \(\triangle \mathrm{DAO}\), where \(\mathrm{O}\) is the mid point of DC?
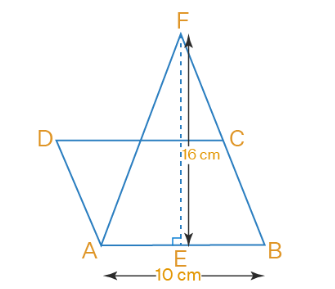 CorrectIncorrect
CorrectIncorrectHint
Given, the area of \(\triangle A F B\) is equal to the area of parallelogram \(A B C D\).
The length of altitude EF is \(16 \mathrm{~cm}\)
We have to find the altitude of the parallelogram to the base \(A B\) of length \(10 \mathrm{~cm}\).
Area of triangle \(=1 / 2 \times\) base \(\times\) height
Area of parallelogram \(=\) base \(\times\) corresponding height
Area of \(\triangle \mathrm{AFB}=\) area of parallelogram \(\mathrm{ABCD}\)
\(
\begin{aligned}
& 1 / 2 \times A B \times E F=A B \times E G \\
& 1 / 2 \times 10 \times 16=10 \times E G \\
& 10 \times 8=10 \times E G \\
& E G=8 \mathrm{~cm}
\end{aligned}
\)
Therefore, the corresponding altitude to the base \(A B\) is \(8 \mathrm{~cm}\).
We have to find the area of \(\triangle D A O\), where \(O\) is the midpoint of \(D C\).
Since \(O\) is the midpoint of \(D C\)
\(
\begin{aligned}
& \mathrm{DC}=\mathrm{DO}+\mathrm{CO} \\
& \mathrm{DO}=\mathrm{CO}=5 \mathrm{~cm}
\end{aligned}
\)
Area of \(\triangle D A O=1 / 2 \times D O \times\) height
\(
\begin{aligned}
& =1 / 2 \times 5 \times 8 \\
& =5(4) \\
& =20 \mathrm{~cm}^2
\end{aligned}
\) -
Question 34 of 50
34. Question
The ratio of the area of \(\Delta W X Y\) to the area of \(\Delta W Z Y\) is \(3: 4\) (Fig. 9.33). If the area of \(\Delta W X Z\) is \(56 \mathrm{~cm}^2\) and \(W Y=8 \mathrm{~cm}\), find the lengths of \(X Y\) and \(Y Z\).
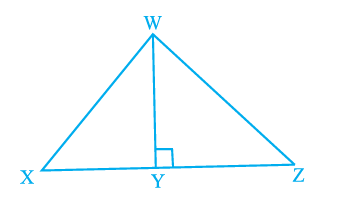 CorrectIncorrect
CorrectIncorrectHint
Given, the ratio of the area of \(\triangle W X Y\) to the area of \(\triangle W Z Y\) is \(3: 4\)
The area of \(\triangle W X Z\) is \(56 \mathrm{~cm}^2\) and \(W Y=8 \mathrm{~cm}\).
We have to find the lengths of \(X Y\) and \(Y Z\).
Area of triangle \(=1 / 2 \times\) base \(\times\) height
Area of \(\triangle W X Y\) : area of \(\triangle W Z Y=3: 4\)
\(1 / 2 \times X Y \times W Y: 1 / 2 \times Y Z \times W Y=3: 4\)
\(X Y: Y Z=3: 4\)
Area of \(\triangle W X Z=1 / 2 \times X Z \times W Y\)
\(56=1 / 2 \times X Z \times 8\)
\(56=4 \times X Z\)
\(X Z=56 / 4\)
\(X Z=14 \mathrm{~cm}\)
From the figure
\(
\begin{aligned}
& X Z=X Y+Y Z \\
& Y Z=X Z-X Y \\
& Y Z=14-X Y \\
& N o w, X Y / Y Z=3 / 4 \\
& X Y /(14-X Y)=3 / 4 \\
& X Y(4)=3(14-X Y) \\
& 4 X Y=3(14)-3 X Y \\
& 4 X Y+3 X Y=3(14) \\
& 7 X Y=3(14) \\
& X Y=3(14) / 7 \\
& X Y=3(2)=6 \mathrm{~cm} \\
& Y Z=14-6=8 \mathrm{~cm}
\end{aligned}
\) -
Question 35 of 50
35. Question
In the figure below, find the area of the parallelogram \(\mathrm{ABCD}\) if the area of the shaded triangle is \(9 \mathrm{~cm}^2\).
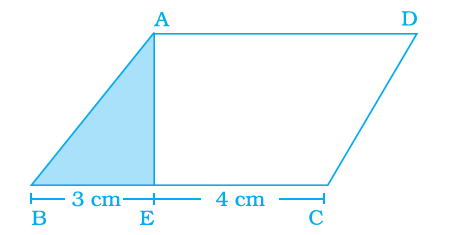 CorrectIncorrect
CorrectIncorrectHint
Given, area of the shaded triangle is \(9 \mathrm{~cm}^2\)
We have to find the area of the parallelogram ABCD.
Area of triangle \(=1 / 2 \times\) base \(\times\) height
\(9=1 / 2 \times 3 \times h\)
\(9(2)=3 \times h\)
\(h=9(2) / 3\)
\(=3(2)\)
\(\mathrm{h}=6 \mathrm{~cm}\)
Area of parallelogram \(=\) base \(\times\) corresponding height
\(=\mathrm{BE} \times \mathrm{h}\)
\(=(3+4) \times 6\)
\(=7(6)\)
\(=42 \mathrm{~cm}^2\)
Therefore, the area of parallelogram is \(42 \mathrm{~cm}^2\). -
Question 36 of 50
36. Question
In the figure below, \(\mathrm{ABCD}\) is a square with \(\mathrm{AB}=15 \mathrm{~cm}\). Find the area of the square BDFE.
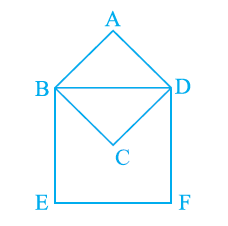 CorrectIncorrect
CorrectIncorrectHint
Given, \(\mathrm{ABCD}\) is a square
\(
A B=15 \mathrm{~cm}
\)
We have to find the area of the square BDFE.
From the figure,
\(\mathrm{BD}\) is the diagonal of the square \(\mathrm{ABCD}\).
Diagonal of square \(=\) side \(\times \sqrt{2}\)
\(=15 \sqrt{ } 2 \mathrm{~cm}\)
So, the length of the side of square BDFE \(=15 \sqrt{ } 2 \mathrm{~cm}\)
Area of square \(=(\text { side })^2\)
\(
\begin{aligned}
& =(15 \sqrt{ } 2)^2 \\
& =(15)^2 \times 2 \\
& =225(2) \\
& =450 \mathrm{~cm}^2
\end{aligned}
\)
Therefore, the area of square BDFE is \(450 \mathrm{~cm}^2\). -
Question 37 of 50
37. Question
Altitudes MN and MO of parallelogram MGHK are \(8 \mathrm{~cm}\) and \(4 \mathrm{~cm}\) long respectively (Figure below). One side GH is \(6 \mathrm{~cm}\) long. Find the perimeter of MGHK.
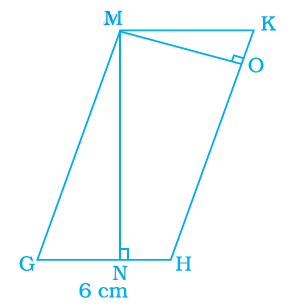 CorrectIncorrect
CorrectIncorrectHint
Given, MGHK is a parallelogram
The altitudes MN and MO of parallelogram are \(8 \mathrm{~cm}\) and \(4 \mathrm{~cm}\)
The length of one side \(\mathrm{GH}\) is \(6 \mathrm{~cm}\).
We have to find the perimeter of MGHK.
Area of parallelogram \(=\) base \(\times\) corresponding height
\(
\begin{aligned}
& =\mathrm{GH} \times \mathrm{MN} \\
& =6 \times 8 \\
& =48 \mathrm{~cm}^2
\end{aligned}
\)
Now, taking base \(\mathrm{HK}\) and altitude \(\mathrm{MO}\)
Area of parallelogram \(=\mathrm{HK} \times M O\)
\(
48=\mathrm{HK} \times 4
\)
\(
\mathrm{HK}=48 / 4
\)
\(
\mathrm{HK}=12 \mathrm{~cm}
\)
Perimeter of parallelogram \(=2\) (length \(+\) breadth \()\)
Perimeter of parallelogram \(\mathrm{MGHK}=2(\mathrm{GH}+\mathrm{HK})\)
\(
\begin{aligned}
& =2(6+12) \\
& =2(18) \\
& =36 \mathrm{~cm}
\end{aligned}
\) -
Question 38 of 50
38. Question
In the figure below, area of \(\triangle \mathrm{PQR}\) is \(20 \mathrm{~cm}^2\) and area of \(\triangle \mathrm{PQS}\) is \(44 \mathrm{~cm}^2\). Find the length RS, if \(\mathrm{PQ}\) is perpendicular to \(\mathrm{QS}\) and \(\mathrm{QR}\) is \(5 \mathrm{~cm}\).
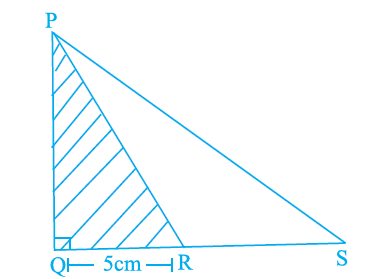 CorrectIncorrect
CorrectIncorrectHint
Given, the area of \(\triangle \mathrm{PQR}\) is \(20 \mathrm{~cm}^2\)
The area of \(\triangle \mathrm{PQS}\) is \(44 \mathrm{~cm}^2\)
\(
\mathrm{QR}=5 \mathrm{~cm}
\)
We have to find the length RS, if \(P Q\) is perpendicular to QS.
Area of triangle \(=1 / 2 \times\) base \(\times\) height
Area of \(\triangle \mathrm{PQR}=1 / 2 \times \mathrm{QR} \times \mathrm{PQ}\)
\(
\begin{aligned}
& 2 O=1 / 2 \times 5 \times P Q \\
& P Q=2 O(2) / 5 \\
& =4(2) \\
& P Q=8 \mathrm{~cm}
\end{aligned}
\)
Area of \(\triangle \mathrm{PQS}=1 / 2 \times \mathrm{QS} \times \mathrm{PQ}\)
\(
\begin{aligned}
& 44=1 / 2 \times Q S \times 8 \\
& Q S=44(2) / 8 \\
& =44 / 4 \\
& Q S=11 \mathrm{~cm}
\end{aligned}
\)
\(P Q\) is perpendicular to \(Q S\).
\(
\begin{aligned}
& \text { So, QS }=Q R+R S \\
& 11=5+R S \\
& R S=11-5 \\
& R S=6 \mathrm{~cm}
\end{aligned}
\) -
Question 39 of 50
39. Question
Find the areas of the shaded region in the figure below.
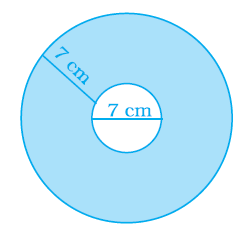 CorrectIncorrect
CorrectIncorrectHint
Consider \(r\) as the radius of smaller circle and \(R\) as the radius of bigger circle
From the figure, we can see,
\(
\begin{aligned}
& r=7 / 2=3.5 \mathrm{~cm} \\
& \mathrm{R}=7 / 2+7=21 / 2=10.5 \mathrm{~cm}
\end{aligned}
\)
We know that
Area of shaded region = Area of bigger circle – Area of smaller circle
\(
=\pi R^2-\pi r^2
\)
Taking \(\pi\) as common
\(
=\pi\left(R^2-r^2\right)
\)
Substituting the values
\(
=\pi\left[(10.5)^2-(3.5)^2\right]
\)
By further calculation
\(
=\pi(110.25-12.25)
\)
Sowe get
\(
\begin{aligned}
& =22 / 7 \times 98 \\
& =308 \mathrm{~cm}^2
\end{aligned}
\) -
Question 40 of 50
40. Question
Find the areas of the shaded region shown in the figure below.
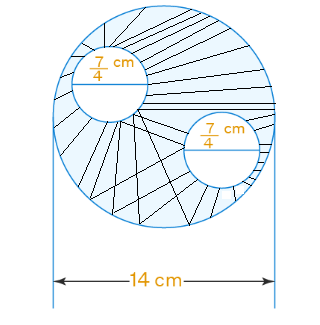 CorrectIncorrect
CorrectIncorrectHint
Given
Diameter of the complete circle \(=14 \mathrm{~cm}\)
We know that
\({\text { Radius }}=14 / 2=7 \mathrm{~cm}\)
Here
Area of the complete circle \(=\pi r^2\)
Substituting the values
\(
\begin{aligned}
& =22 / 7 \times 7 \times 7 \\
& =154 \mathrm{~cm}^2
\end{aligned}
\)
It is given that
Diameter of small circle \(=7 / 4 \mathrm{~cm}\)
Radius \(=7 /(4 \times 2)=7 / 8 \mathrm{~cm}\)
Here
Area of two small circles \(=2 \times \pi r^2\)
Substituting the values
\(
\begin{aligned}
& =2 \times 22 / 7 \times 7 / 8 \times 7 / 8 \\
& =77 / 16=4.8 \mathrm{~cm}^2
\end{aligned}
\)
We know that
Area of shaded region \(=\) Area of complete circle \(–\) Area of two small circles
Substituting the values
\(
\begin{aligned}
& =154-4.8 \\
& 149.2 \mathrm{~cm}^2
\end{aligned}
\)
Therefore, the area of the shaded region is \(149.2 \mathrm{~cm}^2\). -
Question 41 of 50
41. Question
A circle with radius 16 cm is cut into four equal parts and rearranged to form another shape as shown in the figure below.
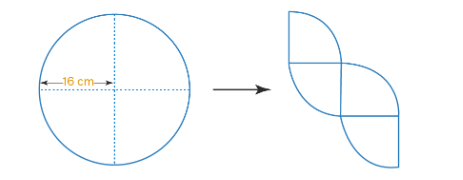
Does the perimeter change? If it does change, by how much does it increase or decrease?
CorrectIncorrectHint
We know that
Curved part of the new shape is \(1 / 4\) th the perimeter of the circle and the radius is the straight line
It is given that
Radius of the original circle \(=16 \mathrm{~cm}\)
Perimeter \(=2 \pi r\)
Substituting the values
\(
\begin{aligned}
& =2 \pi \times 16 \\
& =32 \pi
\end{aligned}
\)
Perimeter of curved part of new shape \(=1 / 4 \times 32 \pi=8 \pi\)
Here
Perimeter of new shape \(=(4 \times\) Perimeter of curved part \()+(2 \times\) radius \()\)
Substituting the values
\(
\begin{aligned}
& =(4 \times 8 \pi)+(2 \times 16) \\
& =32 \pi+32
\end{aligned}
\)
Perimeter is increased by \(32 \mathrm{~cm}\). -
Question 42 of 50
42. Question
Ishika has designed a small oval race track for her remote control car. Her design is shown in the figure below. What is the total distance around the track? Round your answer to the nearest whole cm.
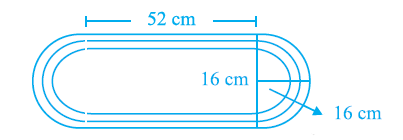 CorrectIncorrect
CorrectIncorrectHint
We know that
Total distance around the track = Length of two parallel strips + Length of two semi circles
Given
Radius \(r=16 \mathrm{~cm}\)
Substituting the values
\(
=(2 \times 52)+(2 \times \pi \times 16)
\)
By further calculation
\(
=104+(2 \times 3.14 \times 16)
\)
Sowe get
\(
\begin{aligned}
& =104+100.5009 \\
& =205 \mathrm{~cm}
\end{aligned}
\)
Therefore, the total distance around the track is \(205 \mathrm{~cm}\). -
Question 43 of 50
43. Question
The dimensions of a plot are \(200 \mathrm{~m} \times 150 \mathrm{~m}\). A builder builds 3 roads which are \(3 \mathrm{~m}\) wide along the length on either side and one in the middle. On either side of the middle road he builds houses to sell. How much area did he get for building the houses?
CorrectIncorrectHint
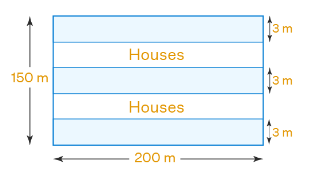
It is given that
Dimension of a plot \(=200 \mathrm{~m} \times 150 \mathrm{~m}\)
Width of road \(=3 \mathrm{~m}\)
We know that
Total area available for houses \(=\) Area of total plot \(–\) Area of 3 roads
Substituting the values
\(
=(200 \times 150)-3 \times(3 \times 200)
\)
By further calculation
\(
\begin{aligned}
& =30000-1800 \\
& =28200 \mathrm{~m}^2
\end{aligned}
\)
Therefore, the area he got for building the houses is \(28200 \mathrm{~m}^2\). -
Question 44 of 50
44. Question
How much distance, in metres, a wheel of 25 cm radius will cover if it rotates 350 times?
CorrectIncorrectHint
It is given that
Radius of wheel \(=25 \mathrm{~cm}=25 / 100 \mathrm{~m}=1 / 4 \mathrm{~m}[\) As \(1 \mathrm{~cm}=1 / 100 \mathrm{~m}]\)
We know that
Distance traveled in one rotation \(=2 \pi r\)
Substituting the values
\(
\begin{aligned}
& =2 \times 22 / 7 \times 1 / 4 \\
& =11 / 7=1.57 \mathrm{~m}
\end{aligned}
\)
Therefore,
Distance traveled in 350 rotations \(=1.57 \times 350\)
\(
=550 \mathrm{~m}
\)
Therefore, the wheel covers a distance of \(550 \mathrm{~m}\). -
Question 45 of 50
45. Question
Calculate the area of the shaded region in the figure below, where all of the short line segments are at right angles to each other and 1 cm long.
 CorrectIncorrect
CorrectIncorrectHint
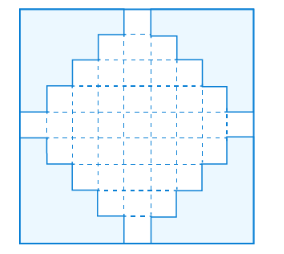
Given, the figure represents a large rectangle in which all of the short line segments are at right angles to each other and 1 cm long.
We have to find the area of the shaded region.
Considering larger square,
\(
\text { side }=9 \mathrm{~cm}
\)
Area of square \(=(\text { side })^2\)
\(
\begin{aligned}
& =(9)^2 \\
& =81 \mathrm{~cm}^2
\end{aligned}
\)
Given, short line segments are at right angles to each other and \(1 \mathrm{~cm}\) long
By joining all the short lines using dotted lines, we obtain 41 identical squares.
Area of square \(=(\text { side })^2\)
Considering one square,
Side \(=1 \mathrm{~cm}\)
Area of square \(=(1)^2=1 \mathrm{~cm}^2\)
Area of 41 identical squares \(=41(1)=41 \mathrm{~cm}^2\)
Area of shaded region \(=\) area of larger square \(–\) area of 41 identical squares
\(
\begin{aligned}
& =81-41 \\
& =40 \mathrm{~cm}^2
\end{aligned}
\)
Therefore, the area of the shaded region is \(40 \mathrm{~cm}^2\). -
Question 46 of 50
46. Question
\(\mathrm{ABCD}\) is a given rectangle with length as \(80 \mathrm{~cm}\) and breadth as \(60 \mathrm{~cm} . \mathrm{P}, \mathrm{Q}, \mathrm{R}, \mathrm{S}\) are the mid points of sides \(\mathrm{AB}, \mathrm{BC}, \mathrm{CD}, \mathrm{DA}\) respectively. A circular rangoli of radius \(10 \mathrm{~cm}\) is drawn at the centre as shown in the figure below. Find the area of shaded portion.
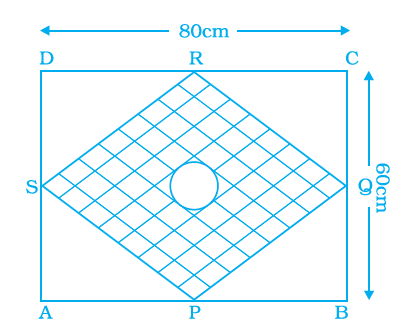 CorrectIncorrect
CorrectIncorrectHint
Given, \(A B C D\) is a rectangle with length \(80 \mathrm{~cm}\) and breadth \(60 \mathrm{~cm}\).
\(P, Q, R\) and \(S\) are the midpoints of \(A B, B C, C D\), and DA respectively.
A circular rangoli of radius \(10 \mathrm{~cm}\) is drawn at the centre.
We have to find the area of the shaded portion.
Area of rectangle \(\mathrm{ABCD}=\) length \(\times\) breadth
\(=80(60)\)
\(=4800 \mathrm{~cm}^2\)
The triangles SAP, PBQ, RCQ and RDS are congruent
\(S\) is the midpoint of DA
So, \(A S=60 / 2=30 \mathrm{~cm}\)
\(P\) is the midpoint of \(A B\)
So, \(A P=80 / 2=40 \mathrm{~cm}\)
Area of triangle \(=1 / 2 \times\) base \(\times\) height
Area of triangle SAP \(=1 / 2 \times \mathrm{AP} \times \mathrm{AS}\)
\(=1 / 2 \times 40 \times 30\)
\(=20(30)\)
\(=600 \mathrm{~cm}^2\)
Area of 4 congruent triangles \(=4(600)\)
\(=2400 \mathrm{~cm}^2\)
Area of circle \(=\pi r^2\)
Area of circular rangoli \(=(3.14)(10)^2\)
\(
\begin{aligned}
& =3.14(100) \\
& =314 \mathrm{~cm}^2
\end{aligned}
\)
Area of shaded portion = area of rectangle PQRS – area of circular rangoli
\(
\begin{aligned}
& =2400-314 \\
& =2086 \mathrm{~cm}^2
\end{aligned}
\)
Therefore, the area of the shaded portion is \(2086 \mathrm{~cm}^2\). -
Question 47 of 50
47. Question
4 squares each of side 10 cm have been cut from each corner of a rectangular sheet of paper of size 100 cm × 80 cm. From the remaining piece of paper, an isosceles right triangle is removed whose equal sides are each of 10 cm length. Find the area of the remaining part of the paper.
CorrectIncorrectHint
Given 4 squares each side \(10 \mathrm{~cm}\) is cut from each corner of a rectangle sheet of paper of size \(100 \mathrm{~cm} \times 80 \mathrm{~cm}\).
An isosceles triangle is removed from the remaining piece of paper whose equal sides are \(10 \mathrm{~cm}\) length.
We have to find the remaining part of the paper.
Area of rectangular sheet \(=\) length \(\times\) breadth
\(
\begin{aligned}
& =100(80) \\
& =8000 \mathrm{~cm}^2
\end{aligned}
\)
Area of one square \(=(\text { side })^2\)
\(
\begin{aligned}
& =(10)^2 \\
& =100 \mathrm{~cm}^2
\end{aligned}
\)
So, area of 4 squares \(=4(100)=400 \mathrm{~cm}^2\)
Area of triangle \(=1 / 2 \times\) base \(\times\) height
Area of isosceles triangle \(=1 / 2 \times 10 \times 10\)
\(
\begin{aligned}
& =10(5) \\
& =50 \mathrm{~cm}^2
\end{aligned}
\)
Area of the remaining part of the sheet \(=\) area of rectangular sheet \(–\) area of 4 squares – area of isosceles triangle
\(
\begin{aligned}
& =8000-400-50 \\
& =7600-50 \\
& =7550 \mathrm{~cm}^2
\end{aligned}
\)
Therefore, the area of the remaining part is \(7550 \mathrm{~cm}^2\). -
Question 48 of 50
48. Question
A dinner plate is in the form of a circle. A circular region encloses a beautiful design as shown in the figure below. The inner circumference is \(352 \mathrm{~mm}\) and outer is \(396 \mathrm{~mm}\). Find the width of circular design.
 CorrectIncorrect
CorrectIncorrectHint
Given, a dinner plate is in the form of a circle.
A circular region encloses a beautiful design.
The inner circumference is \(352 \mathrm{~mm}\) and the outer is \(396 \mathrm{~mm}\).
We have to find the width of the circular design.
Circumference \(=2 \pi r\)
Outer circumference \(=2 \pi R\)
\(
\begin{aligned}
& 396=2(22 / 7) R \\
& 396=(44 / 7) R \\
& R=396(7) / 44 \\
& R=9(7) \\
& R=63 \mathrm{~mm}
\end{aligned}
\)
Inner circumference \(=2 \pi r\)
\(
\begin{aligned}
& 352=2(22 / 7) r \\
& 352=(44 / 7) r \\
& r=352(7) / 44 \\
& r=8(7) \\
& r=56 \mathrm{~mm}
\end{aligned}
\)
Width of circular ring \(=\mathrm{R}-\mathrm{r}\)
\(
\begin{aligned}
& =63-56 \\
& =7 \mathrm{~mm}
\end{aligned}
\)
Therefore, the width of the design is \(7 \mathrm{~mm}\). -
Question 49 of 50
49. Question
The moon is about \(384000 \mathrm{~km}\) from earth and its path around the earth is nearly circular. Find the length of path described by moon in one complete revolution. (Take \(\pi=3.14\) )
CorrectIncorrectHint
Given, the moon is about \(384000 \mathrm{~km}\) from earth and its path around the earth is nearly circular.
We have to find the length of the path described by the moon in one complete revolution.
The length of the path by moon in one complete revolution = circumference
Circumference \(=2 \pi r\)
Given, radius \(=384000 \mathrm{~km}\)
\(=2(3.14)(384000)\)
\(=2(314)(3840)\)
\(=2411520 \mathrm{~km}\)
Therefore, the circumference is \(2411520 \mathrm{~km}\). -
Question 50 of 50
50. Question
A photograph of Billiard/Snooker table has dimensions as \(\frac{1}{10}\) th of its actual size as shown in the figure below. The portion excluding six holes each of diameter \(0.5 \mathrm{~cm}\) needs to be polished at rate of \(₹ 200\) per \(\mathrm{m}^2\). Find the cost of polishing.
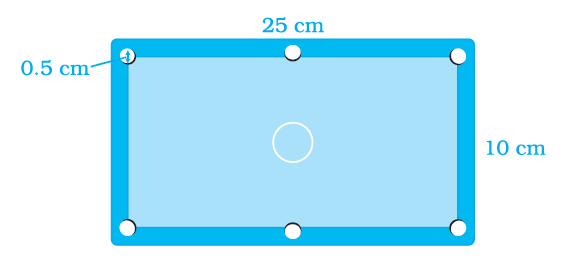 CorrectIncorrect
CorrectIncorrectHint
Given, a photograph of a billiard/snooker table has dimensions as \(1 / 10\) th of its actual size.
The portion excluding six holes each of diameter \(0.5 \mathrm{~cm}\) needs to be polished.
The rate of polishing is \(₹ 200\) per \(\mathrm{m}^2\).
We have to find the total cost of polishing.
Original length \(=25(10)=250 \mathrm{~cm}\)
Original breadth \(=10(10)=100 \mathrm{~cm}\)
Area of table \(=\) length \(\times\) breadth
\(=250(100)\)
\(=25000 \mathrm{~cm}^2\)
Area of circle \(=\pi r^2\)
Given, diameter \(=0.5 \mathrm{~cm}\)
Radius \(=0.5 / 2=0.25 \mathrm{~cm}\)
\(=(22 / 7)(0.25)^2\)
\(=22(0.0625) / 7\)
\(=0.1964 \mathrm{~cm}^2\)
Area of 6 holes \(=6(0.1964)\)
\(=1.179 \mathrm{~cm}^2\)
Area to be polished = area of table \(–\) area of 6 holes
\(
\begin{aligned}
& =25000-1.179 \\
& =24998.82 \mathrm{~cm}^2
\end{aligned}
\)
We know, \(1 \mathrm{~m}=100 \mathrm{~cm}\)
Area to be polished in \(\mathrm{m}^2=24998.82 / 10000\) \(=2.4999 \mathrm{~m}^2\)
Cost of polishing \(1 \mathrm{~m}^2=₹ 200\)
Cost of polishing table \(=200(2.4999)\) \(=₹ 499.98\)
Therefore, the total cost of polishing is \(₹ 499.98\).