A vector is a quantity having direction as well as magnitude, especially as determining the position of one point in space relative to another.

Parallel vectors

Two vectors are said to be parallel if and only if the angle between them is 0 degrees. Parallel vectors are also known as collinear vectors, i.e., two parallel vectors will be always parallel to the same line but they can be either in the same direction or in the exact opposite direction. 

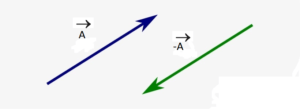
Antiparallel Vectors

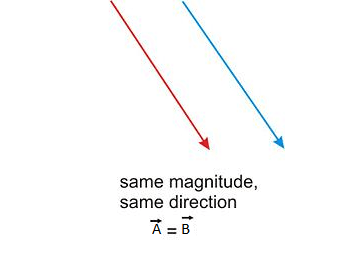
Two vectors are said to be anti-parallel if they are in opposite directions.

Equal vectors

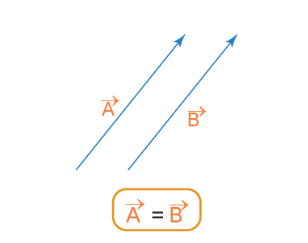
A vector \(\vec{A}\) is called an equal vector to vector \(\vec{A}\) if they have the same magnitude and are pointed in the same direction. 

Negative or opposite vectors

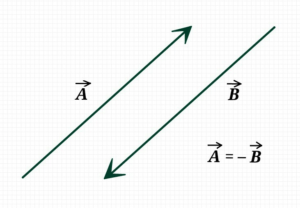
Vectors having equal magnitude but opposite directions.

Null vector or Zero vector

A vector having zero magnitude. The direction of a zero vector is indeterminate.

\(\overrightarrow{\mathrm{A}}+(-\overrightarrow{\mathrm{A}})=\overrightarrow{0}\)

Unit vector

A unit vector is a vector of length 1 (unit vector), sometimes also called a direction vector.

The unit vector \(\hat{\mathbf{A}}\) having the same direction as a given (nonzero) vector \(\vec{A}\) is defined by
\(\hat{\mathbf{A}} \equiv \frac{\vec{A}}{|\vec{A}|}\)

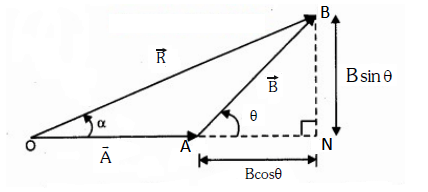
Triangle law of Vector addition

\(
\begin{aligned}
&\overline{\mathrm{R}}=\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}} \\
&\mathrm{R}=\sqrt{\mathrm{A}^{2}+\mathrm{B}^{2}+2 \mathrm{AB} \cos \theta}
\end{aligned}
\)
\(
\tan \alpha=\frac{B \sin \theta}{A+B \cos \theta}
\)
If \(A=B\) then \(R=2 A \cos \frac{\theta}{2}  \&  \alpha=\frac{\theta}{2}\)
\(\mathrm{R}_{\max }=\mathrm{A}+\mathrm{B}\) for \(\theta=0^{\circ} ; \quad \mathrm{R}_{\min }=\mathrm{A}-\mathrm{B}\) for \(\theta=180^{\circ}\)

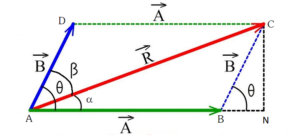
Parallelogram Law of Addition of Two Vectors

If two vectors are represented by two adjacent sides of a parallelogram which are directed away from their common point then their sum (i.e. resultant vector) is given by the diagonal of the parallelogram passing away through that common point.

\(
\begin{gathered}
\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AD}}=\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{R}} \text { or } \overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}=\overrightarrow{\mathrm{R}} \Rightarrow \mathrm{R}=\sqrt{\mathrm{A}^{2}+\mathrm{B}^{2}+2 \mathrm{AB} \cos \theta} \\
\tan \alpha=\frac{\mathrm{B} \sin \theta}{\mathrm{A}+\mathrm{B} \cos \theta} \text { and } \tan \beta=\frac{\mathrm{A} \sin \theta}{\mathrm{B}+\mathrm{A} \cos \theta}
\end{gathered}
\)

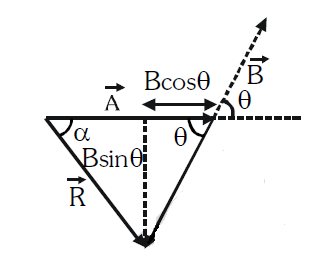
Vector subtraction

\(
\begin{gathered}
\overrightarrow{\mathrm{R}}=\overrightarrow{\mathrm{A}}-\overrightarrow{\mathrm{B}} \Rightarrow \overrightarrow{\mathrm{R}}=\overrightarrow{\mathrm{A}}+(-\overrightarrow{\mathrm{B}}) \\
\mathrm{R}=\sqrt{\mathrm{A}^{2}+\mathrm{B}^{2}-2 \mathrm{AB} \cos \theta}, \quad \tan \alpha=\frac{\mathrm{B} \sin \theta}{\mathrm{A}-\mathrm{B} \cos \theta}
\end{gathered}
\)
If \(A=B\) then \(R=2 A \sin \frac{\theta}{2}\)

Addition of More than Two Vectors (Law of Polygon)

If some vectors are represented by sides of a polygon in same order, then their resultant vector is represented by the closing side of polygon in the opposite order.

\(
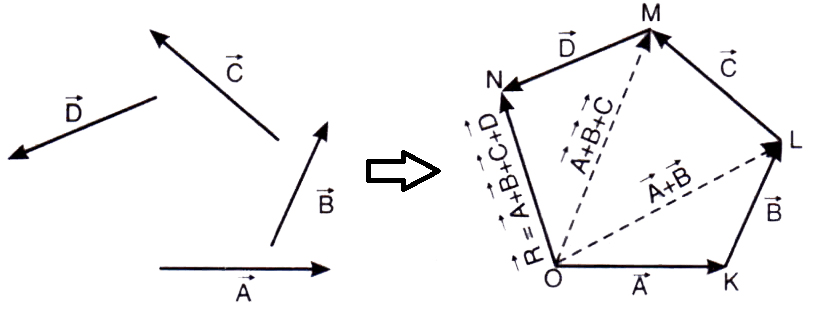
\overrightarrow{\mathrm{R}}=\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}+\overrightarrow{\mathrm{C}}+\overrightarrow{\mathrm{D}}
\)

 

If the polygon is closed, the resultant is a vector of zero magnitude and has no direction. This is called the null vector.

\(
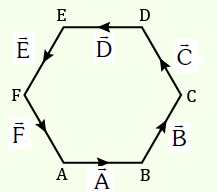
\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}+\overrightarrow{\mathrm{C}}+\overrightarrow{\mathrm{D}}+\overrightarrow{\mathrm{E}}+ \overrightarrow{\mathrm{F}}=0
\)

Rectangular component of a 3-D vector

• \(\vec{A}=A_{x} \hat{i}+A_{y} \hat{j}+A_{z} \hat{k}\)
  Angle made with \(\mathrm{x}\)-axis
  \(
  \cos \alpha=\frac{A_{x}}{A}=\frac{A_{x}}{\sqrt{A_{x}^{2}+A_{y}^{2}+A_{z}^{2}}}=\ell
  \)
  Angle made with \(\mathrm{y}\)-axis
  \(
  \cos \beta=\frac{A_{y}}{A}=\frac{A_{y}}{\sqrt{A_{x}^{2}+A_{y}^{2}+A_{z}^{2}}}=m
  \)
  Angle made with \(z\)-axis
  \(
  \cos \gamma=\frac{A_{z}}{A}=\frac{A_{z}}{\sqrt{A_{x}^{2}+A_{y}^{2}+A_{z}^{2}}}=n
  \)
• \(\ell, \mathrm{m}, \mathrm{n}\) are called direction cosines \(\ell^{2}+m^{2}+n^{2}=\cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma\)
  \(
  =\frac{\mathrm{A}_{\mathrm{x}}^{2}+\mathrm{A}_{\mathrm{y}}^{2}+\mathrm{A}_{\mathrm{z}}^{2}}{\left(\sqrt{\mathrm{A}_{\mathrm{x}}^{2}+\mathrm{A}_{\mathrm{y}}^{2}+\mathrm{A}_{\mathrm{z}}^{2}}\right)^{2}}=1 \text { or } \sin ^{2} \alpha+\sin ^{2} \beta+\sin ^{2} \gamma=2
  \)

General Vector in the x-y plane

\(\vec{r}=x \hat{i}+y \hat{j}=r(\cos \theta \hat{i}+\sin \theta \hat{j})\)

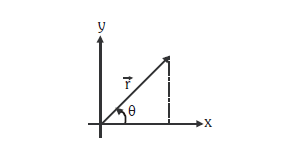
Examples:

1. Construct a vector of magnitude 6 units making an angle of \(60^{\circ}\) with \(x\)-axis.

Solution: \(\vec{r}=r(\cos 60 \hat{\mathrm{i}}+\sin 60 \hat{\mathrm{j}})=6\left(\frac{1}{2} \hat{\mathrm{i}}+\frac{\sqrt{3}}{2} \hat{\mathrm{j}}\right)=3 \hat{\mathrm{i}}+3 \sqrt{3} \hat{\mathrm{j}}\)

2. Construct an unit vector making an angle of \(135^{\circ}\) with \(\mathrm{x}\) axis.

Solution: \(\hat{\mathrm{r}}=1\left(\cos 135^{\circ} \hat{\mathrm{i}}+\sin 135^{\circ} \hat{\mathrm{j}}\right)=\frac{1}{\sqrt{2}}(-\hat{\mathrm{i}}+\hat{\mathrm{j}})\)

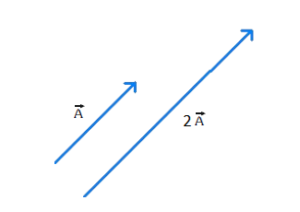
Multiplication of a vector by a number

If \(\vec{b}=k \vec{a}\) then magnitude of \(\vec{b}\) is \(k\) times \(|\vec{a}|\), and direction of \(\vec{b}\) is same as \(\vec{a}\)

Example: Consider a vector \(\vec{A}\). What happens if you multiply this vector by 2? What will the vector \(2 \vec{A}\) represent?

Solution: The new vector will be twice the length of the original vector, but in the same direction as shown below.

How to do the multiplication of two vectors?

A vector has both magnitude and direction. We can multiply two or more vectors by dot product (scalar product) and cross product. 

Dot Product (Scalar product)

The dot product of vectors is also called the scalar product of vectors. The resultant of the dot product of the vectors is a scalar value. Dot Product of vectors is equal to the product of the magnitudes of the two vectors, and the cosine of the angle between the two vectors. The resultant of the dot product of two vectors lie in the same plane of the two vectors. The dot product may be a positive real number or a negative real number.

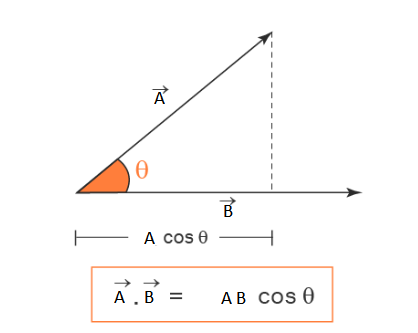
Here, A is the magnitude of \(|\vec{A}|\) and ,B is the magnitude of \(|\vec{B}|\), and \(\theta\) is the angle between them.

Angle between two vectors

\(\theta=\cos ^{-1}\left(\frac{\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}}{\mathrm{AB}}\right)\)

For the scalar multiplication of vectors, the two vectors are expressed in terms of unit vectors, i, j, k, along the \(x, y, z\) axes, then the scalar product is obtained as follows:

\(\text { If } \overrightarrow{\mathrm{A}}=\mathrm{A}_{\mathrm{x}} \hat{\mathrm{i}}+\mathrm{A}_{y} \hat{\mathrm{j}}+\mathrm{A}_{z} \hat{\mathrm{k}}  \&  \overline{\mathrm{B}}=\mathrm{B}_{\mathrm{x}} \hat{\mathrm{i}}+\mathrm{B}_{y} \hat{\mathrm{j}}+\mathrm{B}_{z} \hat{\mathrm{k}} \text { then }\)

\(\vec{\mathrm{A}}.\vec{\mathrm{B}}=\mathrm{A}_{\mathrm{x}} \mathrm{B}_{\mathrm{x}}+\mathrm{A}_{y} \mathrm{B}_{y}+\mathrm{A}_{z} \mathrm{B}_{z} \\\)

and angle between \(\vec{\mathrm{A}}\) & \(\vec{\mathrm{B}} \\\)

\(\cos \theta=\frac{\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}}{\mathrm{AB}}\)

\(
\frac{\mathrm{A_{x}} \mathrm{B_{x}}+\mathrm{A_{y}} \mathrm{B_{y}}+\mathrm{A_{z}} \mathrm{B_{z}}}{\sqrt{\mathrm{A_{x}}^{2}+\mathrm{A_{y}}^{2}+\mathrm{A_{z}}^{2}} \sqrt{\mathrm{B_{x}}^{2}+\mathrm{B_{y}}^{2}+\mathrm{B_{z}}^{2}}  }
\)

• \(
  \hat{\mathrm{i}} . \hat{\mathrm{i}}=1, \hat{\mathrm{j}} \hat{\mathrm{j}}=1, \hat{\mathrm{k}} . \hat{\mathrm{k}}=1, \hat{\mathrm{i}} . \hat{\mathrm{j}}=0, \hat{\mathrm{i}} . \hat{\mathrm{k}}=0, \hat{\mathrm{j}} . \hat{\mathrm{k}}=0
  \)

What is a Projection Vector?

The projection of a vector is the length of the shadow of the given vector on another vector. It is the product of the magnitude of the given vector and the cosine of the angle between the two vectors. 

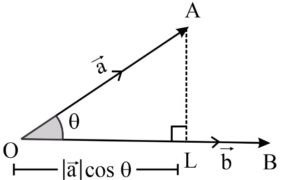
The projection of vector \(\vec{a}\) on vector \(\vec{b}\) is equal to the dot product of vector \(\vec{a}\) and vector \(\vec{b}\), divided by the magnitude of the vector \(\vec{b}\).

\(
\text { The projection of a vector } \vec{a} \text { on vector } \vec{b} \text { is } \frac{\vec{a} \cdot \vec{b}}{|\vec{b}|}
\) \(\text { Similarly, the projection of vector } \vec{b} \text { on vector } \vec{a} \text { is } \frac{\vec{a} \cdot \vec{b}}{|\vec{a}|}\)

 

Example: Find the projection of a vector \(4 \hat{i}+2 \hat{j}+\hat{k}\) on a vector \(5 \hat{i}-3 \hat{j}+3 \hat{k}\).

Solution: Let \(\vec{a}=4 \hat{i}+2 \hat{j}+\hat{k}\) and \(\vec{b}=5 \hat{i}-3 \hat{j}+3 \hat{k}\)
As we know, the projection of a vector \(\vec{a}\) on vector \(\vec{b}\) is \(\frac{\vec{a} \cdot \vec{b}}{|\vec{b}|}\) Therefore, the projection of a vector \(4 \hat{i}+2 \hat{j}+\hat{k}\) on a vector
\(
\begin{aligned}
&5 \hat{i}-3 \hat{j}+3 \hat{k}=\frac{(4 \hat{i}+2 \hat{j}+\hat{k}) \cdot(5 \hat{i}-3 \hat{j}+3 \hat{k})}{|5 \hat{i}-3 \hat{j}+3 \hat{k}|} \\
&=\frac{4 \cdot(5)+2(-3)+1(3)}{\sqrt{5^{2}+(-3)^{2}+(3)^{2}}} \\
&=\frac{20-6+3}{\sqrt{25+9+9}} \\
&=\frac{17}{\sqrt{43}}
\end{aligned}
\)

• Component of a given vector \(\vec{\mathrm{B}}\) along \(\vec{\mathrm{A}}\) is given by the length of \(\vec{\mathrm{B}}\) on \(\vec{\mathrm{A}}\).
  Let \(\theta\) be the angle between both the vectors.
  

  
  Vector component of \(\vec{\mathrm{B}}\) along \(\vec{\mathrm{A}}\) is =\((\vec{\mathrm{B}} \cdot \hat{\mathrm{A}}) \hat{\mathrm{A}}\)

          where \(\hat{\mathrm{A}}=\frac{\vec{\mathrm{A}}}{|\vec{\mathrm{A}}|}\)             

                       

Example: Find the component of \(\vec{a}=2 \hat{i}+3 \hat{j}\) along the direction of \(\hat{i}+\hat{j}\).

Solution: Given that, \(\vec{a}=2 \hat{i}+3 \hat{j}\)
Let \(\vec{b}=\hat{i}+\hat{j}\)
So, the unit vector of \(\vec{b}\) is \(\hat{b}=\frac{\hat{i}+\hat{j}}{|\hat{j}+\hat{j}|}=\frac{1}{\sqrt{2}}(\hat{i}+\hat{j})\)
The component of a vector \(\vec{a}\) along the direction of the vector \(\vec{b}=a \cos \theta\)
\(
=(\vec{a} \cdot \hat{b}) \hat{b} \\\)
\(=\left[(2 \hat{i}+3 \hat{j}) \cdot \frac{1}{\sqrt{2}}(\hat{i}+\hat{j})\right] \frac{1}{\sqrt{2}}(\hat{i}+\hat{j}) \\\)
\(=\left[\frac{1}{\sqrt{2}}(2+3)\right] \frac{1}{\sqrt{2}}(\hat{i}+\hat{j}) \\\)
\(=\frac{5}{2}(\hat{i}+\hat{j})\)

• \(\text {The components of } \vec{B} \text { perpendicular to is } \vec{A}\) \(
  =\vec{B}-\left(\frac{\vec{A} \cdot \vec{B}}{|\vec{A}|^{2}}\right) \vec{A}\) = \(
  \overrightarrow{\mathrm{B}}-(\overrightarrow{\mathrm{B}} \cdot \hat{\mathrm{A}}) \hat{\mathrm{A}}
  \)

\(
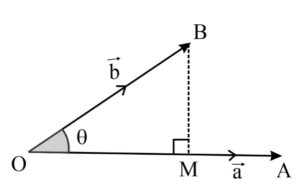
\overrightarrow{M B}=\vec{b}-\overrightarrow{O M}=\vec{b}-\left(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}|^{2}}\right) \vec{a}
\)

Example: Find the component of a vector \(2 \hat{i}+3 \hat{j}+2 \hat{k}\) perpendicular \(\hat{i}+\hat{j}+\hat{k}\)

Solution: Let \(\vec{a}=2 \hat{i}+3 \hat{j}+2 \hat{k}\) and \(\vec{b}=\hat{i}+\hat{j}+\hat{k}\)
As we know, the component of vector \(\vec{a}\) perpendicular to vector \(\vec{b}\) is given by \(\vec{a}-\frac{\vec{a} \cdot \vec{b}}{|\vec{b}|^{2}} \times \vec{b}\)
\(
\begin{aligned}
&=2 \hat{i}+3 \hat{j}+2 \hat{k}-\frac{(2 \hat{i}+3 \hat{j}+2 \hat{k})(\hat{i}+\hat{j}+\hat{k})}{(\sqrt{1+1+1}} \times(\hat{i}+\hat{j}+\hat{k}) \\
&=2 \hat{i}+3 \hat{j}+2 \hat{k}-\frac{1}{(\sqrt{3})^{2}} \times(\hat{i}+\hat{j}+\hat{k}) \\
&=\frac{5}{3}(\hat{i}-2 \hat{j}+\hat{k})
\end{aligned}
\)
Hence, the component of a vector \(\vec{a}\) is perpendicular to vector \(\vec{b}\) is \(\frac{5}{3}(\hat{i}-2 \hat{j}+\hat{k})\).

Cross Product (Vector product)

\(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}=\mathrm{AB} \sin \theta  \hat{\mathrm{n}}\) where \(\hat{\mathrm{n}}\) is the unit vector perpendicular to \(\overrightarrow{\mathrm{A}} \& \overrightarrow{\mathrm{B}}\) or their plane and its direction given by right hand thumb nule.

Where
A (\(|\vec{A}|\))is the magnitude of the vector A or the length of \(\vec{A}\),
B (\(|\vec{B}|\)) is the magnitude of the vector B or the length of \(\vec{B}\).

To get \(\vec{A} \times \vec{B}\) make your fingers sweep from one vector to the other, as if you are rotating \(\vec{A}\) to meet \(\vec{B}\) (dashed arrow below). The cross product direction is where your thumb points.

 

• \(
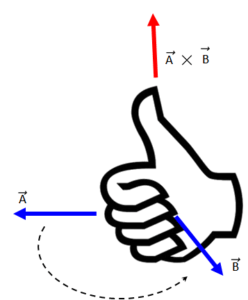
  \begin{aligned}
  &\quad \overrightarrow{\mathrm{A}} \times \overline{\mathrm{B}}=\left|\begin{array}{ccc}
  \hat{\mathrm{i}} & \hat{\mathrm{j}} & \hat{\mathrm{k}} \\
  \mathrm{A}_{\mathrm{x}} & \mathrm{A}_{\mathrm{y}} & \mathrm{A}_{z} \\
  \mathrm{~B}_{\mathrm{x}} & \mathrm{B}_{\mathrm{y}} & \mathrm{B}_{z}
  \end{array}\right|\\
  &=\hat{i}\left(A_{y} B_{z}-A_{z} B_{y}\right)-\hat{j}\left(A_{x} B_{z}-B_{x} A_{z}\right)+\hat{k}\left(A_{x} B_{y}-B_{x} A_{y}\right)
  \end{aligned}
  \)

Example: Find the cross product of two vectors \(\vec{a}=(3,4,5)\) and \(\vec{b}=(7,8,9)\)

Solution:
The cross product is given as,
\(a \times b=\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k} \\ 3 & 4 & 5 \\ 7 & 8 & 9\end{array}\)
\(=[(4 \times 9)-(5 \times 8)] \hat{i}-[(3 \times 9)-(5 \times 7)] \hat{j}+[(3 \times 8)-(4 \times 7)] \hat{k}\)
\(=(36-40) \hat{i}-(27-35) \hat{j}+(24-28) \hat{k}=-4 \hat{i}+8 \hat{j}-4 \hat{k}\)
\(\therefore \vec{a} \times \vec{b}=-4 \hat{i}+8 \hat{j}-4 \hat{k}\)

Example: If \(\vec{a}=(2,-4,4)\) and \(\vec{b}=(4,0,3)\), find the angle between them.

Solution: 

\(
\begin{aligned}
&\vec{a}=2 i-4 j+4 k \\
&\vec{b}=4 i+0 j+3 k
\end{aligned}
\)
The magnitude of \(\vec{a}\) is
\(
|a|=\sqrt{ }\left(2^{2}+4^{2}+4^{2}\right)=\sqrt{ } 36=6
\)
The magnitude of \(\vec{b}\) is
\(
|b|=\sqrt{ }\left(4^{2}+0^{2}+3^{2}\right)=\sqrt{ } 25=5
\)
As per the cross-product formula, we have
\(\vec{a} \times \vec{b}=\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k} \\ 2 & -4 & 4 \\ 4 & 0 & 3\end{array}\)
\(=[(-4 \times 3)-(4 \times 0)] \hat{i}\)
\(-[(3 \times 2)-(4 \times 4)] \hat{j}\)
\(+[(2 \times 0)-(-4 \times 4)] \hat{k}\)
\(=-12 \hat{i}+10 \hat{j}+16 \hat{k}\)
\(\vec{a} \times \vec{b}=(-12,10,16)\)
The length of the \(\vec{c}\) is
\(
\begin{aligned}
&|c|=\sqrt{ }\left(-(12)^{2}+10^{2}+16^{2}\right) \\
&=\sqrt{ }(144+100+256) \\
&=\sqrt{500} \\
&=10 \sqrt{5} \\
&\vec{a} \times \vec{b}=|a||b| \sin \theta \\
&\quad \sin \theta=\frac{\vec{a} \times \vec{b}}{|a||b|} \\
&\sin \theta=10 \sqrt{5} /(5 \times 6) \\
&\sin \theta=\sqrt{5} / 3 \\
&\theta=\sin ^{-1}(\sqrt{5} / 3) \\
&\theta=\sin ^{-1}(0.74) \\
&\theta=48^{\circ}
\end{aligned}
\)

Example: Two vectors have their scalar magnitude as \(|a|=2 \sqrt{3}\) and \(|b|=4\), while the angle between the two vectors is \(60^{\circ}\). Calculate the cross-product of two vectors.

Solution:
We know that \(\sin 60^{\circ}=\sqrt{3} / 2\)
The cross product of the two vectors is given by, \(\vec{a} \times \vec{b}=\) \(|a||b| \sin (\theta) \hat{n}=2 \sqrt{3} \times 4 \times \sqrt{ } 3 / 2=12 \hat{n}\)

• \(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}=- \overrightarrow{\mathrm{B}} \times \overrightarrow{\mathrm{A}} \\\)
• \((\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}) \cdot \overrightarrow{\mathrm{A}}=(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}) \cdot \overrightarrow{\mathrm{B}}=0 \\\)
• \(\hat{\mathrm{i}} \times \hat{\mathrm{i}}= \overrightarrow{0}, \hat{\mathrm{j}} \times \hat{\mathrm{j}}=\overrightarrow{0}, \hat{\mathrm{k}} \times \hat{\mathrm{k}}=\overrightarrow{0} \\\)
• \(\hat{\mathrm{i}} \times \hat{\mathrm{j}}=\hat{\mathrm{k}} ; \hat{\mathrm{j}} \times \hat{\mathrm{k}}=\hat{\mathrm{i}} \\\)
• \(\hat{\mathrm{k}} \times \hat{\mathrm{i}}=\hat{\mathrm{j}} ; \hat{\mathrm{j}} \times \hat{\mathrm{i}}=-\hat{\mathrm{k}} \\\)
• \(\hat{\mathrm{k}} \times \hat{\mathrm{j}}=-\hat{\mathrm{i}}; \hat{\mathrm{i}} \times \hat{\mathrm{k}}=-\hat{\mathrm{j}}\)

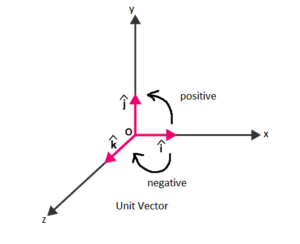
Differentiation

\(\frac{\mathrm{d}}{\mathrm{dt}}(\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}})=\frac{\mathrm{d} \overrightarrow{\mathrm{A}}}{\mathrm{dt}} \cdot \overrightarrow{\mathrm{B}}+\overrightarrow{\mathrm{A}} \cdot \frac{\mathrm{d} \overrightarrow{\mathrm{B}}}{\mathrm{dt}}\)

\(\frac{\mathrm{d}}{\mathrm{dt}}(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}})=\frac{\mathrm{d} \overrightarrow{\mathrm{A}}}{\mathrm{dt}} \times \overrightarrow{\mathrm{B}}+\overrightarrow{\mathrm{A}} \times \frac{\mathrm{d} \overrightarrow{\mathrm{B}}}{\mathrm{dt}}\)

Position Vector

A position vector is defined as a vector that symbolises either the position or the location of any given point with respect to any arbitrary reference point like the origin. The direction of the position vector always points from the origin of that vector towards a given point.

Position Vector Example
The position vector of an object is measured from the origin, in general. Suppose an object is placed in the space as shown below.

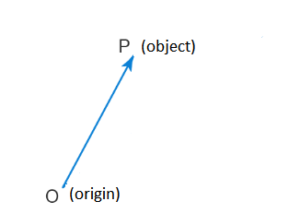
Position vector
\((\vec{r})=x \hat{i}+y \hat{j}+z \hat{k}\)
Where,
\(\hat{i}=\) unit vector along \(x-\) direction
\(\hat{j}=\) unit vector along \(y\)-direction
\(\hat{k}=\) unit vector along \(z\) – direction

Position Vector Formula

To find the position vector of any point in the xy-plane, we should first know the point coordinates. Consider two points A and B whose coordinates are \(\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)\) and \(\left(\mathrm{x}_{2}, \mathrm{y}_{2}\right)\), respectively. To determine the position vector, we need to subtract the corresponding components of \(A\) from \(B\) as follows:
\(
A B=\left(x_{2}-x_{1}\right) i+\left(y_{2}-y_{1}\right) j
\)
The position vector \(A B\) originates from point \(A\) and terminates at point \(B\).

Displacement Vector

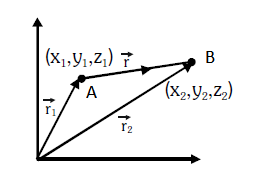
The change in the position vector of an object is known as the displacement vector. Suppose an object is at point A at time = 0 and at point B at time = t. The position vectors of the object at point A and point B are given as:

\(
\begin{aligned}\overrightarrow{\mathrm{r}}_{1} &=\left(\mathrm{x}_{1} \hat{\mathrm{i}}+\mathrm{y}_{1} \hat{\mathrm{j}}+z_{1} \hat{\mathrm{k}}\right)\end{aligned}\);

\(
\begin{aligned}\overrightarrow{\mathrm{r}}_{2} &=\left(\mathrm{x}_{2} \hat{\mathrm{i}}+\mathrm{y}_{2} \hat{\mathrm{j}}+z_{2} \hat{\mathrm{k}}\right)\end{aligned}\)

Now, the displacement vector of the object from time interval 0 to t will be:

\(
\begin{aligned}
\overrightarrow{\mathrm{r}}=\overrightarrow{\mathrm{r}}_{2}-\overrightarrow{\mathrm{r}}_{1} &=\left(\mathrm{x}_{2} \hat{\mathrm{i}}+\mathrm{y}_{2} \hat{\mathrm{j}}+z_{2} \hat{\mathrm{k}}\right)-\left(\mathrm{x}_{1} \hat{\mathrm{i}}+\mathrm{y}_{1} \hat{\mathrm{j}}+z_{1} \hat{\mathrm{k}}\right) \\
&=\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right) \hat{\mathrm{i}}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right) \hat{\mathrm{j}}+\left(z_{2}-z_{1}\right) \hat{\mathrm{k}}
\end{aligned}
\)
Magnitude: \(\mathrm{r}=|\overrightarrow{\mathrm{r}}|=\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}+\left(\mathrm{z}_{2}-\mathrm{z}_{1}\right)^{2}}\)

Lami’s theorem

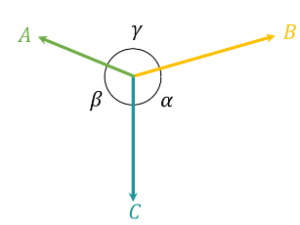
Lami’s Theorem states, “When three forces acting at a point are in equilibrium, then each force is proportional to the sine of the angle between the other two forces”. Referring to the above diagram, consider three forces A, B, C acting on a particle or rigid body making angles \(\alpha, \beta\) and \(\gamma\) with each other.
In the mathematical or equation form, it is expressed as,

\(\frac{A}{\sin \alpha}=\frac{B}{\sin \beta}=\frac{C}{\sin \gamma}\)

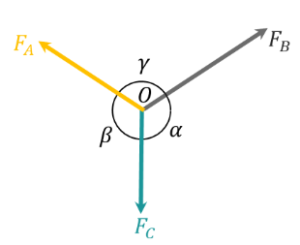
Lami’s Theorem Derivation

Let three force \(F_{A}, F_{B}\) and \(F_{C}\) are acting on a point and the Corresponding angle of them is \(\alpha, \beta\) and \(\gamma\). As shown in the figure.

As Forces are vectors they can move to form a triangle. After moving the forces and writing the angle in a complementary form,

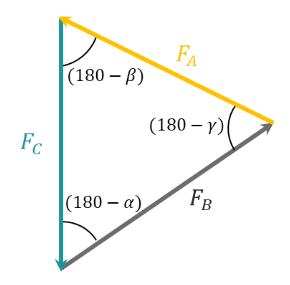
Now using the Sine Rule we get,
\(
\frac{F_{A}}{\sin (180-\alpha)}=\frac{F_{B}}{\sin (180-\beta)}=\frac{F_{C}}{\sin (180-\gamma)}
\)
After simplifying, we have
\(
\frac{F_{A}}{\sin \alpha}=\frac{F_{B}}{\sin \beta}=\frac{F_{C}}{\sin \gamma}
\)
In general, we can write
\(
\frac{A}{\sin \alpha}=\frac{B}{\sin \beta}=\frac{C}{\sin \gamma}
\)

Example: \(1 \mathrm{~A}\) school bell of mass \(30 \mathrm{~kg}\) is hanging from the ceiling with the help of string at point \(\mathrm{A}\) and \(\mathrm{B}\) as shown in the diagram. Find the tension in strings.(Take \(g=10 \mathrm{~m} / \mathrm{s} 2\) )

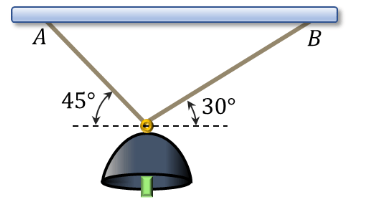
Solution:Given : Mass \(m=30 \mathrm{~kg}\)
Force due to gravity on the bell \(=30 \times 10=300 \mathrm{~N}\)
Now, drawing the free body diagram of the given situation taking bell at point \(\mathrm{C}\),

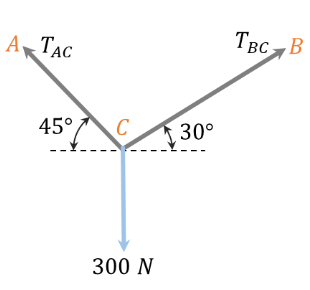
Using lami’s theorem
\(
\frac{A}{\sin \alpha}=\frac{B}{\sin \beta}=\frac{C}{\sin \gamma}
\)
Putting the values from diagram
\(
\frac{T_{A C}}{\sin (90+30)}=\frac{T_{B C}}{\sin (90+45)}=\frac{300}{\sin (180-30-45)}
\)
Taking first and third term,
\(
\frac{T_{A C}}{\sin (90+30)}=\frac{300}{\sin (180-30-45)}
\)
\(
T_{A C}=268.97 \mathrm{~N}
\)
During the second and third term,
Hence, the tensions in Strings are \(268.97 \mathrm{~N}\) and \(219.61 \mathrm{~N}\).

Example: For the triangle shown below, write Lami’s equation

Solution: 

\(\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}\)

Area of triangle

\(
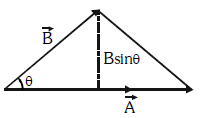
\text { Area }=\frac{|\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}|}{2}=\frac{1}{2} \mathrm{AB} \sin \theta
\)

Area of parallelogram

\(
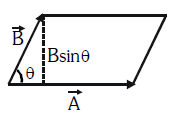
\text { Area }=|\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}|=\mathrm{AB} \sin \theta
\)

For parallel vectors

\(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}=\overrightarrow{0}\)

For perpendicular vectors

\(\vec{A} \cdot \vec{B}=0\)

For coplanar vectors

\(\overrightarrow{\mathrm{A}} \cdot(\overrightarrow{\mathrm{B}} \times \overrightarrow{\mathrm{C}})=0
\)

If \(A, B, C\) points are collinear

\(\overrightarrow{\mathrm{AB}}=\lambda \overrightarrow{\mathrm{BC}}\)

Examples of dot products

• Work, \(W=\vec{F} \cdot \vec{d}=F d \cos \theta\)
  where \(\mathrm{F} \rightarrow\) force, \(\mathrm{d} \rightarrow\) displacement.
• Power, \(\mathrm{P}=\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{v}}=\mathrm{Fv} \cos \theta\)
  where \(\mathrm{F} \rightarrow\) force, \(\mathrm{v} \rightarrow\) velocity.
• Electric flux, \(\phi_{\mathrm{E}}=\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{A}}=\mathrm{EA} \cos \theta\)
  where \(\mathrm{E} \rightarrow\) electric field, \(\mathrm{A} \rightarrow\) Area.
• Magnetic flux, \(\phi_{\mathrm{B}}=\overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{A}}=\mathrm{BA} \cos \theta\)
  where \(\mathrm{B} \rightarrow\) magnetic field, \(\mathrm{A} \rightarrow\) Area.
• Potential energy of dipole in uniform field, \(U=-\vec{p} \cdot \vec{E}\)
  where \(\quad \mathrm{p} \rightarrow\) dipole moment, where \(E \rightarrow\) Electric field.

Examples of Cross-Product

• Torque \(\vec{\tau}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{F}} \quad\) where \(\mathrm{r} \rightarrow\) position vector, \(\mathrm{F} \rightarrow\) force
• Angular momentum \(\overrightarrow{\mathrm{J}}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{p}}\) where \(\rightarrow\) position vector, \(\mathrm{p} \rightarrow\) linear momentum
• Linear velocity \(\vec{v}=\vec{\omega} \times \overrightarrow{\mathrm{r}}\) where \(\mathrm{r} \rightarrow\) position vector, \(\omega \rightarrow\) angular velocity
• Torque on dipole placed in electric field \(\vec{\tau}=\overrightarrow{\mathrm{p}} \times \overrightarrow{\mathrm{E}}\)
  where \(\mathrm{p} \rightarrow\) dipole moment, \(\mathrm{E} \rightarrow\) electric field

Key Points to Remember

• Tensor: A quantity that has different values in different directions is called tensor. I like to visualize tensors as the surface of a cube (similar to visualizing a vector as an arrow): each face of the cube has 3 directions associated with it- one normal, and two tangential. Another Example is Moment of Inertia, In fact, tensors are merely a generalisation of scalars and vectors; a scalar is a zero rank tensor, and a vector is a first rank tensor.
• Electric current is not a vector as it does not obey the law of vector addition.
• A unit vector has no unit.
• To a vector, only a vector of same type can be added and the resultant is a vector of the same type.
• A scalar or a vector can never be divided by a vector.