Units, Dimensions, Measurements and Practical Physics

Units, Dimension, Measurements, and Practical Physics

Fundamental or base quantities

Physical quantities which do not depend upon other quantities for their complete definition are known as fundamental or base quantities. e.g. length, mass, time, temperature, electric current, amount of substance, and luminous intensity, etc.

Derived quantities

Physical quantities that can be expressed as combinations of base (fundamental) quantities are known as derived quantities. e.g. Speed, volume, velocity, acceleration, force, pressure, momentum, energy, etc.

Units of physical quantities

The chosen reference standard of measurement in multiples of which, a physical quantity is expressed is called the unit of that quantity. e.g. \(\text { Physical Quantity }=\text { Numerical Value } \times \text { Unit }\)

System of Units

\(\begin{array}{|c|c|c|c|c|c|}
\hline & \text { MKS } & \text { CGS } & \text { FPS } & \text { MKSQ } & \text { MKSA } \\
\hline \text { (i) } & \begin{array}{c}
\text { Length } \\
(\mathrm{m})
\end{array} & \begin{array}{c}
\text { Length } \\
(\mathrm{cm})
\end{array} & \begin{array}{c}
\text { Length } \\
(\mathrm{ft})
\end{array} & \begin{array}{c}
\text { Length } \\
(\mathrm{m})
\end{array} & \begin{array}{c}
\text { Length } \\
(\mathrm{m})
\end{array} \\
\hline \text { (ii) } & \begin{array}{c}
\text { Mass } \\
(\mathrm{kg})
\end{array} & \begin{array}{c}
\text { Mass } \\
(\mathrm{g})
\end{array} & \begin{array}{c}
\text { Mass } \\
(\text { pound })
\end{array} & \begin{array}{c}
\text { Mass } \\
(\mathrm{kg})
\end{array} & \begin{array}{c}
\text { Mass } \\
(\mathrm{kg})
\end{array} \\
\hline \text { (iii) } & \begin{array}{c}
\text { Time } \\
(\mathrm{s})
\end{array} & \begin{array}{c}
\text { Time } \\
(\mathrm{s})
\end{array} & \begin{array}{c}
\text { Time } \\
(\mathrm{s})
\end{array} & \begin{array}{c}
\text { Time } \\
(\mathrm{s})
\end{array} & \begin{array}{c}
\text { Time } \\
(\mathrm{s})
\end{array} \\
\hline \text { (iv) } & – & – & – & \begin{array}{c}
\text { Charge } \\
(\mathrm{Q})
\end{array} & \begin{array}{c}
\text { Current } \\
(\mathrm{A})
\end{array} \\
\hline
\end{array}\)

 

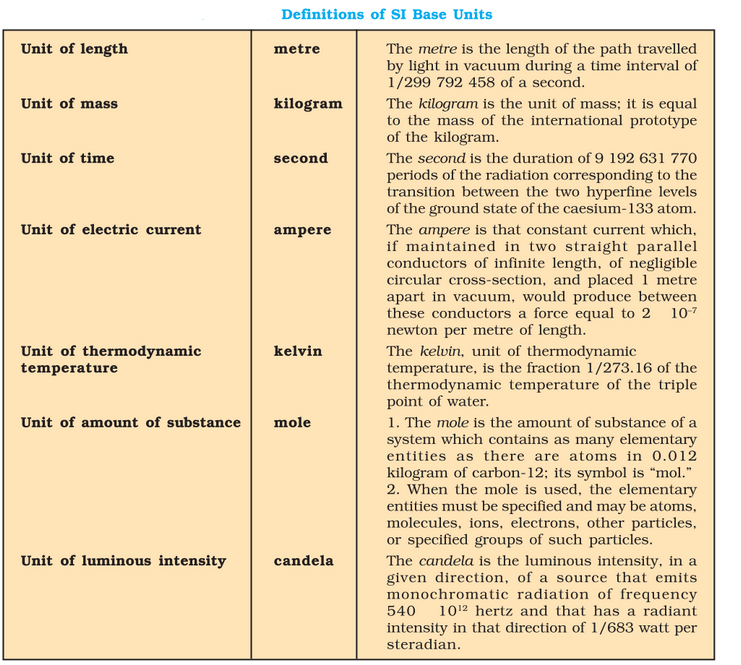
Fundamental Quantities in S.I. System and their units

\(\begin{array}{|c|l|c|c|}
\hline \text { S.N. } & {\text { Physical Qty. }} & \text { Name of Unit } & \text { Symbol } \\
\hline 1 & \text { Mass } & \text { kilogram } & \mathrm{kg} \\
\hline 2 & \text { Length } & \text { meter } & \mathrm{m} \\
\hline 3 & \text { Time } & \text { second } & \mathrm{s} \\
\hline 4 & \text { Temperature } & \text { kelvin } & \mathrm{K} \\
\hline 5 & \text { Luminous intensity } & \text { candela } & \mathrm{Cd} \\
\hline 6 & \text { Electric current } & \text { ampere } & \mathrm{A} \\
\hline 7 & \text { Amount of substance } & \text { mole } & \text { mol } \\
\hline
\end{array}\)

SI Base Quantities and Units

Supplementary Units

• Radian (rad) – for measurement of plane angle
• Steradian (sr) – for measurement of solid angle

Dimensional Formula

Relation which express physical quantities in terms of appropriate powers of fundamental units.

Use of dimensional analysis

• To check the dimensional correctness of a given physical relation.
• To derive the relationship between different physical quantities.
• To convert units of a physical quantity from one system to another.

\(
n_{1} u_{1}=n_{2} u_{2} \Rightarrow n_{2}=n_{1}\left(\frac{M_{1}}{M_{2}}\right)^{a}\left(\frac{L_{1}}{L_{2}}\right)^{b}\left(\frac{T_{1}}{T_{2}}\right)^{c}
\)
where \(\mathrm{u}=\mathrm{M}^{\mathrm{a}} \mathrm{L}^{\mathrm{b}} \mathrm{T}^{\mathrm{c}}\)

Limitations of dimensional analysis

• In Mechanics, the formula for a physical quantity depending on more than three other physical quantities cannot be derived. It can only be checked.
• This method can be used only if the dependency is of multiplication type. The formulae containing exponential, trigonometrical, and logarithmic functions can’t be derived using this method. Formulae containing more than one term which are added or subtracted like \(s=u t+1 / 2\) at \(^{2}\) also can’t be derived.
• The relation derived from this method gives no information about the dimensionless constants.
• If dimensions are given, the physical quantity may not be unique as many physical quantities have the same dimensions.
• It gives no information whether a physical quantity is a scalar or a vector.

 SI Prefixes

Power of 10	Prefix	Symbol
18	exa	E
15	peta	p
12	tera	T
9	giga	G
6	mega	M
3	kilo	k
2	hecto	h
1	deca	da
-1	deci	d
-2	centi	c
-3	milli	m
-6	micro	μ
-9	nano	n
-12	pico	p
-15	femto	f
-18	atto	a

Important dimensions and units

Physical Quantity	Dimension	SI Unit
Force (F)	\(\left[M^{1} L^{1} T^{-2}\right]\)	Newton
Work (W)	\(\left[M^{1} L^{2} T^{-2}\right]\)	joule
Power (P)	\(\left[M^{1} L^{2} T^{-3}\right]\)	Watt
Gravitational constant (G)	\(\left[M^{-1} L^{3} T^{-2}\right]\)	\(N-m^{2} / k g^{2}\)
Angular velocity (ω)	\(\left[T^{-1}\right]\)	radian/s
Angular momentum (L)	\(\left[M^{1} L^{2} T^{-1}\right]\)	\(\mathrm{kg}-\mathrm{m}^{2} / \mathrm{s}\)
Moment of Inertia (I)	\(\left[M^{1} L^{2}\right]\)	\(\mathrm{kg}-\mathrm{m}^{2}\)
Torque \((\tau)\)	\(\left[M^{1} L^{2} T^{-2}\right]\)	N-m
Young’s modulus (Υ)	\(\left[M^{1} L^{-1} T^{-2}\right]\)	\(\mathrm{N} / \mathrm{m}^{2}\)
Surface Tension (S)	\(\left[M^{1} T^{-2}\right]\)	N/m
Co-efficient of Viscocity (η)	\(\left[M^{1} L^{-1} T^{-1}\right]\)	\(\mathrm{N}-\mathrm{s} / \mathrm{m}^{2}\)
Pressure (P)	\(\left[M^{1} L^{-1} T^{-2}\right]\)	\(\mathrm{N} / \mathrm{m}^{2}\) (Pascal)
Electric Field (E)	\(\left[M^{1} L^{1} I^{-1} T^{-3}\right]\)	V/m
Electrical Potential (V)	\(\left[M^{1} L^{2} I^{-1} T^{-3}\right]\)	volt
Electric Flux (Ψ)	\(\left[M^{1} T^{3} I^{-1} L^{-3}\right]\)	volt/m
Capacitance (C)	\(\left[I^{2} T^{4} M^{-1} L^{-2}\right]\)	farad (F)
Permittivity (ε)	\(\left[I^{2} T^{4} M^{-1} L^{-3}\right]\)	\(C^{2} / N-m^{2}\)
Permeability (µ)	\(\left[M^{1} L^{1} I^{-2} T^{-3}\right]\)	Newton/A \({ }^{2}\)
Magnetic Dipole moment (M)	\(\left[I^{1} L^{2}\right]\)	N-m/T
Magnetic Fux (Φ)	\(\left[M^{1} L^{2} I^{-1} T^{-2}\right]\)	Weber (Wb)
Magnetic Field (B)	\(\left[M^{1} I^{-1} T^{-2}\right]\)	tesla
Inductance (L)	\(\left[M^{1} L^{2} I^{-2} T^{-2}\right]\)	henry
Resistance (R)	\(\left[M^{1} L^{2} I^{-2} T^{-3}\right]\)	ohm (Ω)
Intensity of wave (I)	\(\left[M^{1} T^{-3}\right]\)	watt \(/ m^{2}\)
Specific heat capacity (c)	\(\left[L^{2} T^{-2} K^{-1}\right]\)	\(\mathrm{J} / \mathrm{kg}-\mathrm{K}\)
Stephan’s Constant (σ)	\(\left[M^{1} T^{-3} K^{-4}\right]\)	watt \(/ m^{2}-k^{4}\)
Electric dipole moment (p)	\(\left[L^{1} I^{1} T^{1}\right]\)	C-m
Thermal conductivity (k)	\(\left[M^{1} L^{1} T^{-3} K^{-1}\right]\)	watt \(/ m-k\)
Current Density (j)	\(\left[I^{1} L^{-2}\right]\)	ampere \(/ \mathrm{m}^{2}\)
Electrical conductivity (σ)	\(\left[I^{2} T^{3} M^{-1} L^{-3}\right]\)	\(\Omega^{-1} m^{-1}\)

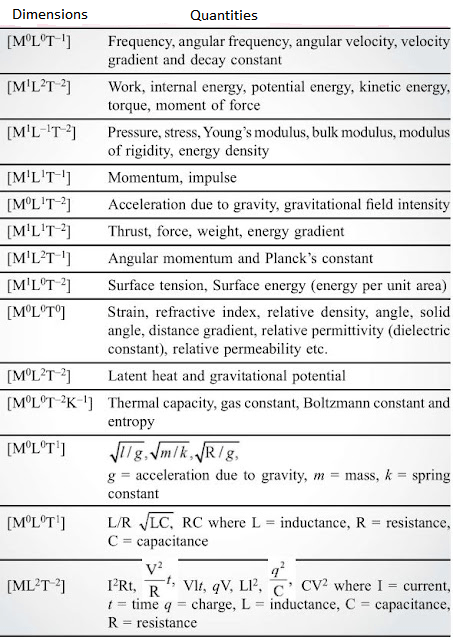
Sets of Quantities having the same dimensions

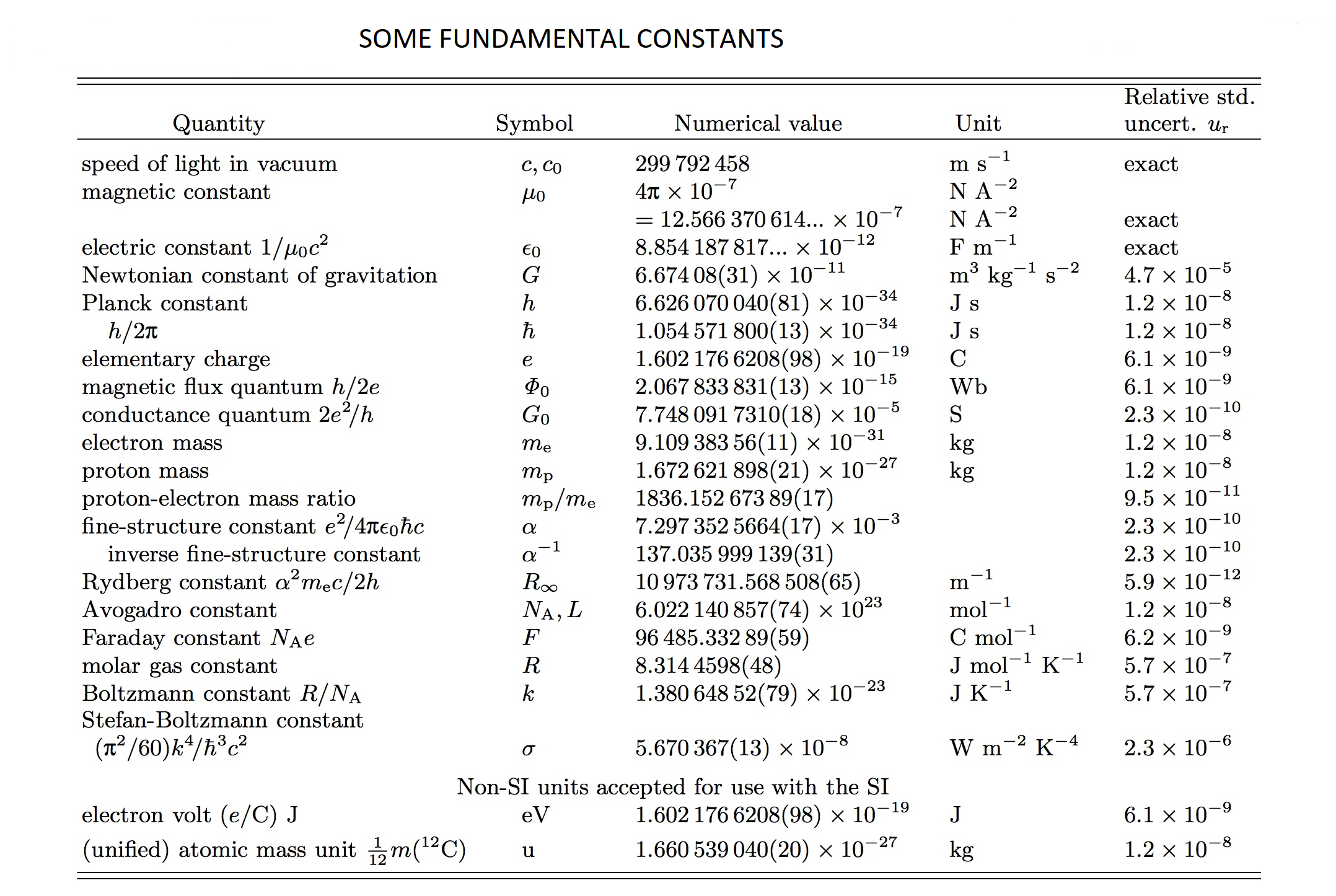
Some Fundamental Constants

Key Points

• Trigonometric functions \(\sin \theta, \cos \theta, \tan \theta\) etc and their arrangements \(\theta\) are dimensionless.
• Dimensions of differential coefficients \(\left[\frac{d^{n} y}{d x^{n}}\right]=\left[\frac{y}{x^{n}}\right]\)
• Dimensions of integrals \(\left[\int y d x\right]=[y x]\)
• We can’t add or subtract two physical quantities of different dimensions.
• Independent quantities may be taken as fundamental quantities in a new system of units.

Rules for Counting Significant Figures

For a number greater than 1

• All non-zero digits are significant.
• All zeros between two non-zero digits are significant. The location of the decimal does not matter.
• If the number is without a decimal part, then the terminal or trailing zeros are not significant.
• Trailing zeros in the decimal part are significant.

For a Number Less than 1
Any zero to the right of a non-zero digit is significant. All zeros between the decimal point and the first non-zero digit are not significant.

Significant Figures

All accurately known digits in measurement plus the first uncertain digit together form the significant figure.

\(
\begin{array}{lll}
\text { Ex. } & 0.108 \rightarrow 3 \mathrm{SF}, & 40.000 \rightarrow 5 \mathrm{SF} \\
& 1.23 \times 10^{-19} \rightarrow 3 \mathrm{SF}, & 0.0018 \rightarrow 2 \mathrm{SF}
\end{array}
\)

Significant Digits

The product or quotient will be reported as having as many significant digits as the number involved in the operation with the least number of significant digits.

For example : \(0.000170 \times 100.40=0.017068\) Another example: \(2.000 \times 10^{4} / 6.0 \times 10^{-3}=\) \(0.33 \times 10^{7}\)

For example : \(3.0 \times 800.0=2.4 \times 10^{3}\)
The sum or difference can be no more precise than the least precise number involved in the mathematical operation. Precision has to do with the number of positions to the RIGHT of the decimal. The more position to the right of the decimal, the more precise the number. So a sum or difference can have no more indicated positions to the right of the decimal as the number involved in the operation with the LEAST indicated positions to the right of its decimal. For example: \(160.45+6.732=167.18\) (after rounding off)

Another example : \(45.621+4.3-6.41=43.5\) (after rounding off)

Rules for rounding off digits:
1. If the digit to the right of the last reported digit is less than 5 round it and all digits to its right off.
2. If the digit to the right of the last reported digit is greater than 5 round it and all digits to its right off and increased the last reported digit by one.
3. If the digit to the right of the last reported digit is a 5 followed by either no other digits or all zeros, round it and all digits to its right off, and if the last reported digit is odd round up to the next even digit. If the last reported digit is even then leave it as is.

For example, if we wish to round off the following number to 3 significant digits : \(18.3682\)

The answer is 18.4. Another example: Round off \(4.565\) to three significant digits.
The answer would be \(4.56\).

Rounding off
\(
\begin{array}{ccc}
6.87 \rightarrow 6.9, & 6.84 \rightarrow 6.8, & 6.85 \rightarrow 6.8, \\
6.75 \rightarrow 6.8, & 6.65 \rightarrow 6.6, & 6.95 \rightarrow 7.0
\end{array}
\)

Order of magnitude
Power of 10 required to represent a quantity
\(
\begin{aligned}
&49=4.9 \times 10^{1} \approx 10^{1} \Rightarrow \text { order of magnitude }=1 \\
&51=5.1 \times 10^{1} \approx 10^{2} \Rightarrow \text { order of magnitude }=2 \\
&0.051=5.1 \times 10^{-2} \approx 10^{-1} \text { order of magnitude }=-1
\end{aligned}
\)

Errors

Whenever an experiment is performed, two kinds of errors can appear in the measured quantity.
(1) random and (2) systematic errors.
1. Random errors appear randomly because of the operator, fluctuations in external conditions, and variability of measuring instruments. The effect of random error can be somewhat reduced by taking the average of measured values. Random errors have no fixed sign or size.
2. Systematic errors occur due to error in the procedure, or miscalibration of the instrument, etc. Such errors have the same size and sign for all the measurements. Such errors can be determined. A measurement with relatively small random error is said to have high precision. A measurement with small random error and small systematic error is said to have high accuracy.

Least Count Error: If the instrument has known least count, the absolute error is taken to be equal to the least count unless otherwise stated.

Relative error \(=\frac{\text { absolute error in a measurement }}{\text { size of the measurement }}\)

Systematic errors

They have a known sign. The systematic error is removed before beginning calculations. Bench error and zero error are examples of systematic error.

Propagation of combination of errors

Error in Summation and Difference: \(x=a+b \text { then } \Delta x=\pm(\Delta a+\Delta b)\)

Error in Product and Division

A physical quantity \(\mathrm{X}\) depend upon \(\mathrm{Y} \& \mathrm{Z}\) as \(\mathrm{X}=\mathrm{Y}^{\mathrm{a}} \mathrm{Z}^{\mathrm{b}}\) then maximum possible fractional error in \(\mathrm{X}\).
\(
\frac{\Delta \mathrm{X}}{\mathrm{X}}=|\mathrm{a}| \frac{\Delta \mathrm{Y}}{\mathrm{Y}}+|\mathrm{b}| \frac{\Delta Z}{\mathrm{Z}}
\)

Error in Power of a Quantity

\(
x=\frac{a^{m}}{b^{n}} \text { then } \frac{\Delta x}{x}=\pm\left[m\left(\frac{\Delta a}{a}\right)+n\left(\frac{\Delta b}{b}\right)\right]
\)

The quotient rule is not applicable if the numerator and denominator are dependent on each other.
e.g if \(\mathrm{R}=\frac{\mathrm{XY}}{\mathrm{X}+\mathrm{Y}}\).

We cannot apply quotient rule to find the error in \(\mathrm{R}\). Instead we write the equation as follows

\(\frac{1}{\mathrm{R}}=\frac{1}{\mathrm{X}}+\frac{1}{\mathrm{Y}}\).

Differentiating both the sides, we get \(-\frac{d R}{R^{2}}=-\frac{d X}{X^{2}}-\frac{d Y}{Y^{2}}\).

Thus \(\quad \frac{r}{R^{2}}=\frac{x}{X^{2}}+\frac{y}{Y^{2}}\)

Least count

The smallest value of a physical quantity which can be measured accurately with an instrument is called the least count of the measuring instrument.

Vernier Callipers

Least count \(=1 \mathrm{MSD}-1 \mathrm{VSD}\)
(MSD \(\rightarrow\) main scale division, VSD \(\rightarrow\) Vernier scale division)

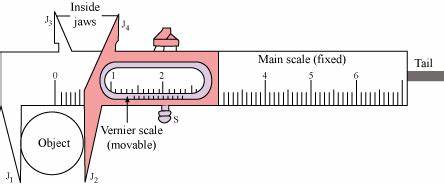
Example: A vernier scale has 10 parts, which are equal to 9 parts of main scale having each path equal to 1 \(\mathrm{mm}\) then least count \(=1 \mathrm{~mm}-\frac{9}{10} \mathrm{~mm}=0.1 \mathrm{~mm}\) \([\because 9 \mathrm{MSD}=10 \mathrm{VSD}]\)

Zero Error

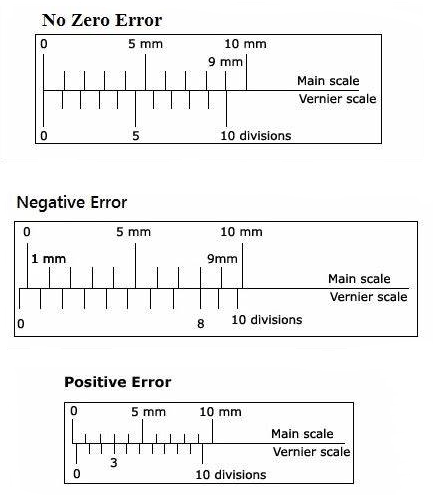
The zero error is always subtracted from the reading to get the corrected value. If the zero error is positive, its value is calculated as we take any normal reading.

Negative zero error \(=-[\) Total no. of vsd \(–\) vsd coinciding] \( \times\) L.C.

Screw Gauge

Least count \(=\frac{\text { pitch }}{\text { total no. of divisions }}\) on circular scale

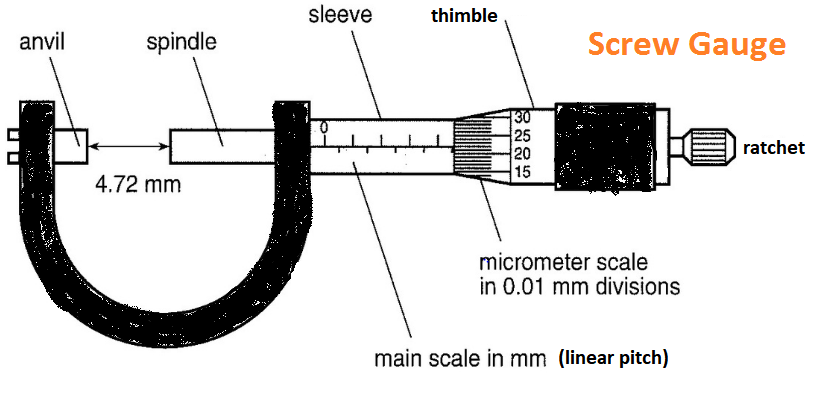
Example: The distance moved by spindle of a screw gauge for each turn of head is \(1 \mathrm{~mm}\). The edge of the humble is provided with a angular scale carrying 100 equal divisions. The least count \(=\frac{1 \mathrm{~mm}}{100}=0.01 \mathrm{~mm}\)

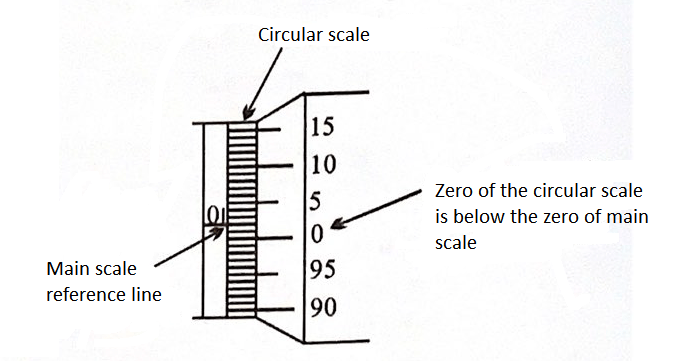
Zero Error

If there is no object between the jaws (i.e. jaws are in contact), the screw gauge should give zero reading. But due to extra material on jaws, even if there is no object, it gives some excess reading. This excess reading is called Zero error.

Negative Zero Error
(3 division error) i.e., \(-0.003 \mathrm{~cm}\)

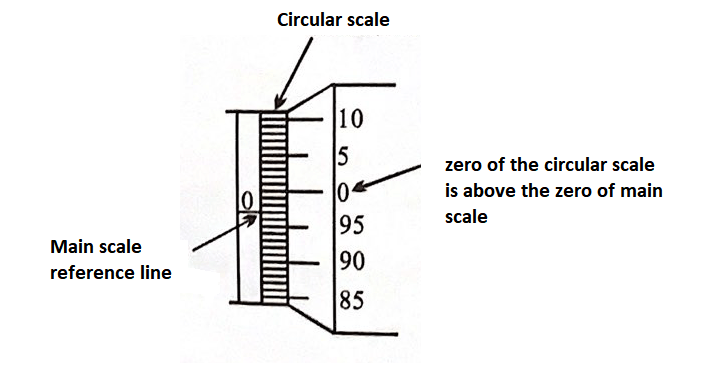
Positive Zero Error
(2 division error) i.e., \(+0.002 \mathrm{~cm}\)