Simple Harmonic Motion (Oscillation)

We are going to study periodic and a basic type of oscillatory motion called simple harmonic motion and its various aspects with the help of some fundamental concepts like period, frequency, amplitude and phase, etc.

Periodic and Oscillatory Motion

Two main categories of motion are given below.

Periodic motion

A motion which repeats itself after a regular intervals of time is termed as periodic motion. e.g. Circular motion, motion of a bouncing ball, motion of planets around the sun, rotation of earth about its polar axis, motion of a pendulum, etc.
One of the simplest periodic function is given by
\(y(t)=A \sin \omega t=A \sin (2 \pi t / T), \quad T=\frac{2 \pi}{\omega}\)
where \(A>0\) is the amplitude (maximum value). The function \(y(t)\) varies between \(A\) and \(-A\), because a sine function varies between +1 and -1. A plot of \(y(t)\) vs. time is shown in Figure below.

Thus, any function \(y(t)\) is periodic with period \(T\), if \(y(t)=y(t+T)\).

The sine function is periodic in time. This means that the value of the function at time t will be exactly the same at a later time \(t^{\prime}=t+T\), where T is the period (the smallest interval of time after which the motion is repeated is called its period). That the sine function satisfies the periodic condition can be seen from
\(
y(t+T)=A \sin \left[\frac{2 \pi}{T}(t+T)\right]=A \sin \left[\frac{2 \pi}{T} t+2 \pi\right]=A \sin \left[\frac{2 \pi}{T} t\right]=y(t)
\)
The frequency, \(f\), is defined to be
\(
f \equiv 1 / T
\)
The SI unit of frequency is inverse seconds, \(\left[\mathrm{s}^{-1}\right]\), or hertz \([\mathrm{Hz}]\). The angular frequency of oscillation is defined to be
\(
\omega \equiv 2 \pi / T=2 \pi f
\)
and is measured in radians per second. (The angular frequency of oscillation is denoted by \(\omega_0\) to distinguish from the angular speed \(\omega=|d \theta / d t|\).) One oscillation per second, 1 Hz , corresponds to an angular frequency of \(2 \pi \mathrm{rad} \cdot \mathrm{s}^{-1}\). (Unfortunately, the same symbol \(\omega\) is used for angular speed in circular motion. For uniform circular motion the angular speed is equal to the angular frequency but for non-uniform motion the angular speed is not constant. The angular frequency for simple harmonic motion is a constant by definition.) We therefore have several different mathematical representations for sinusoidal motion
\(
y(t)=A \sin (2 \pi t / T)=A \sin (2 \pi f t)=A \sin \left(\omega t\right)
\)

Further, a linear combination of sine and cosine functions like
\(
f(t)=A \sin \omega t+B \cos \omega t
\)
is also periodic function with the same time period \(T\).
Thus, any periodic function can be expressed as a superposition of sine and cosine functions of different time periods with suitable coefficients.

Oscillatory (or vibratory) motion

A motion in which a particle moves to and fro (back and forth or up and down) about a fixed point after regular interval of time, is termed as oscillatory (or vibratory) motion. The fixed point about which the particle oscillates (or vibrates) is called mean position or equilibrium position. For example, motion of a pendulum is oscillatory.

Note: Every oscillatory motion is periodic, but every periodic motion need not to be oscillatory. e.g. Motion of the planet around the sun is periodic but not oscillatory.

Simple Harmonic Motion

Simple harmonic motion can be described as an oscillatory motion in which the acceleration of the particle at any position is directly proportional to the displacement from the mean position. It is a special case of oscillatory motion. In this type of oscillatory motion, displacement, velocity and acceleration, and force vary (w.r.t time) in a way that can be described by either sine (or) the cosine functions collectively called sinusoids.

The particle executing simple harmonic motion oscillates such that its acceleration is always directed towards the mean position and magnitude of the acceleration is proportional to the displacement of the particle from the mean position. Mathematically, a simple harmonic motion can be expressed as
\(
\begin{aligned}
& x=A \sin \omega t=A \sin 2 \pi t / T \\
& x=A \cos \omega t=A \cos 2 \pi t / T
\end{aligned}
\)
Here, \(x=\) displacement of body from mean position at any instant \(t\),
\(A=\) amplitude or maximum displacement of the body,
\(\omega=\) angular frequency and \(T=\) time period of SHM.

Types of SHM

SHM are of two types as follows

Linear SHM

When a particle moves back and forth along a straight line around a fixed point (called the equilibrium position), this is referred to as Linear Simple Harmonic Motion. e.g. Motion of a mass connected to spring.

Conditions for Linear Simple Harmonic Motion

The restoring force or acceleration acting on the particle must always be proportional to the particle’s displacement and directed toward the equilibrium position.
\(
\begin{aligned}
& F \propto-x \\
& a \propto-x
\end{aligned}
\)
where
\(F\) is the Restoring Force
\(x\) is the Displacement of Particle from Equilibrium Position
\({a}\) is the Acceleration

Restoring force \((F)\): The force acting on the particle (executing SHM) which tends to bring it towards its mean position, is called restoring force. Restoring force is always directed towards mean position or acts in the direction opposite to that of displacement. Restoring force, \(F=-k x\) where, \(k\) is a constant and \(x\) is displacement about mean position.

Some basic terms related to SHM

Time period \((T)\): The time taken by the particle to complete one oscillation is called time period. Its unit is second.

Frequency \((f)\): The number of oscillations made by the particle (executing SHM) in one second is called frequency.
Frequency, \(f=\frac{1}{\text { Time period }(T)}\)
Its unit is cycles per second or hertz (Hz).

Angular frequency \((\omega)\): The rate of change of phase angle of the particle (executing SHM) with respect to time is called angular frequency. Its unit is radian/second.

Angular frequency 
\(
\begin{aligned}
\omega & =\frac{2 \pi}{\text { Time period }(T)} \\
& =2 \pi \times \text { Frequency }(f)
\end{aligned}
\)

Amplitude \((A)\): The maximum displacement of a particle from its mean position is defined as amplitude.

Phase \((\phi)\): Time-varying quantity, which can fully describe the displacement and velocity of the particle is called phase. Its unit is radian.
In the given graph, two SHM in one second having the same amplitude \(A\) and same angular frequency \(\omega\) are shown.

Their phase angle \(\phi\) are different.

Angular SHM

When a system oscillates angularly with respect to a fixed axis, then its motion is called angular simple harmonic motion. The displacement of the particle in angular simple harmonic motion is measured in terms of angular displacement. e.g. Motion of a bob of simple pendulum.

Another example is the torsional pendulum as shown below is one example of Angular SHM. 

Conditions for Angular Simple Harmonic Motion

The restoring torque (or) angular acceleration acting on the particle should always be proportional to the particle’s angular displacement and oriented towards the equilibrium position.

\(
\therefore \quad \quad \tau \propto-\theta \text { or } \alpha \propto-\theta
\)
where
\(\tau\) is Torque
\({\theta}\) is the Angular Displacement
\({\alpha}\) is the Angular Acceleration

Note: The total mechanical energy of the particle should be conserved (Kinetic energy + Potential energy = constant).

Displacement

The displacement can be represented by a mathematical function of time. In the case of periodic motion, this function is periodic in time. One of the simplest periodic functions is given by
\(
f(t)=A \cos \omega t
\)
If the argument of this function, \(\omega t\), is increased by an integral multiple of \(2 \pi\) radians, the value of the function remains the same. The function \(f(t)\) is then periodic and its period, \(T\), is given by
\(
T=\frac{2 \pi}{\omega}
\)
Thus, the function \(f(t)\) is periodic with period \(T\),
\(
f(t)=f(t+T)
\)
The same result is obviously correct if we consider a sine function, \(f(t)=A \sin \omega t\). Further, a linear combination of sine and cosine functions like.
\(
f(t)=A \sin \omega t+B \cos \omega t \dots(i)
\)
is also a periodic function with the same period T. Taking,
\(
A=D \cos \phi \text { and } B=D \sin \phi
\)
Eq. (i) can be written as,
\(
f(t)=D \sin (\omega t+\phi)
\)
Here \(D\) and \(\phi\) are constant given by
\(
D=\sqrt{A^2+B^2} \text { and } \phi=\tan ^{-1}\left(\frac{B}{A}\right)
\)
The great importance of periodic sine and cosine functions is due to a remarkable result proved by the French mathematician, Jean Baptiste Joseph Fourier (1768-1830): Any periodic function can be expressed as a superposition of sine and cosine functions of different time periods with suitable coefficients.

Simple Harmonic Motion

Consider a particle oscillating back and forth about the origin of an \(x\)-axis between the limits \(+A\) and \(-A\) as shown in Fig. 14.3. This oscillatory motion is said to be simple harmonic if the displacement \(x\) of the particle from the origin varies with time as :
\(
x(t)=A \cos (\omega t+\phi) \dots(14.4)
\)

where \(A, \omega\) and \(\phi\) are constants. 

Let’s assume \(\phi=0\), so \(x(t)=A \cos \omega t\). From this equation let’s calculate the value of displacement at various times (as shown in the table below):
\(
\begin{array}{c|c|c|c|c|c}
t & 0 & T / 4 & T / 2 & 3 T / 4 & T \\
\hline x & A & 0 & -A & 0 & A
\end{array}
\)

Thus, simple harmonic motion (SHM) is not any periodic motion but one in which displacement is a sinusoidal function of time. Fig. 14.4 shows the positions of a particle executing SHM at discrete value of time, each interval of time being \(T / 4\), where \(T\) is the period of motion.

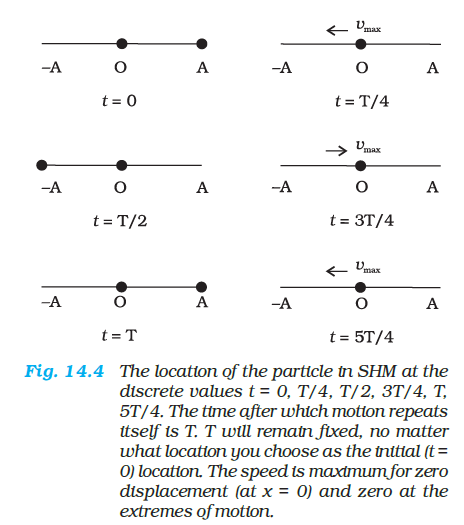
Fig. 14.5 plots the graph of \(x\) versus \(t\), which gives the values of displacement as a continuous function of time.

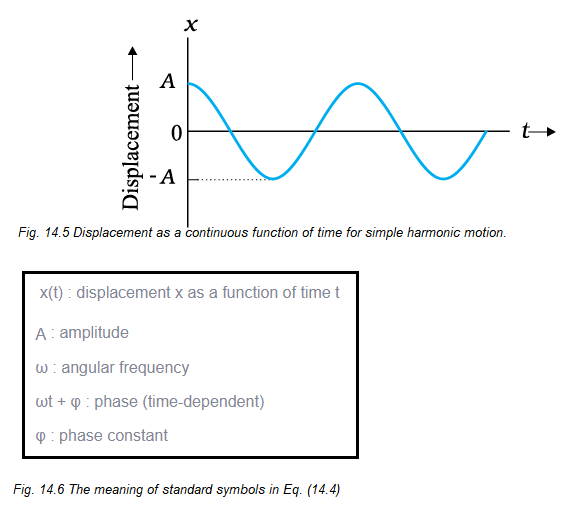
The quantities \(A\), \(\omega\), and \(\phi\) which characterize a given SHM have standard names, as summarised in Fig. 13.6. Let us understand these quantities.

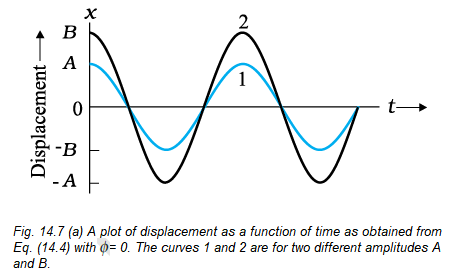
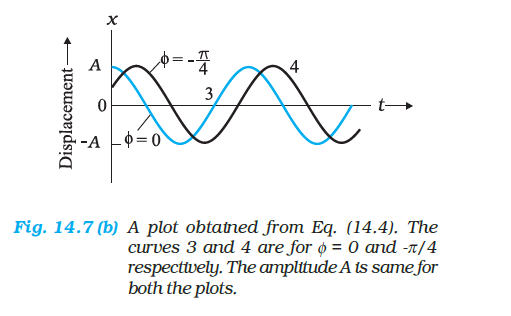
The amplitude \(A\) of SHM is the magnitude of maximum displacement of the particle. [Note, \(A\) can be taken to be positive without any loss of generality]. As the cosine function of time varies from +1 to -1, the displacement varies between the extremes \(A\) and \(-A\). Two simple harmonic motions may have sthe ame \(\omega\) and \(\phi\) but different amplitudes \(A\) and \(B\), as shown in Fig. 14.7 (a).

While the amplitude \(A\) is fixed for a given SHM, the state of motion (position and velocity) of the particle at any time \(t\) is determined by the argument \((\omega t+\phi)\) in the cosine function. This time-dependent quantity, \((\omega t+\phi)\) is called the phase of the motion. The value of phase at \(t=0\) is \(\phi\) and is called the phase constant (or phase angle). If the amplitude is known, \(\phi\) can be determined from the displacement at \(t=0\). Two simple harmonic motions may have the same \(A\) and \(\omega\) but different phase angle \(\phi\), as shown in Fig. 14.7 (b).

Finally, the quantity \(\omega\) can be seen to be related to the period of motion \(T\). Taking, for simplicity, \(\phi=0\) in Eq. (14.4), we have
\(
x(t)=A \cos \omega t
\)
Since the motion has a period \(T, x(t)\) is equal to \(x(t+T)\). That is,
\(
A \cos \omega t=A \cos \omega(t+T)
\)
Now the cosine function is periodic with period \(2 \pi\), i.e., it first repeats itself when the argument changes by \(2 \pi\). Therefore,
\(
\omega(t+T)=\omega t+2 \pi
\)
that is \(\omega=2 \pi / T\)
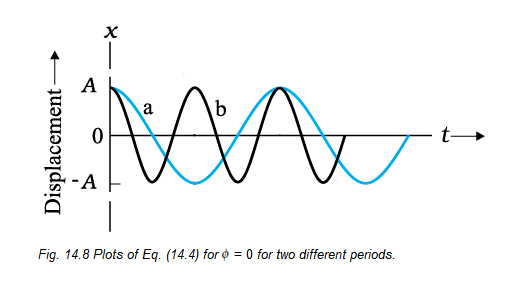
\(\omega\) is called the angular frequency of SHM. Its S.I. unit is radians per second. Since the frequency of oscillations is simply \(1 / \mathrm{T}, \omega\) is \(2 \pi\) times the frequency of oscillation. Two simple harmonic motions may have the same A and \(\phi\), but different \(\omega\), as seen in Fig. 14.8. In this plot the curve (b) has half the period and twice the frequency of the curve (a).

Example 1: Which of the following functions of time represent (a) simple harmonic motion and (b) periodic but not simple harmonic? Give the period for each case.
(a) \(\sin \omega t-\cos \omega t\)
(b) \(\sin ^2 \omega t\)

Solution: (a)
\(
\begin{aligned}
& \sin \omega t-\cos \omega t \\
& \quad=\sin \omega t-\sin (\pi / 2-\omega t)
\end{aligned}
\)
\(
\begin{aligned}
& =2 \cos (\pi / 4) \sin (\omega t-\pi / 4) \\
= & \sqrt{ } 2 \sin (\omega t-\pi / 4)
\end{aligned}
\)
This function represents a simple harmonic motion having a period \(T=2 \pi / \omega\) and a phase angle \((-\pi / 4)\) or \((7 \pi / 4)\)
(b) \(\sin ^2 \omega t =1 / 2-1 / 2 \cos 2 \omega t\)
The function is periodic having a period \(T=\pi / \omega\). It also represents a harmonic motion with the point of equilibrium occurring at \(1 / 2\) instead of zero.

Example 2: Which of the following functions of time represent (a) periodic and (b) non-periodic motion? Give the period for each case of periodic motion [ \(\omega\) is any positive constant].
(i) \(\sin \omega t+\cos \omega t\)
(ii) \(\sin \omega t+\cos 2 \omega t+\sin 4 \omega t\)
(iii) \(\mathrm{e}^{-\omega t}\)
(iv) \(\log (\omega t)\)

Solution: (i) \(\sin \omega t+\cos \omega t\) is a periodic function, it can also be written as \(\sqrt{2} \sin (\omega t+\pi / 4)\).
Now \(\sqrt{2} \sin (\omega t+\pi / 4)=\sqrt{2} \sin (\omega t+\pi / 4+2 \pi)\) \(=\sqrt{2} \sin [\omega(t+2 \pi / \omega)+\pi / 4]\)
The periodic time of the function is \(2 \pi / \omega\).

(ii) This is an example of a periodic motion. It can be noted that each term represents a periodic function with a different angular frequency. Since period is the least interval of time after which a function repeats its value, \(\sin \omega t\) has a period \(T_0=2 \pi / \omega ; \cos 2 \omega t\) has a period \(\pi / \omega=T_o / 2\); and \(\sin 4 \omega t\) has a period \(2 \pi / 4 \omega=T_o / 4\). The period of the first term is a multiple of the periods of the last two terms. Therefore, the smallest interval of time after which the sum of the three terms repeats is \(T_0\), and thus, the sum is a periodic function with a period \(2 \pi / \omega\).

(iii) The function \(e^{-\omega t}\) is not periodic, it decreases monotonically with increasing time and tends to zero as \(t \rightarrow \infty\) and thus, never repeats its value.

(iv) The function \(\log (\omega t)\) increases monotonically with time \(t\). It, therefore, never repeats its value and is a nonperiodic function. It may be noted that as \(t \rightarrow \infty, \log (\omega t)\) diverges to \(\infty\). It, therefore, cannot represent any kind of physical displacement.

Example 3: A harmonic oscillation is represented by \(x=0.34 \cos (3000 t+0.74)\), where \(x\) and \(t\) are in mm and second, respectively. Deduce (i) amplitude (ii) angular frequency (iii) initial phase.

Solution: Given, \(x=0.34 \cos (3000 t+0.74)\)
Comparing with general equation \(x=A \cos (\omega t+\phi)\), we get
(i) Amplitude, \(A=0.34 \mathrm{~mm}=0.034 \mathrm{~cm}\)
(ii) Angular frequency, \(\omega=3000 \mathrm{rads}^{-1}\)
(iii) Initial phase, \(\phi=0.74 \mathrm{rad}\)

Example 4: Find the equation of the simple harmonic motion of a particle whose amplitude is 0.04 and whose frequency is 50 Hz. The initial phase is \(\pi / 3\). Assume that the motion of the particle is started from the mean position.

Solution: From equation of SHM, \(x=A \sin (\omega t+\phi)\)
Here,
\(
\begin{array}{ll}
\text { Here, } & A=0.04 \mathrm{~m}, \quad {f}=50 \mathrm{~Hz}, \quad \phi=\frac{\pi}{3} \\
\therefore & x=0.04 \sin \left(2 \pi \times 50 t+\frac{\pi}{3}\right) \quad(\because \omega=2 \pi f) \\
\text { or } & x=0.04 \sin \left(100 \pi t+\frac{\pi}{3}\right)
\end{array}
\)

Relating Uniform Circular Motion to Simple Harmonic Motion

Looking at an object going around in a circle of radius, \(A\), from the top view gives the relationships involving period, \(\mathbf{T}\) in seconds/cycle, frequency, \({f}\) in cycles/sec, and angular frequency, \({\omega}\) in rad \(/ \mathrm{sec}\) and the direction of velocity \(v_{\tan }\) at a time \(t\) is along the tangent to the circle at the point where the particle is located at that instant.
\(
v_{\tan }=\frac{2 \pi A}{T}
\)
\(
\begin{aligned}
&\text { and rearranging gives }\\
&\frac{v_{\tan }}{A}=\frac{2 \pi}{T}=2 \pi f=\omega A
\end{aligned}
\)
and \(\frac{2 \pi}{T}=\omega\)
so \(2 \pi f=\omega\)

Note: The speed of a particle \(v\) in uniform circular motion is its angular speed \(\omega\) times the radius of the circle \(A\).
\(v=\omega A\)

Looking at that same object going around in a circle of radius, \(\mathbf{A}\), from the edge view reveals that the linear back and forth motion of the object is equivalent to the horizontal motion of an object on the end of a spring. Therefore, the radius, \(\mathbf{A}\), is the same as the maximum amplitude of the mass-spring system and \(\mathbf{v}_{\tan }\) is the same as the maximum velocity of the mass as it passes through the position of the relaxed spring.

Circular motion of a ball in a plane viewed edge-on is SHM.

We show that the projection of uniform circular motion on a diameter of the circle follows simple harmonic motion. A simple experiment (Fig. 14.9) helps us visualise this connection. Tie a ball to the end of a string and make it move in a horizontal plane about a fixed point with a constant angular speed. The ball would then perform a uniform circular motion in the horizontal plane. The ball will appear to execute to and fro motion along a horizontal line with the point of rotation as the midpoint. 

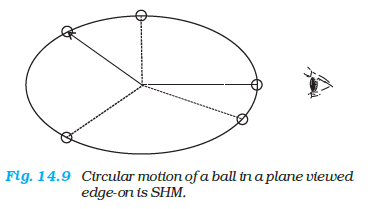
Fig. 14.10 describes the same situation mathematically. Suppose a particle \(P\) is moving uniformly on a circle of radius \(A\) with angular speed \(\omega\). The sense of rotation is anticlockwise.

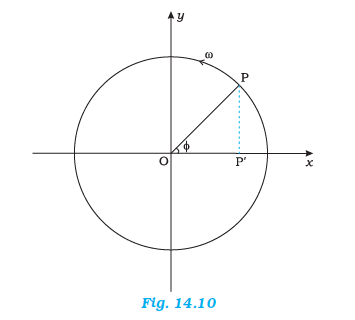
The initial position vector of the particle, i.e., the vector \(\overline{\mathbf{O P}}\) at \(t=0\) makes an angle of \(\phi\) with the positive direction of \(x\)-axis. In time \(t\), it will cover a further angle \(\omega t\) and its position vector will make an angle of \(\omega t+\phi\) with the + ve \(x\)-axis. Next, consider the projection of the position vector OP on the \(x\)-axis. This will be \(\mathrm{OP}^{\prime}\). The position of \(\mathrm{P}^{\prime}\) on the \(x\)-axis, as the particle P moves on the circle, is given by

The initial position vector of the particle, i.e., the vector \(\overline{\mathbf{O P}}\) at \(t=0\) makes an angle of \(\phi\) with the positive direction of \(x\)-axis. In time \(t\), it will cover a further angle \(\omega t\) and its position vector will make an angle of \(\omega t+\phi\) with the + ve \(x\)-axis. Next, consider the projection of the position vector OP on the \(x\)-axis. This will be \(\mathrm{OP}^{\prime}\). The position of \(\mathrm{P}^{\prime}\) on the \(x\)-axis, as the particle P moves on the circle, is given by
\(
x(t)=A \cos (\omega t+\phi)
\)
which is the defining equation of SHM. This shows that if P moves uniformly on a circle, its projection \(\mathrm{P}^{\prime}\) on a diameter of the circle executes SHM. The particle P and the circle on which it moves are sometimes referred to as the reference particle and the reference circle, respectively.

We can take projection of the motion of P on any diameter, say the \(y\)-axis. In that case, the displacement \(y(t)\) of \(\mathrm{P}^{\prime}\) on the \(y\)-axis is given by
\(
y=A \sin (\omega t+\phi)
\)
which is also an SHM of the same amplitude as that of the projection on \(x\)-axis, but differing by a phase of \(\pi / 2\).

In spite of this connection between circular motion and SHM, the force acting on a particle in linear simple harmonic motion is very different from the centripetal force needed to keep a particle in uniform circular motion.

Equations of SHM

Consider a block attached to a spring on a frictionless table (Figure below). The equilibrium position (the position where the spring is neither stretched nor compressed) is marked as \(x=0\). At the equilibrium position, the net force is zero.

Work is done on the block to pull it out to a position of \(x=+A\), and it is then released from rest. The maximum \(x\) position \((A)\) is called the amplitude of the motion. The block begins to oscillate in SHM between \(x=+A\) and \(x=-A\), where \(A\) is the amplitude of the motion and \(T\) is the period of the oscillation.

Velocity

The equation of the position as a function of time for a block on a spring becomes
\(
x(t)=A \cos (\omega t+\phi)
\)
The velocity of the mass on a spring, oscillating in SHM, can be found by taking the derivative of the position equation:
\(
v(t)=\frac{d x(t)}{d t}=\frac{d}{d t}(A \cos (\omega t+\phi))=-A \omega \sin (\omega t+\phi)=-v_{\max } \sin (\omega t+\phi) .
\)
Because the sine function oscillates between -1 and +1, the maximum velocity is the amplitude times the angular frequency, \(v_{\max }=A \omega\). The maximum velocity occurs at the equilibrium position \((x=0)\) when the mass is moving toward \(x=+A\). The maximum velocity in the negative direction is attained at the equilibrium position \((x=0)\) when the mass is moving toward \(x=-A\) and is equal to \(-v_{\max }\). The negative sign shows that \(v({t})\) has a direction opposite to the positive direction of \(x\)-axis.

Proof of the velocity equation in simple harmonic motion 

Displacement in SHM: \({x}={A} \cos (\omega t)\)
\(
v=\frac{d x}{d t}=-A \omega \sin (\omega t)
\)
From \(x=A \cos (\omega t)\), we have \(\cos (\omega t)=\frac{x}{A}\)
Using the identity \(\sin ^2(\omega t)+\cos ^2(\omega t)=1\), we get \(\sin ^2(\omega t)=1-\cos ^2(\omega t)\)
\(
\sin (\omega t)=\sqrt{1-\cos ^2(\omega t)}=\sqrt{1-\left(\frac{x}{A}\right)^2}=\frac{\sqrt{A^2-x^2}}{A}
\)
\(
\begin{aligned}
& v=-A \omega \sin (\omega t) \\
& v=-A \omega \frac{\sqrt{A^2-x^2}}{A} \\
& v=-\omega \sqrt{A^2-x^2}
\end{aligned}
\)
The velocity in simple harmonic motion is \(v=\omega \sqrt{A^2-x^2}\).

Special Cases
(i) When the particle is at the mean position, i.e. \(x=0\), then its velocity is maximum.
\(
\therefore \quad v_{\max }=\omega A
\)

(ii) When the particle is at the extreme position, i.e. \(x= \pm A\), then its velocity is zero.
\(
\therefore \quad v=\omega \sqrt{A^2-A^2}=0
\)
Therefore, the velocity of a particle executing SHM is zero at either of its extreme positions.

Acceleration

The acceleration of the particle executing SHM at any instant is defined as the time rate of change of its velocity at that instant, i.e.
\(
a(t)=d v(t) / d t=\frac{d}{d t}(-A \omega \sin (\omega t+\phi))=-A \omega^2 \cos (\omega t+\varphi)=-a_{\max } \cos (\omega t+\phi)
\)
Acceleration, \(\quad a=-\omega^2 x\)
The maximum acceleration is \(a_{\max }=A \omega^2\). The maximum acceleration occurs at the position \((x=-A)\), and the acceleration at the position \((x=-A)\) and is equal to \(a_{\max }\).

Special Cases
(i) When the particle is at the mean position, i.e. \(x=0\), then acceleration is zero.
\(
\therefore \quad a_{\text {mean position }}=0
\)
(ii) When the particle is at the extreme position, i.e. \(x=A\), then acceleration is maximum.
\(
\therefore \quad a_{\text {(extreme position) }}=-\omega^2 A
\)

The corresponding plots are shown in Fig. 14.13. All quantities vary sinusoidally with time; only their maxima differ and the different plots differ in phase. \(x\) varies between \(-A\) to \(A ; v(t)\) varies from \(-\omega A\) to \(\omega A\) and \(a(t)\) from \(-\omega^2 A\) to \(\omega^2 A\). With respect to the displacement plot, velocity plot has a phase difference of \(\pi / 2\) and the acceleration plot has a phase difference of \(\pi\).

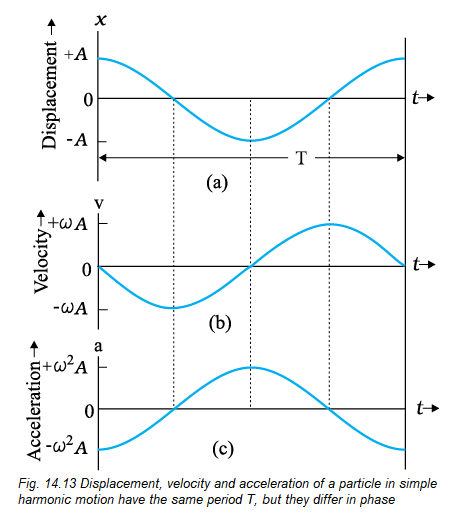
Important points regarding the kinematics of SHM

• In linear SHM, the length of SHM path is 2 A.
• The total work done and displacement in one complete oscillation is zero (Work done is force times displacement. In SHM, the net displacement over one cycle is zero. Therefore, the total work done is zero), but the total traversed length is 4 A (Distance is the total path length traveled. In one complete oscillation, the object travels from the equilibrium position to one extreme ( \(A\) ), back to the equilibrium, to the opposite extreme ( \(A\) ), and back to the equilibrium. Therefore, the total distance traveled is \(A+A+A+A=4 A\)).
• The velocity and acceleration varies with the same frequency as displacement.
• Velocity is ahead of displacement by phase angle of \((\pi / 2)\) rad, acceleration is ahead of velocity by phase angle of ( \(\pi / 2\) ) rad and acceleration is ahead of displacement by phase angle of \(\pi \mathrm{rad}\).

Example 5: The amplitude of a harmonic oscillator is A. When the particle’s velocity of this oscillator is half of the maximum velocity, then determine the position of the particle.

Solution: As, \(v=\omega \sqrt{A^2-x^2}\) but it is given that \(v=\frac{v_{\max }}{2}=\frac{A \omega}{2}\)
\(
\begin{aligned}
& \frac{A \omega}{2}=\omega \sqrt{A^2-x^2} \Rightarrow A^2=4\left(A^2-x^2\right) \\
& x^2=\frac{4 A^2-A^2}{4} \Rightarrow x= \pm \frac{\sqrt{3} A}{2}
\end{aligned}
\)

Example 6: A body oscillates with SHM according to the equation, \(x=(5 \mathrm{~m}) \cos \left[\left(2 \pi \mathrm{rad} \mathrm{s}^{-1}\right) t+\pi / 4\right]\). At \(t=1.5 \mathrm{~s}\), calculate the (i) displacement, (ii) speed and (iii) acceleration of the body.

Solution: The angular frequency \(\omega\) of the body \(=2 \pi \mathrm{rad} \mathrm{s}^{-1}\) and its time period, \(\quad T=1 \mathrm{~s}\)
At \(t=1.5 \mathrm{~s}\),
(i)
\(
\begin{aligned}
\text { Displacement } & =(5 \mathrm{~m}) \cos \left[\left(2 \pi \mathrm{rad} \mathrm{~s}^{-1}\right) \times 1.5 \mathrm{~s}+\pi / 4\right] \\
& =(5 \mathrm{~m}) \cos [(3 \pi+\pi / 4) \mathrm{rad}] \\
& =-5 \times 0.707 \mathrm{~m}=-3.535 \mathrm{~m}
\end{aligned}
\)
(ii) Using \(v=-\omega A \sin (\omega t+\phi)\)
Speed of the body
\(
=-(5 \mathrm{~m})\left(2 \pi \mathrm{~s}^{-1}\right) \sin \left[\left(2 \pi \mathrm{rad} \mathrm{~s}^{-1}\right) \times 1.5 \mathrm{~s}+\frac{\pi}{4}\right]
\)
\(
\begin{aligned}
& =-(5 \mathrm{~m})\left(2 \pi \mathrm{~s}^{-1}\right) \sin \left[\left(3 \pi+\frac{\pi}{4}\right)\right] \\
& =10 \pi \times 0.707 \mathrm{~ms}^{-1}=222 \mathrm{~ms}^{-1}
\end{aligned}
\)
(iii) Acceleration of the body
\(
\begin{aligned}
& =-\left(2 \pi \mathrm{rads}^{-1}\right)^2 \times \text { Displacement } \\
& =-\left(2 \pi \mathrm{rads}^{-1}\right)^2 \times(-3.535 \mathrm{~m})=139.41 \mathrm{~ms}^{-2}
\end{aligned}
\)

Force law for SHM

The acceleration of a particle undergoing SHM is
\(
a(t)=-\omega^2 x(t)
\)
From Newton’s second law of motion, force acting on the particle of mass \(m\) in SHM is \(F(t)=m a(t)\), we get
\(
F(t)=-m \omega^2 x(t)=-k x(t)
\)
where, \(k=m \omega^2\) or \(\omega=\sqrt{\frac{k}{m}}\)
Thus, in SHM, the force is directly proportional and opposite to the displacement and is always directed towards the mean position. This force is called restoring force.
Further, since \(\omega=\frac{2 \pi}{T}=\sqrt{\frac{k}{m}}\)
\(\therefore\) Time period, \(T=2 \pi \sqrt{\frac{m}{k}}\)
and frequency, \(f=\frac{1}{2 \pi} \sqrt{\frac{k}{m}}\)

Notes:
In different types of SHM, the quantities \(m\) and \(k\) will go on taking different forms and names. In general, \(m\) is called inertial factor and \(k\) is called spring factor.
In linear SHM, the general formula for time period is
\(
T=2 \pi \sqrt{\frac{\text { Inertial factor }}{\text { Spring factor }}}
\)
In linear SHM, the spring factor stands for force per unit displacement and the inertial factor for the mass of the body executing SHM.
Thus, in linear SHM,
\(
\begin{aligned}
& T=2 \pi \sqrt{\frac{m}{k}}=2 \pi \sqrt{\frac{m}{\left(\frac{\text { Force }}{\text { Displacement }}\right)}} \\
& T=2 \pi \sqrt{\frac{\text { Displacement }}{\text { Acceleration }}}
\end{aligned}
\)

Example 7: Frequency of oscillation of a body is 6 Hz when force \(F_1\) is applied and 8 Hz when \(F_2\) is applied. If both forces \(F_1\) and \(F_2\) are applied together, then find out the frequency of oscillation.

Solution: According to question, \(F_1=-k_1 x\) and \(F_2=-k_2 x\)
So, \(f_1=\frac{1}{2 \pi} \sqrt{\frac{k_1}{m}}=6 \mathrm{~Hz},\)
\(
f_2=\frac{1}{2 \pi} \sqrt{\frac{k_2}{m}}=8 \mathrm{~Hz}
\)
Now, \(F=F_1+F_2=-\left(k_1+k_2\right) x\)
Therefore, \(n=\frac{1}{2 \pi} \sqrt{\frac{k_1+k_2}{m}}\)
\(
f=\frac{1}{2 \pi} \sqrt{\frac{4 \pi^2 f_1^2 m+4 \pi^2 f_2^2 m}{m}} \left(\mathrm{As}, k=4 \pi^2 f^2 m\right)
\)
\(
=\sqrt{f_1^2+f_2^2}=\sqrt{8^2+6^2}=10 \mathrm{~Hz}
\)

Energy in SHM

The particle executing SHM has both types of energy: potential energy and kinetic energy. When a body is displaced from its equilibrium position by doing work upon it, the body acquires potential energy. However, when the body is released, it begins to move back with a velocity, thus acquiring kinetic energy.

Kinetic energy

The relation for kinetic energy of a particle executing SHM can be expressed in two forms, i.e. in terms of displacement and in terms of time. Let us consider
\(
\begin{aligned}
& x=A \sin (\omega t+\phi) \\
& v=A \omega \cos (\omega t+\phi)=\omega \sqrt{A^2-x^2}
\end{aligned}
\)
\(
\begin{aligned}
& \text { KE}=\frac{1}{2} m v^2 \quad\left[\text { Since, } v^2=A^2 \omega^2 \cos ^2(\omega t+\phi)\right] \\
& =\frac{1}{2} m \omega^2 A^2 \cos ^2(\omega t+\phi) \\
& =\frac{1}{2} m \omega^2\left(A^2-x^2\right) \\
& \therefore \text { KE }=\frac{1}{2} m \omega^2 A^2 \cos ^2(\omega t+\phi)=\frac{1}{2} m \omega^2\left(A^2-x^2\right)
\end{aligned}
\)
where, \(A=\) amplitude of SHM.
As, \(\quad \omega=\sqrt{\frac{k}{m}} \Rightarrow m \omega^2=k \therefore {KE}=\frac{1}{2} k\left(A^2-x^2\right)\)

In terms of time Kinetic energy of a particle executing SHM at any time \(t\) is given by
\(
KE=\frac{1}{2} m \omega^2 A^2 \cos ^2 \omega t
\)
i.e. kinetic energy of a particle executing SHM is a periodic function of time.
The kinetic energy versus time graph is given below:

From the graph above, it is clear that at \(t=0, T / 2\), \(T\), etc., kinetic energy has its maximum value. For \(x= \pm A\) or \(t=\frac{T}{4}, \frac{3 T}{4}\), the kinetic energy has its minimum value.

Special cases:

• Kinetic energy is maximum at the mean position, i.e. at \(x=0\)
  \(
  \mathrm{KE}_{\max }=\frac{1}{2} m \omega^2 A^2
  \)
• Kinetic energy is minimum (zero) at the extreme position, i.e. at \(x= \pm A, \mathrm{KE}_{\min }=\) zero

Potential energy

Work done by the restoring force while displacing the particle from the mean position \((x=0)\) to \(x=x\) :

The work done by restoring force when the particle has been displaced from the position \(x\) to \({x}+{dx}\) is given by
\(
d w=F d x=-k x~ d x
\)
\(
\begin{aligned}
& w=\int d w=\int_0^x-k x~ d x=\frac{-k x^2}{2} \\
& =-\frac{m \omega^2 x^2}{2} \quad \left[k=m \omega^2\right]
\end{aligned}
\)
\(
=-\frac{m \omega^2}{2} A^2 \sin ^2(\omega t+\phi)
\)
Potential Energy = -(work done by restoring force)
Potential Energy \(U=\frac{m \omega^2 x^2}{2}=\frac{1}{2} k x^2=\frac{m \omega^2 A^2}{2} \sin ^2(\omega t+\phi)\)

Special cases:

• Potential energy is maximum at the extreme position, i.e. at \(x= \pm A\)
  \(
  U_{\max }=\frac{1}{2} m \omega^2 A^2
  \)
  Potential energy is minimum (zero) at the mean position, i.e. at \(x=0, U_{\min }=0\)
• In terms of time Potential energy of a particle executing SHM at any time \(t\) is given by
  \(
  U=\frac{1}{2} m \omega^2 A^2 \sin ^2 \omega t
  \)
  The potential energy versus time graph is given below

From the graph, it is clear that at mean position (i.e. \(x=0\) or \(t=0, T / 2, T \ldots)\), potential energy is minimum and at extreme position (i.e. \(\mathrm{t} x= \pm A\) or \(t=T / 4,3 T / 4\) ), its value is maximum. Clearly, twice in each cycle, potential energy acquires its peak values.
Hence, the potential energy is the periodic function of time with a period of \(T / 2\).

Total Mechanical Energy of the Particle Executing Simple Harmonic Motion

The total energy of the system of a block and a spring is equal to the sum of the potential energy stored in the spring plus the kinetic energy of the block and is proportional to the square of the amplitude.
\(
\begin{gathered}
E=KE+U=\frac{1}{2} m \omega^2\left(A^2-x^2\right)+\frac{1}{2} m \omega^2 x^2 \\
E=\frac{1}{2} m \omega^2 A^2 \text { or } E=\frac{1}{2} k A^2
\end{gathered}
\)
which is a constant quantity, i.e. it remains the same at all instants and at all displacement.

The figure below shows the variation of kinetic energy \((K)\), potential energy \((U)\), and total energy \((E)\) as a function of time [shown in Figure (a)] and displacement [shown in Figure (b)] for a particle executing SHM.

\(\therefore\) From the above graph, it can be concluded that

• The total energy remains constant at all \(t\) or \(x\). So, it is shown by a straight line parallel to time.
• Also, \(U=\frac{1}{2} k x^2\) and \(K=\frac{1}{2} k\left(A^2-x^2\right)\), so the graphs of \(U\) and \(K\) versus \(x\) are parabolic.
• Both kinetic energy and potential energy reach maximum value twice, during each period of SHM.
• In the course of motion, kinetic energy increases at the expense of potential energy or vice-versa. Therefore, we may say that during an oscillation, there is a continuous exchange of kinetic and potential energies.

Important points regarding energy in SHM

• The frequency of oscillation of potential energy and kinetic energy is twice as that of displacement or velocity or acceleration.
• The average value of kinetic energy and potential energy is
  \(
  \begin{aligned}
  KE_{\mathrm{av}} & =U_{\mathrm{av}} \\
  & =\frac{1}{2} E=\frac{1}{4} k A^2
  \end{aligned}
  \)

Example 8: The potential energy of a particle executing SHM is 2.5 J when its displacement is half of the amplitude, then determine the total energy of the particle.

Solution: As, potential energy \(=\frac{1}{2} k x^2\)
\(
\Rightarrow \quad \frac{1}{2} k \frac{A^2}{4}=2.5 \mathrm{~J} \quad\left(\because x=\frac{A}{2}\right)
\)
where, \(x\) is the displacement of the particle and \(A\) is the amplitude.
\(
\Rightarrow \quad \text { Total energy }=\frac{1}{2} k A^2=2.5 \times 4=10 \mathrm{~J}
\)

Example 9: A harmonic oscillator of force constant \(4 \times 10^6 \mathrm{Nm}^{-1}\) and amplitude 0.01 m has total energy 240 J . What is maximum kinetic energy and minimum potential energy?

Solution: Given, \(k=4 \times 10^6 \mathrm{~N} / \mathrm{m}, A=0.01 \mathrm{~m}\), total energy \(=240 \mathrm{~J}\) Maximum kinetic energy
\(
=\frac{1}{2} m \omega^2 A^2=\frac{1}{2} k A^2=\frac{1}{2} \times 4 \times 10^6 \times(0.01)^2=200 \mathrm{~J}
\)
Minimum potential energy \(=\) Total energy – Maximum kinetic energy \(=40 \mathrm{~J}\)

Example 10: A linear harmonic oscillator has a total mechanical energy of 200 J . Potential energy of it at mean position is 50 J. Find
(i) the minimum potential energy,
(ii) the maximum kinetic energy,
(iii) the potential energy at extreme positions.

Solution: (i) At mean position, potential energy is minimum. Hence, \(\quad U_{\min }=50 \mathrm{~J}\)
(ii) At the mean position, kinetic energy is maximum.
\(
\therefore \quad K_{\max }=E-U_{\min }=200-50=150 \mathrm{~J}
\)
(iii) At extreme positions, kinetic energy is zero and potential energy is maximum.
\(
\therefore \quad U_{\max }=E=200 \mathrm{~J} \text { (From law of conservation of energy) }
\)

Example 11: A particle executes SHM, at what value of displacement are the kinetic and potential energies equal?

Solution: We know that, kinetic energy \(=\frac{1}{2} m \omega^2\left(A^2-x^2\right)\) and potential energy \(U=\frac{1}{2} m \omega^2 x^2\)
Since, \(KE=U\)
\(
\Rightarrow \frac{1}{2} m \omega^2\left(A^2-x^2\right)=\frac{1}{2} m \omega^2 x^2 \text { or } 2 x^2=A^2
\)
\(
x=\frac{A}{\sqrt{2}}=0.707 A
\)

Example 12: A particle starts oscillating simple harmonically from its equilibrium position with time period \(T\). Determine the ratio of kinetic energy and potential energy of the particle at time \(t=\frac{T}{12}\).

Solution: At \(t=\frac{T}{12}, x=A \sin \frac{2 \pi}{T} \times \frac{T}{12}=A \sin \frac{\pi}{6}=\frac{A}{2}\)
So, kinetic energy, \(\mathrm{KE}=\frac{1}{2} k\left(A^2-x^2\right)=\frac{3}{4} \times \frac{1}{2} k A^2\) and potential energy, \(\mathrm{PE}=\frac{1}{2} k x^2=\frac{1}{4} \times \frac{1}{2} k A^2\)
\(
\therefore \quad \frac{\mathrm{KE}}{\mathrm{PE}}=\frac{3}{1}
\)

Example 13: A particle of mass 0.2 kg is executing \(S H M\) of amplitude 0.2 m. When it passes through the mean position, its kinetic energy is \(64 \times 10^{-3} \mathrm{~J}\). Obtain the equation of motion of this particle, if the initial phase of oscillation is \(\pi / 4\).

Solution: Here, \(A=0.2 \mathrm{~m}, \phi=\frac{\pi}{4}, \mathrm{KE}=64 \times 10^{-3} \mathrm{~J}\)
As we know that, \(\mathrm{KE}=\frac{1}{2} m \omega^2 A^2\) where, \(m=\) mass of particle \(=0.2 \mathrm{~kg}\)
\(
\begin{array}{ll}
\Rightarrow & 64 \times 10^{-3}=\frac{1}{2} \times 0.2 \times \omega^2 \times(0.2)^2 \\
\Rightarrow & \omega^2=\frac{128 \times 10^{-3}}{0.2 \times 0.2 \times 0.2} \text { or } \omega=4 \mathrm{~s}^{-1}
\end{array}
\)
\(\therefore\) Equation of motion can be written as
\(
x=A \sin (\omega t+\phi)=0.2 \sin \left(4 t+\frac{\pi}{4}\right)
\)

Example 14: A particle executes SHM with amplitude A and time period T. When the displacement from the equilibrium position is half the amplitude, what fractions of the total energy are kinetic and potential?

Solution: Total energy, \(E=\frac{1}{2} k A^2\)
When
\(
x= \pm \frac{A}{2} \text {, then }
\)
Potential energy, \(U=\frac{1}{2} k x^2=\frac{1}{2} k \cdot\left( \pm \frac{A}{2}\right)^2\)
\(
=\frac{1}{4} \cdot \frac{1}{2} k A^2=\frac{1}{4} E=25 \% \text { of } E
\)
\(\therefore\) Kinetic energy, \(E-U=E-\frac{1}{4} E=\frac{3}{4} E=75 \%\) of \(E\)

Example 15: The potential energy of a particle oscillating on \(X\)-axis is given as, \(U=20+(x-2)^2\) Here, \(U\) is in joule and \(x\) is in metre. The total mechanical energy of the particle is 36 J.
(i) State whether the motion of the particle is simple harmonic or not.
(ii) Find the mean position.
(iii) Find the maximum kinetic energy of the particle.

Solution: (i) \(F=-\frac{d U}{d x}=-2(x-2)\)
By assuming \(x-2=X\), we get
Since,
\(
\begin{aligned}
& F=-2 X \\
& F \propto-X
\end{aligned}
\)
The motion of the particle is simple harmonic.
(ii) The mean position of the particle is \(X=0\) or \(x-2=0\), which gives \(x=2 \mathrm{~m}\)
(iii) At \(x=2 \mathrm{~m}\) (mean position),
\(
U_{\min }=20+(2-2)^2=20 \mathrm{~J}
\)
\(\therefore \quad\) Maximum kinetic energy of the particle,
\(
K_{\max }=E-U_{\min }=36-20=16 \mathrm{~J}
\)
Note: \(U_{\text {min }}\) is 20 J at mean position or at \(x=2 \mathrm{~m}\).

The Simple Pendulum

Consider simple pendulum, a small bob of mass \(m\) tied to an inextensible massless string of length \(L\). The other end of the string is fixed to a rigid support. The bob oscillates in a plane about the vertical line through the support. Fig. 14.18(a) shows this system. Fig. 14.18(b) is a kind of ‘free-body’ diagram of the simple pendulum showing the forces acting on the bob.

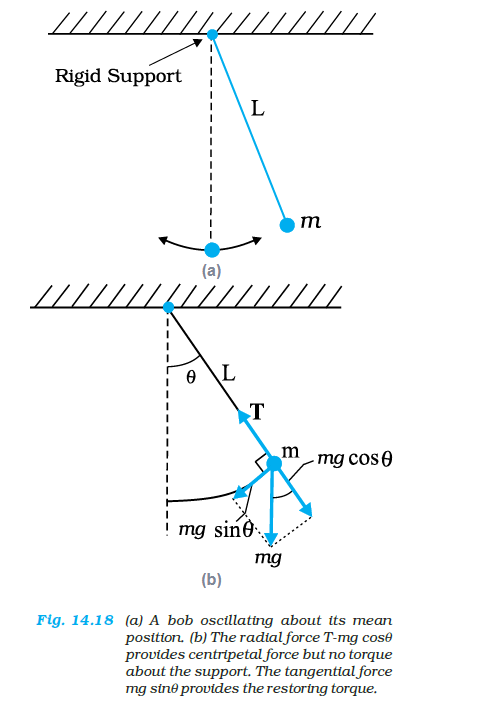
Let \(\theta\) be the angle made by the string with the vertical. When the bob is at the mean position, \(\theta=0\)

There are only two forces acting on the bob; the tension T along the string and the vertical force due to gravity \((=m g)\). The force \(m g\) can be resolved into the component \(m g \cos \theta\) along the string and \(m g \sin \theta\) perpendicular to it. Since the motion of the bob is along a circle of length \(L\) and centre at the support point, the bob has a radial acceleration \(\left(\omega^2 L\right)\) and also a tangential acceleration; the latter arises since motion along the arc of the circle is not uniform. The radial acceleration is provided by the net radial force \(\mathrm{T}-m g \cos \theta\), while the tangential acceleration is provided by \(m g \sin \theta\). It is more convenient to work with torque about the support since the radial force gives zero torque. Torque \(\tau\) about the support is entirely provided by the tangential component of force
\(
\tau=-L(m g \sin \theta) \dots(i)
\)
This is the restoring torque that tends to reduce angular displacement, hence the negative sign. By Newton’s law of rotational motion,
\(
\tau=I \alpha \dots(ii)
\)
where \(I\) is the moment of inertia of the system about the support and \(\alpha\) is the angular acceleration. Thus,
\(
I \alpha=-m g \sin \theta \quad L \dots(iii)
\)
Or, \(\alpha=-\frac{m g L}{I} \sin \theta \dots(iv)\)

We can simplify Eq. (iv) if we assume that the displacement \(\theta\) is small. We know that \(\sin \theta\) can be expressed as,
\(
\sin \theta=\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!} \pm \ldots(v)
\)
where \(\theta\) is in radians.
Now if \(\theta\) is small, \(\sin \theta\) can be approximated by \(\theta\) and Eq. (iv) can then be written as,
\(
\alpha=-\frac{m g L}{I} \theta \dots(vi)
\)
In Table below, we have listed the angle \(\theta\) in degrees, its equivalent in radians, and the value of the function \(\sin \theta\). From this table it can be seen that for \(\theta\) as large as 20 degrees, \(\sin \theta\) is nearly the same as \(\theta\) expressed in radians.
\(
\begin{array}{|c|c|c|}
\hline \theta \text { (degrees) } & \theta \text { (radians) } & \sin \theta \\
\hline 0 & 0 & 0 \\
\hline 5 & 0.087 & 0.087 \\
\hline 10 & 0.174 & 0.174 \\
\hline 15 & 0.262 & 0.259 \\
\hline 20 & 0.349 & 0.342 \\
\hline
\end{array}
\)
Equation (vi) is mathematically, identical to Eq. \(a=-\omega^2 x\)) except that the variable is angular displacement. Hence we have proved that for small \(\theta\), the motion of the bob is simple harmonic. From Eqs. (vi) and \(a=-\omega^2 x\)),
\(
\omega=\sqrt{\frac{m g L}{I}}
\)
and \(T=2 \pi \sqrt{\frac{I}{m g L}} \dots(vii)\)
Now since the string of the simple pendulum is massless, the moment of inertia \(I\) is simply \(\mathrm{mL}^2\). Eq. (vii) then gives the well-known formula for time period of a simple pendulum.
\(
T=2 \pi \sqrt{\frac{L}{g}} \dots(viii)
\)

Note that the time period is independent of the mass of the pendulum. This formula is valid only when radius of point mass of pendulum is negligible as compared to length of the pendulum.

Effect of acceleration

• Above or below the surface of earth, \(g\) decreases. Hence, time period of simple pendulum increases.
• At the centre of earth or in a satellite or in a freely falling lift, the value of \(g\) is zero, so time period of simple pendulum becomes infinity. That means, it will not oscillate and remain as it is, where it is left.
• If a simple pendulum is suspended at the ceiling of a lift which is accelerating upwards with acceleration \(a\), then time period of simple pendulum, \(T^{\prime}=2 \pi \sqrt{\frac{l}{g+a}}\), hence time period will decrease.
• If a simple pendulum is suspended at the ceiling of a lift which is accelerating downwards with acceleration \(a\), then time period of simple pendulum, \(T^{\prime}=2 \pi \sqrt{\frac{l}{g-a}}\). i.e. Time period will increase.
• If a simple pendulum in a car which is accelerating horizontally with acceleration ‘ \(a\) ‘, then time period of pendulum will be \(T^{\prime}=2 \pi \sqrt{\frac{l}{g_{\text {eff }}}}\) where \(g_{\text {eff }}=\sqrt{g^2+a^2}\), i.e. time period will decrease. In this case, the equilibrium position will not be vertical but will make an angle \(\theta=\tan ^{-1}(a / g)\) to the vertical in a direction opposite to the acceleration.

             

Example 16: Two pendulums whose lengths differ by 22 cm oscillate at the same place, so that one of them makes 30 oscillations and the other 36 oscillations during same time. Find the lengths of the pendulum.

Solution: According to the question,
\(
30 \times 2 \pi \sqrt{\frac{l_1}{g}}=36 \times 2 \pi \sqrt{\frac{l_2}{g}}
\)
\(
\frac{l_1}{l_2}=\frac{36 \times 36}{30 \times 30}=\frac{36}{25}
\)
Also, \(\quad l_1-l_2=22 \mathrm{~cm}, \frac{l_1}{l_2}-1=\frac{22}{l_2}\)
\(
\begin{aligned}
\frac{22}{l_2} & =\frac{36}{25}-1 \quad \text { or } \quad \frac{l_2}{22}=\frac{25}{11} \\
l_2 & =50 \mathrm{~cm} \\
l_1 & =22+l_2=(22+50) \mathrm{cm}=72 \mathrm{~cm}
\end{aligned}
\)

Example 17: The length of a simple pendulum is 16 cm. It is suspended by the roof of a lift which is moving upwards with an acceleration of \(6.2 \mathrm{~ms}^{-2}\). Find the time period of the pendulum.

Solution: Given, the length of the pendulum, \(l=16 \mathrm{~cm}=0.16 \mathrm{~m}\) Acceleration of the lift, \(a=6.2 \mathrm{~ms}^{-2}\)
\(
\begin{aligned}
\because \text { Time period, } T & =2 \pi \sqrt{\frac{l}{(g+a)}}=2 \times 3.14 \sqrt{\frac{0.16}{(9.8+6.2)}} \\
& =6.28 \times \sqrt{\frac{0.16}{16}}=6.28 \times \sqrt{\frac{1}{100}}=\frac{6.28}{10} \\
& =0.628 \mathrm{~s}
\end{aligned}
\)

Example 18: A simple pendulum of length \(l\) is suspended from the ceiling of a cart which is sliding without friction on an inclined plane of inclination \(\theta\). What will be the time period of the pendulum?

Solution: Here, point of suspension has an acceleration, \(a=g \sin \theta\) (down the plane). Further, \(g\) can be resolved into two components \(g \sin \theta\) (along the plane) and \(g \cos \theta\) (perpendicular to plane).

\(\therefore \quad g_{\text {eff }}=g \cos \theta \quad\) (perpendicular to plane)
\(
T=2 \pi \sqrt{\frac{l}{\left|g_{\mathrm{eff}}\right|}}=2 \pi \sqrt{\frac{l}{g \cos \theta}}
\)

Example 19: A bob of simple pendulum is suspended by a metallic wire. If \(\alpha\) is the coefficient of linear expansion and \(d \theta\) is the change in temperature, then prove that percentage change in time period is \(50 \alpha d \theta\).

Solution:  With change in temperature \(d \theta\), the effective length of wire becomes \(l^{\prime}=l(1+\alpha d \theta)\)
\(
T^{\prime}=2 \pi \sqrt{\frac{l^{\prime}}{g}} \text { and } T=2 \pi \sqrt{\frac{l}{g}}
\)
Hence, \(\frac{T^{\prime}}{T}=\sqrt{\frac{l^{\prime}}{l}}=(1+\alpha d \theta)^{1 / 2}\)
\(
=1+\frac{1}{2} \alpha d \theta
\)
Percentage increase in time period
\(
\begin{aligned}
& =\left(\frac{T^{\prime}-T}{T}\right) \times 100=\left(\frac{T^{\prime}}{T}-1\right) \times 100 \\
& =\left(1+\frac{\alpha d \theta}{2}-1\right) \times 100 \\
& =50 \alpha d \theta
\end{aligned}
\)

Example 20: A simple pendulum consists of a small sphere of mass \(m\) suspended by a thread of length 1. The sphere carries a positive charge \(q\). The pendulum is placed in a uniform electric field of strength \(E\) directed vertically upwards. With what period will the pendulum oscillate, if the electrostatic force acting on the sphere is less than the gravitational force?

Solution: 

The two forces acting on the bob are shown in figure.
\(g_{\text {eff }}\) in this case will be \(\frac{w-F_e}{m}\)
\(
\begin{aligned}
g_{\mathrm{eff}} & =\frac{m g-q E}{m}=g-\frac{q E}{m} \\
T & =2 \pi \sqrt{\frac{l}{g_{\mathrm{eff}}}}=2 \pi \sqrt{\frac{l}{g-\frac{q E}{m}}}
\end{aligned}
\)

Example 21: Find the period of the function, \(y=\sin \omega t+\sin 2 \omega t+\sin 3 \omega t\)

Solution: The given function can be written as,
Here,
\(
\begin{aligned}
& y=y_1+y_2+y_3 \\
& y_1=\sin \omega t, T_1=\frac{2 \pi}{\omega} \\
& y_2=\sin 2 \omega t, T_2=\frac{2 \pi}{2 \omega}=\frac{\pi}{\omega} \\
& y_3=\sin 3 \omega t, T_3=\frac{2 \pi}{3 \omega} \\
& T_1=2 T_2 \quad \text { and } T_1=3 T_3
\end{aligned}
\)

So, the time period of the given function is \(T_1\) or \(\frac{2 \pi}{\omega}\).
Because in time \(T=\frac{2 \pi}{\omega}\), first function completes one oscillation, the second function two oscillations and the third three.

Vector Method of Combining Two or More Simple Harmonic Motions

A simple harmonic motion is produced when a force (called restoring force) proportional to the displacement acts on a particle. If a particle is acted upon by two such forces the resultant motion of the particle is a combination of two simple harmonic motions. Suppose the two individual motions are represented by,
\(
\begin{aligned}
& x_1=A_1 \sin \omega t \\
& x_2=A_2 \sin (\omega t+\phi)
\end{aligned}
\)
Both the simple harmonic motions have the same angular frequency \(\omega\).

The resultant displacement of the particle is given by,
\(
\begin{aligned}
x & =x_1+x_2 \\
& =A_1 \sin \omega t+A_2 \sin (\omega t+\phi) \\
& =A \sin (\omega t+\alpha)
\end{aligned}
\)
Here, \(A=\sqrt{A_1^2+A_2^2+2 A_1 A_2 \cos \phi}\)
\(
\tan \alpha=\frac{A_2 \sin \phi}{A_1+A_2 \cos \phi}
\)

Example 22: Find the displacement equation of the simple harmonic motion obtained by combining the motions.
\(
x_1=2 \sin \omega t, \quad x_2=4 \sin \left(\omega t+\frac{\pi}{6}\right) \text { and } x_3=6 \sin \left(\omega t+\frac{\pi}{3}\right)
\)

Solution: The resultant equation is,

\(
\begin{aligned}
x & =A \sin (\omega t+\phi) \\
\Sigma A_x & =2+4 \cos 30^{\circ}+6 \cos 60^{\circ}=8.46 \\
\Sigma A_y & =4 \sin 30^{\circ}+6 \cos 30^{\circ}=7.2
\end{aligned}
\)
\(
\begin{aligned}
A & =\sqrt{\left(\Sigma A_x\right)^2+\left(\Sigma A_y\right)^2} \\
& =\sqrt{(8.46)^2+(7.2)^2} \\
& =11.25
\end{aligned}
\)
\(
\begin{aligned}
\tan \phi & =\frac{\Sigma A_y}{\Sigma A_x} \\
& =\frac{7.2}{8.46}=0.85 \\
\phi & =\tan ^{-1}(0.85) \\
& =40.4^{\circ}
\end{aligned}
\)
Thus, the displacement equation of the combined motion is,
\(
\begin{aligned}
& x=11.25 \sin (\omega t+\phi) \\
& \text { where, }\phi=40.4^{\circ}
\end{aligned}
\)

Spring block system

Let us consider a massless spring placed on a frictionless horizontal surface. Its one end is attached to a rigid support and the other end to a body of mass \(m\). When it is pulled on one side through a small distance \(x\) and released, it moves to and fro about a mean position. Let \(x=0\) be the position of the centre of the body when the spring is at the mean position.

By Hooke’s law, a restoring force \(F\) is developed in the spring on stretching and compressing it through a small displacement \(x\),
\(
\Rightarrow \quad \begin{aligned}
F & =-k x \\
a & =-\frac{k}{m} x
\end{aligned}
\)
The time period of such oscillations is given by
\(
T=2 \pi \sqrt{\frac{m}{k}}
\)
where, \(k\) is force constant of spring and \(m\) is mass of the object connected to the spring.
If the stretch in a vertically loaded spring is \(y\), then for equilibrium of mass \(m, \quad T=2 \pi \sqrt{y / g}\)

Special cases:

• If the spring has a mass \(M\) and a mass \(m\) is suspended from it, then time period is given by
  \(
  T=2 \pi \sqrt{\frac{M_{\mathrm{eff}}}{k}}, \text { where } M_{\mathrm{eff}}=m+\frac{M}{3}
  \)
• If two masses \(m_1\) and \(m_2\) are connected by a spring of spring constant \(k\) and made to oscillate on horizontal surface. Then, time period is given by
  \(
  T=2 \pi \sqrt{\frac{\mu}{k}}
  \)

       

        Here, \(\mu=\) reduced mass \(=\frac{m_1 m_2}{m_1+m_2}\)

Example 23: A 2.5 kg collar is attached to a spring of spring constant \(250 \mathrm{Nm}^{-1}\). It slides without friction over a horizontal surface. It is displaced from its equilibrium position by 20 cm and released. Calculate the period of oscillation and the maximum speed.

Solution: The period of oscillation,
\(
\begin{aligned}
T & =2 \pi \sqrt{\frac{m}{k}}=2 \pi \sqrt{\frac{2.5}{250}} \\
& =\frac{2 \times 3.14}{10}=0.63 \mathrm{~s}
\end{aligned}
\)
Maximum speed, \(v_m=A \omega=0.2 \sqrt{\frac{k}{m}}=0.2 \times \sqrt{\frac{250}{2.5}}\)
\(
=0.2 \times 10=2 \mathrm{~ms}^{-1}
\)

Example 24: A spring-mass system is hanging from the ceiling of an elevator in equilibrium. The elevator suddenly starts accelerating upwards with acceleration a, find
(i) the frequency and
(ii) the amplitude of the resulting SHM.

Solution: (i) Frequency \(=2 \pi \sqrt{m / k}\)
(Frequency is independent of \(g\) in spring mass system)
(ii) Initial extension in spring in equilibrium \(=\frac{m g}{k}\)
Extension in spring in equilibrium when lift starts accelerating upwards \(=\frac{m(g+a)}{k}\)
\(\therefore\) Amplitude \(=\frac{m(g+a)}{k}-\frac{m g}{k}=\frac{m a}{k}\)

Example 25: A body of mass \(m\) attached to a spring which is oscillating with time period 4 s. If the mass of the body is increased by 4 kg, its time period increases by 2 s. Determine the value of initial mass \(m\).

Solution: \(\text { In } 1 \text { st case, } T=2 \pi \sqrt{\frac{m}{k}} \Rightarrow 4=2 \pi \sqrt{\frac{m}{k}} \dots(i)\)
\(
\text { In 2nd case, } 6=2 \pi \sqrt{\frac{m+4}{k}} \dots(ii)
\)
On dividing Eq. (i) by Eq. (ii), we get
\(
\frac{4}{6}=\sqrt{\frac{m}{m+4}} \Rightarrow \frac{16}{36}=\frac{m}{m+4} \Rightarrow m=3.2 \mathrm{~kg}
\)

Example 26: A block with a mass of 3 kg is suspended from an ideal spring having negligible mass and stretches the spring upto 0.2 m .
(i) What is the force constant of the spring?
(ii) What is the period of oscillation of the block, if it is pulled down and released?

Solution: (i) In equilibrium, \(k l=m g\)
\(
\therefore \quad k=\frac{m g}{l}
\)
Substituting the given values, we get
\(
k=\frac{(3)(9.8)}{0.2}=147 \mathrm{Nm}^{-1}
\)
(ii) \(T=2 \pi \sqrt{\frac{l}{g}}=2 \pi \sqrt{\frac{0.2}{9.8}}=0.897 \mathrm{~s}\)

Example 27: Two rigid bodies \(A\) and \(B\) of masses 1 kg and 2 kg respectively are rigidly connected to a spring of force constant \(400 \mathrm{Nm}^{-1}\). The body \(B\) rests on a horizontal table. From the rest position, the body \(A\) is compressed by 2 cm and then released. Deduce (i) the frequency of oscillation, (ii) total oscillation energy, (iii) the amplitude of the harmonic vibration of the reaction of the table on body \(B\).

Solution: Since it is the body \(A\) which is oscillating, \(m=1 \mathrm{~kg}\)
(i) Frequency of oscillation, \(v=\frac{1}{2 \pi} \sqrt{\frac{k}{m}}\)
\(
v=\frac{1}{2 \pi} \sqrt{\frac{400}{1}}=\frac{10}{\pi}=3.185 \mathrm{~Hz}
\)
(ii) Total oscillation energy, \(E=\frac{1}{2} m A^2 \omega^2\)
\(
\begin{aligned}
E & =\frac{1}{2} m A^2\left(\frac{k}{m}\right)=\frac{1}{2} k A^2 \\
& =\frac{1}{2} \times 400 \times(0.02)^2 \quad(\because A=2 \mathrm{~cm}=0.02 \mathrm{~m}) \\
& =0.08 \mathrm{~J}
\end{aligned}
\)
(iii) Total force acting on the table
\(
=(1+2) \mathrm{kg}-\mathrm{wt}=3 \mathrm{~kg}-\mathrm{wt}=3 \times 9.8 \mathrm{~N}=29.4 \mathrm{~N}
\)
This is the mean upward reaction. Now, due to oscillations, the maximum tension developed in the spring is given by
\(
F=k A=400 \times 0.02 \mathrm{~N}=8 \mathrm{~N}
\)
Therefore, the net reaction of the table will vary from \((29.4+8) \mathrm{N}\) to \((29.4) \mathrm{N}\).

Example 28: In the following arrangements, block is slightly displaced vertically downwards from its equilibrium position and released. Find time period of vertical oscillations. Assume the pulley to be light.

Solution: (i) Let at some instant extension of spring is \(x\), tension in the string \(T=k x\)

Restoring force, \(F=T=-k x \quad \text { (Hooke’s law) }\)
where, \(k=\) spring constant
Time period, \(T_0=2 \pi \sqrt{\frac{m}{k}}\)

(ii) Let block move down by \(x\), pulley will move by \(x / 2\).

\(
2 T=\frac{k x}{2} \Rightarrow T=\frac{k x}{4}
\)
Comparing it with equation \(F=-k x\), we get
\(
k^{\prime}=k / 4 \quad \therefore \quad T_0=2 \pi \sqrt{\frac{m}{k^{\prime}}}
\)
\(
T_0=2 \pi \sqrt{\frac{m}{k / 4}}=4 \pi \sqrt{\frac{m}{k}}
\)

(iii) If block moves by \(x\), pulley also moves \(x\) and hence, spring is stretched by \(2 x\).

Tension produced in spring, \(T=4 k x\)
Restoring force, \(F=-4 k x\)
Comparing it with equation \(F=-k^{\prime} x\), we get
\(
k^{\prime}=+4 k
\)
\(
\therefore \quad T_0=2 \pi \sqrt{\frac{m}{k^{\prime}}} \Rightarrow T_0=2 \pi \sqrt{\frac{m}{4 k}}=\pi \sqrt{\frac{m}{k}}
\)

Oscillations of spring combination

Series combination:

Two springs of spring constants \(k_1\) and \(k_2\) are joined in series as shown in the figure.

Then, the resultant spring constant of the combination is given by
\(
\frac{1}{k_s}=\frac{1}{k_1}+\frac{1}{k_2}=\frac{k_1+k_2}{k_1 k_2} \Rightarrow k_s=\frac{k_1 k_2}{k_1+k_2}
\)
and hence,
\(
T=2 \pi \sqrt{\frac{m}{k_s}}=2 \pi \sqrt{\frac{\left(k_1+k_2\right) m}{k_1 k_2}}
\)

Parallel combination

Two springs of spring constants \(k_1\) and \(k_2\) are joined in parallel as shown in the figure.

Then, spring constant, \(k_p=k_1+k_2\)
Time period, \(T=2 \pi \sqrt{\frac{m}{k_p}}=2 \pi \sqrt{\frac{m}{\left(k_1+k_2\right)}}\)

Important points regarding spring block system

• If the length of the spring is made \(n\) times, then the effective force constant becomes \(1 / n\) times and the time period becomes \(\sqrt{n}\) times.
• If a spring of spring constant \(k\) is divided into \(n\) equal parts, the spring constant of each part becomes \(n k\), and time period becomes \(\frac{1}{\sqrt{n}}\) times.
• The force constant of a stiffer spring is more than that of a soft spring.

Example 29: One body is suspended from a spring of length \(l\), spring constant \(k\) and has time period T. Now, if the spring is divided in two equal parts which are joined in parallel and the same body is suspended from this arrangement, then determine the new time period.

Solution: When a spring of spring constant \(k\) is divided into 2 parts, the spring constant of each part becomes \(2 k\).
\(\therefore\) Spring constant in parallel combination \(k^{\prime}=2 k+2 k=4 k\)
\(
\begin{aligned}
\therefore & =2 \pi \sqrt{\frac{m}{k^{\prime}}}=2 \pi \sqrt{\frac{m}{4 k}} \\
& =2 \pi \sqrt{\frac{m}{k}} \times \frac{1}{\sqrt{4}}=\frac{T}{\sqrt{4}}=\frac{T}{2}
\end{aligned}
\)

Example 30: Two identical springs of spring constant \(k\) are attached to a block of mass \(m\) and to fixed supports as shown in the figure. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.

Solution: Let the mass be displaced by a small distance \(x\) to the right side of the equilibrium position as shown in the figure.

Under this situation, the spring on the left side gets elongated by a length equal to \(x\), and that on the right side gets compressed by the same length. The forces acting on the mass are then
\(F_1=-k x\) (force exerted by the spring on the left side, trying to pull the mass towards the mean position)
\(F_2=-k x\) (force exerted by the spring on the right side, trying to push the mass towards the mean position)
The net force \(F\) acting on the mass is then given by, \(F=-2 k x\). Hence, the force acting on the mass is proportional to the displacement and is directed towards the mean position, therefore the motion executed by the mass is simple harmonic. The time period of oscillations is \(T=2 \pi \sqrt{\frac{m}{2 k}}\).

Example 31: Periodic time of oscillation \(T_1\) is obtained when a mass is suspended from a spring and if another spring is used with same mass, then the periodic time of oscillation is \(T_2\). Now, if this mass is suspended from series combination of above springs, then calculate the time period.

Solution:

As, \(T_1=2 \pi \sqrt{\frac{m}{k_1}}\)
\(
\begin{aligned}
& \Rightarrow T_1^2=4 \pi^2 \frac{m}{k_1} \Rightarrow k_1=\frac{4 \pi^2 m}{T_1^2} \\
& \text { and } T_2=2 \pi \sqrt{\frac{m}{k_2}} \Rightarrow T_2^2=4 \pi^2 \frac{m}{k_2} \Rightarrow k_2=\frac{4 \pi^2 m}{T_2^2}
\end{aligned}
\)
Now, \(T=2 \pi \sqrt{\frac{m}{k^{\prime}}}\)
where, \(\frac{1}{k^{\prime}}=\frac{1}{k_1}+\frac{1}{k_2}\)
\(
\Rightarrow \quad k^{\prime}=\frac{k_1 k_2}{k_1+k_2}=\frac{\left(\frac{4 \pi^2 m}{T_1^2}\right)\left(\frac{4 \pi^2 m}{T_2^2}\right)}{\frac{4 \pi^2 m}{T_1^2}+\frac{4 \pi^2 m}{T_2^2}}
\)
\(
k^{\prime}=\frac{4 \pi^2 m\left(\frac{4 \pi^2 m}{T_1^2 T_2^2}\right)}{4 \pi^2 m\left(\frac{1}{T_1^2}+\frac{1}{T_2^2}\right)}=\frac{4 \pi^2 m}{T_1^2+T_2^2}
\)
\(\therefore \quad T=2 \pi \sqrt{\frac{m}{k^{\prime}}}=2 \pi \sqrt{\frac{m}{\frac{4 \pi^2 m}{T_1^2+T_2^2}}}=\sqrt{T_1^2+T_2^2}\)

The physical pendulum

Any rigid body suspended from a rigid support capable of oscillating about a horizontal axis passing through it constitutes a physical pendulum (or compound pendulum). The figure given below shows a rigid body pivoted at \(O\), so that it can oscillate without friction about an axis passing through \(O\).
In equilibrium, the centre of gravity \((G)\) is directly below \(O\). In the position shown in the figure, the body is displaced from equilibrium by an angle \(\theta\). The distance from \(O\) to the centre of gravity is \(l\). Let, the moment of inertia of the body about the axis of rotation through \(O\) is \(I\) and the total mass is \(m\). In the displaced position, the weight \(m g\) causes a restoring torque, \(\tau=-(m g)(l \sin \theta)\)

The negative sign shows that the restoring torque is clockwise when the displacement is counterclockwise and vice-versa.
For small oscillations,
\(
\sin \theta \approx \theta \text { and } \Sigma \tau=I \alpha \Rightarrow-(m g l) \theta=I \alpha
\)
As \(\alpha\) is proportional to \(-\theta\), the motion is simple harmonic, the time period of which is
\(
T=2 \pi \sqrt{\left|\frac{\theta}{\alpha}\right|}
\)
or \(T=2 \pi \sqrt{\frac{I}{m g l}}\)

Note: Time period of some common physical pendulum
(i) \(B a r, T=2 \pi \sqrt{\frac{2 l}{3 g}}\)
(ii) Ring, \(T=2 \pi \sqrt{\frac{2 R}{g}}\)
(iii) Disc, \(T=2 \pi \sqrt{\frac{3 R}{2 g}}\)

Example 32: A uniform circular disc of radius \(R\) oscillates in a vertical plane about a horizontal axis. Find the distance of the axis of rotation from the centre for which the period is minimum. What is the value of this period?

Solution: The time period of a compound pendulum is minimum when its length is equal to the radius of gyration about its centre of gravity, i.e. \(l=K\)
Since, the moment of inertia of a disc about an axis perpendicular to its plane and passing through its centre is equal to, \(\quad I=M K^2=\frac{1}{2} M R^2 \Rightarrow K=\frac{R}{\sqrt{2}}\)
Thus, the disc will oscillate with the minimum time period when the distance of the axis of rotation from the centre is \(\frac{R}{\sqrt{2}}\).
and the value of this minimum time period will be
\(
T_{\min }=2 \pi \sqrt{\frac{2 R / \sqrt{2}}{g}}=2 \pi \sqrt{\frac{\sqrt{2} R}{g}} \text { or } T_{\min } \approx 2 \pi \sqrt{\frac{1.414 R}{g}}
\)

Example 33: Find the period of small oscillations of a uniform rod with length \(l\), pivoted at one end.

Solution: Time period of a uniform rod which is the same as the physical pendulum,

\(
T=2 \pi \sqrt{\frac{I_0}{m g(O G)}}
\)
Here, \(I_0=\frac{1}{3} m l^2\) and \(O G=\frac{l}{2}\)
\(\therefore \quad T=2 \pi \sqrt{\frac{\left(\frac{1}{3} m l^2\right)}{(m)(g)\left(\frac{l}{2}\right)}}\)
or \(\quad T=2 \pi \sqrt{\frac{2 l}{3 g}}\)

Example 34: A ring of radius \(r\) is suspended from a point on its circumference. Determine its angular frequency of small oscillations.

Solution: It is a physical pendulum, the time period of which is,
\(
T=2 \pi \sqrt{\frac{I}{m g l}}
\)
Here, \(I=\) moment of inertia of the ring about point of suspension
\(
=m r^2+m r^2=2 m r^2
\)
and \(l=\) distance of point of suspension from centre of gravity \(=r\)
\(\therefore\) \(T=2 \pi \sqrt{\frac{2 m r^2}{m g r}}=2 \pi \sqrt{\frac{2 r}{g}}\)
Hence, angular frequency, \(\omega=\frac{2 \pi}{T}\) or \(\quad \omega=\sqrt{\frac{g}{2 r}}\)