Orbital Velocity is the minimum velocity required to put the satellite into its orbit around the Earth.

Derivation of Orbital Velocity

For the derivation, let us consider a satellite of mass \((m)\) revolving around the earth having mass \((M)\) and the radius \((R)\) in a circular radius \((r)\) at a height \((h)\) from the surface of the Earth. To revolve around the Earth, the Gravitational force between the satellite and the Earth provides a centripetal force.

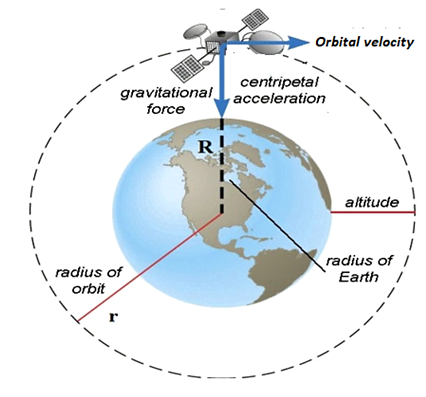
As we know that, According to the law of gravitation, the force of gravity on the satellite at an altitude of \(h\) is given by
\(
F_g=frac{G M m}{(r)^2}=frac{G M m}{(R+h)^2}(r=R+h) ldots(1)
\)
And, the centripetal force required by the satellite to keep it in its orbit is given as
\(
F_r=frac{m V_o^2}{r}=frac{m V_o^2}{R+h} quad ldots ldots(2)
\)
So, the satellite will orbit the earth if,
\(
begin{aligned}
&F_{text {Gravitational }}=F_{text {Centripetal }} \
&Rightarrow frac{G M m}{(R+h)^2}=frac{m V_o^2}{R+h} \
&Rightarrow V_o^2=frac{G M}{R+h} \
&Rightarrow V_o=sqrt{frac{G M}{R+h}}
end{aligned}
\)
Now when the satellite revolves close to the surface of the Earth then, \((h=0\), on comparing with the radius of the earth), and the orbital velocity becomes
\(
Rightarrow V_o=sqrt{frac{G M}{R}} ldots(3)
\)
Where,
\(M=\) Mass of the Earth,
\(R=\) Radius of the Earth,
\(m=\) Mass of the Satellite
\(V_o=\) Orbital Velocity of the Satellite
\(H=\) Height of the satellite above the earth’s surface

Relation Between Escape Velocity and Orbital Velocity

There exists a relationship between escape velocity and orbital velocity. The mathematical relation between the escape velocity and the orbital velocity will be
From the expression of the Escape velocity,
We have:- \(v_e=sqrt{frac{2 G M}{R}} quad cdots(4)\)
And from the expression of the orbital velocity,
We have:- \(V_o=sqrt{frac{G M}{R}} quad cdots(5)\)
Now, On dividing Eq (4) and Eq (5)
We have
\(
begin{aligned}
&frac{v_e}{V_o}=sqrt{frac{2 G M}{R}} times sqrt{frac{R}{G M}} \
&Rightarrow v_e=sqrt{2} V_o quad cdots(6)
end{aligned}
\)
The above relation is valid for any orbit at a distance of \(r\) from the earth’s centre.

Calculation of Escape Velocity from the Surface of the Earth

To escape from the earth’s surface, we calculate the escape velocity, As we know that
The Mass of the Earth \(=5.98 times 10^{24} mathrm{~kg}\)
The Radius of the Earth \(=6.38 times 10^6 mathrm{~m}\)
Newtons Gravitational Constant, \(G=6.673 times 10^{-11} mathrm{Nm}^2 mathrm{~kg}^{-2}\).
Now we can find the escape velocity from the earth using the escape velocity formula:-
\(
v_e=sqrt{frac{2 G M}{R}}
\)
Now substituting all the above values, we have:-
\(
begin{aligned}
&v_e=sqrt{frac{2 timesleft(6.673 times 10^{11}right)left(5.98 times 10^{24}right)}{6.38 times 10^6}} \
&Rightarrow v_e=sqrt{frac{left(7.981 times 10^{14}right)}{6.38 times 10^6}} \
&Rightarrow v_e=sqrt{1.251 times 10^8} \
&Rightarrow v_e=11184 mathrm{~m} mathrm{~s}^{-1} \
&Rightarrow v_e=11.2 mathrm{~km} mathrm{~s}^{-1}
end{aligned}
\)
Therefore, the escape velocity from the Earth is \(11.2 mathrm{~km} mathrm{~s}^{-1}\).