4.2 Inheritance of One Gene

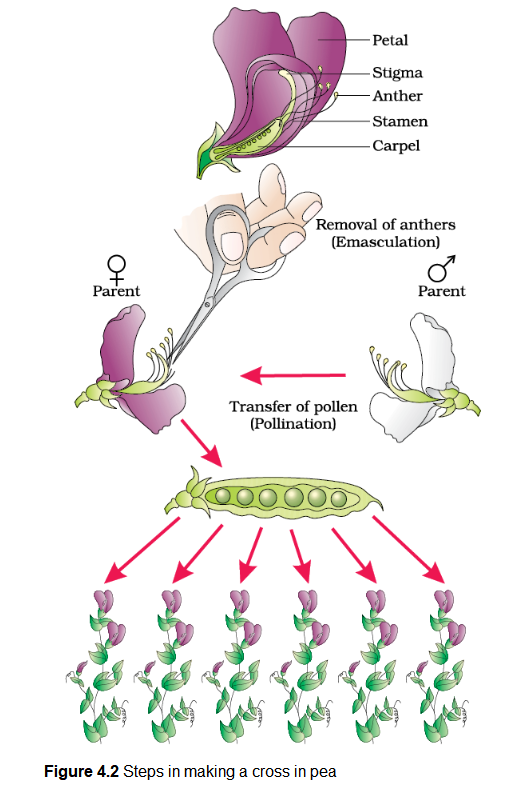
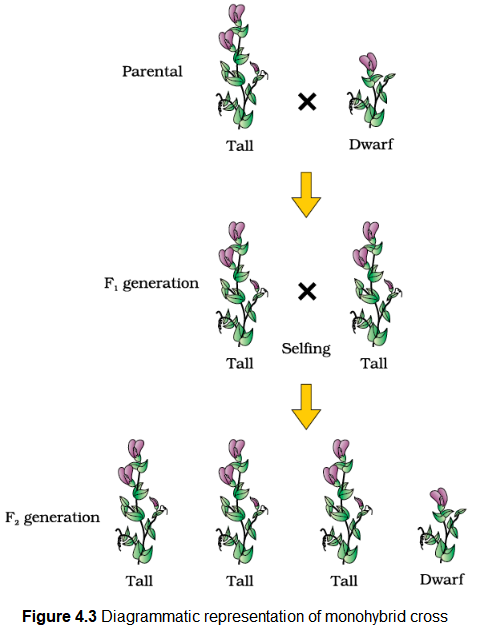
Let us take the example of one such hybridisation experiment carried out by Mendel where he crossed tall and dwarf pea plants to study the inheritance of one gene (Figure 4.2). He collected the seeds produced as a result of this cross and grew them to generate plants of the first hybrid generation. This generation is also called the Filial\(_1\) progeny or the \(\mathbf{F}_{\mathbf{1}}\). Mendel observed that all the \(\mathrm{F}_1\) progeny plants were tall, like one of its parents; none were dwarf (Figure 4.3). He made similar observations for the other pairs of traits – he found that the \(\mathrm{F}_1\) always resembled either one of the parents, and that the trait of the other parent was not seen in them.

Mendel then self-pollinated the tall \(\mathrm{F}_1\) plants and to his surprise found that in the Filial \(_2\) generation some of the offspring were ‘dwarf’; the character that was not seen in the \(\mathrm{F}_1\) generation was now expressed. The proportion of plants that were dwarf were \(1 / 4^{\text {th }}\) of the \(\mathrm{F}_2\) plants while \(3 / 4^{\text {th }}\) of the \(\mathrm{F}_2\) plants were tall. The tall and dwarf traits were identical to their parental type and did not show any blending, that is all the offspring were either tall or dwarf, none were of inbetween height (Figure 4.3).

Similar results were obtained with the other traits that he studied: only one of the parental traits was expressed in the \(\mathrm{F}_1\) generation while at the \(\mathrm{F}_2\) stage both the traits were expressed in the proportion \(3: 1\). The contrasting traits did not show any blending at either \(\mathrm{F}_1\) or \(\mathrm{F}_2\) stage.

Based on these observations, Mendel proposed that something was being stably passed down, unchanged, from parent to offspring through the gametes, over successive generations. He called these things as ‘factors’. Now we call them as genes. Genes, therefore, are the units of inheritance. They contain the information that is required to express a particular trait in an organism. Genes which code for a pair of contrasting traits are known as alleles, i.e., they are slightly different forms of the same gene.

If we use alphabetical symbols for each gene, then the capital letter is used for the trait expressed at the \(F_1\) stage and the small alphabet for the other trait. For example, in case of the character of height, \(\mathbf{T}\) is used for the Tall trait and \(\mathbf{t}\) for the ‘dwarf’, and \(\mathbf{T}\) and \(\mathbf{t}\) are alleles of each other. Hence, in plants the pair of alleles for height would be \(\mathbf{TT}\), \(\mathbf{Tt}\) or \(\mathbf{t t}\). Mendel also proposed that in a true breeding, tall or dwarf pea variety the allelic pair of genes for height are identical or homozygous, \(\mathbf{TT}\) and \(\mathbf{t t}\), respectively. \(\mathbf{TT}\) and \(\mathbf{t t}\) arre called the genotype of the plant while the descriptive terms tall and dwarf are the phenotype. What then would be the phenotype of a plant that had a genotype \(\mathbf{T t}\) ?

As Mendel found the phenotype of the \(\mathrm{F}_1\) heterozygote \(\mathbf{T t}\) to be exactly like the \(\mathbf{TT}\) parent in appearance, he proposed that in a pair of dissimilar factors, one dominates the other (as in the \(\mathrm{F}_1\) ) and hence is called the dominant factor while the other factor is recessive. In this case \(\mathbf{T}\) (for tallness) is dominant over \(\mathbf{t}\) (for dwarfness), that is recessive. He observed identical behaviour for all the other characters/trait-pairs that he studied.

It is convenient (and logical) to use the capital and lower case of an alphabetical symbol to remember this concept of dominance and recessiveness. (Do not use \(\mathbf{T}\) for tall and \(\mathbf{d}\) for dwarf because you will find it difficult to remember whether \(\mathbf{T}\) and \(\mathbf{d}\) are alleles of the same gene/character or not). Alleles can be similar as in the case of homozygotes \(\mathbf{T T}\) and \(\mathbf{t t}\) or can be dissimilar as in the case of the heterozygote \(\mathbf{T t}\). Since the \(\mathbf{T t}\) plant is heterozygous for genes controlling one character (height), it is a monohybrid and the cross between \(\mathbf{T T}\) and \(\mathbf{t t}\) is a monohybrid cross.

From the observation that the recessive parental trait is expressed without any blending in the \(\mathrm{F}_2\) generation, we can infer that, when the tall and dwarf plant produce gametes, by the process of meiosis, the alleles of the parental pair separate or segregate from each other and only one allele is transmitted to a gamete. This segregation of alleles is a random process and so there is a 50 per cent chance of a gamete containing either allele, as has been verified by the results of the crossings. In this way the gametes of the tall \(\mathbf{TT}\) plants have the allele \(\mathbf{T}\) and the gametes of the dwarf \(\mathbf{t t}\) plants have the allele \(\mathbf{t}\). During fertilisation the two alleles, \(\mathbf{T}\) from one parent say, through the pollen, and \(\mathbf{t}\) from the other parent, then through the egg, are united to produce zygotes that have one \(\mathbf{T}\) allele and one \(\mathbf{t}\) allele. In other words the hybrids have \(\mathbf{Tt}\). Since these hybrids contain alleles which express contrasting traits, the plants are heterozygous. The production of gametes by the parents, the formation of the zygotes, the \(\mathrm{F}_1\) and \(\mathrm{F}_2\) plants can be understood from a diagram called Punnett Square as shown in Figure 4.4. It was developed by a British geneticist, Reginald C. Punnett. It is a graphical representation to calculate the probability of all possible genotypes of offspring in a genetic cross. The possible gametes are written on two sides, usually the top row and left columns. All possible combinations are represented in boxes below in the squares, which generates a square output form.

The Punnett Square shows the parental tall \(\mathbf{TT}\) (male) and dwarf \(\mathbf{tt}\) (female) plants, the gametes produced by them and, the \(\mathrm{F}_1 \mathbf{T t}\) progeny. The \(\mathrm{F}_1\) plants of genotype \(\mathbf{T t}\) are self-pollinated. The symbols are used to denote the female (eggs) and male (pollen) of the \(\mathrm{F}_1\) generation, respectively. The \(\mathrm{F}_1\) plant of the genotype \(\mathbf{Tt}\) when self-pollinated, produces gametes of the genotype \(\mathbf{T}\) and \(\mathbf{t}\) in equal proportion. When fertilisation takes place, the pollen grains of genotype \(\mathbf{T}\) have a 50 per cent chance to pollinate eggs of the genotype \(\mathbf{T}\), as well as of genotype \(\mathbf{t}\). Also pollen grains of genotype \(\mathbf{t}\) have a 50 per cent chance of pollinating eggs of genotype \(\mathbf{T}\), as well as of genotype \(\mathbf{t}\). As a result of random fertilisation, the resultant zygotes can be of the genotypes \(\mathbf{TT}\), \(\mathbf{Tt}\) or \(\mathbf{tt}\)

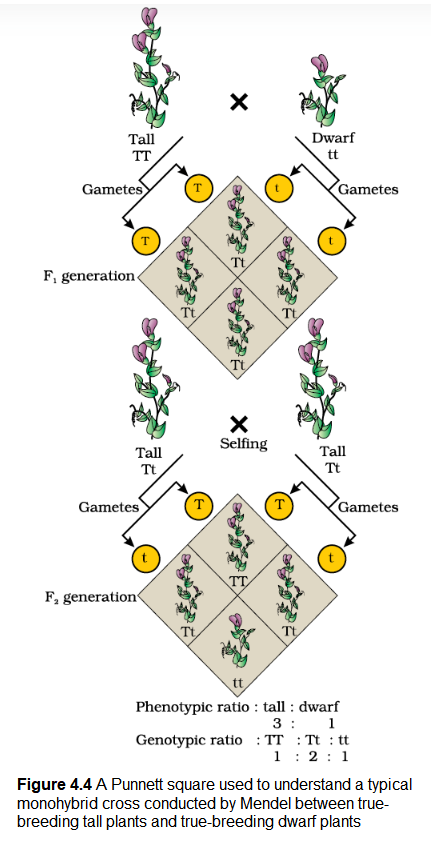
From the Punnett square it is easily seen that \(1 / 4^{\text {th }}\) of the random fertilisations lead to \(\mathbf{TT}\), \(1 / 2\) lead to \(\mathbf{Tt}\) and \(1 / 4^{\text {th }}\) to \(\mathbf{t t}\). Though the \(\mathrm{F}_1\) have a genotype of \(\mathbf{T t}\), but the phenotypic character seen is ‘tall’. At \(\mathrm{F}_2\), \(3 / 4^{\text {th }}\) of the plants are tall, where some of them are \(\mathbf{TT}\) while others are \(\mathbf{Tt}\). Externally it is not possible to distinguish between the plants with the genotypes \(\mathbf{TT}\) and \(\mathbf{Tt}\). Hence, within the genopytic pair \(\mathbf{Tt}\) only one character ‘\(\mathbf{T}\)‘ tall is expressed. Hence the character \(\mathbf{T}\) or ‘tall’ is said to dominate over the other allele \(\mathbf{t}\) or ‘dwarf’ character. It is thus due to this dominance of one character over the other that all the \(\mathrm{F}_1\) are tall (though the genotype is \(\mathbf{Tt}\) ) and in the \(\mathrm{F}_2 3 / 4^{\text {th }}\) of the plants are tall (though genotypically \(1 / 2\) are \(\mathbf{Tt}\) and only \(1 / 4^{\mathrm{th}}\) are \(\mathbf{TT}\)). This leads to a phenotypic ratio of \(3 / 4^{\text {th }}\) tall : \((1 / 4 \mathbf{T T}+1 / 2 \mathbf{T t})\) and \(1 / 4^{\text {th }} \mathbf{t t}\), i.e., a 3:1 ratio, but a genotypic ratio of 1:2:1.

The \(1 / 4: 1 / 2: 1 / 4\) ratio of \(\mathbf{T T}\) : \(\mathbf{Tt}\): \(\mathbf{t t}\) is mathematically condensable to the form of the binomial expression (ax +by\()^2\), that has the gametes bearing genes \(\mathbf{T}\) or \(\mathbf{t}\) in equal frequency of \(1 / 2\). The expression is expanded as given below :
\(
(1 / 2 \mathbf{T}+1 / 2 \mathbf{t})^2=(1 / 2 \mathbf{T}+1 / 2 \mathbf{t}) \mathrm{X}(1 / 2 \mathbf{T}+1 / 2 \mathbf{t})=1 / 4 \mathbf{~T T}+1 / 2 \mathbf{~T} \mathbf{t}+1 / 4 \mathbf{~t t}
\)

Mendel self-pollinated the \(\mathrm{F}_2\) plants and found that dwarf \(\mathrm{F}_2\) plants continued to generate dwarf plants in \(\mathrm{F}_3\) and \(\mathrm{F}_4\) generations. He concluded that the genotype of the dwarfs was homozygous – \(\mathbf{tt}\). What do you think he would have got had he self-pollinated a tall \(\mathrm{F}_2\) plant?

From the preceeding paragraphs it is clear that though the genotypic ratios can be calculated using mathematical probability, by simply looking at the phenotype of a dominant trait, it is not possible to know the genotypic composition. That is, for example, whether a tall plant from \(F_1\) or \(\mathrm{F}_2\) has \(\mathbf{T T}\) or \(\mathbf{T t}\) composition, cannot be predicted. Therefore, to determine the genotype of a tall plant at \(\mathrm{F}_2\), Mendel crossed the tall plant from \(\mathrm{F}_2\) with a dwarf plant. This he called a test cross. In a typical test cross an organism (pea plants here) showing a dominant phenotype (and whose genotype is to be determined) is crossed with the recessive parent instead of self-crossing. The progenies of such a cross can easily be analysed to predict the genotype of the test organism. Figure 4.5 shows the results of typical test cross where violet colour flower (W) is dominant over white colour flower (w).

Using Punnett square, try to find out the nature of offspring of a test cross.
What ratio did you get?
Using the genotypes of this cross, can you give a general definition for a test cross?

Based on his observations on monohybrid crosses Mendel proposed two general rules to consolidate his understanding of inheritance in monohybrid crosses. Today these rules are called the Principles or Laws of Inheritance: the First Law or Law of Dominance and the Second Law or Law of Segregation.

Law of Dominance

• (i) Characters are controlled by discrete units called factors.
• (ii) Factors occur in pairs.
• (iii) In a dissimilar pair of factors one member of the pair dominates (dominant) the other (recessive).

The law of dominance is used to explain the expression of only one of the parental characters in a monohybrid cross in the \(\mathrm{F}_1\) and the expression of both in the \(\mathrm{F}_2\). It also explains the proportion of \(3: 1\) obtained at the \(\mathrm{F}_2\).

Law of Segregation

This law is based on the fact that the alleles do not show any blending and that both the characters are recovered as such in the \(\mathrm{F}_2\) generation though one of these is not seen at the \(\mathrm{F}_1\) stage. Though the parents contain two alleles during gamete formation, the factors or alleles of a pair segregate from each other such that a gamete receives only one of the two factors. Of course, a homozygous parent produces all gametes that are similar while a heterozygous one produces two kinds of gametes each having one allele with equal proportion.

Incomplete Dominance

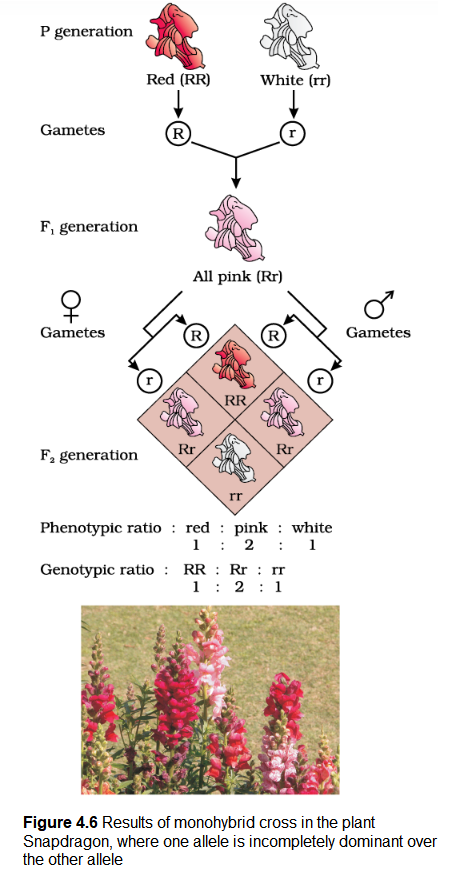
When experiments on peas were repeated using other traits in other plants, it was found that sometimes the \(\mathrm{F}_1\) had a phenotype that did not resemble either of the two parents and was in between the two. The inheritance of flower colour in the dog flower (snapdragon or Antirrhinum sp.) is a good example to understand incomplete dominance. In a cross between true-breeding red-flowered (\(\mathbf{R R}\)) and truebreeding white-flowered plants ( \(\mathbf{r r}\) ), the \(\mathrm{F}_1(\mathbf{R r})\) was pink (Figure 4.6). When the \(\mathrm{F}_1\) was self-pollinated the \(\mathrm{F}_2\) resulted in the following ratio 1 (RR) Red: 2 (\(\mathbf{R r}\)) Pink: 1 (\(\mathbf{r r}\)) White. Here the genotype ratios were exactly as we would expect in any mendelian monohybrid cross, but the phenotype ratios had changed from the \(3: 1\) dominant : recessive ratio. What happened was that \(\mathbf{R}\) was not completely dominant over \(\mathbf{r}\) and this made it possible to distinguish \(\mathbf{R r}\) as pink from \(\mathbf{R R}\) (red) and \(\mathbf{r r}\) (white).

Explanation of the concept of dominance: What exactly is dominance? Why are some alleles dominant and some recessive? To tackle these questions, we must understand what a gene does. Every gene, as you know by now, contains the information to express a particular trait. In a diploid organism, there are two copies of each gene, i.e., as a pair of alleles. Now, these two alleles need not always be identical, as in a heterozygote. One of them may be different due to some changes that it has undergone (about which you will read further on, and in the next chapter) which modifies the information that particular allele contains.

Let’s take an example of a gene that contains the information for producing an enzyme. Now there are two copies of this gene, the two allelic forms. Let us assume (as is more common) that the normal allele produces the normal enzyme that is needed for the transformation of a substrate S. Theoretically, the modified allele could be responsible for production of-

• (i) the normal/less efficient enzyme, or
• (ii) a non-functional enzyme, or
• (iii) no enzyme at all

In the first case, the modified allele is equivalent to the unmodified allele, i.e., it will produce the same phenotype/trait, i.e., result in the transformation of substrate S . Such equivalent allele pairs are very common. But, if the allele produces a non-functional enzyme or no enzyme, the phenotype may be effected. The phenotype/trait will only be dependent on the functioning of the unmodified allele. The unmodified (functioning) allele, which represents the original phenotype is the dominant allele and the modified allele is generally the recessive allele. Hence, in the example above the recessive trait is seen due to non-functional enzyme or because no enzyme is produced.

Co-dominance

Till now we were discussing crosses where the \(\mathrm{F}_1\) resembled either of the two parents (dominance) or was in-between (incomplete dominance). But, in the case of co-dominance the \(\mathrm{F}_1\) generation resembles both parents. A good example is different types of red blood cells that determine ABO blood grouping in human beings. ABO blood groups are controlled by the gene \(\boldsymbol{I}\). The plasma membrane of the red blood cells has sugar polymers that protrude from its surface and the kind of sugar is controlled by the gene. The gene \((\boldsymbol{I})\) has three alleles \(\boldsymbol{I}^{\boldsymbol{A}}, \boldsymbol{I}^{\boldsymbol{B}}\) and \(\boldsymbol{i}\). The alleles \(\boldsymbol{I}^{\boldsymbol{A}}\) and \(\boldsymbol{I}^{\boldsymbol{B}}\) produce a slightly different form of the sugar while allele \(\boldsymbol{i}\) does not produce any sugar. Because humans are diploid organisms, each person possesses any two of the three \(\boldsymbol{I}\) gene alleles. \(\boldsymbol{I}^{\boldsymbol{A}}\) and \(\boldsymbol{I}^{\boldsymbol{B}}\) are completely dominant over \(\boldsymbol{i}\), in other words when \(\boldsymbol{I}^{\boldsymbol{A}}\) and \(\boldsymbol{i}\) are present only \(\boldsymbol{I}^{\boldsymbol{A}}\) expresses (because \(\boldsymbol{i}\) does not produce any sugar), and when \(\boldsymbol{I}^{\boldsymbol{B}}\) and \(\boldsymbol{i}\) are present \(\boldsymbol{I}^{\boldsymbol{B}}\) expresses. But when \(\boldsymbol{I}^{\boldsymbol{A}}\) and \(\boldsymbol{I}^{\mathbf{B}}\) are present together they both express their own types of sugars: this is because of co-dominance. Hence red blood cells have both A and B types of sugars. Since there are three different alleles, there are six different combinations of these three alleles that are possible, and therefore, a total of six different genotypes of the human ABO blood types (Table 4.2). How many phenotypes are possible?

Table 4.2: Table Showing the Genetic Basis of Blood Groups in Human Population
\(
\begin{array}{|l|l|l|l|}
\hline \begin{array}{l}
\text { Allele from } \\
\text { Parent 1 }
\end{array} & \begin{array}{l}
\text { Allele from } \\
\text { Parent 2 }
\end{array} & \begin{array}{l}
\text { Genotype of } \\
\text { offspring }
\end{array} & \begin{array}{l}
\text { Blood } \\
\text { types of } \\
\text { offspring }
\end{array} \\
\hline I^A & I^A & I^A I^A & \mathrm{~A} \\
\hline I^A & I^B & I^A I^B & \mathrm{AB} \\
\hline I^A & i & I^A i & \mathrm{~A} \\
\hline I^B & I^A & I^A I^B & \mathrm{AB} \\
\hline I^B & I^B & I^B I^B & \mathrm{~B} \\
\hline I^B & i & I^B i & \mathrm{~B} \\
\hline i & i & i i & \mathrm{O} \\
\hline
\end{array}
\)

Do you realise that the example of ABO blood grouping also provides a good example of multiple alleles? Here you can see that there are more than two, i.e., three alleles, governing the same character. Since in an individual only two alleles can be present, multiple alleles can be found only when population studies are made.

Occasionally, a single gene product may produce more than one effect. For example, starch synthesis in pea seeds is controlled by one gene. It has two alleles (\(\mathbf{B}\) and \(\mathbf{b}\)). Starch is synthesised effectively by \(\mathbf{B B}\) homozygotes and therefore, large starch grains are produced. In contrast, \(\mathbf{b b}\) homozygotes have lesser efficiency in starch synthesis and produce smaller starch grains. After maturation of the seeds, B B seeds are round and the \(\mathbf{b b}\) seeds are wrinkled. Heterozygotes produce round seeds, and so \(\mathbf{B}\) seems to be the dominant allele. But, the starch grains produced are of intermediate size in \(\mathbf{B b}\) seeds. So if starch grain size is considered as the phenotype, then from this angle, the alleles show incomplete dominance.

Therefore, dominance is not an autonomous feature of a gene or the product that it has information for. It depends as much on the gene product and the production of a particular phenotype from this product as it does on the particular phenotype that we choose to examine, in case more than one phenotype is influenced by the same gene.