Sample Math Problems
Q1: Evaluate \(3 \times 10-(8 \times 6-15)+4 \times 20 \div 4\).
Answer: 17
Step1: The numbers inside the parentheses should be evaluated first, that is \((8 \times 6-15)\). As multiplication has higher precedence over subtraction 8×6 is evaluated and then the result gets subtracted with 15. Therefore we get (48-15) = 33. Therefore after step1 we have \(3 \times 10-33+4 \times 20 \div 4\)
Step2: Next we need to execute multiplication and division from left to right order. Multiplication is executed first (3×10 = 30 and 4×20 = 80) and then division (80 ÷ 4 = 20). Therefore we get \(30-33+80 \div 4\) = \(30-33+20\).
Step3: Finally we execute addition and subtraction, so here’s what we have:
\(30-33+20\) = \(-3+20\) =\(17\)
Q2: Execute \(5 \times 4^{2}+8-(11+4)^{2} \div 3\).
Answer: 13
step1: parentheses \(5 \times 4^{2}+8-(225) \div 3\)
step2: Exponents \(5 \times 16+8-225 \div 3\)
step3: Multiplication/Division \(80+8-75\)
step4: Addition and subtraction 13
Points to Remember: The arithmetic operator’s Precedence rules are given below:
- Parentheses (Execute the operation within the parentheses first as it has the highest precedence)
- Exponents (Exponents have the second-highest precedence after parentheses)
- Multiplication and Division (As both multiplication and division have equal precedence order of execution should be from left to right)
- Addition and Subtraction ((As both Addition and multiplication have equal precedence order of execution should be from left to right)
Note: When you have a bunch of operations having equal precedence, you just operate from left to right.
Q3: Evaluate the multiplication 95 X 95 =?
Answer: 9025
Step 1: Multiply: \(5 \times 5=25\)
Step 2: Multiply 9 with the number that is one greater(10): \(10 \times 9=90\)
Step 3: Join the numbers from step1 & step2: 9025
Trick: Any time you square a two-digit number that ends in 5, the last digits of the answer will be 25, and the digits before that are given by multiplying the first digit of the number by the number that’s one greater.
Q4. \(\text { Evaluate }(109)^{2}=?\)
Answer: 11881
\((109)^{2}\) is + 9 away from 100
Step 1: Add \(+9\) with \(109=118\) is the first 3 numbers
Step 2: Square \(9=81\) is the last 2 numbers
Step 3: 11881
Trick: This is a neat way to square numbers near 100 without having to multiply it out the long way.
Q5. At the entrance of the zoo, there are 12 children in line. Lily is the 7th from the front and John is the second from the back. How many children are there between Lucy and Sam in the line?
Answer: 3
Q6. What fraction is shown by the shaded region in the figure below?
Answer: 2/4
Q7. What is the sum of the first ten whole numbers greater than 0?
Answer: 55
Trick: \(\left(\frac{n(n+1)}{2}=10 \times 11 / 2=55\right)\)
Q8. Sam scored 15 points fewer than Bob, who scored 35 points. Carol scored half as many points as Lilia. How many points did Carol score?
Answer: 10
Solution: Bob scored 35 points and Sam scores 15 less so you start with 35 – 15 = 20. Then you want to divide 20 by 2 because Carol scored half as much as Sam. Your equation is 20 ÷ 2 = 10.
Q9. The seats on a children’s merry-go-round are labeled as 1, 2, 3, . . .. On the merry-go-round. Akash is sitting on seat number 2, exactly opposite Sahil, who is sitting on seat number 6. How many seats are there on the merry-go-round?
Answer: 8
Q10. Sam’s locker number is a three-digit multiple of 5. The tens digit is the sum of the hundreds digit and the ones digit. The sum of all three digits is 16. No digit is repeated. What is Sam’s locker number?
Answer: 385
Solution: Sam’s locker number ends in 0 or 5 (given 3-digit number is multiple of 5). It can’t be 0 because then the hundreds digit and the tens digit would be the same. The only other choice for the one’s digit is 5. Since the tens digit is 5 more than the hundreds digit, her locker number is one of the following: 165, 275, 385, 495. Of these, only 385 have a digit sum of 16. Ashley’s locker number is 385.
Q11. Ten friends have an average of 5 toy soldiers each. John joins them, and now the average is 6 toy soldiers each. How many toy soldiers does John have?
Answer: 16
Solution: The ten friends have a total of 10 × 5 = 50 toy soldiers. When John joins the group, the 11 friends have a total of 11 × 6 = 66 toy soldiers. Then John has 66 – 50 = 16 toy soldiers.
Q12. What is the least multiple of 9 that is greater than 150?
Answer: 153
Solution: Start with a known multiple of 9. Continue adding 9 until the sum first exceeds 150. For example: 99, 108, 117, 126, 135, 144, 153. Therefore 153 is the least multiple of 9 greater than 150.
Q13. What is the next number in the given series?
\(258,130,66,34,18, ? \)Answer: 10
Q14. What is the missing number in the following series: 11, 13, 17, 19, 23, 29, 31, 37, 41,?
(a) 42
(b) 43
(c) 44
(d) 45
Answer: 43
Q15. A train travelling with a speed \(60 \mathrm{~km} / \mathrm{h}\) catches another train travelling in the same direction and then leavers it \(120 \mathrm{~m}\) behind in \(18 \mathrm{~s}\). The speed of the second train is
(a) \(26 \mathrm{~km} / \mathrm{h}\)
(b) \(35 \mathrm{~km} / \mathrm{h}\)
(c) \(36 \mathrm{~km} / \mathrm{h}\)
(d) \(63 \mathrm{~km} / \mathrm{h}\)
Answer: (c)
Solution:
\(\begin{aligned}&\text { Let speed of another train }=x \mathrm{~km} / \mathrm{h}\\&\therefore \quad(60-x)=\frac{120}{18} \times 3.6\\
&\Rightarrow \quad 60-x=24\\
&\therefore \quad x=60-24=36 \mathrm{~km} / \mathrm{h}
\end{aligned}\)
Q16. If a man travels at a speed of \(30 \mathrm{~km} / \mathrm{h}\), he reaches his destination 10 min late and if he travels at a speed of \(42 \mathrm{~km} / \mathrm{h}\), he reaches his destination \(10 \mathrm{~min}\) early. The distance travelled is
(a) \(36 \mathrm{~km}\)
(b) \(35 \mathrm{~km}\)
(c) \(40 \mathrm{~km}\)
(d) \(42 \mathrm{~km}\)
Answer: (b)
Solution: According to the question (late case), speed \(=30 \mathrm{~km} / \mathrm{h}\), time \(=\left(t+\frac{10}{60}\right) \mathrm{h}=\left(t+\frac{1}{6}\right) \mathrm{h}\)
By using, Speed \(=\frac{\text { Distance }}{\text { Time }}\)
\(\operatorname{Distance}(S)=30 \times\left(t+\frac{1}{6}\right)\)
According to the question (early case),
Speed \(=42 \mathrm{~km} / \mathrm{h}\)
Time \(=\left(t-\frac{10}{60}\right) \mathrm{h}=\left(t-\frac{1}{6}\right) \mathrm{h}\) \(\Rightarrow\) Distance \((S)=42 \times\left(t-\frac{1}{6}\right)\)
From the two cases
\(\operatorname{Distance}(S)=30\left(t+\frac{1}{6}\right)=42 \times\left(t-\frac{1}{6}\right)\)
\(\Rightarrow 5\left(t+\frac{1}{6}\right)=7\left(t-\frac{1}{6}\right)\)
\(\Rightarrow \quad 5 t+\frac{5}{6}=7 t-\frac{7}{6}\)
\(\Rightarrow \quad 2 t=\frac{12}{6}\)
\(\therefore \quad t=1 \mathrm{~h}\)
Hence, distance \((S)=30\left(t+\frac{1}{6}\right)\)
\(=30\left(1+\frac{1}{6}\right)=30 \times \frac{7}{6}=35 \mathrm{~km}\)
Q17. The ratio between boys and girls in a school is \(4: 6\), respectively. If the number of boys is increased by 200 the ratio becomes \(5: 6\), respectively. How many girls are there in the school?
(a) 1200
(b) 800
(c) 1000
(d) 900
Answer: (a)
Solution: Let the number of boys and girls be \(4 x\) and \(6 x\), respectively. According to the question, \(\frac{4 x+200}{6 x}=\frac{5}{6}\)
\(
\begin{array}{ll}
\Rightarrow & 5 x=4 x+200 \\
\Rightarrow & x=200
\end{array}
\)
Therefore, number of girls \(=6 x=6 \times 200=1200\)
Q18. A person borrowed a sum of ₹ 20000 for 2 yr on simple interest. He had to repay \(₹ 24800\) including interest after \(2 \mathrm{yr}\). The rate of interest per annum was?
Answer: 12%
Solution:
\(\begin{aligned}&\because \text { Amount }=₹ 24800\\
&\text { Principal }=₹ 20000\\
&\therefore \quad \text { SI }=\text { Amount – Principal }\\
&=24800-20000=₹ 4800\\
&\text { Rate of interest }=\frac{\mathrm{SI} \times 100}{P \times T}=\frac{4800 \times 100}{20000 \times 2}=12 \%
\end{aligned}\)
Q19. A person buys a radio for \(₹ 1030\) and he spent ₹ 50 on its repairs. If he sold it for \(₹ 1200\), What is the profit percent?
(a) \(10 \frac{1}{3}\)
(b) \(11 \frac{1}{9}\)
(c) \(12 \frac{1}{2}\)
(d) None of these
Answer: (b)
Solution:
Total cost \(=1030+50=₹ 1080\); \(S P =₹ 1200\) \(
\begin{aligned} \therefore \text { Profit per cent }=\frac{1200-1080}{1080} \times 100 =\frac{120}{1080} \times 100=11 \frac{1}{9} \% \end{aligned}
\)
Q20. In the given questions, there is a question figure and four answer figures. [(1),(2),(3), and (4). Find out which answer figure can appear when a piece of paper is folded, punched, and opened?

Answer: (1)
Q21. In the given questions, there is a question figure and four answer figures (1), (2), (3), and (4). Find out the correct answer figure when a mirror is held on the XY line.
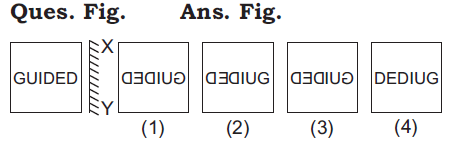
Answer: (1)
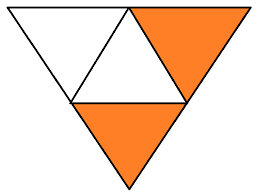
Q22. How many triangles are there in the given image below?

Answer: 13
Q23. Frank is 12 years older than David. Five years ago, the sum of their ages was 28. How old are they now?
Answer: Frank = 25, David = 13
Solution: Five years ago, the sum of their ages was 28
\(
\begin{aligned}
(D+7)+(D-5) &=28 \\
2 D+2 &=28 \\
-2 &=-2 \\
2 D &=26 \\
D &=\frac{26}{2}=13
\end{aligned}
\)
Therefore, Frank’s age is David’s age 13+12 years =25 years old.
Q24. There is a three-digit number. The second digit is four times as big as the third digit, while the first digit is three less than the second digit. What is the number?
Answer: 141
Q25. If 1st October 2012 is a Monday, what day will it be on 21st December 2013?
Answer: Saturday
Solution: 1st October 2012 to 1st October 2013, is 1 ordinary year (365 days). Rest number of days up to 21st December is 81. So total number of days = 365 + 81 = 446 days. 446/7 = 63 with remainder 5. Therefore the weekday on 21st December 2013 will be 5 days after Monday which is a Saturday.