Quiz Level-3

Hint

Let the distance between the stations \(A\) and \(B\) be \(x \mathrm{~km}\).
\(
\begin{aligned}
& \text { Time taken }=45 \mathrm{~min}=\frac{3}{4} \mathrm{hr} \\
& \therefore \text { Original speed }=\left(x \times \frac{4}{3}\right) \mathrm{km} / \mathrm{hr}=\frac{4 x}{3} \mathrm{~km} / \mathrm{hr} \\
& \text { New speed }=\left(\frac{4 x}{3}-5\right) \mathrm{km} / \mathrm{hr}=\left(\frac{4 x-15}{3}\right) \mathrm{km} / \mathrm{hr} . \\
& \therefore \quad \frac{x}{\left(\frac{4 x-15}{3}\right)}=\frac{48}{60} \Rightarrow \frac{3 x}{4 x-15}=\frac{4}{5} \\
& \Rightarrow 15 x=16 x-60 \Rightarrow x=60 .
\end{aligned}
\)

Hint

Let the speed of the train be \(x \mathrm{~km} / \mathrm{hr}\).
Then, \(\frac{600}{x}-\frac{600}{x+5}=4 \Leftrightarrow 4 x(x+5)=3000\)
\(
\begin{aligned}
& \Leftrightarrow 4 x^2+20 x-3000=0 \Leftrightarrow x^2+5 x-750=0 \\
& \Leftrightarrow(x+30)(x-25)=0 \Leftrightarrow x=25 . \\
& \therefore \text { Speed of the train }=25 \mathrm{~km} / \mathrm{hr} .
\end{aligned}
\)

Hint

Let the usual speed be \(x \mathrm{~km} / \mathrm{hr}\).
Then, \(\frac{75}{x}-\frac{75}{x+10}=\frac{15}{60} \Leftrightarrow x(x+10)=3000\)
\(
\begin{aligned}
& \Leftrightarrow x^2+10 x-3000=0 \Leftrightarrow(x+60)(x-50)=0 \Leftrightarrow x=50 . \\
& \therefore \text { Required time }=\left(\frac{300}{60}\right) \text { hrs }=5 \text { hrs. }
\end{aligned}
\)

Hint

Let the distance be \(x \mathrm{~km}\)
Then, \(\frac{x}{7 \frac{1}{2}}-\frac{x}{8}=4 \Leftrightarrow \frac{2 x}{15}-\frac{x}{8}=4 \Leftrightarrow x=480 \mathrm{~km}\).

Hint

Let the distance be \(x \mathrm{~km}\).
Then, \(\frac{x}{3}-\frac{x}{3.75}=\frac{1}{2} \Leftrightarrow 2.5 x-2 x=3.75\)
\(
\Leftrightarrow \quad x=\frac{3.75}{0.50}=\frac{15}{2}=7.5 \mathrm{~km} \text {. }
\)

Hint

Let the actual distance travelled be \(x \mathrm{~km}\) Then, \(\frac{x}{10}=\frac{x+20}{14} \Leftrightarrow 14 x=10 x+200\) \(\Leftrightarrow \quad 4 x=200 \Leftrightarrow x=50 \mathrm{~km}\).

Hint

The ratio of speeds \(=3: 4\). The ratio of times taken \(=4: 3\).
Suppose \(A\) takes \(4 x\) hrs and \(B\) takes \(3 x\) hrs to reach the destination. Then,
\(4 x-3 x=\frac{30}{60}=\frac{1}{2}\) or \(x=\frac{1}{2}\)
\(\therefore\) Time taken by \(A=4 x\) hrs \(=\left(4 \times \frac{1}{2}\right)\) hrs \(=2\) hrs

Hint

Let Abhay’s speed be \(x \mathrm{~km} / \mathrm{hr}\).
Then, \(\frac{30}{x}-\frac{30}{2 x}=3 \Leftrightarrow 6 x=30 \Leftrightarrow x=5 \mathrm{~km} / \mathrm{hr}\).

Hint

Ratio of speeds \(=4: 3: 5\).
\(
\therefore \text { Ratio of times taken }=\frac{1}{4}: \frac{1}{3}: \frac{1}{5}=15: 20: 12
\)

Hint

Let the speed of the fast train be \(x \mathrm{~km} / \mathrm{hr}\). Then, speed of the slow train \(=(x-16) \mathrm{km} / \mathrm{hr}\).
\(
\begin{aligned}
& \therefore \frac{192}{x-16}-\frac{192}{x}=2 \Rightarrow \frac{1}{x-16}-\frac{1}{x}=\frac{1}{96} \\
& \Leftrightarrow x^2-16 x-1536=0 \Leftrightarrow(x-48)(x+32)=0 \Leftrightarrow x=48 .
\end{aligned}
\)

Hint

Let the original planned duration of the flight be \(x\) hours.
Then, \(\frac{6000}{x}-\frac{6000}{\left(x+\frac{1}{2}\right)}=400 \Leftrightarrow \frac{6000}{x}-\frac{12000}{(2 x+1)}=400\)
\(
\begin{aligned}
& \Leftrightarrow \quad \frac{15}{x}-\frac{30}{(2 x+1)}=1 \Leftrightarrow 2 x^2+x-15=0 \\
& \Leftrightarrow \quad(x+3)(2 x-5)=0 \Leftrightarrow x=\frac{5}{2}=2 \frac{1}{2} .
\end{aligned}
\)

Hint

Let the distance covered at \(440 \mathrm{kmph}\) be \(x \mathrm{~km}\) Then, distance covered at \(660 \mathrm{kmph}=(x-770) \mathrm{km}\) Total distance covered \(=(x+x-770) \mathrm{km}\)
\(
\begin{aligned}
& =(2 x-770) \mathrm{km} . \\
& \therefore \quad \frac{2 x-770}{500}=\frac{x}{440}+\frac{x-770}{660} \Leftrightarrow \frac{2 x-770}{25}=\frac{x}{22}+\frac{(x-770)}{33} \\
& \Leftrightarrow \quad 66(2 x-770)=25(5 x-1540) \\
& \Leftrightarrow \quad 7 x=12320 \Leftrightarrow x=1760 .
\end{aligned}
\)
Hence, total distance covered \(=(2 x-770)\)
\(
=(2 \times 1760-770) \mathrm{km}=2750 \mathrm{~km}
\)

Hint

Let A’s speed \(=x \mathrm{~km} / \mathrm{hr}\).
Then, B’s speed \(=(x+4) \mathrm{km} / \mathrm{hr}\).
Clearly, time taken by B to cover \((60+12)\) i.e., \(72 \mathrm{~km}\)
= Time taken by \(A\) to cover \((60-12)\) i.e., \(48 \mathrm{~km}\)
\(\therefore \frac{72}{x+4}=\frac{48}{x} \Rightarrow 72 x=48 x+192 \Rightarrow 24 x=192 \Rightarrow x=8\).
Hence, A’s speed \(=8 \mathrm{~km} / \mathrm{hr}\).

Hint

Let the cyclist’s speed without wind be \(x \mathrm{~km} / \mathrm{hr}\) and the speed of the wind be \(y \mathrm{~km} / \mathrm{hr}\).
Then, \(\quad \frac{1}{x+y}=\frac{3}{60} \Rightarrow x+y=20 \dots(i)\)
And, \(\quad \frac{1}{x-y}=\frac{4}{60} \Rightarrow x-y=15 \dots(ii)\)
Adding (i) and (ii), we get : \(2 x=35\) or \(x=17.5\). Putting \(x=17.5\) in (i), we get: \(y=2.5\).
Time taken to drive \(17.5 \mathrm{~km}\) without wind \(=1 \mathrm{hr}\). Time taken to drive \(1 \mathrm{~km}\) without wind \(=\left(\frac{1}{17.5}\right) \mathrm{hr}=\left(\frac{1}{17.5} \times 60\right) \min =3 \frac{3}{7} \min\).

Hint

Let the speeds of the train and the car be \(x \mathrm{~km} / \mathrm{hr}\) and \(y \mathrm{~km} / \mathrm{hr}\) respectively.
Then, \(\frac{160}{x}+\frac{600}{y}=8 \Rightarrow \frac{20}{x}+\frac{75}{y}=1 \dots(i)\)
And, \(\quad \frac{240}{x}+\frac{520}{y}=8 \frac{1}{5} \Rightarrow \frac{240}{x}+\frac{520}{y}=\frac{41}{5} \dots(ii)\)
Multiplying (i) by 12 and subtracting (ii) from it, we get : \(\frac{380}{y}=12-\frac{41}{5}=\frac{19}{5} \Rightarrow y=\left(380 \times \frac{5}{19}\right)=100\).
Putting \(y=100\) in (i), we get: \(\frac{20}{x}+\frac{3}{4}=1 \Rightarrow \frac{20}{x}=\frac{1}{4} \Rightarrow x=80\).
Hence, speed of car \(=100 \mathrm{~km} / \mathrm{hr}\), speed of train \(=80 \mathrm{~km} / \mathrm{hr}\)

Hint

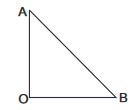
Suppose the two trawlers start from a point \(O\) and move in the directions \(O A\) and \(O B\) respectively.
Let the speeds of the two sea trawlers be \(x \mathrm{~km} / \mathrm{hr}\) and y \(\mathrm{km} / \mathrm{hr}\). respectively.
\(
\text { Then, } \quad\left(x \times \frac{1}{2}\right)^2+\left(y \times \frac{1}{2}\right)^2=(17)^2
\)
\(
\Rightarrow \frac{x^2}{4}+\frac{y^2}{4}=289 \Rightarrow x^2+y^2=1156 \dots(i)
\)
And, \(\left(x \times \frac{3}{4}\right)-\left(y \times \frac{3}{4}\right)=10.5 \Rightarrow x-y=10.5 \times \frac{4}{3}=14 \dots(ii)\)
Now, \((x+y)^2+(x-y)^2=2\left(x^2+y^2\right)\)
\(
\Rightarrow(x+y)^2=2 \times 1156-(14)^2=2312-196=2116
\)
\(
\Rightarrow x+y=\sqrt{2116}=46 \dots(iii)
\)
Adding (ii) and (iii), we get : \(2 x=60\) or \(x=30\).
Putting \(x=30\) in (ii), we get : \(y=16\).
Hence, the speeds of the two sea-trawlers are \(30 \mathrm{~km} / \mathrm{hr}\) and \(16 \mathrm{~km} / \mathrm{hr}\).

Hint

Let \(C^{\prime}\) s speed \(=x \mathrm{~km} / \mathrm{hr}\). Then, \(B^{\prime}\) s speed \(=3 x \mathrm{~km} / \mathrm{hr}\) and \(A^{\prime}\) s speed \(=6 x \mathrm{~km} / \mathrm{hr}\).
\(\therefore\) Ratio of speeds of \(A, B, C=6 x: 3 x: x=6: 3: 1\).
Ratio of times taken \(=\frac{1}{6}: \frac{1}{3}: 1=1: 2: 6\).
If \(C\) takes \(6 \mathrm{~min}\), then \(A\) takes \(1 \mathrm{~min}\).
If \(C\) takes \(72 \mathrm{~min}\), then \(A\) takes \(\left(\frac{1}{6} \times 72\right) \min =12 \mathrm{~min}\).

Hint

Quantity of water let in by the leak in 1 min
\(
=\left(\frac{3 \frac{3}{4}}{12}\right) \text { tonnes }=\left(\frac{15}{4} \times \frac{1}{12}\right) \text { tonnes }=\frac{15}{48} \text { tonnes. }
\)
Quantity of water thrown out by the pumps in 1 min \(=\left(\frac{12}{60}\right)\) tonnes \(=\frac{1}{5}\) tonnes.
Net quantity of water filled in the ship in 1 min
\(
=\left(\frac{15}{48}-\frac{1}{5}\right) \text { tonnes }=\frac{27}{240} \text { tonnes. }
\)
\(\frac{27}{240}\) tonnes water is filled in 1 min.
60 tonnes water is filled in \(\left(\frac{240}{27} \times 60\right) \mathrm{min}\)
\(
=\frac{1600}{3} \min =\frac{80}{9} \mathrm{hrs}
\)
\(
\begin{aligned}
& \text { Hence, required speed }=\frac{40}{(80 / 9)} \mathrm{km} / \mathrm{hr} \\
&=\left(40 \times \frac{9}{80}\right) \mathrm{km} / \mathrm{hr}=\frac{9}{2} \mathrm{~km} / \mathrm{hr}=4 \frac{1}{2} \mathrm{~km} / \mathrm{hr} .
\end{aligned}
\)

Hint

Quantity of petrol consumed in 1 hour
\(
=\left(\frac{40}{10}+\frac{1}{2}\right) \text { litres }=4 \frac{1}{2} \text { litres. }
\)
\(
\begin{aligned}
\text { Time for which the fuel lasted } & =\left[\frac{18}{\left(4 \frac{1}{2}\right)}\right] \mathrm{hrs} \\
& =\left(18 \times \frac{2}{9}\right) \mathrm{hrs}=4 \mathrm{hrs} .
\end{aligned}
\)
\(\therefore\) Required distance \(=(40 \times 4) \mathrm{km}=160 \mathrm{~km}\)

Hint

To be \(0.5 \mathrm{~km}\) apart, they take 1 hour.
To be \(8.5 \mathrm{~km}\) apart, they take \(\left(\frac{1}{0.5} \times 8.5\right) \mathrm{hrs}=17 \mathrm{hrs}\).

Hint

Since \(A\) and \(B\) move in the same direction along the circle, so they will first meet each other when there is a difference of one round between the two.
Relative speed of \(A[latex] and [latex]B=(6-1)=5\) rounds per hour.
Time taken to complete one round at this speed
\(
=\frac{1}{5} \mathrm{hr}=12 \mathrm{~min} .
\)

Hint

Perimeter of the field \(=2(400+300) \mathrm{m}=1400 \mathrm{~m}=1.4 \mathrm{~km}\) Since A and B move in the same direction, so they will first meet each other when there is a difference of one round i.e., \(1.4 \mathrm{~km}\) between the two.
Relative speed of \(A\) and \(B=(3-2.5) \mathrm{km} / \mathrm{hr}=0.5 \mathrm{~km} / \mathrm{hr}\).
Time take to cover \(1.4 \mathrm{~km}\) at this speed \(=\left(\frac{1.4}{0.5}\right) \mathrm{hr}\)
\(
=2 \frac{4}{5} \mathrm{hr}=2 \mathrm{hr} 48 \mathrm{~min} .
\)
So they shall first cross each other at \(9: 48\) a.m. and again, \(2 \mathrm{hr} 48 \mathrm{~min}\) after \(9: 48 \mathrm{am}\) i.e., \(12: 36 \mathrm{pm}\).
Thus, till \(12: 30 \mathrm{pm}\) they will cross each other once.

Hint

Distance covered by first person in time \(t\)
\(
=\left(\frac{2}{8}\right) \text { rounds }=\frac{1}{4} \text { round. }
\)
Distance covered by second person in time \(t=\frac{3}{8}\) round. Speed of first person \(=\frac{1}{4 t}\)
Speed of second person \(=\frac{3}{8 t}\).
Since the two persons start from \(A\) and \(B\) respectively, so they shall meet each other when there is a difference of \(\frac{7}{8}\) round between the two.
Relative speed of \(A\) and \(B=\left(\frac{3}{8 t}-\frac{1}{4 t}\right)=\frac{1}{8 t}\).
Time taken to cover \(\frac{7}{8}\) round at this speed \(=\left(\frac{7}{8} \times 8 t\right)=7 t\).

Hint

Suppose after \(x \mathrm{~km}\) from the start \(B\) catches up with \(A\). Then, the difference in the time taken by \(A\) to cover \(x \mathrm{~km}\) and that taken by \(B\) to cover \(x \mathrm{~km}\) is 4 hours.
\(
\therefore \frac{x}{4}-\frac{x}{10}=4 \text { or } x=26.7 \mathrm{~km}
\)

Hint

Suppose the two trains meet \(x \mathrm{~km}\) from Delhi.
Then, \(\frac{x}{60}-\frac{x}{80}=2 \Leftrightarrow x=480\).

Hint

Relative speed of the thief and policeman
\(
=(11-10) \mathrm{km} / \mathrm{hr}=1 \mathrm{~km} / \mathrm{hr} \text {. }
\)
Distance covered in \(\begin{aligned} 6 \text { minutes } & =\left(\frac{1}{60} \times 6\right) \mathrm{km} \\ & =\frac{1}{10} \mathrm{~km}=100 \mathrm{~m} .\end{aligned}\)
\(\therefore\) Distance between the thief and policeman
\(
=(200-100) \mathrm{m}=100 \mathrm{~m}
\)

Hint

\(\begin{aligned} \text { Relative speed of the car wr.t. bus } & =(50-30) \mathrm{km} / \mathrm{hr} \\ & =20 \mathrm{~km} / \mathrm{hr} .\end{aligned}\)
Required distance \(=\) Distance covered in 15 min at relative
\(
\text { speed }=\left(20 \times \frac{1}{4}\right) \mathrm{km}=5 \mathrm{~km}
\)

Hint

Relative speed \(=(10-8) \mathrm{km} / \mathrm{hr}=2 \mathrm{~km} / \mathrm{hr}\).
Required time \(=\) Time taken to cover \(100 \mathrm{~m}\) at relative speed
\(
=\left(\frac{100}{2000}\right) \mathrm{hr}=\frac{1}{20} \mathrm{hr}=\left(\frac{1}{20} \times 60\right) \mathrm{min}=3 \mathrm{~min} .
\)

Hint

Suppose the thief is overtaken \(x\) hrs after \(2.30 \mathrm{p} . \mathrm{m}\). Then, Distance covered by the thief in \(x\) hrs = Distance covered by the owner in \(\left(x-\frac{1}{2}\right)\) hrs.
\(\therefore 60 x=75\left(x-\frac{1}{2}\right) \Leftrightarrow 15 x=\frac{75}{2} \Leftrightarrow x=\frac{5}{2}\) hrs.
So, the thief is overtaken at \(5 \mathrm{p}. \mathrm{m.}\)

Hint

Distance covered by Aryan in \(5 \mathrm{~min}=(40 \times 5) \mathrm{m}=200 \mathrm{~m}\) Relative speed of Rahul wr.t. Aryan \(=(50-40) \mathrm{m} / \mathrm{min}\) \(=10 \mathrm{~m} / \mathrm{min}\).
Time taken to cover \(200 \mathrm{~m}\) at relative speed
\(
=\left(\frac{200}{10}\right) \min =20 \mathrm{~min} .
\)
Distance covered by the dog in \(20 \mathrm{~min}=(60 \times 20) \mathrm{m}\) \(=1200 \mathrm{~m}\)

Hint

Let the thief be caught \(x\) metres from the place where the policeman started running.
Let the speed of the policeman and the thief be \(5 y \mathrm{~m} / \mathrm{s}\) and \(4 y \mathrm{~m} / \mathrm{s}\) respectively.
Then, time taken by the policeman to cover \(x\) metres \(=\) time taken by the thief to cover \((x-100) \mathrm{m}\)
\(
\Rightarrow \frac{x}{5 y}=\frac{(x-100)}{4 y} \Rightarrow 4 x=5(x-100) \Rightarrow x=500 \text {. }
\)
So, the thief ran \((500-100)\) i.e. \(400 \mathrm{~m}\) before being caught.

Hint

Distance covered by \(A\) in 4 hrs \(=(4 \times 4) \mathrm{km}=16 \mathrm{~km}\) Relative speed of \(B\) w.r.t. \(A=(10-4) \mathrm{km} / \mathrm{hr}=6 \mathrm{~km} / \mathrm{hr}\). Time taken to cover \(16 \mathrm{~km}\) at relative speed
\(
=\left(\frac{16}{6}\right) \mathrm{hrs}=\frac{8}{3} \mathrm{hrs} .
\)
Distance covered by B in \(\frac{8}{3}\) hrs \(=\left(10 \times \frac{8}{3}\right) \mathrm{km}=\left(\frac{80}{3}\right) \mathrm{km}\) \(=26.7 \mathrm{~km}\).

Hint

Let the speed of the goods train be \(x \mathrm{~km} / \mathrm{hr}\). Then, relative speed \(=(80-x) \mathrm{km} / \mathrm{hr}\).
Distance covered by goods train in \(6 \mathrm{hrs}\) at \(x \mathrm{~km} / \mathrm{hr}\) \(=\) Distance covered by passenger train in \(4 \mathrm{hrs}\) at \((80-x)\) \(\mathrm{km} / \mathrm{hr}\)
\(
\Rightarrow 6 x=4(80-x) \Rightarrow 10 x=320 \Rightarrow x=32 \mathrm{~km} / \mathrm{hr}
\)

Hint

Error = Time taken to cover \(10 \mathrm{~m}\) at \(300 \mathrm{~m} / \mathrm{sec}\)
\(
=\left(\frac{10}{300}\right) \mathrm{sec}=\frac{1}{30} \sec \approx 0.03 \mathrm{sec}
\)

Hint

Clearly, the two persons would be maximum distance apart when they stand in opposite directions to the point at which sound is produced, and minimum distance apart when they stand in the same direction.
\(\therefore\) Maximum distance between the two persons
\(=\) Distance covered by sound in \((6+5)\) seconds, i.e. \(11 \mathrm{sec}\) \(=(300 \times 11) \mathrm{m}=3300 \mathrm{~m}=3.3 \mathrm{~km}\)
And, minimum distance between the two persons
\(=\) Distance covered by sound in \((6-5)\) sec., i.e. \(1 \mathrm{sec}\)
\(=300 \mathrm{~m}=0.3 \mathrm{~km}\)

Hint

Let the speed of the man be \(x \mathrm{~m} / \mathrm{sec}\).
Then, Distance travelled by the man in \(5 \mathrm{~min} 52 \mathrm{sec}\)
\(=\) Distance travelled by sound in \(8 \mathrm{sec}\)
\(
\begin{aligned}
\Leftrightarrow x & \times 352=330 \times 8 \\
\Leftrightarrow x & =\left(\frac{330 \times 8}{352}\right) \mathrm{m} / \mathrm{sec} \\
& =\left(\frac{330 \times 8}{352} \times \frac{18}{5}\right) \mathrm{km} / \mathrm{hr}=27 \mathrm{~km} / \mathrm{hr}
\end{aligned}
\)

Hint

To be \((18+20) \mathrm{km}\) apart, they take 1 hour.
To be \(47.5 \mathrm{~km}\) apart, they take \(\left(\frac{1}{38} \times 47.5\right) \mathrm{hrs}=1 \frac{1}{4} \mathrm{hrs}\).

Hint

\(
\text { Suppose they meet after } x \text { hours. Then, }
\)
Distance travelled by \(P\) in \(x\) hrs + Distance travelled by \(Q\) in \(x\) hrs \(=10 \mathrm{~km}\)
\(
\Leftrightarrow 3 x+2 x=10 \Rightarrow 5 x=10 \Rightarrow x=2 \text { hrs. }
\)
Distance travelled by \(P\) in 2 hrs \(=(3 \times 2) \mathrm{km}=6 \mathrm{~km}\).

Hint

Suppose they meet \(x\) hrs after \(9 \mathrm{am}\). Then,
Distance travelled by car \(X\) in \((x-1)\) hrs + Distance travelled by car \(Y\) in \(x\) hrs \(=700 \mathrm{~km}\)
\(
\begin{aligned}
& \Rightarrow 60(x-1)+60 x=700 \Rightarrow 120 x=760 \\
& \Rightarrow x=\frac{760}{120}=\frac{19}{3} \mathrm{hrs}=6 \mathrm{hr} 20 \mathrm{~min} .
\end{aligned}
\)
So, they cross each other \(6 \mathrm{hr} 20 \mathrm{~min}\) after 9 a.m i.e., at \(3: 20 \mathrm{pm}\)

Hint

Suppose the trains meet after \(x\) hrs. Then,
Distance covered by 1st train in \(x\) hrs
+ Distance covered by 2 nd train in \(\left(x-\frac{3}{4}\right) \mathrm{hrs}=232 \mathrm{~km}\)
\(\Rightarrow 48 x+50\left(x-\frac{3}{4}\right)=232\)
\(\Rightarrow 98 x=232+\frac{75}{2}=\frac{539}{2} \Rightarrow x=\frac{539}{196} \mathrm{hrs}\).
Required distance
\(=\) Distance travelled by 1st train in \(\left(\frac{539}{196}\right)\) hrs.
\(=\left(48 \times \frac{539}{196}\right) \mathrm{km}=132 \mathrm{~km}\)

Hint

Clearly, the two will meet when they are \(726 \mathrm{~m}\) apart. To be \((4.5+3.75)=8.25 \mathrm{~km}\) apart, they take 1 hour.
To be \(726 \mathrm{~m}\) apart, they take \(\left(\frac{100}{825} \times \frac{726}{1000}\right)\) hrs
\(
=\left(\frac{242}{2750} \times 60\right) \mathrm{min}=5.28 \mathrm{~min} .
\)

Hint

Relative speed \(=(2+3)=5\) rounds per hour.
So, they cross each other 5 times in an hour and 2 times in half an hour.
Hence, they cross each other 7 times before \(9.30 \mathrm{am}\).

Hint

Time taken by the two cyclists to cover one round of the track is \(\frac{300}{7}\) sec and \(\frac{300}{8}\) sec respectively.
\(
\therefore \text { Required time }=\text { L.CM. of } \frac{300}{7} \text { and } \frac{300}{8}=300 \mathrm{sec} .
\)

Hint

Relative speed \(=(200+200) \mathrm{km} / \mathrm{hr}=400 \mathrm{~km} / \mathrm{hr}\)
Distance covered in \(1 \mathrm{hr} 30 \mathrm{~min}\)
\(
\begin{gathered}
=\left(400 \times \frac{1}{2}+200 \times \frac{1}{2}+100 \times \frac{1}{2}\right) \mathrm{km} \\
=(200+100+50) \mathrm{km}=350 \mathrm{~km}
\end{gathered}
\)
[ \(\because\) speed reduces by half every half an hour]
Hence, distance between the trains
\(
=(425-350) \mathrm{km}=75 \mathrm{~km}
\)

Hint

Time taken by \(A\) to cover \(120 \mathrm{~km}=\left(\frac{120}{6}\right) \mathrm{hrs}=20 \mathrm{hrs}\). So, \(A\) will reach his destination \(20 \mathrm{hrs}\) after 6 a.m, i.e., at 2 a.m the next day.

Hint

\(
\begin{aligned}
\text { Required difference } & =\left(\frac{120}{4}-\frac{120}{6}\right) \mathrm{hrs} \\
& =(30-20) \mathrm{hrs}=10 \mathrm{hrs} .
\end{aligned}
\)

Hint

\(
A^{\prime} \text { s speed }=6 \mathrm{~km} / \mathrm{hr} \text {. }
\)

Hint

Let the speed of train \(Z\) be \(z \mathrm{mph}\).
Distance travelled by train \(X\) in \(1 \mathrm{hr}=x\) miles.
Relative speed of train \(\mathrm{Z}\) w.r.t. train \(\mathrm{X}=(z-x) \mathrm{mph}\).
To catch train \(X\) at 5 : 30 AM., train \(Z\) will have to cover \(x\) miles at relative speed in \(3 \mathrm{hr} 30 \mathrm{~min}\), i.e. \(\frac{7}{2}\) hrs.
\(
\therefore \quad(z-x) \times \frac{7}{2}=x \Rightarrow \frac{7}{2} z=\frac{9}{2} x \Rightarrow z=\left(\frac{9}{2} \times \frac{2}{7}\right) x=\frac{9}{7} x .
\)

Hint

Let the speed of the second lady be \(x \mathrm{~km} / \mathrm{hr}\).
Then, speed of first lady \(=(x+2) \mathrm{km} / \mathrm{hr}\).
\(
\begin{aligned}
& \therefore \quad \frac{24}{x}-\frac{24}{(x+2)}=1 \Rightarrow x(x+2)=48 \\
& \Rightarrow x^2+2 x-48=0 \Rightarrow x^2+8 x-6 x-48=0 \\
& \Rightarrow \quad x(x+8)-6(x+8)=0 \Rightarrow(x+8)(x-6)=0 \\
& \Rightarrow \quad x=6 \text {. } \\
&
\end{aligned}
\)
Hence, speed of first lady \(=8 \mathrm{~km} / \mathrm{hr}\); speed of second lady \(=6 \mathrm{~km} / \mathrm{hr}\).

Hint

Let the speed of the man be \(x \mathrm{~km} / \mathrm{hr}\). Then, Distance covered by the bus in 2 min \(=\) Distance covered by the man in \(8 \mathrm{~min}\)
\(
\Rightarrow 20 \times \frac{2}{60}=x \times \frac{8}{60} \Rightarrow x=\left(\frac{2}{3} \times \frac{60}{8}\right)=5 \mathrm{~km} / \mathrm{hr} .
\)

Hint

Suppose the two men meet in \(n\) hours.
Then Sum of distances covered by two men in \(n\) hours = 76
\(
\begin{aligned}
& \Rightarrow 4 \frac{1}{2} n+\left(3 \frac{1}{4}+3 \frac{3}{4}+\ldots \ldots \ldots . . \text { upto } n \text { terms }\right)=76 \\
& \Rightarrow \frac{9}{2} n+\frac{n}{2}\left[2 \times \frac{13}{4}+(n-1) \times \frac{1}{2}\right]=76
\end{aligned}
\)
[Sum to \(n\) terms of an AP.]
\(
\begin{aligned}
& \Rightarrow \frac{9 n}{2}+\frac{n}{2}\left[\frac{13}{2}+\frac{1}{2} n-\frac{1}{2}\right]=76 \\
& \Rightarrow \frac{9 n}{2}+\frac{n}{2}\left(6+\frac{n}{2}\right)=76
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \frac{9 n}{2}+\frac{6 n}{2}+\frac{n^2}{4}=76 \Rightarrow \frac{15 n}{2}+\frac{n^2}{4}=76 \\
& \Rightarrow 30 n+n^2=304 \Rightarrow n^2+30 n-304=0 \\
& \Rightarrow(n+38)(n-8)=0 \Rightarrow n=8 .
\end{aligned}
\)
Distance travelled by first man in 8 hours
\(
=\left(\frac{9}{2} \times 8\right) \mathrm{km}=36 \mathrm{~km} \text {. }
\)
Distance travelled by second man \(=(76-36) \mathrm{km}=40 \mathrm{~km}\) Thus, the meeting point is \(36 \mathrm{~km}\) from \(R\) and \(40 \mathrm{~km}\) from \(S\), i.e. \((40-36)=4 \mathrm{~km}\) nearer to \(R\) than \(S\).
Hence, \(x=4\).

Hint

Let their speeds be \(x \mathrm{~m} / \mathrm{sec}\) and \(y \mathrm{~m} / \mathrm{sec}\) respectively.
Then, \(\quad \frac{1200}{x+y}=15 \Rightarrow x+y=80 \dots(i)\)
And, \(\quad \frac{1200}{x-y}=60 \Rightarrow x-y=20 \dots(ii)\)
Adding (i) and (ii), we get : \(2 x=100\) or \(x=50\).
Putting \(x=50\) in (i), we get : \(y=30\).
Hence, speed of slower plane \(=30 \mathrm{~m} / \mathrm{s}=0.03 \mathrm{~km} / \mathrm{s}\).

Hint

Let the speed of the faster and slower cyclists be \(x \mathrm{~km}\) / \(\mathrm{hr}\) and \(y \mathrm{~km} / \mathrm{hr}\) respectively,
Then, \(\frac{k}{x-y}=r \Rightarrow(x-y) r=k \dots(i)\)
And, \(\quad \frac{k}{x+y}=t \Rightarrow(x+y) t=k \dots(ii)\)
From (i) and (ii), we have :
\(
\begin{aligned}
& (x-y) r=(x+y) t \Rightarrow x r-y r=x t+y t \Rightarrow x r-x t=y r+y t \\
& \Rightarrow x(r-t)=y(r+t) \Rightarrow \frac{x}{y}=\frac{r+t}{r-t}
\end{aligned}
\)

Hint

Let the distance between points \(X\) and \(Y\) be \(d \mathrm{~km}\) Suppose the bus takes \(x\) hours to travel from \(X\) to \(Y\).
Then, speed of bus \(=\frac{d}{x}\) and speed of car \(=\frac{d}{x-2}\).
Now, sum of distances travelled by car and bus in \(1 \frac{1}{3} \mathrm{hrs}\) i.e. \(\frac{4}{3} \mathrm{hrs}=d\)
\(
\begin{aligned}
& \Rightarrow\left(\frac{d}{x} \times \frac{4}{3}\right)+\left(\frac{d}{x-2} \times \frac{4}{3}\right)=d \\
& \Rightarrow \frac{4}{3 x}+\frac{4}{3(x-2)}=1 \\
& \Rightarrow 4(x-2)+4 x=3 x(x-2) \\
& \Rightarrow 3 x^2-14 x+8=0 \\
& \Rightarrow 3 x^2-12 x-2 x+8=0 \Rightarrow 3 x(x-4)-2(x-4)=0 \\
& \Rightarrow(x-4)(3 x-2)=0 \Rightarrow x=4\left[\because x \neq \frac{2}{3}\right] \\
& \therefore \text { Required time }=4 \text { hours. }
\end{aligned}
\)

Hint

In the same time, they cover \(110 \mathrm{~km}\) and \(90 \mathrm{~km}\) respectively.
\(
\therefore \text { Ratio of their speeds }=110: 90=11: 9 .
\)

Hint

At the time of meeting, let the distance travelled by the first train be \(x \mathrm{~km}\).
Then, distance covered by the second train \(=(x+120) \mathrm{km}\)
\(
\begin{aligned}
\therefore \quad \frac{x}{50}=\frac{x+120}{60} & \Leftrightarrow 60 x=50 x+6000 \\
& \Leftrightarrow 10 x=6000 \Leftrightarrow x=600 .
\end{aligned}
\)
So, distance between \(A\) and \(B=(x+x+120) \mathrm{km}=1320 \mathrm{~km}\)

Hint

Distance covered by train A from \(11 \mathrm{a.m}\) to \(2 \mathrm{pm}\) i.e., in \(3 \mathrm{hrs}=(60 \times 3)=180 \mathrm{~km}\)
Relative speed \(=(72-60) \mathrm{km} / \mathrm{hr}=12 \mathrm{~km} / \mathrm{hr}\).
Time taken to cover \(180 \mathrm{~km}\) at relative speed
\(
=\left(\frac{180}{12}\right) \mathrm{hrs}=15 \mathrm{hrs} \text {. }
\)
So, the two trains will meet \(15 \mathrm{hrs}\) after \(2 \mathrm{pm}\). i.e., at 5 a.m. on the next day.

Hint

Let the distance between stations \(X\) and \(Y\) be \(x \mathrm{~km}\) and let the trains meet \(y\) hours after \(7 \mathrm{a} . \mathrm{m}\).
Clearly, M covers \(x \mathrm{~km}\) in \(4 \mathrm{hrs}\) and \(N\) covers \(x \mathrm{~km}\) in (7/2) hrs.
\(\therefore \quad\) Speed of \(M=\frac{x}{4} \mathrm{kmph}\), Speed of \(N=\frac{2 x}{7} \mathrm{kmph}\).
Distance covered by \(M\) in \((y+2)\) hrs + Distance covered by \(N\) in \(y\) hrs \(=x\).
\(
\begin{aligned}
& \therefore \quad \frac{x}{4}(y+2)+\frac{2 x}{7} \times y=x \Leftrightarrow \frac{(y+2)}{4}+\frac{2 y}{7}=1 \\
& \Leftrightarrow y=\frac{14}{15} \mathrm{hrs}=\left(\frac{14}{15} \times 60\right) \mathrm{min} .=56 \mathrm{~min} .
\end{aligned}
\)
Hence, the trains meet at \(7.56 \mathrm{am}\)

Hint

Suppose the three trains meet \(x\) hours after \(9 \mathrm{pm}\).
Let the speed of train \(C\) be \(y \mathrm{~km} / \mathrm{hr}\).
Distance travelled by Train \(A\) in \((x+3)\) hrs = Distance travelled by Train \(B\) in \(x\) hrs
\(
\Rightarrow 60(x+3)=90 x \Rightarrow 30 x=180 \Rightarrow x=6 \text {. }
\)
Also, dist. travelled by Train \(B\) in \(x\) hrs + Dist. travelled by train \(C\) in \(x\) hrs \(=1260 \mathrm{~km}\)
\(
\Rightarrow 90 x+y x=1260 \Rightarrow 540+6 y=1260 \Rightarrow 6 y=720 \Rightarrow y
\)
\(
=120 \text {. }
\)
Hence, speed of Train \(C=120 \mathrm{~km} / \mathrm{hr}\).

Hint

Let the distance be \(x \mathrm{~km}\). Then,
(Time taken to walk \(x \mathrm{~km}\) ) + (Time taken to drive \(x \mathrm{~km}\) ) \(=\frac{27}{4}\) hrs
\(\Rightarrow\) (Time taken to walk \(2 x \mathrm{~km}\) ) + (Time taken to drive \(2 x \mathrm{~km}\) ) \(=\frac{27}{2}\) hrs.
But time taken to drive \(2 x \mathrm{~km}=\frac{19}{4}\) hrs.
\(\therefore\) Time taken to walk \(2 x \mathrm{~km}=\left(\frac{27}{2}-\frac{19}{4}\right) \mathrm{hrs}\) \(=\frac{35}{4} \mathrm{hrs}=8 \mathrm{hrs} 45 \mathrm{~min}\).

Hint

Since 10 minutes are saved, it means that Reena’s father drives from the meeting point to the station and back to the meeting point in \(10 \mathrm{~min}\) i.e. he can drive from the meeting point to the station in \(\left(\frac{10}{2}\right)=5 \mathrm{~min}\).
But he reaches the station daily at \(7 \mathrm{pm}\). So Reena and her father meet on the way at \(6: 55 \mathrm{pm}\). Thus, Reena walked for \(25 \mathrm{~min}\) before her father picked her up.

Hint

Clearly, the coachman needed 2 hours to reach the station from Mr X’s house or 4 hours for the entire round trip.
But now he took \((4-1)=3\) hours for the round trip.
Thus he went one way in \(1 \frac{1}{2}\) hrs i.e.,
Mr \(X\) walked for \(1 \frac{1}{2}\) hrs.
Distance covered in \(1 \frac{1}{2} \mathrm{hrs}\) while walking \(=\left(4 \times \frac{3}{2}\right)\) miles \(=6\) miles.
But this distance would have been covered by the coachman in \(\left(2-1 \frac{1}{2}\right) \mathrm{hr}=\frac{1}{2} \mathrm{hr}\).
Speed of the coachman \(=\left(6 \div \frac{1}{2}\right) \mathrm{mph}=12 \mathrm{mph}\).
\(\therefore\) Distance between the house and the station
\(=\) Distance covered by coachman in \(2 \mathrm{hrs}\)
\(=(12 \times 2)\) miles \(=24\) miles.

Hint

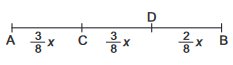
Let length \(A B=x\).
Then, if \(C\) is the position of the
cat, we have \(A C=\frac{3}{8} x\)
When the cat runs towards the entrance, the train catches it at the entrance. This means that when the train reaches the entrance, the cat has travelled a distance of \(\frac{3}{8} x\).
Let us now consider the case when the cat runs towards the exit.

So, when the train reaches \(A\), the cat reaches a point \(D\) such that \(\mathrm{CD}=\frac{3}{8} x\).
Then, \(B D=\left[x-\left(\frac{3}{8} x+\frac{3}{8} x\right)\right]=\frac{x}{4}\).
Since the train catches the cat at the exit, so the train covers distance \(x(=A B)\) in the same time in which the cat covers distance \(\frac{x}{4}(=B D)\).
\(\therefore\) Required ratio \(=x: \frac{x}{4}=4: 1\).

Hint

On attaching 9 compartments to the engine, we have : reduction in speed \(=k \sqrt{9},=3 k\) where \(k\) is a constant. \(\therefore 42-3 k=24\) or \(3 k=18\) or \(k=6\).
For the speed of the engine to be zero, let the number of compartments attached be \(x\).
Then, \(42-6 \sqrt{x}=0 \Rightarrow 6 \sqrt{x}=42 \Rightarrow \sqrt{x}=7 \Rightarrow x=49\).
Hence, maximum number of compartments that the engine can pull \(=(49-1)=48\).

Hint

Since \(A\) and \(B\) are \(5 \mathrm{~km}\) apart and Ram’s speed is \(5 \mathrm{~km} /\) \(\mathrm{hr}\), so Ram reaches \(B\) in 1 hour i.e., at \(10 \mathrm{am}\) Thus, when Ram reaches B, Shyam has travelled from 9 : \(45 \mathrm{am}\) to \(10 \mathrm{am}\) i.e. \(15 \mathrm{~min}\). So, distance covered by Shyam when Ram reaches
\(
B=\left(10 \times \frac{15}{60}\right) \mathrm{km}=\frac{5}{2} \mathrm{~km}
\)
Now, Ram starts travelling from \(B\) to \(A\).
So, relative speed \(=(10+5) \mathrm{km} / \mathrm{hr}=15 \mathrm{~km} / \mathrm{hr}\).
Distance between Ram and Shyam \(=\left(5-\frac{5}{2}\right) \mathrm{km}=\frac{5}{2} \mathrm{~km}\).
Time taken to cover \(\frac{5}{2} \mathrm{~km}\) at relative speed
\(
=\left(\frac{5}{2} \times \frac{1}{15}\right) h r=\frac{1}{6} h r=10 \mathrm{~min}
\)
Hence, Ram and Shyam meet each other 10 minutes after \(10 \mathrm{a} . \mathrm{m}\) i.e., at \(10: 10 \mathrm{am}\)

Hint

Time taken by Shyam to reach \(B\) from \(A\) \(=\left(\frac{5}{10}\right) h r=\frac{1}{2} h r=30 \mathrm{~min}\).
So, Shyam reaches \(B\) at \(10: 15 \mathrm{a.m}\).
Now, Shyam starts travelling from \(B\) to \(A\).
Distance between Ram and Shyam \(=\) Distance travelled by Ram in 15 min \(=\left(5 \times \frac{1}{4}\right) \mathrm{km}=\frac{5}{4} \mathrm{~km}\).
Relative speed \(=(10-5) \mathrm{km} / \mathrm{hr}=5 \mathrm{~km} / \mathrm{hr}\).
\(\therefore\) Time taken to cover \(\frac{5}{4} \mathrm{~km}\) at \(5 \mathrm{~km} / \mathrm{hr}\) \(=\left(\frac{5}{4} \times \frac{1}{5}\right) \mathrm{hr}=\frac{1}{4} \mathrm{hr}=15 \mathrm{~min}\).
Hence, Shyam overtakes Ram at 15 min past 10 : \(15 \mathrm{am}\) i.e., at \(10: 30 \mathrm{a} . \mathrm{m}\).

Hint

Suppose the escalator has \(n\) steps.
Let man’s speed be \(x\) steps per sec. and the speed of the escalator be \(y\) steps per sec.
Then, \(x+y=\frac{n}{30}\) and \(x-y=\frac{n}{90}\).
Adding, we get : \(2 x=\frac{4 n}{90}=\frac{2 n}{45}\) or \(x=\frac{n}{45}\).
\(\therefore\) Required time \(=\frac{n}{(n / 45)}=45 \mathrm{sec}\).

Hint

60 leaps of the hare \(=\left(60 \times 1 \frac{3}{4}\right) \mathrm{m}=105 \mathrm{~m}\).
So, the hound should gain \(105 \mathrm{~m}\) over the hare.
When the hound travels \(\left(3 \times 2 \frac{3}{4}\right) \mathrm{m}=\frac{33}{4} \mathrm{~m}\), the hare travels \(\left(4 \times 1 \frac{3}{4}\right) \mathrm{m}=7 \mathrm{~m}\).
In 3 leaps of the hound, the hound gains \(\left(\frac{33}{4}-7\right) \mathrm{m}=\frac{5}{4} m\).
\(
\therefore \text { Number of leaps required }=\left(105 \times \frac{4}{5} \times 3\right)=252 .
\)

Hint

Let the total distance be \(x \mathrm{~km}\) and time spent in riding be \(y\) hours.
Then, distance covered by riding \(=\left(\frac{x}{3}\right) \mathrm{km}\).
Distance covered by walking \(=\left(x-\frac{x}{3}\right) \mathrm{km}=\frac{2 x}{3} \mathrm{~km}\).
Time spent in walking \(=(20 y)\) hrs.
\(
\begin{aligned}
& \text { Riding speed }=\left(\frac{\frac{x}{3}}{y}\right) \mathrm{km} / \mathrm{hr}=\left(\frac{x}{3 y}\right) \mathrm{km} / \mathrm{hr} \text {. } \\
& \text { Walking speed }=\frac{\left(\frac{2 x}{3}\right)}{20 y} \mathrm{~km} / \mathrm{hr}=\left(\frac{x}{30 y}\right) \mathrm{km} / \mathrm{hr} \\
& \therefore \text { Required ratio }=\frac{x}{3 y}: \frac{x}{30 y}=1: \frac{1}{10}=10: 1 . \\
&
\end{aligned}
\)

Hint

Suppose after meeting the bus, the car travelled \(x \mathrm{~km}\) to reach Jaipur.
Then, it travelled \(x \mathrm{~km}\) in \(1 \frac{1}{2}\) hours.
Again, it travelled back to meet the bus again in \(1 \frac{1}{2}\) hours.
Now, distance travelled in \(\frac{1}{2}\) hour \(=\frac{x}{3} \mathrm{~km}\).
The bus travelled \(\left(x-\frac{x}{3}\right)=\frac{2 x}{3} \mathrm{~km}\) in 3 hours.
So, it will travel \(x \mathrm{~km}\) in \(\left(3 \times \frac{3}{2 x} \times x\right) \mathrm{hrs}=\frac{9}{2} \mathrm{hrs}=4 \frac{1}{2} \mathrm{hrs}\).
Hence, the bus will reach Jaipur
\(4 \frac{1}{2}\) hours after \(4: 30\) p.m i.e. at 9 p.m

Hint

Speed of Karan \(=60 \mathrm{kmph}\)
Time \(=9\) hrs.
Distance \(=\) Speed \(\times\) Time \(=60 \times 9=540 \mathrm{~km}\).
\(\therefore\) Time taken to cover \(540 \mathrm{~km}\) at \(90 \mathrm{~km} / \mathrm{ph}\)
\(
=\frac{540}{90}=6 \text { hours. }
\)

Hint

Speed of bus \(=72 \mathrm{~km} / \mathrm{ph}=\left(\frac{72 \times 5}{18}\right) \mathrm{m} / \mathrm{sec} .=20 \mathrm{~m} / \mathrm{sec}\)
Let distance covered by bus in \(5 \mathrm{sec}\) be \(x\)
\(\therefore\) Distance \(=\) Speed \(\times\) Time
\(\Rightarrow x=20 \times 5=100\) meter

Hint

Let the distance covered be \(2 x \mathrm{~km}\).
\(
\text { Time }=\frac{\text { Distance }}{\text { Speed }}
\)
Time taken to covers the first half and second half of the journey in \(t_1\) and \(t_1\) hours
\(
\begin{aligned}
& \Rightarrow \frac{a}{60}=t_1 \dots(i)\\
& \Rightarrow \frac{a}{45}=t_2 \dots(ii)
\end{aligned}
\)
Adding (i) and (ii) we get
\(
\begin{aligned}
& \frac{a}{60}+\frac{a}{45}=t_1+t_2 \\
& \frac{a}{60}+\frac{a}{45}=5 \frac{15}{60}=5 \frac{1}{4} \\
& \Rightarrow \frac{3 a+4 a}{180}=\frac{21}{4} \\
& \Rightarrow 7 a=\frac{21}{4} \times 180 \\
& \Rightarrow a=\frac{21 \times 180}{4 \times 7}=135 \mathrm{~km} \\
& \therefore \text { Length of total journey. } \\
& =2 \times 135=270 \mathrm{~km} .
\end{aligned}
\)

Hint

Speed of Ashok \(=39 \mathrm{~km} / \mathrm{ph}\)
Speed of Rahul \(=47 \mathrm{~km} / \mathrm{ph}\)
Distance between place \(\mathrm{A}\) and \(\mathrm{B}=637 \mathrm{~km}\)
Distance covered by Ashok (from \(8 \mathrm{am}\) to \(10 \mathrm{am}\) ) in 2 hours \(=2 \times 39=78 \mathrm{~km}\)
\(\therefore\) Remaining distance \(=637-78=559\)
Relative speed \(=39+47=86 \mathrm{~km} / \mathrm{ph}\)
\(\therefore\) Time taken to travel \(559 \mathrm{~km}=\frac{559}{86}=6.5\) hours
So, they meet at \(=(10 \mathrm{am}+6.5)\) hours \(=4: 30 \mathrm{pm}\)

Hint

Distance between the Speed of \(\mathrm{P}\) and \(\mathrm{Q}\) \(=3 \frac{1}{2}-3=\frac{7}{2}-3=\frac{1}{2} \mathrm{~km} / \mathrm{hr}\).
So, Distance \(=\) Speed \(\times\) Time
Time \(=4\) hours
\(
\Rightarrow D=\frac{1}{2} \times 4=2 \mathrm{~km}
\)

Hint

Let the total distance be covered \(3 a \mathrm{~km}\)
\(2 a \mathrm{~km}\) distance covered in 2 hours 30 minutes at the rate of \(k \mathrm{~km} / \mathrm{ph}\).
According to the question
Speed \(\times\) Time \(=\) Distance
\(
\begin{aligned}
& x \times 2 \frac{30}{60}=2 a \\
& \Rightarrow x \times 2 \frac{1}{2}=2 a \\
& \therefore x \times \frac{5}{2}=2 a \\
& \Rightarrow 5 x=4 a \dots(i)
\end{aligned}
\)
Then, ‘ \(a\) ‘ \(\mathrm{km}\) distance covered in 50 minutes at the rate of \((x+2) \mathrm{km} / \mathrm{ph}\).
\(
(x+2) \times \frac{50}{60}=a
\)
\(
\Rightarrow(x+2) \times 5=6 a \dots(ii)
\)
On dividing equation (ii) by (i).
\(
\begin{aligned}
& \frac{(x+2) \times 5}{5 x}=\frac{6 a}{4 a} \\
& \Rightarrow \frac{x+2}{x}=\frac{3}{2} \\
& \Rightarrow 3 x=2 x+4 \\
& \Rightarrow x+4 \\
& \text { From equation (i) } \\
& 5 \times 4=4 a \\
& \Rightarrow a=5 \\
& \therefore \text { Total distance }=3 a=3 \times 5=15 \mathrm{~km}
\end{aligned}
\)

Hint

Difference between time \(=1\) hour
Distance between point \(\mathrm{AB}=x \mathrm{~km}\)
According to the question
\(
\frac{x}{18}-\frac{x}{24}=1
\)
\(\mathrm{LCM}\) of 18 and \(24=72\)
\(
\begin{aligned}
& \Rightarrow \frac{4 x-3 x}{72}=1 \\
& \Rightarrow x=72 \mathrm{~km}
\end{aligned}
\)
Time taken at \(18 \mathrm{~km} / \mathrm{ph}\) to cover \(72 \mathrm{~km}[latex] [latex]=\frac{72}{18}=4\) hours
\(\therefore\) Speed to cover \(72 \mathrm{~km}\) in 2 hours
\(
=\frac{72}{2}=36 \mathrm{~km} / \mathrm{ph}
\)

Hint

Let the distance between school and home be \(=D\) According to the given information
\(
\begin{aligned}
& \frac{D}{2 \frac{1}{2}}-\frac{D}{3}=16 \text { minutes } \\
& \therefore \frac{2 D}{5}-\frac{D}{3}=\frac{16}{60} \\
& \Rightarrow \frac{6 D-5 D}{15}=\frac{16}{60} \\
& \Rightarrow D=\frac{16}{60} \times 15=4 \mathrm{~km}
\end{aligned}
\)

Hint

Let the speed of \(\operatorname{Kim}\) be \(a\) and that of \(\mathrm{Om}\) be \(b\).
Distance between point \(A\) and \(B=400 \mathrm{~km}\)
Then, \(\frac{400}{a}-\frac{400}{b}=1\)
Let, \(\frac{1}{a}=x\) and \(\frac{1}{b}=y\)
\(400 x-500 y=1 \dots(i)\)
Speed of \(\mathrm{km}\) doubles and she will take lets time i.e. 1 hour 30 minutes than 0 meter
Again, \(\frac{400}{b}-\frac{400}{2 b}=\frac{3}{2}\)
\(
\begin{aligned}
& \therefore 400 y-200 x=\frac{3}{2} \\
& 800 y-400 x=3 \dots(ii)
\end{aligned}
\)
Solving (i) and (ii), we get
\(
\begin{aligned}
& 400 x-400 y=1 \\
& \frac{-400 x+800 y=3}{400 y=4} \\
& \therefore y=\frac{4}{400}=\frac{1}{100} \mathrm{~km} \\
& \therefore b=100 \mathrm{~km}
\end{aligned}
\)
Now, \(\frac{400}{a}-\frac{400}{100}=4\)
Or, \(\frac{400}{a}\)
\(\therefore a=80 \mathrm{kmph}\).

Hint

Let distance covered be \(x\) in 15 minutes
\(
\begin{aligned}
& \text { Average speed }=\frac{\text { Time distance }}{\text { Time taken }} \\
& =\left(\frac{650+850}{12+18}\right) \mathrm{kmph} \\
& =\left(\frac{1500}{30}\right) \mathrm{kmph} \\
& =50 \mathrm{kmph}
\end{aligned}
\)

Hint

\(
\begin{aligned}
& \text { Speed of vehicle }=80 \mathrm{kmph} \\
& =\left(\frac{80 \times 1000}{60}\right) \mathrm{m} / \mathrm{min} . \\
& =\left(\frac{4000}{3}\right) \mathrm{m} / \mathrm{min} . \\
& \therefore \text { Required distance } x=\frac{4000}{3} \times 15=20000 \text { meter }
\end{aligned}
\)

Hint

According to given information
\(
\begin{aligned}
& \frac{2 x}{4}+\frac{3}{5}=\frac{3}{2} \\
& \Rightarrow \frac{2 x}{12}+\frac{x}{15}=\frac{3}{2} \\
& \Rightarrow \frac{x}{6}+\frac{x}{15}=\frac{3}{2} \\
& \Rightarrow \frac{5 x+2 x}{30}=\frac{3}{2} \\
& \Rightarrow \frac{7 x}{30}=\frac{3}{2} \\
& \Rightarrow 14 x=90 \\
& \Rightarrow x=\frac{90}{14}=6.4 \mathrm{~km}
\end{aligned}
\)

Hint

Rani goes to school from her house \(=30\) minutes Raja goes to school from her house \(=45\) minutes Required ratio \(=30: 45=2: 3\)

Hint

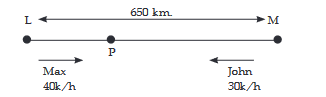
Speed of John \(=30 \mathrm{~km} / \mathrm{h}\)
Speed of Max \(=40 \mathrm{~km} / \mathrm{h}\)
Distance between \(L\) and \(M=650 \mathrm{~km}\)
Distance travelled by John in \(3 \mathrm{hrs} .=30 \times 3=90 \mathrm{kms}\) Time taken by Max and John to travel remaining
\(
\begin{aligned}
& (650-90=560) \\
& =\frac{560}{40+30}=8 \text { hours. }
\end{aligned}
\)
Distance travelled by John to reach point
\(
\mathrm{P}=8 \times 30=240 \mathrm{kms}
\)
Distance between \(\mathrm{P}\) and \(\mathrm{M}=240+90=330 \mathrm{kms}\)

Hint

Let the distance travelled by a car be \(x \mathrm{~km}\).
First \(\frac{x}{3} \mathrm{~km}\) distance cover at speed of \(10 \mathrm{~km} / \mathrm{hr}\)
Second \(\frac{x}{3} \mathrm{~km}\) distance cover at speed \(=20 \mathrm{~km} / \mathrm{hr}\)
Third \(\frac{x}{3} \mathrm{~km}\) distance cover at speed \(=60 \mathrm{~km} / \mathrm{hr}\)
According to given information
\(
\begin{aligned}
\text { Total time } & =\frac{x}{3 \times 10}+\frac{x}{3 \times 20}+\frac{x}{3 \times 60} \\
& =\frac{x}{30}+\frac{x}{60}+\frac{x}{180} \\
& =\frac{6 x+3 x+x}{180} \\
& =\frac{10 x}{180}=\frac{x}{18}
\end{aligned}
\)
Average speed \(=\frac{x \times 18}{x} \mathrm{~km} / \mathrm{hr} .=18 \mathrm{~km} / \mathrm{hr}\)

Hint

Let the speed of car be \(x \mathrm{~km} / \mathrm{hr}\)
Distance \(=\) speed \(\times\) time
Distance \(=8 x \mathrm{~km}\)
According to given information
\(
\begin{aligned}
& (x+4) \times 7.5=8 x \\
& \Rightarrow 7.5 x+30=8 x \\
& \Rightarrow 8 x-7.5 x=30 \\
& 30=0.5 x \\
& x=\frac{30}{0.5}=60 \mathrm{~km} / \mathrm{hr}
\end{aligned}
\)
\(
\text { Required distance }=8 \times 60=480 \mathrm{~km} \text {. }
\)

Hint

Speed of thief \(=10 \mathrm{~km} / \mathrm{hr}\)
Speed of policeman \(=11 \mathrm{~km} / \mathrm{hr}\)
Relative speed of policeman with respect to thief \(=(11-10) \mathrm{km} / \mathrm{hr}=1 \mathrm{~km} / \mathrm{hr}\)
The thief is noticed by a policeman from a distance of \(200 \mathrm{~m}\)
Distance covered in 6 minutes \(\frac{1000}{60} \times 6=100 \mathrm{~m}\)
Distance between them after 6 minutes \(=200-100=100 \mathrm{~m}\)

Hint

Let total distance covered by man be \(x \mathrm{~km}\) Journey covered by rail \(=\frac{2 x}{15}\)
Journey covered by bus \(=\frac{9 x}{20}\)
Remaining covered by Cycle \(=10 \mathrm{~km}\)
\(
\therefore x\left(1-\frac{2}{15}-\frac{9}{20}\right)=10
\)
\(\mathrm{LCM}\) of 15 and \(20=60\)
\(
\begin{aligned}
& x\left(\frac{60-8-27}{60}\right)=10 \\
& \Rightarrow x\left(\frac{25}{60}\right)=10 \\
& x=\frac{10 \times 60}{25}=24 \mathrm{~km}
\end{aligned}
\)

Hint

Speed of Ramesh \(=10 \mathrm{kmph}\)
Ramesh will take rest four times during his journey
\(\therefore\) Required time
\(=\left(5 \times \frac{1}{10} \times 60\right)\) minutes \(+(5 \times 4)\) minutes
\(=(30+20)\) minutes
\(=50\) minutes
Ramesh takes time to cover a distance of \(5 \mathrm{kms}\)

Hint

According to the question,
\(
\begin{aligned}
& \therefore 50 \mathrm{~m}=20 \mathrm{~m} \\
& \therefore 1 \mathrm{~m}=\frac{20}{50} \mathrm{~m} \\
& \therefore 1000 \mathrm{~m}=\left(\frac{20}{50} \times 1000\right) \mathrm{m} \equiv 400 \mathrm{~m}
\end{aligned}
\)