Quiz Level-2
Quiz Summary
0 of 40 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 40 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 40
1. Question
If two dice are rolled, find the probability that the sum of the faces of the dice is 7.
CorrectIncorrectHint
Let \(E\) represent the event that the sum of the faces of two dice is 7.
The possible cases for the sum to be equal to 7 are: \((1,6),(2,5),(3,4),(4,3),(5,2)\), and \((6,1)\), so event \(E\) is
\(
E=\{(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)\}
\)
The probability of the event \(E[latex] is
[latex]
P(E)=6 / 36 \text { or } 1 / 6 \text {. }
\) -
Question 2 of 40
2. Question
One 6 sided die is rolled once. Find the probability that the result is greater than 4.
CorrectIncorrectHint
The sample space consists of the following six possibilities in set \(\mathrm{S}: \mathrm{S}=1,2,3,4, 5, 6\) Let \(\mathrm{E}\) be the event that the number rolled is greater than four: \(\mathrm{E}=5,6\) Therefore, the probability of \(\mathrm{E}\) is: \(\mathrm{P}(\mathrm{E})=2 / 6\) or \(1 / 3\).
-
Question 3 of 40
3. Question
A jar contains 3 red, 4 white, and 3 blue marbles. If a marble is chosen at random, what is the probability that the marble is a red marble or a blue marble?
CorrectIncorrectHint
We assume the marbles are \(r_1, r_2, r_3, w_1, w_2, w_3, w_4, b_1, b_2, b_3\). Let the event \(\mathrm{C}\) represent that the marble is red or blue.
The sample space \(\mathrm{S}=\left\{\mathrm{r}_1, \mathrm{r}_2, \mathrm{r}_3, \mathrm{w}_1, \mathrm{w}_2, \mathrm{w}_3, \mathrm{w}_4, \mathrm{~b}_1, \mathrm{~b}_2, \mathrm{~b}_3\right\}\).
And the event \(\mathrm{C}=\left\{\mathrm{r}_1, \mathrm{r}_2, \mathrm{r}_3, \mathrm{~b}_1, \mathrm{~b}_2, \mathrm{~b}_3\right\}\)
Therefore, the probability of \(\mathrm{C}\),
\(
\mathrm{P}(\mathrm{C})=6 / 10 \text { or } 3 / 5
\) -
Question 4 of 40
4. Question
A jar contains three marbles numbered 1, 2, and 3. If two marbles are drawn without replacement, what is the probability that the sum of the numbers is 5?
Note: The two marbles in this example are drawn consecutively without replacement. That means that after a marble is drawn it is not replaced in the jar, and therefore is no longer available to select on the second draw.
CorrectIncorrectHint
Since two marbles are drawn without replacement, the sample space consists of the following six possibilities.
\(
\mathrm{S}=\{(1,2),(1,3),(2,1),(2,3),(3,1),(3,2)\}
\)
Note that \((1,1),(2,2)\) and \((3,3)\) are not listed in the sample space. These outcomes are not possible when drawing without replacement, because once the first marble is drawn but not replaced into the jar, that marble is not available in the jar to be selected again on the second draw.
Let the event \(\mathrm{E}\) represent that the sum of the numbers is five. Then
\(
\mathrm{E}=\{(2,3),(3,2)\}
\)
Therefore, the probability of \(\mathrm{E}\) is
\(
\mathrm{P}(\mathrm{E})=2 / 6 \text { or } 1 / 3 \text {. }
\) -
Question 5 of 40
5. Question
A jar contains three marbles numbered 1, 2, and 3. If two marbles are drawn with replacement, what is the probability that the sum of the numbers is 5?
Note: The two marbles in this example are drawn consecutively with replacement. That means that after a marble is drawn it is replaced in the jar, and therefore is available to select again on the second draw.
CorrectIncorrectHint
When two marbles are drawn with replacement, the sample space consists of the following nine possibilities.
\(
\mathrm{S}=\{(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)\}
\)
Note that \((1,1),(2,2)\) and \((3,3)\) are listed in the sample space. These outcomes are possible when drawing with replacement, because once the first marble is drawn and replaced, that marble is not available in the jar to be drawn again.
Let the event \(E\) represent that the sum of the numbers is four. Then
\(
\mathrm{E}=(2,3),(3,2)
\)
Therefore, the probability of \(\mathrm{F}\) is \(\mathrm{P}(\mathrm{E})=2 / 9\) -
Question 6 of 40
6. Question
A jar contains three marbles numbered 1,2 , and 3. If two marbles are drawn with replacement, what is the probability that the sum of the numbers is at least 4?
CorrectIncorrectHint
The sample space when drawing with replacement consists of the following nine possibilities.
\(
\mathrm{S}=(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)
\)
Let the event \(\mathrm{F}\) represent that the sum of the numbers is at least four. Then
\(
\mathrm{F}=(1,3),(3,1),(2,3),(3,2),(2,2),(3,3)
\)
Therefore, the probability of \(\mathrm{F}\) is
\(
\mathrm{P}(\mathrm{F})=6 / 9 \text { or } 2 / 3 \text {. }
\) -
Question 7 of 40
7. Question
Five cards are drawn from a deck. Find the probability of obtaining two pairs, that is, two cards of one value, two of another value, and one other card.
CorrectIncorrectHint
Let us first do an easier problem-the probability of obtaining a pair of kings and queens.
Since there are four kings, and four queens in the deck, the probability of obtaining two kings, two queens and one other card is
\(
\mathrm{P}(\text { A pair of kings and queens })=\frac{{ }^4 C_2 \times { }^4 C_2 \times { }^44 C_1}{{ }^{52} C_5}
\)
To find the probability of obtaining two pairs, we have to consider all possible pairs.
Since there are altogether 13 values, that is, aces, deuces, and so on, there are \({ }^{13} C_2\) different combinations of pairs.
\(
P(\text { Two pairs })=^{13} C_2 \cdot \frac{{ }^4 C_2 \times { }^4 C_2 \times { }^{44} C_1}{{ }^{52} C_5}=.04754
\) -
Question 8 of 40
8. Question
A cell phone store receives a shipment of 15 cell phones that contains 8 iPhones and 7 Android phones. Suppose that 6 cell phones are randomly selected from this shipment. Find the probability that a randomly selected set of 6 cell phones consists of 2 iPhones and 4 Android phones.
CorrectIncorrectHint
There are \({ }^8 C_2\) ways of selecting 2 out of the 8 iPhones.
and \({ }^7 C_4\) ways of selecting 4 out of the 7 Android phones
But altogether there are \({ }^{15} C_6\) ways of selecting 6 out of 15 cell phones.
Therefore we have
\(
P(2 \text { iPhones and } 4 \text { Android phones })=\frac{{ }^8 C_2 \times { }^7 C_4}{{ }^{15} C_6}=\frac{(28)(35)}{5005}=\frac{980}{5005}=0.1958
\) -
Question 9 of 40
9. Question
One afternoon, a bagel store still has 53 bagels remaining: 20 plain, 15 poppyseed, and 18 sesame seed bagels. Suppose that the store owner packages up a bag of 9 bagels to bring home for tomorrow’s breakfast, and selects the bagels randomly. Find the probability that the bag contains 4 plain, 3 poppyseed, and 2 sesame seed.
CorrectIncorrectHint
There are \({ }^{20} C_4\) ways of selecting 4 out of the 20 plain bagels, and \({ }^{15} C_3\) ways of selecting 3 out of the 15 poppyseed bagels, and \({ }^{18} C_2\) ways of selecting 2 out of the 18 sesame seed bagels.
But altogether there are \({ }^{53} C_9\) ways of selecting 9 out of the 53 bagels.
\(
\begin{aligned}
\mathrm{P}(4 \text { plain, } 3 \text { poppyseed, and } 2 \text { sesame seed }) & =\frac{{ }^{20} C_4 \times { }^{15} C_3 \times { }^{18} C_2}{{ }^{53} C_9} \\
& =\frac{(4845)(455)(153)}{4431613550} \\
& =0.761
\end{aligned}
\) -
Question 10 of 40
10. Question
If there are 25 people in a room, what is the probability that at least two people have the same birthday?
CorrectIncorrectHint
Let event \(\mathrm{E}\) represent that at least two people have the same birthday.
We first find the probability that no two people have the same birthday.
We analyze as follows.
Suppose there are 365 days to every year. According to the multiplication axiom, there are \(365^{25}\) possible birthdays for 25 people. Therefore, the sample space has \(365^{25}\) elements. We are interested in the probability that no two people have the same birthday. There are 365 possible choices for the first person and since the second person must have a different birthday, there are 364 choices for the second, 363 for the third, and so on. Therefore,
\(
\mathrm{P}(\text { No two have the same birthday })=\frac{365 \cdot 364 \cdot 363 \cdots 341}{365^{25}}=\frac{365 \mathrm{P} 25}{365^{25}}
\)
Since \(\mathrm{P}\) (at least two people have the same birthday) \(=1-\mathrm{P}\) (No two have the same birthday),
\(
\text { P at least two people have the same birthday })=1-\frac{365 \mathrm{P} 25}{365^{25}}=.5687
\) -
Question 11 of 40
11. Question
You are rolling a pair of dice to see who goes first in a board game. You only need to beat a 4 to win the chance to go first. What is the probability that you will roll greater than a 4?
CorrectIncorrectHint
It is easier to count the number of ways to roll a 4 or less. There is one way \((1,1)\) to roll a 2 , there are 2 ways to roll a \(3(1,2)\) and \((2,1)\), and 3 ways to roll a 4 \((1,3),(2,2)\), and \((3,1)\) for a total of 6 out of the \(6^2=\) 36 possible rolls, leaving 30 ways to roll greater than a \(4.30 / 36=5 / 6\).
-
Question 12 of 40
12. Question
The digits 1 through 4 are randomly arranged to create a four-digit number. What is the probability that the number formed is not divisible by 4?
CorrectIncorrectHint
There are \(4 !=24\) ways to arrange the digits. To be be divisible by 4 , the integer formed must end in either 12,24 , or 32 . Two of each of these makes 6 numbers divisible by \(4: 3,412 ; 4,312 ; 1,324 ; 3,124 ; 1,432\); and 4,132 . This means there are 18 out of the 24 that are not divisible by 4 or \(3 / 4\).
-
Question 13 of 40
13. Question
Three coins are flipped. What is the probability of flipping at least one heads and at least one tails?
CorrectIncorrectHint
There are \(2^3=8\) ways to flip 2 coins. Only HHH and TTT do not show at least one tails or one heads, so there are 6 of 8 possibilities which show at least one of each,making the probability \(3 / 4\).
-
Question 14 of 40
14. Question
A pair of standard dice is rolled, and the product of the digits is calculated. What is the probability that the product is even?
CorrectIncorrectHint
It is easiest to calculate the probability that the product is odd, which requires that both rolls be odd. The probability of rolling an odd number is \(1 / 2\), so the probability of rolling two odds in a row is \((1 / 2)^2=1 / 4\). Subtract this from 1 to get the probability that the product of the two rolls is even: \(3 / 4\).
-
Question 15 of 40
15. Question
For any date in history, Luke can quickly tell you what day of the week it was. You choose three dates at random and Luke tells you the day of the week for each. What is the probability that at least two of the dates occurred on the same day of the week?
CorrectIncorrectHint
We will find the probability that no two dates fall on the same day of the week and subtract this from 1 . The first date selected can be on any one the seven days. The second date must fall on one of the six remaining days, and the third date must fall on one of the remaining 5 days for a probability of: \(\frac{7}{7} \cdot \frac{6}{7} \cdot \frac{5}{7}=\frac{30}{49}\), making the probability that at least two f the dates fall on the same day of the week
\(
1-\frac{30}{49}=\frac{19}{49}
\) -
Question 16 of 40
16. Question
There are nine blocks in a bag: three red, three white, and three blue. Three blocks are selected at random and without replacement. What is the probability that at least two of the blocks will be different colored?
CorrectIncorrectHint
It is much simpler to calculate the probability that all three are the same color. There are three blocks of each color, so the probability is the same for each: \(\frac{3}{9} \cdot \frac{2}{8} \cdot \frac{1}{7}=\frac{1}{84}\). Multiply this by 3 because there are three colors to get \(1 / 28\). The probability that no two blocks will be different colors is \(1 / 28\), so the probability that at least two will be different colored is 27/28.
-
Question 17 of 40
17. Question
The first nine letters of the alphabet are randomly placed into three equal piles of three letters each. What is the probability that the letters A and B end up in different piles?
CorrectIncorrectHint
We will look for the probability that \(\mathrm{A}\) and \(\mathrm{B}\) end up in the same pile. There are \({ }^9 C_3=84\) ways to choose 3 of 9 letters for a pile. There are 7 possible sets that include A, B, and one of the remaining 7 letters. This makes the probability that any pile of 3 letters will include both \(\mathrm{A}\) and \(\mathrm{B} 7 / 84=1 / 12\). There are 3 piles, so the probability that 1 of 3 piles will include both \(A\) and \(B\) is \(3(1 / 12)=3 / 12\) or \(1 / 4\). The probability that \(A\) and \(B\) will be in different piles is therefore \(1-1 / 4=\) \(3 / 4\). Alternatively, place the \(A\) first:
A _ _ _ _ _ _ _ _This leaves 8 places for the B. 2 of those places are in the same pile as the \(A\), while 6 are in one of the other piles. \(6 / 8=3 / 4\).
-
Question 18 of 40
18. Question
If the digits 1 through 5 are randomly arranged so that one digit fills each of the five circles, what is the probability that at least two consecutive integers will be connected by a line segment?
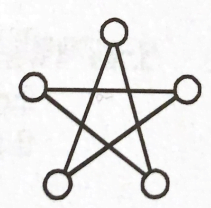 CorrectIncorrect
CorrectIncorrectHint
Start by placing the 3. Any arrangement can be rotated so that the three is located on top. When we place the three on top, this leaves 4 blanks to fill with 4 integers for \(4 !=24\) possible ways to complete the diagram. To avoid consecutive integers, we can have a 1 and a 5 connected to the three as shown in two ways with the 2 and the 4 forced (depending on the placement of the 1 and the 5). This gives us just 2 ways to avoid consecutive integers (shown), so there are \(22 / 24=\mathbf{1 1} / 12\) arrangements with at least one connected pair of consecutive integers.
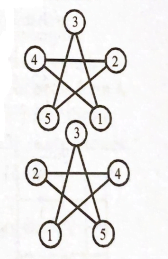
-
Question 19 of 40
19. Question
A pizza place offers 14 different toppings. How many different three-topping pizzas can you order?
CorrectIncorrectHint
\(
{ }^3 C_{14}=\left(\begin{array}{c}
14 \\
3
\end{array}\right)=\frac{14 !}{3 !(14-3) !}=\frac{14 \cdot 13 \cdot 12}{3 \cdot 2 \cdot 1}=364
\) -
Question 20 of 40
20. Question
Suppose we have 5 red balls and 4 black balls and get 5 balls randomly. What’s the probability of getting 3 red balls and 2 black balls?
CorrectIncorrectHint
Let’s denote the event of getting 3 red balls and 2 black balls by \(A\), so
\(
P(A)=\frac{n(A)}{n(S)}=\frac{\left(\begin{array}{l}
5 \\
3
\end{array}\right) \times\left(\begin{array}{l}
4 \\
2
\end{array}\right)}{\left(\begin{array}{l}
9 \\
5
\end{array}\right)}=\frac{10 \times 6}{126}=\frac{30}{63}
\) -
Question 21 of 40
21. Question
Suppose we have a dice that the probability of odd numbers is 5 times more than even numbers.
Find the probability that dice shows 6.CorrectIncorrectHint
\(
\begin{aligned}
& P(1)=P(3)=P(5)=5 P(2)=5 P(4)=5 P(6) \\
& P(1)+P(2)+P(3)+P(4)+P(5)+P(6)=1 \\
& 5 P(6)+P(6)+5 P(6)+P(6)+5 P(6)+P(6)=1 \\
& 18 P(6)=1 \\
& P(6)=1 / 18
\end{aligned}
\) -
Question 22 of 40
22. Question
Bob and Alice each have a bag that contains one ball of each of the colors blue, green, orange, red, and violet. Alice randomly selects one ball from her bag and puts it into Bob’s bag. Bob then randomly selects one ball from his bag and puts it into Alice’s bag. What is the probability that after this process the contents of the two bags are the same?
CorrectIncorrectHint
Since there are the same amount of total balls in Alice’s bag as in Bob’s bag, and there is an equal chance of each ball being selected, the color of the ball that Alice puts in Bob’s bag doesn’t matter. Without loss of generality, let the ball Alice puts in Bob’s bag be red.
For both bags to have the same contents, Bob must select one of the 2 red balls out of the 6 balls in his bag.
So the desired probability is \(\frac{2}{6}=\frac{1}{3}\). -
Question 23 of 40
23. Question
For a particular peculiar pair of dice, the probabilities of rolling
 ,
,  ,
,  ,
,  ,
,  , and 6, on each die are in the ratio
, and 6, on each die are in the ratio  . What is the probability of rolling a total of
. What is the probability of rolling a total of  on the two dice?CorrectIncorrect
on the two dice?CorrectIncorrectHint
Let \(x\) be the probability of rolling a 1 . The probabilities of rolling a \(2,3,4,5\), and 6 are \(2 x, 3 x, 4 x, 5 x\), and \(6 x\), respectively. The sum of the probabilities of rolling each number must equal 1, so
\(
\begin{aligned}
& x+2 x+3 x+4 x+5 x+6 x=1 \\
& 21 x=1 \\
& x=\frac{1}{21}
\end{aligned}
\)
So the probabilities of rolling a \(1,2,3,4,5\), and 6 are respectively \(\frac{1}{21}, \frac{2}{21}, \frac{3}{21}, \frac{4}{21}, \frac{5}{21}\), and \(\frac{6}{21}\).
The possible combinations of two rolls that total 7 are: \((1,6) ;(2,5) ;(3,4) ;(4,3) ;(5,2) ;(6,1)\)
The probability \(P\) of rolling a total of 7 on the two dice is equal to the sum of the probabilities of rolling each combination.
\(
P=\frac{1}{21} \cdot \frac{6}{21}+\frac{2}{21} \cdot \frac{5}{21}+\frac{3}{21} \cdot \frac{4}{21}+\frac{4}{21} \cdot \frac{3}{21}+\frac{5}{21} \cdot \frac{2}{21}+\frac{6}{21} \cdot \frac{1}{21}=\frac{8}{63}
\) -
Question 24 of 40
24. Question
Two cards are drawn from the pack of 52 cards. Find the probability that both are diamonds or both are kings.
CorrectIncorrectHint
Total no. of ways \(={ }^{52} \mathrm{C}_2\)
Case I: Both are diamonds \(={ }^{13} \mathrm{C}_2\)
Case II: Both are kings \(={ }^4 \mathrm{C}_2\)
\(P\) (both are diamonds or both are kings) \(=\left({ }^{13} \mathrm{C}_2+{ }^4 \mathrm{C}_2\right) /{ }^{52} \mathrm{C}_2\) -
Question 25 of 40
25. Question
A problem is given to three persons P, Q, R whose respective chances of solving it are 2/7, 4/7, 4/9 respectively. What is the probability that the problem is solved?
CorrectIncorrectHint
Probability of the problem getting solved \(=1-\) (Probability of none of them solving the problem)
\(
P(P)=\frac{2}{7} \Rightarrow P(\bar{P})=1-\frac{2}{7}=\frac{5}{7}, P(Q)=\frac{4}{7} \Rightarrow P(\bar{Q})=1-\frac{4}{7}=\frac{3}{7}, P(R)=\frac{4}{9} \Rightarrow P(\bar{R})=1-\frac{4}{9}=\frac{5}{9}
\)
Probability of problem getting solved \(=1-(5 / 7) \times(3 / 7) \times(5 / 9)=(122 / 147)\) -
Question 26 of 40
26. Question
Find the probability that a leap year has 52 Sundays.
CorrectIncorrectHint
A leap year can have 52 Sundays or 53 Sundays. In a leap year, there are 366 days out of which there are 52 complete weeks & remaining 2 days. Now, these two days can be (Sat, Sun) (Sun, Mon) (Mon, Tue) (Tue, Wed) (Wed, Thur) (Thur, Friday) (Friday, Sat).
So there are total 7 cases out of which (Sat, Sun) (Sun, Mon) are two favorable cases. So, P (53 Sundays) \(=2 / 7\)
Now, \(\mathrm{P}(52\) Sundays \()+\mathrm{P}(53\) Sundays \()=1\)
So, \(P(52\) Sundays \()=1-P(53\) Sundays \()=1-(2 / 7)=(5 / 7)\) -
Question 27 of 40
27. Question
Three bags contain 3 red, 7 black; 8 red, 2 black, and 4 red & 6 black balls respectively. 1 of the bags is selected at random and a ball is drawn from it. If the ball drawn is red, find the probability that it is drawn from the third bag.
CorrectIncorrectHint
Let E1, E2, E3 and A are the events defined as follows.
\(\mathrm{E} 1\) = First bag is chosen
E2 = Second bag is chosen
E3 \(=\) Third bag is chosen
\(A=\) Ball drawn is red
Since there are three bags and one of the bags is chosen at random, so \(P(E 1)=P(E 2)=P(E 3)=1 / 3\)
If \(\mathrm{E} 1\) has already occurred, then first bag has been chosen which contains 3 red and 7 black balls. The probability of drawing 1 red ball from it is \(3 / 10\). So, \(P\left(A / E_1\right)=3 / 10\), similarly \(P\left(A / E_2\right)=8 / 10\), and \(P\left(A / E_3\right)=\) 4/10. We are required to find \(P\left(E_3 / A\right)\) i.e. given that the ball drawn is red, what is the probability that the ball is drawn from the third bag by Baye’s rule
\(
=\frac{\frac{1}{3} \times \frac{4}{10}}{\frac{1}{3} \times \frac{3}{10}+\frac{1}{3} \times \frac{8}{10}+\frac{1}{3} \times \frac{4}{10}}=\frac{4}{15} .
\) -
Question 28 of 40
28. Question
The thirteen diamonds are separated from a standard deck of cards. What is the probability that all three face cards (KQJ) are in a set of five randomly selected cards from this set?
CorrectIncorrectHint
There are \({ }^{13} C_5=1,287\) ways to choose 5 cards from a set of 13. If we have \(\mathrm{KQJ}\) in the set, we must choose 2 of the remaining 10 cards to complete the set. There are \({ }^{10} C_2=45\) ways to complete the set, making the probability \(45 / 1,287=5 / 143\).
-
Question 29 of 40
29. Question
Three students are randomly selected from a group of twelve that includes twins Billy and Adam. What is the probability that Adam is selected but Billy is not?
CorrectIncorrectHint
There are \({ }^{12} C_3=220\) ways to select three students from a group of 12. If Adam is selected, there are 10 students left (excluding Billy) and we need to choose two to pair with Adam. \({ }^{10} \mathrm{C}_2=45\) pairs can be selected, meaning there are 45 groups of 3 students which include Adam but not Billy out of the 220 possible groups. \(45 / 220=9 / 44\).
-
Question 30 of 40
30. Question
There are 3 vegetarians in a class of 20 students. If 3 students are chosen at random, what is the probability that exactly one of the 3 is a vegetarian?
CorrectIncorrectHint
There are \({ }^{20} C_3=1,140\) sets of 3 students who can be chosen from a group of 20 . We are looking to form a group with 1 vegetarian and 2 non-vegetarians. There are \({ }^3 C_1=3\) ways to choose the vegetarian and \({ }^{17} \mathrm{C}_2=136\) ways to choose the non-vegetarians, for a total of \(3 \cdot 136=408\) ways to form a group with one vegetarian and two non-vegetarians, which gives us a probability of \(408 / 1,140=34 / 95\). Alternatively, The probability of selecting vegetarian, non-vegetarian, non-vegetarian in that order is: \(\frac{3}{20} \cdot \frac{17}{19} \cdot \frac{16}{18}=\frac{34}{285}\), and we can arrange these picks three different ways (the veg. can be \(1^{\text {st }}, 2^{\text {nd }}\), or \(3^{\text {rd }}\) ), which gives us: \(3 \cdot \frac{34}{285}=\frac{34}{95}\)
-
Question 31 of 40
31. Question
A circle is inscribed inside a square. If a point inside the square is selected at random, what is the probability that the point will also be inside the circle?
CorrectIncorrectHint
The probability of the point being inside the circle is the ratio of the area of the circle to the area of the square. If we suppose that the circle has radius \(r\), then the square must have side \(2 r\). The area of the circle is \(\pi r^2\) and the area of the square is \((2 r)^2=(4 r)^2\), so the proportion of the areas is \(\left(\pi r^2\right) / (4 r)^2=\pi / 4\).
-
Question 32 of 40
32. Question
If x is chosen at random from the set (4, 6, 7, 9, 11) and y is chosen at random from the set (12, 13, 15, 17) then what is the probability that xy is odd?
CorrectIncorrectHint
If \(x\) is chosen at random from the set \((4,6,7,9,11)\) and \(y\) is chosen at random from the set \((12,13,15,17)\) then what is the probability that \(x y\) is odd?
Here we have 5 possible choices for \(x\) and 4 possible choices for \(y\), giving us \(5 \times 4=20\) possible outcomes.
We know that odd times odd = odd; even times even = even; and even times odd = even. Thus we need all of the outcomes where \(x\) and \(y\) are odd. We have 3 possibilities of odd numbers for \(x\), and 3 possibilities of odd numbers for \(y\), so we will have 9 outcomes of our total 20 outcomes where \(x y\) is odd, giving us a probability of \(9 / 20\). -
Question 33 of 40
33. Question
Mike has a bag of marbles, 4 white, 8 blue, and 6 red. He pulls out one marble from the bag and it is red. What is the probability that the second marble he pulls out of the bag is white?
CorrectIncorrectHint
There are 18 marbles in total. One of them is removed so now there are 17 marbles. This is our denominator. All of the original white marbles are still in the bag so there is a 4 out of 17 or \(4 / 17\) chance that the next marble taken out of the bag will be white.
-
Question 34 of 40
34. Question
Michael tosses three fair coins. What is the probability that at least one of these coins will land on heads?
CorrectIncorrectHint
Michael can toss at least one head, or he can toss zero heads. The sum of these two probabilities must equal one, because they represent all of the ways that Michael could toss the coins. He could either toss at least on head, or he could toss no heads at all.
Probability of tossing at least one head + probability of tossing no heads \(=1\)
The probability of tossing no heads is only possible with the combination TTT. The probability of tossing three tails is equal to \((1 / 2)(1 / 2)\) \((1 / 2)=1 / 8\)
Probability of tossing at least one head \(+1 / 8=1\)
Probability of tossing at least one head \(=1-1 / 8=7 / 8\). -
Question 35 of 40
35. Question
A jar of marbles has 125 marbles in it. 25 are blue marbles, 65 are red marble, 15 are green marbles and 20 are yellow marbles. What is the probability that the first three marbles picked are green or blue?
CorrectIncorrectHint
Probability of each event \(=(\#\) green marbles \(+\) \# blue marbles \() /\) Total # of Marbles
\(
\mathrm{P} 1=(15+25) / 125=40 / 125
\)
Second event assumes a blue or green was chosen for first event so there is one fewer marble on top and also one fewer marble in the total number of marbles.
\(
\mathrm{P} 2=(14+25) / 124=39 / 124
\)
Third event assumes a blue or green was chosen for first and second events so there are two fewer marbles on top and also two fewer marbles in the total number of marbles.
\(
\mathrm{P} 3=(13+25) / 124=38 / 123
\)
Probability for multiple events \(=\mathrm{P} 1 \times \mathrm{P} 2 \times \mathrm{P} 3\)
\(
\begin{aligned}
& (40 / 125) \times (39 / 124) \times (38 / 123) \\
& (40 \times 39 \times 38) /(125 \times 124 \times 123)=59280 / 1906500=0.031
\end{aligned}
\) -
Question 36 of 40
36. Question
How many positive four-digit integers are multiples of 5 and less than 7,000?
CorrectIncorrectHint
First, observe that multiples of 5 are all those numbers that have a 0 or a 5 as their final digit \((5,10,15,20,25\), etc.), so the question is asking how many 4-digit integers under 7000 end in a 0 or a 5 . Second, notice that the smallest 4-digit integer is 1,000. So, to rephrase the question, we want to find how many integers that are between 1000 and 6999 end in a 0 or a 5.
Writing the 4-digit integer as \(W X Y Z\), we see that there are six possibilties for \(W(1,2,3,4,5\), and 6\()\), ten possibilities for \(X(0-9)\), ten possibilities for \(Y(0-9)\), and two possibilities for \(Z(0\) and 5). So there are \(6 \times 10 \times 10 \times 2=1200\) total integers between 1000 and 6999 that end in a 0 or a 5. Therefore, there are 1200 four-digit integers that are multiples of 5 and less than 7,000.
-
Question 37 of 40
37. Question
A street light in Anytown, USA, completes a cycle from red to green to yellow, and back to red, in 50 seconds. During this time, the light will be red for 20 seconds, green for 25 seconds, and yellow for the remaining time. Over a period of 100 seconds, what is the probability that the light will be yellow at a randomly chosen time?
CorrectIncorrectHint
First, find the amount of time that the light is yellow, which is \(50-20-25=5\) seconds out of a 50 second cycle. The period of 100 seconds is irrelevant because the probability of getting a yellow light would be the same for any complete period or number of complete periods. So the probability of getting a yellow light would be \(5 / 50=1 / 10\).
-
Question 38 of 40
38. Question
Judy is practicing to be a magician and has an ordinary deck of 52 playing cards, a regular 6-sided die, and a fair coin. What is the probability that Judy rolls a 6 on the die, then flips the coin head face up, and then draws a spade from the deck of cards?
CorrectIncorrectHint
We can find the individual probabilities of these three events occuring first.
\(P(\) rolling a 6\()=1 / 6\)
\(P(\) head \()=1 / 2\)
\(P(\) spade \()=13 / 52=1 / 4\)
Now, to find the probability of rolling a 6 AND flipping a head AND drawing a spade, we must multiply the individual probabilities. So the answer is \(1 / 6 \times 1 / 2 \times 1 / 4=1 / 48\). -
Question 39 of 40
39. Question
A bag of marbles has 7 yellow marbles, 5 red marbles, 3 blue marbles, and 6 white marbles. What is the probability of choosing a yellow marble, putting it back and choosing a blue marble, and then NOT putting the blue marble back and picking a white marble?
CorrectIncorrectHint
There are a total of \(7+5+3+6=21\) marbles. The probability of picking a yellow marble is \(7 / 21=1 / 3\). Then we put it back and choose a blue marble with probability \(3 / 21=1 / 7\). We do NOT put this blue marble back, but then we grab for a white. The probability of picking a white is now \(6 / 20=3 / 10\), because now we are choosing from 20 marbles instead of 21 . So putting it together, the probability of choosing a yellow marble, replacing it and then choosing a blue and a white, is \(1 / 3 \times 1 / 7 \times 3 / 10=1 / 70\).
-
Question 40 of 40
40. Question
Jackie is a contestant on a gameshow. She has to pick marbles out of a big bag to win various amounts of money. The bag contains a total of 200 marbles.
There are 100 red marbles worth \($ 10\) each, 50 blue marbles worth \($ 20\) each, 30 green marbles worth \($ 50\) each, 15 white marbles worth \($ 100\) each and 5 black marbles worth \( 1000\) each. If she picks once, what percent chance does she have of picking a \($ 1000\) marble?
CorrectIncorrectHint
\(
\text { There are } 5 \text { black marbles worth } \$ 1000 \text { dollars out of the total of } 200 \text { marbles. } 5 \div 200=.025 \text { or } 2.5 \%
\)