Complementary Counting and Probability

It is often easier to compute the probability of what we do not want. Subtracting this from 1 gives us the probability of what we do want. We can calculate using the formula below as we know Event A plus all outcomes that are not Event A make up all possible outcomes.

\(P(A)=1-P\left(A^{\prime}\right)\), where

\({P ( A )} \text { means “Probability of Event A” }\)

\({P}\left({A}^{\prime}\right) \text { means “Probability of the complement of Event A” }\)

Example 1: Throw two dice. What is the probability the two scores are different?

Solution:

Different scores are like getting a 2 and 3, or a 6 and 1. It is a long list:
\(
\begin{gathered}
A=\{(1,2),(1,3),(1,4),(1,5),(1,6), \\
(2,1),(2,3),(2,4),(1,5),(1,6), \\
(3,1),(3,2), \ldots \text { etc } !\}
\end{gathered}
\)
But the compliment (which is when the two scores are the same) is only \({6}\) outcomes:
\(
A^{\prime}=\{(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)\}
\)
And its probability is:
\(
P\left(A^{\prime}\right)=\frac{6}{36}=\frac{1}{6}
\)
Knowing that \(\mathrm{P}({A})\) and \({P}\left({A}^{\prime}\right)\) together make 1 , we can calculate:
\(
\begin{aligned}
P(A) & =1-P\left(A^{\prime}\right) \\
& =1-\frac{1}{6} \\
& =\frac{5}{6}
\end{aligned}
\)
So in this case (and many others) it is easier to work out \({P}\left({A}^{\prime}\right)\) first, then calculate \({P}({A})=\) \(1-{P}\left({A}^{\prime}\right)\)

Example 2: Two dice are thrown. What is the probability that the sum of the numbers appearing on the two dice is 11 if 5 appears on the first?

Solution:

5 appears on the first. Hence to get the sum 11, the number on the second die must be 6. So required probability = 1/36.

Example 3: A number is chosen at random from a set of whole numbers from 1 to 50. Calculate the probability that the chosen number is not a perfect square.

Solution:

Let B denotes the event of choosing a perfect square.
Let \(\mathrm{B}^{\prime}\) denote the event that the number chosen is not a perfect square.
\(
B=\{1,4,9,16,25,36,49\}
\)
Number of elements in \(B=n(B)=7\)
\(
\begin{aligned}
& P(B)=n(B) / n(S)=7 / 50 \\
& P\left(B^{\prime}\right)=1-P(A) \\
& =1-(7 / 50) \\
& =43 / 50
\end{aligned}
\)
So the required probability is \(43 / 50\).

Example 3: Suppose you know that the probability of getting the flu this winter is 0.43. What is the probability that you will not get the flu?

Solution:

Let the event \(A\) be getting the flu this winter. We are given \(P(A)=0.43\). The event not getting the flu is \(A^{\prime}\). Thus, \(P\left(A^{\prime}\right)=1-P(A)=1-0.43=0.57\).

Example 4: Two coins are tossed simultaneously. Let event A be observing at least one head. What is the complement of A, and how would you calculate the probability of A by using the Complement Rule?

Solution:

Since the sample space of event \(A=\{H T, T H, H H\}\), the complement of \(A\) will be all events in the sample space that are not in \(A\). In other words, the complement will be all the events in the sample space that do not involve heads. That is, \(A^{\prime}=\{T T\}\).
We can draw a simple Venn diagram that shows \(A\) and \(A^{\prime}\) when tossing two coins as follows:

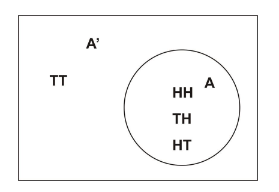
The second part of the problem is to calculate the probability of \(A\) using the Complement Rule. Recall that \(P(A)=1-P\left(A^{\prime}\right)\). This means that by calculating \(P\left(A^{\prime}\right)\), we can easily calculate \(P(A)\) by subtracting \(P\left(A^{\prime}\right)\) from 1 .
\(
\begin{aligned}
& P\left(A^{\prime}\right)=P(T T)=\frac{1}{4} \\
& P(A)=1-P\left(A^{\prime}\right)=1-\frac{1}{4}=\frac{3}{4}
\end{aligned}
\)

Example 5: Consider the experiment of tossing a coin ten times. What is the probability that we will observe at least one head?

Solution:

We are being asked to calculate the probability that we will observe at least one head. You will probably find it difficult to calculate since heads will almost always occur at least once during 10 consecutive tosses. However, if we determine the probability of the complement of \(A\) (i.e., the probability that no heads will be observed), our answer will become a lot easier to calculate. The complement of \(A\) contains only one event: \(A^{\prime}=\{T T T T T T T T T T\}\). This is the only event in which no heads appear, and since all simple events are equally likely, \(P\left(A^{\prime}\right)=\frac{1}{1024}\).
Using the Complement Rule, \(P(A)=1-P\left(A^{\prime}\right)=1-\frac{1}{1024}=\frac{1023}{1024}=0.999\).
That is a very high percentage chance of observing at least one head in ten tosses of a coin.

Example 6: A single coin is tossed 4 times. What is the probability that you will get at least one tail?

Solution:

\(
P(\text { at least one tail })=1-P(\text { no tails })=1-P(4 \text { heads })=1-\left(\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}\right)=1-\frac{1}{16}=\frac{15}{16}
\)

Example 7: A teacher is asking some students to read for the class, the lesson of the day if the teacher is going to put to read to 7 of his 40 students, but most of the students are very shy to read for the class. What are the chances for each student to not read out loud?

Solution:

First we find \(P(R)\) where \(R\) is reading for the class
\(
\begin{aligned}
& P(R)=7 / 40=0.175
\end{aligned}
\)
And finally we find \(P(R^{\prime})\)
\(
\begin{aligned}
& P(R^{\prime})=1-0.175 \\
& P(R^{\prime})=0.825 \\
& P(R^{\prime})=0.825 * 100 \% \\
& P(R^{\prime})=82.5 \%
\end{aligned}
\)

Example 8: In an ice cream shop there are 4 types of flavors, according to the statistics of the shop, the favorite flavor of its clients is the chocolate flavor, and because of this the chocolate flavor is running out of stock and the people from the ice cream shop do not want people to ask for this flavor because they would be out of chocolate too fast, knowing this what is the probability that the next client asks for any flavor but chocolate.

Solution:

we find \(P(C)\) being \(C\) the chocolate flavor
\(
\begin{aligned}
& P(C)=1 / 4 \\
& P(C)=0.25
\end{aligned}
\)
And we find \(P(C^{\prime})\)
\(
\begin{gathered}
& P(C^{\prime})=1-0.25 \\
& P(C^{\prime})=0.75 \\
& P(C^{\prime})=0.75 \times 100 \% \\
& P(C^{\prime})=75 \%
\end{gathered}
\)

Example 9: A young man goes to buy a new phone model which has a 10 different color collection, but he does not like two of those colors when he buys the phone they give him a random color. What are the chances of him getting a color that he actually likes?

Solution:

First, we find \(P(C)\) being \(C\) getting one of the unwished colors.

\(
\begin{aligned}& P(C)=2 / 10 \\
& P(C)=0.2
\end{aligned}
\)
And we find \(P(C^{\prime})\)
\(
\begin{gathered}
& P(C^{\prime})=1-0.2 \\
& P(C^{\prime})=0.80 \\
& P(C^{\prime})=0.8 \times 100 \% \\
& P(C^{\prime})=80 \%
\end{gathered}
\)

Example 10: In a company, they are making their employees work overtime one day of the next week between Monday and Saturday, but one of the workers has a surprise party for his son´s birthday next Friday, so if this extra hour are given randomly, what is the probability that this worker has to work overtime any day but Friday.

Solution:

irst we find \(P(O)\), \(O\)=overtime work friday
\(
\begin{aligned}
& P(O)=1 / 6 \\
\end{aligned}
\)
And we find \(P(O^{\prime})\)
\(
\begin{gathered}
P(O^{\prime})=1-0.1667=0.8333 \\
P(O^{\prime})=0.8333 \times 100 \% \\
P(O^{\prime})=83.33 \%
\end{gathered}
\)

Example 11: The chance of rain for each of the next five days is \(25 \%\). What is the probability that it will rain at least once in the next five days? Express your answer to the nearest tenth of a percent.

Solution:

We only need to calculate the probability that it will not rain at all. If there is a \(25 \%\) chance of rain for each of the next five days, there is a \(75 \%\) chance that it will not rain, or \(3 / 4\) for each of five days:
\(
\left(\frac{3}{4}\right)^5=\frac{243}{1024} \approx 23.7 \% \text { or }(0.75)^5=0.2373 \ldots \approx 23.7 \%
\)

Example 12: You hold the \(Q\) in a game of Scrabble, and need a \(U\) to be able to make a word. There are 9 letters left in the bag and two are U’s. If you select four letters at random, what is the probability that you will get at least one U?

Solution:

It is easier to compute the probability that you will not get a U. Beginning with two U’s and seven letters which are not U’s, we get the probability of not drawing a \(\mathrm{U}\) as:
\(
\frac{7}{9} \cdot \frac{6}{8} \cdot \frac{5}{7} \cdot \frac{4}{6}=\frac{5}{18}
\)
This means: \(1-\frac{5}{18}=\frac{13}{18}\) of the time you would draw a U.

With counting techniques: there are a total of \({ }^9 C_4=126\) combinations of four letters and \({ }^7 C_4=35\) combinations which do not include a \(\mathrm{U}\), which means the probability of not drawing a \(\mathrm{U}\) is \(35 / 126=5 / 18\). This leaves a \(13 / 18\) probability of drawing the \(\mathrm{U}\).