A compound event is an event that includes two or more simple events. Simple events are events that can have only one outcome, while compound events can have multiple different outcomes. Compound events can be made up of a number of independent events or dependent events.  A compound event’s probability is the ratio of the number of favorable outcomes and the number of possible outcomes, just like a single event.

\(
\mathrm{P} \text { (Event) }=\frac{\text { The number of favorable outcomes }}{\text { Number of possible outcomes }}
\)

For example, Imagine tossing two fair coins. The result of the first event has no bearing on the outcome of the second. So, these are called independent events.

Imagine drawing a marble from a bag and, without replacing it, drawing a second marble from the bag. In this case, the outcome of the second event is determined by the first event’s outcome. These are called dependent events.

Example 1:  Consider that if a coin is tossed and a dice is rolled, the following would be the possible outcomes. If so, what will be the probability of rolling a number greater than 2 and flipping tails?

\(
\begin{array}{|l|l|l|l|l|l|l|}
\hline \text { Cube } & 1 & 2 & 3 & 4 & 5 & 6 \\
\hline \text { Coin head } & 1 \mathrm{H} & 2 \mathrm{H} & 3 \mathrm{H} & 4 \mathrm{H} & 5 \mathrm{H} & 6 \mathrm{H} \\
\hline \text { Coin tail } & 1 \mathrm{~T} & 2 \mathrm{~T} & 3 \mathrm{~T} & 4 \mathrm{~T} & 5 \mathrm{~T} & 6 \mathrm{~T} \\
\hline
\end{array}
\)

Solution:

There are four favorable outcomes in the sample space for rolling a number greater than 2 and flipping tails: \(3 T\), \(4 T\), \(5 T\) and \(6 T\).
\(
P(\text { Event })=\frac{\text { number of favorable outcomes }}{\text { total possible outcomes }}
\)
\(\mathrm{P}(\) greater than 2 and tails \()=\frac{4}{12}\)
\(
=\frac{1}{3} \text { or } 33 \%
\)
The outcome of tossing the coin does not affect the outcome of tossing the cube. Hence they are independent events and not dependent events.

Example 2: If we throw a coin twice, what is the probability of getting “heads” both times?

Solution:

We are asked to find the probability of getting heads both times:  getting a head on the first throw and getting a head on the second throw of the coin. We can illustrate all the possible outcomes on a tree diagram to help us find the probability of getting “heads” both times. The first set of branches represents the first throw, with the two possible outcomes “heads” and “tails.”

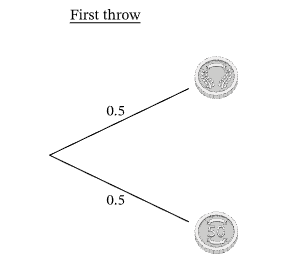
The probabilities for “heads” and “tails” are each 1/2. Now if we attach branches to each of these outcomes, covering all possible outcomes for the second throw, we can work out the compound probability of getting “heads” both times.

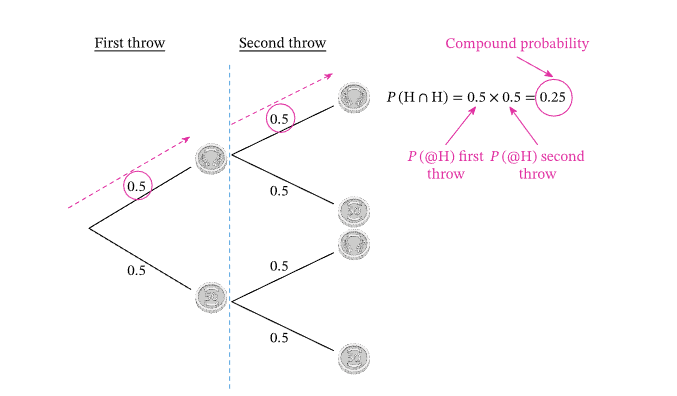
Using the same unbiased coin, the probability of getting “heads” on our second throw has not changed from \(\frac{1}{2}\) or \(0.5\). And we obtain the compound probability of getting one “head” after another by multiplying the probability of “head” on the first throw with the probability of “head” on the second throw. We can write this as
\(
P(\text { Heads } \cap \text { Heads })=0.5 \times 0.5=0.25 .
\)

Example 3: If these two spinners are spun, what is the probability that the sum of the numbers the arrows land on is a multiple of 5?

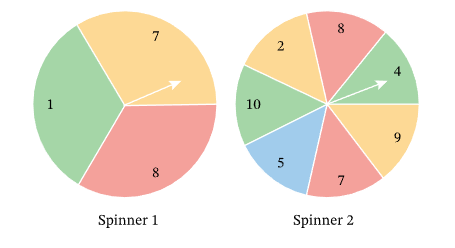
Solution:

To find the probability that the sum of the numbers the two arrows land on is a multiple of 5, let us first put all possible outcomes into a table. All possibilities for spinner 2 are in the blue block across the top and those for spinner 1 are in the red block down the left-hand side. The sums of the values on the two spinners are in the body of the table. So, for example, if spinner 2 lands with the pointer on 8 and spinner 1 lands with the pointer on 7, the sum is 15, which is below the column headed “8” and across the row labeled “7.”

To find the probability that the sum of the numbers on the two spinners is a multiple of 5, we need to know two things:

1. How many of the results are multiples of 5,
2. How many possibilities there are in total?

First, considering multiples of 5, we note that the range of values in the table is from 3 to 18. Between these two, the multiples of 5 are 5, 10, and 15. Let us mark the instances of 5, 10, and 15 in our table and count how many we have.

As we can see, there is one instance of the number 5 and two instances each of the numbers 10 and 15. We, therefore, have \(1+2+2=5\) “favorable outcomes,” that is, 5 instances where the sum on the two spinners is a multiple of 5.

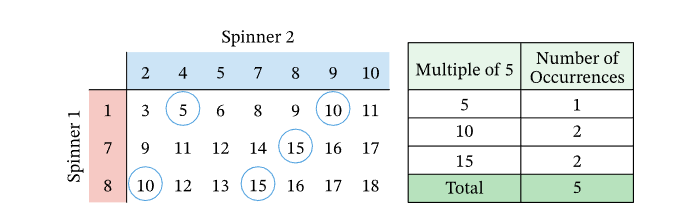
Remember, we are working out the probability that the sum of the two numbers is a multiple of 5. The second number we need in order to calculate this is the number of possibilities in total. We can find this by multiplying the number of rows by the number of columns in the body of our spinner results table (the number of rows corresponds to the number of segments on spinner 1 and the number of columns is the number of segments on spinner 2).
The total number of possible outcomes is therefore \(3 \times 7=21\); hence,
\(
\begin{aligned}
P(\text { sum is a multiple of } 5) & =\frac{\text { number of ways sum is a multiple of } 5}{\text { total possible outcomes }} \\
& =\frac{5}{21} .
\end{aligned}
\)

Independent Events

Two events are independent if the result of the first has no effect on the second. That is if the event \(A\) occurs does not affect the probability of event \(B\) occurring, If the probability of an event occurring is \(P(A)\), and the probability of a second event occurring is \(P(B)\), then the probability that both events will occur is:

For independent events,\(P(A \text { and } B)\)=\(P(A \cap B)=P(A) \times P(B)\)

Note: The total probability of events that are independent is found by multiplying the probability of these events. Many probability problems involve the blind selection of objects. If objects are selected with replacement, the events are treated as independent of one another. Selections of objects without replacement are dependent events.

Example 4: \(A\) and \(B\) are independent events, where \(P(A)=\frac{1}{3}\) and \(P(B)=\frac{2}{5}\). What is the probability that events \(A\) and \(B\) both occur?

Solution:

Given that events \(A\) and \(B\) are independent, the probability that they both occur is
\(
\begin{aligned}
P(A \cap B) & =P(A) \times P(B) \\
& =\frac{1}{3} \times \frac{2}{5} \\
& =\frac{2}{15}
\end{aligned}
\)

Example 5: Consider an example of rolling a die. If \(A\) is the event ‘the number appearing is odd’ and B is the event ‘the number appearing is a multiple of 3 ‘, then find the probability that the number appearing is odd and a multiple of 3.

Solution:

\(
P(A)=3 / 6=1 / 2 \text { and } P(B)=2 / 6=1 / 3
\)
Also \(\mathrm{A}\) and \(\mathrm{B}\) is the event ‘the number appearing is odd and a multiple of 3 ‘ so that
\(
P(A \cap B)=P(A) \times P(B)=1 / 2 \times 1 / 3=1 / 6
\)

Example 6: A juggler has seven red, five green, and four blue balls. During his stunt, he accidentally drops a ball and then picks it up. As he continues, another ball falls. What is the probability that the first ball that was dropped is blue, and the second ball is green?

Solution:

As we know that the first ball is picked by the juggler, the size of the sample space for both balls is 16, because these events are independent.

The probability that the first ball is blue or \(P(\) blue ball \()=4 / 16\)
The probability that the second ball is green or \(\mathrm{P}\) (green ball \()=\) \(4 / 16\)

The probability that the first ball is blue and the second ball is green:
\(P(\) blue and green \()=P(\) blue \() \times P(\) green \()=4 / 16 \times 4 / 16=1 / 16\)

Example 7: Two coins are flipped simultaneously. What is the probability of getting heads on either of these coins?

Solution:

The first thing that you realise is that these are independent events. Let us call the first coin toss as \(A\) and the second coin toss as \(B\).
Therefore we can write: \(P(A)=1 / 2\) i.e. probability of getting a head on the first coin toss \(=1 / 2\).

Similarly, the probability of getting a head on the second coin’s toss \(=1 / 2\). In other words, we can write that \(\mathrm{P}({B})=1 / 2\).
Hence the probability that either of the two coins will turn up a head \(=1 / 2 \times 1 / 2=\) \(1 / 4\)

Example 8: A die is cast twice and a coin is tossed twice. What is the probability that the die will turn a 6 each time and the coin will turn a tail every time?

Solution:

Each time the die is cast, it is an independent event. The probability of getting a 6 is \(=1 / 6\). So the probability of getting a 6 when the die is cast twice \(=1 / 6\) \(\times 1 / 6=1 / 36\)
Similarly the probability of getting a tail in two flips that follow each other (are independent \()=(1 / 2) \times(1 / 2)=1 / 4\)
Therefore as the two events i.e. casting the die and tossing the coin are independent, and the probability of both the events \(=(1 / 36) \times(1 / 4)=1 / 144\).

Mutually exclusive events

In probability theory, two events are said to be mutually exclusive if they cannot occur at the same time or simultaneously. In other words, mutually exclusive events are called disjoint events. If two events are considered disjoint events, then the probability of both events occurring at the same time will be zero.

If two events are mutually exclusive the probability of either event occurring is the sum of probabilities of each event occurring. If \(A\) and \(B\) are said to be mutually exclusive events then the probability of an event \(A\) occurring or the probability of event \(B\) occurring that is \(P(A \cup B)\) formula is given by 
\(P(A\) or \(B)=P(A \cup B)=P(A)+P(B)\)

If \(A\) and \(B\) are the two events, then the probability of disjoint of event \(A\) and \(B\) is written by:
Probability of Disjoint (or) Mutually Exclusive Event \(={P}({A}\) and \({B})=P(A \cap B)=0\)

Rules for Mutually Exclusive Events

From the definition of mutually exclusive events, certain rules for probability are concluded.

• Addition Rule: \(P(A+B)=1\)
• Subtraction Rule: \(P(A \cup B)^{\prime}=0\)
• Multiplication Rule: \(P(A \cap B)=0\)

Some of the examples of mutually exclusive events are:

• When tossing a coin, the event of getting head and tail are mutually exclusive. Because the probability of getting head and tail simultaneously is 0.
• In a six-sided die, the events “4” and “6” are mutually exclusive. We cannot get both events 4 and 6 at the same time when we threw one die.
• In a deck of 52 cards, drawing a red card and drawing a club are mutually exclusive events because all the clubs are black.

Note:
If the events \(A\) and \(B\) are not mutually exclusive, the probability of getting \(A[latex] or [latex]B\) that is \(P(A \cup B)\) formula is given as follows:
\(
P(A \cup B)=P(A)+P(B)-P(A \text { and } B)
\)

Example 9: Three coins are tossed at the same time. We say A as the event of receiving at least 2 heads. Likewise, B denotes the event of getting no heads and C is the event of getting heads on the second coin. Which of these is mutually exclusive?

Solution:

Firstly, let us create a sample space for each event. For the event \(A\) we have to get at least two heads. Therefore, we have to include all the events that have two or more heads.

Or we can write: \({A}=\{\mathrm{HHT}, \mathrm{HTH}, \mathrm{THH}, \mathrm{HHH}\}\).
This set \(A\) has 4 elements or events in it i.e. \(n(A)=4\)
In the same way, for event B, we can write the sample as:
\(B=\{\mathrm{TTT}\}\) and \(n(B)=1\)
Again using the same logic, we can write;
\({C}=\{\mathrm{THT}, \mathrm{HHH}, \mathrm{HHT}, \mathrm{THH}\}\) and \(\mathrm{n}(C)=4\)
So events \(B \& C\) and events \(A \& B\) are mutually exclusive since they have nothing in their intersection.

Example 10: \(\text { If } P(A)=2 / 3, P(B)=1 / 2 \text { and } P(A \cup B)=7 / 6 \text { then events } A \text { and } B \text { are: mutually exclusive or not? }
\)

Solution:

\(
\begin{aligned}
& P(A \cup B)=P(A)+P(B)-P(A \cap B) \\
& 7 / 6=(2 / 3)+(1 / 2)-P(A \cap B) \\
& \Rightarrow P(A \cap B)=0
\end{aligned}
\)
Therefore, events A and B are mutually exclusive.

Example 11:  The likelihood of the 3 teams A, B, and C winning a football match are 1 / 3, 1 / 5, and 1 / 9 respectively. Find the probability that

(i) out of the three teams, either team a or team b will win
(ii) either team a or team b or team c will win
(iii) none of the teams will win the match
(iv) neither team a nor team b will win the match

Solution:

(i) \(\mathrm{P}(\mathrm{A}\) or \(\mathrm{B}\) will win \()=1 / 3+1 / 5=8 / 15\)
(ii) \(P(A\) or \(B\) or \(C\) will win \()=1 / 3+1 / 5+1 / 9=29 / 45\)
(iii) \(P(\) none will win \()=1-P(A\) or \(B\) or C will win \()=1-29 / 45=16 / 45\)
(iv) \(P\) (neither \(A\) nor \(B\) will win \()=1-P(\) either \(A\) or \(B\) will win)
\(
\begin{aligned}
& =1-8 / 15 \\
& =7 / 15
\end{aligned}
\)

Example 12: A card is drawn at random from a well-shuffled deck of 52 cards. Find the probability that the card drawn is a king or an ace.

Solution:

As per the definition of mutually exclusive events, selecting an ace and selecting a king from a well-shuffled deck of 52 cards are termed mutually exclusive events.
Assume \(A\) to be the event of drawing a king and \(B\) to be the event of drawing an ace.
In a standard deck of 52 cards, there exist 4 kings and 4 aces.
\(P(\) an event \()=\) count of favourable outcomes \(/\) total count of outcomes
\(P(\) selecting a king from a standard deck of 52 cards \()=P(A)=4 / 52=1 / 13\)
\(P(\) selecting an ace from a standard deck of 52 cards \()=P(B)=4 / 52=1 / 13\)
To compute \(\mathrm{P}\) (king or ace).
By the formula of the addition theorem for mutually exclusive events,
\(
\begin{aligned}
& P(A \cup B)=P(A)+P(B) \\
& P(A \cup B)=(1 / 13)+(1 / 13) \\
& =2 / 13
\end{aligned}
\)
The probability of selecting a king or an ace from a well-shuffled deck of 52 cards \(=2 / 13\).

Dependent Events

If the two events are dependent, then the result of the first affects the outcome of the second. That is the event \(A\) occurs does affect the probability of \(B\) occurring.

When two events, \(A\) and \(B\) are dependent, the probability of occurrence of \(A\) and \(B\) is:
\(
P(A \text { and } B)=P(A \cap B)=P(A) \cdot P(B \mid A)
\)

\(P(B \mid A)\) represents the probability of event \(B\) knowing that event \(A\) has occurred already.
\(P(B \mid A)\) represents the conditional probability of event \(B\) given \(A\).

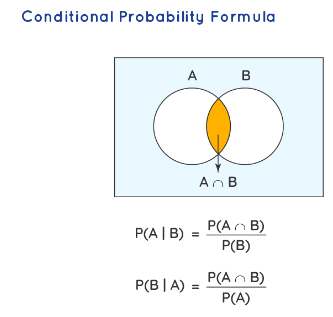
Conditional Probability

\({P}({A} \mid {B})={P}({A} \cap {B}) / {P}({B})(\) Note that \(P(B) \neq 0\) here)
Similarly, we can define \(P(B \mid A)\) as follows:
\(
{P}({B} \mid {A})={P}({A} \cap {B}) / {P}({A}) \text { (Note that } P(A) \neq 0 \text { here) }
\)

\(P(A \mid B)=\) The probability of A given \(B\) (or) the probability of \(A\) which happens after \(B\)
\(P(B \mid A)=\) The probability of \(B\) given \(A\) (or) the probability of \(B\) which happens after \(A\)
\(P(A \cap B)=\) The probability of happening of both \(A\) and \(B\)
\(P(A)=\) The probability of \(A\)
\(P(B)=\) The probability of \(B\)

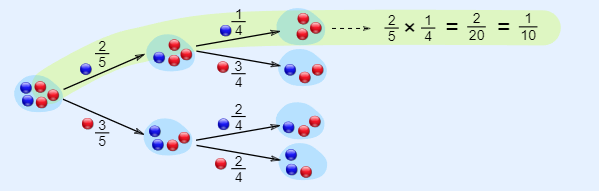
Example 13: Consider the Marbles in a Bag problem. If 2 blue and 3 red marbles are in a bag, What are the chances of getting a blue marble?

Solution:

The first time, the chance of getting a blue marble from the bag is = 2/5, as shown in the figure below.

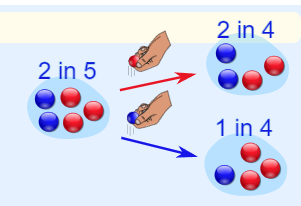
But after taking one out the chances changed (dependent event). So the next time: 

If we got a red marble before, then the chance of a blue marble next is 2/4. If we got a blue marble before, then the chance of a blue marble next is 1/4. This is because we are removing marbles from the bag. So the next event depends on what happened in the previous event and is called dependent.

A tree diagram is a wonderful way to picture what is going on, so let’s build one for the marble example. There is a 2/5 chance of pulling out a Blue marble, and a 3/5 chance for Red:

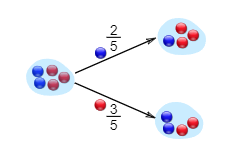
We can go one step further and see what happens when we pick a second marble:

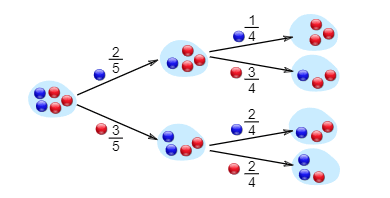
If a blue marble was selected first there is now a 1/4 chance of getting a blue marble and a 3/4 chance of getting a red marble.

If a red marble was selected first there is now a 2/4 chance of getting a blue marble and a 2/4 chance of getting a red marble.

“What are the chances of drawing 2 blue marbles?”

It is a 2/5 chance followed by a 1/4 chance. Therefore, the chance of drawing 2 blue marbles is 1/10.

Example 14: Find the probability of drawing 2 Kings from a Deck of 52 cards.

Solution:

Let’s assume event \(A\) is drawing a king first and \(B\) is drawing a king second.

For the first card, the chance of drawing a King is 4 out of 52 (there are 4 Kings in a deck of 52 cards):
\(
P(A)=4 / 52
\)
But after removing a King from the deck the probability of the 2 nd card drawn is less likely to be a King (only 3 of the 51 cards left are Kings):
\(
P(B \mid A)=3 / 51
\)
And so:
\(
{P}({A} \text { and } {B})={P}({A}) \times {P}({B} \mid {A})=(4 / 52) \times(3 / 51)=12 / 2652={1} / {2 2 1}
\)

Example 15: \(70 \%\) of your friends like Chocolate, and \(35 \%\) like Chocolate and like Strawberry. What percent of those who like Chocolate also like Strawberry?

Solution:

\({P}(\) Strawberry \(\mid\) Chocolate \()={P}(\) Chocolate and Strawberry \() / {P}(\) Chocolate \()\)
\(
0.35 / 0.7=50 \%
\)
\(50 \%\) of your friends who like Chocolate also like Strawberry

Example 16:  Ashok has to select two students from a class of 23 girls and 25 boys. What is the probability that both students chosen are boys?

Solution:

Total number of students \(=23+25=48\)
Probability of choosing the first boy, say Boy \(1=25 / 48\)
Probability of choosing the second boy, say Boy \(2=24 / 47\)
Now,
\(P(\) Boy 1 and Boy 2\()=P(\) Boy 1\()\) and \(P(\) Boy \(2 \mid\) Boy 1\()\)
\(=(25 / 48) \times(24 / 47)\)
\(=600 / 2256\)

Example 18:  In a survey found that 10 out of 15 people walk to the office. 3 persons are selected randomly. What is the probability that all three walk to the office?

Solution:

The probability that all three walk to the office = (3/15) × (2/14) × (1/13) = 6/2730

Example 19: A bag contains 6 red,  5 blue, and 4 yellow balls. 2 balls are drawn, but the first ball is drawn without replacement. Find the following. (i) P (red, then blue) (ii) P (blue, then blue).

Solution:

(i) There are six red balls and a total of fifteen balls.
\(
P(\text { red })=6 / 15
\)
The probability of the second draw affected the first.
Number of blue balls \(=5\)
Total number of balls left \(=14\)
\(P(\) drawing blue after red \()=5 / 14\)
\(P(\) drawing red, then blue \()=P(\) drawing red \() \times P\) (blue after red \()\)
\(
=\frac{6}{15} \times \frac{5}{14}=\frac{1}{7}
\)
1/ 7 will be the probability value of drawing a red ball followed by a blue ball.

(ii) Number of blue balls \(=5\)
Total number of balls left \(=15\)
The probability of drawing a blue ball \(=5 / 15\)
The probability of the second draw affected the first.
Now there are 4 blue balls left and a total of 14 balls left.
\(P(\) drawing a blue ball after a blue ball \()=4 / 14\)
\(P(\) blue, then blue \()=P(\) drawing blue ball \() \times (\) drawing a blue ball after a blue ball \()\)
\(
=\frac{5}{15} \times \frac{4}{14}=\frac{2}{21}
\)
Hence, the probability of drawing a red ball followed by a blue ball is \(2 / 21\).

Example 20:  In a pack of 52 cards, a card is drawn at random without replacement. Find the probability of drawing a king followed by a jack.

Solution:

\(P\) (drawing a king in the first place \()=4 / 52\)
\(P\) (drawing jack in the second place given that king is in the first place) \(=4 / 51\)
\(P\) (drawing a king followed by a jack)
\(
=\frac{4}{52} \times \frac{4}{51}=\frac{16}{2652}=\frac{4}{663}
\)

Example 21: A wallet contains 4 bills of 5 dollars, 5 bills of 10 dollars, and 3 bills of 20 dollars. 2 bills are chosen randomly without replacement. Find the P (drawing a 5-dollar bill followed by a 5-dollar bill).

Solution:

Number of 5 dollar bills \(=4\)
Total number of bills given \(=12\)
\(P(\) drawing a 5 dollar bill \()=4 / 12\)
The probability of the second draw affected the first.
Number of 5 dollar bills left \(=3\)
A total of 11 bills are left.
\(P\) (drawing a 5 dollar bill after a 5 dollar bill) \(=3 / 11\)
\(P\) (drawing a 5 dollar bill followed by a 5 dollar bill \()=P(\) drawing a 5 dollar bill \() \times\)  \(P\) (drawing a 5 dollar bill after a 5 dollar bill)
\(
=\frac{4}{12} \times \frac{3}{11}=\frac{1}{11}
\)
Hence the \(P\) (drawing a 5 dollar bill followed by a 5 dollar bill) \(=1 / 11\)

Example 22: Four green blocks and three red blocks are placed in a bag and selected at random. What is the probability of selecting two red blocks without replacement?

Solution:

The total number of blocks = 4+3=7.
There are 3 red blocks. The probability of selecting a red block is 3/7.
Once a red block is drawn, only 2 of 6 blocks that remain in the bag are red.
So the probability of the second block being red is 2/6.
Therefore, probability of selecting two red blocks without replacement = \(3 / 7 \times 2 / 6=1 / 7\)

Example 23: Four green blocks and three red blocks are placed in a bag and selected at random. What is the probability of selecting a green block and then a red block with a replacement?

Solution:

The total number of blocks = 4+3=7.
There are 4 green blocks. The probability of selecting a green block is 4/7.
Once it is replaced, the probability of the second block being red is 3/7.
Therefore, the probability of selecting a green block and then a red block with a replacement= \(4 / 7 \times 3 / 7=12 / 49\)

Example 24: Four green blocks and three red blocks are placed in a bag and selected at random. What is the probability of selecting three blocks of the same color without replacement?

Solution:Let the probability of selecting three green blocks = \(P(GGG)\)
Let the probability of selecting three red blocks = \(P(RRR)\)
So the probability of selecting three green blocks = \(P(GGG)=4/7 \times 3/6 \times 2/5=4/35\)
So the probability of selecting three red blocks = \(P(RRR)=3/7 \times 2/6 \times 1/5=1/35\)
Therefore, \(P(G G G \text { or } R R R)=4/35 + 1/35 = 5/35=1/7\)

Example 25: Andrews has to select two students from 35 girls and 15 boys to be part of a club. What is the probability that both students are girls?

Solution:

The total number of students \(=35+15=50\)
Probability of choosing the first girl, \(P(\) girl 1\()=\frac{35}{50}\)
Probability of choosing the second girl, \(\mathrm{P}(\) girl 2 \()=\frac{34}{49}\)
Now,
The probability that both students have chosen are girls
\(\mathrm{P}\) (first girl and second girl)
\(=\mathrm{P}(\) first girl \() \times \mathrm{P}(\) second girl \(\mid\) first girl \()\)
\(=\frac{35}{50} \times \frac{34}{49}\)
\(=\frac{1190}{1666}\)
\(=\frac{85}{119}\)