Projections

The best way to understand projections is to see a couple of sketches. So, given two vectors \(\vec{a}\) and \(\vec{b}\) we want to determine the projection of \(\vec{b}\) onto \(\vec{a}\). The projection is denoted by \(\operatorname{proj}_\vec{a} \vec{b}\). Here are a couple of sketches illustrating the projection.

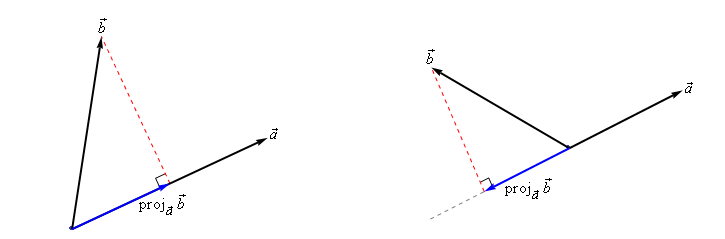
So, to get the projection of \(\vec{b}\) onto \(\vec{a}\) we drop straight down from the end of \(\vec{b}\) until we hit (and form a right angle) with the line that is parallel to \(\vec{a}\). The projection is then the vector that is parallel to \(\vec{a}\), starts at the same point both of the original vectors started at and ends where the dashed line hits the line parallel to \(\vec{a}\).
There is a nice formula for finding the projection of \(\vec{b}\) onto \(\vec{a}\). Here is the formula

\(
\operatorname{proj}_\vec{a} \vec{b}=\frac{\vec{a} \cdot \vec{b}}{\mid\vec{a}\mid^2} \vec{a}
\)

Silimarly, the projection of \(\vec{a}\) onto \(\vec{b}\) is given by
\(
\operatorname{proj}_\vec{b} \vec{a}=\frac{\vec{a} \cdot \vec{b}}{\mid\vec{b}\mid^2} \vec{b}
\)

Example 1: \(\text { Determine the projection of } \vec{b}=\langle 2,1,-1\rangle \text { onto } \vec{a}=\langle 1,0,-2\rangle \text {. }\)

Solution:

We need the dot product and the magnitude of \(\vec{a}\).
\(
\vec{a} \cdot \vec{b}=4, \quad\mid\vec{a}\mid^2=5
\)
The projection is then,
\(
\begin{aligned}
\operatorname{proj}_\vec{a} \vec{b} & =\frac{\vec{a} \cdot \vec{b}}{\mid\vec{a}\mid^2} \vec{a} \\
& =\frac{4}{5}\langle 1,0,-2\rangle \\
& =\left\langle\frac{4}{5}, 0,-\frac{8}{5}\right\rangle
\end{aligned}
\)

Example 2: \(\text { Determine the projection of } \vec{a}=\langle 1,0,-2\rangle \text { onto } \vec{b}=\langle 2,1,-1\rangle \text {. }\)

Solution:

We need the dot product and the magnitude of \(\vec{b}\).
\(
\vec{a} \cdot \vec{b}=4, \quad\mid\vec{b}\mid^2=6
\)
The projection is then,
\(
\begin{aligned}
\operatorname{proj}_\vec{b} \vec{a} & =\frac{\vec{a} \cdot \vec{b}}{\mid\vec{b}\mid^2} \vec{b} \\
& =\frac{4}{6}\langle 2,1,-1\rangle \\
& =\left\langle\frac{4}{3}, \frac{2}{3},-\frac{2}{3}\right\rangle
\end{aligned}
\)

Direction Cosines

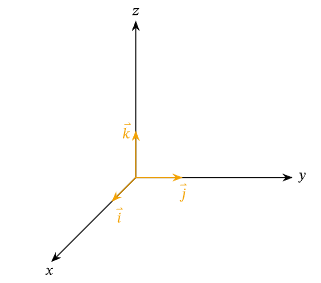
We know, in three-dimensional coordinate space, we have the \(x\)-, \(y\)-, and \(z\)-axes. These are perpendicular to one another as seen in the diagram below. The unit vectors \(\vec{i}, \vec{j}\), and \(\vec{k}\) act in the \(x-, y\)-, and \(z\)-directions respectively.

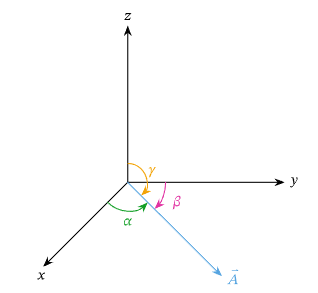
Definition: The Direction Angles

Given a vector \(\vec{A}=\left(A_x, A_y, A_z\right)\), the angles that this vector makes with the \(x\)-, \(y\)-, and \(z\)-axes, respectively, are \(\alpha, \beta\), and \(\gamma\). These are known as the direction angles and are written \((\alpha, \beta, \gamma)\).

These direction angles lead us to a definition for the direction cosines. We know, in right-angled trigonometry, the cosine of any angle \(\theta\) is equal to the length of the side adjacent to the angle divided by the length of the hypotenuse:
\(
\cos \theta=\frac{\text { adj }}{\text { hyp }} .
\)

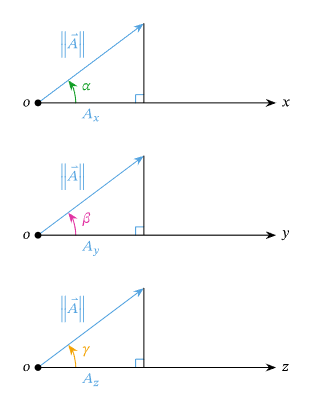
Definition: The Direction Cosines

The direction cosines are the cosines of the three direction angles, \(\alpha, \beta\), and \(\gamma\) : \(\cos \alpha=\frac{A_x}{\|\vec{A}\|}, \quad \cos \beta=\frac{A_y}{\|\vec{A}\|}, \quad \cos \gamma=\frac{A_z}{\|\vec{A}\|}\).
\(A_x, A_y\), and \(A_z\) are the \(x\)-, \(y\)-, and \(z\)-components of vector \(\vec{A}\), and \(\|\vec{A}\|\) is the magnitude or norm of this vector, where \(\|\vec{A}\|=\sqrt{\left(A_x\right)^2+\left(A_y\right)^2+\left(A_z\right)^2}\).

We can rearrange the three equations such that \(\alpha=\cos ^{-1}\left(\frac{A_x}{\|\vec{A}\|}\right), \quad \beta=\cos ^{-1}\left(\frac{A_y}{\|\vec{A}\|}\right), \quad \gamma=\cos ^{-1}\left(\frac{A_z}{\|\vec{A}\|}\right)\).

Example 3: Find vector \(\vec{A}\) whose norm is 41 and whose direction angles are \(\left(135^{\circ}, 120^{\circ}, 60^{\circ}\right)\).

Solution: The norm of a vector is its magnitude or length, and the direction angles \(\alpha, \beta\), and \(\gamma\) are the angles between the vector and the \(x-, y\)-, and \(z\)-axes respectively.
Using the formulae for the direction cosines, we know that, for a vector \(\vec{A}=\left(A_x, A_y, A_z\right)\), \(\cos \alpha=\frac{A_x}{\|\vec{A}\|}, \quad \cos \beta=\frac{A_y}{\|\vec{A}\|}, \quad \cos \gamma=\frac{A_z}{\|\vec{A}\|}\).
\(
\begin{aligned}
A_x & =\|\vec{A}\| \cos \alpha \\
& =41 \cos 135^{\circ} \\
& =\frac{-41 \sqrt{2}}{2}, \\
A_y & =\|\vec{A}\| \cos \beta \\
& =41 \cos 120^{\circ} \\
& =\frac{-41}{2},
\end{aligned}
\)
\(
\begin{aligned}
A_z & =\|\vec{A}\| \cos \gamma \\
& =41 \cos 60^{\circ} \\
& =\frac{41}{2}
\end{aligned}
\)
Multiplying each of these equations by \(\|\vec{A}\|\), the components of \(\vec{A}\) are as follows: Therefore, \(\vec{A}=\left(\frac{-41 \sqrt{2}}{2}, \frac{-41}{2}, \frac{41}{2}\right)\).

Formula that links the direction cosines

Consider the direction cosines as follows:
\(
\begin{aligned}
& \text { Consider the direction cosines as follows: } \cos \alpha=\frac{A_x}{\|\vec{A}\|}, \quad \cos \beta=\frac{A_y}{\|\vec{A}\|}, \quad \cos \gamma=\frac{A_z}{\|\vec{A}\|} . \\
& \text { Squaring } \quad \text { both } \quad \text { sides } \quad \text { of } \quad \text { these } \quad \text { three } \quad \text { equations } \\
& \cos ^2 \alpha=\frac{\left(A_x\right)^2}{(\|\vec{A}\|)^2}, \quad \cos ^2 \beta=\frac{\left(A_y\right)^2}{(\|\vec{A}\|)^2}, \quad \cos ^2 \gamma=\frac{\left(A_z\right)^2}{(\|\vec{A}\|)^2} .
\end{aligned}
\)
\(
\cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \gamma=\frac{\left(A_x\right)^2+\left(A_y\right)^2+\left(A_z\right)^2}{(\|\vec{A}\|)^2} .
\)
Adding these three equations, we get
We also know that \(\|\vec{A}\|=\sqrt{\left(A_x\right)^2+\left(A_y\right)^2+\left(A_z\right)^2}\).
So, \((\|\vec{A}\|)^2=\left(A_x\right)^2+\left(A_y\right)^2+\left(A_z\right)^2\).
This means that the right-hand side of the equation is equal to 1 . Therefore, \(\cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \gamma=1\).

Remarks

• Formula: Property of Direction Cosines for a Three-Dimensional Vector
  If \(\alpha, \beta\), and \(\gamma\) are the three direction angles and \(\cos \alpha, \cos \beta\), and \(\cos \gamma\) are their corresponding direction cosines, then \(\cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \gamma=1\).

Example 4: Suppose that \(31^{\circ}, 65^{\circ}\), and \(\theta\) are the direction angles of a vector. Which of the following, to the nearest hundredth, is \(\theta\) ?
A. \(72.88^{\circ}\)
B. \(85.03^{\circ}\)
C. \(264.00^{\circ}\)
D. \(84.00^{\circ}\)

Solution: In order to answer this question, we will use the fact that if the three direction angles of a vector are \(\alpha\), \(\beta\), and \(\gamma\), then \(\cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \gamma=1\).
\(
\begin{aligned}
\cos ^2 31^{\circ}+\cos ^2 65^{\circ}+\cos ^2 \theta & =1 \\
0.91334+\cos ^2 \theta & \approx 1
\end{aligned}
\)
If we let \(\alpha=31^{\circ}, \beta=65^{\circ}\), and \(\gamma=\theta^{\circ}\), we have,
\(
\cos ^2 \theta \approx 1-0.91334 .
\)
Taking the square root of both sides of our equation, \(\cos \theta \approx 0.29437\).
Taking the inverse cosine of both sides, \(\theta \approx 72.8797^{\circ}\).
So, the value of \(\theta\), to the nearest hundredth, is \(72.88^{\circ}\).

Example 5: Find the direction cosines of the vector \(\vec{A}=(5,2,8)\).

Solution: Given any vector \(\vec{A}\) with components \(A_x, A_y\), and \(A_z\), the direction cosines are \(\cos \alpha=\frac{A_x}{\|\vec{A}\|}, \quad \cos \beta=\frac{A_y}{\|\vec{A}\|}, \quad \cos \gamma=\frac{A_z}{\|\vec{A}\|}, \quad\) where \(\|\vec{A}\|=\sqrt{\left(A_x\right)^2+\left(A_y\right)^2+\left(A_z\right)^2}\).
\(
\|\vec{A}\|=\sqrt{(5)^2+(2)^2+(8)^2}
\)
Substituting \(A_x=5, A_y=2\), and \(A_z=8\), we have \(\|\vec{A}\|=\sqrt{93}\).
Therefore, \(\cos \alpha=\frac{5}{\sqrt{93}}, \quad \cos \beta=\frac{2}{\sqrt{93}}, \quad \cos \gamma=\frac{8}{\sqrt{93}}\).
The direction cosines of the vector \(\vec{A}\) are \(\left(\frac{5}{\sqrt{93}}, \frac{2}{\sqrt{93}}, \frac{8}{\sqrt{93}}\right)\).

Example 6: \(\text { Determine the direction cosines and direction angles for } \vec{a}=\langle 2,1,-4\rangle \text {. }\)

Solution:

We will need the magnitude of the vector.
\(
\mid\vec{a}\mid=\sqrt{4+1+16}=\sqrt{21}
\)
The direction cosines and angles are then,
\(
\begin{array}{ll}
\cos \alpha=\frac{2}{\sqrt{21}}, & \alpha=1.119 \text { radians }=64.123 \text { degrees } \\
\cos \beta=\frac{1}{\sqrt{21}}, & \beta=1.351 \text { radians }=77.396 \text { degrees } \\
\cos \gamma=\frac{-4}{\sqrt{21}}, & \gamma=2.632 \text { radians }=150.794 \text { degrees }
\end{array}
\)

Example 7: Find the direction angles of the vector \(\left(\frac{21}{2}, \frac{21 \sqrt{2}}{2}, \frac{21}{2}\right)\).

Solution: Given any vector \(\vec{A}\) with components \(A_x, A_y\), and \(A_z\), the direction cosines are
\(
\cos \alpha=\frac{A_x}{\|\vec{A}\|}, \quad \cos \beta=\frac{A_y}{\|\vec{A}\|}, \quad \cos \gamma=\frac{A_z}{\|\vec{A}\|},
\)
\(
\text { where }\|\vec{A}\|=\sqrt{\left(A_x\right)^2+\left(A_y\right)^2+\left(A_z\right)^2} \text {. }
\)
\(
\begin{aligned}
& \|\vec{A}\|=\sqrt{\left(\frac{21}{2}\right)^2+\left(\frac{21 \sqrt{2}}{2}\right)^2+\left(\frac{21}{2}\right)^2} \\
& \|\vec{A}\|=\sqrt{441}=21
\end{aligned}
\)
\(
\text { Substituting } A_x=\frac{21}{2}, A_y=\frac{21 \sqrt{2}}{2} \text {, and } A_z=\frac{21}{2} \text {, we have }
\)
Therefore, \(\quad \cos \alpha=\frac{\frac{21}{2}}{21}, \quad \cos \beta=\frac{\frac{21 \sqrt{2}}{2}}{21}, \quad \cos \gamma=\frac{\frac{21}{2}}{21}, \quad\) which simplify \(\quad\) to \(\cos \alpha=\frac{1}{2}, \quad \cos \beta=\frac{\sqrt{2}}{2}, \quad \cos \gamma=\frac{1}{2}\).
Taking the inverse cosine of both sides of these three equations, \(\alpha=60^{\circ}, \quad \beta=45^{\circ}, \gamma=60^{\circ}\).
The direction angles of the vector \(\left(\frac{21}{2}, \frac{21 \sqrt{2}}{2}, \frac{21}{2}\right)\) are \(\left(60^{\circ}, 45^{\circ}, 60^{\circ}\right)\).

Example 8: Find the measure of the direction angles of the vector \(\vec{F}\), represented by the given figure, corrected to one decimal place.

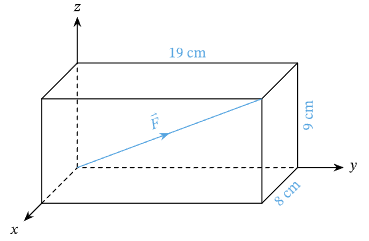
Solution: We begin by writing the vector \(\vec{F}\) in terms of its three components, where we will define 1 unit to be \(1 cm\).
In the \(x\)-direction, we travel \(8 cm\), so the \(x\)-component is 8 . In the \(y\)-direction, we travel \(19 cm\), so the \(y\)-component is 19 . In the \(z\)-direction, we travel \(9 cm\), so the \(z\)-component is 9 : \(\vec{F}=(8,19,9)\).
The magnitude of the vector is \(\|\vec{F}\|=\sqrt{\left(F_x\right)^2+\left(F_y\right)^2+\left(F_z\right)^2}\), where \(F_x, F_y\), and \(F_z\) are the \(x-, y\)-,and \(z\)-components of vector \(\vec{F}\).
\(
\begin{aligned}
\|\vec{F}\| & =\sqrt{(8)^2+(19)^2+(9)^2} \\
\|\vec{F}\| & =\sqrt{506} .
\end{aligned}
\)
Given any vector \(\vec{F}\) with components \(F_x, F_y\), and \(F_z\) and direction angles \(\theta_x, \theta_y\), and \(\theta_z\),
\(
\begin{gathered}
\theta_x=\cos ^{-1}\left(\frac{F_x}{\|\vec{F}\|}\right) \\
\theta_y=\cos ^{-1}\left(\frac{F_y}{\|\vec{F}\|}\right) \\
\theta_z=\cos ^{-1}\left(\frac{F_z}{\|\vec{F}\|}\right) \\
\theta_x=\cos ^{-1}\left(\frac{8}{\sqrt{506}}\right) \\
\theta_x=69.2^{\circ}, \\
\theta_y=\cos ^{-1}\left(\frac{19}{\sqrt{506}}\right) \\
\theta_y=32.4^{\circ}, \\
\theta_z=\cos ^{-1}\left(\frac{9}{\sqrt{506}}\right)
\end{gathered}
\)
So, \(\theta_z=66.4^{\circ}\).
Therefore, the direction angles of the vector \(\vec{F}\) are \(\theta_x=69.2^{\circ}, \theta_y=32.4^{\circ}, \theta_z=66.4^{\circ}\).

Key Points

• The direction angles \(\alpha, \beta\), and \(\gamma\) are the angles between a vector and the \(x-, y\)-, and \(z\)-axes respectively.
• The direction cosines are the cosines of the three direction angles, \(\alpha, \beta\), and \(\gamma\), such that \(\cos \alpha=\frac{A_x}{\|\vec{A}\|}, \quad \cos \beta=\frac{A_y}{\|\vec{A}\|}, \quad \cos \gamma=\frac{A_z}{\|\vec{A}\|}\).
• This means that \(\alpha, \beta\), and \(\gamma\) are as follows: \(\alpha=\cos ^{-1}\left(\frac{A_x}{\|\vec{A}\|}\right), \quad \beta=\cos ^{-1}\left(\frac{A_y}{\|\vec{A}\|}\right), \quad \gamma=\cos ^{-1}\left(\frac{A_z}{\|\vec{A}\|}\right)\).
• The following formula links the three direction cosines: \(\cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \gamma=1\).