Quiz
RELATION BETWEEN SYSTEM OF MEASUREMENT OF ANGLES :
\(\begin{aligned}
& \frac{ D }{90}=\frac{ G }{100}=\frac{2 C }{\pi} \\
& 1 \text { Radian }=\frac{180}{\pi} \text { degree } \approx 57^{\circ} 17^{\prime} 15^{\prime \prime} \text { (approximately) } \\
& 1 \text { degree }=\frac{\pi}{180} \text { radian } \approx 0.0175 \text { radian }
\end{aligned}
\)
BASIC TRIGONOMETRIC IDENTITIES
- \(\sin ^2 \theta+\cos ^2 \theta=1\) or \(\sin ^2 \theta=1-\cos ^2 \theta\) or \(\cos ^2 \theta=1-\sin ^2 \theta\)
- \(\sec ^2 \theta-\tan ^2 \theta=1\) or \(\sec ^2 \theta=1+\tan ^2 \theta\) or \(\tan ^2 \theta=\sec ^2 \theta-1\)
- If \(\sec \theta+\tan \theta= k \Rightarrow \sec \theta-\tan \theta=\frac{1}{ k } \Rightarrow 2 \sec \theta= k +\frac{1}{ k }\)
- \(\operatorname{cosec}^2 \theta-\cot ^2 \theta=1\) or \(\operatorname{cosec}^2 \theta=1+\cot ^2 \theta\) or \(\cot ^2 \theta=\operatorname{cosec}^2 \theta-1\)
- If \(\operatorname{cosec} \theta+\cot \theta= k \Rightarrow \operatorname{cosec} \theta-\cot \theta=\frac{1}{ k } \Rightarrow 2 \operatorname{cosec} \theta= k +\frac{1}{ k }\)
TRIGONOMETRIC FUNCTIONS OF ALLIED ANGLES
- \(\sin (2 n \pi+\theta)=\sin \theta, \cos (2 n \pi+\theta)=\cos \theta\), where \(n \in I\)
- \(\sin (-\theta)=-\sin \theta\)
\(
\begin{aligned}
& \cos (-\theta)=\cos \theta \\
& \cos \left(90^{\circ}-\theta\right)=\sin \theta \\
& \cos \left(90^{\circ}+\theta\right)=-\sin \theta \\
& \cos \left(180^{\circ}-\theta\right)=-\cos \theta \\
& \cos \left(180^{\circ}+\theta\right)=-\cos \theta \\
& \cos \left(270^{\circ}-\theta\right)=-\sin \theta \\
& \cos \left(270^{\circ}+\theta\right)=\sin \theta
\end{aligned}
\)
\(
\sin \left(90^{\circ}-\theta\right)=\cos \theta
\)
\(
\sin \left(90^{\circ}+\theta\right)=\cos \theta
\)
\(
\sin \left(180^{\circ}-\theta\right)=\sin \theta
\)
\(
\sin \left(180^{\circ}+\theta\right)=-\sin \theta
\)
\(
\sin \left(270^{\circ}-\theta\right)=-\cos \theta
\)
\(
\sin \left(270^{\circ}+\theta\right)=-\cos \theta
\)
Note :
(i) \(\sin n \pi=0 ; \cos n \pi=(-1)^n ; \tan n \pi=0\), where \(n \in I\)
(ii) \(\sin (2 n+1) \frac{\pi}{2}=(-1)^n ; \cos (2 n+1) \frac{\pi}{2}=0\), where \(n \in I\)
IMPORTANT TRIGONOMETRIC FORMULAE
- \(\quad \sin ( A + B )=\sin A \cos B +\cos A \sin B\).
- \(\quad \sin ( A – B )=\sin A \cos B -\cos A \sin B\).
- \(\quad \cos ( A + B )=\cos A \cos B -\sin A \sin B\)
- \(\quad \cos ( A – B )=\cos A \cos B +\sin A \sin B\)
- \(\tan (A+B)=\frac{\tan A+\tan B}{1-\tan A \tan B}\)
- \(\tan (A-B)=\frac{\tan A-\tan B}{1+\tan A \tan B}\)
- \(\cot ( A + B )=\frac{\cot B \cot A -1}{\cot B +\cot A }\)
- \(\cot ( A – B )=\frac{\cot B \cot A +1}{\cot B -\cot A }\)
- \(\quad 2 \sin A \cos B =\sin ( A + B )+\sin ( A – B )\).
- \(\quad 2 \cos A \sin B=\sin (A+B)-\sin (A-B)\).
- \(2 \cos A \cos B =\cos ( A + B )+\cos ( A – B )\)
- \(\quad 2 \sin A \sin B =\cos ( A – B )-\cos ( A + B )\)
- \(\sin C +\sin D =2 \sin \left(\frac{ C + D }{2}\right) \cos \left(\frac{ C – D }{2}\right)\)
- \(\sin C -\sin D =2 \cos \left(\frac{ C + D }{2}\right) \sin \left(\frac{ C – D }{2}\right)\)
- \(\quad \cos C +\cos D =2 \cos \left(\frac{ C + D }{2}\right) \cos \left(\frac{ C – D }{2}\right)\)
- \(\cos C -\cos D =2 \sin \left(\frac{ C + D }{2}\right) \sin \left(\frac{ D – C }{2}\right)\)
- \(\sin 2 \theta=2 \sin \theta \cos \theta=\frac{2 \tan \theta}{1+\tan ^2 \theta}\)
- \(\cos 2 \theta=\cos ^2 \theta-\sin ^2 \theta=2 \cos ^2 \theta-1=1-2 \sin ^2 \theta=\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta}\)
- \(1+\cos 2 \theta=2 \cos ^2 \theta\) or \(|\cos \theta|=\sqrt{\frac{1+\cos 2 \theta}{2}}\)
- \(1-\cos 2 \theta=2 \sin ^2 \theta\) or \(|\sin \theta|=\sqrt{\frac{1-\cos 2 \theta}{2}}\)
- \(\tan \theta=\frac{1-\cos 2 \theta}{\sin 2 \theta}=\frac{\sin 2 \theta}{1+\cos 2 \theta}\)
- \(\tan 2 \theta=\frac{2 \tan \theta}{1-\tan ^2 \theta}\)
- \(\cos 2 \theta=\cos ^2 \theta-\sin ^2 \theta=2 \cos ^2 \theta-1=1-2 \sin ^2 \theta=\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta}\)
- \(1+\cos 2 \theta=2 \cos ^2 \theta\) or \(|\cos \theta|=\sqrt{\frac{1+\cos 2 \theta}{2}}\)
- \(1-\cos 2 \theta=2 \sin ^2 \theta\) or \(|\sin \theta|=\sqrt{\frac{1-\cos 2 \theta}{2}}\)
- \(\tan \theta=\frac{1-\cos 2 \theta}{\sin 2 \theta}=\frac{\sin 2 \theta}{1+\cos 2 \theta}\)
- \(\tan 2 \theta=\frac{2 \tan \theta}{1-\tan ^2 \theta}\)
- \(\sin 3 \theta=3 \sin \theta-4 \sin ^3 \theta\).
- \(\cos 3 \theta=4 \cos ^3 \theta-3 \cos \theta\).
- \(\tan 3 \theta=\frac{3 \tan \theta-\tan ^3 \theta}{1-3 \tan ^2 \theta}\)
- \(\sin ^2 A-\sin ^2 B=\sin ( A + B ) \cdot \sin ( A – B )=\cos ^2 B-\cos ^2 A\).
- \(\cos ^2 A-\sin ^2 B=\cos ( A + B ) \cdot \cos ( A – B )\).
MAXIMUM & MINIMUM VALUES OF TRIGONOMETRIC EXPRESSIONS
- \(a\cos \theta+ b \sin \theta\) will always lie in the interval \(\left[-\sqrt{a^2+b^2}, \sqrt{a^2+b^2}\right]\), i.e. the maximum and minimum values are \(\sqrt{ a ^2+ b ^2},-\sqrt{ a ^2+ b ^2}\) respectively.
- Minimum value of \(a ^2 \tan ^2 \theta+ b ^2 \cot ^2 \theta=2 ab\), where \(a , b >0\)
- Minimum value of \(a^2 \cos ^2 \theta+b^2 \sec ^2 \theta\left(\right.\) or \(\left.a^2 \sin ^2 \theta+b^2 \operatorname{cosec}^2 \theta\right)\) is either 2 ab (when \(| a | \geq| b |\) ) or \(a ^2+ b ^2\) (when \(| a | \leq| b |\) ).
IMPORTANT RESULTS
- \(\sin \theta \sin \left(60^{\circ}-\theta\right) \sin \left(60^{\circ}+\theta\right)=\frac{1}{4} \sin 3 \theta\)
- \(\cos \theta \cdot \cos \left(60^{\circ}-\theta\right) \cos \left(60^{\circ}+\theta\right)=\frac{1}{4} \cos 3 \theta\)
- \(\tan \theta \tan \left(60^{\circ}-\theta\right) \tan \left(60^{\circ}+\theta\right)=\tan 3 \theta\)
- \(\cot \theta \cot \left(60^{\circ}-\theta\right) \cot \left(60^{\circ}+\theta\right)=\cot 3 \theta\)
- (i) \(\sin ^2 \theta+\sin ^2\left(60^{\circ}+\theta\right)+\sin ^2\left(60^{\circ}-\theta\right)=\frac{3}{2}\)
(ii) \(\cos ^2 \theta+\cos ^2\left(60^{\circ}+\theta\right)+\cos ^2\left(60^{\circ}-\theta\right)=\frac{3}{2}\) - (i) If \(\tan A+\tan B+\tan C=\tan A \tan B \tan C\), then \(A + B + C = n \pi, n \in I\)
(ii) If \(\tan A \tan B +\tan B \tan C +\tan C \tan A =1\), then \(A+B+C=(2 n+1) \frac{\pi}{2}, n \in I\) - \(\cos \theta \cos 2 \theta \cos 4 \theta \ldots \cdot \cos \left(2^{n-1} \theta\right)=\frac{\sin \left(2^n \theta\right)}{2^n \sin \theta}\)
- \(\cot A-\tan A =2 \cot 2 A\)
CONDITIONAL IDENTITIES
If \(A + B + C =180^{\circ}\), then
- \(\tan A+\tan B+\tan C=\tan A \tan B \tan C\)
- \(\cot A \cot B +\cot B \cot C +\cot C \cot A =1\)
- \(\tan \frac{ A }{2} \tan \frac{ B }{2}+\tan \frac{ B }{2} \tan \frac{ C }{2}+\tan \frac{ C }{2} \tan \frac{ A }{2}=1\)
- \(\cot \frac{ A }{2}+\cot \frac{ B }{2}+\cot \frac{ C }{2}=\cot \frac{ A }{2} \cot \frac{ B }{2} \cot \frac{ C }{2}\)
- \(\sin 2 A+\sin 2 B+\sin 2 C =4 \sin A \sin B \sin C\)
- \(\cos 2 A+\cos 2 B+\cos 2 C =-1-4 \cos A \cos B \cos C\)
- \(\sin A +\sin B +\sin C =4 \cos \frac{ A }{2} \cos \frac{ B }{2} \cos \frac{ C }{2}\)
- \(\cos A +\cos B +\cos C =1+4 \sin \frac{ A }{2} \sin \frac{ B }{2} \sin \frac{ C }{2}\)
DOMAINS, RANGES ANDPERIODICITY OF TRIGONOMETRIC FUNCTIONS
\(\begin{array}{llcr}
\text { T-Ratio } & \text{ Domain } & \text { Range } & \text { Period } \\
\sin x & R & {[-1,1]} & 2 \pi \\
\cos x & R & {[-1,1]} & 2 \pi \\
\tan x & R-\{(2 n+1) \pi / 2 ; n \in I\} & R & \pi \\
\cot x & R-[n \pi: n \in I] & R & \pi \\
\sec x & R-\{(2 n+1) \pi / 2: n \in I\} & (-\infty,-1] \cup[1, \infty) & 2 \pi \\
\operatorname{cosec} x & R-\{n \pi: n \in I\} & (-\infty,-1] \cup[1, \infty) & 2 \pi
\end{array}
\)
IMPORTANT NOTES
- The sum of interior angles of a polygon of \(n\)-sides
\(
=( n -2) \times 180^{\circ}=( n -2) \pi \text {. }
\) - Each interior angle of a regular polygon of n sides
\(
=\frac{( n -2)}{ n } \times 180^{\circ}=\frac{( n -2)}{ n } \pi \text {. }
\) - Sum of exterior angles of a polygon of any number of sides \(=360^{\circ}=2 \pi\).
GENERAL SOLUTIONS OF SOME TRIGONOMETRIC EQUATIONS (TO BE REMEMBERED)
- If \(\sin \theta=0\), then \(\theta= n \pi, n \in I\) (set of integers)
- If \(\cos \theta=0\), then \(\theta=(2 n+1) \frac{\pi}{2}, n \in I\)
- If \(\tan \theta=0\), then \(\theta= n \pi, n \in I\)
- If \(\sin \theta=\sin \alpha\), then \(\theta= n \pi+(-1)^{ n } \alpha, n \in I\)
- If \(\cos \theta=\cos \alpha\), then \(\theta=2 n \pi \pm \alpha, n \in I\)
- If \(\tan \theta=\tan \alpha\), then \(\theta= n \pi+\alpha, n \in I\)
- If \(\sin \theta=1\), then \(\theta=2 n \pi+\frac{\pi}{2}=(4 n+1) \frac{\pi}{2}, n \in I\)
- If \(\cos \theta=1\) then \(\theta=2 n \pi, n \in I\)
(i) If \(\sin ^2 \theta=\sin ^2 \alpha\) or \(\cos ^2 \theta=\cos ^2 \alpha\) or \(\tan ^2 \theta=\tan ^2 \alpha\), then \(\theta= n \pi \pm \alpha, n \in I\)
(j) \(\begin{aligned} & \sin ( n \pi+\theta)=(-1)^{ n } \sin \theta, n \in I \\ & \cos ( n \pi+\theta)=(-1)^{ n } \cos \theta, n \in I \end{aligned}\)
GENERAL SOLUTION OF EQUATION \(a \sin \theta+ b \cos \theta= c\)
Consider, \(a \sin \theta+ b \cos \theta= c \dots(i)\)
\(\therefore \frac{ a }{\sqrt{ a ^2+ b ^2}} \sin \theta+\frac{ b }{\sqrt{ a ^2+ b ^2}} \cos \theta=\frac{ c }{\sqrt{ a ^2+ b ^2}}\)
equation (i) has the solution only if \(|c| \leq \sqrt{a^2+b^2}\)
let \(\frac{ a }{\sqrt{ a ^2+ b ^2}}=\cos \phi, \frac{ b }{\sqrt{ a ^2+ b ^2}}=\sin \phi \quad \& \phi=\tan ^{-1} \frac{ b }{ a }\)
by introducing this auxiliary argument \(\phi\), equation (i) reduces to
\(
\sin (\theta+\phi)=\frac{c}{\sqrt{a^2+b^2}}
\)
Now this equation can be solved easily.
Quiz Summary
0 of 100 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 100 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 100
1. Question
\(
\text { Solve the equation exactly: } 2 \cos \theta-3=-5,0 \leq \theta<2 \pi \text {. }
\)CorrectIncorrectHint
\(
\begin{gathered}
2 \cos \theta-3=-5 \\
2 \cos \theta=-2 \\
\cos \theta=-1 \\
\theta=\pi
\end{gathered}
\) -
Question 2 of 100
2. Question
\(
\text { Solve the equation exactly using an identity: } 3 \cos \theta+3=2 \sin ^2 \theta, 0 \leq \theta<2 \pi \text {. }
\)CorrectIncorrectHint
If we rewrite the right side, we can write the equation in terms of cosine:
\(
\begin{aligned}
3 \cos \theta+3 & =2 \sin ^2 \theta \\
3 \cos \theta+3 & =2\left(1-\cos ^2 \theta\right) \\
3 \cos \theta+3 & =2-2 \cos ^2 \theta \\
2 \cos ^2 \theta+3 \cos \theta+1 & =0 \\
(2 \cos \theta+1)(\cos \theta+1) & =0 \\
2 \cos \theta+1 & =0 \\
\cos \theta & =-\frac{1}{2} \\
\theta & =\frac{2 \pi}{3}, \frac{4 \pi}{3} \\
\cos \theta+1 & =0 \\
\cos \theta & =-1 \\
\theta & =\pi
\end{aligned}
\)
Our solutions are \(\theta=\frac{2 \pi}{3}, \frac{4 \pi}{3}, \pi\). -
Question 3 of 100
3. Question
\(
\text { what is the cosine of } 370^{\circ} \text { ? }
\)CorrectIncorrectHint
\(370^{\circ}\) is greater than \(360^{\circ}\) so let us subtract \(360^{\circ}\)
\(
\begin{gathered}
370^{\circ}-360^{\circ}=10^{\circ} \\
\cos \left(370^{\circ}\right)=\cos \left(10^{\circ}\right)=\mathbf{0 . 9 8 5} \text { (to } 3 \text { decimal places) }
\end{gathered}
\) -
Question 4 of 100
4. Question
Find the missing angle measure in the triangle given below.
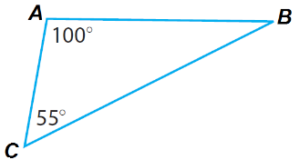 CorrectIncorrect
CorrectIncorrectHint
\(
m \angle B+155^{\circ}=180^{\circ}
\)\(
m \angle B=25^{\circ}
\) -
Question 5 of 100
5. Question
\(
\text { What is the sine of } 35^{\circ} \text { ? }
\)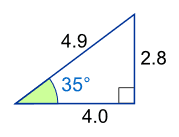 CorrectIncorrect
CorrectIncorrectHint
\(
\begin{aligned}
\sin \left(35^{\circ}\right) & =\frac{\text { Opposite }}{\text { Hypotenuse }} \\
& =\frac{2.8}{4.9} \\
& =\mathbf{0 . 5 7}
\end{aligned}
\) -
Question 6 of 100
6. Question
Two friends, Rakesh and Vishal started climbing a pyramid-shaped hill. Rakesh climbs 315 m and finds that the angle of depression is 72.3 degrees from his starting point. How high is he from the ground?
CorrectIncorrectHint
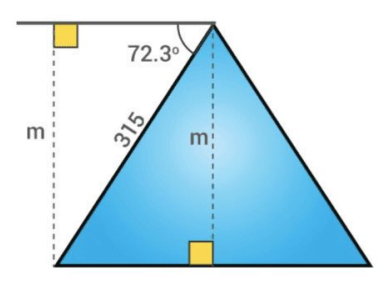
To solve \(m\), use the sine ratio.
\(\operatorname{Sin} 72.3^{\circ}=m / 315\)
\(0.953=\mathrm{m} / 315\)
\(m=315 \times 0.953\)
\(m=300.195 \mathrm{mtr}\)
The man is \(300.195 \mathrm{mtr}\) above the ground. -
Question 7 of 100
7. Question
A man is observing a pole of height 55 foot. According to his measurement, pole cast a 23 feet long shadow. Can you help him to know the angle of elevation of the sun from the tip of the shadow?
CorrectIncorrectHint
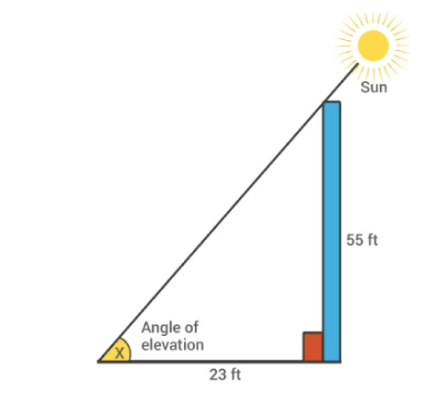
Let \(x\) be the angle of elevation of the sun, then
\(
\begin{aligned}
& \tan x=55 / 23=2.391 \\
& x=\tan ^{-1}(2.391)
\end{aligned}
\)
or \(x=67.30\) degrees -
Question 8 of 100
8. Question
\(
\text { From the given figure, find } \tan P-\cot R \text {. }
\)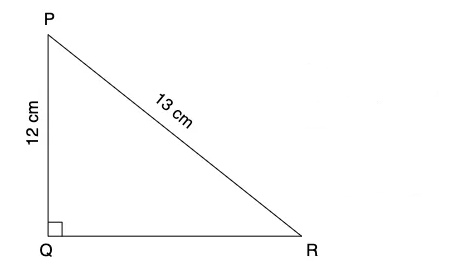 CorrectIncorrect
CorrectIncorrectHint
From the given,
\(
\begin{aligned}
& P Q=12 \mathrm{~cm} \\
& \mathrm{PR}=13 \mathrm{~cm}
\end{aligned}
\)
In the right triangle \(P Q R, Q\) is right angle.
By Pythagoras theorem,
\(
\begin{aligned}
& \mathrm{PR}^2=\mathrm{PQ}^2+\mathrm{QR}^2 \\
& \mathrm{QR}^2=(13)^2-(12)^2 \\
& =169-144 \\
& =25 \\
& \mathrm{QR}=5 \mathrm{~cm} \\
& \tan \mathrm{P}=\mathrm{QR} / \mathrm{PQ}=5 / 12 \\
& \cot \mathrm{R}=\mathrm{QR} / \mathrm{PQ}=5 / 12
\end{aligned}
\)
So, \(\tan \mathrm{P}-\cot \mathrm{R}=(5 / 12)-(5 / 12)=0\) -
Question 9 of 100
9. Question
\(
\left(\sin ^4 \theta-\cos ^4 \theta+1\right) \operatorname{cosec}^2 \theta=?
\)CorrectIncorrectHint
\(
\begin{aligned}
& \left(\sin ^4 \theta-\cos ^4 \theta+1\right) \operatorname{cosec}^2 \theta \\
& =\left[\left(\sin ^2 \theta-\cos ^2 \theta\right)\left(\sin ^2 \theta+\cos ^2 \theta\right)+1\right] \operatorname{cosec}^2 \theta \\
& \text { Using the identity } \sin ^2 A+\cos ^2 A=1 \\
& =\left(\sin ^2 \theta-\cos ^2 \theta+1\right) \operatorname{cosec}^2 \theta \\
& =\left[\sin ^2 \theta-\left(1-\sin ^2 \theta\right)+1\right] \operatorname{cosec}^2 \theta \\
& =2 \sin ^2 \theta \operatorname{cosec}^2 \theta \\
& =2 \sin ^2 \theta\left(1 / \sin ^2 \theta\right) \\
& =2
\end{aligned}
\) -
Question 10 of 100
10. Question
\(
\text { If } \sin 3 A=\cos \left(A-26^{\circ}\right) \text {, where } 3 A \text { is an acute angle, find the value of } A \text {. }
\)CorrectIncorrectHint
Given,
\(\sin 3 A=\cos \left(A-26^{\circ}\right) ; 3 A\) is an acute angle
\(
\begin{aligned}
& \cos \left(90^{\circ}-3 A\right)=\cos \left(A-26^{\circ}\right)\left\{\text { since } \cos \left(90^{\circ}-A\right)=\sin A\right\} \\
& \Rightarrow 90^{\circ}-3 A=A-26 \\
& \Rightarrow 3 A+A=90^{\circ}+26^{\circ} \\
& \Rightarrow 4 A=116^{\circ} \\
& \Rightarrow A=116^{\circ} / 4 \\
& \Rightarrow A=29^{\circ}
\end{aligned}
\) -
Question 11 of 100
11. Question
\(
\text { If } \tan \theta+\sec \theta=l \text {, then } \sec \theta=?
\)CorrectIncorrectHint
Given,
\(
\tan \theta+\sec \theta=l \text {….(i) }
\)
We know that,
\(
\begin{aligned}
& \sec ^2 \theta-\tan ^2 \theta=1 \\
& (\sec \theta-\tan \theta)(\sec \theta+\tan \theta)=1 \\
& (\sec \theta-\tan \theta) l=1\{\text { from (i) }\} \\
& \sec \theta-\tan \theta=1 / l \ldots \text { (ii) } \\
& \text { Adding (i) and (ii), } \\
& \tan \theta+\sec \theta+\sec \theta-\tan \theta=l+(1 / l) \\
& 2 \sec \theta=\left(l^2+1\right) l \\
& \sec \theta=\left(l^2+1\right) / 2 l
\end{aligned}
\) -
Question 12 of 100
12. Question
\(
\text { If } a \sin \theta+b \cos \theta=c \text {, then } a \cos \theta-b \sin \theta=?
\)CorrectIncorrectHint
Given,
\(a \sin \theta+b \cos \theta=c\)
Squaring on both sides,
\((a \sin \theta+b \cos \theta)^2=c^2\)
\(a^2 \sin ^2 \theta+b^2 \cos ^2 \theta+2 a b \sin \theta \cos \theta=c^2\)
Using the identity \(\sin ^2 A+\cos ^2 A=1\),
\(a^2\left(1-\cos ^2 \theta\right)+b^2\left(1-\sin ^2 \theta\right)+2 a b \sin \theta \cos \theta=c^2\)
\(a^2-a^2 \cos ^2 \theta+b^2-b^2 \sin ^2 \theta+2 a b \sin \theta \cos \theta=c^2\)
\(a^2+b^2-c^2=a^2 \cos ^2 \theta+b^2 \sin ^2 \theta-2 a b \sin \theta \cos \theta\)
\(a^2+b^2-c^2=(a \cos \theta-b \sin \theta)^2\)
\(\Rightarrow a \cos \theta-b \sin \theta=\sqrt{ }\left(a^2+b^2-c^2\right)\) -
Question 13 of 100
13. Question
An airplane is approaching point A along a straight line and at a constant altitude h. At 10:00 am, the angle of elevation of the airplane is \(20^{\circ}\) and at 10:01 it is \(60^{\circ}\). What is the altitude \(h\) of the airplane if the speed of the airplane is constant and equal to 600 miles/hour? (round answer to 2 decimal places).
CorrectIncorrectHint
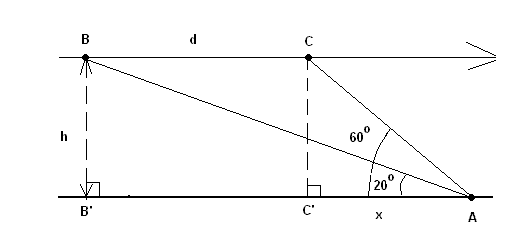
We first calculate distance \(d\) using the time and speed ( 1 minute \(=1 / 60\) hour)
\(
d=600 \times (1 / 60)=10 \text { miles }
\)
We next express the tangent of the given angles of elevation as follows
\(
\tan \left(20^{\circ}\right)=h /(d+x)
\)
and
\(
\tan \left(60^{\circ}\right)=\mathrm{h} / \mathrm{x}
\)
Eliminate \(x\) in the two equations above to find a relationship between \(\mathrm{h}\) and \(\mathrm{d}\)
\(
\mathrm{h}=\mathrm{d} /\left[1 / \tan \left(20^{\circ}\right)-1 / \tan \left(60^{\circ}\right)\right]
\)
\(=4.6\) miles (rounded to 2 decimal places) -
Question 14 of 100
14. Question
\(
\text { Determine the exact value of } \cos \left(\frac{5 \pi}{6}\right) \text { without using a calculator. }
\)CorrectIncorrectHint
First, we can notice that \(\pi-\frac{\pi}{6}=\frac{5 \pi}{6}\) and so the terminal line for \(\frac{5 \pi}{6}\) will form an angle of \(\frac{\pi}{6}\) with the negative \(x\)-axis in the second quadrant and we’ll have the following unit circle for this problem.
The coordinates of the line representing \(\frac{5 \pi}{6}\) will be the same as the coordinates of the line representing \(\frac{\pi}{6}\) except that the \(x\) coordinate will now be negative. So, our new coordinates will then be \(\left(-\frac{\sqrt{3}}{2}, \frac{1}{2}\right)\) and so the answer is,
\(
\cos \left(\frac{5 \pi}{6}\right)=-\frac{\sqrt{3}}{2}
\)
-
Question 15 of 100
15. Question
\(
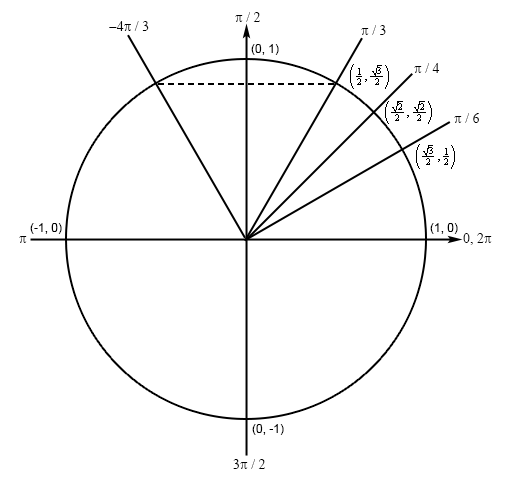
\text { Determine the exact value of } \sin \left(-\frac{4 \pi}{3}\right) \text { without using a calculator. }
\)CorrectIncorrectHint
First we can notice that \(-\pi-\frac{\pi}{3}=-\frac{4 \pi}{3}\) and so (remembering that negative angles are rotated clockwise) we can see that the terminal line for \(-\frac{4 \pi}{3}\) will form an angle of \(\frac{\pi}{3}\) with the negative \(x\)-axis in the second quadrant and we’ll have the following unit circle for this problem. The coordinates of the line representing \(-\frac{4 \pi}{3}\) will be the same as the coordinates of the line representing \(\frac{\pi}{3}\) except that the \(x\) coordinate will now be negative. So, our new coordinates will then be \(\left(-\frac{1}{2}, \frac{\sqrt{3}}{2}\right)\) and so the answer is,
\(
\sin \left(-\frac{4 \pi}{3}\right)=\frac{\sqrt{3}}{2}
\)
-
Question 16 of 100
16. Question
Find the value of x of the right isosceles triangle.
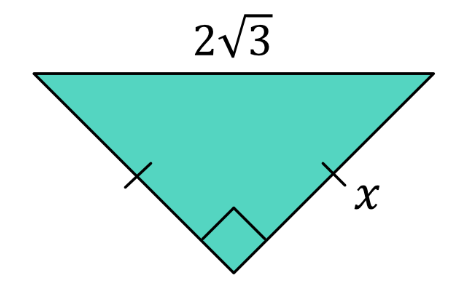 CorrectIncorrect
CorrectIncorrectHint
\(x^2+x^2=12\) and solve for x.
-
Question 17 of 100
17. Question
Shane marched 3 m east and 6 m north. How far is he from his starting point?
CorrectIncorrectHint
First, sketch the scenario. The path taken by Shane forms a right-angled triangle. The distance from the starting point forms the hypotenuse.
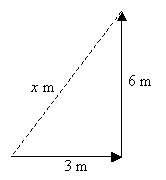
\(
x=\sqrt{3^2+6^2}=6.71 \mathrm{~m}
\) -
Question 18 of 100
18. Question
In the following diagram of a circle, \(\mathrm{O}\) is the centre and the radius is 12 \(\mathrm{cm}\). \(A B\) and \(E F\) are straight lines. \(
\text { Find the length of } E F \text { if the length of } O P \text { is } 6 \mathrm{~cm} \text {. }
\)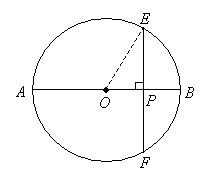 CorrectIncorrect
CorrectIncorrectHint
\(\mathrm{OE}\) is the radius of the circle, which is \(12 \mathrm{~cm}\)
\(
\begin{aligned}
& O P^2+P E^2=O E^2 \\
& 6^2+P E^2=12^2 \\
& P E=\sqrt{12^2-6^2} \\
& E F=2 \times P E=20.78 \mathrm{~cm}
\end{aligned}
\) -
Question 19 of 100
19. Question
A 35-foot ladder is leaning against the side of a building and it is positioned such that the base of the ladder is 21 feet from the base of the building. Find the distance above the ground where the point of the ladder touches the building.
CorrectIncorrectHint
Let the point above the ground \(=x\)
As given in the question,
Length of the foot ladder \(=35\)
Base of the ladder \(=21\) feet
Let the equation be \(a^2+b^2=c^2\)
\(
(21)^2+(x)^2=(35)^2
\)
\(441+x=1225\)
Subtracting by 441 on both sides
\(
x^2=784
\)
Squaring and both sides
\(
x=\sqrt{ } 784=28
\)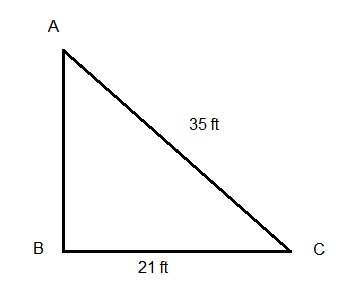
-
Question 20 of 100
20. Question
The main mast of a fishing boat is supported by a sturdy rope that extends from the top of the mast to the deck. If the mast is 20 feet tall and the rope is attached to the deck 15 feet away from the base of the mast, how long is the rope?
CorrectIncorrectHint
\(
\begin{aligned}
15^2+20^2 & =r^2 \\
225+400 & =r^2 \\
\sqrt{625} & =\sqrt{r^2} \\
25 & =r
\end{aligned}
\) -
Question 21 of 100
21. Question
Two cars leave an intersection. One car travels north; the other east. When the car traveling north had gone 15 mi, the distance between the cars was 5 mi more than the distance traveled by the car heading east. How far had the eastbound car traveled?
CorrectIncorrectHint
\(
\text { Draw a diagram, letting } x \text { be the distance covered by the car travelling eastbound. }
\)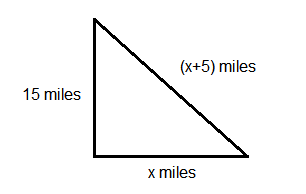
By Pythagorean theorem (since the directions east and north make a right angle) we have:
\(
\begin{aligned}
& 15^2+x^2=(x+5)^2 \\
& 225+x^2=x^2+10 x+25 \\
& 225-25=10 x \\
& 200=10 x \\
& x=20
\end{aligned}
\)
Hence, the eastbound car has travelled 20 miles. -
Question 22 of 100
22. Question
Shari went to a level field to fly a kite. She let out all 650 feet of the string and tied it to a stake. Then, she walked out on the field until she was directly under the kite, which was 600 feet from the stake. How high was the kite from the ground?
CorrectIncorrectHint
Because this forms a right triangle, with the 650 feet of string being the hypotenuse, use the pythagorean theorem, \(a^2+b^2=c^2\). A is \(600 \mathrm{ft}\) and \(c\) is \(650 \mathrm{ft}\).
Set up the equation:
\(
\begin{aligned}
& 600^2+x^2=650^2 \\
& 360000+x^2=422500 \\
& x^2=62500 \\
& x=250
\end{aligned}
\)
The kite was 250 feet high off the ground. -
Question 23 of 100
23. Question
If the height of a triangle is 17 inches less than the length of its base and the length of the hypotenuse is 25 inches, find the base and the height.
CorrectIncorrectHint
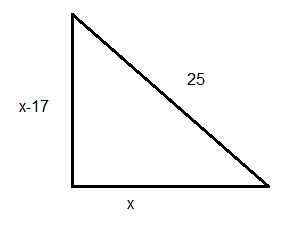
In the right triangle above, according to the Pythagorean theorem, we have
\(
(x-17)^2+x^2=25^2
\)
\(
x=-7 \text { or } x=24
\)
Because the base of a triangle can never be a negative value, we can ignore \(x=-7\).
So, the value \(x\) is 24 .
Then,
\(
x-17=24-17=7
\)
So, the base and height of the right triangle are 24 inches and 7 inches respectively. -
Question 24 of 100
24. Question
\(
\text { Determine the smallest integer } p \text { for which the equation } 4 \sin x=p \text { has no solution. }
\)CorrectIncorrectHint
\(
\begin{aligned}
& -1 \leq \sin x \leq 1 \\
& -4 \leq 4 \sin x \leq 4 \\
& p=4+1=5
\end{aligned}
\) -
Question 25 of 100
25. Question
According to the map, the scouts were supposed to proceed through the forest perpendicular to its straight edge, where the goal was \(3 \mathrm{~km}\) away from the starting point. They already deviated from the correct direction by \(5^{\circ}\) at the start. How far from the target did they get out of the forest?
CorrectIncorrectHint
\(
\begin{aligned}
& a=3 \mathrm{~km} \\
& \alpha=5^{\circ} \\
& \tan \alpha=x / a \\
& x=a \cdot \tan \alpha=a \cdot \tan 5^{\circ}=3 \cdot \tan 5^{\circ}=3 \cdot 0.087489=0.262=0.2625 \mathrm{~km}
\end{aligned}
\) -
Question 26 of 100
26. Question
\(
\text { When the sun is } 22^{\circ} \text { above the horizon, how long is the shadow cast by a building that is } 60 \text { meters high? }
\)CorrectIncorrectHint
To solve this problem, first set up a diagram that shows all of the info given in the problem.
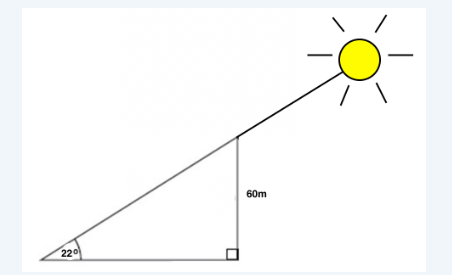
Next, we need to interpret which side length corresponds to the shadow of the building, which is what the problem is asking us to find. Is it the hypotenuse, or the base of the triangle? Think about when you look at a shadow. When you see a shadow, you are seeing it on something else, like the ground, the sidewalk, or another object. We see the shadow on the ground, which corresponds to the base of our triangle, so that is what we’ll be solving for. We’ll call this base \(b\).
Next, think about which trig functions relate our known angle, \(22^{\circ}\), to the base (or adjacent) and the opposite sides of the triangle. If you thought tangent (or cotangent), you are correct! We know that \(\tan x=\frac{\text { opposite }}{\text { adjacent }}\) and \(\cot x=\frac{\text { adjacent }}{\text { opposite }}\). For simplicity’s sake, we’ll use tangent to solve this problem. We have:
\(
\begin{aligned}
& \tan 22^{\circ}=\frac{60}{b} \\
& b=\frac{60}{\tan 22^{\circ}} \\
& b=\frac{60}{.4} \text { (Use a calculator and round to two places to find that } \tan 22^{\circ}=.40 \text { ) } \\
& b=150 \text { meters }
\end{aligned}
\)
Therefore the shadow cast by the building is 150 meters long. -
Question 27 of 100
27. Question
From the top of a lighthouse that sits 105 meters above the sea, the angle of depression of a boat is \(19^{\circ}\). How far from the boat is the top of the lighthouse?
CorrectIncorrectHint
To solve this problem, we need to create a diagram, but in order to create that diagram, we need to understand the vocabulary that is being used in this question. The following diagram clarifies the difference between an angle of depression (an angle that looks downward; relevant to our problem) and the angle of elevation (an angle that looks upward; relevant to other problems, but not this specific one.) Imagine that the top of the blue altitude line is the top of the lighthouse, the green line labelled GroundHorizon is sea level, and point B is where the boat is.
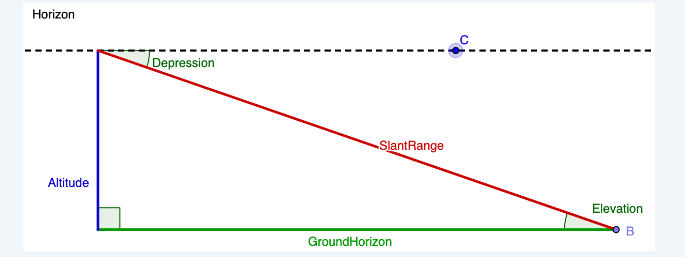
Merging together the given info and this diagram, we know that the angle of depression is \(19^{\circ}\) and and the altitude (blue line) is 105 meters. While the blue line is drawn on the left hand side in the diagram, we can assume is it is the same as the right hand side. Next, we need to think of the trig function that relates the given angle, the given side, and the side we want to solve for. The altitude or blue line is opposite the known angle, and we want to find the distance between the boat (point B) and the top of the lighthouse. That means that we want to determine the length of the hypotenuse, or red line labelled SlantRange. The sine function relates opposite and hypotenuse, so we’ll use that here. We get:
\(\sin 19^{\circ}=\frac{105}{d}\) (where \(d\) is the distance between the top of the lighthouse and the boat)
\(d=\frac{105}{\sin 19^{\circ}}\)
\(d=\frac{105}{.33}\) (using a calculator in degree mode and rounding to two digits, we get that \(\sin 19^{\circ}=.33\) )
\(d=318.18\) meters -
Question 28 of 100
28. Question
Angelina just got a new car, and she wants to ride it to the top of a mountain and visit a lookout point. If she drives 4000 meters along a road that is inclined \(22^{\circ}\) to the horizontal, how high above her starting point is she when she arrives at the lookout?
CorrectIncorrectHint
As with other trig problems, begin with a sketch of a diagram of the given and sought-after information.
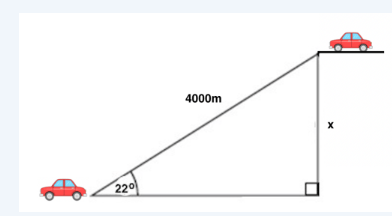
Angelina and her car start at the bottom left of the diagram. The road she is driving on is the hypotenuse of our triangle, and the angle of the road relative to flat ground is \(22^{\circ}\). Because we want to find the change in height (also called elevation), we want to determine the difference between her ending and starting heights, which is labelled \(\mathrm{x}\) in the diagram. Next, consider which trig function relates together an angle and the sides opposite and hypotenuse relative to it; the correct one is sine. Then, set up:
\(
\begin{aligned}
& \sin 22^{\circ}=\frac{x}{4000} \\
& 4000 \cdot \sin 22^{\circ}=x \\
& 4000 \cdot .37=x \text { (using a calculator in degree mode and rounding to two decimals we get that } \sin 22^{\circ}=.37 \text { ) } \\
& 1480=x
\end{aligned}
\)
Therefore the change in height between Angelina’s starting and ending points is 1480 meters. -
Question 29 of 100
29. Question
Two buildings with flat roofs are 50 feet apart. The shorter building is 40 feet tall. From the roof of the shorter building, the angle of elevation to the edge of the taller building is \(48^{\circ}\). How high is the taller building?
CorrectIncorrectHint
To solve this problem, let’s start by drawing a diagram of the two buildings, the distance in between them, and the angle between the tops of the two buildings. Then, label in the given lengths and angle.
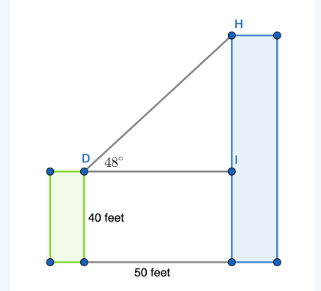
We are being asked to find the height of the taller building, but this diagram does not provide a triangle that has as one of its sides the entire height of the larger (rightmost and blue) building. However, we can instead find the distance \(\overline{\mathrm{HI}}\), and then add that to the 40 foot height of the shorter building to find the entire height of the taller building. Start by finding \(\overline{\mathrm{HI}}\) :
\(
\begin{aligned}
& \tan 48^{\circ}=\frac{\overline{\mathrm{HI}}}{50} \\
& 50 \cdot \tan 48^{\circ}=\overline{\mathrm{HI}} \\
& 50 \cdot 1.11=\overline{\mathrm{HI}} \\
& 55.5=\overline{\mathrm{HI}}
\end{aligned}
\)
Remember that this is not the full height of the larger building. To find that, we need to add \(55.5+40=95.5\) feet. Therefore, the taller building is \(95.5\) feet tall. -
Question 30 of 100
30. Question
\(
\text { Find the principal solutions of the equation } \tan x=-1 /(\sqrt{ } 3) \text {. }
\)CorrectIncorrectHint
We know that \(\tan (\pi / 6)=1 /(\sqrt{3})\)
Since, \(\tan (\pi-\pi / 6)=-\tan (\pi / 6)=-1 /(\sqrt{ } 3)\)
Further, \(\tan (2 \pi-\pi / 6)=-\tan (\pi / 6)=-1 /(\sqrt{3})\)
Hence, the principal solutions are \(\tan (\pi-\pi / 6)=\tan (5 \pi / 6)\) and \(\tan (2 \pi-\pi / 6)=\tan (11 \pi / 6)\) -
Question 31 of 100
31. Question
\(
\text { Evaluate the value of } \sin (11 \pi / 12) \text {. }
\)CorrectIncorrectHint
\(
\begin{aligned}
& \sin (11 \pi / 12) \text { can be written as } \sin (2 \pi / 3+\pi / 4) \\
& \text { using formula, } \sin (x+y)=\sin x \cos y+\cos x \sin y \\
& \sin (11 \pi / 12)=\sin (2 \pi / 3+\pi / 4)=\sin (2 \pi / 3) \cos \pi / 4+\cos (2 \pi / 3) \sin \pi / 4 \\
& =(\sqrt{ } 3) / 2 \times \sqrt{ } 2 / 2+(-1 / 2) \times \sqrt{ } 2 / 2 \\
& =\sqrt{6} / 4-(\sqrt{ } 2) / 4 \\
& =(\sqrt{ } 6-\sqrt{ } 2) / 4
\end{aligned}
\) -
Question 32 of 100
32. Question
\(
\text { Evaluate } \operatorname{cosec} x=2 \text {. }
\)CorrectIncorrectHint
We know, \(\operatorname{cosec} x=\operatorname{cosec} \pi / 6=2\) or \(\sin x=\sin \pi / 6=1 / 2\).
Or, \(x=n \pi+(-1)^n \pi / 6\) -
Question 33 of 100
33. Question
\(
\text { Solve } 5 \cos ^2 y+2 \sin y=0
\)CorrectIncorrectHint
\(5 \cos ^2 y+2 \sin y=0\)
or \(5\left(1-\sin ^2 y\right)+2 \sin y=0\)
or \(5 \sin ^2 y-2 \sin y-5=0\)
i.e., \(\sin y=1.2\) or \(\sin y=-0.8\).
Since sin y can not be greater than 1 ,
\(\sin y=-0.8=\sin (\pi+\pi / 3)\)
or \(\sin y=\sin 4 \pi / 3\), and hence, the solution is given by \(y=n \pi+(-1)^n 4 \pi / 3\) -
Question 34 of 100
34. Question
\(
\text { Find the principal solutions of the equation } \sin x=(\sqrt{3}) / 2 \text {. }
\)CorrectIncorrectHint
We know that, \(\sin \pi / 3=(\sqrt{3}) / 2\) and \(\sin 2 \pi / 3=\sin (\pi-\pi / 3)=\sin \pi / 3=(\sqrt{3}) / 2\)
Therefore, the principal solutions are \(x=\pi / 3\) and \(2 \pi / 3\). -
Question 35 of 100
35. Question
\(
\text { Solve } \cos ^2(\alpha)+\cos (\alpha)=\sin ^2(\alpha) \text { on the interval } 0^{\circ} \leq x<360^{\circ}
\)CorrectIncorrectHint
I can use a trig identity to get a quadratic in cosine:
\(
\begin{aligned}
& \cos ^2(\alpha)+\cos (\alpha)=\sin ^2(\alpha) \\
& \cos ^2(\alpha)+\cos (\alpha)=1-\cos ^2(\alpha) \\
& 2 \cos ^2(\alpha)+\cos (\alpha)-1=0 \\
& (2 \cos (\alpha)-1)(\cos (\alpha)+1)=0 \\
& \cos (\alpha)=\frac{1}{2} \text { or } \cos (\alpha)=-1
\end{aligned}
\)
The first trig equation, \(\cos (\alpha)=\frac{1}{2}\), gives me \(\alpha=60^{\circ}\) and \(\alpha=300^{\circ}\). The second equation gives me \(\alpha=\) \(180^{\circ}\). So my complete solution is:
\(
\alpha=60^{\circ}, 180^{\circ}, 300^{\circ}
\) -
Question 36 of 100
36. Question
\(
\text { Solve } \sin ^2(\theta)-\sin (\theta)=2 \text { on the interval } 0 \leq \theta<2 \pi
\)CorrectIncorrectHint
First, I’ll get everything over to one side of the “equals” sign:
\(
\sin ^2(\theta)-\sin (\theta)-2=0
\)
This equation is “a quadratic in sine”; that is, the form of the equation is the quadratic-equation format:
\(
a \mathrm{X}^2+b \mathrm{X}+c=0
\)
In the case of the equation they’re wanting me to solve, \(\mathrm{X}=\sin (\theta), a=1, b=-1\), and \(c=-2\).
Since this is quadratic in form, I can apply some quadratic-equation methods. In the case of this equation, I can factor the quadratic:
\(
\begin{aligned}
& \sin ^2(\theta)-\sin (\theta)-2=0 \\
& (\sin (\theta)-2)(\sin (\theta)+1)=0
\end{aligned}
\)
The first factor gives me the related trig equation:
\(
\sin (\theta)=2
\)
But the sine is never more than 1 , so this equation is not solvable; it has no solution.
The other factor gives me the second related trig equation:
\(
\begin{aligned}
& \sin (\theta)+1=0 \\
& \sin (\theta)=-1 \\
& \theta=\frac{3}{2} \pi
\end{aligned}
\) -
Question 37 of 100
37. Question
\(
\text { Solve } \ln \left(2-\sin ^2(x)\right)=0 \text { on } 0^{\circ} \leq x<360^{\circ}
\)CorrectIncorrectHint
The natural log (well, any log) is zero when the argument is 1 , so this gives me:
\(
\begin{aligned}
& 2-\sin ^2(x)=1 \\
& 1-\sin ^2(x)=0 \\
& (1-\sin (x))(1+\sin (x))=0 \\
& 1=\sin (x) \text { or } 1=-\sin (x)
\end{aligned}
\)
From what I know of the sine wave, my solution is:
\(
x=90^{\circ}, 270^{\circ}
\) -
Question 38 of 100
38. Question
\(
\text { Solve } \log _3(2 \sin (x))=\frac{1}{2} \text { on }[0,2 \pi)
\)CorrectIncorrectHint
By nature of logarithms, the equivalent exponential equation is:
\(
\begin{aligned}
& 2 \sin (x)=3^{1 / 2} \\
& 2 \sin (x)=\sqrt{3} \\
& \sin (x)=\frac{\sqrt{3}}{2}
\end{aligned}
\)
The sine takes on this value at \(x=\frac{\pi}{3}\) and also at \(x=\pi-\frac{\pi}{3}=\frac{2 \pi}{3}\). Then my solution is:
\(
x=\frac{\pi}{3}, \frac{2 \pi}{3}
\) -
Question 39 of 100
39. Question
\(
\text { Solve for } x \text { : } \sqrt{3} \sin x-2 \sin x \cos x=0,0 \leq x<2 \pi \text {. }
\)CorrectIncorrectHint
\(
\begin{aligned}
& \sin x \sqrt{3}-2 \sin x \cos x=0 \\
& (\sin x)(\sqrt{3}-2 \cos x)=0 \\
& \sin x=0, x=0, \pi \\
&
\end{aligned}
\)
\(
\begin{aligned}
& \sqrt{3}-2 \cos x=0 \\
& \cos x=\frac{\sqrt{3}}{2} \\
& x=\frac{\pi}{6}, \frac{11 \pi}{6}
\end{aligned}
\)
\(
x=0, \frac{\pi}{6}, \pi, \frac{11 \pi}{6}
\) -
Question 40 of 100
40. Question
\(
\text { Solve for } x \text { : } \sin ^2 x+\sin x-2=0,0 \leq x<2 \pi \text {. }
\)CorrectIncorrectHint
\(
\begin{aligned}
& \sin ^2 x+\sin x-2=0 \\
& (\sin x-1)(\sin x+2)=0 \\
& \sin x-1=0 \\
& \sin x=1 \\
& x=\frac{\pi}{2}
\end{aligned}
\)
\(
\begin{aligned}
& \sin x+2=0 \\
& \sin x=-2
\end{aligned}
\)
No solution. (Since the minimum value of \(\sin x\) is \(-1\), it cannot equal \(-2\).) -
Question 41 of 100
41. Question
In a \(\triangle A B C, \angle B<\angle C\) and the values of \(B\) and \(C\) satisfy the equation \(2 \tan x-k\left(1+\tan ^2 x\right)=0\), where \((0<k<1)\). Then, the measure of \(\angle A\) is
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (c) } \because k=\frac{2 \tan x}{1+\tan ^2 x}=\sin 2 x \\
& \Rightarrow \quad \sin 2 C=\sin 2 B \\
& \text { But } \quad \angle C>\angle B \\
& \Rightarrow \quad 2 C=\pi-2 B \Rightarrow B+C=\frac{\pi}{2} \\
& \therefore \quad \angle A=\frac{\pi}{2} \\
&
\end{aligned}
\) -
Question 42 of 100
42. Question
If \(M\) and \(m\) are maximum and minimum value of the function \(f(x)=\frac{\tan ^2 x+4 \tan x+9}{1+\tan ^2 x}\), then \((M+m)\) equals
CorrectIncorrectHint
(c) Given, \(f(x)=\frac{\tan ^2 x+4 \tan x+9}{1+\tan ^2 x}\) \(=\frac{2(2 \tan x)}{1+\tan ^2 x}+4\left(\frac{1-\tan ^2 A}{1+\tan ^2 A}\right)+5\)
\(
\begin{aligned}
& =2 \sin 2 x+4 \cos 2 x+5 \\
\therefore \quad R_f & =[{5}-\sqrt{20}, 5+\sqrt{20}]
\end{aligned}
\)
Hence, \((M+m)=10\).Hence, the maximum and minimum values of trigonometrical functions of the form \(a \sin x+b \cos x\) are \(\sqrt{a^2+b^2}\) and \(-\sqrt{a^2+b^2}\), respectively.
-
Question 43 of 100
43. Question
The value of \(4 \cos \frac{\pi}{10}-3 \sec \frac{\pi}{10}-\tan \frac{\pi}{10}\) is equal to
CorrectIncorrectHint
(d) We have, \(4 \cos 18^{\circ}-\frac{3}{\cos 18^{\circ}}-2 \tan 18^{\circ}\)
\(
\begin{aligned}
& =\frac{4 \cos ^2 18^{\circ}-3-2 \sin 18^{\circ}}{\cos 18^{\circ}} \\
& =\frac{2\left(1+\cos 36^{\circ}\right)-2 \sin 18^{\circ}-3}{\cos 18^{\circ}} \\
& =\frac{2\left(1+\cos 36^{\circ}-\sin 18^{\circ}\right)-3}{\cos 18^{\circ}} \\
& =\frac{2\left(1+\frac{1}{2}\right)-3}{\cos 18^{\circ}}=0
\end{aligned}
\) -
Question 44 of 100
44. Question
For \(0<A<\frac{\pi}{2}\), the value of \(\log _{\frac{1}{2}}\left(\frac{1}{1+2 \cos ^2 A}+\frac{2}{\sec ^2 A+2}\right)\) is equal to
CorrectIncorrectHint
(d)
\(
\begin{aligned}
& \text { As, }\left(\frac{1}{1+2 \cos ^2 A}+\frac{2}{\sec ^2 A+2}\right) \\
& =\left(\frac{1}{1+2 \cos ^2 A}+\frac{2 \cos ^2 A}{1+2 \cos ^2 A}\right) \\
& =\frac{\left(1+2 \cos ^2 A\right)}{\left(1+2 \cos ^2 A\right)}=1 \\
&
\end{aligned}
\)
Hence, \(\log _{\frac{1}{2}}(1)=0\). -
Question 45 of 100
45. Question
The \(\operatorname{sum} \frac{1}{\sin 45^{\circ} \sin 46^{\circ}}+\frac{1}{\sin 47^{\circ} \sin 48^{\circ}}\) \(+\frac{1}{\sin 49^{\circ} \sin 50^{\circ}}+\ldots+\frac{1}{\sin 133^{\circ} \sin 134^{\circ}}\) is equal to
CorrectIncorrectHint
\(
\begin{aligned}
T_1=\frac{1}{\sin 1^{\circ}} & {\left[\frac{\sin \left(46^{\circ}-45^{\circ}\right)}{\sin 45^{\circ} \sin 46^{\circ}}\right]=\frac{1}{\sin 1^{\circ}}\left[\cot 45^{\circ}-\cot 46^{\circ}\right] } \\
T_2 & =\frac{1}{\sin 1^{\circ}}\left[\frac{\sin \left(48^{\circ}-47^{\circ}\right)}{\sin 48^{\circ} \sin 47^{\circ}}\right] \\
& =\frac{1}{\sin 1^{\circ}}\left[\cot 47^{\circ}-\cot 48^{\circ}\right] \\
T_l & =\frac{1}{\sin 1^{\circ}}\left[\frac{\sin \left(133^{\circ}-134^{\circ}\right)}{\sin 133^{\circ} \sin 134^{\circ}}\right] \\
& =\frac{1}{\sin 1^{\circ}}\left[\cot 133^{\circ}-\cot 134^{\circ}\right]
\end{aligned}
\)
On adding
\(
\sum_{r=1}^l T_r=\frac{1}{\sin 1^{\circ}}\left[\left\{\cot 45^{\circ}+\cot 47^{\circ}\right.\right.\left.+\cot 49^{\circ}+\ldots+\cot 133^{\circ}\right\}\left.-\left\{\cot 46^{\circ}+\cot 48^{\circ}+\cot 50^{\circ}+\ldots+\cot 134^{\circ}\right\}\right]
\)
\(
=\operatorname{cosec} 1^{\circ}
\)
[all terms cancelled except \(\cot 45^{\circ}\) remains] -
Question 46 of 100
46. Question
If \(f(\theta)=\frac{1-\sin 2 \theta+\cos 2 \theta}{2 \cos 2 \theta}\), then value of \(f\left(11^{\circ}\right) \cdot f\left(34^{\circ}\right)\) equals
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (a) } f(\theta)=\frac{1-\sin 2 \theta+\cos 2 \theta}{2 \cos 2 \theta} \\
& =\frac{(\cos \theta-\sin \theta)^2+\left(\cos ^2 \theta-\sin ^2 \theta\right)}{2(\cos \theta-\sin \theta)(\cos \theta+\sin \theta)} \\
& =\frac{(\cos \theta-\sin \theta)+(\cos \theta+\sin \theta)}{2(\cos \theta+\sin \theta)} \\
& =\frac{2 \cos \theta}{2(\cos \theta+\sin \theta)}=\frac{1}{1+\tan \theta} \\
& f\left(11^{\circ}\right) \cdot f\left(34^{\circ}\right)=\frac{1}{\left(1+\tan 11^{\circ}\right)} \cdot \frac{1}{\left(1+\tan 34^{\circ}\right)} \\
& =\frac{1}{\left(1+\tan 11^{\circ}\right)} \cdot \frac{1}{\left(1+\tan \left(45^{\circ}-11^{\circ}\right)\right)} \\
& =\frac{1}{\left(1+\tan 11^{\circ}\right)} \cdot \frac{1}{1+\frac{1-\tan 11^{\circ}}{1+\tan 11^{\circ}}} \\
& =\frac{1}{\left(1+\tan 11^{\circ}\right)} \cdot \frac{1+\tan 11^{\circ}}{2}=\frac{1}{2} \\
&
\end{aligned}
\) -
Question 47 of 100
47. Question
The variable ‘ \(x\) ‘ satisfying the equation \(|\sin x \cos x|+\sqrt{2+\tan ^2 x+\cot ^2 x}=\sqrt{3}\), belongs to the interval
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (d) }|\sin x \cos x|+|\tan x+\cot x|=\sqrt{3} \\
& \Rightarrow \quad|\sin x \cos x|+\frac{1}{|\sin x \cos x|}=\sqrt{3} \\
& \text { but } \quad|\sin x \cos x|+\frac{1}{|\sin x \cos x|} \geq 2
\end{aligned}
\)
Hence, no solution. -
Question 48 of 100
48. Question
In a \(\triangle A B C\), if \(4 \cos A \cos B+\sin 2 A\) \(+\sin 2 B+\sin 2 C=4\), then \(\triangle A B C\) is
CorrectIncorrectHint
(c) We have, \(4 \cos A \cos B+4 \sin A \sin B \sin C=4\)
\(
\begin{array}{ll}
\Rightarrow & \sin C=\frac{1-\cos A \cos B}{\sin A \cos B} \leq 1 \\
\Rightarrow & 1 \leq \sin A \sin B+\cos A \cos B \\
\Rightarrow & \cos (A-B) \geq 1 \\
\Rightarrow & A=B \text { and } \sin C=\frac{1-\cos ^2 A}{\sin ^2 A}=1 \\
\therefore & C=90^{\circ} \\
\text { and } & A=B=\frac{\pi}{4} \text { (each). }
\end{array}
\) -
Question 49 of 100
49. Question
If \(A, B, C\) are interior angles of \(\triangle A B C\) such that \((\cos A+\cos B+\cos C)^2+(\sin A+\sin B+\sin C)^2=9\), then number of possible triangles is
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (d) }(\Sigma \cos A)^2+(\Sigma \sin A)^2=9 \\
& \Sigma\left(\cos ^2 A+\sin ^2 A\right)+2(\Sigma \cos A \cos B+\sin A \sin B) \\
& 3+2 \Sigma \cos (A-B) \leq 3+2(3)=9 .
\end{aligned}
\)
Equality holds if \(A=B=C\)
\(\Rightarrow \triangle A B C\) is equilateral \(\Rightarrow\) Infinite many equilateral
[Note We can vary side length of equilateral triangle] -
Question 50 of 100
50. Question
If \(\operatorname{cosec} \frac{\pi}{32}+\operatorname{cosec} \frac{\pi}{16}+\operatorname{cosec} \frac{\pi}{8}+\operatorname{cosec} \frac{\pi}{4}+\) \(\operatorname{cosec} \frac{\pi}{2}=\cot \frac{\pi}{k}\), then the value of \(k\) is
CorrectIncorrectHint
\(
\text { (a) } T_1=\operatorname{cosec} \theta=\frac{\sin \left(\theta-\frac{\theta}{2}\right)}{\sin \frac{\theta}{2} \sin \theta} ; \theta=\frac{\pi}{32}
\)
\(
\left.\begin{array}{l}
T_1=\cot \frac{\theta}{2}-\cot \theta \\
T_2=\cot \theta-\cot 2 \theta \\
T_3=\cot 2 \theta-\cos 2^2 \theta \\
T_4=\cot 2^2 \theta-\cos 2^3 \theta \\
T_5=1
\end{array}\right] \text { sum }=1+\cot \frac{\theta}{2}-\cot 8 \theta
\)
\(
\begin{aligned}
\text { Sum } & =1+\cot \frac{\theta}{2}-\cot 8 \theta \\
& =1+\cot \frac{\pi}{64}-\cot \frac{\pi}{4}=\cot \frac{\pi}{64}=\cot \frac{\pi}{k} \therefore k=64
\end{aligned}
\) -
Question 51 of 100
51. Question
If \(\cos 5 \theta=a \cos \theta+b \cos ^3 \theta+c \cos ^5 \theta+d\), then
CorrectIncorrectHint
(d) Put \(\theta=\frac{\pi}{2}\) in the given inequality, we get \(d=0\)
Put \(\theta=0\) in the given inequality, we get
\(
a+b+c+d=1 \dots(i)
\)
So, (d) is correct and (c) is not correct.
Now differentiate both sides with respect to \(\theta\), we get
\(
\begin{array}{r}
-5 \sin \theta=-a \sin \theta-3 b \cos ^2 \theta \sin \theta \\
-5 c \cos ^4 \theta \sin \theta \dots(ii)
\end{array}
\)Put
\(
\theta=\frac{\pi}{2} \text {, then } a=5 \dots(iii)
\)Again putting \(\theta=\frac{\pi}{4}\) in the given expression or in (ii), we get
\(
4 a+2 b+c=-4 \dots(iv)
\)From (i), (iii) and (iv) we have \(b=-20\) and \(c=16\)
-
Question 52 of 100
52. Question
If A and \(B\) are acute positive angles satisfying the equations \(3 \sin ^2 A+2 \sin ^2 B=1\) and \(3 \sin 2 A-2 \sin 3 B=0\), then \(A+2 B\) is equal to
CorrectIncorrectHint
(b) From the given relations, we have
\(
\sin 2 B=\left(\frac{3}{2}\right) \sin 2 A \text { and } 3 \sin ^2 A=1-2 \sin ^2 B=\cos 2 B
\)
so that
\(
\begin{aligned}
\cos (A+2 B) & =\cos A \cos 2 B-\sin A \sin 2 B \\
& =\cos A \cdot 3 \sin ^2 A-\left(\frac{3}{2}\right) \sin A \sin 2 A \\
& =3 \cos A \sin ^2 A-3 \sin ^2 A \cos A=0 \\
A+2 B & =\frac{\pi}{2}
\end{aligned}
\) -
Question 53 of 100
53. Question
If \(k_1=\tan 27 \theta-\tan \theta\) and \(k_2=\frac{\sin \theta}{\cos 3 \theta}+\frac{\sin 3 \theta}{\cos 9 \theta}+\frac{\sin 9 \theta}{\cos 27 \theta}\) then,
CorrectIncorrectHint
(b) We can write
\(
\begin{aligned}
& k_1=\tan 27 \theta-\tan 9 \theta+\tan 9 \theta-\tan 3 \theta+\tan 3 \theta-\tan \theta \\
& \text { But } \tan 3 \theta-\tan \theta=\frac{\sin 3 \theta \cos \theta-\cos 3 \theta \sin \theta}{\cos 3 \theta \cos \theta} \\
&=\frac{\sin 2 \theta}{\cos 3 \theta \cos \theta} \\
&=\frac{2 \sin \theta}{\cos 3 \theta} \\
& \therefore \quad k_1=2\left[\frac{\sin 9 \theta}{\cos 27 \theta}+\frac{\sin 3 \theta}{\cos 9 \theta}+\frac{\sin \theta}{\cos 3 \theta}\right]=2 k_2
\end{aligned}
\) -
Question 54 of 100
54. Question
If \(a^2-2 a \cos x+1=674\) and \(\tan \left(\frac{x}{2}\right)=7\) then the integral value of \(a\) is
CorrectIncorrectHint
(a)
\(
\begin{aligned}
674=a^2 & -2 a \frac{1-\tan ^2\left(\frac{x}{2}\right)}{1+\tan ^2\left(\frac{x}{2}\right)}+1 \\
& =a^2-2 a \times \frac{1-49}{1+49}+1 \\
& =a^2+2 a \times \frac{48}{50}+1
\end{aligned}
\)
\(
\begin{aligned}
& 25 a^2+48 a-673 \times 25=0 \\
&(a-25)(25 a+673)=0 \\
& a=25 \quad \text { (taking the integral value of } a \text { ). }
\end{aligned}
\) -
Question 55 of 100
55. Question
The value of expression \(\frac{\sin ^3 x}{1+\cos x}+\frac{\cos ^3 x}{1-\sin x}\) is/are
CorrectIncorrectHint
(a) Let \(\frac{\sin ^3 x}{1+\cos x}+\frac{\cos ^3 x}{1-\sin x}=A\), then
\(
\begin{aligned}
& A=\frac{\left(\sin ^3 x+\cos ^3 x\right)+\left(\cos ^4 x-\sin ^4 x\right)}{(1+\cos x)(1-\sin x)} \\
& \left\{\left(\sin ^3 x+\cos ^3 x\right)\right\} \\
& \frac{+\left\{\begin{array}{l}
(\cos x+\sin x)(\cos x-\sin x) \\
\left(\cos ^2 x+\sin ^2 x\right)
\end{array}\right\}}{(1+\cos x)(1-\sin x)} \\
& (\sin x+\cos x)\{(1-\sin x \cos x) \\
&
\end{aligned}
\)
\(
\begin{aligned}
& A=\sin x+\cos x \\
& A=\sqrt{2}\left[\frac{1}{\sqrt{2}} \sin x+\frac{1}{\sqrt{2}} \cos x\right] \dots(i)
\end{aligned}
\)
\(
\begin{aligned}
A & =\sqrt{2}\left[\cos \frac{\pi}{4} \sin x+\sin \frac{\pi}{4} \cos x\right] \\
& =\sqrt{2} \sin \left[\frac{\pi}{4}+x\right]
\end{aligned}
\)
Again, by Eq. (i)
\(
\begin{aligned}
A & =\sqrt{2}\left[\sin \frac{\pi}{4} \sin x+\cos \frac{\pi}{4} \cos x\right] \\
& =\sqrt{2} \cos \left[\frac{\pi}{4}-x\right]
\end{aligned}
\) -
Question 56 of 100
56. Question
Let \(0 \leq \theta \leq \frac{\pi}{2}\) and \(x=X \cos \theta+Y \sin \theta\), \(y=X \sin \theta-Y \cos \theta\) such that \(x^2+2 x y+y^2=a X^2+b Y^2\), where \(a\) and \(b\) are constant, then
CorrectIncorrectHint
\(
\text { (c) } \begin{aligned}
x^2+y^2 & =X^2+Y^2 \\
x y & =\left(X^2-Y^2\right) \sin \theta \cdot \cos \theta-X Y\left(\cos ^2 \theta-\sin ^2 \theta\right) \\
x^2 & +4 x y+y^2=X^2+Y^2+2\left(X^2-Y^2\right)\sin 2 \theta-2 X Y \cos 2 \theta
\end{aligned}
\)
\(
=(1+2 \sin 2 \theta) X^2+(1-2 \sin 2 \theta) Y^2-2 \cos 2 \theta \cdot X Y
\)
From the question,
\(
\begin{aligned}
a & =1+2 \sin 2 \theta, b=1-2 \sin 2 \theta, \cos 2 \theta=0 \\
\cos 2 \theta & =0 \Rightarrow \theta=\frac{\pi}{4}, \text { then } \\
a & =1+2 \sin \frac{\pi}{2}, b=1-2 \sin \frac{\pi}{2} \\
\therefore \quad a & =3, b=-1
\end{aligned}
\) -
Question 57 of 100
57. Question
If \(a=\sin \frac{\pi}{18} \sin \frac{5 \pi}{18} \sin \frac{7 \pi}{18}\), and \(x\) is the solution the equation \(y=2[x]+2\) and \(y=3[x-2]\), where \([x]\) denotes the integral part of \(x\), then a is equal to
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (b) } a=\sin \frac{\pi}{18} \sin \frac{5 \pi}{18} \sin \frac{7 \pi}{18} \\
& =\sin 10^{\circ} \sin 50^{\circ} \sin 70^{\circ} \\
& =\frac{1}{2}\left[2 \sin 70^{\circ} \sin 10^{\circ}\right] \sin 50^{\circ} \\
& =\frac{1}{2}\left[\cos 60^{\circ}-\cos 80^{\circ}\right] \sin 50^{\circ} \\
& =\frac{1}{4} \sin 50^{\circ}-\frac{1}{4}\left(2 \cos 80^{\circ} \sin 50^{\circ}\right) \\
& =\frac{1}{4} \sin 50^{\circ}-\frac{1}{4}\left(\sin 130^{\circ}-\sin 30^{\circ}\right) \\
& =\frac{1}{4} \sin 50^{\circ}-\frac{1}{4} \sin 50^{\circ}+\frac{1}{4} \cdot \frac{1}{2}=\frac{1}{8} \\
& y=2[x]+2 \text { and } y=3[x-2] \\
& \Rightarrow 2[x]+2=3[x-2] \\
& =3[x]+3[-2] \Rightarrow[x]=8 \\
& \therefore \quad a=\frac{1}{[x]} \\
&
\end{aligned}
\) -
Question 58 of 100
58. Question
The value of \(\cos \frac{2 \pi}{7}+\cos \frac{4 \pi}{7}+\cos \frac{6 \pi}{7}\) is equal to
CorrectIncorrectHint
\(
\begin{aligned}
\cos \left(\frac{2 \pi}{7}\right) & +\cos \left(\frac{4 \pi}{7}\right)+\cos \left(\frac{6 \pi}{7}\right) \\
& =\operatorname{Re}\left\{e^{\frac{2 \pi i}{7}}+e^{\frac{4 \pi i}{7}}+e^{\frac{6 \pi i}{7}}\right\}
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{e^{\frac{2 \pi i}{7}}+e^{\frac{4 \pi i}{7}}+e^{\frac{6 \pi i}{7}}+e^{\frac{-4 \pi i}{7}}+e^{\frac{-4 \pi i}{7}}+e^{\frac{-6 \pi i}{7}}}{2} \\
& =\frac{-1+\left(1+e^{\frac{2 \pi i}{7}}+e^{\frac{4 \pi i}{7}}+e^{\frac{6 \pi i}{7}}+e^{\frac{-2 \pi i}{7}}+e^{\frac{-4 \pi i}{7}}+e^{\frac{-6 \pi i}{7}}\right)}{2} \\
& =\frac{-1+\text { (Sum of seven roots of unity) }}{2} \\
& =\frac{-1+0}{2}=-\frac{1}{2}
\end{aligned}
\) -
Question 59 of 100
59. Question
If \(\alpha, \beta, \gamma\) are acute angles and \(\cos \theta=\sin \beta / \sin \alpha\), \(\cos \phi=\sin \gamma / \sin \alpha\) and \(\cos (\theta-\phi)=\sin \beta \sin \gamma\), then the value of \(\tan ^2 \alpha-\tan ^2 \beta-\tan ^2 \gamma\) is equal to
CorrectIncorrectHint
(b) From the third relation we get
\(
\begin{aligned}
& \cos \theta \cos \phi+\sin \theta \sin \phi=\sin \beta \sin \gamma \\
& \Rightarrow \quad \sin ^2 \theta \sin ^2 \phi=(\cos \theta \cos \phi-\sin \beta \sin \gamma)^2 \\
& \Rightarrow \quad\left(1-\frac{\sin ^2 \beta}{\sin ^2 \alpha}\right)\left(1-\frac{\sin ^2 \gamma}{\sin ^2 \alpha}\right) \\
& =\left(\frac{\sin \beta \sin \gamma}{\sin ^2 \alpha}-\sin \beta \sin \gamma\right)^2 \\
& \Rightarrow \quad\left(\sin ^2 \alpha-\sin ^2 \beta\right)\left(\sin ^2 \alpha-\sin ^2 \gamma\right) \\
& =\sin ^2 \beta \sin ^2 \gamma\left(1-\sin ^2 \alpha\right)^2 \\
& \Rightarrow \quad \sin ^4 \alpha\left(1-\sin ^2 \beta \sin ^2 \gamma\right) \\
& -\sin ^2 \alpha\left(\sin ^2 \beta+\sin ^2 \gamma-2 \sin ^2 \beta \sin ^2 \gamma\right)=0 \\
&
\end{aligned}
\)
\(
\begin{aligned}
& \therefore \quad \sin ^2 \alpha=\frac{\sin ^2 \beta+\sin ^2 \gamma-2 \sin ^2 \beta \sin ^2 \gamma}{1-\sin ^2 \beta \sin ^2 \gamma} \\
& \text { and } \quad \cos ^2 \alpha=\frac{1-\sin ^2 \beta-\sin ^2 \gamma+\sin ^2 \beta \sin ^2 \gamma}{1-\sin ^2 \beta \sin ^2 \gamma} \\
& \Rightarrow \quad \tan ^2 \alpha=\frac{\sin ^2 \beta-\sin ^2 \beta \sin ^2 \gamma+\sin ^2 \gamma-\sin ^2 \beta \sin ^2 \gamma}{\cos ^2 \beta-\sin ^2 \gamma\left(1-\sin ^2 \beta\right)} \\
& =\frac{\sin ^2 \beta \cos ^2 \gamma+\cos ^2 \beta \sin ^2 \gamma}{\cos ^2 \beta \cos ^2 \gamma} \\
& =\tan ^2 \beta+\tan ^2 \gamma \\
& \Rightarrow \quad \tan ^2 \alpha-\tan ^2 \beta-\tan ^2 \gamma=0 \\
&
\end{aligned}
\) -
Question 60 of 100
60. Question
If \(\sqrt{2} \cos A=\cos B+\cos ^3 B\), and \(\sqrt{2} \sin A=\sin B-\sin ^3 B\) then \(\sin (A-B)=\)
CorrectIncorrectHint
(c) \(\sqrt{2} \cos A=\cos B+\cos ^3 B \dots(i)\)
and \(\sqrt{2} \sin A=\sin B-\sin ^3 B \dots(ii)\)
\(
\begin{aligned}
\Rightarrow \sqrt{2} & \sin A \cos B-\sqrt{2} \cos A \sin B \\
& =\left(\sin B-\sin ^3 B\right) \cos B-\left(\cos B+\cos ^3 B\right) \sin B \\
& =-\sin B \cos B
\end{aligned}
\)
\(
\Rightarrow \sin (A-B)=\frac{-1}{2 \sqrt{2}} \sin 2 B
\)
Now squaring and adding Eqs. (i) and (ii), we get
\(
2=\cos ^2 B+\sin ^2 B+\cos ^6 B+\sin ^6 B+2\left(\cos ^4 B-\sin ^4 B\right)
\)
\(
\begin{aligned}
& \Rightarrow \quad 1=\left(\cos ^2 A+\sin ^2 A\right)^3-3 \cos ^2 A \sin ^2 \\
& A\left(\cos ^2 A+\sin ^2 A\right)+2 \cos 2 B
\end{aligned}
\)
\(
\begin{array}{lc}
\Rightarrow & 1=1-\left(\frac{3}{4}\right) \sin ^2 2 B+2 \cos 2 B \\
\Rightarrow & -3 \sin ^2 2 B+8 \cos 2 B=0 \\
\Rightarrow & 3 \cos ^2 2 B+8 \cos 2 B-3=0 \\
\Rightarrow & \cos 2 B=\frac{1}{3} \\
\Rightarrow & \sin 2 B= \pm \frac{2 \sqrt{2}}{3} \\
\therefore & \sin (A-B)= \pm \frac{1}{3}
\end{array}
\) -
Question 61 of 100
61. Question
Evaluate \(\cos 55^{\circ}+\cos 65^{\circ}+\cos 175^{\circ} \text {. }\)
CorrectIncorrectHint
\(
\begin{aligned}
& =\cos 55^{\circ}+\cos 65^{\circ}+\cos 175^{\circ} \\
& =2 \cos \frac{55^{\circ}+65^{\circ}}{2} \cos \frac{55^{\circ}-65^{\circ}}{2}+\cos 17 \\
& =2 \cos 60^{\circ} \cos \left(-5^{\circ}\right)+\cos 175^{\circ} \\
& =2 \times \frac{1}{2} \cos 5^{\circ}+\cos \left(180^{\circ}-5^{\circ}\right) \\
& =\cos 5^{\circ}-\cos 5^{\circ}=0
\end{aligned}
\) -
Question 62 of 100
62. Question
Evaluate \(\frac{\sin A+\sin 2 A+\sin 4 A+\sin 5 A}{\cos A+\cos 2 A+\cos 4 A+\cos 5 A}\)
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{\sin A+\sin 2 A+\sin 4 A+\sin 5 A}{\cos A+\cos 2 A+\cos 4 A+\cos 5 A} \\
& =\frac{(\sin 5 A+\sin A)+(\sin 4 A+\sin 2 A)}{(\cos 5 A+\cos A)+(\cos 4 A+\cos 2 A)} \\
& =\frac{2 \sin 3 A \cos 2 A+2 \sin 3 A \cos A}{2 \cos 3 A \cos 2 A+2 \cos 3 A \cos A} \\
& =\frac{2 \sin 3 A(\cos 2 A+\cos A)}{2 \cos 3 A(\cos 2 A+\cos A)}=\tan 3 A \\
&
\end{aligned}
\) -
Question 63 of 100
63. Question
\(\text { Evaluate } \sin 20^{\circ} \sin 40^{\circ} \sin 80^{\circ}=\frac{\sqrt{3}}{8}\)
CorrectIncorrectHint
\(
\begin{aligned}
& \sin 20^{\circ} \sin 40^{\circ} \sin 80^{\circ}=\frac{1}{2}\left(2 \sin 80^{\circ} \sin 40^{\circ}\right) \sin 20^{\circ} \\
& =\frac{1}{2}\left[\cos \left(80^{\circ}-40^{\circ}\right)-\cos \left(80^{\circ}+40^{\circ}\right) \sin 20^{\circ}\right. \\
& =\frac{1}{2}\left(\cos 40^{\circ}-\cos 120^{\circ}\right) \sin 20^{\circ} \\
& =\frac{1}{4}\left(2 \cos 40^{\circ} \sin 20^{\circ}-2 \cos 120^{\circ} \sin 20^{\circ}\right) \\
& =\frac{1}{4}\left[\sin \left(40^{\circ}+20^{\circ}\right)-\sin \left(40^{\circ}-20^{\circ}\right)-2\left(-\frac{1}{2}\right) \sin 20^{\circ}\right] \\
& =\frac{1}{4}\left[\sin 60^{\circ}-\sin 20^{\circ}+\sin 20^{\circ}\right]=\frac{1}{4} \sin 60^{\circ} \\
& =\frac{1}{4} \cdot \frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{8}
\end{aligned}
\) -
Question 64 of 100
64. Question
Evaluate \(\sqrt{2+\sqrt{2+\sqrt{2+2 \cos 8}}}\)
CorrectIncorrectHint
\(
\begin{aligned}
& \text { We have, }\sqrt{2+\sqrt{2+\sqrt{2(1+\cos 8 \theta)}}} \\
& \Rightarrow \sqrt{2+\sqrt{2+\sqrt{2\left(2 \cos ^2 4 \theta\right)}}} \left[\because 1+\cos 8 \theta=2 \cos ^2 \frac{8 \theta}{2}\right]
\end{aligned}
\)
\(
\begin{array}{ll}
\Rightarrow & \sqrt{2+\sqrt{2+\sqrt{\left(4 \cos ^2 4 \theta\right)}}} \\
\Rightarrow & \sqrt{2+\sqrt{2+2 \cos 4 \theta}} \\
\Rightarrow & \sqrt{2+\sqrt{2(1+\cos 4 \theta)}} \\
\Rightarrow & \sqrt{2+\sqrt{2\left(2 \cos ^2 2 \theta\right)}} \quad\left[\because 1+\cos 4 \theta=2 \cos ^2 2 \theta\right] \\
\Rightarrow & \sqrt{2+2 \cos 2 \theta}=\sqrt{2(1+\cos 2 \theta)}
\end{array}
\)
\(
\begin{aligned}
& =\sqrt{2+2 \cos 2 \theta}=\sqrt{2(1+\cos 2 \theta)} \\
& =\sqrt{2\left(2 \cos ^2 \theta\right)}=2 \cos \theta
\end{aligned}
\) -
Question 65 of 100
65. Question
\(\left(1+\cos \frac{\pi}{8}\right)\left(1+\cos \frac{3 \pi}{8}\right)\) \(\left(1+\cos \frac{5 \pi}{8}\right)\left(1+\cos \frac{7 \pi}{8}\right)=?\).
CorrectIncorrectHint
We have \(\cos \frac{7 \pi}{8}=\cos \left(\pi-\frac{\pi}{8}\right)=-\cos \frac{\pi}{8}\)
\(
\begin{aligned}
& \cos \frac{5 \pi}{8}=\cos \left(\pi-\frac{3 \pi}{8}\right)=-\cos \frac{3 \pi}{8} \\
& \left(1+\cos \frac{\pi}{8}\right)\left(1+\cos \frac{3 \pi}{8}\right)\left(1+\cos \frac{5 \pi}{8}\right)\left(1+\cos \frac{7 \pi}{8}\right)=\frac{1}{b} \\
& =\left(1-\cos ^2 \frac{\pi}{8}\right)\left(1-\cos ^2 \frac{3 \pi}{8}\right) \\
& =\sin ^2 \frac{\pi}{8} \sin ^2 \frac{3 \pi}{8} \\
& =\frac{1}{4}\left(2 \sin ^2 \frac{\pi}{8}\right)\left(2 \sin ^2 \frac{3 \pi}{8}\right) \\
& =\frac{1}{4}\left[\left(1-\cos \frac{\pi}{4}\right)\left(1-\cos \frac{3 \pi}{4}\right)\right] \because\left[1-\cos \theta=2 \sin ^2 \frac{\theta}{2}\right] \\
& =\frac{1}{4}\left[\left(1-\frac{1}{\sqrt{2}}\right)\left(1+\frac{1}{\sqrt{2}}\right)\right]=\frac{1}{4}\left(1-\frac{1}{2}\right)=\frac{1}{8}
\end{aligned}
\) -
Question 66 of 100
66. Question
Determine the smallest positive value of \(x\) (in degrees) for which \(\tan \left(x+100^{\circ}\right)=\tan \left(x+50^{\circ}\right)\) \(\tan x \tan \left(x-50^{\circ}\right)\)
CorrectIncorrectHint
\(
\begin{aligned}
& \text { We have, } \tan \left(x+100^{\circ}\right)=\tan \left(x+50^{\circ}\right) \tan x \tan \left(x-50^{\circ}\right) \\
& \Rightarrow \quad \frac{\tan \left(x+100^{\circ}\right)}{\tan \left(x+50^{\circ}\right)}=\tan \left(x+50^{\circ}\right) \tan x^{\circ} \\
& \Rightarrow \quad \frac{\sin \left(x+100^{\circ}\right) \cos \left(x-50^{\circ}\right)}{\cos \left(x+100^{\circ}\right) \sin \left(x-50^{\circ}\right)}=\frac{\sin \left(x+50^{\circ}\right) \sin x}{\cos \left(x+50^{\circ}\right) \cos x} \\
& \Rightarrow \frac{\sin \left(x+100^{\circ}\right) \cos \left(x-50^{\circ}\right)+\cos \left(x+100^{\circ}\right) \sin \left(x-50^{\circ}\right)}{\sin \left(x+100^{\circ}\right) \cos \left(x-50^{\circ}\right)-\cos \left(x+100^{\circ}\right) \sin \left(x-50^{\circ}\right)} \\
& \quad=\frac{\sin \left(x+50^{\circ}\right) \sin x+\cos \left(x+50^{\circ}\right) \cos x}{\sin \left(x+50^{\circ}\right) \sin x-\cos \left(x+50^{\circ}\right) \cos x} \\
& \Rightarrow \quad \frac{\sin \left(x+100^{\circ}+x-50^{\circ}\right)}{\sin \left(x+100^{\circ}-x+50^{\circ}\right)}=\frac{\cos \left(x+50^{\circ}-x\right)}{-\cos \left(x+50^{\circ}+x\right)} \\
& \Rightarrow \quad \frac{\sin \left(2 x+50^{\circ}\right)}{\sin 150^{\circ}}=\frac{\cos 50^{\circ}}{-\cos \left(2 x+50^{\circ}\right)}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad \sin \left(2 x+50^{\circ}\right) \cos \left(2 x+50^{\circ}\right)=-\sin 150^{\circ} \cos 50^{\circ} \\
& \Rightarrow \quad 2 \sin \left(2 x+50^{\circ}\right) \cos \left(2 x+50^{\circ}\right)=-2 \cos 60^{\circ} \cos 50^{\circ} \left[\because \sin 150^{\circ}=\cos 60^{\circ}\right]
\end{aligned}
\)
\(
\begin{array}{ll}
\Rightarrow & \sin \left(4 x+100^{\circ}\right)=\sin \left(270-50^{\circ}\right) \\
\Rightarrow & \sin \left(4 x+100^{\circ}\right)=\sin 220^{\circ} \\
\Rightarrow & 4 x+100^{\circ}=220^{\circ} \Rightarrow x=30^{\circ}
\end{array}
\) -
Question 67 of 100
67. Question
If \(\alpha=112^{\circ} 30^{\prime}\), find the value of \(\sin \alpha\)
CorrectIncorrectHint
Given, \(\alpha=112^{\circ} 30^{\prime}\)
\(
\begin{aligned}
& \therefore \quad 2 \alpha=225^{\circ} \\
& \text { or } \quad \cos 2 \alpha=\cos 225^{\circ}=\cos \left(180^{\circ}+45^{\circ}\right) \\
& =-\cos 45^{\circ}=-\frac{1}{\sqrt{2}} \\
&
\end{aligned}
\)
Now, \(\sin ^2 \alpha=\frac{1-\cos 2 \alpha}{2}\)
Since \(\alpha\) lies in the 2 nd quadrant \(\therefore \sin \alpha\) is positive
\(
\begin{aligned}
\therefore \quad \sin \alpha & =\sqrt{\frac{1-\cos 2 \alpha}{2}}=\sqrt{\frac{1-\left(-\frac{1}{\sqrt{2}}\right)}{2}} \\
& =\sqrt{\frac{\sqrt{2}+1}{2 \sqrt{2}}}=\frac{\sqrt{2+2 \sqrt{2}}}{2} \\
\text { Hence, } \sin \alpha & =\frac{\sqrt{2+2 \sqrt{2}}}{2}
\end{aligned}
\) -
Question 68 of 100
68. Question
\(
\cos 6^{\circ} \cos 42^{\circ} \cos 66^{\circ} \cos 78^{\circ}=?
\)CorrectIncorrectHint
\(
\begin{aligned}
& \cos 6^{\circ} \cos 42^{\circ} \cos 66^{\circ} \cos 78^{\circ} \\
& =\frac{1}{4}\left(2 \cos 66^{\circ} \cos 6^{\circ}\right)\left(2 \cos 78^{\circ} \cos 42^{\circ}\right) \\
& =\frac{1}{4}\left[\cos \left(66^{\circ}+6^{\circ}\right)+\cos \left(66^{\circ}-6^{\circ}\right)\right] \\
& \quad \times\left[\cos \left(78^{\circ}+42^{\circ}\right)+\cos \left(78^{\circ}-42^{\circ}\right)\right] \\
& =\frac{1}{4}\left(\cos 72^{\circ}+\cos 60^{\circ}\right)\left(\cos 120^{\circ}+\cos 36^{\circ}\right)
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{1}{4}\left(\sin 18^{\circ}+\frac{1}{2}\right)\left(-\frac{1}{2}+\cos 36^{\circ}\right) \\
& =\frac{1}{4}\left[\frac{(\sqrt{5}-1)}{4}+\frac{1}{2}\right]\left[-\frac{1}{2}+\frac{(\sqrt{5}-1)}{4}\right] \\
& {\left[\because \sin 18^{\circ}=\frac{(\sqrt{5}-1)}{4} \text { and } \cos 36^{\circ}=\frac{(\sqrt{5}+1)}{4}\right]} \\
& =\frac{1}{4} \cdot \frac{(\sqrt{5}+1)}{4} \cdot \frac{(\sqrt{5}-1)}{4}=\frac{(5-1)}{64} \\
& =\frac{4}{64}=\frac{1}{16}
\end{aligned}
\) -
Question 69 of 100
69. Question
\(
\sin \frac{\pi}{5} \sin \frac{2 \pi}{5} \sin \frac{3 \pi}{5} \sin \frac{4 \pi}{5}=?
\)CorrectIncorrectHint
\(
\begin{aligned}
& \sin \frac{\pi}{5} \sin \frac{2 \pi}{5} \sin \frac{3 \pi}{5} \sin \frac{4 \pi}{5} \\
& =\sin \frac{\pi}{5} \sin \frac{2 \pi}{5} \sin \left(\pi-\frac{2 \pi}{5}\right) \sin \left(\pi-\frac{\pi}{5}\right) \\
& =\sin ^2 \frac{\pi}{5} \sin ^2 \frac{2 \pi}{5} \\
& =\left(\sin 36^{\circ}\right)^2 \times\left(\sin 72^{\circ}\right)^2 \\
& =\left(\sin 36^{\circ}\right)^2 \times\left(\cos 18^{\circ}\right)^2 \\
& {\left[\because \sin 72^{\circ}=\sin \left(90^{\circ}-18^{\circ}\right)=\cos 18^{\circ}\right]}
\end{aligned}
\)
\(
\begin{aligned}
& =\frac{(10-2 \sqrt{5})}{16} \times \frac{(10+2 \sqrt{5})}{16}=\frac{(100-20)}{(16 \times 16)} \\
& {\left[\begin{array}{l}
\because \sin 36^{\circ}=\frac{\sqrt{10-2 \sqrt{5}}}{4} \\
\text { and } \cos 18^{\circ}=\frac{\sqrt{10+2 \sqrt{5}}}{4}
\end{array}\right]} \\
& =\frac{80}{(16 \times 16)}=\frac{5}{16} \\
&
\end{aligned}
\) -
Question 70 of 100
70. Question
The value of \(x\) in \((0, \pi / 2)\) satisfying the equation, \(\frac{\sqrt{3}-1}{\sin x}+\frac{\sqrt{3}+1}{\cos x}=4 \sqrt{2}\) is
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{\sqrt{3}-1}{2 \sqrt{2} \sin x}+\frac{\sqrt{3}+1}{2 \sqrt{2} \cos x}=2 \\
& \sin \frac{\pi}{12} \cos x+\cos \frac{\pi}{12} \sin x=\sin 2 x \\
& \sin 2 x=\sin \left(x+\frac{\pi}{12}\right)
\end{aligned}
\)
\(
\begin{aligned}
2 x & =x+\frac{\pi}{12} \\
\text { or } 2 x & =\pi-x-\frac{\pi}{12} \\
x & =\frac{\pi}{12} \\
\text { or } 3 x & =\frac{11 \pi}{12} \\
x & =\frac{\pi}{12} \text { or } \frac{11 \pi}{36}
\end{aligned}
\) -
Question 71 of 100
71. Question
In \(\triangle A B C, \tan B+\tan C=5\) and \(\tan A \tan C=3\), then
CorrectIncorrectHint
\(
\begin{aligned}
& \text { (a,c) } \tan A+\tan B+\tan C=\tan A \tan B \tan C \\
& \Rightarrow \quad \tan A+5=3 \tan B \\
& \Rightarrow \quad 5+\tan A=3(5-\tan C) \\
& \Rightarrow \quad 5+\tan A=15-\frac{9}{\tan A} \\
& \Rightarrow \quad \tan ^2 A-10 \tan A+9=0 \\
& \Rightarrow \quad \tan A=1 \text { or } \tan A=9 \\
&
\end{aligned}
\)
\(\Rightarrow \tan B\) and \(\tan C\) are 2,3 or \(\frac{14}{3}, \frac{1}{3}\), respectively
\(\Rightarrow \triangle A B C\) is always on acute angled triangle and sum of all possible values of \(\tan A\) is 10 . -
Question 72 of 100
72. Question
Let \(y=\sin ^2 x+\cos ^4 x\). Then, for all real \(x\)
CorrectIncorrectHint
(b, c) \(y=\cos ^4 x-\cos ^2 x+1\)
\(
=\left(\cos ^2 x-\frac{1}{2}\right)^2+\frac{3}{4}
\)
\(\therefore y_{\min }=\frac{3}{4}\) and \(y\) is maximum when \(\left(\cos ^2 x-\frac{1}{2}\right)^2\) is then maximum
\(
\therefore \quad y_{\max }=\frac{1}{4}+\frac{3}{4}=1
\) -
Question 73 of 100
73. Question
If in \(\triangle A B C, \tan A+\tan B+\tan C=6\) and \(\tan A \tan B=2\), then \(\sin ^2 A: \sin ^2 B: \sin ^2 C\) is
CorrectIncorrectHint
\(
\begin{aligned}
& (b, c) \tan A+\tan B+\tan C=6 \dots(i) \\
& \Rightarrow \tan A \tan B \tan C=6 \\
& 2 \tan C=6 \\
& \therefore \quad \tan C=3 \\
& \therefore \quad \sin ^2 C=\frac{\tan ^2 C}{1+\tan ^2 C}=\frac{9}{1+9}=\frac{9}{10} \\
&
\end{aligned}
\)
From Eq. (i), \(\tan A+\tan B=3\) and \(\tan A \tan B=2\)
\(\tan A-\tan B\)
\(
\begin{aligned}
& = \pm \sqrt{\left.\left\{(\tan A+\tan B)^2-4 \tan A \tan B\right)\right\}} \\
& = \pm 1
\end{aligned}
\)
we get, \(\tan A=2,1\) and \(\tan B=1,2\)
\(
\begin{array}{ll}
\therefore & \sin ^2 A=\frac{4}{1+4}, \frac{1}{1+1} \text { and } \sin ^2 B=\frac{1}{1+1}, \frac{4}{1+4} \\
\Rightarrow & \sin ^2 A=\frac{8}{10}, \frac{5}{10} \text { and } \sin ^2 B=\frac{5}{10}, \frac{8}{10} \\
\therefore & \sin ^2 A: \sin ^2 B: \sin ^2 C=8: 5: 9 \text { or } 5: 8: 9
\end{array}
\) -
Question 74 of 100
74. Question
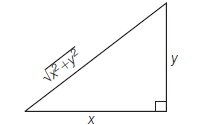
If \(x \sin ^3 \theta+y \cos ^3 \theta=\sin \theta \cos \theta\) and \(x \sin \theta-y \cos \theta=0\) then \((x, y)\) lie one
CorrectIncorrectHint
(a) We have, \(x \sin ^3 \theta+y \cos ^3 \theta=\sin \theta \cos \theta\) and \(x \sin \theta-y \cos \theta=0 \dots(i)\)
From Eq. (ii), \(\tan \theta=\frac{y}{x} \dots(ii)\)
\(
\therefore \quad \sin \theta=\frac{y}{\sqrt{\left(x^2+y^2\right)}} \text { and } \cos \theta=\frac{x}{\sqrt{\left(x^2+y^2\right)}}
\)
\(
\begin{aligned}
& \text { From Eq., (i) } x \times \frac{y^3}{\left(x^2+y^2\right)^{\frac{3}{2}}}+y \times \frac{x^3}{\left(x^2+y^2\right)^{\frac{3}{2}}} \\
& =\frac{x y}{\left(x^2+y^2\right)} \\
& \text { or } \quad \frac{\left(x^2+y^2\right)}{\left(x^2+y^2\right)^{\frac{3}{2}}}=\frac{1}{\left(x^2+y^2\right)} \Rightarrow\left(x^2+y^2\right)^{\frac{1}{2}}=1 \\
& \text { or } \quad x^2+y^2=1 \text { which is a circle }
\end{aligned}
\) -
Question 75 of 100
75. Question
Maximum value of the expression \(\log _3\left(9-2 \cos ^2 \theta-4 \sec ^2 \theta\right)\) is equal to
CorrectIncorrectHint
For the expression \(a \cos ^2 \theta+b \sec ^2 \theta\) if \(b>a\), then minimum value attains at \(\cos ^2 \theta=\sec ^2 \theta=1\)
\(\Rightarrow \max\) of \(\left\{9-\left(2 \cos ^2 \theta+4 \sec ^2 \theta\right)\right\}=3\)
So, maximum of \(\left.\log _3\left(9-2 \cos ^2 \theta+4 \sec ^2 \theta\right)\right)=1\) -
Question 76 of 100
76. Question
If \(\sec A \tan B+\tan A \sec B=91\), then the value of \((\sec A \sec B+\tan A \tan B)^2\) is equal to
CorrectIncorrectHint
\(
(\sec A \sec B+\tan A \tan B)^2-(\sec A \tan B+\tan A \sec B)^2
\)
\(
\begin{aligned}
& =\left[\frac{1+\sin A \sin B}{\cos A \cos B}\right]^2-\left[\frac{\sin B+\sin A}{\cos A \cos B}\right]^2 \\
& =\frac{1+\sin ^2 A \sin ^2 B-\sin ^2 B-\sin ^2 A}{\cos ^2 A \cos ^2 B} \\
& =\frac{1-\sin ^2 B \cos ^2 A-\sin ^2 A}{\cos ^2 A \cos ^2 B} \\
& =\frac{\cos ^2 A \cos ^2 B}{\cos ^2 A \cos ^2 B}=1
\end{aligned}
\)
\(
\Rightarrow(\sec A \sec B+\tan A \tan B)^2=(91)^2+1=8282
\) -
Question 77 of 100
77. Question
If \(4 \sin 27^{\circ}=\sqrt{\alpha}+\sqrt{\beta}\), then the value of \((\alpha+\beta-\alpha \beta+2)^4\) must be
CorrectIncorrectHint
\(
\text { We know }\left(\cos 27^{\circ}+\sin 27^{\circ}\right)^2
\)
\(
\begin{aligned}
& =1+\sin 54=1+\cos 36^{\circ} \\
& \Rightarrow \quad \cos 27^{\circ}+\sin 27^{\circ}=\sqrt{\left(1+\cos 36^{\circ}\right)} \quad[\because \text { LHS }>0]
\end{aligned}
\)
Also, \(\cos 27^{\circ}-\sin 27^{\circ}=\sqrt{\left(1-\cos 36^{\circ}\right)}\)
\(
\begin{aligned}
& {\left[\because \cos 27^{\circ}>\sin 27^{\circ}\right]} \\
& \therefore \quad 2 \sin 27^{\circ}=\sqrt{\left(1+\cos 36^{\circ}\right)}-\sqrt{\left(1-\cos 36^{\circ}\right)} \\
& =\sqrt{\left(1+\left(\frac{\sqrt{5}+1}{4}\right)\right)}-\sqrt{\left(1-\left(\frac{\sqrt{5}+1}{4}\right)\right)} \\
& \therefore \quad 4 \sin 27^{\circ}=\sqrt{(5+\sqrt{5})}-\sqrt{(3-\sqrt{5})} \\
&
\end{aligned}
\)
On comparing, we get
\(
\begin{aligned}
& \alpha=5+\sqrt{5}, \beta=3-\sqrt{5} \\
& \therefore \quad \alpha+\beta=8, \alpha \beta=10-2 \sqrt{5} \\
& \alpha+\beta-\alpha \beta+2=2 \sqrt{5} \\
& \therefore(\alpha+\beta-\alpha \beta+2)^4=400
\end{aligned}
\) -
Question 78 of 100
78. Question
If \(0<A<\frac{\pi}{2}\) and \(\sin A+\cos A+\tan A\)
\(+\cot A+\sec A+\operatorname{cosec} A=7\) and \(\sin A\) and \(\cos A\) are the roots of the equation \(4 x^2-3 x+a=0\), then the value of \(25 a\) must beCorrectIncorrectHint
\(\sin A\) and \(\cos A\) are the roots of the equation \(4 x^2-3 x+a=0\), then
\(
\sin A+\cos A=\frac{3}{4}, \sin A \cos A=\frac{a}{4}
\)
Also, \(\sin A+\cos A+\tan A+\cot A+\sec A+\operatorname{cosec} A=7\)
\(
\begin{aligned}
& \Rightarrow \quad(\sin A+\cos A)+\left(\frac{\sin A}{\cos A}+\frac{\cos A}{\sin A}\right) \\
& +\left(\frac{1}{\cos A}+\frac{1}{\sin A}\right)=7 \\
& \Rightarrow \quad(\sin A+\cos A)+\frac{1}{\sin A \cos A}+\frac{(\sin A+\cos A)}{\sin A \cos A}=7 \\
& \Rightarrow \quad \frac{3}{4}+\frac{4}{a}+\frac{3}{a}=7 \\
& \Rightarrow \quad \frac{3}{4}+\frac{7}{a}=7 \\
& \Rightarrow \quad \frac{7}{a}=7-\frac{3}{4}=\frac{25}{4} \\
& \therefore \quad 25 a=28 \\
&
\end{aligned}
\) -
Question 79 of 100
79. Question
If \(\frac{1}{\cos 290^{\circ}}+\frac{1}{\sqrt{3} \sin 250^{\circ}}=\lambda\), then the value of \(9 \lambda^4+81 \lambda^2+97\) must be
CorrectIncorrectHint
Here, \(\cos 290^{\circ}=\cos \left(270^{\circ}+20^{\circ}\right)=\sin 20^{\circ}\) and \(\sin 250^{\circ}=\sin \left(270^{\circ}-20^{\circ}\right)=-\cos 20^{\circ}\)
\(
\begin{aligned}
& \therefore \text { The given expression }=\frac{1}{\sin 20^{\circ}}-\frac{1}{\sqrt{3} \cos 120^{\circ}}=\lambda \\
& \Rightarrow \quad \frac{1}{\sin 20^{\circ}}-\frac{\cos 60^{\circ}}{\sin 60^{\circ} \cos 20^{\circ}}=\lambda \\
& \Rightarrow \quad \frac{\sin 60^{\circ} \cos 20^{\circ}-\cos 60^{\circ} \sin 20^{\circ}}{\sin 20^{\circ} \cos 20^{\circ} \sin 60^{\circ}}=\lambda \\
& \Rightarrow \quad \frac{\sin \left(60^{\circ}-20^{\circ}\right)}{\frac{\sin 40^{\circ}}{2} \times \frac{\sqrt{3}}{2}}=\lambda \\
& \therefore \quad \lambda=\frac{4}{\sqrt{3}} \\
& \Rightarrow \quad \lambda^2=\frac{16}{3} \\
&
\end{aligned}
\)
Then, \(9 \lambda^4+81 \lambda^2+97=9 \times \frac{256}{9}+81 \times \frac{16}{3}+97\)
\(
=256+432+97=785
\) -
Question 80 of 100
80. Question
If \(\log _{10} \sin x+\log _{10} \cos x=-1\) and \(\log _{10}(\sin x+\cos x)=\frac{\left(\log _{10} n\right)-1}{2}\), then the value of ‘ \(n / 3\) ‘ is
CorrectIncorrectHint
\(
\begin{gathered}
\log _{10}\left(\frac{\sin 2 x}{2}\right)=-1 \\
\frac{\sin 2 x}{2}=\frac{1}{10} \\
\sin 2 x=\frac{1}{5}
\end{gathered}
\)
\(
\text { Also } \log _{10}(\sin x+\cos x)=\frac{\log _{10}\left(\frac{n}{10}\right)}{2}
\)
\(
\begin{aligned}
& \log _{10}(\sin x+\cos x)^2=\log _{10}\left(\frac{n}{10}\right) \\
& 1+\sin 2 x=\frac{n}{10} \\
& 1+\frac{1}{5}=\frac{n}{10} \text { or } \frac{6}{5}=\frac{n}{10} \\
& \frac{n}{3}=4
\end{aligned}
\) -
Question 81 of 100
81. Question
\(5\left(\tan ^2 x-\cos ^2 x\right)=2 \cos 2 x+9\), then the value of \(\cos 4 x\) is
CorrectIncorrectHint
Given, \(5\left(\tan ^2 x-\cos ^2 x\right)=2 \cos 2 x+9\)
\(
\Rightarrow \quad 5\left(\frac{1-\cos 2 x}{1+\cos 2 x}-\frac{1+\cos 2 x}{2}\right)=2 \cos 2 x+9
\)
Put \(\cos 2 x=y\), we have
\(
5\left(\frac{1-y}{1+y}-\frac{1+y}{2}\right)=2 y+9
\)
\(
\begin{aligned}
& 5\left(2-2 y-1-y^2-2 y\right)=2(1+y)(2 y+9) \\
& 5\left(1-4 y-y^2\right)=2\left(2 y+9+2 y^2+9 y\right) \\
& 5-20 y-5 y^2=22 y+18+4 y^2 \\
& 9 y^2+42 y+13=0 \\
& 9 y^2+3 y+39 y+13=0 \\
& 3 y(3 y+1)+13(3 y+1)=0 \\
& (3 y+1)(3 y+13)=0 \\
& y=-\frac{1}{3},-\frac{13}{3} \\
& \cos 2 x=-\frac{1}{3},-\frac{13}{3} \\
& \cos 2 x=-\frac{1}{3} \quad\left[\because \cos 2 x \neq-\frac{13}{3}\right] \\
&
\end{aligned}
\)
Now,
\(
\begin{aligned}
\cos 4 x & =2 \cos ^2 2 x-1=2\left(-\frac{1}{3}\right)^2-1 \\
& =\frac{2}{9}-1=-\frac{7}{9}
\end{aligned}
\) -
Question 82 of 100
82. Question
The expression \(\frac{\tan A}{1-\cot A}+\frac{\cot A}{1-\tan A}\) can be written as
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{\tan A}{1-\cot A}+\frac{\cot A}{1-\tan A}=\frac{\sin A}{\cos A} \times \frac{\sin A}{\sin A-\cos A} \\
& \quad+\frac{\cos A}{\sin A} \times \frac{\cos A}{\cos A-\sin A} \\
&= \frac{1}{\sin A-\cos A}\left\{\frac{\sin ^3 A-\cos ^3 A}{\cos A \sin A}\right\} \\
&= \frac{\sin ^2 A+\sin A \cos A+\cos ^2 A}{\sin A \cos A} \\
&= \frac{1+\sin A \cos A}{\sin A \cos A} \\
&= 1+\sec A \operatorname{cosec} A
\end{aligned}
\) -
Question 83 of 100
83. Question
In a \(\triangle P Q R\), if \(3 \sin P+4 \cos Q=6\) and \(4 \sin Q+3 \cos P=1\), then the angle \(R\) is equal to
CorrectIncorrectHint
Given \(A \triangle P Q R\) such that
\(
\begin{aligned}
& 3 \sin P+4 \cos Q=6 \dots(i) \\
& 4 \sin Q+3 \cos P=1 \dots(ii)
\end{aligned}
\)
On squaring and adding Eqs. (i) and (ii) both sides we get
\(
\begin{aligned}
& (3 \sin P+4 \cos Q)^2+(4 \sin Q+3 \cos P)^2=36+1 \\
& \Rightarrow 9\left(\sin ^2 P+\cos ^2 P\right)+16\left(\sin ^2 Q+\cos ^2 Q\right) \\
& +2 \times 3 \times 4(\sin P \cos Q+\sin Q \cos P)=37 \\
& \Rightarrow \quad 24[\sin (P+Q)]=37-25 \\
& \Rightarrow \quad \sin (P+Q)=\frac{1}{2} \\
&
\end{aligned}
\)
Since, \(P\) and \(Q\) are angles of \(\triangle P Q R\), hence \(0^{\circ}<P, Q<180^{\circ}\).
\(
\begin{aligned}
& \Rightarrow \quad P+Q=30^{\circ} \text { or } 150^{\circ} \\
& \Rightarrow \quad R=150^{\circ} \text { or } 30^{\circ} \\
&
\end{aligned}
\)
Hence, two cases arise here.
\(
\begin{aligned}
& \text { Case I } \quad R=150^{\circ} \\
& R=150^{\circ} \Rightarrow P+Q=30^{\circ} \\
& \Rightarrow \quad 0<P, Q<30^{\circ} \\
& \Rightarrow \quad \sin P<\frac{1}{2}, \cos Q<1 \\
& \Rightarrow \quad 3 \sin P+4 \cos Q<\frac{3}{2}+4 \\
& \Rightarrow \quad 3 \sin P+4 \cos Q<\frac{11}{2}<6 \\
& \Rightarrow 3 \sin P+4 \cos Q \Rightarrow 6 \text { is not possible. } \\
& \text { Case II } \quad R=30^{\circ} \\
&
\end{aligned}
\)
Hence, \(R=30^{\circ}\) is the only possibility. -
Question 84 of 100
84. Question
If \(A=\sin ^2 x+\cos ^4 x\), then for all real \(x\)
CorrectIncorrectHint
\(
\begin{aligned}
& A=\sin ^2 x+\cos ^4 x \\
& A=1-\cos ^2 x+\cos ^4 x
\end{aligned}
\)
\(
\begin{aligned}
& =\cos ^4 x-\cos ^2 x+\frac{1}{4}+\frac{3}{4} \\
& =\left(\cos ^2 x-\frac{1}{2}\right)^2+\frac{3}{4} \dots(i)
\end{aligned}
\)
\(
\begin{array}{ll}
\text { where, } & 0 \leq\left(\cos ^2 x-\frac{1}{2}\right)^2 \leq \frac{1}{4} \dots(ii) \\
\therefore & \frac{3}{4} \leq A \leq 1
\end{array}
\) -
Question 85 of 100
85. Question
Let \(\cos (\alpha+\beta)=\frac{4}{5}\) and \(\sin (\alpha-\beta)=\frac{5}{13}\), where \(0 \leq \alpha, \beta \leq \frac{\pi}{4}\). Then, \(\tan 2 \alpha\) is equal to
CorrectIncorrectHint
\(
\cos (\alpha+\beta)=\frac{4}{5} \Rightarrow \alpha+\beta \in \text { Ist quadrant }
\)
and \(\sin (\alpha-\beta)=\frac{5}{13} \Rightarrow \alpha-\beta \in\) Ist quadrant
Now, \(\quad 2 \alpha=(\alpha+\beta)+(\alpha-\beta)\)
\(
\therefore \quad \tan 2 \alpha=\frac{\tan (\alpha+\beta)+\tan (\alpha-\beta)}{1-\tan (\alpha+\beta) \tan (\alpha-\beta)}=\frac{\frac{3}{4}+\frac{5}{12}}{1-\frac{3}{4} \cdot \frac{5}{12}}=\frac{56}{33}
\) -
Question 86 of 100
86. Question
Let \(A\) and \(B\) denote the statements
\(
\begin{gathered}
A: \cos \alpha+\cos \beta+\cos \gamma=0 \\
B: \sin \alpha+\sin \beta+\sin \gamma=0
\end{gathered}
\)
If \(\cos (\beta-\gamma)+\cos (\gamma-\alpha)+\cos (\alpha-\beta)=-\frac{3}{2}\), thenCorrectIncorrectHint
\(
\begin{aligned}
& \cos (\beta-\gamma)+\cos (\gamma-\alpha)+\cos (\alpha-\beta)=-\frac{3}{2} \\
& \Rightarrow 2[\cos (\beta-\gamma)+\cos (\gamma-\alpha)+\cos (\alpha-\beta)]+3=0
\end{aligned}
\)
\(
\Rightarrow 2[\cos (\beta-\gamma)+\cos (\gamma-\alpha)+\cos (\alpha-\beta)]+\sin ^2 \alpha+\cos ^2 \alpha+\sin ^2 \beta+\cos ^2 \beta+\sin ^2 \gamma+\cos ^2 \gamma=0
\)
\(
\Rightarrow(\sin \alpha+\sin \beta+\sin \gamma)^2+(\cos \alpha+\cos \beta+\cos \gamma)^2=0
\)
It is possible when,
\(
\text { and } \quad \begin{aligned}
\sin \alpha+\sin \beta+\sin \gamma & =0 \\
\cos \alpha+\cos \beta+\cos \gamma & =0
\end{aligned}
\)
Hence, both statements \(A\) and \(B\) are true. -
Question 87 of 100
87. Question
A triangular park is enclosed on two sides by a fence and on the third side by a straight river bank. The two sides having fence are of same length \(x\). The maximum area enclosed by the park is
CorrectIncorrectHint
\(
\text { Area }=\frac{1}{2} \times \text { Base } \times \text { Altitude }
\)
\(
=\frac{1}{2} \times(2 x \cos \theta) \times(x \sin \theta)=\frac{1}{2} x^2 \sin 2 \theta
\)
[since, maximum value of \(\sin 2 \theta\) is 1]
\(\therefore\) Maximum area \(=\frac{1}{2} x^2\) -
Question 88 of 100
88. Question
If \(0<x<\pi\) and \(\cos x+\sin x=\frac{1}{2}\), then \(\tan x\) is
CorrectIncorrectHint
Given, \(\quad \cos x+\sin x=\frac{1}{2}\)
\(
\therefore \frac{1-\tan ^2 \frac{x}{2}}{1+\tan ^2 \frac{x}{2}}+\frac{2 \tan \frac{x}{2}}{1+\tan ^2 \frac{x}{2}}=\frac{1}{2}
\)
Let \(\tan \frac{x}{2}=t \Rightarrow \frac{1-t^2}{1+t^2}+\frac{2 t}{1+t^2}=\frac{1}{2}\)
\(\Rightarrow \quad 2\left(1-t^2+2 t\right)=1+t^2 \Rightarrow 3 t^2-4 t-1=0\)
\(\Rightarrow \quad t=\frac{2 \pm \sqrt{7}}{3}\)
As \(0<x<\pi \Rightarrow 0<\frac{x}{2}<\frac{\pi}{2}\)
So, \(\tan \frac{x}{2}\) is positive.
\(\therefore \quad t=\tan \frac{x}{2}=\frac{2+\sqrt{7}}{3}\)
Now, \(\quad \tan x=\frac{2 \tan \frac{x}{2}}{1-\tan ^2 \frac{x}{2}}=\frac{2 t}{1-t^2}\)
\(\Rightarrow \quad \tan x=\frac{2\left(\frac{2+\sqrt{7}}{3}\right)}{1-\left(\frac{2+\sqrt{7}}{3}\right)^2}\)
\(\Rightarrow \quad \tan x=\frac{-3(2+\sqrt{7})}{1+2 \sqrt{7}} \times \frac{1-2 \sqrt{7}}{1-2 \sqrt{7}}\)
\(\Rightarrow \quad \tan x=-\left(\frac{4+\sqrt{7}}{3}\right)\) -
Question 89 of 100
89. Question
In a \(\triangle P Q R, \angle R=\frac{\pi}{2}\). If \(\tan \left(\frac{P}{2}\right)\) and \(\tan \left(\frac{Q}{2}\right)\) are the roots of \(a x^2+b x+c=0, a \neq 0\), then
CorrectIncorrectHint
\(
\begin{aligned}
& \text { Since, } \quad \angle R=\frac{\pi}{2} \\
& \Rightarrow \quad \angle P+\angle Q=\frac{\pi}{2} \\
& \Rightarrow \quad \frac{\angle P}{2}=\frac{\pi}{4}-\frac{\angle Q}{2} \\
& \therefore \quad \tan \frac{P}{2}=\tan \left(\frac{\pi}{4}-\frac{Q}{2}\right) \\
& =\frac{\tan \frac{\pi}{4}-\tan \frac{Q}{2}}{1+\tan \frac{\pi}{4} \tan \frac{Q}{2}} \\
& \Rightarrow \quad \tan \frac{P}{2}+\tan \frac{P}{2} \tan \frac{Q}{2}=1-\tan \frac{Q}{2} \\
& \Rightarrow \quad \tan \frac{P}{2}+\tan \frac{Q}{2}=1-\tan \frac{P}{2} \tan \frac{Q}{2} \\
& \Rightarrow \quad-\frac{b}{a}=1-\frac{c}{a} \\
& \Rightarrow \quad-b=a-c \\
& \Rightarrow \quad c=a+b \\
&
\end{aligned}
\) -
Question 90 of 100
90. Question
If \(\frac{\sin ^4 x}{2}+\frac{\cos ^4 x}{3}=\frac{1}{5}\), then
CorrectIncorrectHint
\(
\begin{aligned}
& \frac{\sin ^4 x}{2}+\frac{\cos ^4 x}{3}=\frac{1}{5} \\
& \Rightarrow \quad \frac{\sin ^4 x}{2}+\frac{\left(1-\sin ^2 x\right)^2}{3}=\frac{1}{5} \\
& \Rightarrow \quad \frac{\sin ^4 x}{2}+\frac{1+\sin ^4 x-2 \sin ^2 x}{3}=\frac{1}{5}
\end{aligned}
\)
\(
\begin{aligned}
& \Rightarrow \quad 5 \sin ^4 x-4 \sin ^2 x+2=\frac{6}{5} \\
& \Rightarrow \quad 25 \sin ^4 x-20 \sin ^2 x+4=0 \\
& \Rightarrow \quad\left(5 \sin ^2 x-2\right)^2=0 \\
& \Rightarrow \quad \sin ^2 x=\frac{2}{5} \\
& \cos ^2 x=\frac{3}{5}, \tan ^2 x=\frac{2}{3} \\
& \therefore \quad \frac{\sin ^8 x}{8}+\frac{\cos ^8 x}{27}=\frac{1}{125} \\
&
\end{aligned}
\) -
Question 91 of 100
91. Question
\(
\text { The value of } \sum_{n=1}^{10}\left(\sin \frac{2 n \pi}{11}-\cos \frac{2 n \pi}{11}\right) \text { is equal to }
\)CorrectIncorrectHint
\(
\begin{aligned}
= & \left(\sin \frac{2 \pi}{11}-\cos \frac{2 \pi}{11}\right)+\left(\sin \frac{4 \pi}{11}-\cos \frac{4 \pi}{11}\right) \\
& +\left(\sin \frac{6 \pi}{11}-\cos \frac{6 \pi}{11}\right)+\ldots+\left(\sin \frac{20 \pi}{11}-\cos \frac{20 \pi}{11}\right) \\
= & \left(\sin \frac{2 \pi}{11}+\sin \frac{4 \pi}{11}+\ldots+\sin \frac{20 \pi}{11}\right) \\
= & \frac{\sin \pi \cdot \sin \frac{10 \pi}{11}}{\sin \frac{\pi}{11}}-\frac{\cos \frac{2 \pi}{11}+\cos \frac{4 \pi}{11}+\ldots+\sin \frac{10 \pi}{11}}{\sin \frac{\pi}{11}} \\
= & 0+\frac{\sin \left(\pi-\frac{\pi}{11}\right)}{\sin \frac{\pi}{11}}=1
\end{aligned}
\) -
Question 92 of 100
92. Question
The minimum value of the function \(f(x)=(3 \sin x-4 \cos x-10)(3 \sin x+4 \cos x-10)\), is
CorrectIncorrectHint
\(
\begin{aligned}
& f(x)=9 \sin ^2 x-16 \cos ^2 x-10(3 \sin x-4 \cos x) \\
& -10(3 \sin x+4 \cos x)+100 \\
& =25 \sin ^2 x-60 \sin x+84 \\
& =(5 \sin x-6)^2+48 \\
& \therefore f(x)_{\min } \text { occurs when } \sin x=1 \\
& \text { Minimum value }=49 \\
&
\end{aligned}
\) -
Question 93 of 100
93. Question
The value of expression \(\sum_{\theta=0}^8 \frac{1}{1+\tan ^3(10 \theta)^{\circ}}\) equal is to
CorrectIncorrectHint
\(
S=\frac{1}{1+\tan ^3 0^{\circ}}+\frac{1}{1+\tan ^3 10^{\circ}}+\ldots+\frac{1}{1+\tan ^3 80^{\circ}}
\)
Now, \(\frac{1}{1+\tan ^3 \theta}+\frac{1}{1+\tan ^3(90-\theta)}\)
\(
\begin{aligned}
& =\frac{1}{1+\tan ^3 \theta}+\frac{1}{1+\cot ^3 \theta} \\
& =\frac{1}{1+\tan ^3 \theta}+\frac{\tan ^3 \theta}{1+\tan ^3 \theta} \\
& =\frac{1+\tan ^3 \theta}{1+\tan ^3 \theta}=1
\end{aligned}
\)
Hence, \(S=1+(1+1+1+1)=5\) -
Question 94 of 100
94. Question
\(
\text { The value of } \sqrt{1-\sin ^2 110^{\circ}} \cdot \sec 110^{\circ} \text { is equal to }
\)CorrectIncorrectHint
\(
\text { Clearly, } \sqrt{1-\sin ^2 110^{\circ}} \cdot \sec 110^{\circ}
\)
\(
\begin{aligned}
& =\left|\cos 110^{\circ}\right| \sec 110^{\circ} \\
& =-\cos 110^{\circ} \sec 110^{\circ}=-1
\end{aligned}
\) -
Question 95 of 100
95. Question
The value of the product
\(
\sin \left(\frac{\pi}{2^{2009}}\right) \cos \left(\frac{\pi}{2^{2009}}\right) \cos \left(\frac{\pi}{2^{2008}}\right)
\)
\(\cos \left(\frac{\pi}{2^{2007}}\right) \cos \left(\frac{\pi}{2^{2006}}\right) \ldots \cos \left(\frac{\pi}{2^3}\right) \cos \left(\frac{\pi}{2^2}\right), \)isCorrectIncorrectHint
Let \(A\) be the expression. Multiplying \(A\) by \(2^{2008}\) and using \(2 \sin \theta \cos \theta=\sin 2 \theta\),
we have
\(
2^{2008} A=\sin \frac{\pi}{2}=1 . A=\frac{1}{2^{2008}}
\)Alternatively
\(\sin \left(\frac{\pi}{2^{2009}}\right) \cos \left(\frac{\pi}{2^{2009}}\right)=\frac{1}{2} \sin \left(\frac{\pi}{2^{2008}}\right)\)
\(
\begin{aligned}
& =\frac{1}{2^2} \cdot 2 \sin \left(\frac{\pi}{2^{2008}}\right) \cos \left(\frac{\pi}{2^{2008}}\right) \\
& =\frac{1}{2^2} \sin \left(\frac{\pi}{2^{2007}}\right)
\end{aligned}
\)
Similarly, continued product upto,
\(
\cos \left(\frac{\pi}{2^2}\right)=\frac{1}{2^{2008}} \sin \left(\frac{\pi}{2}\right)=\frac{1}{2^{2008}}
\) -
Question 96 of 100
96. Question
The value of \(\left(\cos ^4 1^{\circ}+\cos ^4 2^{\circ}+\cos ^4 3^{\circ}+\ldots+\cos ^4 179^{\circ}\right)-\) \(\left(\sin ^4 1^{\circ}+\sin ^4 2^{\circ}+\sin ^4 3^{\circ}+\ldots+\sin ^4 179^{\circ}\right)\) equals to
CorrectIncorrectHint
\(
\begin{aligned}
&\left(\cos ^4 1^{\circ}+\cos ^4 2^{\circ}+\cos ^4 3^{\circ}+\ldots+\cos ^4 179^{\circ}\right) \\
&-\left(\sin ^4 1^{\circ}+\sin ^4 2^{\circ}+\sin ^4 3^{\circ}+\ldots+\sin ^4 179^{\circ}\right) \\
&=\cos 2^{\circ}+\cos 4^{\circ}+\cos 6^{\circ}+\ldots+\cos \left(358^{\circ}\right) \\
&=\cos \frac{\left(\frac{2^{\circ}+358^{\circ}}{2}\right) \cdot \sin \left(179 \times 1^{\circ}\right)}{\sin 1^{\circ}} \\
&= \cos \left(180^{\circ}\right)=-1 .
\end{aligned}
\) -
Question 97 of 100
97. Question
Suppose that ‘ \(a\) ‘ is a non-zero real number for which \(\sin x+\sin y=a\) and \(\cos x+\cos y=2 a\). The value of \(\cos (x-y)\), is
CorrectIncorrectHint
\(
\begin{aligned}
& \sin x+\sin y=a \dots(i)\\
& \quad \cos x+\cos y=2 a \dots(ii)
\end{aligned}
\)
On squaring and adding Eqs. (i) and (ii), we get
\(
\begin{aligned}
2+2 \cos (x-y) & =5 a^2 \\
\cos (x-y) & =\frac{5 a^2-2}{2}
\end{aligned}
\) -
Question 98 of 100
98. Question
The value of \(\sum_{r=1}^{18} \cos ^2(5 r)^{\circ}\), where \(x^{\circ}\) denotes the \(x\) degrees, is equal to
CorrectIncorrectHint
\(
\sum_{r=1}^{18} \cos ^2(5 r)^{\circ}=\cos ^2 5^{\circ}+\cos ^2 10^{\circ}+\cos ^2 15^{\circ}+\ldots+\cos ^2 85^{\circ}+\cos ^2 90^{\circ}
\)
\(
\begin{aligned}
= & \left(\cos ^2 5^{\circ}+\cos ^2 85^{\circ}\right)+\left(\cos ^2 10^{\circ}+\cos ^2 80^{\circ}\right) \\
& +\left(\cos ^2 15^{\circ}+\cos ^2 75^{\circ}\right)+\ldots+\left(\cos ^2 40^{\circ}+\cos ^2 50^{\circ}\right)+\cos ^2 45^{\circ} \\
= & \left(\cos ^2 5^{\circ}+\sin ^2 5^{\circ}\right)+\left(\cos ^2 10^{\circ}+\sin ^2 10^{\circ}\right) \\
& +\left(\cos ^2 15^{\circ}+\sin ^2 15^{\circ}\right)+\ldots+\left(\cos ^2 40^{\circ}+\sin ^2 40^{\circ}\right)+\cos ^2 45^{\circ}
\end{aligned}
\)
\(
=1+1+1+\ldots+1+\frac{1}{2}=8+\frac{1}{2}=\frac{17}{2}
\) -
Question 99 of 100
99. Question
If \(A=\sin 44^{\circ}+\cos 44^{\circ}, B=\sin 45^{\circ}+\cos 45^{\circ}\) and \(C=\sin 46^{\circ}+\cos 46^{\circ}\). Then, correct option(s) is/are
CorrectIncorrectHint
\(
\begin{aligned}
& A=\sin 44^{\circ}+\cos 44^{\circ} \\
&=\cos 46^{\circ}+\sin 46^{\circ}=C \\
& B=\sin 45^{\circ}+\cos 45^{\circ}=\sqrt{2}\left[\sin 90^{\circ}\right] \\
& A=\sqrt{2}\left[\frac{1}{\sqrt{2}} \sin 44^{\circ}+\frac{1}{\sqrt{2}} \cos 44^{\circ}\right] \\
&=\sqrt{2}\left[\sin 44^{\circ} \cdot \cos 45^{\circ}+\cos 44^{\circ} \cdot \sin 45^{\circ}\right] \\
&=\sqrt{2} \sin 89^{\circ} \\
& \Rightarrow \quad B>A
\end{aligned}
\) -
Question 100 of 100
100. Question
If \(4 \cos 36^{\circ}+\cot \left(7 \frac{1}{2}^{\circ}\right)=\sqrt{n_1}+\sqrt{n_2}+\sqrt{n_3}+\sqrt{n_4}+\sqrt{n_5}\) \(+\sqrt{n_6}\), then the value of \(\sum_{i=1}^6 n_i^2\) must be
CorrectIncorrectHint
\(
\begin{aligned}
\cot \left(7 \frac{1^{\circ}}{2}\right)= & \frac{1+\cos 15^{\circ}}{\sin 15^{\circ}} \\
& =\frac{1+\frac{\sqrt{3}+1}{2 \sqrt{2}}}{\frac{\sqrt{3}-1}{2 \sqrt{2}}}=\frac{2 \sqrt{2}+\sqrt{3}+1}{\sqrt{3}-1} \\
& =\frac{(2 \sqrt{2}+\sqrt{3}+1)(\sqrt{3}+1)}{2}
\end{aligned}
\)
\(
\begin{aligned}
& =\sqrt{1}+\sqrt{2}+\sqrt{3}+\sqrt{4}+\sqrt{5}+\sqrt{6} \\
& \therefore \quad n_1=1, n_2=2, n_3=3, n_4=4, n_5=5 \text { and } n_6=6 \\
& \therefore \sum_{i=1}^6 n_i^2=n_1^2+n_2^2+n_3^2+n_4^2+n_5^3+n_6^2 \\
& =1^2+2^2+3^2+4^2+5^2+6^2 \\
& =91 \\
&
\end{aligned}
\)