Quiz
Quiz Summary
0 of 26 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 26 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 26
1. Question
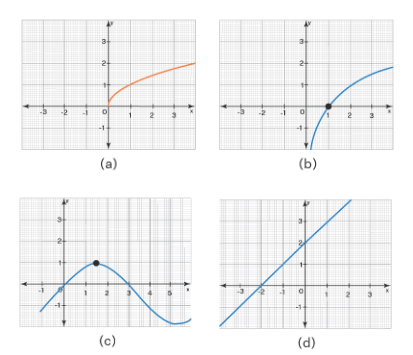
Which of the following graphs represents nonlinear functions?
 CorrectIncorrect
CorrectIncorrectHint
We know that a nonlinear function’s graph is not a straight line. So among the given graphs, (a), (b), and (c) are nonlinear whereas (d) is a linear function.
-
Question 2 of 26
2. Question
Which of the following represents a nonlinear function?
CorrectIncorrect -
Question 3 of 26
3. Question
Is this equation linear or nonlinear?
\(y=2^x\)
CorrectIncorrect -
Question 4 of 26
4. Question
Solve the following system of nonlinear equations:
\(
\begin{aligned}
& -x^2+y+3 x=7 \\
& 5=-y-x^2+7 x
\end{aligned}
\)CorrectIncorrectHint
We can start by rearranging each equation so that \(y\) is on one side:
\(
\begin{aligned}
& -x^2+y+3 x=7 \rightarrow y=x^2-3 x+7 \\
& 5=-y-x^2+7 x \rightarrow y=-x^2+7 x-5
\end{aligned}
\)
Now that both equations are equal to \(\mathrm{y}\), we can set the right sides equal to each other and solve for \(\mathrm{x}\) :
\(
\begin{aligned}
& x^2-3 x+7=-x^2+7 x-5 \rightarrow 2 x^2-10 x+12=0 \\
& 2\left(x^2-5 x+6\right)=0 \rightarrow 2(x-2)(x-3)=0 \\
& x=2, x=3
\end{aligned}
\)
Our last step is to plug these values of \(x\) into either equation to find the \(y\) values of our solutions:
\(
\begin{aligned}
& y=x^2-3 x+7=(2)^2-3(2)+7=5 \\
& y=x^2-3 x+7=(3)^2-3(3)+7=7
\end{aligned}
\)
So our solutions are the following two points:
\(
(2,5),(3,7)
\) -
Question 5 of 26
5. Question
Solve the following system of equations
\(
\begin{aligned}
& x^2+y^2=117 \\
& y-x=3
\end{aligned}
\)CorrectIncorrectHint
Our first step is to solve the bottom equation for \(y\)
\(
y=x+3
\)
We can now substitute it into the top equation:
\(
x^2+(x+3)^2=117
\)
and solve for our \(x\) values:
\(
\begin{aligned}
& x^2+x^2+6 x+9=117 \\
& 2 x^2+6 x+9-117=0 \\
& 2 x^2+6 x-108=0 \\
& 2\left(x^2+3 x-54\right)=0 \\
& 2(x+9)(x-6)=0
\end{aligned}
\)
our values are then: \(x=6,-9\)
We can now plug our values into the bottom equation we had solved for \(y\) and arrive at our solutions:
\(
y=6+3=9 \quad y=-9+3=-6
\)
So, our solutions are \((6,9),(-9,-6)\) -
Question 6 of 26
6. Question
Solve the following system of nonlinear equations
\(
\begin{aligned}
& x^2+y^2=5 \\
& x^2+3 x^2 y=x^4
\end{aligned}
\)CorrectIncorrectHint
Our first step is to solve the bottom equation for \(x^2\) :
\(
\begin{aligned}
& x^2(1+3 y)=x^4 \\
& (1+3 y)=\frac{x^4}{x^2} \\
& (1+3 y)=x^2
\end{aligned}
\)
so we can substitute it into the top equation:
\(
\begin{aligned}
& (1+3 y)+y^2=5 \\
& 1+3 y+y^2-5=0 \\
& y^2+3 y-4=0 \\
& (y-1)(y+4)=0 \\
& y=1,-4
\end{aligned}
\)
Now we can plug in our \(y\)-values into the bottom equation to find our \(\mathrm{x}\)-values:
\(
\begin{aligned}
& (1+3(1))=x^2 \\
& 4=x^2 \\
& x=\pm 2
\end{aligned}
\)
\(
\begin{aligned}
& (1+3(-4))=x^2 \\
& 1-12=x^2 \\
& -11=x^2
\end{aligned}
\)
Remember we cannot take a square root of a negative number without getting an imaginary number. As such, we’ll just focus on the \(x=\pm 2\) values.
Our solution is then: \((2,1),(-2,1)\) -
Question 7 of 26
7. Question
Solve the following system for \(y>0\) :
\(
\begin{aligned}
4 y & =x^2+2 x \\
y^2 & =36
\end{aligned}
\)CorrectIncorrectHint
The first step is to solve the bottom equation for \(y\) :
\(y=\sqrt{36}=\pm 6\) since our question specifies for \(y>0\) we just focus on \(y=6\)
We now substitute this equation into the top equation:
\(
\begin{aligned}
& 4(6)=x^2+2 x \\
& 0=x^2+2 x-24 \\
& 0=(x+6)(x-4) \\
& x=-6,4
\end{aligned}
\)
we can now plug in our \(x\)-values into the bottom equation to find our \(y\)-values:
\(
\begin{array}{lc}
4 y=(-6)^2+2(-6) & 4 y=(4)^2+2(4) \\
4 y=36-12 & 4 y=16+8 \\
4 y=24 & 4 y=24 \\
y=6 & y=6
\end{array}
\)
The solutions are then: \((-6,6),(4,6)\) -
Question 8 of 26
8. Question
Solve the following system of nonlinear equations
\(
\begin{aligned}
& y^2+x^2+6 x=18 \\
& y^2=x^2-2
\end{aligned}
\)CorrectIncorrectHint
We can solve this equation by using substitution since the bottom equation is already solved for \(y^2\). Substituting the bottom equation into the top we get:
\(
\left(x^2-2\right)+x^2+6 x=18
\)
We then solve the equation for our \(x\) values:
\(
\begin{aligned}
& \left(x^2-2\right)+x^2+6 x-18=0 \\
& 2 x^2+6 x-20=0 \\
& 2\left(x^2+3 x-10\right)=0 \\
& 2(x-2)(x+5)=0 \\
& x=2,-5
\end{aligned}
\)
Finally, we substitute our values into the bottom equation to get our \(y\) values:
\(
\begin{array}{ll}
y^2=(2)^2-2 & y^2=(-5)^2-2 \\
y^2=2 & y^2=23 \\
y=\pm \sqrt{2} & y=\pm \sqrt{23}
\end{array}
\)
Our different solutions are then: \((2, \sqrt{2}),(2,-\sqrt{2}),(-5, \sqrt{23}),(-5,-\sqrt{23})\) -
Question 9 of 26
9. Question
Solve graphically. Estimate your answer.
\(
\begin{aligned}
& y=x^2 \\
& x y=4
\end{aligned}
\)CorrectIncorrectHint
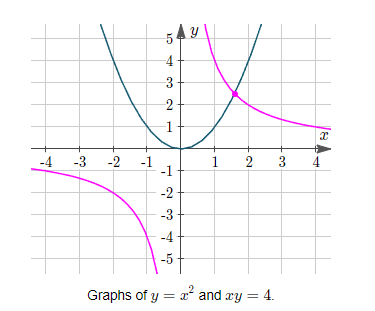
\(y=x^2\) is a parabola
\(x y=4\) is a hyperbola.
\(
\text { We see that the intersection point (the graphical solution) is at approximately }(1.5,2.5) \text {. }
\) -
Question 10 of 26
10. Question
Solve graphically. Estimate your answer:
\(
\begin{aligned}
& y=4 x-x^2 \\
& y=2 \cos x
\end{aligned}
\)CorrectIncorrectHint
We see that the solutions are approximately
(0.5,1.8)(0.5,1.8) & (4.2,−0.9)(4.2,−0.9).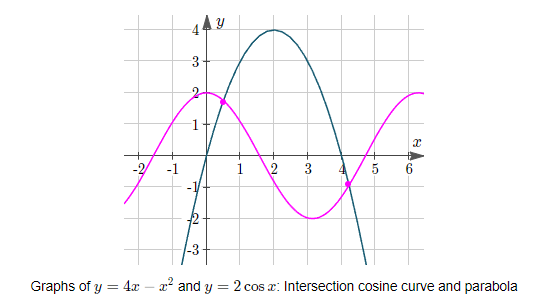
-
Question 11 of 26
11. Question
\(
\text { Find an equation of the circle with centre at }(0,0) \text { and radius } r \text {. }
\)CorrectIncorrectHint
By the distance formula, we have
i.e.
\(
\begin{aligned}
& \sqrt{(x-h)^2+(y-k)^2}=r \\
& (x-h)^2+(y-k)^2=r^2
\end{aligned}
\)\(
\text { Here } h=k=0 \text {. Therefore, the equation of the circle is } x^2+y^2=r^2 \text {. }
\) -
Question 12 of 26
12. Question
\(
\text { Find the equation of the circle with centre }(-3,2) \text { and radius } 4 \text {. }
\)CorrectIncorrectHint
Here \(h=-3, k=2\) and \(r=4\). Therefore, the equation of the required circle is
\(
(x+3)^2+(y-2)^2=16
\) -
Question 13 of 26
13. Question
\(
\text { Find the centre and the radius of the circle } x^2+y^2+8 x+10 y-8=0
\)CorrectIncorrectHint
The given equation is
\(
\left(x^2+8 x\right)+\left(y^2+10 y\right)=8
\)
Now, completing the squares within the parenthesis, we get
\(
\begin{aligned}
& \left(x^2+8 x+16\right)+\left(y^2+10 y+25\right)=8+16+25 \\
& (x+4)^2+(y+5)^2=49 \\
& \{x-(-4)\}^2+\{y-(-5)\}^2=7^2
\end{aligned}
\)
Therefore, the given circle has centre at \((-4,-5)\) and radius 7. -
Question 14 of 26
14. Question
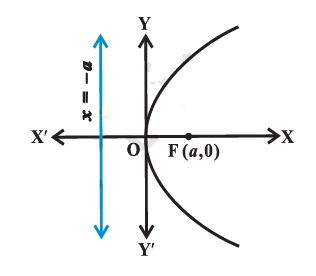
Find the equation of the parabola shown below.
 CorrectIncorrect
CorrectIncorrectHint
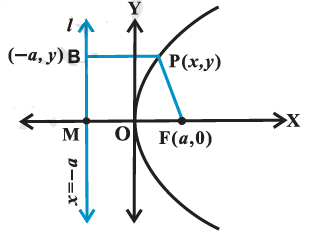
Let \(\mathrm{F}\) be the focus and \(l\) the directrix. Let FM be perpendicular to the directrix and bisect FM at the point O. Produce MO to X. By the definition of parabola, the mid-point \(\mathrm{O}\) is on the parabola and is called the vertex of the parabola. Take \(O\) as origin, OX the \(x\)-axis and OY perpendicular to it as the \(y\)-axis. Let the distance from the directrix to the focus be \(2 a\). Then, the coordinates of the focus are \((a, 0)\), and the equation of the directrix is \(x+a=0\) as in above. Let \(\mathrm{P}(x, y)\) be any point on the parabola such that \(\mathrm{PF}=\mathrm{PB} \dots(1)\)
where \(\mathrm{PB}\) is perpendicular to \(l\). The coordinates of \(\mathrm{B}\) are \((-a, y)\). By the distance formula, we have
\(
\mathrm{PF}=\sqrt{(x-a)^2+y^2} \text { and } \mathrm{PB}=\sqrt{(x+a)^2}
\)
Since \(\mathrm{PF}=\mathrm{PB}\), we have
\(
\sqrt{(x-a)^2+y^2}=\sqrt{(x+a)^2}
\)
i.e. \((x-a)^2+y^2=(x+a)^2\)
or \(x^2-2 a x+a^2+y^2=x^2+2 a x+a^2\)
or \(y^2=4 a x(a>0)\).Hence, any point on the parabola satisfies
\(
y^2=4 a x \dots(2)
\)
Conversely, let \(\mathrm{P}(x, y)\) satisfy the equation (2)
\(
\begin{aligned}
\mathrm{PF} & =\sqrt{(x-a)^2+y^2}=\sqrt{(x-a)^2+4 a x} \\
& =\sqrt{(x+a)^2}=\mathrm{PB} \dots(3)
\end{aligned}
\)
and so \(\mathrm{P}(x, y)\) lies on the parabola.
Thus, from (2) and (3) we have proved that the equation to the parabola with vertex at the origin, focus at \((a, 0)\) and directrix \(x=-a\) is \(y^2=4 a x\). -
Question 15 of 26
15. Question
\(
\text { Find the equation of the parabola with vertex at }(0,0) \text { and focus at }(0,2) \text {. }
\)CorrectIncorrectHint
Since the vertex is at \((0,0)\) and the focus is at \((0,2)\) which lies on \(y\)-axis, the \(y\)-axis is the axis of the parabola. Therefore, equation of the parabola is of the form \(x^2=4 a y\). thus, we have
\(
x^2=4(2) y \text {, i.e., } x^2=8 y
\) -
Question 16 of 26
16. Question
Find the equation of the hyperbola with foci \((0, \pm 3)\) and vertices
\(
\left(0, \pm \frac{\sqrt{11}}{2}\right)
\)CorrectIncorrectHint
Since the foci is on y-axis, the equation of the hyperbola is of the form \(\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\)
Since vertices are \(\left(0, \pm \frac{\sqrt{11}}{2}\right), a=\frac{\sqrt{11}}{2}\)
Also, since foci are \((0, \pm 3) ; c=3\) and \(b^2=c^2-a^2=\frac{25}{4}\).
Therefore, the equation of the hyperbola is
\(
\frac{y^2}{\left(\frac{11}{4}\right)}-\frac{x^2}{\left(\frac{25}{4}\right)}=1, \text { i.e., } 100 y^2-44 x^2=275
\) -
Question 17 of 26
17. Question
Which of the following function is nonlinear?
CorrectIncorrectHint
The power of \(x\) in \(3 x^2\) and \(2 x\) are 2 and 1 respectively. So its highest power is 2 .
So it is a Nonlinear function -
Question 18 of 26
18. Question
Solve the system of equations
\(
\begin{aligned}
& y=x^2+x-1 \\
& y=-2 x+3
\end{aligned}
\)CorrectIncorrectHint
Step 1 The equations are already solved for \(y\).
Step 2 Substitute \(-2 x+3\) for \(y\) in Equation 1 and solve for \(x\).
\(
\begin{array}{rlrl}
-2 x+3 & =x^2+x-1 \\
3 & =x^2+3 x-1 \\
0 & =x^2+3 x-4 \\
0 & =(x+4)(x-1) \\
x+4 & =0 \quad \text { or } & x-1=0 \\
x & =-4 \quad \text { or } \quad x=1
\end{array}
\)
Step 3 Substitute \(-4\) and 1 for \(x\) in Equation 2 and solve for \(y\).
\(
\begin{array}{rlrlrl}
y & =-2(-4)+3 & \text { Substitute for } x \text { in Equation 2. } & & y & =-2(1)+3 \\
& =11 & \text { Simplify. } & & =1
\end{array}
\)
So, the solutions are \((-4,11)\) and \((1,1)\). -
Question 19 of 26
19. Question
Solve the system of equations by elimination.
\(
\begin{aligned}
& y=x^2-3 x-2 \\
& y=-3 x-8
\end{aligned}
\)CorrectIncorrectHint
Subtract Equation 2 from Equation 1 .
\(
\begin{aligned}
0=x^2 \quad+6
\end{aligned}
\)Solve for \(x\).
\(
\begin{aligned}
0 & =x^2+6 \\
-6 & =x^2
\end{aligned}
\)
The square of a real number cannot be negative. So, the system has no real solutions. -
Question 20 of 26
20. Question
The difference of two numbers is 3, and the sum of their cubes is 407. Find the numbers.
CorrectIncorrectHint
\(
\text { Let’s set up a system of non-linear equations: }\left\{\begin{array}{l}
x-y=3 \\
x^3+y^3=407
\end{array}\right.
\)
\(
\text { Substituting the } y \text { from the first equation into the second and solving yields: }
\)
\(
\begin{aligned}
x^3+(x-3)^3 & =407 \\
x^3+(x-3)\left(x^2-6 x+9\right) & =407 \\
x^3+x^3-6 x^2+9 x-3 x^2+18 x-27 & =407 \\
2 x^3-9 x^2+27 x-434 & =0
\end{aligned}
\)
\(
x=7 \text { works, and to find } y \text {, we use } y=x-3 \text {. When } x=7, y=4 \text {. The two numbers are } 4 \text { and } 7.
\) -
Question 21 of 26
21. Question
Lacy is speeding in her car and sees a parked police car on the side of the road right next to her at \(t=0\) seconds. She immediately decelerates, but the police car accelerates to catch up with her. (Assume the two cars are going in the same direction in parallel paths).
The distance that Lacy has traveled in feet after \(t\) seconds can be modeled by the equation \(d(t)=150+75 t-1.2 t^2\). The distance that the police car travels after \(t\) seconds can be modeled by the equation \(d(t)=4 t^2\). How long will it take the police car to catch up to Lacy?CorrectIncorrectHint
Quadratic Formula to solve:
\(
\begin{aligned}
& \left\{\begin{array}{l}
d(t)=150+75 t-1.2 t^2 \\
d(t)=4 t^2
\end{array}\right. \\
& 150+75 t-1.2 t^2=4 t^2 \\
& 5.2 t^2-75 t-150=0 \\
& t=\frac{-(-75) \pm \sqrt{(-75)^2-4(5.2)(-150)}}{2(5.2)} \\
& t \approx 16.20 \\
&
\end{aligned}
\)
Note that we only want the positive value for \(t\), so in \(16.2\) seconds, the police car will catch up with Lacy. -
Question 22 of 26
22. Question
A motorboat whose speed is 18kmph in still water takes 1 hour more to go 24 km upstream than to return downstream to the exact location. Find the speed of the stream.
CorrectIncorrectHint
Let the speed of the stream be \(x \mathrm{kmph}\).
We know that when the boat travels upstream, the relative speed between the boat and the stream \(=(18-x) \mathrm{kmph}\)
When the boat travels downstream, the relative speed between the boat and the stream \(=(18+x) \mathrm{kmph}\)
The time required to go upstream \(=\frac{\text { Distance }}{\text { Speed }}=\frac{24}{18-x}\) hours
Similarly, the time required to go downstream \(=\frac{\text { Distance }}{\text { Speed }}=\frac{24}{18+x}\) hours
Now, according to the question, \(\frac{24}{18-x}-\frac{24}{18+x}=1 \Rightarrow 24\left[\frac{1}{18-x}-\frac{1}{18+x}\right]=1 \Rightarrow\left[\frac{1}{18-x}-\frac{1}{18+x}\right]=\frac{1}{24}\)
To solve the for \(x\) we need to convert the above equation into the standard form of the quadratic equation.
\(
\begin{aligned}
& \Rightarrow\left[\frac{(18+x)-(18-x)}{(18-x)(18+x)}\right]=\frac{1}{24} \Rightarrow\left[\frac{18+x-18+x}{(18-x)(18+x)}\right]=\frac{1}{24} \\
& \Rightarrow\left[\frac{2 x}{18^2-x^2}\right]=\frac{1}{24} \text { (using the algebraic identity } a^2-b^2=(a+b)(a-b)
\end{aligned}
\)
Now, cross multiplying we have, \(\Rightarrow 48 x=324-x^2\)
\(
\Rightarrow x^2+48 x-324=0 \Rightarrow x^2+2 \times 24 \times x-324=0
\)
Now, to make the perfect square, we need to add and subtract \((24)^2\) from LHS
\(
\Rightarrow x^2+2 \times 24 \times x+(24)^2-(24)^2-324=0 \Rightarrow(x+24)^2-(24)^2-324=0
\)
Transferring \(-(24)^2-324\) from LHS to RHS we have,
\(
\Rightarrow(x+24)^2=+324+(24)^2
\)
Taking square root on both sides we have,
\(
\begin{aligned}
& \Rightarrow x+24=\pm \sqrt{900} \\
& \Rightarrow x=\pm 30-24 \\
& \Rightarrow x=+30-24 =6\\
& \Rightarrow x=-30-24=-54
\end{aligned}
\)
We will consider the positive value of \(x\) as speed can not be negative.
Hence, the speed of the stream is \(6 \mathrm{kmph}\). -
Question 23 of 26
23. Question
Priya decides to build a prayer hall of her house having a carpet area of 300 square meters with its length of 25 meters more than its breadth. What should be the breadth and length of the prayer hall?
CorrectIncorrectHint
Let us assume breadth is \(x\), and the length is \((x+25)\). According to the question, \(x(x+25)=300 \Rightarrow x^2+25 x-300=0\)
\(\Rightarrow\) From the given quadratic equation \(a=1, b=25, c=-300\)
Quadratic equation formula is given by \(x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
\(x=\frac{-(25) \pm \sqrt{(25)^2-4 \times 1 \times(-300)}}{2 \times 1}=\frac{-25 \pm \sqrt{1825}}{2}\)
\(x=\frac{-25+\sqrt{1825}}{2}=8.86\) (approx) or \(x=\frac{-25-\sqrt{1825}}{2}=-33.86\) (approx) We will avoid the negative value of \(x\) as breadth can not be negative.
Hence, the breadth is, \(x=8.86\) (approx) and the length is \(x+25=8.86\) (approx) \(+25=33.86\) (approx) -
Question 24 of 26
24. Question
The product of two odd consecutive positive integers is 63. Find the numbers.
CorrectIncorrectHint
Let the two odd integers be \(x, x+2\). We have:
Now, according to the statement,
\(
\begin{aligned}
& x(x+2)=63 \Rightarrow x^2+2 x-63=0 \\
& \Rightarrow x^2+(9-7) x-63=0 \Rightarrow x^2+9 x-7 x-63=0 \\
& \Rightarrow x(x+9)-7(x+9)=0 \Rightarrow(x+9)(x-7)=0
\end{aligned}
\)
So, \(x=-9\) or, \(x=7\)
Here, we need to find the positive odd integers. So, avoid the negative value of \(x\).
Hence, the two odd consecutive integers are \(x=7\) and \(x+2=7+2=9\). -
Question 25 of 26
25. Question
The product of Rime’s age two years ago and her age four years from now is one more than twice her present age. What is her present age?
CorrectIncorrectHint
Let her present age be \(x\).
Two years ago, her age was \((x-2)\).
Her age after four years from now is \((x+4)\).
One more than twice her present age is \((1+2 x)\).
According to the statement,
\(
\begin{aligned}
& (x-2)(x+4)=1+2 x x^2+4 x-2 x-8=1+2 x \\
& x^2+2 x-2 x-8-1=0 \\
& x^2-9=0 x^2=9
\end{aligned}
\)
Thus, \(x=\pm 3\)
Now, age can not be negative.
Hence, Rime’s present age is 3 years -
Question 26 of 26
26. Question
If the speed of a car is increased by \(10 \mathrm{~km} / \mathrm{hr}\), the time of journey for a distance of \(72 \mathrm{~km}\) is reduced by 36 minutes. Find the initial speed of the car.
CorrectIncorrectHint
Let the initial speed of the car is \(x \mathrm{kmph}\).
Speed of the car after increasing the speed is \((x+10), \mathrm{kmph}\).
Distance is \(72 \mathrm{~km}\) (given).
Time taken to cover the distance is \(\left(\frac{72}{x}\right)\) hours
Time taken after increasing the speed is \(\left(\frac{72}{x+10}\right)\) hours
According to the question,
\(
\begin{aligned}
& \Rightarrow\left(\frac{1}{x}\right)-\left(\frac{1}{x+10}\right)=\frac{36}{60 \times 72} \\
& \Rightarrow\left[\frac{x+10-x}{x(x+10)}\right]=\frac{1}{120} \Rightarrow x^2+10 x-1200=0 \\
& \Rightarrow x^2+40 x-30 x-1200=0 \\
& \Rightarrow x(x+40)-30(x+40)=0 \\
& \Rightarrow(x+40)(x-30)=0 \Rightarrow x=-40 \text { or } x=30
\end{aligned}
\)