A function that is not linear is called a nonlinear function, any function whose graph is not a straight line should represent a nonlinear function. Let’s understand the terms like symmetry, and vertex commonly used for a nonlinear quadratic function like a parabola.

Axis of Symmetry

The axis of symmetry is an imaginary line that divides a figure into two identical parts such that each part is a mirror reflection of one another. We can say the axis of symmetry is the vertical line that cuts the figure in half. It can be either horizontal, vertical, or lateral. If we fold and unfold an object along the axis of symmetry, the two sides are identical. Different shapes have different lines of symmetry. A square has four lines of symmetry, a rectangle has 2 lines of symmetry, a circle has infinite lines of symmetry and a parallelogram has no line of symmetry. A regular polygon of ‘n’ sides has ‘n’ axes of symmetry.

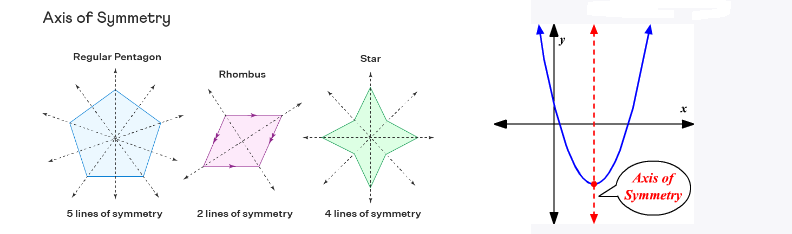
Vertex

The vertex is the point where the axis of symmetry intersects the parabola. 

Axis of Symmetry of a Parabola

A parabola has one line of symmetry. The axis of the symmetry is the straight line that divides a parabola into two symmetrical parts. The parabola can be in four forms. It can be either horizontal or vertical, facing left or right.

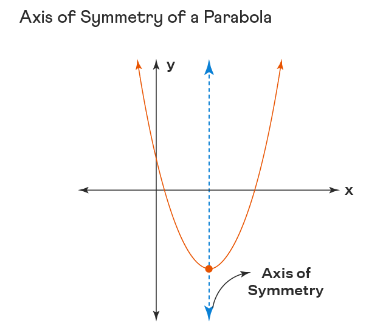
The axis of symmetry which is horizontal has zero slope, and the axis of symmetry which is vertical has an undefined slope.

The equation of the axis of symmetry can be represented when a parabola is in two forms:

• Standard form
• Vertex form

Standard Form: The quadratic equation in standard form is, \(y=a x^2+b x+c\) where \(a, b\), and \(c\) are real numbers.
Here, the axis of symmetry formula is: \(\mathbf{x}=-\mathbf{b} / \mathbf{2} \mathbf{a}\).

Vertex Form: The quadratic equation in vertex form is, \(y=a(x-h)^2+k\) where \((h, k)\) is the vertex of the parabola. Here, the axis of the symmetry formula is \(\mathbf{x}=\mathbf{h}\).

Derivation of the Axis of Symmetry for Parabola

The axis of symmetry always passes through the vertex of the parabola. Thus identification of the vertex helps us to calculate the position of the axis of symmetry. Axis of symmetry formula for a parabola is, \(x=-b / 2 a\). Let us derive the equation of the axis of symmetry.
The quadratic equation of a parabola is, \(y=a x^2+b x+c\) (up/down parabola).

The constant term ‘ \(c\) ‘ does not affect the parabola. Therefore, let us consider, \(y=a x^2+b x\).
The axis of symmetry is the midpoint of its two x-intercepts. To find the \(x\)-intercept, substitute \(y=0\).
\(
x(a x+b)=0
\)
\(x=0\) and \((a x+b)=0\)
\(x=0\) and \(x=-b / a\)
The mid-point formula is \(x=\left(x_1+x_2\right) / 2\)
\(
x=[0+(-b / a)] / 2
\)
Therefore \(x=-b / 2 a\)

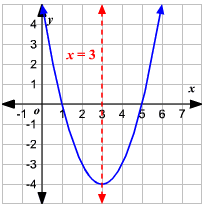
Example 1: \(\text { Find the axis of symmetry of the graph of } y=x^2-6 x+5 \text { using the formula. }\)

Solution:

For a quadratic function in standard form, \(y=a x^2+b x+c\), the axis of symmetry is a vertical line \(x=-\frac{b}{2 a}\).
Here, \(a=1, b=-6\) and \(c=5\).
Substitute.
\(
x=-\frac{-6}{2(1)}
\)
Simplify.
\(
\begin{aligned}
x & =\frac{6}{2} \\
& =3
\end{aligned}
\)
Therefore, the axis of symmetry is \(x=3\).

Here are some examples of non-linear functions. Let’s understand how to plot the graph from the given equation.

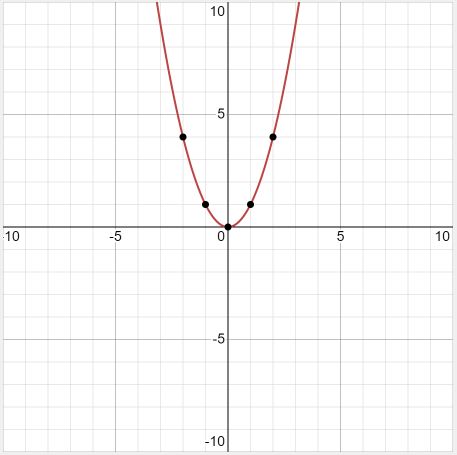
Example 2: \(y=x^2\)

Solution:

Let’s find the values and form a table and draw the graph.

\(
\begin{array}{|c|c|c|c|c|c|}
\hline x & -2 & -1 & 0 & 1 & 2 \\
\hline y & 4 & 1 & 0 & 1 & 4 \\
\hline
\end{array}
\)

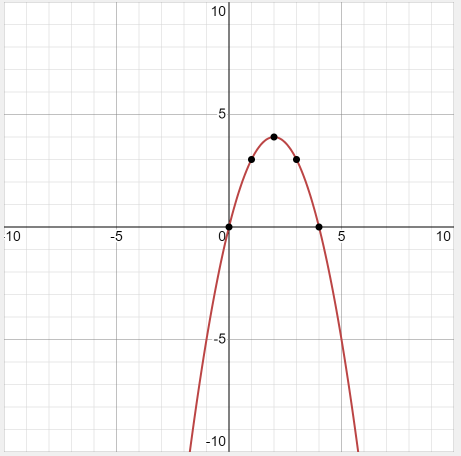
Example 3:  Graph\(y=-(x-2)^2+4\)

Solution:

Let’s form the table and draw the graph.

\(
\begin{array}{|c|c|c|c|c|c|}
\hline x & 0 & 1 & 2 & 3 & 4 \\
\hline y & 0 & 3 & 4 & 3 & 0 \\
\hline
\end{array}
\)

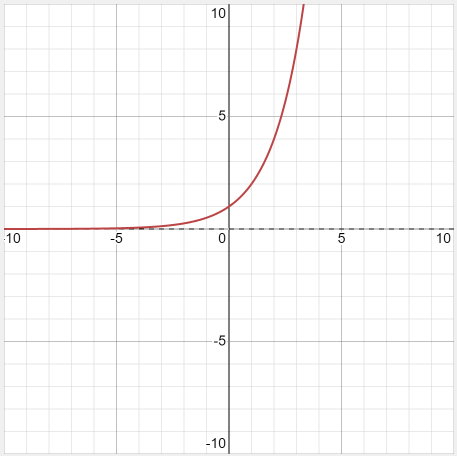
Example 4: Graph \(y=2^x\)

Solution:

\(
\begin{array}{|c|c|c|c|c|c|}
\hline x & 0 & 1 & 2 & 3 & 4 \\
\hline y & 1 & 2 & 4 & 8 & 16 \\
\hline
\end{array}
\)

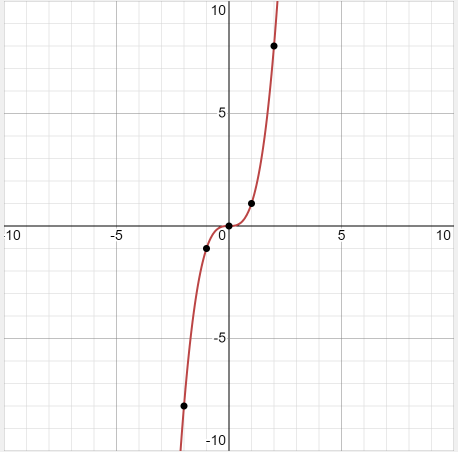
Example 5: Graph \(y=x^3\)

Solution:

\(
\begin{array}{|c|c|c|c|c|c|c|c|}
\hline x & -2 & -1 & 0 & 1 & 2 & 3 & 4 \\
\hline y & -8 & -1 & 0 & 1 & 8 & 27 & 64 \\
\hline
\end{array}
\)

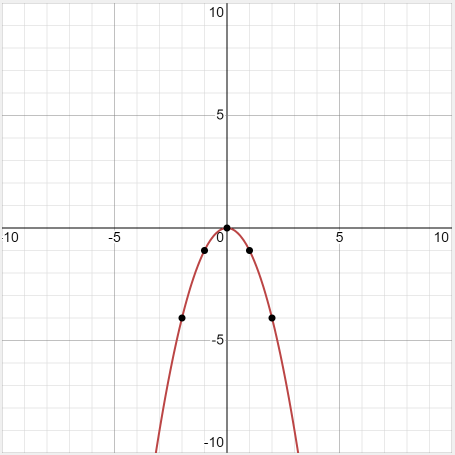
Example 6: Graph \(y = -x^2\)

Solution:

\(
\begin{array}{|c|c|c|c|c|c|}
\hline x & -2 & -1 & 0 & 1 & 2 \\
\hline y & -4 & -1 & 0 & -1 & -4 \\
\hline
\end{array}
\)

Example 7: Graph \(y=|x|\)

Solution:

\(
\begin{array}{|c|c|c|c|c|c|}
\hline x & -2 & -1 & 0 & 1 & 2 \\
\hline y & 2 & 1 & 0 & 1 & 2 \\
\hline
\end{array}
\)

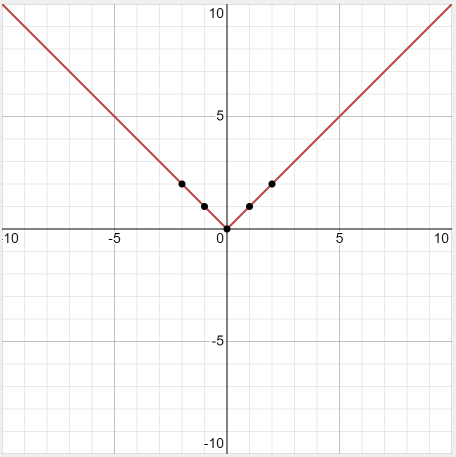
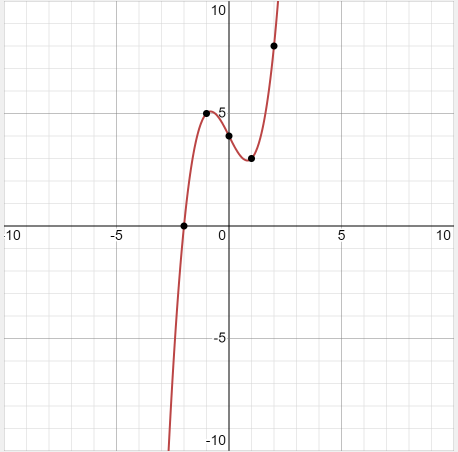
Example 8: Graph \(f(x)=x^3-2 x+4\)

Solution:

\(
\begin{array}{|c|c|c|c|c|c|}
\hline x & -2 & -1 & 0 & 1 & 2 \\
\hline y & 0 & 5 & 4 & 3 & 8 \\
\hline
\end{array}
\)

Example 9: Graph \(f(x)=\sin x\)

Solution:

\(f(x)=\sin x\) is a trigonometric function and hence it is nonlinear.

\(
\begin{array}{|c|c|c|c|c|c|}
\hline x & 0 & \pi/2 & \pi & 3\pi/2 & 2\pi \\
\hline y & 0 & 1 & 0 & -1 & 0 \\
\hline
\end{array}
\)

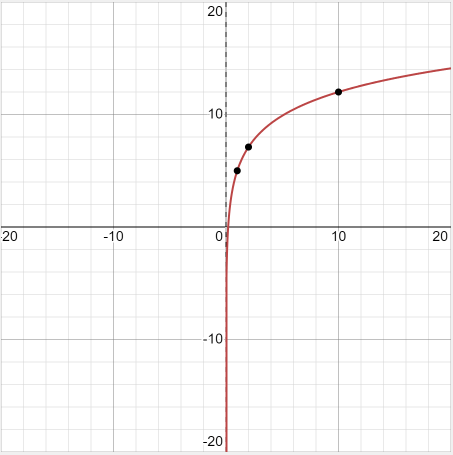
Example 10: Graph \(h(x)=7 \log x+5\)

Solution:

\(
\begin{array}{|c|c|c|c|c|c|}
\hline x & 1 & 2 & 10 & 15 & 20 \\
\hline y & 5 & 7.107 & 12 & 13.23 & 14.10 \\
\hline
\end{array}
\)

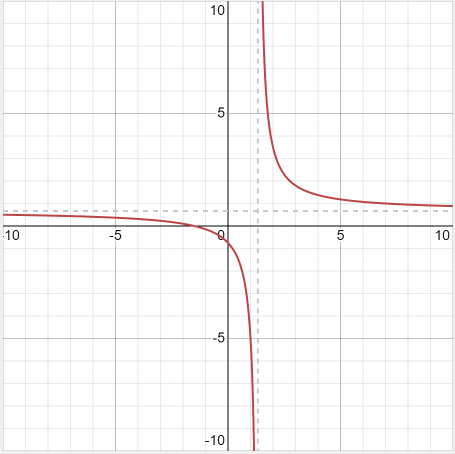
Example 11: \(f(x)=\frac{(2 x+3)}{(3 x-4)}\)

Solution:

\(
\begin{array}{|c|c|c|c|c|c|}
\hline x & -1 & 0 & 1 & 2 & 5 \\
\hline y & -1/7 & -3/4 & -5 & 7/2 & 13/11 \\
\hline
\end{array}
\)

Example 12: If the axis of symmetry of the equation \(y=q x^2-32 x-10\) is 8, then find the value of \(q\).

Solution:

\(
y=q x^2-32 x-10
\)
Axis of symmetry is \(x=8\)
Using the formula:
\(
x=-b / 2 a
\)
where \(a=q, b=-32\) and \(x=8\)
\(
\begin{aligned}
& 8=-(-32) /(2 \times q) \\
& 8=32 / 2 q \\
& 16 q=32 \\
& q=2
\end{aligned}
\)
Therefore, the value of \(q=2\).

Example 13: Find the equation of the axis of symmetry of the given parabola. Also, identify the vertex.

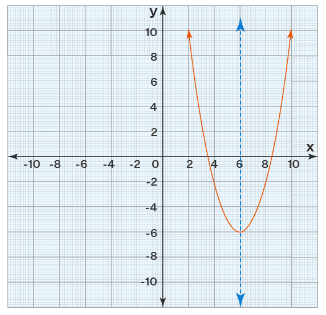
Solution:

Here the vertex \(=(6,-6)\)
The axis of symmetry intersects the parabola at its vertex and it is a vertical line since the parabola opens up.
Hence its equation is:
\(x=6\)

Example 14: Find the equation of the line that divides the given parabola into two equal parts.

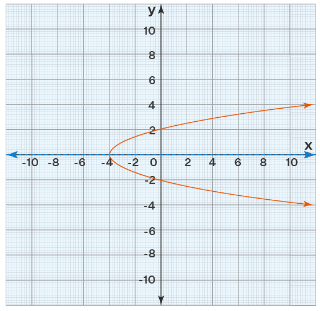
Solution:

Here the vertex \(=(-4,0)\).
The axis of symmetry intersects the parabola at its vertex and is a horizontal line in this case as the parabola opens sideways.
Hence, its equation is \(\mathrm{y}=0\)