Area of a Triangle Formula in Coordinate Geometry

If \(\left(x_1, y_1\right),\left(x_2, y_2\right)\), and \(\left(x_3, y_3\right)\) are the three vertices of a triangle on the coordinate plane, then its area is calculated by the formula (1/2) \(\mid x_1\left(y_2-\right.\) \(\left.y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right) \mid\).

Proof: In coordinate geometry, if we need to find the area of a triangle, we use the coordinates of the three vertices. Consider \(\triangle A B C\) as given in the figure below with vertices \(A\left(x_1, y_1\right), B\left(x_2, y_2\right)\), and \(C\left(x_3, y_3\right)\). In this figure, we have drawn perpendiculars \(A E, C F\), and \(B D\) from the vertices of the triangle to the horizontal axis. Notice that three trapeziums are formed: BAED, ACFE, and BCFD.

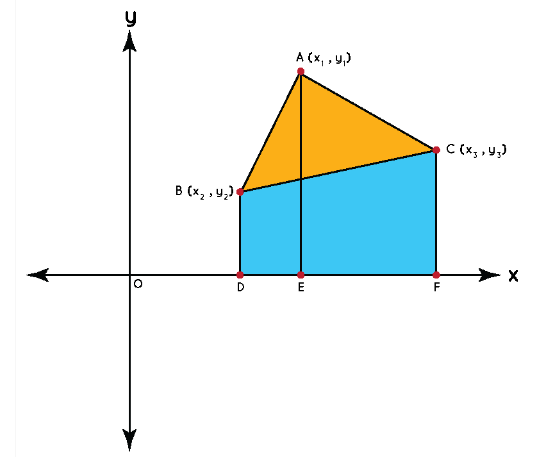
We can express the area of a triangle in terms of the areas of these three trapeziums.
\(
\operatorname{Area}(\triangle A B C )=\operatorname{Area}(\text { Trap.BAED} +\text { Area(Trap.ACFE) }- \text { Area(Trap.BCFD) }
\)
Now, the area of a trapezium in terms of the lengths of the parallel sides (the bases of the trapezium) and the distance between the parallel sides (the height of the trapezium):

Trapezium Area \(=(1 / 2) \times\) Sum of base \(\times\) Height
Consider any one trapezium, say BAED. Its bases are BD and AE, and its height is DE. BD and AE can easily be seen to be the y coordinates of \(B\) and \(A\), while \(D E\) is the difference between the \(x\) coordinates of \(A\) and \(B\). Similarly, the bases and heights of the other two trapeziums can be easily calculated. Thus, we have:
\(
\begin{aligned}
& \text { Area }(\text { Trap.BAED })=(1 / 2) \times(B D+A E) \times D E \\
& =(1 / 2) \times\left(y_2+y_1\right) \times\left(x_1-x_2\right) \\
& \text { Area }(\text { Trap.ACFE })=(1 / 2) \times(A E+C F) \times E F \\
& =(1 / 2) \times\left(y_1+y_3\right) \times\left(x_3-x_1\right) \\
& \text { Area }(\text { Trap.BCFD })=(1 / 2) \times(B D+C F) \times D F \\
& =(1 / 2) \times\left(y_2+y_3\right) \times\left(x_3-x_2\right)
\end{aligned}
\)
The expression for the area of the triangle in terms of the coordinates of its vertices can thus be given as,
\(
\begin{aligned}
& \text { Area }(\triangle A B C)=\text { Area(Trap.BAED) + Area(Trap.ACFE) – Area(Trap.BCFD) } \\
& =(1 / 2) \times\left[\left(y_2+y_1\right) \times\left(x_1-x_2\right)\right]+(1 / 2) \times\left[\left(y_1+y_3\right) \times\left(x_3-x_1\right)\right]-(1 / 2) \times \\
& {\left[\left(y_2+y_3\right) \times\left(x_3-x_2\right)\right]}
\end{aligned}
\)
However, we should try to simplify it so that it is easy to remember.
For that, we simplify the product of the two brackets in each terms:
\(
\begin{aligned}
& =(1 / 2)\left(x_1 y_2-x_2 y_2+x_1 y_1-x_2 y_1\right)+(1 / 2)\left(x_3 y_1-x_1 y_1+x_3 y_3-x_1 y_3\right)- \\
& (1 / 2)\left(x_3 y_2-x_2 y_2+x_3 y_3-x_2 y_3\right)
\end{aligned}
\)
Take the common term \(1 / 2\) outside the bracket.
\(
\begin{aligned}
& =(1 / 2)\left(x_1 y_2-x_2 y_2+x_1 y_1-x_2 y_1-x_3 y_1-x_1 y_1+x_3 y_3-x_1 y_3-x_3 y_2+\right. \\
& \left.x_2 y_2-x_3 y_3+x_2 y_3\right)
\end{aligned}
\)
Thus,
\(
\operatorname{Area}(\triangle A B C)=(1 / 2)\left\{x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right\}
\)
As the area is always positive. Hence, we take the absolute value sign.
\(
(\triangle A B C)=(1 / 2)\left|x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right|
\)
This is a symmetric expression, and there is an easy technique to remember it, which we will now discuss as Determinants Method.

To calculate the area of a triangle using determinants, we use the formula as shown below,
\(
\text { Area }=1 / 2\left[\begin{array}{lll}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
x_3 & y_3 & 1
\end{array}\right]
\)
\(
\text { Area }=(1 / 2)\left|x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right|
\)

Distance of a Point From a Line

 

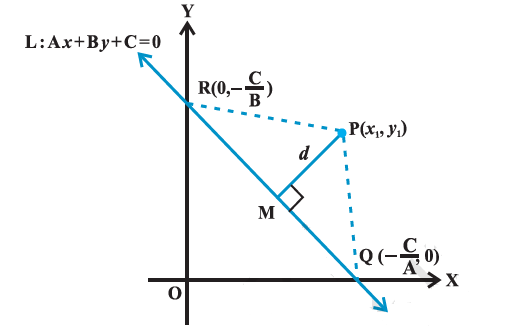
The distance of a point from a line is the length of the perpendicular drawn from the point to the line. Let \(\mathrm{L}: \mathrm{A} x+\mathrm{By}+\mathrm{C}=0\) be a line, whose distance from the point \(\mathrm{P}\left(x_1, y_1\right)\) is \(d\). Draw a perpendicular PM from the point \(\mathrm{P}\) to the line \(\mathrm{L}\) (Figure above). If the line meets the \(x\)-and \(y\)-axes at the points \(\mathrm{Q}\) and \(\mathrm{R}\), respectively. Then, coordinates of the points are \(Q\left(-\frac{C}{A}, 0\right)\) and \(R\left(0,-\frac{C}{B}\right)\). Thus, the area of the triangle PQR is given by
area \((\triangle \mathrm{PQR})=\frac{1}{2} \mathrm{PM} \cdot \mathrm{QR}\), which gives \(\mathrm{PM}=\frac{2 \text { area }(\triangle \mathrm{PQR})}{\mathrm{QR}} \dots(1)\)

In coordinate geometry, the area of triangle with vertices \(\left(x_1, y_1\right),\left(x_2, y_2\right)\) and \(\left(x_3, y_3\right)\) is
\(
\Delta=(1 / 2)\left|x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right|
\)
Here,
\(
\begin{aligned}
& \left(x_1, y_1\right)=P\left(x_1, y_1\right) \\
& \left(x_2, y_2\right)=Q(-C / A, 0) \\
& \left(x_3, y_3\right)=R(0,-C / B)
\end{aligned}
\)

Also area
\(
(\Delta \mathrm{PQR})=\frac{1}{2}\left|x_1\left(0+\frac{\mathrm{C}}{\mathrm{B}}\right)+\left(-\frac{\mathrm{C}}{\mathrm{A}}\right)\left(-\frac{\mathrm{C}}{\mathrm{B}}-y_1\right)+0\left(y_1-0\right)\right|
\)
\(
=\frac{1}{2}\left|x_1 \frac{\mathrm{C}}{\mathrm{B}}+y_1 \frac{\mathrm{C}}{\mathrm{A}}+\frac{\mathrm{C}^2}{\mathrm{AB}}\right|
\)
\(
\text { or } 2 \text { area }(\triangle \mathrm{PQR})=\left|\frac{\mathrm{C}}{\mathrm{AB}}\right| .\left|\mathrm{A} x_1+\mathrm{B} y_1+\mathrm{C}\right| \text {, and Distance }
\)
\(
\mathrm{QR}=\sqrt{\left(0+\frac{\mathrm{C}}{\mathrm{A}}\right)^2+\left(\frac{\mathrm{C}}{\mathrm{B}}-0\right)^2}=\left|\frac{\mathrm{C}}{\mathrm{AB}}\right| \sqrt{\mathrm{A}^2+\mathrm{B}^2}
\)
\(
\text { Substituting the values of area }(\triangle \mathrm{PQR}) \text { and } \mathrm{QR} \text { in (1), we get }
\)
\(
\mathrm{PM}=\frac{\left|\mathrm{A} {x_1}+\mathrm{B} y_1+\mathrm{C}\right|}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}
\)
or
\(
d=\frac{\left|\mathrm{A}_{x_1}+\mathrm{B} y_1+\mathrm{C}\right|}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}
\)
Thus, the perpendicular distance \((d)\) of a line \(\mathrm{A} x+\mathrm{B} y+\mathrm{C}=0\) from a point \(\left(x_1, y_1\right)\) is given by
\(
d=\frac{\left|\mathrm{A} x_1+\mathrm{B} y_1+\mathrm{C}\right|}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}} .
\)

Example 1: \(\text { Find the distance of the point }(3,-5) \text { from the line } 3 x-4 y-26=0 \text {. }\)

Solution:

Given line is \(\quad 3 x-4 y-26=0 \dots(1)\)
Comparing (1) with general equation of line \(\mathrm{Ax}+\mathrm{B} y+\mathrm{C}=0\), we get
\(
\mathrm{A}=3, \mathrm{~B}=-4 \text { and } \mathrm{C}=-26 \text {. }
\)
Given point is \(\left(x_1, y_1\right)=(3,-5)\). The distance of the given point from given line is
\(
d=\frac{\left|\mathrm{A} x_1+\mathrm{B} y_1+\mathrm{C}\right|}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}=\frac{|3.3+(-4)(-5)-26|}{\sqrt{3^2+(-4)^2}}=\frac{3}{5}
\)

Distance between two parallel lines

We know that the slopes of two parallel lines are equal. Therefore, two parallel lines can be taken in the form

\(y=m x+c_1 \dots(1)\)

and \(y =m x+c_2 \dots(2)\)
Line (1) will intersect \(x\)-axis at the point \(\mathrm{A}\left(-\frac{c_1}{m}, 0\right)\) as shown in figure below.

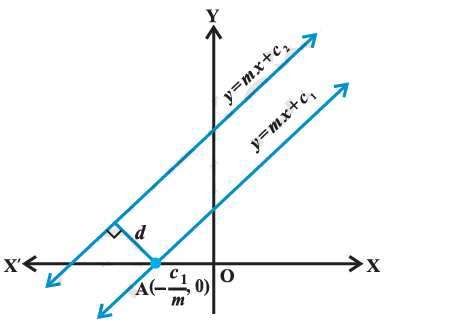
The perpendicular distance would be the required distance between two lines, The distance between the point A and the line \(y=m x+c_2\)
can be given by using the formula:
\(d = \frac{\left|A x_1+B y_1+C\right|}{\sqrt{A^2+B^2}} \dots(3)\)
We can write the equation \(y=m x+c_2\) as \(~y-m x-c_2\) and compare it with the standard equation \(A x+B y+C\)
we get, \(B=1, A=-m \text { and } C=-c_2\) and \((x_1, y_1)=\left(-\frac{c_1}{m}, 0\right)\)
Replacing these values in eqn (3) we get distance between two lines is equal to the length of the perpendicular from point A to line (2). Therefore, distance between the lines (1) and (2) is
\(
\frac{\left|(-m)\left(-\frac{c_1}{m}\right)+\left(-c_2\right)\right|}{\sqrt{1+m^2}} \text { or } d=\frac{\left|c_1-c_2\right|}{\sqrt{1+m^2}} .
\)
Thus, the distance \(d\) between two parallel lines \(y=m x+c_1\) and \(y=m x+c_2\) is given by
\(
d=\frac{\left|c_1-c_2\right|}{\sqrt{1+m^2}} .
\)
If lines are given in general form, i.e., \(\mathrm{Ax}+\mathrm{By}+\mathrm{C}_1=0\) and \(\mathrm{Ax}+\mathrm{By}+\mathrm{C}_2=0\),
\(
\text { then above formula will take the form } d=\frac{\left|\mathrm{C}_1-\mathrm{C}_2\right|}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}
\)

Example 2: Find the distance between the parallel lines \(3 x-4 y+7=0\) and \(3 x-4 y+5=0\)

Solution:

Here \(\mathrm{A}=3, \mathrm{~B}=-4, \mathrm{C}_1=7\) and \(\mathrm{C}_2=5\). Therefore, the required distance is
\(
d=\frac{|7-5|}{\sqrt{3^2+(-4)^2}}=\frac{2}{5} .
\)

Example 3: If the lines \(2 x+y-3=0,5 x+k y-3=0\) and \(3 x-y-2=0\) are concurrent, find the value of \(k\).

Solution:

Three lines are said to be concurrent, if they pass through a common point, i.e., the point of intersection of any two lines lies on the third line. Here given lines are
\(
\begin{aligned}
& 2 x+y-3=0 \dots(1) \\
& 5 x+k y-3=0 \dots(2)
\end{aligned}
\)
\(
3 x-y-2=0 \dots(3)
\)
Solving (1) and (3) by cross-multiplication method, we get
\(
\frac{x}{-2-3}=\frac{y}{-9+4}=\frac{1}{-2-3} \quad \text { or } \quad x=1, y=1 \text {. }
\)
Therefore, the point of intersection of two lines is \((1,1)\). Since the above three lines are concurrent, the point \((1,1)\) will satisfy equation (2) so that
\(
5.1+k .1-3=0 \text { or } k=-2 \text {. }
\)

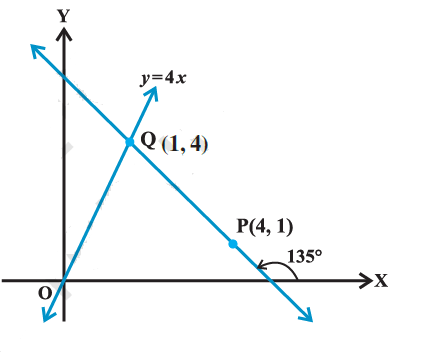
Example 4: Find the distance of the line \(4 x-y=0\) from the point \(P(4,1)\) measured along the line making an angle of \(135^{\circ}\) with the positive \(x\)-axis.

Solution:

Given line is \(4 x-y=0 \dots(1)\)
In order to find the distance of the line (1) from the point \(P(4,1)\) along another line, we have to find the point of intersection of both lines. For this purpose, we will first find the equation of the second line (Figure below). The slope of second line is \(\tan 135^{\circ}=-1\). Equation of the line with slope \(-1\) through the point \(\mathrm{P}(4,1)\) is
\(
y-1=-1(x-4) \text { or } x+y-5=0 \dots(2)
\)
Solving (1) and (2), we get \(x=1\) and \(y=4\) so that point of intersection of the two lines is \(Q(1,4)\). Now, the distance of line (1) from the point \(P(4,1)\) along the line (2) \(=\) the distance between the points \(P(4,1)\) and \(\mathrm{Q}(1,4)\). \(=\sqrt{(1-4)^2+(4-1)^2}=3 \sqrt{2}\) units.

Example 5: Assuming that straight lines work as the plane mirror for a point, find the image of the point \((1,2)\) in the line \(x-3 y+4=0\).

Solution:

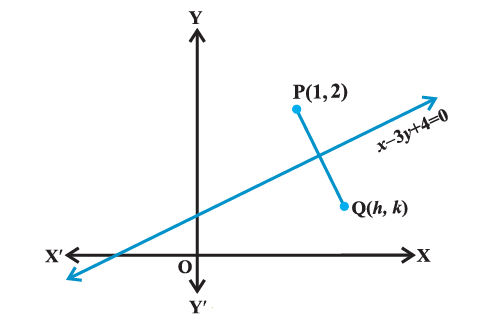
Let \(\mathrm{Q}(h, k)\) is the image of the point \(\mathrm{P}(1,2)\) in the line
\(
x-3 y+4=0 \dots(1)
\)
Therefore, line (1) is the perpendicular bisector of line segment PQ (Figure above).
Hence Slope of line \(P Q=\frac{-1}{\text { Slope of line } x-3 y+4=0}\)
so that \(\frac{k-2}{h-1}=\frac{-1}{\frac{1}{3}}\) or \(3 h+k=5 \dots(2)\)
and the mid-point of PQ, i.e., point \(\left(\frac{h+1}{2}, \frac{k+2}{2}\right)\) will satisfy the equation (1) so that
\(
\frac{h+1}{2}-3\left(\frac{k+2}{2}\right)+4=0 \text { or } h-3 k=-3 \dots(3)
\)
Solving (2) and (3), we get \(h=\frac{6}{5}\) and \(k=\frac{7}{5}\).
Hence, the image of the point \((1,2)\) in the line (1) is \(\left(\frac{6}{5}, \frac{7}{5}\right)\).

Example 6: Show that the area of the triangle formed by the lines
\(
y=m_1 x+c_1, y=m_2 x+c_2 \text { and } x=0 \text { is } \frac{\left(c_1-c_2\right)^2}{2\left|m_1-m_2\right|} .
\)

Solution:

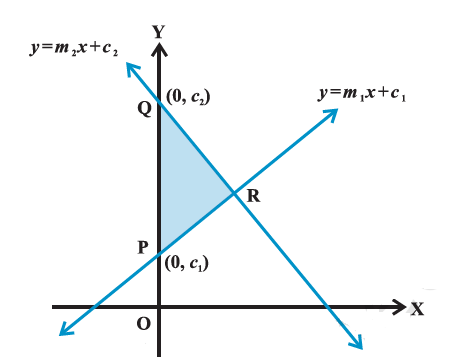
Given lines are
\(
\begin{aligned}
& y=m_1 x+c_1 \dots(1) \\
& y=m_2 x+c_2 \dots(2) \\
& x=0 \dots(3)
\end{aligned}
\)
We know that line \(y=m x+c\) meets the line \(x=0\) ( \(y\)-axis) at the point \((0, c)\). Therefore, two vertices of the triangle formed by lines (1) to (3) are \(\mathrm{P}\left(0, c_1\right)\) and \(\mathrm{Q}\left(0, c_2\right)\) (Figure above). Third vertex can be obtained by solving equations (1) and (2). Solving (1) and (2), we get
\(
x=\frac{\left(c_2-c_1\right)}{\left(m_1-m_2\right)} \quad \text { and } y=\frac{\left(m_1 c_2-m_2 c_1\right)}{\left(m_1-m_2\right)}
\)
\(
\text { Therefore, third vertex of the triangle is } \mathrm{R}\left(\frac{\left(c_2-c_1\right)}{\left(m_1-m_2\right)}, \frac{\left(m_1 c_2-m_2 c_1\right)}{\left(m_1-m_2\right)}\right) \text {. }
\)
\(
\text { Now, the area of the triangle is }
\)
\(
=\frac{1}{2} \mid 0\left(\frac{m_1 c_2-m_2 c_1}{m_1-m_2}-c_2\right)+\frac{c_2-c_1}{m_1-m_2}\left(c_2-c_1\right)+0 \quad\left(c_1-\frac{m_1 c_2-m_2 c_1}{m_1-m_2}\right)=\frac{\left(c_2-c_1\right)^2}{2\left|m_1-m_2\right|}
\)

Example 7: A line is such that its segment between the lines
\(5 x-y+4=0\) and \(3 x+4 y-4=0\) is bisected at the point \((1,5)\). Obtain its equation.

Solution:

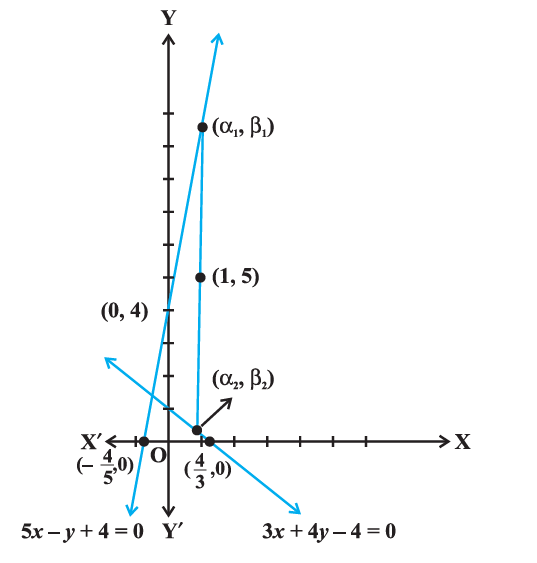
Given lines are
\(
\begin{aligned}
& 5 x-y+4=0 \dots(1)\\
& 3 x+4 y-4=0 \dots(2)
\end{aligned}
\)
Let the required line intersects the lines (1) and (2) at the points, \(\left(\alpha_1, \beta_1\right)\) and \(\left(\alpha_2, \beta_2\right)\), respectively (Figure above). Therefore
\(5 \alpha_1-\beta_1+4=0\) and
\(3 \alpha_2+4 \beta_2-4=0\)
or \(\beta_1=5 \alpha_1+4\) and \(\beta_2=\frac{4-3 \alpha_2}{4}\)
We are given that the mid point of the segment of the required line between \(\left(\alpha_1, \beta_1\right)\) and \(\left(\alpha_2, \beta_2\right)\) is \((1,5)\). Therefore
\(
\begin{aligned}
& \frac{\alpha_1+\alpha_2}{2}=1 \text { and } \frac{\beta_1+\beta_2}{2}=5, \\
& \alpha_1+\alpha_2=2 \text { and } \frac{5 \alpha_1+4+\frac{4-3 \alpha_2}{4}}{2}=5, \\
& \text { or } \alpha_1+\alpha_2=2 \text { and } 20 \alpha_1-3 \alpha_2=20 \dots(3)
\end{aligned}
\)
Solving equations in (3) for \(\alpha_1\) and \(\alpha_2\), we get
\(
\alpha_1=\frac{26}{23} \text { and } \alpha_2=\frac{20}{23} \text { and hence, } \beta_1=5 \cdot \frac{26}{23}+4=\frac{222}{23} \text {. }
\)
Equation of the required line passing through \((1,5)\) and \(\left(\alpha_1, \beta_1\right)\) is
\(
y-5=\frac{\beta_1-5}{\alpha_1-1}(x-1) \text { or } y-5=\frac{\frac{222}{23}-5}{\frac{26}{23}-1}(x-1)
\)
or \(\quad 107 x-3 y-92=0\),
which is the equation of the required line.

Example 8: Show that the path of a moving point such that its distances from two lines \(3 x-2 y=5\) and \(3 x+2 y=5\) are equal is a straight line.

Solution:

Given lines are
\(
\begin{aligned}
& 3 x-2 y=5 \dots(1) \\
& 3 x+2 y=5 \dots(2)
\end{aligned}
\)
\(
\text { and } \quad 3 x+2 y=5
\)
Let \((h, k)\) is any point, whose distances from the lines (1) and (2) are equal. Therefore
\(
\frac{|3 h-2 k-5|}{\sqrt{9+4}}=\frac{|3 h+2 k-5|}{\sqrt{9+4}} \text { or }|3 h-2 k-5|=|3 h+2 k-5|,
\)
which gives \(3 h-2 k-5=3 h+2 k-5\) or \(-(3 h-2 k-5)=3 h+2 k-5\).
Solving these two relations we get \(k=0\) or \(h=\frac{5}{3}\). Thus, the point \((h, k)\) satisfies the equations \(y=0\) or \(x=\frac{5}{3}\), which represent straight lines. Hence, path of the point equidistant from the lines (1) and (2) is a straight line.

Example 9: If three lines whose equations are \(y=m_1 x+c_1, y=m_2 x+c_2\) and \(y=m_3 x+c_3\) are concurrent, then show that \(m_1\left(\mathrm{c}_2-\mathrm{c}_3\right)+m_2\left(\mathrm{c}_3-\mathrm{c}_1\right)+m_3\left(\mathrm{c}_1-\mathrm{c}_2\right)=0\).

Solution:

\(
\begin{aligned}
& y=m_1 x+c_1 \dots(i)\\
& y=m_2 x+c_2 \dots(ii)\\
& y=m_3 x+c_3 \dots(iii)
\end{aligned}
\)
Subtracting (i) and (ii), we get
\(
\mathrm{x}=\frac{c_2-c_1}{m_1-m_2}
\)
Putting in eqn(i), we get,
\(
\begin{aligned}
& y=\frac{m_1\left(c_2-c_1\right)}{m_1-m_2}+c_1 \\
& y=\frac{m_1 c_2-m_2 c_1}{m_1-m_2}
\end{aligned}
\)
Putting it the eqn(iii), we get
\(
\frac{m_1 c_2-m_2 c_1}{m_1-m_2}=\frac{m_3\left(c_2-c_1\right)+m_1 c_3-m_2 c_3}{m_1-m_2}
\)
Rearranging, we get
\(
m_1\left(c_2-c_3\right)+m_2\left(c_3-c_1\right)+m_3\left(c_1-c_2\right)=0
\)

Example 10: Show that the equation of the line passing through the origin and making an angle \(\theta\) with the line \(y=m x+c\) is \(\frac{y}{x}=\frac{m \pm \tan ,}{1 \mp m \tan ,}\).

Solution:

Let the equation of the line passing through the origin be \(y=m_1 x\). From this, \(m_1=y / x\).

If this line makes an angle of \(\theta\) with line \(y=m x+c\), then angle \(\theta\) is given by
\(
\begin{aligned}
& \tan \theta=\left|\left(m_1-m\right) /\left(1+m_1 m\right)\right| \\
& \tan \theta=|(y / x-m) /(1+(y / x) m)| \\
& \tan \theta=\pm(y / x-m) /(1+(y / x) m) \\
& \tan \theta=(y / x-m) /(1+(y / x) m) \text { or } \tan \theta=-[(y / x-m) /(1+(y / x) m)]
\end{aligned}
\)

Case I:
\(
\begin{aligned}
& \tan \theta=(y / x-m) /(1+(y / x) m) \\
& \tan \theta+(y / x) m \tan \theta=y / x-m \\
& m+\tan \theta=y / x(1-m \tan \theta) \\
& y / x=(m+\tan \theta) /(1-m \tan \theta)
\end{aligned}
\)

Case II:
\(
\begin{aligned}
& \tan \theta=-[(y / x-m) / 1+(y / x) m] \\
& \tan \theta+(y / x) m \tan \theta=-y / x+m \\
& m-\tan \theta=y / x(1+m \tan \theta) \\
& y / x=(m-\tan \theta) /(1+m \tan \theta)
\end{aligned}
\)
Thus, the required line is given by \(y / x=m \pm \tan \theta / 1 \mp \tan \theta\)

Example 11: If the sum of the perpendicular distances of a variable point \(\mathrm{P}(x, y)\) from the lines \(x+y-5=0\) and \(3 x-2 y+7=0\) is always 10. Show that \(\mathrm{P}\) must move on a line.

Solution:

It is given that the sum of perpendicular distances of a variable point \(P(x, y)\) from the lines \(x+y-5=0\) and \(3 x-2 y+7=\) 0 is always 10
\(
\begin{aligned}
& \therefore\left|\frac{x+y-5}{\sqrt{1^2+1^2}}\right|+\left|\frac{3 x-2 y+7}{\sqrt{3^2+2^2}}\right|=10 \\
& \Rightarrow\left|\frac{x+y-5}{\sqrt{2}}\right|+\left|\frac{3 x-2 y+7}{\sqrt{13}}\right|=10 \\
& (3 \sqrt{2}+\sqrt{13}) x+(\sqrt{13}-2 \sqrt{2}) y+(7 \sqrt{2}-5 \sqrt{13}-10 \sqrt{26})=0
\end{aligned}
\)
It is a straight line. Thus, point P must move on a line

Example 12: Prove that the product of the lengths of the perpendiculars drawn from the points \(\left(\sqrt{a^2-b^2}, 0\right)\) and \(\left(-\sqrt{a^2-b^2}, 0\right)\) to the line \(\frac{x}{a} \cos \theta+\frac{y}{b} \sin \theta=1\) is \(b^2\).

Solution:

The equation of the given line is
\(
x / a \cos \theta+y / b \sin \theta=1
\)
\(
b x \cos \theta+a y \sin \theta-a b=0 \dots(1)
\)
Length of the perpendicular from point \(\left(\sqrt{a^2-b^2}, 0\right)\) to the line (1) is
\(
\begin{aligned}
& p_1=\left|b \cos \theta\left(\sqrt{a^2-b^2}\right)+a \sin \theta(0)-a b\right| / \sqrt{b^2 \cos ^2 \theta+a^2 \sin ^2 \theta} \\
& =\left|b \cos \theta\left(\sqrt{a^2-b^2}\right)-a b\right| / \sqrt{b^2 \cos ^2 \theta+a^2 \sin ^2 \theta} \ldots . \text { (2) }
\end{aligned}
\)
\(
\text { Length of the perpendicular from point }\left(-\sqrt{a^2-b^2}, 0\right) \text { to the line (2) is }
\)
\(
p_2=\left|b \cos \theta\left(-\sqrt{a^2-b^2}\right)+a \sin \theta(0)-a b\right| / \sqrt{b^2 \cos ^2 \theta+a^2 \sin ^2 \theta}
\)
\(
=\left|b \cos \theta\left(\sqrt{a^2-b^2}\right)+a b\right| / \sqrt{b^2 \cos ^2 \theta+a^2 \sin ^2 \theta} \dots(3)
\)
On multiplying equations (2) and (3), we obtain
\(\left[\left|b \cos \theta\left(\sqrt{a^2-b^2}\right)-a b\right|\left|b \cos \theta\left(\sqrt{a^2-b^2}\right)+a b\right|\right] /\left(\sqrt{b^2 \cos ^2 \theta+a^2 \sin ^2 \theta}\right)^2\) \(=\left[\left|b \cos \theta\left(\sqrt{a^2-b^2}\right)-a b\right|\left|b \cos \theta\left(\sqrt{a^2-b^2}\right)+a b\right|\right] /\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right)\) \(=\left|\left(b \cos \theta \sqrt{a^2-b^2}\right)^2-(a b)^2\right| /\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right)\)
\(
\begin{aligned}
& =\left|\left(b \cos \theta \sqrt{a^2-b^2}\right)^2-(a b)^2\right| /\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right) \\
& =\left|b^2 \cos ^2 \theta\left(a^2-b^2\right)-a^2 b^2\right| /\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right) \\
& =\left|a^2 b^2 \cos ^2 \theta-b^4 \cos ^2 \theta-a^2 b^2\right| /\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right) \\
& =b^2\left|a^2 \cos ^2 \theta-b^2 \cos ^2 \theta-a^2\right| /\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right) \\
& =b^2\left|a^2 \cos ^2 \theta-b^2 \cos ^2 \theta-a^2 \sin ^2 \theta-a^2 \cos ^2 \theta\right| /\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right)\left[\because \sin ^2 \theta+\right. \\
& \left.\cos ^2 \theta=1\right] \\
& =b^2\left|-\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right)\right| /\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right) \\
& =b^2\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right) /\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right) \\
& =b^2 \\
& \text { Hence, proved }
\end{aligned}
\)

Summary

• Slope \((m)\) of a non-vertical line passing through the points \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) is given by \(m=\frac{y_2-y_1}{x_2-x_1}=\frac{y_1-y_2}{x_1-x_2}, \quad x_1 \neq x_2\).
• If a line makes an angle á with the positive direction of \(x\)-axis, then the slope of the line is given by \(m=\tan \alpha, \alpha \neq 90^{\circ}\).
• Slope of horizontal line is zero and slope of vertical line is undefined.
• An acute angle (say \(\theta\) ) between lines \(\mathrm{L}_1\) and \(\mathrm{L}_2\) with slopes \(m_1\) and \(m_2\) is given by \(\tan \theta=\left|\frac{m_2-m_1}{1+m_1 m_2}\right|, 1+m_1 m_2 \neq 0\).
• Two lines are parallel if and only if their slopes are equal.
• Two lines are perpendicular if and only if the product of their slopes is \(-1\).
• Three points \(\mathrm{A}, \mathrm{B}\) and \(\mathrm{C}\) are collinear, if and only if slope of \(\mathrm{AB}=\) slope of \(\mathrm{BC}\).
• The equation of the horizontal line having distance \(a\) from the \(x\)-axis is either \(y=a\) or \(y=-a\).
• Equation of the vertical line having distance \(b\) from the \(y\)-axis is either \(x=b\) or \(x=-b\).
• The point \((x, y)\) lies on the line with slope \(m\) and through the fixed point \(\left(x_{\mathrm{o}}, y_{\mathrm{o}}\right)\), if and only if its coordinates satisfy the equation \(y-y_{\mathrm{o}}=m\left(x-x_{\mathrm{o}}\right)\).
• Equation of the line passing through the points \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\) is given by

           \(y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right) .\)

• The point \((x, y)\) on the line with slope \(m\) and \(y\)-intercept \(c\) lies on the line if and only if \(y=m x+c\).
• If a line with slope \(m\) makes \(x\)-intercept \(d\). Then equation of the line is \(y=m(x-d)\).
• Equation of a line making intercepts \(a\) and \(b\) on the \(x\)-and \(y\)-axis, respectively, is \(\frac{x}{a}+\frac{y}{b}=1\).
• The equation of the line having normal distance from origin \(p\) and angle between normal and the positive \(x\)-axis \(\omega\) is given by \(x \cos \omega\) – \(y \sin \omega=p\).
• Any equation of the form \(\mathrm{Ax}+\mathrm{By}+\mathrm{C}=0\), with \(\mathrm{A}\) and \(\mathrm{B}\) are not zero, simultaneously, is called the general linear equation or general equation of a line.
• The perpendicular distance \((d)\) of a line \(\mathrm{A} x+\mathrm{B} y+\mathrm{C}=0\) from a point \(\left(x_1, y_1\right)\) is given by \(d=\frac{\left|\mathrm{A} x_1+\mathrm{B} y_1+\mathrm{C}\right|}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}\).
• Distance between the parallel lines \(\mathrm{A} x+\mathrm{B} y+\mathrm{C}_1=0\) and \(\mathrm{A} x+\mathrm{B} y+\mathrm{C}_2=0\), is given by \(d=\frac{\left|\mathrm{C}_1-\mathrm{C}_2\right|}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}\).