3D shapes are solids that consist of 3 dimensions – length, breadth (width), and height. 3D in the word 3D shapes means three-dimensional. Some examples of 3D shapes are cube, Rectangular Parallelopiped, cone, and cylinder. We will study how to calculate the area, volume, and other parameters of various 3D shapes.

Rectangular Parallelopiped

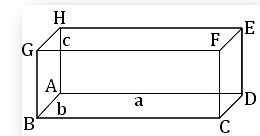
If \(a, b\) and \(c\) be the length, breadth, and height respectively of a rectangular parallelopiped then,

• the area of its surfaces \(=2(a b+b c+c a)\)
• its volume \(=a b c\) and
• the length of diagonal \(=\sqrt{\left(a^2+b^2+c^2\right)}\). 

Cube

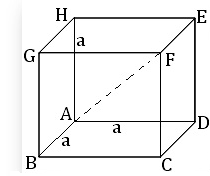
If the length of the side of a cube be a then, 

• the area of its surfaces \(=6 a^2\)
• its volume \(=\mathrm{a}^3\) and
• the length of the diagonal \(=\sqrt{{3} a}\)

Cylinder

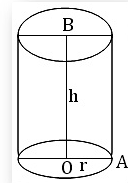
Let \(r(=O A)\) be the radius of the base and \(h(=O B)\) be the height of a right circular cylinder ; then

• area of its curved surface \(=\) perimeter of base \(\times\) height \(=2 \pi r h\)
• area of the whole surface \(=\) area of its curved surface \(+2 \times\) area of circular base
  \(
  \begin{aligned}
  & =2 \pi r h+2 \pi r^2 \\
  & =2 \pi r(h+r)
  \end{aligned}
  \)
• volume of cylinder \(=\) area of base \(\times\) height
  \(
  =\pi r^2 \mathrm{~h}
  \)

Cone

\(l^2=h^2+r^2\)

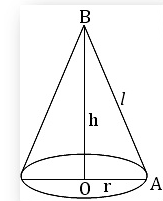
• area of its curved surface
  \(=(1 / 2) \times\) perimeter of the base \(\times\) slant height \(=(1 / 2) \cdot 2 \pi r \cdot l=\pi r l\)
• area of its whole surface \(=\) area of the curved surface \(+\) area of the circular base
  \(=\pi r l+\pi r^2=\pi r l+\pi r(l+r)\).
• volume of the cone \(=(1 / 3) \times\) area of the base \(\times\) height \(=(1 / 3) \pi r^2 h\)

Sphere

• Surface area of the sphere will be covered completely fill the region of four circles, all of the same radius as of the sphere. So the Surface area of a Sphere with radius \((r)=4 \times\left(\pi r^2\right)=4 \pi r^2\)
• Volume of a sphere is equal to \(4 \pi / 3\) times the cube of its radius.
  Volume of a sphere \(=\frac{4}{3} \pi r^3\)

Hemisphere

The solid sphere is divided into two equal parts and its each half part is called a hemisphere.

• Surface area of the hemisphere having two faces. There is curved face (Cap Area) and flat face (base area).
  Surface area of a Sphere with radius \((r)=4 \pi r^2\)
  Then cap area of hemisphere is half surface area of the sphere
  i.e Cap Area or Curved surface area of the hemisphere \(=1 / 2\left(4 \pi r^2\right)=2 \pi r^2\)
  Flat surface area or base area of the hemisphere = Area of the circle with same radius \(=\pi r^2\)
  Total Surface Area of the Hemisphere \(=3 \pi r^2\)
• Volume of a Hemisphere
  Hemisphere is half of a sphere
  Volume of a hemisphere \(=(1 / 2)\left(4 / 3 \pi r^2\right)=\frac{2}{3} \pi r^3\)
• Surface Area and Volume of Hemisphere shell
  Take external radius is \(R\) and inner radius is \(r\) of hemisphere
  then
  Curved surface area of hemisphere shell \(=2 \pi\left(R^2+r^2\right)\) ( Considered inside and outside area of hemisphere)
  Volume of Hemisphere shell \(=\frac{2}{3} \pi\left(R^3-r^3\right)\)

Volume of Hollow Sphere

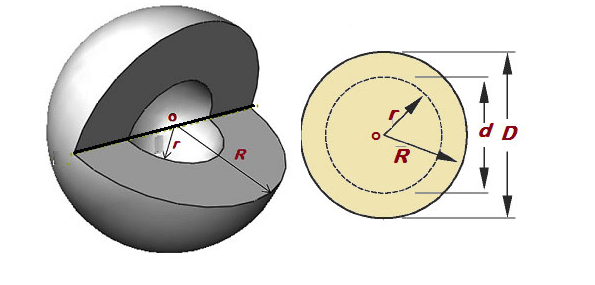
Assuming Hollow sphere inner radius \(\mathrm{r}\) and outer radius \(\mathrm{R}\)
Volume of hollow sphere \(=\frac{4}{3} \pi\left(R^3-r^3\right)\)

Pyramid

 

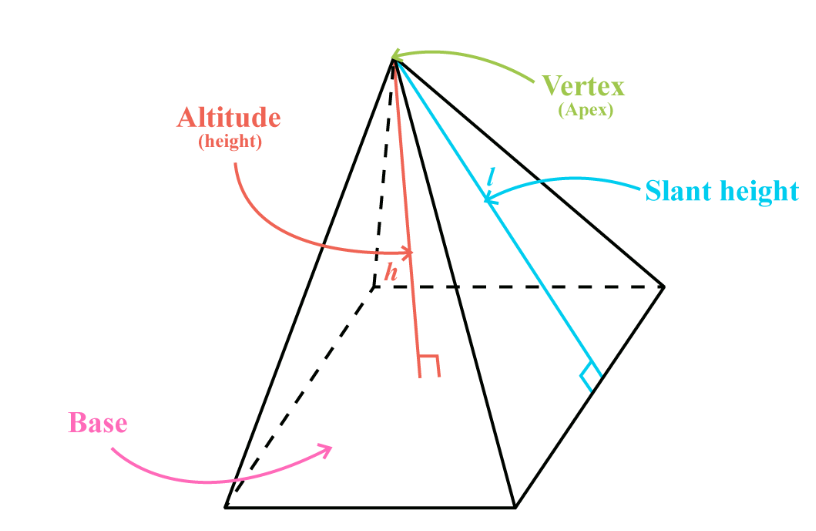
The volume of any pyramid is one-third the area of the base times the height. Let \(b\) = area of the base and \(h\)= altitude length.

\(V=\frac{1}{3} b h\)

 

Let \(P\) be the perimeter of the base and \(l\) be the slant height of the pyramid.

The lateral area is the sum of the area of a regular pyramid’s lateral faces and is found by taking half the product of the perimeter of the base and the slant height of one of the lateral faces.

\(L=\frac{1}{2} P l\)

The surface area of a pyramid is the sum of the area of the base and the lateral area.

Surface Area=\(b+L\)

Square Pyramid

A square pyramid is a three-dimensional geometric shape that has a square base and four triangular sides that are joined at a vertex.  A square pyramid has 5 faces, 4 side faces that are triangles, a square base, 5 vertices, and 8 edges.

\(
\begin{aligned}
\text { Volume } & =\frac{1}{3} a^2 h \\
\text { Curved Surface Area } & =2 a \sqrt{\left(\frac{a^2}{4}+h^2\right)} \text { or 2al } \\
\text { Total Surface Area } & =a^2+2 a \sqrt{\left(\frac{a^2}{4}+h^2\right)} \text { or } a^2+2 a l
\end{aligned}
\)

Prism

A prism is a polyhedron with two congruent, parallel faces, called bases. I like to think of them as the “top” and “bottom” of the prism. The other faces of a prism are called lateral faces, and they are parallelograms formed by connecting the corresponding vertices of the bases together.

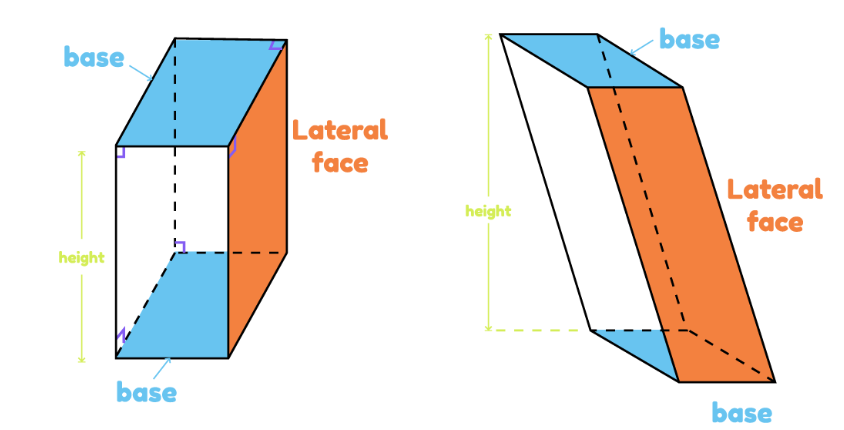
Surface Area \(=(\) Perimeter of Base \()\) (Height of Prism \()+2(\) Base Area \()\)
\(S A=P h+2 B\)

Volume \(=(\) Base Area \()(\) Height of Prism \()\)
\(V=B h\)

Rectangular Prism

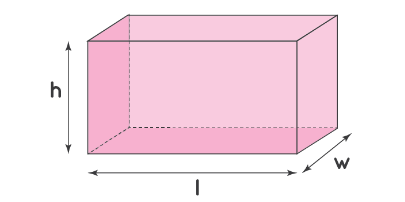
\(l\) is the base length
\(w\) is the base width
\(h\) is the height of the prism

Area of a rectangular prism \(A= l \times w+l \times h+h \times w\)

Volume of a rectangular prism \(V=l \times w \times h\)

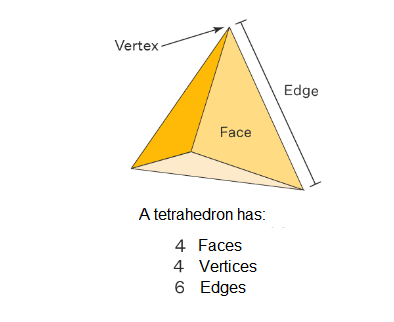
Tetrahedron

A tetrahedron is a polyhedron with 4 faces, 6 edges, and 4 vertices, in which all the faces are triangles. It is also known as a triangular pyramid whose base is also a triangle. A regular tetrahedron has equilateral triangles, therefore, all its interior angles measure \(60^{\circ}\). The interior angles of a tetrahedron in each plane add up to \(180^{\circ}\) as they are triangular.

Area of One Face of Regular Tetrahedron Formula:
\(A=\frac{1}{4} \sqrt{3} a^2\)

The altitude of a Regular Tetrahedron Formula:
\(h=\frac{a \sqrt{6}}{3}\)

Lateral Surface Area of a Tetrahedron

LSA of Regular Tetrahedron \(=\) Sum of 3 congruent equilateral triangles (i.e. lateral faces)
\(=3 \times(\sqrt{3}) / 4 \mathrm{a}^2\) square units
where \(\mathrm{a}\) is the side length (edge) of a regular tetrahedron.

Total Surface Area of a Tetrahedron

The total surface area of a tetrahedron is defined as the surface area of all the faces of a tetrahedron. The formula to calculate the total surface area of a regular tetrahedron is given as, TSA of Regular Tetrahedron \(=\) Sum of 4 congruent equilateral triangles (i.e. lateral faces) \(=4 \times(\sqrt{3}) / 4 a^2=\sqrt{3} a^2\) square units where \(\mathrm{a}\) is the side length of the regular tetrahedron.

Volume of Tetrahedron

The volume of a tetrahedron is defined as the total space occupied by it in a three-dimensional plane. The formula to calculate the tetrahedron volume is given as,

The volume of regular tetrahedron \(=(1 / 3) \times\) area of the base \(\times\) height \(=\) \((1 / 3) \cdot(\sqrt{3}) / 4 \cdot a^2 \times(\sqrt{2}) /(\sqrt{3}) a\) \(=(\sqrt{2} / 12) a^3\) cubic units where \(a\) is the side length of the regular tetrahedron.