The 2-D shapes are flat shapes that have only two dimensions, length, and width as in squares, rectangles, circles, and triangles, etc. Some of the geometry formulas for common 2D shapes are listed below.

Triangle

\(
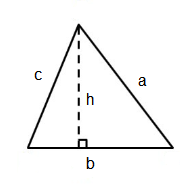
\begin{gathered}
b=\text { base of the triangle} \\
h=\text { height of the triangle} \\
a,c=\text { sides of the triangle} \\
\end{gathered}
\)

Perimeter: \(P=a+b+c\)

Area: \(\text { Area }=\frac{1}{2} \mathrm{x} \text { base } \mathrm{x} \text { height }\)

\(A=\frac{1}{2} b h\)

Equilateral Triangle

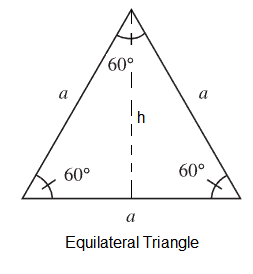
latex]a=[/latex] length of sides of an equilateral triangle. An equilateral triangle also has three equal \(60^{\circ}\) angles.

\(h=a \sin 60^{\circ}=\frac{1}{2} \sqrt{3} a\)

Perimeter: \(P=3 \times a\)

Area: \(A=\frac{1}{2} a h=\frac{1}{4} \sqrt{3} a^2\)

Rectangle:

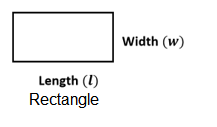
\(\text { Length }(l)\), \(\text { Width (w) }\)

Perimeter: \(P=2(l+w)\)

Area: \(A=l \times w\)

Square

\(a =\text { length of side of the square }\)

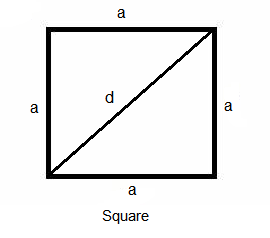
Perimeter: \(P=4 \times a\)

Area: \(A =a^2\)

Diagonal: \(d=\sqrt{2} a\)

Parallelogram

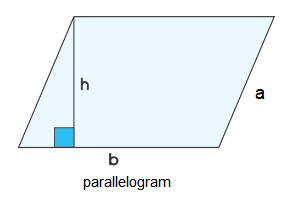
\(b=\) base of parallelogram, \(h\) =height of parallelogram

Perimeter: \(P=\mathbf{2}(\mathbf{a}+\mathbf{b})\)

Area: \(A=b \times h\)

Trapezoid

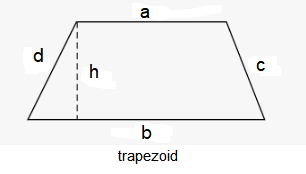
\(a, b=\) length of parallel sides \(h\) = distance between the parallel sides of trapezoid.

Perimeter: \(P=a+b+c+d\)

Area: \(A=\frac{1}{2}(a+b) \times h\)

Circle

\(
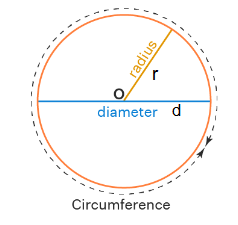
\begin{gathered}
r=\text { radius } \\
d=\text { diameter }
\end{gathered}
\)

Perimeter or Circumference: \(P=2 \pi r\),

Area: \(A=\pi r^2\)

Sector Of Circle

\(r=\text { radius, } \theta=\text { angle in radians }\)

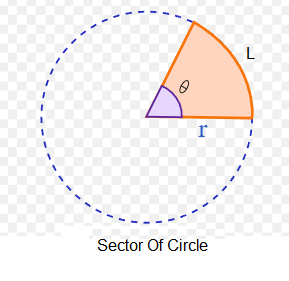
Arc Length: \( L=\theta r\)

Area: \(A=\frac{1}{2} \theta r^2\)

Ellipse

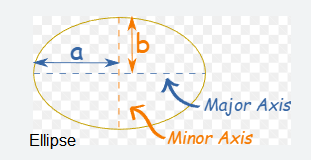
\(a=\) semimajor axis
\(b=\) semiminor axis

Circumference: \(C \approx \pi(3(a+b)-\sqrt{(a+3 b)(b+3 a)})\)

Area: \(A=\pi a b\)

Annulus Shape

\(
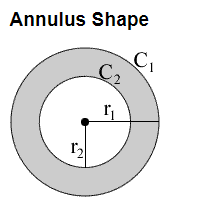
\begin{aligned}
& r_1=\text { outer radius } \\
& r_2=\text { inner radius } \\
& C_1=\text { outer circumference } \\
& C_2=\text { inner circumference }
\end{aligned}
\)

Circumference: 

\(C_1=2 \pi r_1\), \(C_2=2 \pi r_2\)

Area: \(A=\pi\left(r_1{ }^2-r_2^2\right)\)

Rhombus

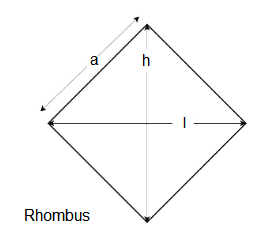
\(\text { length }=l\), \(\text { height}=h\), \(\text { side }=a\)

Perimeter: \(P=4 a\)

Area: \(A=\frac{(h \times l)}{2}\)

Scalene Triangle

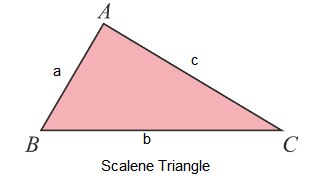
a, b, and c are the side length of the triangle.

Perimeter: \(P=(a+b+c)\)

Semi-perimeter: \(s=(a+b+c)/2\)

Area: \(A=\sqrt{s(s-a)(s-b)(s-c)}\)

Formula to find the area under a curve

The area under the curve can be calculated through three simple steps.

Step 1: First, we need to know the equation of the curve(y = f(x)), the limits across which the area is to be calculated, and the axis enclosing the area.

Step 2: Secondly, we have to find the integration (antiderivative) of the curve.

Step 3: Finally, we need to apply the upper limit and lower limit to the integral answer and take the difference to obtain the area under the curve.

For example, let’s consider the curve below.

\(
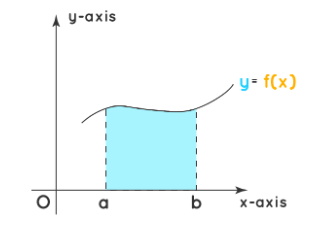
\begin{aligned}
\text { Area } & =\int_a^b y \cdot d x \\
& =\int_a^b f(x) \cdot d x \\
& =[g(x)]_a^b \\
& =g(b)-g(a)
\end{aligned}
\)

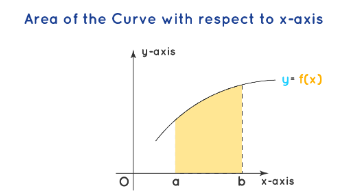
Case 1: Area with respect to the x-axis:

Here we shall first look at the area enclosed by the curve \(y=f(x)\) and the \(x\)-axis. The below figures present the area enclosed by the curve and the \(x\)-axis. The bounding values for the curve with respect to the \(x\)-axis are \(a\) and \(b\) respectively. The formula to find the area under the curve with respect to the

\(x\)-axis is \(\mathrm{A}=\) \(\int_a^b f(x) \cdot d x\)

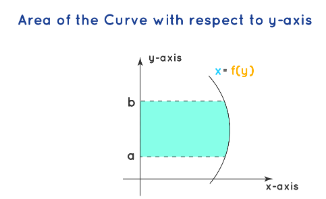
Case 2: Area with respect to the y-axis:

The area of the curve bounded by the curve \(x=f(y)\), the \(y\)-axis, across the lines \(y=a\) and \(y=b\) is given by the following below expression. Further, the area between the curve and the \(y\)-axis can be understood from the below graph.
\(
A=\int_a^b x \cdot d y={ }_a \int^b f(y) \cdot d y
\)

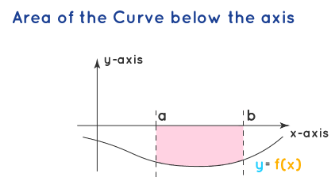
Case 3: Area below the axis:

The area of the curve below the axis is a negative value and hence the modulus of the area is taken. The area of the curve \(y\) \(=f(x)\) below the \(x\)-axis and bounded by the \(x\)-axis is obtained by taking the limits \(a\) and \(b\). The formula for the area above the curve and the \(x\)-axis is as follows.
\(
A=\int_a^b f(x) \cdot d x \mid
\)

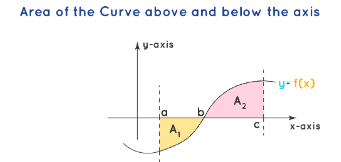
Case 4: Area above and below the axis:

The area of the curve which is partly below the axis and partly above the axis is divided into two areas and separately calculated. The area under the axis is negative, and hence a modulus of the area is taken. Therefore the overall area is equal to the sum of the two areas \(\left(A=\left|A_1\right|+A_2\right)\).
\(
A=\int_a^b f(x) \cdot d x +\int_b^c f(x) \cdot d x
\)

A regular polygon is a polygon in which all the angles and sides are equal. There are 2 types of angles in a regular polygon:

• Interior Angles: The angles that lie inside a shape, generally a polygon, are said to be its interior angles.
• Exterior Angles: An exterior angle of a polygon is the angle between a side and its adjacent extended side.

Sum of Interior Angles in a Polygon

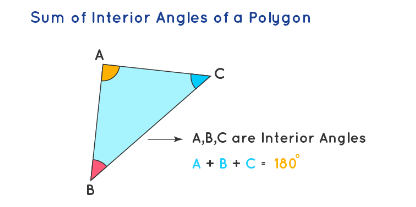
The interior angles of a polygon are those angles that lie inside the polygon. Observe the interior angles A, B, and C in the following triangle. The interior angles in a regular polygon are always equal to each other. Therefore, to find the sum of the interior angles of a polygon, we use the formula:

Sum of interior angles \(=(n-2) \times 180^{\circ}\) where ‘ \(n=\) the number of sides of a polygon.

Another way to calculate the sum of the interior angles is by checking the number of triangles formed inside the polygon with the help of the diagonals. Since the interior angles of a triangle sum up to \(180^{\circ}\), the sum of the interior angles of any polygon can be calculated by multiplying \(180^{\circ}\) with the number of triangles formed inside the polygon.

For example, a quadrilateral can be divided into two triangles using the diagonals, therefore, the sum of the interior angles of a quadrilateral is 2 \(\times 180^{\circ}=360^{\circ}\). Similarly, a pentagon can be divided into 3 triangles, so, the pentagon’s interior angles will sum up to \(3 \times 180^{\circ}=540^{\circ}\).

Sum of Exterior Angles in a Polygon

An exterior angle (outside angle) of any shape or regular polygon is the angle formed by one side and the extension of the adjacent side of that polygon. Observe the exterior angles shown in the following polygon.

The sum of the exterior angles of a polygon is equal to \(360^{\circ}\). This can be proved with the following steps:

• We know that the sum of the interior angles of a regular polygon with \(n\) sides \(=180(n-2)\).
• The interior and exterior angle at each vertex form a linear pair. Therefore, there will be \(n\) linear pairs in the polygon. Now, since each linear pair sums upto \(180^{\circ}\), the sum of all linear pairs will be: \(180 n^{\circ}\).
• So, the sum of exterior angles = Sum of all linear pairs – Sum of interior angles
• This means: Sum of exterior angles \(=180 n-180(n-2)=180 n-180 n\) \(+360\). Hence, the sum of exterior angles of a pentagon equals \(360^{\circ}\).

Area of a regular Polyon

Let’s study how to derive the formula for the area of a regular polygon by breaking it down into a set of \(n\) isosceles triangles, where \(n\) is the number of sides. As shown below, a regular polygon can be broken down into a set of congruent isosceles triangles. In this case, the hexagon has six of them.

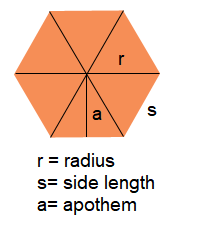
A regular hexagon is a six-sided polygon where each side is of equal length.

\(\text { Perimeter }=\mathbf{6 s}\)

Case 1: Given the side length s

If we look at one of the triangles and draw a line from the apex to the midpoint of the base it will form a right angle. Let the length of this line be \(h\). The base of the triangle is \(s\), the side length of the polygon.

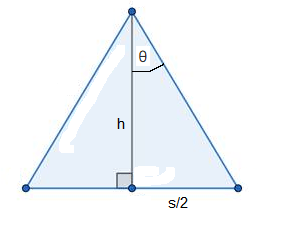
The whole angle at the apex is dependent on the number of sides \(n\) :
\(\frac{360}{n}\)
So the angle \(\theta\) is half that, which simplifies to
\(\frac{180}{n}\)
We know that the tan of an angle is opposite side over adjacent side, so
\(\tan {\theta}=\frac{\left(\frac{s}{2}\right)}{h}\)
Rearranging to solve for \(h\):
\(
h=\frac{\left(\frac{s}{2}\right)}{\tan {\theta}} \text { or } h=\frac{s}{2 \tan {\theta}}
\)
The area of any triangle is half the base times height, so area of each triangle
\(
=\frac{s}{2} \cdot \frac{s}{2 \tan {\theta}}
\)
Which simplifies to
\(
\frac{s^2}{4 \tan {\theta}}
\)
Finally since have \(\boldsymbol{n}\) triangles, multiply by \(\boldsymbol{n}\) :
\(
\text { Area of polygon }=\frac{s^2 n}{4 \tan {\theta}}
\)

Given the radius r

The radius of a regular polygon is the distance from the center to any vertex. In the figure below the leg of the isosceles triangle is a radius \(r\) of the polygon. We add a perpendicular \(\boldsymbol{h}\) from the apex to the base. In this case, let \(\theta\) be the whole angle at the apex.

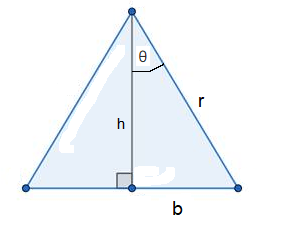
From the figure, we see that
\(
h=r \cos {\theta} \text { and } b=r \sin {\theta}
\)
The area of any triangle is half the base times height, and since \(b\) is already half the base:
triangle area \(=b h\)
Substituting \(b, h\) :
triangle area \(=r \cos {\theta} \cdot r \sin {\theta}=r^2 \sin {\theta} \cos {\theta}\)
\(
\text { triangle area }=r^2 \cdot \frac{1}{2} \sin 2 {\theta}
\)
The whole angle \(2 {\theta}\) at the apex is dependent on the number of sides: \(\boldsymbol{n}\)
\(
2 {\theta}=\frac{360}{n}
\)
Substituting this for \(2 {\theta}\).
\(
\frac{1}{2} r^2 \sin \left(\frac{360}{n}\right)
\)
Finally, there are \(n\) triangles in the polygon so
\(
\text { Area of polygon }=\frac{1}{2} r^2 n \sin \left(\frac{360}{n}\right)
\)

Given the apothem a

The apothem of a regular polygon is a line from the center to the midpoint of a side, which it meets at right angles. In the figure below, the apothem is labelled \(\boldsymbol{a}\).

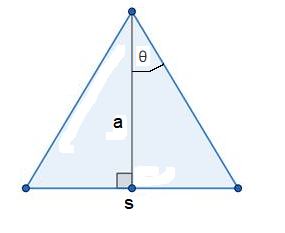
The whole angle at the apex is dependent on the number of sides \(n\) :
\(
\frac{360}{n}
\)
So the angle \(\theta\) is half that, which simplifies to
\(
\frac{180}{n}
\)
We know that the tan of an angle is opposite side over adjacent side, so
\(
\tan \frac{180}{n}=\frac{\left(\frac{s}{2}\right)}{a}=\frac{s}{2 a}
\)
Transposing we solve this for s
\(
s=2 a \tan \left(\frac{180}{n}\right)
\)
The area of any triangle is half the base times height, so
\(
\text { Area of triangle }=\frac{2 a \tan \left(\frac{180}{n}\right) \cdot a}{2}
\)
Which simplifies to
\(
\text { Area of triangle }=a^2 \tan \left(\frac{180}{n}\right)
\)
Finally since have \(\boldsymbol{n}\) triangles, multiply by \(\boldsymbol{n}\) :
\(
\text { Area of polygon }=a^2 n \tan \left(\frac{180}{n}\right)
\)

Example 1: Prove that area of the circle is \(2 \pi r\)

Proof:

The area of the circle is calculated by first calculating the area of the part of the circle in the first quadrant. We know the equation of a circle is given by

\(x^2+y^2=r^2\)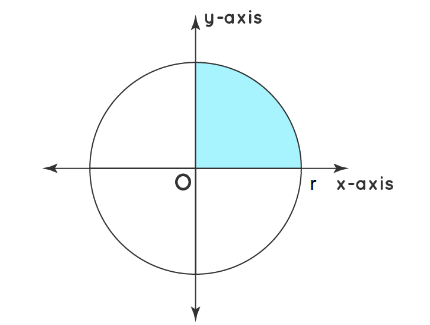

The area of the circle is four times the area of the quadrant of the circle. The area of the quadrant is calculated by integrating the equation of the curve across the limits in the first quadrant.

\(
\begin{aligned}
& A=4 \int_0^r y \cdot d x \\
& =4 \int_0^r \sqrt{r^2-x^2} \cdot d x \\
& =4\left[\frac{x}{2} \sqrt{r^2-x^2}+\frac{r^2}{2} \operatorname{Sin}^{-1} \frac{x}{r}\right]_0^r \\
& =4\left[\left((r / 2) \times 0+\left(r^2 / 2\right) \operatorname{Sin}^{-1} 1\right)-0\right] \\
& =4\left(r^2 / 2\right)(\pi / 2) \\
& =\pi r^2
\end{aligned}
\)
Hence the area of the circle is \(\pi \mathrm{r}^2\) square units.

Example 2: Calculate the Area Under a Parabola Curve.

Solution:

A parabola has an axis that divides the parabola into two symmetric parts. Here we take a parabola that is symmetric along the \(\mathrm{x}\)-axis and has an equation \(y^2=4 a x\). We first find the area of the parabola in the first quadrant with respect to the x-axis and along the limits from 0 to a. Here we integrate the equation within the boundary and double it, to obtain the area of the whole parabola. 

\(
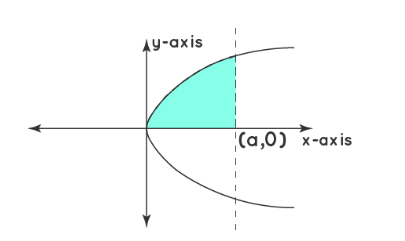
\begin{aligned}
A & =2 \int_0^a y \cdot d x \\
& =2 \int_0^a \sqrt{4 a x} \cdot d x \\
& =4 \sqrt{a} \int_0^a \sqrt{x} \cdot d x \\
& =4 \sqrt{a}\left[\frac{2}{3} \cdot x^{\frac{3}{2}}\right]_0^a \\
& =4 \sqrt{a}\left(\left(\frac{2}{3} \cdot a^{\frac{3}{2}}\right)-0\right) \\
& =\frac{8 a^2}{3}
\end{aligned}
\)
Therefore the area under the curve enclosed by the parabola is \(\frac{8 \mathrm{a}^2}{3}\) square units.

Example 3: Calculate the area of an Ellipse.

Solution:

The equation of the ellipse with the major axis of \(2 a\) and a minor axis of \(2 b\) is \(x^2 / a^2+y^2 / b^2=1\). This equation can be transformed in the form as \(y\) \(=b / a \cdot \sqrt{ }\left(a^2-x^2\right)\). Here we calculate the area bounded by the ellipse in the first coordinate and with the x-axis, and further multiply it with 4 to obtain the area of the ellipse. The boundary limits taken on the \(x\)-axis is from \(\mathrm{O}\) to \(\mathrm{a}\).

\(
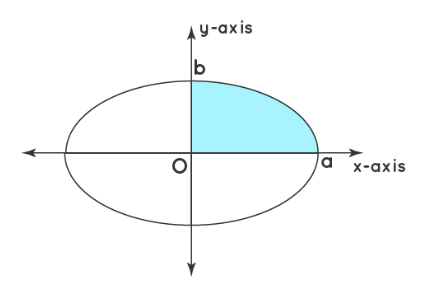
\begin{aligned}
A & =4 \int_0^a y \cdot d x \\
& =4 \int_0^4 \frac{b}{a} \cdot a^2-x^2 \cdot d x \\
& =\frac{4 b}{a}\left[\frac{x}{2} \cdot \sqrt{a^2-x^2}+\frac{a^2}{2} \operatorname{Sin}^{-1} \frac{x}{a}\right]_0^a \\
& \left.=\frac{4 b}{a}\left[\left(\frac{a}{2} \times 0\right)+\frac{a^2}{2} \cdot \operatorname{Sin}^{-1} 1\right)-0\right] \\
& =\frac{4 b}{a} \cdot \frac{a^2}{2} \cdot \frac{\pi}{2} \\
& =\pi a b
\end{aligned}
\)
Therefore the area of the ellipse is \(\pi a b\) sq units.

Example 4: Find the area between two curves

Solution:

The area between two curves can be conveniently calculated by taking the difference of the areas of one curve from the area of another curve. Here the boundary with respect to the axis for both curves is the same. The below figure shows two curves \(y_1=f(x)\), and \(y_2=g(x)\), and the objective is to find the area between these two curves.

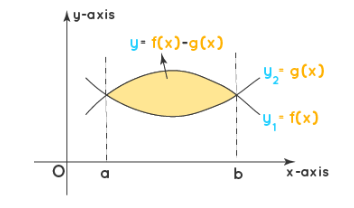
Here we take the integral of the difference of the two curves and apply the boundaries to find the resultant.
\(
A=\int_a^b[f(x)-g(x)] \cdot d x
\)

Example 5: Find the area of the region bounded above by \(y=x^2+1\), bounded below by \(y=x\), and bounded on the sides by \(x=0\) and \(x=1\).

Solution:

The upper boundary curve is \(y=x^2+1\) and the lower boundary curve is \(y=\mathrm{x}\).
Using the formula for area bounded by curves,
\(
\begin{aligned}
A & =\int_0^1\left[\left(x^2+1\right)-x\right] d x \\
& =\int_0^1\left(x^2-x+1\right) d x \\
& \left.=\frac{x^3}{3}-\frac{x^2}{2}+x\right]_0^1 \\
& =\frac{1}{3}-\frac{1}{2}+1=\frac{5}{6}
\end{aligned}
\)

Example 6: Find the area between the two curves \(y=x^2\) and \(y=2 x-x^2\).

Solution:

Step 1: Find the points of intersection of the two parabolas by solving the equations simultaneously.
\(
\begin{aligned}
& x^2=2 x-x^2 \\
& 2 x^2-2 x=0 \\
& 2 x(x-1)=0 \\
& x=0 \text { or } 1
\end{aligned}
\)
The points of intersection are \((0,0)\) and \((1,1)\)
Step 2: Find the area between \(x=0\) and \(x=1\)
\(
\begin{aligned}
A & =\int_0^1\left[\left(2 x-x^2\right)-x^2\right] d x \\
& =\int_0^1\left(2 x-2 x^2\right) d x \\
& =2 \int_0^1\left(x-x^2\right) d x \\
& =2\left[\frac{x^2}{2}-\frac{x^3}{3}\right]_0^1 \\
& =2\left(\frac{1}{2}-\frac{1}{3}\right)=\frac{1}{3}
\end{aligned}
\)

Example 7: In the Figure below, a circle of radius \(7.5 \mathrm{~cm}\) is inscribed in a square. Find the area of the shaded region (Use \(\pi=3.14\) )

Solution:

Area of the circle \(=\pi r^2\)
\(
\begin{aligned}
& =3.14 \times(7.5)^2 \mathrm{~cm}^2 \\
& =176.625 \mathrm{~cm}^2
\end{aligned}
\)
Clearly, side of the square \(=\) diameter of the circle \(=15 \mathrm{~cm}\)
So, area of the square \(=15^2 \mathrm{~cm}^2=225 \mathrm{~cm}^2\)
Therefore, the area of the shaded region
\(
=225 \mathrm{~cm}^2-176.625 \mathrm{~cm}^2=48.375 \mathrm{~cm}^2
\)

Example 8: Find the area of the shaded field shown in the Figure below.

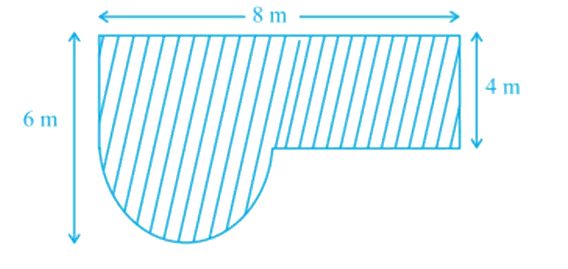
Solution:

Area = \((32+2 \pi) m^2\)

Example 9: Find the area of the shaded region in Figure below, where arcs drawn with centres \(\mathrm{A}, \mathrm{B}, \mathrm{C}\) and D intersect in pairs at mid-points \(P, Q, R\) and \(S\) of the sides \(A B, B C, C D\) and \(D A\) respectively of a square \(A B C D\) of side \(12 \mathrm{~cm}\). [Use \(\pi=3.14\) ]

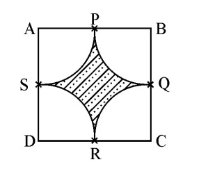
Solution:

Radius of each are drawn \(=6 \mathrm{~cm}\)
Area of one quadrant \(=(3.14) \times \frac{36}{4}\)
Area of four quadrants \(=3.14 \times 36=113.04 \mathrm{~cm}^2\)
Area of square \(\mathrm{ABCD}=12 \times 12=144 \mathrm{~cm}^2\)
Hence, Area of shaded region = \(144-113.04\) \(=30.96 \mathrm{~cm}^2\)

Example 10: In Figure below arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.

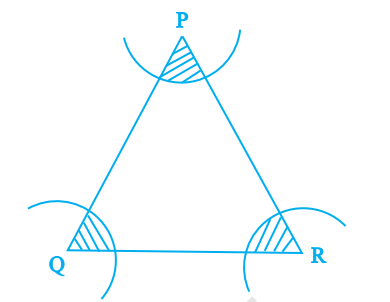
Solution:

Given, radii of each arc, \(r=14 \mathrm{~cm}\)
Let \(\theta_1, \theta_2\) and \(\theta_3\) be the three angles of \(\triangle P Q R\).
\(
\begin{aligned}
\therefore \text { Area of sector with centre at } P= & \frac{\angle P}{360^{\circ}} \times \pi r^2 \\
& =\frac{\angle P}{360^{\circ}} \times \pi \times(14)^2 \mathrm{~cm}^2
\end{aligned}
\)
Also, area of sector with centre at \(Q=\frac{\angle Q}{360^{\circ}} \times \pi r^2=\frac{\angle Q}{360^{\circ}} \times \pi \times(14)^2 \mathrm{~cm}^2\)
And area of sector with centre at \(R=\frac{\angle R}{360^{\circ}} \times \pi r^2=\frac{\angle R}{360^{\circ}} \times \pi \times(14)^2 \mathrm{~cm}^2\)
Now, area of shaded region \(=\) Sum of the areas of three sectors
\(
\begin{aligned}
& =\frac{\angle P}{360^{\circ}} \times \pi r^2+\frac{\angle Q}{360^{\circ}} \times \pi r^2+\frac{\angle R}{360^{\circ}} \times \pi r^2 \\
& =\frac{\pi r^2}{360^{\circ}}(\angle P+\angle Q+\angle R) \quad (\text { Sum of angles of a triangle }=180^{\circ}) \\
& =\frac{\pi r^2}{360^{\circ}} \times 180^{\circ}=\frac{22 \times 14 \times 14}{7 \times 2}=308 \mathrm{~cm}^2
\end{aligned}
\)
Hence, the required area of the shaded region is \(308 \mathrm{~cm}^2\)

Example 11: Find the area of the scalene triangle ABC with the sides 8 cm, 6 cm and 4 cm.

Solution:

Let \(a=8 \mathrm{~cm}\)
\(
b=6 \mathrm{~cm}
\)
\(
\mathrm{c}=4 \mathrm{~cm}
\)
If all the sides of a triangle are given, then use Heron’s formula.
Area of the triangle \(A=\sqrt{s(s-a)(s-b)(s-c)}\) square units Now, find the semi perimeter value
\(
\begin{aligned}
& s=(a+b+c) / 2 \\
& s=(8+6+4) / 2 \\
& s=18 / 2 \\
& s=9
\end{aligned}
\)
Now substitute the value of \(S\) in the area formula,
\(
\begin{aligned}
& \text { Area }=\sqrt{9(9-8)(9-6)(9-4)} \\
& =\sqrt{9(1)(3)(5)} \\
& =\sqrt{135} \\
& =11.6
\end{aligned}
\)
Therefore, the area of the scalene triangle \(=11.6 \mathrm{~cm}^2\)