Quiz Level-2
Quiz Summary
0 of 30 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 30 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 30
1. Question
How many ways can five keys be placed in the ring?
CorrectIncorrectHint
Since clockwise and anticlockwise are same in case of ring.
If the anti-clockwise and clockwise sequence and movement are not different then the number of circular permutations of \(n\) distinct items is
\(
=(n-1) ! / 2
\)
Required number of ways \(=(5-1) ! / 2=4 ! / 2=12\) -
Question 2 of 30
2. Question
What would be the number of arrangements, If eleven members of a committee sit at a round table so that the President and Secretary always sit together?
CorrectIncorrectHint
By the fundamental property of circular permutation
The count of circular permutations of \(n\) different things are ( \(n-1)\) !Since two positions are fixed so we have
The required number of ways \((11-2) ! \times 2=9 ! \times 2=725760\) -
Question 3 of 30
3. Question
What would be the number of ways 6 men and 5 women can eat at a round table if no two women can sit together?
CorrectIncorrectHint
The count of circular permutations of n different things are (n-1)!
The number of ways in which 6 men can be arranged at a round table = (6 – 1)! =5!
Now women can be arranged in 6! ways and the Total Number of ways = 6! × 5!
-
Question 4 of 30
4. Question
Find the number of ways in which 5 men and 5 women can be seated at a round table in such a way that no two persons of same-sex sit together.
CorrectIncorrectHint
If we fix one man round a table then their permutations \(={ }^4 \mathrm{P}_4=24\)
Now if women sit between the two men then their permutations \(={ }^5 \mathrm{P}_5=120\)
So total permutations \(=24 \times 120=2880\)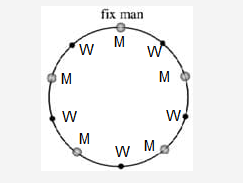
-
Question 5 of 30
5. Question
In how many ways can 4 keys be arranged on a circular key ring?
CorrectIncorrectHint
Number of keys \(=4\)
Fixing one key we have permutation \(={ }^3 \mathrm{P}_3=6\)
Since the above figures of arrangement are reflections of each other. Therefore permutations \(=1 / 2 \times 6=3\)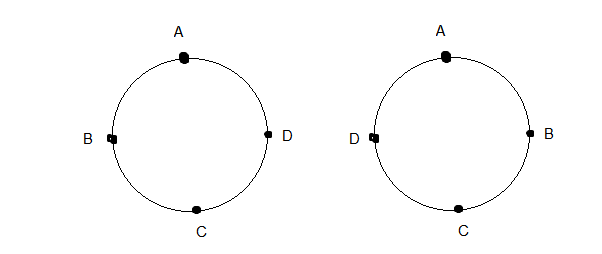
-
Question 6 of 30
6. Question
How many necklaces can be made from 6 beads of different colours?
CorrectIncorrectHint
Number of beads \(=6\)
Fixing one bead, we have permutation \(={ }^5 \mathrm{P}_5=120\)
Since above figures of arrangement are reflections of each other, therefore permutations \(=1 / 2 \times 120=60\)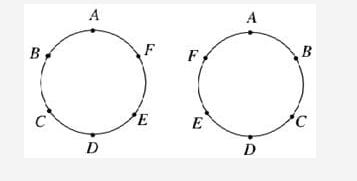
-
Question 7 of 30
7. Question
In how many ways 4 boys and 4 girls can be seated on a circular table such that boys and girls sit on alternate positions?
CorrectIncorrectHint
Boys can sit on the circular table in (4-1)! ways. The girls can be seated in 4 places in 4! ways. So. the number of ways =3!×4!
-
Question 8 of 30
8. Question
The Governor of New York calls a meeting of 12 officers. In how many ways can they be seated at a round table?
CorrectIncorrectHint
Fixing one officer on a particular seat, we have permutations of the remaining 11 officers.
=(12-1)!=11!=39916800 -
Question 9 of 30
9. Question
The D.C.Os of 11 districts meet to discuss the law and order situation in their districts. In how many ways can they be seated at a round table, when two particular D.C.Os insist on sitting together?
CorrectIncorrectHint
Number of D.C.O’s \(=9\)
Let \(D_1\) and \(D_2\) be the two D.C.O’s insisting to sit together so consider them one.
If \(D_1 D_2\) sit together then permutations
\(
={ }^9 P_9=362880
\)
If \(D_2 D_1\) sit together then permutations
\(
={ }^9 P_9=362880
\)
So total permutations \(=362880+362880\) \(=725760\)Alternate:
\(
2 ! \cdot(11-2) !=2 \times 362880=725760
\) -
Question 10 of 30
10. Question
Fatima invites 14 people to a dinner. There are 9 males and 5 females who are seated at two different tables so that guests of one sex seat at one round table and the guests of the other sex at the second table. Find the number of ways in which all guests are seated.
CorrectIncorrectHint
9 males can be seated on a round table
\(
={ }^8 P_8=40320
\)
And 5 females can be seated on a round table
\(
={ }^4 P_4=24
\)
So permutations of both \(=40320 \times 24\)
\(
=967680 .
\)Alternate:
\(
=(9-1) ! \times(5-1) !
\) -
Question 11 of 30
11. Question
How many arrangements of the letters of the following word, taken all together, can be made:
PAKPATTANCorrectIncorrectHint
PAKPATTAN
Total number of letters \(=9\)
\(\mathrm{P}\) is repeated 2 times
A is repeated 3 times
\(\mathrm{T}\) is repeated 2 times
\(\mathrm{K}\) and \(\mathrm{N}\) come only once.
Required number of permutations =
\(
\begin{aligned}
& =\frac{9 !}{2 ! \times 3 ! \times 2 \backslash \times 1 \times 1 !} \\
& =\frac{362880}{(2)(6)(2)}=15120 .
\end{aligned}
\) -
Question 12 of 30
12. Question
How many 6-digits numbers can be formed from the digits 2, 2, 3, 3, 4, 4?
CorrectIncorrectHint
Total number of digits \(=6\)
Number of 2’s \(=2\)
Number of 3’s =2
Number of 4 ‘s \(=2\)
So number formed by these 6 digits
\(
\begin{aligned}
& =\frac{6 !}{(2 !)(2 !)(2 !)} \\
& =\frac{720}{(2)(2)(2)}=90 .
\end{aligned}
\) -
Question 13 of 30
13. Question
The number of 6-digit numbers that can be formed from the digits 2, 2, 3, 3, 4, and 4 is 90. How many of them will lie between 400,000 and 430,000?
CorrectIncorrectHint
Total number of digits \(=6\)
Number of 2’s \(=2\)
Number of 3’s =2
Number of 4 ‘s \(=2\)
So number formed by these 6 digits
\(
\begin{aligned}
& =\frac{6 !}{(2 !)(2 !)(2 !)} \\
& =\frac{720}{(2)(2)(2)}=90 .
\end{aligned}
\)
The numbers lie between 400,000 and 430,000 are only of the form \(42^{* * * *}\), where each * can be filled by \(2,3,3,4\).
Here number of digits \(=4\).
Number of 2’s \(=1\)
Number of 3’s \(=2\)
Number of 4’s = 1
\(
\begin{aligned}
\text { So number formed }
& =\frac{4 !}{(1 !)(2 !)(1 !)} \\
& =\frac{24}{2}=12
\end{aligned}
\) -
Question 14 of 30
14. Question
11 members of a club form 4 committees of 3, 4, 2, 2 members so that no member is a member is a member of more than one committee. Find the number of committees.
CorrectIncorrectHint
Total members =11
Members in first committee =3
Members in second committee =4
Members in third committee =2
Members in fourth committee =2
So required number of committees
\(
\begin{aligned}
& =\frac{11 !}{3 ! \cdot 4 ! \cdot 2 ! \cdot 2 !} \\
& =\frac{39916800}{(6)(24)(2)(2)}=69300 .
\end{aligned}
\) -
Question 15 of 30
15. Question
How many arrangements of the letters of the word ATTACKED can be made, if each arrangement begins with C and ends with K?
CorrectIncorrectHint
If \(C\) be the first letter and \(K\) is the last letter then words are of the form \(\mathrm{C} * * * * * * \mathrm{~K}\). where each * can be replaced with A, T, T, A, E, D.
So number of letters \(=6\)
\(\mathrm{A}\) is repeated 2 times
\(\mathrm{T}\) is repeated 2 times
\(E\) and D come only once.
\(
\begin{gathered}
\text { So required permutations }
& =\frac{6 !}{2 ! \times 2 \times 1 \times 1 !}=\frac{720}{4}=180 .
\end{gathered}
\) -
Question 16 of 30
16. Question
How many numbers greater than 1000,000 can be formed from the digits 0, 2, 2, 2,3,4,4?
CorrectIncorrectHint
The number greater than 1000000 are of the following forms.
If numbers are of the form \(2 * * * * * *\),
where each \(*\) can be filled with \(0,2,2,3,4,4\)
Then number of digits \(=6\)
2 is repeated 2 times
4 is repeated 2 times
0 and 3 come only once.
So number formed
\(
=\frac{6 !}{2 ! \times 2 \times 1 \times 1 \times 1 !}=\frac{720}{4}=180 \text {. }
\)
Now if numbers are of the form \(3 * * * * *\), where each \(*\) can be filled with \(0,2,2,2,4,4\)
Then number of digits \(=6\)
2 is repeated 3 times
4 is repeated 2 times
0 comes only once.
So number formed
\(
=\frac{6 !}{3 ! \times 2 \times 1 !}=\frac{720}{12}=60 \text {. }
\)
Now if numbers are of the form \(4 * * * * * *\), where each \(*\) can be filled with \(0,2,2,2,3,4\)
Then number of digits \(=6\)
2 is repeated 3 times
0,3 and 4 come only once.
So number formed \(=\frac{6 !}{3 ! \times 1 \times 1 !}\)
\(
=\frac{720}{6}=120 \text {. }
\)
So required numbers greater than 1000000
\(
\begin{aligned}
& =180+60+120 \\
& =360 .
\end{aligned}
\) -
Question 17 of 30
17. Question
How many permutations of the letters of the word PANAMA can be made, if P is to be the first letter in each arrangement?
CorrectIncorrectHint
If \(P\) is the first letter then words are of the form \(\mathrm{P} * * * * *\), where five \(*\) can be replace with \(\mathrm{A}, \mathrm{N}, \mathrm{A}, \mathrm{M}, \mathrm{A}\).
So number of letters \(=5\)
\(\mathrm{A}\) is repeated 3 times
\(\mathrm{M}, \mathrm{N}\) appears only once
\(
\begin{aligned}
\text { So required permutations }
& =\frac{5 !}{3 ! \times 1 ! \times 1 !} \\
& =\frac{120}{6}=20 .
\end{aligned}
\) -
Question 18 of 30
18. Question
A necklace is to be prepared with 16 beads. 5 out of these beads are similar and 3 of the other beads are similar, How many distinct necklaces can be prepared with the help of these beads?
CorrectIncorrectHint
A necklace of 16 beads can be arranged in \(15 ! / 2\) ways since a necklace is same when turned upside down. Now it has 5 and 3 similar beads. Hence the total number of distinct necklaces that can be made
\(
=\frac{15 !}{2 \times 5 ! \times 3 !}=\frac{1}{16} \times \frac{16 !}{2 \times 5 ! \times 3 !}
\)
The following solution below shows that number of clockwise circular permutations is equal to the number of anticlockwise circular permutations -
Question 19 of 30
19. Question
Consider 23 different colored beads in a necklace. In how many ways can the beads be placed in the necklace so that 3 specific beads always remain together?
CorrectIncorrectHint
By theory, let us consider 3 beads as one. Hence we have, in effect, 21 beads, ‘n’ = 21.
The number of arrangements = (n − 1)! = 20!
Also, the number of ways in which 3 beads can be arranged between themselves is 3! = 3 x 2 x 1 = 6.
Thus the total number of arrangements = (1/2) x 20! x 3!
-
Question 20 of 30
20. Question
In how many ways 10 boys and 5 girls can sit around a circular table so that no two girls sit together?
CorrectIncorrectHint
10 boys can be seated in a circle in 9! ways. There are 10 spaces in between the boys, which can be occupied by 5 girls in \({ }^{10} p_5\) ways.
Hence the total number of ways
\(
=9 !{ }^{10} p_5=9 ! 10 ! / 5 !
\) -
Question 21 of 30
21. Question
In how many ways can 15 persons be seated around a table for dinner if there are 9 chairs?
CorrectIncorrectHint
In case of circular table the clockwise and anticlockwise arrangements will be treated as different arrangements.
Hence the total number of ways is
\(
{ }^{15} \mathrm{P}_9 / 9
\) -
Question 22 of 30
22. Question
In how many different ways can the letters of the word ‘DIRECTOR’ be arranged so that the vowels are always together?
CorrectIncorrectHint
In the given word, we treat the vowels IEO as 1 letter.
Thus, we have DRCTR (IEO).
This group has 6 letters in which R occurs 2 times and others are all different.Number of ways of arranging these letters = 6 ! / 2 !
\(
\frac{(6 \times 5 \times 4 \times 3 \times 2 \times 1)}{2}=360
\)Now, 3 vowels can be arranged among themselves in 3 ! = 6 ways.
Required number of ways = (360 × 6) = 2160.
-
Question 23 of 30
23. Question
In how many different ways can the letters of the word ‘DIGEST’ be arranged so that the vowels are never together?
CorrectIncorrectHint
In the given word DIGEST, we take the vowels IE as one letter.
Then, we can write it as DGST (IE).
This word has 5 letters which can be arranged among themselves in
5! = (5 × 4 × 3 × 2 × 1) = 120 ways.
The letters of IE can be arranged in 2 ways.
∴ Number of ways of arranging the letters of given word with vowels together
= (120 × 2) = 240 ways.
Number of ways of arranging all the letters of the given word
= 6! = (6 × 5 × 4 × 3 × 2 × 1) = 720 ways.
∴ Number of ways of arrangements so that the vowels are never together
= (720 – 240) = 480. -
Question 24 of 30
24. Question
In how many different ways can the letters of the word ‘DETAIL’ be arranged so that the vowels occupy only the odd positions?
CorrectIncorrectHint
There are 6 letters in the given word, out of which there are 3 consonants and 3 vowels.
Let us mark these positions as (1) (2) (3) (4) (5) (6).
Now, 3 vowels can be placed at any of 3 places, marked 1, 3,5 .
Number of these arrangements \(={ }^3 P_3=3!=6\).
Also, 3 consonants can be placed at the remaining 3 places.
Number of these arrangements \(={ }^3 P_3=3!=6\).
Total number of ways \(=(6 \times 6)=36\). -
Question 25 of 30
25. Question
In how many different ways can the letters of the word JUDGE be arranged in such a way that the vowels always come together?
CorrectIncorrectHint
The given word contains 5 different letters.
Keeping the vowels UE together, we suppose them as 1 letter.
Then, we have to arrange the letters JDG(UE).
Now, 4 letters can be arranged in \(4!=24\) ways.
The vowels (UE) can be arranged among themselves in 2 ways.
\(\therefore\) Required no. of ways \(=(24 \times 2)=48\) -
Question 26 of 30
26. Question
There are six teachers. Out of them, two are primary teachers and two are secondary teachers. They are to stand in a row, so as the primary teachers, middle teachers and secondary teachers are always in a set. The number of ways in which they can do so is
CorrectIncorrectHint
There are 2 primary teachers.
They can stand in a row in P(2, 2) = 2! = 2 × 1 ways = 2 ways
∴ Two middle teachers.
They can stand in a row in P(2, 2) = 2! = 2 × 1 = 2 ways
There are two secondary teachers.
They can stand in a row in P(2, 2) = 2! = 2 × 1 = 2 ways
These three sets can be arranged themselves in 3! Ways = 3 × 2 × 1 = 6 ways
Hence, the required number of ways
= 2 × 2 × 2 × 6 = 48 ways -
Question 27 of 30
27. Question
Five students are running a race. In how many ways can the three of five students place \(1^{\text {s. }}, 2^{\text {ad }}\), and \(3^{\text {rd }}\) ?
CorrectIncorrectHint
5 students can win the 1st place, leaving 4 who can place second and then 3 for third place. This makes \(5 \cdot 4 \cdot 3=60\) ways that students can place \(1^{st}, 2^{\text {nd }}\), and \(3^{\text {rd }}\)
-
Question 28 of 30
28. Question
An organization is choosing colors for the three pentagons in its logo. They have narrowed their choice to 7 colors, and want to have three different colors in their logo. How many possible logos can be created by choosing three of the seven colors and using one for each pentagon?
CorrectIncorrectHint
The first pentagon can be one of seven different colors, the second can be any one of six, and there are five colors which remain for the final pentagon. \(7 \cdot 6 \cdot 5=210\) ways to color the logo.
-
Question 29 of 30
29. Question
How many different five-letter “words” (letter arrangements) can be formed by rearranging the letters in the word BEAST?
CorrectIncorrectHint
There are 5 letters to choose from for the first spot, leaving 4 for the second, 3 for the third, 2 for the fourth, and there is 1 remaining for the end of the word: \(P(5,5)=5 !=5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=120\) “words”.
-
Question 30 of 30
30. Question
How many different seven-letter “words” can be formed by rearranging the letters in the word ALGEBRA?
CorrectIncorrectHint
Notice that there are two A’s. No need to panic, just pretend for a moment that the A’s are different. We’ll call one of them \(A_1\) and the other \(A_2\). \(P(7,7)=7 !=7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=5,040\) “words”.
However, we over-counted. A LGEBRA is the same as \(A_2 L G E B R A_1\), just like \(A_1 A_2 L E G B R\) is the same as \(A_2 A_1\) LEGBR. To eliminate the extra cases, we need to divide by the ways that the A’s can be arranged, which in this case is just \(2 !=2\).
\(
\frac{P(7,7)}{2}=\frac{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{2}=2,520 \text { “words”. }
\)