Quiz Level-3
Quiz Summary
0 of 40 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 40 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- Current
- Review
- Answered
- Correct
- Incorrect
-
Question 1 of 40
1. Question
Boxes that are 12 inches tall are being stacked next to boxes that are 18 inches tall. What is the shortest height at which the two stacks will be the same height?
CorrectIncorrectHint
\(
\begin{aligned}
& 12-12,24, \underline{\mathbf{3 6}} \\
& 18-18, \underline{\mathbf{3 6}}
\end{aligned}
\)
\(
\text { LCM = } 36
\)
The two stacks will be the same height at \(\mathbf{3 6}\) inches. -
Question 2 of 40
2. Question
Beginning at 8:30 A.M., tours of the National Capitol and the White House begin at a tour agency. Tours for the National Capitol leave every 15 minutes. Tours for the White House leave every 20 minutes. How often do the tours leave at the same time?
CorrectIncorrectHint
\(
\begin{aligned}
& 15-15,30,45, \underline{60} \\
& 20-20,40, \underline{60}
\end{aligned}
\)
LCM = 60
The tours leave at the same time every 60 minutes. -
Question 3 of 40
3. Question
Two neon lights are turned on at the same time. One blinks every 4 seconds and the other blinks every 6 seconds. In 60 seconds, how many times will they blink at the same time?
CorrectIncorrectHint
\(
\begin{aligned}
& 4-4,8,12,16,20, \underline{\mathbf{2 4}} \\
& 6-6,12,18, \underline{\mathbf{2 4}} \\
& 60 \div 24=2.5
\end{aligned}
\)
\(
\text { LCM }=\mathbf{2 4}
\)
In 60 seconds, the lights will blink twice at the same time. -
Question 4 of 40
4. Question
The table below shows the number of students in the school choir.
\(
\begin{aligned}
&\text { School Choir }\\
&\begin{array}{|l|c|}
\hline \text { Students } & \text { Number } \\
\hline \text { Girls } & 48 \\
\hline \text { Boys } & 64 \\
\hline
\end{array}
\end{aligned}
\)The choir teacher plans to arrange the students in equal rows. Only girls or boys will be in each row. What is the greatest number of students that could be in each row?
CorrectIncorrectHint
\(
\begin{aligned}
& 48-1,2,3,4,6,8,12, \underline{\mathbf{1 6}}, 24,48 \\
& 64-1,2,4,8, \underline{\mathbf{1 6}}, 32,64 \quad \text { GCF }=\mathbf{1 6}
\end{aligned}
\) -
Question 5 of 40
5. Question
At a display booth at an amusement park, every visitor gets a gift bag. Some of the bags have items in them as shown in the table below.
\(
\begin{aligned}
&\text { Items in the Gift Bags }\\
&\begin{array}{|l|l|}
\hline {\text { Items }} & {\text { Bags }} \\
\hline \text { Hat } & \text { Every } 2^{\text {nd }} \text { visitor } \\
\hline \text { T-shirt } & \text { Every } 7^{\text {th }} \text { visitor } \\
\hline \text { Backpack } & \text { Every } 10^{\text {th }} \text { visitor } \\
\hline
\end{array}
\end{aligned}
\)How often will a bag contain all three items?
CorrectIncorrectHint
\(
\begin{aligned}
& 2-2,4,6,8,10 \ldots .70 \\
& 7-7,14,21,28,35,42,49,56,63, \underline{70} \\
& 10-10,20,30,40,50,60, \underline{70} \\
& \text { GCF }=70 \\
&
\end{aligned}
\) -
Question 6 of 40
6. Question
Bridget has swimming lessons every fifth day and diving lessons every third day. If she had a swimming lesson and a diving lesson on May 5, when will be the next date on which she has both swimming and diving lessons?
CorrectIncorrectHint
\(
\begin{aligned}
& 5 \times 3=15 \\
& 5+15=20
\end{aligned}
\)
\(
L C M=15
\)
Bridget will have both swimming and diving lessons on May \(\mathbf{2 0}^{\text {th }}\). -
Question 7 of 40
7. Question
The 3 colors in the Christmas lights blink at different times. The yellow light blinks every 3 seconds, the green light blinks every 4 seconds, and the red blinks every 2 seconds. If the three lights blink now when is the next time the three lights will blink at the same time?
CorrectIncorrectHint
Multiples of \(3: 3,6,9,12,15,18\)
\(4: 4,8,12,16,20\)
\(2: 2,4,6,8,10,12, 14,16\)
The three lights will blink together after 12 seconds. -
Question 8 of 40
8. Question
Ed bought 24 hamburgers, 48 chocolate bars, and 36 cans of soda to celebrate his birthday with his classmates. In 5 hours, he prepared the food so that each of his classmates would receive the same amount of food. How many classmates did he prepare food for? How many hamburgers, chocolate bars, and cans of soda will each classmate receive?
CorrectIncorrectHint
Factors of 24: \(1,2,3,4,6,8, \underline{12}, 24\)
\(36: 1,2,3,4,6,9, \underline{12}, 18,36\)
\(48: 1,2,3,4,6,8,\underline{12},16,24,48\)
He prepared the food for 12 classmates.
Hamburgers: \(24 \div 12=2\)
Chocolate bars: \(48 \div 12=4\)
Soda: \(36 \div 12=3\)
Each of his classmates will receive 2 hamburgers, 4 chocolate bars and 3 cans of soda. -
Question 9 of 40
9. Question
Junie has 3 different colors of marbles. There are 35 red marbles, 63 white marbles, and 56 green marbles. She placed them in plastic containers containing equal numbers of each color. Without any leftover, how many marbles will she put in each plastic container?
CorrectIncorrectHint
Factors of \(35: 1,5, \underline{\mathbf{7}}, 35\)
\(63: 1,3, \underline{\mathbf{7}}, 9,12,63\)
\(56: 1,2,4, \underline{\mathbf{7}}, 8,14\)
She will put 7 marbles in each plastic container. -
Question 10 of 40
10. Question
The Mathematics Club adviser wants to group the members for their activity. She can group the club members into 6, 8 or 12 members without any members left behind. At least how many club members are there in the Mathematics Club?
CorrectIncorrectHint
Multiples of 6: \(6,12,28, \underline{\mathbf{2 4}}, 30\)
\(8: 8, 16, \underline{\mathbf{2 4}}, 32\)
\(12: 12, \underline{\mathbf{2 4}}, 36, 48\)
There are at least 24 members in the Mathematics Club. -
Question 11 of 40
11. Question
At a birthday party, Alexander has 12 one-dollar bills, 18 quarters, and 24 pennies which will be given to the winners of 3 games. The prizes will be given such that each winner will receive the same amount of money. How many winners can receive a prize?
CorrectIncorrectHint
Factors of \(12: 1,2,3,4, \underline{\mathbf{6}}, 12\)
18: \(1,2,3, \underline{\mathbf{6}}, 9,19\)
\(24: 1,2,3,4, \underline{6}, 8,12,24\)
There would be 6 winners.
Dollar bill: \(12 \div 6=2\)
Quarter coin: \(18 \div 6=3\)
Penny: \(24 \div 6=4\)
Each winner will receive 2 one-dollar bills, 3 quarters and 4 pennies for a total amount of \( $2.79\) each. -
Question 12 of 40
12. Question
At the gym, Hillary swims every 6 days, runs every 4 days, and cycles every 16 days. If she did all three activities today, in how many days will she do all three activities again on the same day?
CorrectIncorrectHint
Multiples of \(4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, \underline{48}, 52\).
\(6: 6,12,18,24,30,36,42, \underline{48}, 54\).
16: \(16,32, \underline{48}\)
In 48 days, she will do all three on the same day. -
Question 13 of 40
13. Question
Oscar needs to ship 14 rock CDs, 12 classical CDs, and 8 pop CDs. He can pack only one type of CD in each box, and he must pack the same number of CDs in each box. What is the greatest number of CDs Oscar can pack in each box?
CorrectIncorrectHint
Factors of \(14: 1, \underline{\mathbf{2}}, 7,14\)
12: 1, \(\underline{\mathbf{2}},3,4,6,12\)
8: \(1, \underline{\mathbf{2}}, 4,8\)
He can pack 2 CDs in each box. -
Question 14 of 40
14. Question
I want to plant 45 sunflower plants, 81 corn plants, and 63 tomato plants in my garden. If I put the same number of plants in each row and each row has only one type of plant, what is the greatest number of plants I can put in one row?
CorrectIncorrectHint
actors of \(45: 1,3,5, \underline{\mathbf{9}}, 15,45\)
\(81: 1,3, \underline{\mathbf{9}}, 27,81\)
63: 1, 3, \(, \underline{\mathbf{9}}, 21,63\)
I can put 9 in each row. -
Question 15 of 40
15. Question
Cups are sold 6 to a package and plates are sold 8 to a package. If you want to have the same number of each item for a party, what is the least number of packages of each you need to buy?
CorrectIncorrectHint
Multiples of \(6: 6,12,18, \underline{24}, 30,36,42,48,54\).
\(8: 8,16,\underline{24}, 32,40,48,56,64,72\)
He needs to buy at least 24 of each, so 4 packages cups and 3 packages of plates.
He needs to buy 4 packages of cups and 3 packages of plates. -
Question 16 of 40
16. Question
A full moon occurs every 30 days. If the last full moon occurred on a Friday, how many days will pass before a full moon occurs again on a Friday?
CorrectIncorrectHint
To find a common multiple, we can multiply 30 days by 7 days in a Week (to end up on Friday again). \(30 \times 7=210\) It will take 210 days.
-
Question 17 of 40
17. Question
There are 28 girls and 42 boys from 6 sections registered to participate in a science quiz bee. The quiz master divided the participants into teams with the same number of boys and girls on each team. How many teams will there be?
CorrectIncorrectHint
Factors of \(28: 1,2,4, \underline{\mathbf{7}}, 14,28\)
42: \(1,2,3,6, \underline{\mathbf{7}}, 14,21,42\)
There would be 7 teams.
Girls: \(28 \div 7=4\)
Boys: \(42 \div 7=6\)
There would be 4 girls and 6 boys on each team. -
Question 18 of 40
18. Question
Carina has 24 apples, 36 bundles of bananas, and 12 lemons. She wants to put all of the fruit into plastic containers, each with the same number of pieces of fruit in it. What is the greatest number of pieces of fruit she can put in each plastic container?
CorrectIncorrectHint
Factors of \(24: 1,2,3,4,6,8, \underline{12}, 24\)
\(36: 1,2,3,4,6,9,\underline{12},18,36\)
12: \(1,2,3,4,6, \underline{12}\)
There would be \({12}\) pieces of fruit in each plastic container. -
Question 19 of 40
19. Question
Rudy and Lynn are working delivering newspapers and magazines from a publishing company for 7 months. Rudy
delivers newspapers every 3 days in a village. Lynn also delivers magazines every 7 days in the same village. If the two students deliver today, when is the next time they will deliver on the same day?CorrectIncorrectHint
Multiples of \(3: 3,6,9,12,15,18, \underline{\mathbf{2 1}}, 24,27,30\)
\(7: 7,14, \underline{\mathbf{2 1}}, 28,35,42,49\).
They will deliver on the same day again 21 days later.
-
Question 20 of 40
20. Question
Anna Marie needs to pack 15 pencils, 12 boxes of crayons, and 9 pens into bundles. She must pack one item in each bundle and each bundle must have the same number of items. What is the greatest number of the same items she must pack in a bundle?
CorrectIncorrect -
Question 21 of 40
21. Question
The 3 bells ring at the factory at intervals of 3, 6, and 10 minutes simultaneously starting at 8:00 in the morning. At what time will the three bells ring together at the same time?
CorrectIncorrectHint
Multiples of \(3: 3,6,9,12,15,18,21,24,27, \underline{30}\)
\(6: 6,12,18,24, \underline{30}, 36,42\)
\(10: 10,20, \underline{30}, 40,50\) The three bells will ring together at 8:30 am. -
Question 22 of 40
22. Question
Magellan has decided to make party baskets for the fund raiser. Balloons are sold in bags of 20, party horns are sold in
bags of 10, and there are 8 candy bars in a package. How many of each should he buy so there are an equal number of
balloons, horns, and candy bars in each basket?CorrectIncorrectHint
Multiples of \(8: 8,16,24,32, \underline{40}, 48\)
20: \(20, \underline{40}, 60\)
10: \(10, 20, 30, \underline{40}, 50\)
In order to have 40 of each item, Magellan should buy 5 packages of candy bars, 4 bags of horns and 2 bags of balloons. -
Question 23 of 40
23. Question
A radio station is having a promotion in which every 12th caller receives a free concert ticket, and every 15th caller receives a limo ride. Which caller will be the first one to win both?
CorrectIncorrectHint
Multiples of \(12: 12,24,36,48, \underline{\mathbf{6 0}}, 72\)
\(15: 15, 30, 45, \underline{\mathbf{6 0}}, 75\)
The \(60^{\text {th }}\) caller will win both. -
Question 24 of 40
24. Question
Cups are sold 5 to a package and plates are sold 10 to a package. If you want to have the same number of each item for a party, what is the least number of packages of each you need to buy?
CorrectIncorrectHint
Multiples of \(5: 5, \underline{10}, 15,20,25\)
\(10: \underline{10}, 20, 30\)
You should buy 10 of each. So, you need 2 packages of cups \((5 \times 2=10)\) and 1 of plates \((10 \times 1=10)\).
You should buy 2 packages of cups and 1 package of plates. -
Question 25 of 40
25. Question
Tony needs to ship 12 comedy DVDs, 24 animated DVDs, and 30 musical DVDs. He can pack only one type of DVD in each box, and he must pack the same number of DVDs in each box. What is the greatest number of DVDs Tony can pack in each box?
CorrectIncorrectHint
Factors of \(12: 1,2,3,4, \underline{\mathbf{6}}, 12\)
\(24: 1, 2, 3, 4, \underline{\mathbf{6}}, 8, 12, 24\)
\(30: 1,2,3,5, \underline{\mathbf{6}}, 10,15,30\)
He can pack 6 DVDs in each box. -
Question 26 of 40
26. Question
Mei has 15 oranges, 9 peaches, and 18 pears. She wants to put all of the fruit into baskets with each basket having the same number of pieces of fruit in it. Without mixing the fruit, what is the greatest number of pieces of fruit Mei can put in each basket?
CorrectIncorrectHint
Factors of \(15: 1, \underline{\mathbf{3}}, 5,15\)
9: \(1, \underline{3}, 9\)
18: \(1,2, \underline{\mathbf{3}}, 6,9,18\)
She can pack 3 pieces of fruit in each basket. -
Question 27 of 40
27. Question
Andrew is having a barbecue. He is going to the store to buy the groceries, and he realized hot dogs come in packs of 10 and buns come in packs of 8. If he wants the same number of hot dogs and buns, what is the (fewest)number of hot dogs he needs in all?
CorrectIncorrectHint
LCM of (8,10) = 2 x 4 x 5 = 40.
How many packs of hot dogs should he buy?
Take the LCM and divide by the number of dogs in a pack: 40/10 = 4 packs.How many packs of buns should he buy?
Take the LCM and divide by the number of buns in a pack: 40/8 = 5 packs. -
Question 28 of 40
28. Question
Brock wants to create groups of different types of sports balls for his birthday party. If he has 16 footballs, 24 baseballs and 40 golf balls, what is the maximum number of groups he can create?
CorrectIncorrectHint
GCF of (16,24,40) = 8
How many footballs will be in each group?
Take the number of footballs and divide by the GCF: 16/8 = 2How many baseballs will be in each group?
Take the number of baseballs and divide by the GCF: 24/8 = 3How many golf balls will be in each group?
Take the number of golf balls and divide by the GCF: 40/8 = 5 -
Question 29 of 40
29. Question
Use a Venn diagram to find the GCF and LCM for 36, 48 , and 90 .
CorrectIncorrectHint
\(
\begin{aligned}
& 36=2 \cdot 2 \cdot 3 \cdot 3 \\
& 48=2 \cdot 2 \cdot 2 \cdot 2 \cdot 3 \\
& 90=2 \cdot 3 \cdot 3 \cdot 5
\end{aligned}
\)
The GCF is 6 .
The LCM is 720 .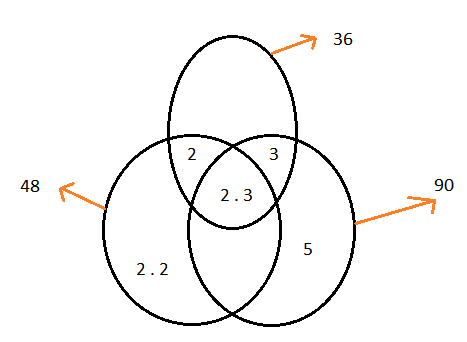
-
Question 30 of 40
30. Question
The GCF of two distinct perfect squares is 4, and their product is 3,600. What is the least positive difference between the two perfect squares?
CorrectIncorrectHint
If their GCF is 4 and their product is 3,600 , then their LCM is \(3,600 / 4=900\). We are looking for two perfect squares \(a\) and \(b\) which are mutually prime and have a product of \(900 / 4=225.225=3^2 \cdot 5^2\), so we can use \(a=9\) and \(b=25\) or \(a=1\) and \(b=225\). To minimize the positive difference we use 9 and 25, so \(9 \cdot 4=36\) and \(25 \cdot 4=100\). Their positive difference is 64.
-
Question 31 of 40
31. Question
You are buying cups, plates, and napkins for a school picnic. Cups come in packs of 24, plates come in packs of 30, and napkins come in packs of 100. What is the least number of packs of napkins will you need to buy if you want to buy the exact same number of cups, plates, and napkins?
CorrectIncorrectHint
We find the LCM of 24,30, and 100 is 600, so you must buy 6 packs of napkins to have the same number of cups, plates, and napkins.
-
Question 32 of 40
32. Question
Janice and Kiera begin jogging around a track, starting at the finish line and going the same direction. Janice completes a lap every 78 seconds, while Kiera takes 90 seconds to complete each lap. At the end of their workout, they cross the finish line together in a whole number of minutes for the first time. How many more laps did Janice run than Kiera?
CorrectIncorrectHint
The LCM of 90 and 78 seconds gives us the amount of time it takes for Janice and Kiera to finish a lap at the same time. The LCM is 1,170 seconds, which is equal to 19.5 minutes. They will need to run for another 19.5 minutes to cross the finish line in a whole number of minutes (39 minutes). In 39 minutes (2,340 seconds), Kiera completes 2,340/90= 26 laps, while Janice completes 2,340/78 = 30 laps, or 4 more laps than Kiera. We could also have found the LCM of 60 (seconds), 78, and 90 to get the number of seconds it would take Janice and Kiera to cross the finish line at the same time in a whole number of minutes.
-
Question 33 of 40
33. Question
Ken gets his hair cut every 20 days. Larry gets his cut every 26 days. Ken and Larry get their hair cut on the same Tuesday. What day of the week is it the next time they get their hair cut on the same day?
CorrectIncorrectHint
The number of days it takes for Ken and Larry to get their hair cut again on the same day is the LCM of 20 and 26, which is 260. 7 divides 259 ( 37 times), so the \(259^{\text {th }}\) day is Tuesday again, and day 260 is a Wednesday.
-
Question 34 of 40
34. Question
Positive integers \(a, b\), and \(c\), satisfy the following conditions:
\(
\begin{aligned}
& \operatorname{GCF}(a, b, c)=1 \\
& \operatorname{GCF}(a, b)=3 . \\
& \operatorname{GCF}(a, c)=4 \\
& \operatorname{GCF}(b, c)=5
\end{aligned}
\)
What is the least possible value of \(\operatorname{LCM}(a, b, c)\)?CorrectIncorrectHint
We solve with a Venn diagram:
\(\operatorname{LCM}(a, b, c)=\mathbf{6 0}\)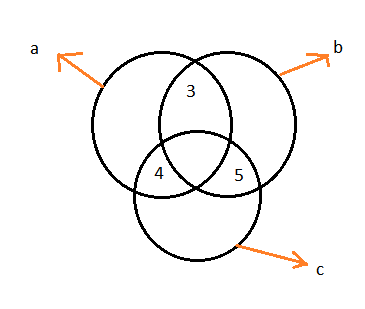
-
Question 35 of 40
35. Question
Kinsie has 80 chocolate chips, 112 pecans, and 128 M&Ms. She wants to bake a batch of giant cookies using all of the toppings she has. What is the greatest number of identical cookies she can make?
CorrectIncorrectHint
We must divide the chips, pecans, and M&Ms into an equal number of cookies, so we look for the GCF of 80,112, and 128, which is 16. (Each giant cookie gets 5 chocolate chips, 7 pecans, and \(6 \mathrm{M} \& \mathrm{Ms}\) ).
-
Question 36 of 40
36. Question
Including the endpoints, how many lattice points (points on the coordinate plane whose \(x\) and \(y\) coordinates are both integers) are on the line segment which connects \((126,162)\) to the origin?
CorrectIncorrectHint
The slope of the line is \(162 / 126\), which simplifies to \(9 / 7\). Any \(x\)-coordinate which is a multiple of 7 on this line segment will have a corresponding \(y\)-coordinate that is an integer multiple of 9: \((0,0),(7,9),(14,18) \ldots\) \((126,162)\). There are \(126 / 7+1=19\) multiples of 7 from 0 to 126 (remember to include 0 ) and 19 corresponding multiples of 9 for a total of 19 lattice points.
-
Question 37 of 40
37. Question
Tim has a bag of 36 orange-flavoured sweets and Peter has a bag of 44 grape-flavoured sweets. They have to divide up the sweets into small trays with equal number of sweets; each tray containing either orange-flavoured or grape-flavoured sweets only. If there is no remainder, find the largest possible number of sweets in each tray.
CorrectIncorrectHint
GCF, is the greatest factor that divides two numbers, thus in the question, we will be calculating the GCF.
Tim has a bag of 36 orangeflavoured sweets and Peter has a bag of 44 grape-flavoured sweets. For calculating, we need to calculate the factors of 36 and 44.
Factors of \(36=2 \times 2 \times 3 \times 3 ;\) Factors of \(44=2 \times 2 \times 11\) Thus GCF \(=2 \times 2=4\), Therefore the largest possible number of sweets in each tray is 4. -
Question 38 of 40
38. Question
Janice and Jasmine were each given a piece of ribbon of equal length. Janice cuts her ribbons into equal lengths of 2 m, while Jasmine cuts her ribbons into equal lengths of 5 m. If there was no remainder in both cases, find the shortest possible length of ribbon given to them.
CorrectIncorrectHint
The shortest possible length of ribbon can be calculated by measuring the lowest common multiple (LCM) of the lengths of ribbon cut by Janice and Jasmine. Since 2 and 5 are both prime numbers, so to find their LCM, we will multiply them to get the shortest length of ribbon =2×5=10.
-
Question 39 of 40
39. Question
On a track for remote-controlled racing cars, racing car A completes the track in 28 seconds, while racing car B completes it in 24 seconds. If they both start at the same time, after how many seconds will they be side by side again?
CorrectIncorrectHint
On a track for remote controlled racing cars racing car A completes the track in 28 seconds while racing car B completes it in 24 seconds.
To know after how many seconds will they be side by side again, we will find the LCM of 24 and 28.
\(
\begin{aligned}
& 24=2 \times 2 \times 2 \times 3 \\
& 28=2 \times 2 \times 7 \\
& \text { LCM is }=2 \times 2 \times 2 \times 3 \times 7=168
\end{aligned}
\)
Hence, after 168 seconds, both the cars will be side by side again. -
Question 40 of 40
40. Question
Two wires are 12 m and 16 m long. The wires are to be cut into pieces of equal length. Find the maximum length of each piece.
CorrectIncorrectHint
To find the maximum length, we need to find the H.C.F. of 12 and 16.
First let’s list down the factors of 12 and 16.
Factors of 12: 1, 2, 3, 4, 6, 12
Factors of 16: 1, 2, 4, 8, 16
Common factors of 12 and 16: 1, 2, and 4.
Therefore, the H.C.F. = 4
Therefore, the maximum length of each piece should be 4 m.