Definition of a Factor

Factors are numbers that can be multiplied together to get another number. This also means that the division of a number with all the factors will result in 0 remainders. In simple words, we can say that a factor of a particular number is an exact divisor of that number.

For instance, take 3 x 2 = 6. Here 3 and 2 are factors of 6.

How to find how many factors

Add 1 to each exponent in the prime factorization and multiply.

Example 1: How many factors does the number 180 have?

Solution:

\(180 = 2^2 \times 3^2 \times 5^1\)

Number of factors = (2+1)(2+1)(1+1)=18

Factors of \(180: 1,2,3,4,5,6,9,10,12,15,18,20,30,36,45,60,90\) and 180.
Prime Factorization of \(180: 2 \times 2 \times 3 \times 3 \times 5\) or \(2^2 \times 3^2 \times 5\).

What are Prime Factors?

A prime factor is a factor that is a prime quantity, meaning that it can only be formed as the product of 1 and itself. For example, 3 × 7 = 21. In this problem, 3 and 7 are prime factors, since they are both prime numbers. 

For example, 2, 2, and 5 are the prime factors of 20, i.e., 2 × 2 × 5 = 20. It should be noted that all the factors of a number may not necessarily be prime factors.

How to Find Prime Factors of a Number?

There are two important methods of finding prime factors of a given number. They are:

• Prime Factors by Division Method
• Prime Factors using Factor Tree

Prime Factors by Division Method

Let us find the prime factors of 40 using this method.

\(
\begin{array}{r|r}
2 & 40 \\
\hline 2 & 20 \\
\hline 2 & 10 \\
\hline 5 & 5 \\
\hline & 1
\end{array}
\)
Prime factorization of \(40=2 \times 2 \times 2 \times 5=2^3 \times 5\)

Prime Factors using Factor Tree

The below figure shows the prime factor of 80 using the factor tree.

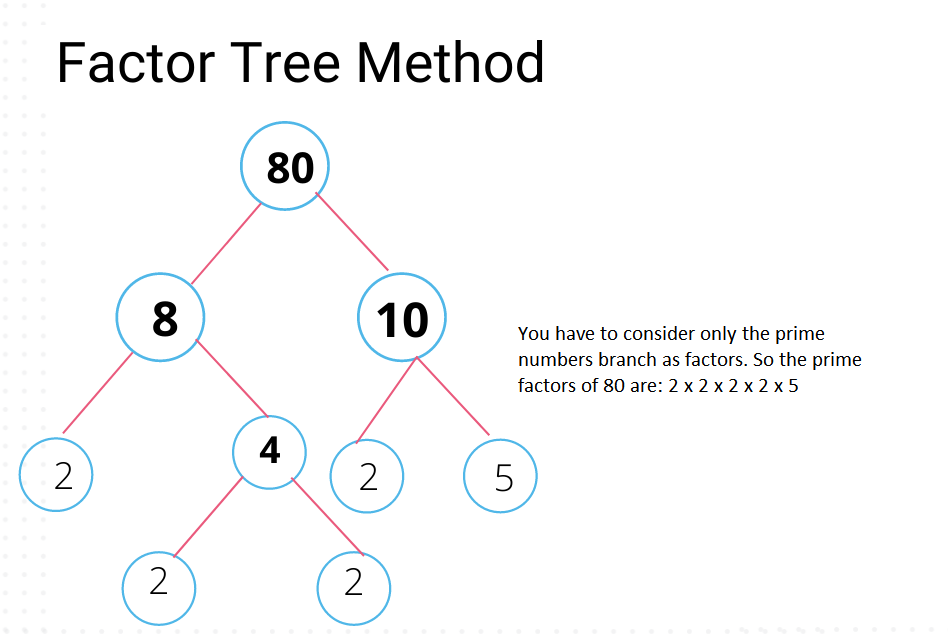
Prime Factorization

Prime factorization is a way of expressing a number as a product of its prime factors. A prime number is a number that has exactly two factors, 1 and the number itself.

For example, if we take the number 30. We know that 30 = 5 × 6, but 6 is not a prime number. The number 6 can further be factorized as 2 × 3, where 2 and 3 are prime numbers. Therefore, the prime factorization of 30 = 2 × 3 × 5, where all the factors are prime numbers.

Let us see the prime factorization chart of a few numbers in the table given below:

\(
\begin{array}{|l|l|}
\hline \text { Numbers } & \text { Prime Factorization } \\
\hline 36 & 2^2 \times 3^2 \\
\hline 24 & 2^3 \times 3 \\
\hline 60 & 2^2 \times 3 \times 5 \\
\hline 18 & 2 \times 3^2 \\
\hline 72 & 2^3 \times 3^2 \\
\hline 45 & 3^2 \times 5 \\
\hline 40 & 2^3 \times 5 \\
\hline 50 & 2 \times 5^2 \\
\hline 48 & 2^4 \times 3 \\
\hline 30 & 2 \times 3 \times 5 \\
\hline 42 & 2 \times 3 \times 7 \\
\hline
\end{array}
\)

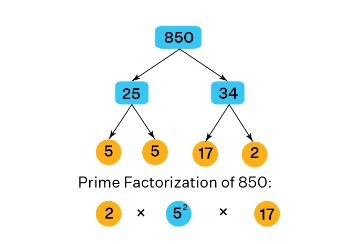
Example 2: Do the prime factorization of 850 using the factor tree.

Solution: Let us get the prime factors of 850 using the factor tree given below.

• Step 1: Place the number, 850, on top of the factor tree.
• Step 2: Then, write down the corresponding pair of factors as the branches of the tree. Here, they are 25 and 34.
• Step 3: Factorize the composite factors that are found in step 2, and write down the pair of factors as the next branches of the tree. Here, 25 can be further factorized into \(5 \times 5\), and 34 can be factorized into \(17 \times 2\)
• Step 4: Repeat step 3, until we get the prime factors of all the composite factors. So, we get the prime factors of \(850=2 \times 5^2 \times 17\)

Example 3: Find all the prime factors of 627.

Solution: 

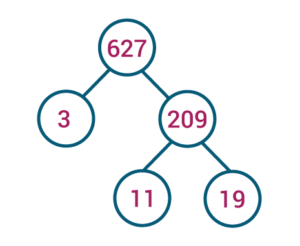
Thus, 3,11,19 are the prime factors of 627. That is 627 = 3 × 11 × 19.

How to check if the number n is Prime?

Check for divisibility by primes less than \(\sqrt{n}\) starting from least to greatest.

Example 4: \(\mathrm{n}=16\)
\(
\sqrt{16}=4
\)
We can factorize 16 in pairs as : \((1,16),(2,8),(4,4),(8,2),(16,1)\)
In every pair, it can be observed that one factor is less than the square root.

Example 5: \(\mathrm{n}=36\)
\(
\sqrt{36}=6
\)
We can factorize 36 in pairs as: \((1,36),(2,18),(3,12),(4,9),(6,6),(9,4),(12,3),(18,2),(36,1)\)
Again, it can be observed that one factor in every pair is less than the square root of \(n\).

Perfect Square

36, 81, 100, 441, 256, and 576 are all perfect squares. If a number is a perfect square, each of the prime factors will have an even exponent in its prime factorization.

Example 6: Is the number 2025 a perfect square?

Solution:

\(2025 = 3^4 \times 5^2 = (3^2 \times 5)^2 = 45^2\). Exponents of 3 and 5 are even.

Tricky Factor counting

Example 7: How many odd numbers are factors of 240?

Solution: We will begin by looking at the prime factorization of 240
\(
240=2^4 \cdot 3^1 \cdot 5^1
\)
Any number multiplied by 2 is even, so the odd factors are the ones that have no 2 ‘s in their prime factorization. We can only use the 3 ‘s and 5 ‘s as factors for a total of \(2 \cdot 2=4\) factors: \(1,3,5\), and 15.

Example 8: How many even numbers are factors of 240?

Solution: This is a case where complementary counting makes the most sense. Count the total number of factors (20) and subtract the number of odd factors (4) from above for a total of 16 even factors. This is much easier than counting all of the factors that include a two.

Example 9: How many perfect squares are factors of 360?

Solution:

Again, look at the prime factorization:
\(
360=2^3 \cdot 3^2 \cdot 5^1
\)
We need to find factors that include only even powers of 2,3 , and \(5: 2^0\) or \(2^2\) and \(3^0\) or \(3^2 .5^1\) cannot be part of the prime factorization of a perfect square. This gives us \(2 \cdot 2=4\) perfect square factors:
\(
2^0=1,2^2=4,3^2=9 \text {, and } 2^2 \cdot 3^2=36 .
\)
Notice that this is simply a matter of multiplying the number of choices for 2’s and 3’s in the prime factorization of a perfect square factor. Do not forget to include 1 when counting perfect squares.

The Product Of Factors

Now that you can count the number of factors of any natural number (positive integer) quickly, lets find a quick way to find the product of those factors.

Begin again by making a list of all factors of 96 , and 196 :
\(
\begin{array}{cc}
\frac{96:}{1 \times 96} & \underline{196:} \\
2 \times 48 & 1 \times 196 \\
3 \times 32 & 2 \times 98 \\
4 \times 24 & 4 \times 49 \\
6 \times 16 & 7 \times 28 \\
8 \times 12 & 14^2
\end{array}
\)

The product of the factors for a number \(n\) with \(x\) factors can be expressed as:
\(
n^{\left(\frac{x}{2}\right)}
\)
Try not to memorize a formula without understanding it. Continue to use logical reasoning like the statements on the previous page until you understand the formula. Once you understand it, there is no need to memorize it.

Example 10: Find the product of the factors of 40, then 225.

Solution:

40 is not a perfect square. Its prime factorization is \(2^3 \cdot 5\), so 40 has 8 factors. The product of each pair of factors is 40 , so the product of the four pairs is \(40^4\) which equals \(\left(2^3 \cdot 5\right)^4=2^{12} \cdot 5^4\).

225 is a perfect square. Its prime factorization is \(3^2 \cdot 5^2\), so it has 9 factors. Think of each of these factors as the square root of \(225(15)\) so the product of the factors of 225 is \(15^9\), which equals \(3^9 \cdot 5^9\).

Example 11: Write the prime factorization of the product of the factors of 45.

Solution:

Prime factorization of 45
Without Exponents:
\(
45=3 \times 3 \times 5
\)
With Exponents:
\(
45=3^2 \times 5
\)

which means 45 has 3 x 2 = 6 factors (3 pairs) and each pair of factors has a product of 45 (\(3^2 \times 5\)), so the product of these factors is (\(3^2 \times 5)^3=3^6 \times 5^3\).

Example 12: A number \(a\) has \(2 b\) factors. What is the product of the factors of \(a\) in terms of \(a\) and \(b\)?

Solution: If \(a\) has \(2 b\) factors, it has \(b\) pairs of factors, each of which has a product \(a\). The product of factors of \(a\) is therefore \(a^b\)

Example 13: The product of the factors of 30 is equal to \(2^x \cdot 3^x \cdot 5^x\) Find \(x\).

Solution: 

\(30 = 2 \cdot 3 \cdot 5\), so 30 has 8 factors of 4 pairs of factors with each pair having a product of 30, so we have the product \(30^4=(2 . 3 . 5)^4=2^4 . 3^4 . 5^4\). Therefore \(x=4\)

Sum of the Factors

One of my favorite number theory tricks involves finding the sum of the factors of a number. Let’s take an example.

Example 14: What is the sum of the factors of 20? 

Solution:

First, as usual, we need the prime factorization: \( 20=2^2 \cdot 5 \)
Take a look at what happens when we distribute the sum of the powers of 2 to the sum of the powers of 5 :
\(
\begin{aligned}
\left(2^0+2^1+2^2\right)\left(5^0+5^1\right) & = \\
(1+2+4)(1+5) & = \\
1(1+5)+2(1+5)+4(1+5) & = \\
1+5+2+10+4+20 & =42
\end{aligned}
\)
The distribution gives us every factor! Of course, we don’t need to distribute to find the sum of the factors. Skip the distribution:
\(
(1+2+4)(1+5)=(7)(6)=42 .
\)
This is much more important with bigger numbers.

Example 15: Find the sum of the factors of 408.

Solution:

\(408=2^3 \cdot 3 \cdot 17\)

The sum of factors of 408: \((1+2+4+8)(1+3)(1+17)=1,080\)

Note: The sum of the factors of \(2^n\) is \(2^{n+1} – 1\). For example, 64 = \(2^6\) whose factor sum is (1+2+4+8+16+32+64) =127 = \(2^7 -1\)

A Perfect Number

A perfect number is one whose factor sum is equal to twice the number. Another way of saying this is that the sum of a number’s proper divisors (factors other than itself) is equal to the number. For example, the number 6 is perfect because the sum of its factors is 12, 28 is the second smallest perfect number and 496 is the third smallest perfect number, and 8128 is the fourth smallest perfect number.

A Perfect Number \(n\), is a positive integer that is equal to the sum of its factors, excluding \(n\) itself.

If you know the prime number, you can find its perfect number using the following formula:

\(2^{p-1}\left(2^p-1\right)\), where \(p\) is a prime number.

Example 16: Find all the perfect numbers from 1 to 500.

Solution:

We know that every perfect number can be expressed as \(2^{p-1}\left(2^p-1\right)\) where \(p\) is a prime number.
Using the above formula let us find the perfect numbers from 1 to 500.
For \(n=2,2^2-1\left(2^2-1\right)=2(4-1)=2 \times 3=6\).
For \(n=3,2^{3-1}\left(2^3-1\right)=2^2(8-1)=4 \times 7=28\)
For \(n=5,2^{5-1}\left(2^5-1\right)=2^4\left(3^2-1\right)=16 \times 31=496\)
\(\therefore\) the perfect numbers between 1 to 500 are 6,28 and 496.

Example 17: Check whether 282 is a perfect number or not.

Solution:

Factors of 282 are 1, 2, 3, 6, 47, 94, 141, 282.
The proper divisors of 282 are \(1,2,3,6,47,94,141\)(282 excluded).
Now,
\(1+2+3+6+47+94+141=294 \neq 282\)
Thus, 282 is not a perfect number.