Let \(P Q\) be a curve representing the relation between two quantities \(x\) and \(y\) (figure below). The point \(P\) corresponds to \(x=a\) and \(Q\) corresponds to \(x=b\). Draw perpendiculars from \(P\) and \(Q\) on the \(X\)-axis so as to cut it at \(A\) and \(B\) respectively. We are interested in finding the area \(P A B Q\). Let us denote the value of \(y\) at \(x\) by the symbol \(y=f(x)\).

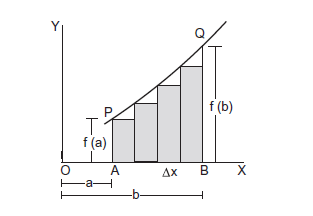
Let us divide the length \(A B\) in \(N\) equal elements each of length \(\Delta x=\frac{b-a}{N}\). From the ends of each small length, we draw lines parallel to the \(Y\)-axis. From the points where these lines cut the given curve, we draw short lines parallel to the \(X\)-axis. This constructs the rectangular bars shown shaded in the figure. The sum of the areas of these \(N\) rectangular bars is
\(
\begin{gathered}
I^{\prime}=f(a) \Delta x+f(a+\Delta x) \Delta x+f(a+2 \Delta x) \Delta x+\ldots \\
\ldots+f[a+(N-1) \Delta x] \Delta x .
\end{gathered}
\)
This may be written as
\(
I^{\prime}=\sum_{i=1}^N f\left(x_i\right) \Delta x \dots(3)
\)
where \(x_i\) takes the values \(a, a+\Delta x, a+2 \Delta x, . ., b-\Delta x\).

This area differs slightly from the area \(P A B Q\). This difference is the sum of the small triangles formed just under the curve. Now the important point is the following. As we increase the number of intervals \(N\), the vertices of the bars touch the curve \(P Q\) at more points, and the total area of the small triangles decreases. As \(N\) tends to infinity ( \(\Delta x\) tends to zero because \(\Delta x=\frac{b-a}{N}\) ) the vertices of the bars touch the curve at infinite number of points and the total area of the triangles tends to zero. In such a limit the sum (eq-3) becomes the area \(I\) of \(P A B Q\). Thus, we may write,

\(
I=\lim _{\Delta x \rightarrow 0} \sum_{i=1}^N f\left(x_i\right) \Delta x .
\)

The limit is taken as \(\Delta x\) tends to zero or as \(N\) tends to infinity. In mathematics, this quantity is denoted as

\(
I=\int_a^b f(x) d x
\)

and is read as the integral of \(f(x)\) with respect to \(x\) within the limits \(x=a\) to \(x=b\). Here \(a\) is called the lower limit and \(b\) the upper limit of integration. The integral is the sum of a large number of terms of the type \(f(x) \Delta x\) with \(x\) continuously varying from \(a\) to \(b\) and the number of terms tending to infinity.

Derivative and Integral Relationship

Now look for a function \(F(x)\) such that the derivative of \(F(x)\) is \(f(x)\) that is, \(\frac{d F(x)}{d x}=f(x)\). If you can find such a function \(F(x)\), then
\(
\int_a^b f(x) d x=F(b)-F(a) ;
\)
\(F(b)-F(a)\) is also written as \([F(x)]_a^b\).

\(F(x)\) is called the indefinite integration or the antiderivative of \(f(x)\). We also write \(\int f(x) d x=F(x)\). This may be treated as another way of writing \(\frac{d F(x)}{d x}=f(x)\)

Example 1: Evaluate \(\frac{d}{d x}\left(\frac{1}{2} x^2\right)\) and \(\int_a^b x d x\)

Solution:

\(\frac{d}{d x}\left(\frac{1}{2} x^2\right)=\frac{1}{2} \frac{d}{d x}\left(x^2\right)=\frac{1}{2} \cdot 2 x=x\).

Thus, \(\quad \int_a^b x d x=\left[\frac{1}{2} x^2\right]_a^b\)
\(
\begin{aligned}
&=\left(\frac{1}{2} b^2\right)-\left(\frac{1}{2} a^2\right) \\
&=\frac{1}{2}\left(b^2-a^2\right)
\end{aligned}
\)

Integration Formulae

\(
\begin{aligned}
&\begin{array}{llll}
\hline f(x) & F(x)=\int f(x) d x & f(x) & F(x)=\int f(x) d x
\end{array}\\
&\begin{array}{llll}
\hline \sin x & -\cos x & x^n(n \neq-1) & \frac{x^{n+1}}{n+1} \\
\cos x & \sin x & \frac{1}{x} & \ln x \\
\sec ^2 x & \tan x & \frac{1}{x^2+a^2} & \frac{1}{a} \tan ^{-1} \frac{x}{a} \\
\operatorname{cosec}^2 x & -\cot x & \frac{1}{\sqrt{a^2-x^2}} & \sin ^{-1} \frac{x}{a} \\
\sec x \tan x & \sec x & & \\
\operatorname{cosec} x \cot x & -\operatorname{cosec} x & & \\
\hline
\end{array}
\end{aligned}
\)

Some useful rules for integration are as follows:
(a) \(\int c f(x) d x=c \int f(x) d x\) where \(c\) is a constant
(b) Let \(\int f(x) d x=F(x)\), then \(\int f(c x) d x=\frac{1}{c} F(c x)\).
(c) \(\int[f(x)+g(x)] d x=\int f(x) d x+\int g(x) d x\).

Example 2: \(\text { Evaluate } \int_3^6\left(2 x^2+3 x+5\right) d x\)

Solution:

\(
\begin{aligned}
\int\left(2 x^2+\right.&3 x+5) d x \\
&=\int 2 x^2 d x+\int 3 x d x+\int 5 d x \\
&=2 \int x^2 d x+3 \int x d x+5 \int x^0 d x
\end{aligned}
\)
\(
\begin{aligned}
&=2 \frac{x^3}{3}+3 \frac{x^2}{2}+5 \frac{x^1}{1}\\
&=\frac{2}{3} x^3+\frac{3}{2} x^2+5 x \text {. }\\
&\text { Thus, } \int_3^6\left(2 x^2+3 x+5\right) d x=\left[\frac{2}{3} x^3+\frac{3}{2} x^2+5 x\right]_3^6\\
&=\frac{2}{3}(216-27)+\frac{3}{2}(36-9)+5(6-3)\\
&=126+40 \cdot 5+15=181 \cdot 5 \text {. }
\end{aligned}
\)