Cross Product or Vector Product of Two Vectors
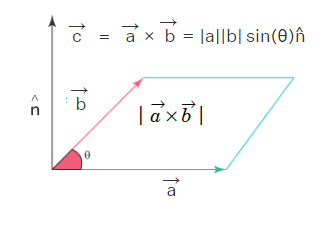
The cross product or the vector product of two vectors \(\vec{a}\) and \(\vec{b}\), denoted by \(\vec{a} \times \vec{b}\) is itself a vector. The magnitude of this vector is
\(
|\vec{a} \times \vec{b}|=|a||b| \sin \theta \text {. }
\)
- The angle between \(\vec{a}\) and \(\vec{c}\) is always \(90^{\circ}\).i.e., \(\vec{a}\) and \(\vec{c}\) are orthogonal vectors.
- The angle between \(\vec{b}\) and \(\vec{c}\) is always \(90^{\circ}\).i.e., \(\vec{b}\) and \(\vec{c}\) are orthogonal vectors.
- We can position \(\vec{a}\) and \(\vec{b}\) parallel to each other or at an angle of \(0^{\circ}\), making the resultant vector a zero vector.
- To get the greatest magnitude, the original vectors must be perpendicular(angle of \(90^{\circ}\) ) so that the cross product of the two vectors will be maximum.
Cross Product Formula
Cross product formula between any two vectors gives the area between those vectors. The cross product formula gives the magnitude of the resultant vector which is the area of the parallelogram (as shown in above figure) that is spanned by the two vectors.
The cross product of the two vectors is given by the formula:
\(\vec{a} \times \vec{b}=|\vec{a}||\vec{b}| \sin (\theta) \hat{n}\)
Where
\(|\vec{a}|\) is the magnitude of the vector a or the length of \(\vec{a}\),
\(|\vec{b}|\) is the magnitude of the vector b or the length of \(\vec{b}\).
\(\theta\) is the angle between two vectors. \(\hat{n}\) is the unit vector perpendicular to the plane containing the given two vectors, in the direction given by the right hand rule.
Cross product of two vectors Formula
Consider two vectors \(\vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}\) and \(\vec{b}=b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}\).
The cross product of two vectors is also represented using the cross product formula as:
\(
\begin{aligned}
&\vec{a} \times \vec{b}=\hat{i}\left(a_2 b_3-a_3 b_2\right) -\hat{j}\left(a_1 b_3-a_3 b_1\right) +\hat{k}\left(a_1 b_2-a_2 b_1\right)
\end{aligned}
\)
where \(\hat{i}, \hat{j}\), and \(\hat{k}\) are the unit vectors in the direction of \(x\) axis, \(y\)-axis, and \(z\)-axis respectively.
Cross Product Matrix
We can also derive the formula for the cross product of two vectors using the determinant of the matrix as given below.
\(\begin{aligned}&\vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}, \quad \vec{b}=b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}\\
&\vec{c}=\vec{a} \times \vec{b}\\
&\vec{c}=\left|\begin{array}{lll}
\hat{i} & \hat{j} & \hat{k} \\
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3
\end{array}\right|\\
&\vec{c}=\hat{i}\left|\begin{array}{ll}
a_2 & a_3 \\
b_2 & b_3
\end{array}\right|-\hat{j}\left|\begin{array}{ll}
a_1 & a_3 \\
b_1 & b_3
\end{array}\right|+\hat{k}\left|\begin{array}{ll}
a_1 & a_2 \\
b_1 & b_2
\end{array}\right|\\
&\vec{c}=\hat{i}\left|a_2 b_3-a_3 b_2\right|-\hat{j}\left|a_1 b_3-a_3 b_1\right|+\hat{k}\left|a_1 b_2-a_2 b_1\right|
\end{aligned}\)
Right-Hand Rule – Cross Product of Two Vectors
We can find out the direction of the vector which is produced on doing cross product of two vectors by the right-hand rule. We follow the following procedure to find out the direction of the result of the cross-product of two vectors:
- Align your index finger towards the direction of the first \(\operatorname{vector}(\overrightarrow{\mathrm{a}})\).
- Align the middle finger in the direction of the second vector \(\vec{b}\).
- Now the thumb points in the direction of the cross-product of two vectors.
This is shown in the figure below.
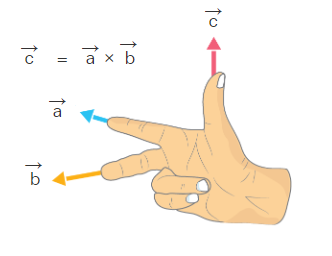
Here are few examples of right hand rule:
The right-hand rule is a mnemotechnic method using the right hand that allows us to find the direction (up or down) of \(\vec{A} \times \vec{B}\) with respect to the plane defined by \(\vec{A}\) and \(\vec{B}\) (considered horizontal).
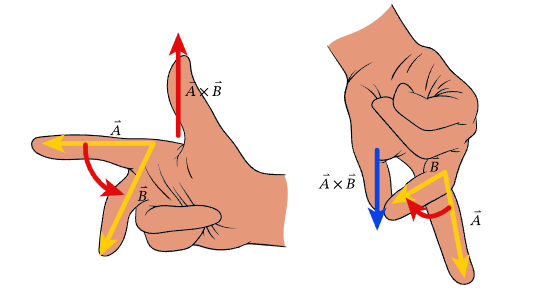
Taking our right hand, aligning our first finger with \(\vec{A}\) and the second with \(\vec{B}\), the direction of the thumbup or down-indicates the direction of \(\vec{A} \times \vec{B}\).
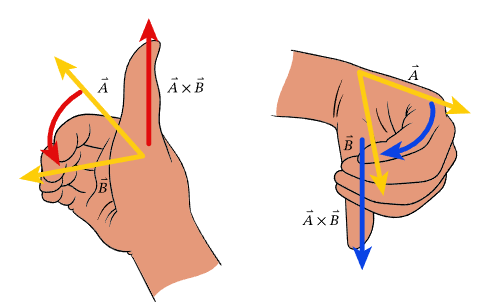
In a slightly different version, we use a half-closed right hand with the fingers showing the angle from \(\vec{A}\) to \(\vec{B}\), and the thumb then gives the direction of \(\vec{A} \times \vec{B}\).
Vector Decomposition and the Vector Product: Cartesian Coordinates
We first calculate that the magnitude of vector product of the unit vectors \(\hat{ i }\) and \(\hat{ j }\) :
\(
|\hat{ i } \times \hat{ j }|=|\hat{ i } \| \hat{ j }| \sin (\pi / 2)=1
\)
because the unit vectors have magnitude \(|\hat{ i }|=|\hat{ j }|=1\) and \(\sin (\pi / 2)=1\). By the right hand rule, the direction of
\(
\hat{ i } \times \hat{ j }
\)
is in the \(+\hat{ k }\) as shown in Figure below. Thus \(\hat{ i } \times \hat{ j }=\hat{ k }\)
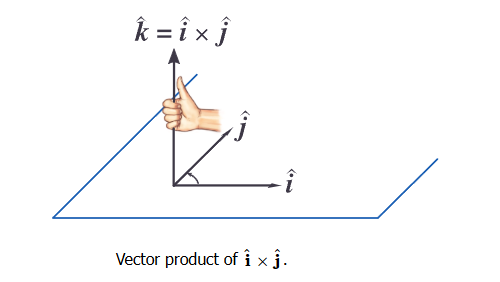
We note that the same rule applies for the unit vectors in the \(y\) and \(z\) directions,
\(
\hat{ j } \times \hat{ k }=\hat{ i }, \quad \hat{ k } \times \hat{ i }=\hat{ j }
\)
By the anti-commutative property of the vector product,
\(
\hat{ j } \times \hat{ i }=-\hat{ k }, \quad \hat{ i } \times \hat{ k }=-\hat{ j }
\)
The vector product of the unit vector \(\hat{ i }\) with itself is zero because the two unit vectors are parallel to each other, \((\sin (0)=0)\),
\(
|\hat{ i } \times \hat{ i }|=|\hat{ i }||\hat{ i }| \sin (0)=0 .
\)
The vector product of the unit vector \(\hat{ j }\) with itself and the unit vector \(\hat{ k }\) with itself are also zero for the same reason,
\(
|\hat{ j } \times \hat{ j }|=0, \quad|\hat{ k } \times \hat{ k }|=0
\)
Cross Product of Two Vectors Properties
The properties of the cross-product of two vectors are as follows:
- The length of the cross product of two vectors \(=\vec{a} \times \vec{b}=|a||b| \sin (\theta)\).
- Anti-commutative property: \(\vec{a} \times \vec{b}=-\vec{b} \times \vec{a}\) (The vector product is anti-commutative because changing the order of the vectors changes the direction of the vector product by the right-hand rule)
- Distributive property: \(\vec{a} \times(\vec{b}+\vec{c})=(\vec{a} \times \vec{b})+(\vec{a} \times \vec{c})\)
- Cross product of the zero vector: \(\vec{a} \times \overrightarrow{0}=\overrightarrow{0}\)
- Cross product of the vector with itself: \(\vec{a} \times \vec{a}=\overrightarrow{0}\)
- Multiplied by a scalar quantity: \(k(\vec{a} \times \vec{b})=k \vec{a} \times \vec{b}=\vec{a} \times k \vec{b}\)
- The cross product of the unit vectors: \(\hat{i} \times \hat{i}=\hat{j} \times \hat{j}=\hat{k} \times \hat{k}=0\)
- \(\hat{i} \times \hat{j}=\hat{k}\); \(\hat{j} \times \hat{k}=\hat{i}\); \(\hat{k} \times \hat{i}=\hat{j}\)
- \(\hat{j} \times\hat{i}=-\hat{k}\); \(\hat{k} \times \hat{j}=-\hat{i}\); \(\hat{i} \times \hat{k}=-\hat{j}\)
- Cross product of perpendicular vectors \(\vec{a} \times \vec{b}=|\vec{a}| \cdot|\vec{b}| \sin \theta = |\vec{a}| \cdot|\vec{b}| \sin 90^{\circ} = |\vec{a}| \cdot|\vec{b}|\), which is equal to the area of a rectangle. Hence, the cross product of the perpendicular vectors becomes \(\vec{a} \times \vec{b}=|\vec{a}| \cdot|\vec{b}|\)
- Cross product of parallel vectors \(\vec{a} \times \vec{b}=|\vec{a}| \cdot|\vec{b}| \sin \theta = |\vec{a}| \cdot|\vec{b}| \sin 0^{\circ} = 0\), Hence, the cross product of the parallel vectors becomes \(\vec{a} \times \vec{b}=0\)
Magnitude of Cross Product
Let us assume two vectors, \(\overrightarrow{ A }=A_x \hat{ i }+A_y \hat{ j }+A_z \hat{ k }\) and \(\overrightarrow{ B }=B_x \hat{ i }+B_y \hat{ j }+B_z \hat{ k }\). Then their cross product is given by
\(
\overrightarrow{ A } \times \overrightarrow{ B }=\left(A_y B_z-A_z B_y\right) \hat{ i }+\left(A_z B_x-A_x B_z\right) \hat{ j }+\left(A_x B_y-A_y B_x\right) \hat{ k }
\)
Then the magnitude of two vectors is given by the formula,
\(
\begin{aligned}
&|\vec{A}|=\sqrt{A_x^2+A_y^2+A_z^2} \\
&|\vec{B}|=\sqrt{B_x^2+B_y^2+B_z^2}
\end{aligned}
\)
Hence, the magnitude of the cross product of two vectors is given by the formula,
\(
|\vec{A} \times \vec{B}|=|\vec{A}||\vec{B}|\sin \theta
\)
Example 1: Find the cross product of the given two vectors:
\(
\vec{X}=5 \hat{i}+6 \hat{j}+2 \hat{k} \text { and } \vec{Y}=\hat{i}+\hat{j}+\hat{k}
\)
Solution:
Given:
\(
\begin{aligned}
&\vec{X}=5 \hat{i}+6 \hat{j}+2 \hat{k} \\
&\vec{Y}=\hat{i}+\hat{j}+\hat{k}
\end{aligned}
\)
To find the cross product of two vectors, we have to write the given vectors in determinant form. Using the determinant form, we can find the cross product of two vectors as:
\(
\vec{X} \times \vec{Y}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
5 & 6 & 2 \\
1 & 1 & 1
\end{array}\right|
\)
By expanding,
\(
\vec{X} \times \vec{Y}=(6-2) \hat{i}-(5-2) \hat{j}+(5-6) \hat{k}
\)
Therefore,
\(
\vec{X} \times \vec{Y}=4 \hat{i}-3 \hat{j}-\hat{k}
\)
Example 2: If \(\vec{a}=(2,-4,4)\) and \(\vec{b}=(4,0,3)\), find the angle between them.
Solution:
\(
\begin{aligned}
&\vec{a}=2 \hat{i}-4 \hat{j}+4 \hat{k} \\
&\vec{b}=4 \hat{i}+0 \hat{j}+3 \hat{k}
\end{aligned}
\)
The magnitude of \(\vec{a}\) is
\(|a|=\sqrt{ 2^2+4^2+4^2}=\sqrt{36 }=6\)
The magnitude of \(\vec{b}\) is
\(|b|=\sqrt{4^2+0^2+3^2 }=\sqrt{ 25}=5\)
As per the cross-product formula, we have
\(\vec{c}=\vec{a} \times \vec{b}=\left|\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k} \\ 2 & -4 & 4 \\ 4 & 0 & 3\end{array}\right|\)
\(=[(-4 \times 3)-(4 \times 0)] \hat{i}\)
\(-[(3 \times 2)-(4 \times 4)] \hat{j}\)
\(+[(2 \times 0)-(-4 \times 4)] \hat{k}\)
\(=-12 \hat{i}+10 \hat{j}+16 \hat{k}\)
\(\vec{c}=\vec{a} \times \vec{b}=(-12,10,16)\)
The length of the \(\vec{c}\) is
\(
\begin{aligned}
&|c|=\sqrt{-(12)^2+10^2+16^2} \\
&=\sqrt{(144+100+256)} \\
&=\sqrt{500} \\
&=10 \sqrt{5}
\end{aligned}
\)
\(
\begin{aligned}
&\vec{a} \times \vec{b}=|a||b| \sin \theta \\
&\sin \theta=\frac{\vec{a} \times \vec{b}}{|a||b|} \\
&\sin \theta=10 \sqrt{5} /(5 \times 6) \\
&\sin \theta=\sqrt{5} / 3 \\
&\theta=\sin ^{-1}(\sqrt{5} / 3) \\
&\theta=\sin ^{-1}(0.74) \\
&\theta=48^{\circ}
\end{aligned}
\)
Example 3: The vector \(\vec{A}\) has a magnitude of 5 unit, \(\vec{B}\) has a magnitude of 6 unit and the cross product of \(\vec{A}\) and \(\vec{B}\) has a magnitude of 15 unit. Find the angle between \(\vec{A}\) and \(\vec{B}\).
Solution: If the angle between \(\vec{A}\) and \(\vec{B}\) is \(\theta\), the cross product will have a magnitude
\(|\vec{A} \times \vec{B}|=A B \sin \theta\)
or, \(\quad 15=5 \times 6 \sin \theta\)
or, \(\quad \sin \theta=\frac{1}{2}\).
Thus, \(\quad \theta=30^{\circ}\) or, \(150^{\circ}\).
Example 4: Find a unit vector perpendicular to \(\overrightarrow{ A }=\hat{ i }+\hat{ j }-\hat{ k }\) and \(\overrightarrow{ B }=-2 \hat{ i }-\hat{ j }+3 \hat{ k }\).
Solution: The vector product \(\overrightarrow{ A } \times \overrightarrow{ B }\) is perpendicular to both \(\overrightarrow{ A }\) and \(\overrightarrow{ B }\). Therefore the unit vectors \(\hat{ n }= \pm \overrightarrow{ A } \times \overrightarrow{ B } /|\overrightarrow{ A } \times \overrightarrow{ B }|\) are perpendicular to both \(\overrightarrow{ A }\) and \(\overrightarrow{ B }\). We first calculate
\(
\begin{aligned}
\overrightarrow{ A } \times \overrightarrow{ B } & =\left(A_y B_z-A_z B_y\right) \hat{ i }+\left(A_z B_x-A_x B_z\right) \hat{ j }+\left(A_x B_y-A_y B_x\right) \hat{ k } \\
& =((1)(3)-(-1)(-1)) \hat{ i }+((-1)(2)-(1)(3)) \hat{ j }+((1)(-1)-(1)(2)) \hat{ k } \\
& =2 \hat{ i }-5 \hat{ j }-3 \hat{ k }
\end{aligned}
\)
We now calculate the magnitude
\(
|\overrightarrow{ A } \times \overrightarrow{ B }|=\left(2^2+5^2+3^2\right)^{1 / 2}=(38)^{1 / 2}
\)
Therefore, the perpendicular unit vectors are
\(
\hat{ n }= \pm \overrightarrow{ A } \times \overrightarrow{ B } /|\overrightarrow{ A } \times \overrightarrow{ B }|= \pm(2 \hat{ i }-5 \hat{ j }-3 \hat{ k }) /(38)^{1 / 2}
\)
Example 5: Calculate the Vector Product of Two Vectors That Lie in the \(x y\) plane given Their Components. Consider the two vectors \(\vec{A}=3 \hat{i}+2\hat{j}\) and \(\vec{B}=5 \hat{i}+8 \hat{j}\). Calculate \(\vec{A} \times \vec{B}\).
Solution: We can use the formula \(\vec{A} \times \vec{B}=\left(A_x B_y-A_y B_x\right) \hat{k}\) to work out the vector product of \(\vec{A}\) and \(\vec{B}\).
\(
\vec{A} \times \vec{B}=(3 \times 8-2 \times 5) \hat{k}=14 \hat{k}
\)
The result of \(\vec{A} \times \vec{B}\) is \(14 \hat{k}\). Note that both \(\vec{A}\) and \(\vec{B}\) lie in the \(x y\)-plane, while their vector product points along the \(z\)-axis, normal to the \(x y\)-plane.